Approaches for Joint Retrieval of Wind Speed and Significant Wave Height and Further Improvement for Tiangong-2 Interferometric Imaging Radar Altimeter
Abstract
:1. Introduction
2. Datasets
2.1. TG2-InIRA Observations
2.2. NDBC Buoys Data
2.3. ECMWF ERA-5 Data
2.4. ETOPO1 Data
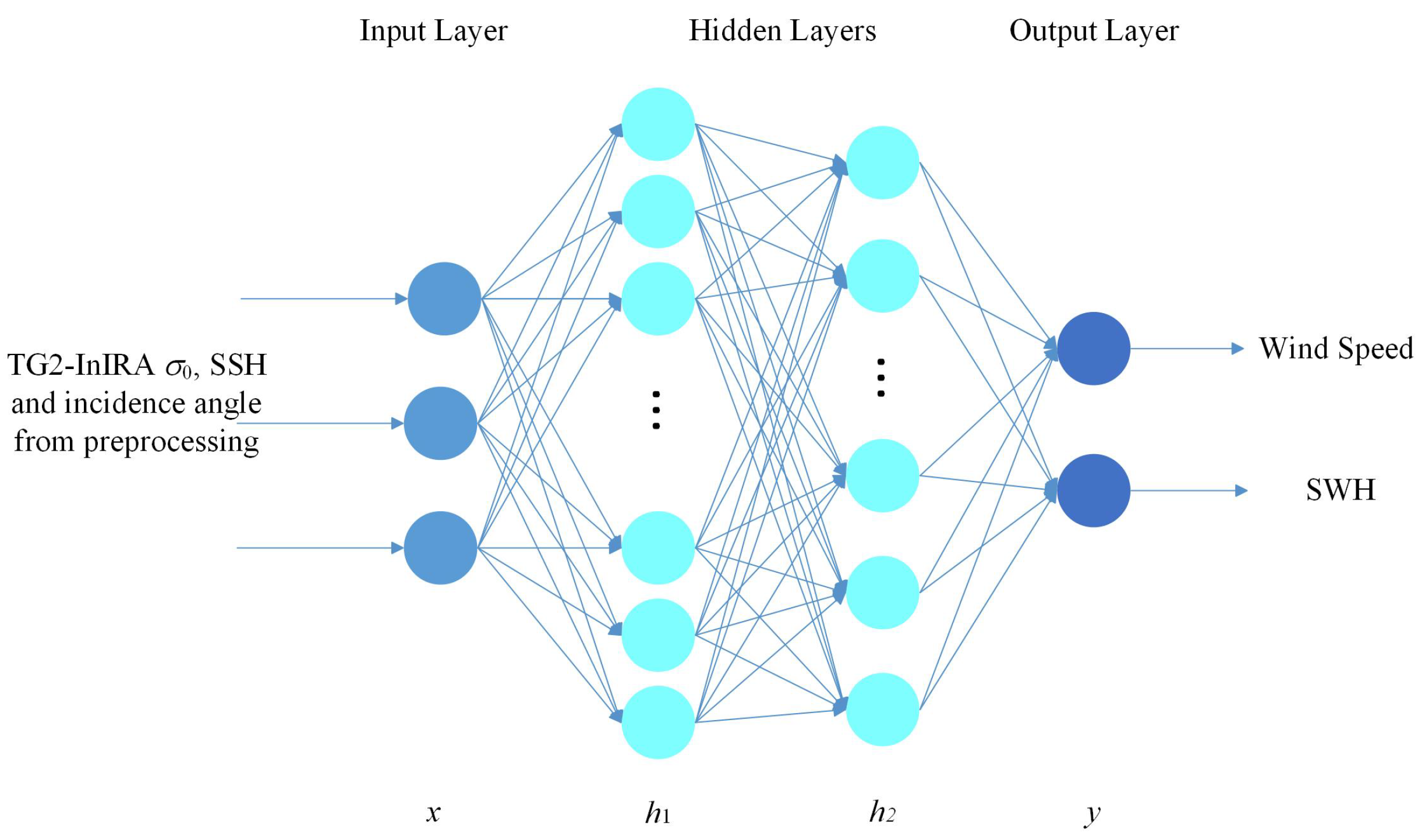
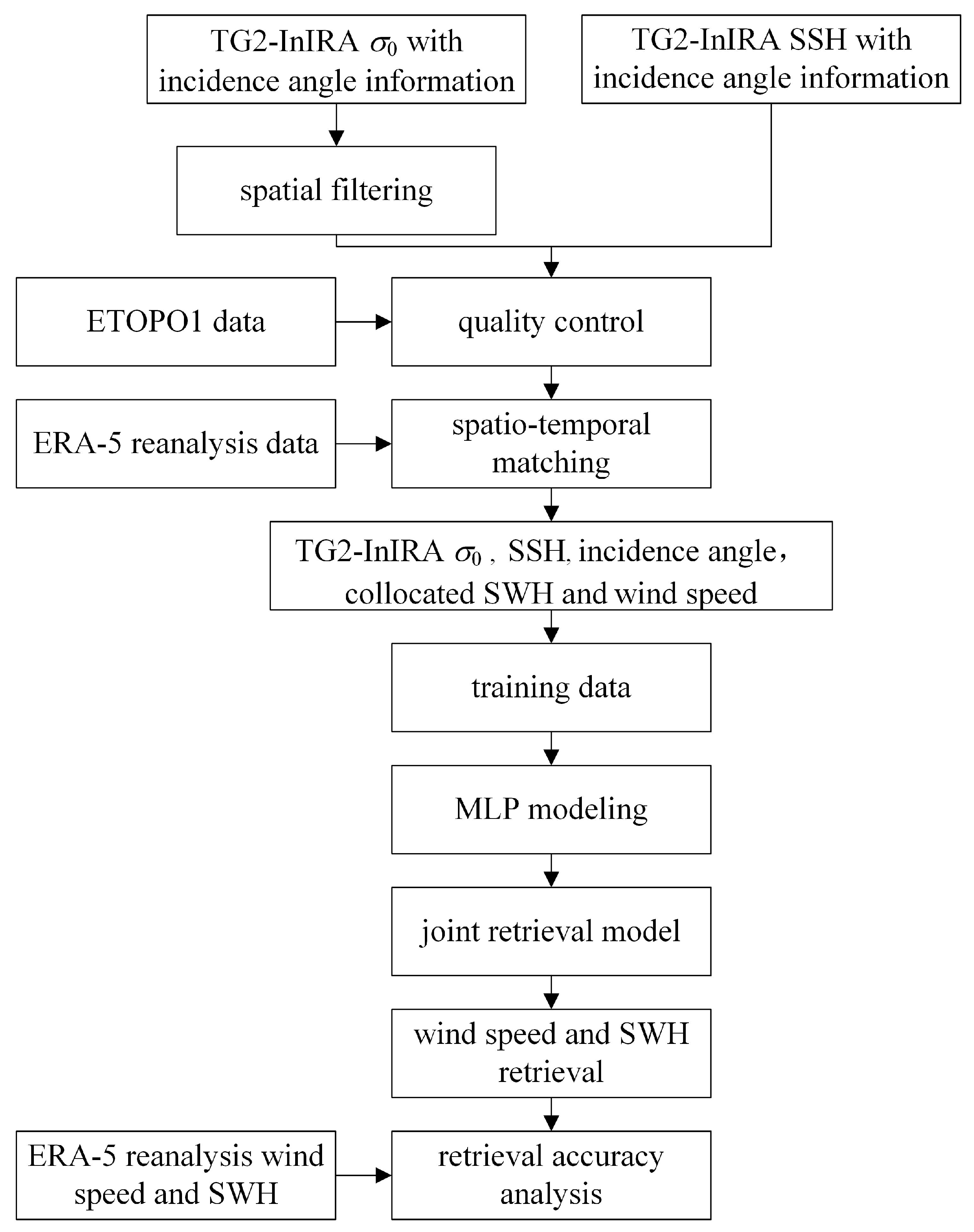
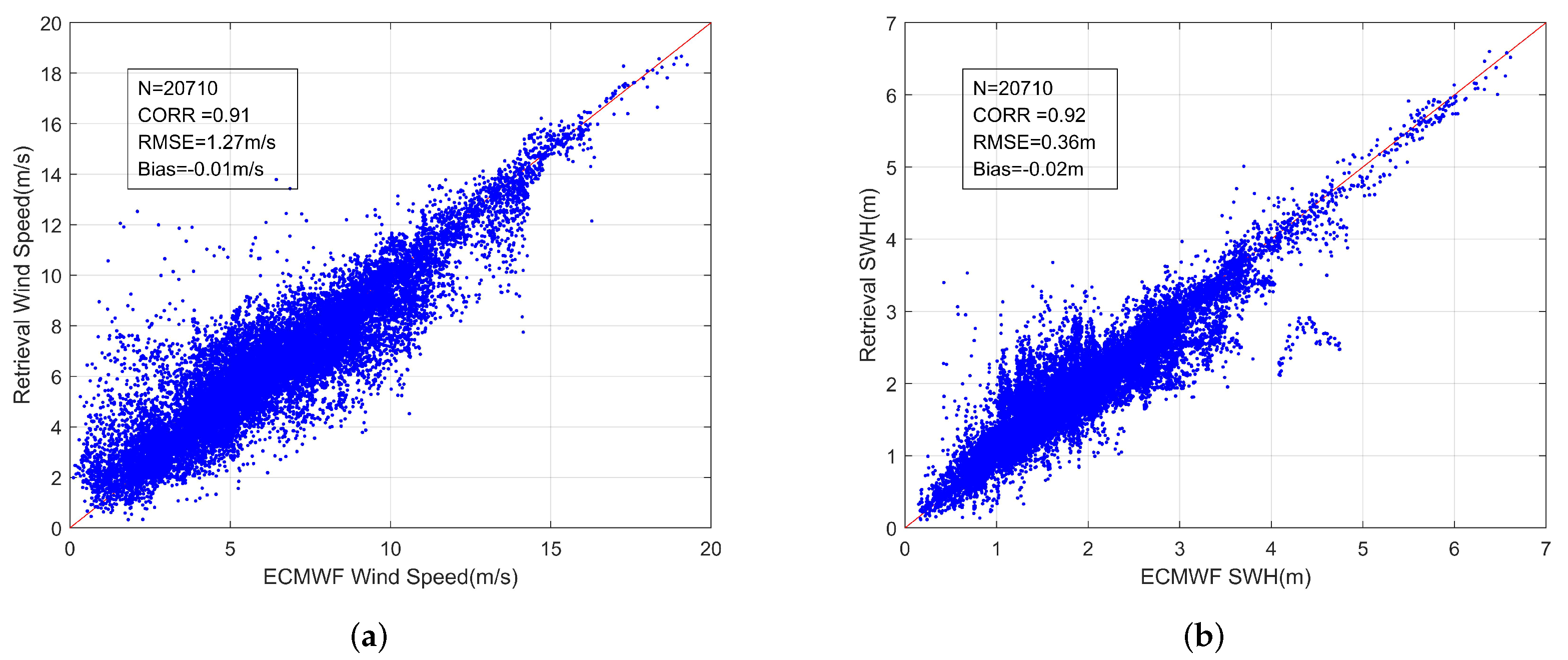
3. Joint Retrieval Model for Wind Speed and SWH
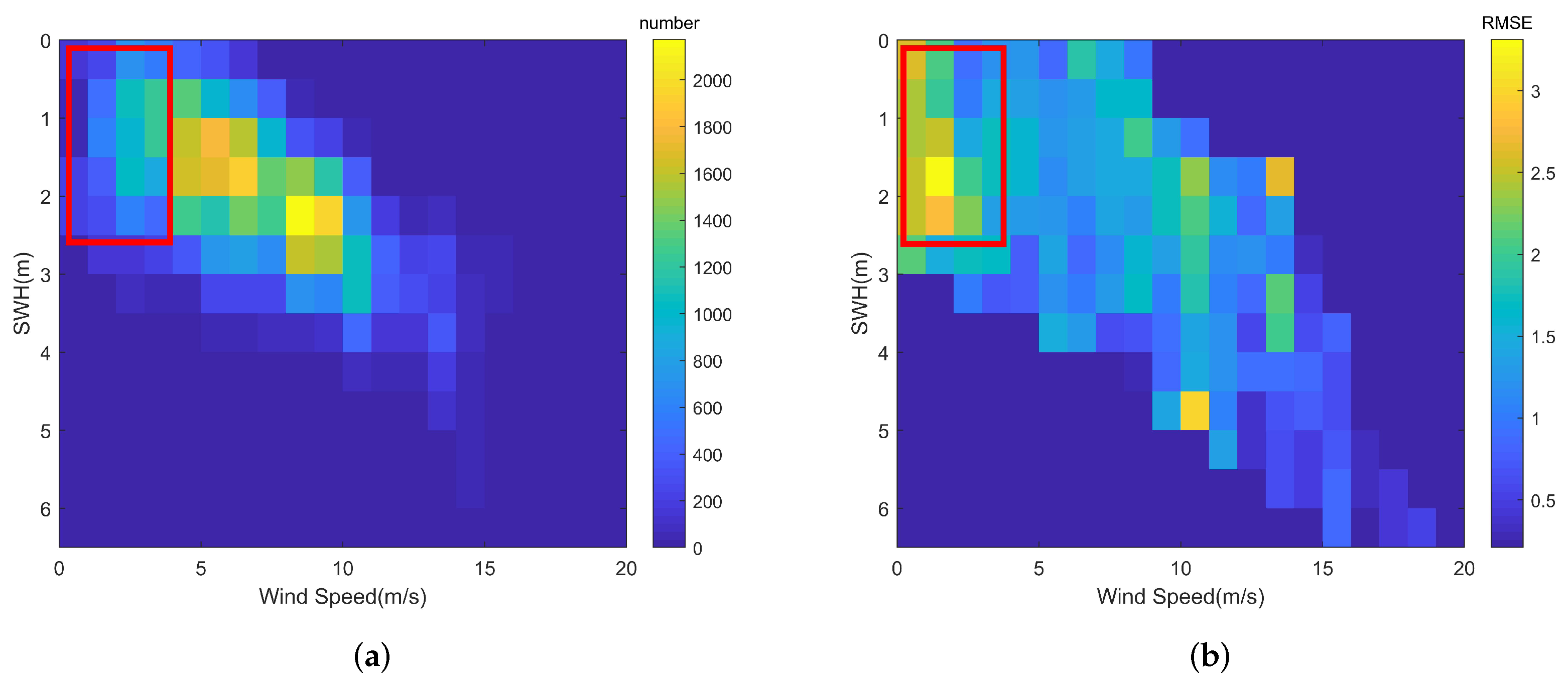
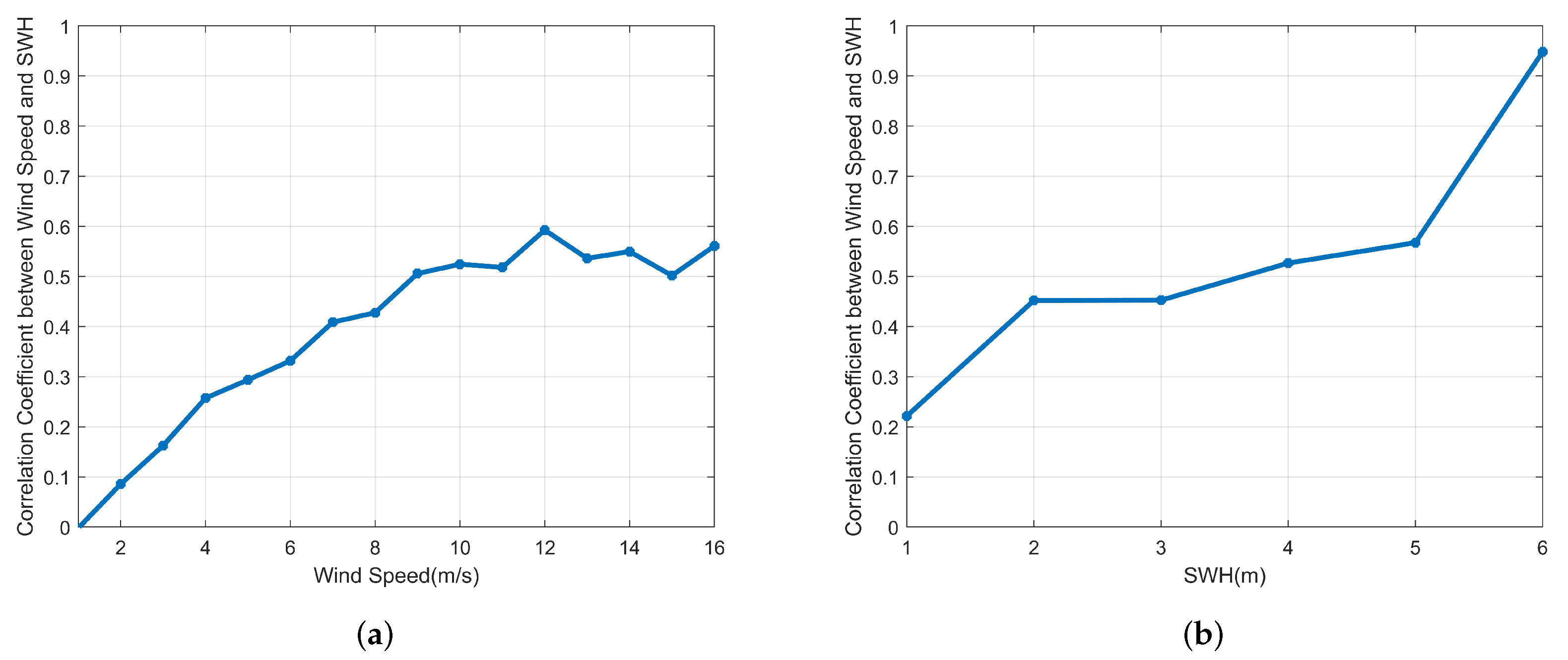
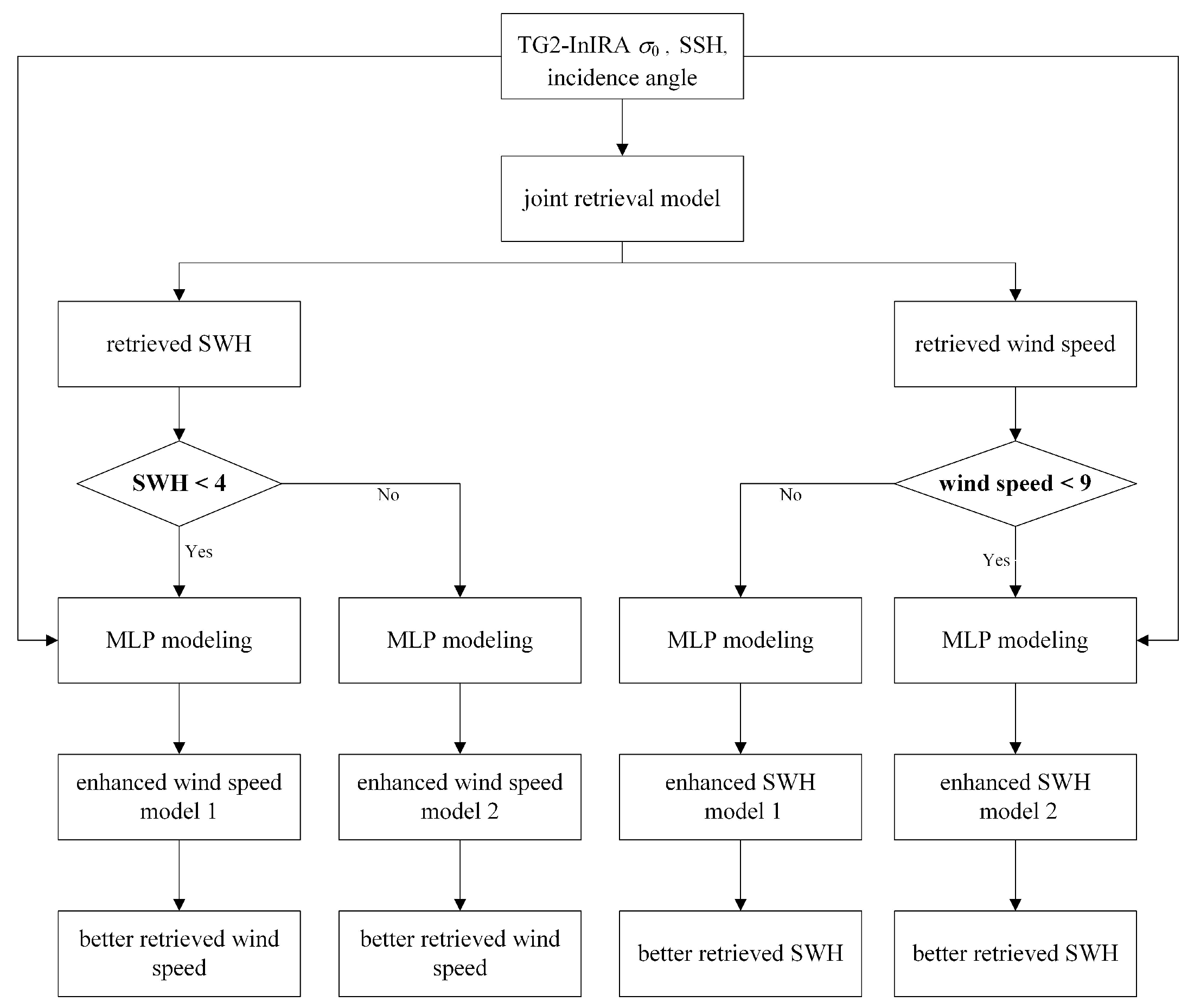
4. Enhanced Joint Retrieval of Wind Speed and SWH
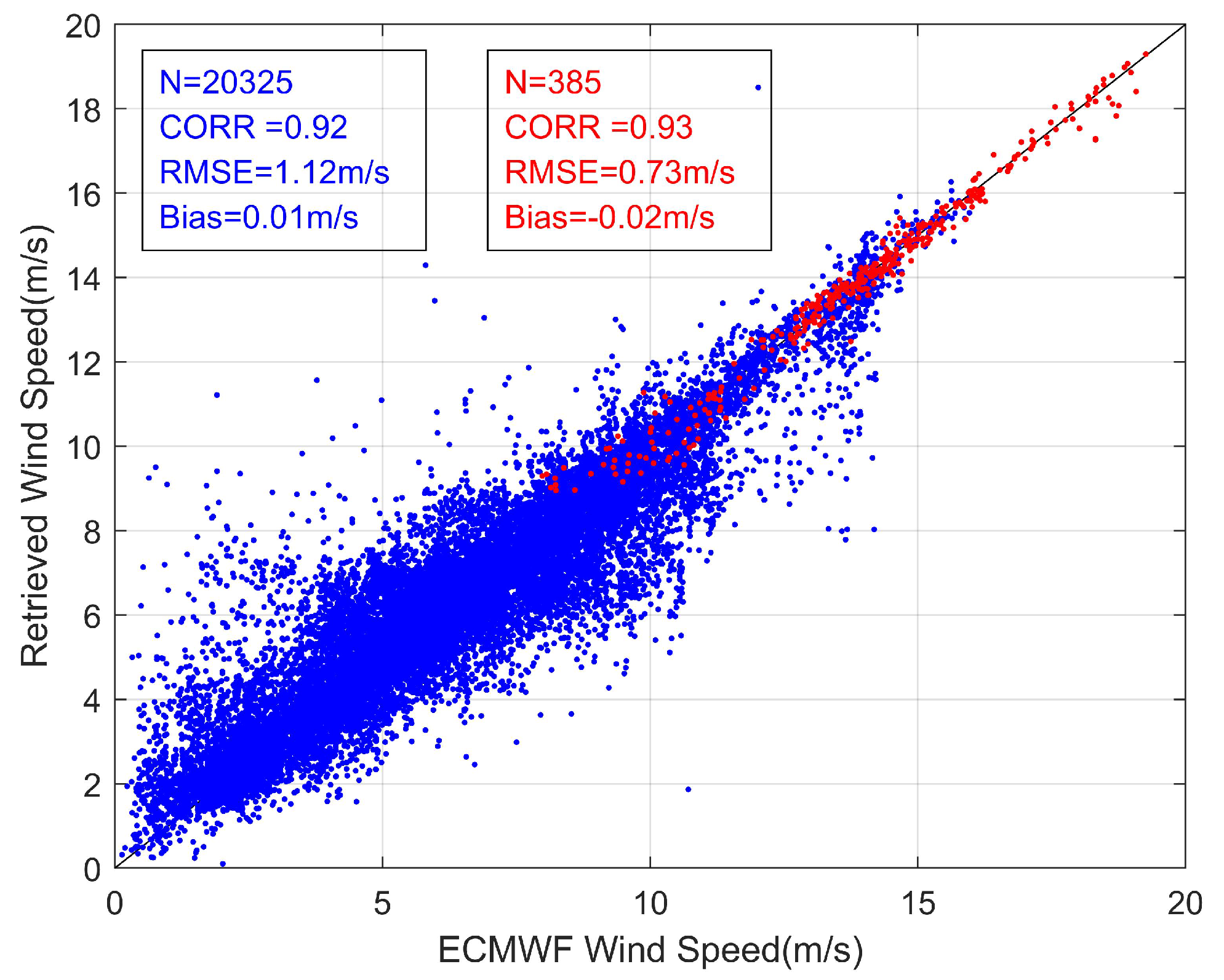
5. Validated by Buoy and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Horstmann, J.; Schiller, H.; Schulz-Stellenfleth, J.; Lehner, S. Global Wind Speed Retrieval from Sar. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2277–2286. [Google Scholar] [CrossRef] [Green Version]
- Witter, D.L.; Chelton, D.B. A Geosat Altimeter Wind Speed Algorithm and a Method for Altimeter Wind Speed Algorithm Development. J. Geophys. Res. 1991, 96, 8853–8860. [Google Scholar] [CrossRef]
- Monaldo, F.; Thompson, D.; Pichel, W.; Clemente-Colon, P. A Systematic Comparison of QuikSCAT and SAR Ocean Surface Wind Speeds. IEEE Trans. Geosci. Remote Sens. 2004, 42, 283–291. [Google Scholar] [CrossRef]
- Brown, G.; Stanley, H.; Roy, N. The Wind-Speed Measurement Capability of Spaceborne Radar Altimeters. IEEE J. Ocean. Eng. 1981, 6, 59–63. [Google Scholar] [CrossRef]
- Chelton, D.B.; McCabe, P.J. A Review of Satellite Altimeter Measurement of Sea Surface Wind Speed: With a Proposed New Algorithm. J. Geophys. Res. 1985, 90, 4707–4720. [Google Scholar] [CrossRef]
- Monaldo, F.; Dobson, E. On Using Significant Wave Height and Radar Cross Section to Improve Radar Altimeter Measurements of Wind Speed. J. Geophys. Res. 1989, 94, 12699–12701. [Google Scholar] [CrossRef]
- Lefevre, J.M.; Barckicke, J.; Ménard, Y. A Significant Wave Height Dependent Function for TOPEX/POSEIDON Wind Speed Retrieval. J. Geophys. Res. 1994, 99, 25035–25049. [Google Scholar] [CrossRef]
- Hasselmann, K.; Hasselmann, S. On the Nonlinear Mapping of an Ocean Wave Spectrum into a Synthetic Aperture Radar Image Spectrum and Its Inversion. J. Geophys. Res. 1991, 96, 10713–10729. [Google Scholar] [CrossRef]
- Engen, G.; Johnsen, H. SAR-ocean Wave Inversion Using Image Cross Spectra. IEEE Trans. Geosci. Remote Sens. 1995, 33, 1047–1056. [Google Scholar] [CrossRef]
- Li, X.; Lehner, S.; Bruns, T. Ocean Wave Integral Parameter Measurements Using Envisat ASAR Wave Mode Data. IEEE Trans. Geosci. Remote Sens. 2011, 49, 155–174. [Google Scholar] [CrossRef] [Green Version]
- Schulz-Stellenfleth, J.; Konig, T.; Lehner, S. An Empirical Approach for the Retrieval of Ocean Wave Parameters from Synthetic Aperture Radar Data. In Proceedings of the 2006 IEEE International Symposium on Geoscience and Remote Sensing, Denver, CO, USA, 31 July–4 August 2006; pp. 1875–1878. [Google Scholar] [CrossRef]
- Stopa, J.E.; Mouche, A. Significant Wave Heights from Sentinel-1 SAR: Validation and Applications: EMPIRICAL WAVE PARAMETERS FOR SENTINEL-1. J. Geophys. Res. Oceans 2017, 122, 1827–1848. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.; Li, X.; Pichel, W.G.; Li, Z. Comparison of Ocean Surface Winds From ENVISAT ASAR, MetOp ASCAT Scatterometer, Buoy Measurements, and NOGAPS Model. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4743–4750. [Google Scholar] [CrossRef]
- Zhang, B.; Mouche, A.; Lu, Y.; Perrie, W.; Zhang, G.; Wang, H. A Geophysical Model Function for Wind Speed Retrieval From C-Band HH-Polarized Synthetic Aperture Radar. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1521–1525. [Google Scholar] [CrossRef]
- Apel, J.R. An Improved Model of the Ocean Surface Wave Vector Spectrum and Its Effects on Radar Backscatter. J. Geophys. Res. 1994, 99, 16269–16291. [Google Scholar] [CrossRef]
- Romeiser, R.; Alpers, W. An Improved Composite Surface Model for the Radar Backscattering Cross Section of the Ocean Surface: 2. Model Response to Surface Roughness Variations and the Radar Imaging of Underwater Bottom Topography. J. Geophys. Res. Oceans 1997, 102, 25251–25267. [Google Scholar] [CrossRef]
- Chen, K.; Fung, A.; Weissman, D. A Backscattering Model for Ocean Surface. IEEE Trans. Geosci. Remote Sens. 1992, 30, 811–817. [Google Scholar] [CrossRef]
- Stoffelen, A.; Anderson, D. Scatterometer Data Interpretation: Estimation and Validation of the Transfer Function CMOD4. J. Geophys. Res. Oceans 1997, 102, 5767–5780. [Google Scholar] [CrossRef]
- Portabella, M. Toward an Optimal Inversion Method for Synthetic Aperture Radar Wind Retrieval. J. Geophys. Res. 2002, 107, 3086. [Google Scholar] [CrossRef]
- Xie, X.; Chen, K.; Yu, W.; Hu, W.; Zeng, Q.; Fang, Y. A Study on Geophysical Model Function Modeling with Water Surface Temperature as One of the Input Parameters. In Proceedings of the IGARSS 2008—2008 IEEE International Geoscience and Remote Sensing Symposium, Boston, MA, USA, 6–11 July 2008; Volume 1, pp. I-398–I-401. [Google Scholar] [CrossRef]
- Stiles, B.W.; Danielson, R.E.; Poulsen, W.L.; Brennan, M.J.; Hristova-Veleva, S.; Shen, T.P.; Fore, A.G. Optimized Tropical Cyclone Winds From QuikSCAT: A Neural Network Approach. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7418–7434. [Google Scholar] [CrossRef]
- Liu, Y.; Collett, I.; Morton, Y.J. Application of Neural Network to GNSS-R Wind Speed Retrieval. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9756–9766. [Google Scholar] [CrossRef]
- Thiria, S.; Mejia, C.; Badran, F.; Crepon, M. A Neural Network Approach for Modeling Nonlinear Transfer Functions: Application for Wind Retrieval from Spaceborne Scatterometer Data. J. Geophys. Res. 1993, 98, 22827–22841. [Google Scholar] [CrossRef]
- Kumar, N.K.; Savitha, R.; Al Mamun, A. Ocean Wave Height Prediction Using Ensemble of Extreme Learning Machine. Neurocomputing 2018, 277, 12–20. [Google Scholar] [CrossRef]
- Gao, D.; Liu, Y.; Meng, J.; Jia, Y.; Fan, C. Estimating Significant Wave Height from SAR Imagery Based on an SVM Regression Model. Acta Oceanol. Sin. 2018, 37, 103–110. [Google Scholar] [CrossRef]
- Xue, S.; Geng, X.; Yan, X.H.; Xie, T.; Yu, Q. Significant Wave Height Retrieval from Sentinel-1 SAR Imagery by Convolutional Neural Network. J. Oceanogr. 2020, 76, 465–477. [Google Scholar] [CrossRef]
- Chu, X.; He, Y.; Karaev, V.Y. Relationships Between Ku-Band Radar Backscatter and Integrated Wind and Wave Parameters at Low Incidence Angles. IEEE Trans. Geosci. Remote Sens. 2012, 50, 4599–4609. [Google Scholar] [CrossRef]
- Yan, Q.; Zhang, J.; Fan, C.; Meng, J. Analysis of Ku- and Ka-Band Sea Surface Backscattering Characteristics at Low-Incidence Angles Based on the GPM Dual-Frequency Precipitation Radar Measurements. Remote Sens. 2019, 11, 754. [Google Scholar] [CrossRef] [Green Version]
- Karaev, V.Y.; Kanevsky, M.B.; Balandina, G.N.; Cotton, P.D.; Challenor, P.G.; Gommenginger, C.P.; Srokosz, M.A. On the Problem of the near Ocean Surface Wind Speed Retrieval by Radar Altimeter: A Two-Parameter Algorithm. Int. J. Remote Sens. 2002, 23, 3263–3283. [Google Scholar] [CrossRef]
- Gourrion, J.; Vandemark, D.; Bailey, S.; Chapron, B.; Gommenginger, G.P.; Challenor, P.G.; Srokosz, M.A. A Two-Parameter Wind Speed Algorithm for Ku-Band Altimeters. J. Atmos. Ocean. Technol. 2002, 19, 2030–2048. [Google Scholar] [CrossRef]
- Glazman, R.E.; Greysukh, A. Satellite Altimeter Measurements of Surface Wind. J. Geophys. Res. Oceans 1993, 98, 2475–2483. [Google Scholar] [CrossRef]
- Jiang, H.; Zheng, H.; Mu, L. Improving Altimeter Wind Speed Retrievals Using Ocean Wave Parameters. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 1917–1924. [Google Scholar] [CrossRef]
- Webster, P.J.; Moore, A.M.; Loschnigg, J.P.; Leben, R.R. Coupled Ocean–Atmosphere Dynamics in the Indian Ocean during 1997–98. Nature 1999, 401, 356–360. [Google Scholar] [CrossRef]
- Stewart, R.H. Introduction to Physical Oceanography; Prentice-Hall: Upper Saddle River, NJ, USA, 2008. [Google Scholar]
- Dong, X.; Zhang, Y.; Zhai, W. Design and Algorithms of the Tiangong-2 Interferometric Imaging Radar Altimeter Processor. In Proceedings of the 2017 Progress in Electromagnetics Research Symposium-Spring (PIERS), St. Petersburg, Russia, 22–25 May 2017; pp. 3802–3803. [Google Scholar] [CrossRef]
- Zhang, Y.; Shi, X.; Wang, H.; Tan, Y.; Zhai, W.; Dong, X.; Kang, X.; Yang, Q.; Li, D.; Jiang, J. Interferometric Imaging Radar Altimeter on Board Chinese Tiangong-2 Space Laboratory. In Proceedings of the 2018 Asia-Pacific Microwave Conference (APMC), Kyoto, Japan, 6–9 November 2018; pp. 851–853. [Google Scholar] [CrossRef]
- Ren, L.; Yang, J.; Jia, Y.; Dong, X.; Wang, J.; Zheng, G. Sea Surface Wind Speed Retrieval and Validation of the Interferometric Imaging Radar Altimeter Aboard the Chinese Tiangong-2 Space Laboratory. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 4718–4724. [Google Scholar] [CrossRef]
- Zhang, Y.; Bao, Q.; Lin, M.; Lang, S. Wind Speed Inversion and In-Orbit Assessment of the Imaging Altimeter on Tiangong-2 Space Station. Acta Oceanol. Sin. 2020, 39, 114–120. [Google Scholar] [CrossRef]
- Li, G.; Zhang, Y.; Dong, X. New Ku-Band Geophysical Model Function and Wind Speed Retrieval Algorithm Developed for Tiangong-2 Interferometric Imaging Radar Altimeter. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 1981–1991. [Google Scholar] [CrossRef]
- Ren, L.; Yang, J.; Dong, X.; Jia, Y.; Zhang, Y. Preliminary Significant Wave Height Retrieval from Interferometric Imaging Radar Altimeter Aboard the Chinese Tiangong-2 Space Laboratory. Remote Sens. 2021, 13, 2413. [Google Scholar] [CrossRef]
- Khotanzad, A.; Lu, J.H. Distortion Invariant Character Recognition by a Multi-Layer Perceptron and Back-Propagation Learning. In Proceedings of the IEEE 1988 International Conference on Neural Networks, San Diego, CA, USA, 24–27 July 1988; Volume 1, pp. 625–632. [Google Scholar] [CrossRef]
- Pal, S.; Mitra, S. Multilayer Perceptron, Fuzzy Sets, and Classification. IEEE Trans. Neural Netw. 1992, 3, 683–697. [Google Scholar] [CrossRef]
- Thomas, B.R.; Kent, E.C.; Swail, V.R. Methods to Homogenize Wind Speeds from Ships and Buoys. Int. J. Climatol. 2005, 25, 979–995. [Google Scholar] [CrossRef]
- Amante, C. ETOPO1 1 Arc-Minute Global Relief Model: Procedures, Data Sources and Analysis; National Geophysical Data Center, NOAA: Washington, DC, USA, 2009. [CrossRef]
- Gaspar, P.; Florens, J.P. Estimation of the Sea State Bias in Radar Altimeter Measurements of Sea Level: Results from a New Nonparametric Method. J. Geophys. Res. Oceans 1998, 103, 15803–15814. [Google Scholar] [CrossRef]
- Andersen, O.B. Marine Gravity and Geoid from Satellite Altimetry. In Geoid Determination; Sansò, F., Sideris, M.G., Eds.; Springer: Berlin/Heidelberg, Germnay, 2013; Volume 110, pp. 401–451. [Google Scholar] [CrossRef]
- Chelton, D.B. The Sea State Bias in Altimeter Estimates of Sea Level from Collinear Analysis of TOPEX Data. J. Geophys. Res. 1994, 99, 24995. [Google Scholar] [CrossRef]
- Fowler, J.; Cohen, L.; Jarvis, P. Practical Statistics for Field Biology; Wiley: Hoboken, NJ, USA, 1998. [Google Scholar]
- Wu, K.; Li, X.M.; Huang, B. Retrieval of Ocean Wave Heights From Spaceborne SAR in the Arctic Ocean With a Neural Network. J. Geophys. Res. Oceans 2021, 126, e2020JC016946. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning Representations by Back Propagating Errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Tran, N.; Chapron, B.; Vandemark, D. Effect of Long Waves on Ku-Band Ocean Radar Backscatter at Low Incidence Angles Using TRMM and Altimeter Data. IEEE Geosci. Remote Sens. Lett. 2007, 4, 542–546. [Google Scholar] [CrossRef] [Green Version]
- Zheng, Y.; Shi, Z.; Lu, Z.; Ma, W. A Method for Detecting Rainfall From X-Band Marine Radar Images. IEEE Access 2020, 8, 19046–19057. [Google Scholar] [CrossRef]
- Chen, X.; Huang, W.; Zhao, C.; Tian, Y. Rain Detection From X-Band Marine Radar Images: A Support Vector Machine-Based Approach. IEEE Trans. Geosci. Remote Sens. 2020, 58, 2115–2123. [Google Scholar] [CrossRef]

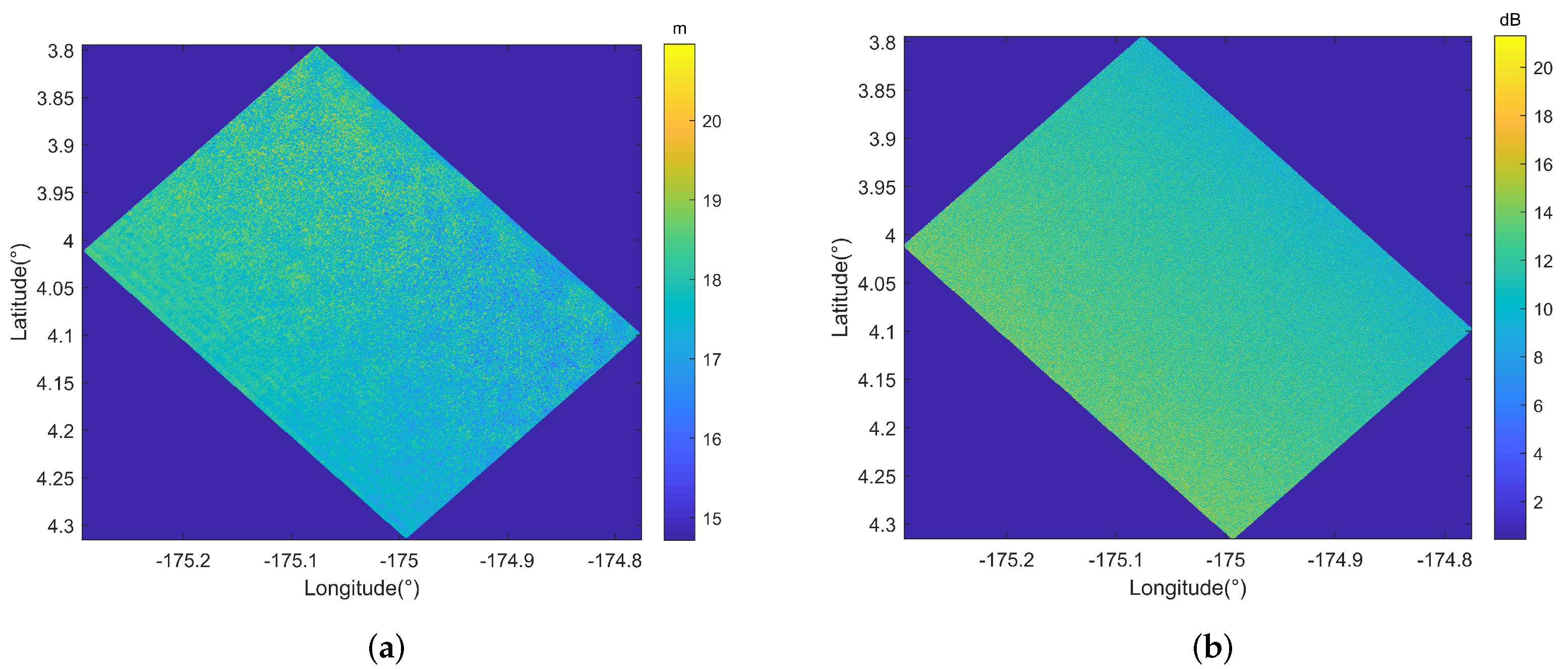

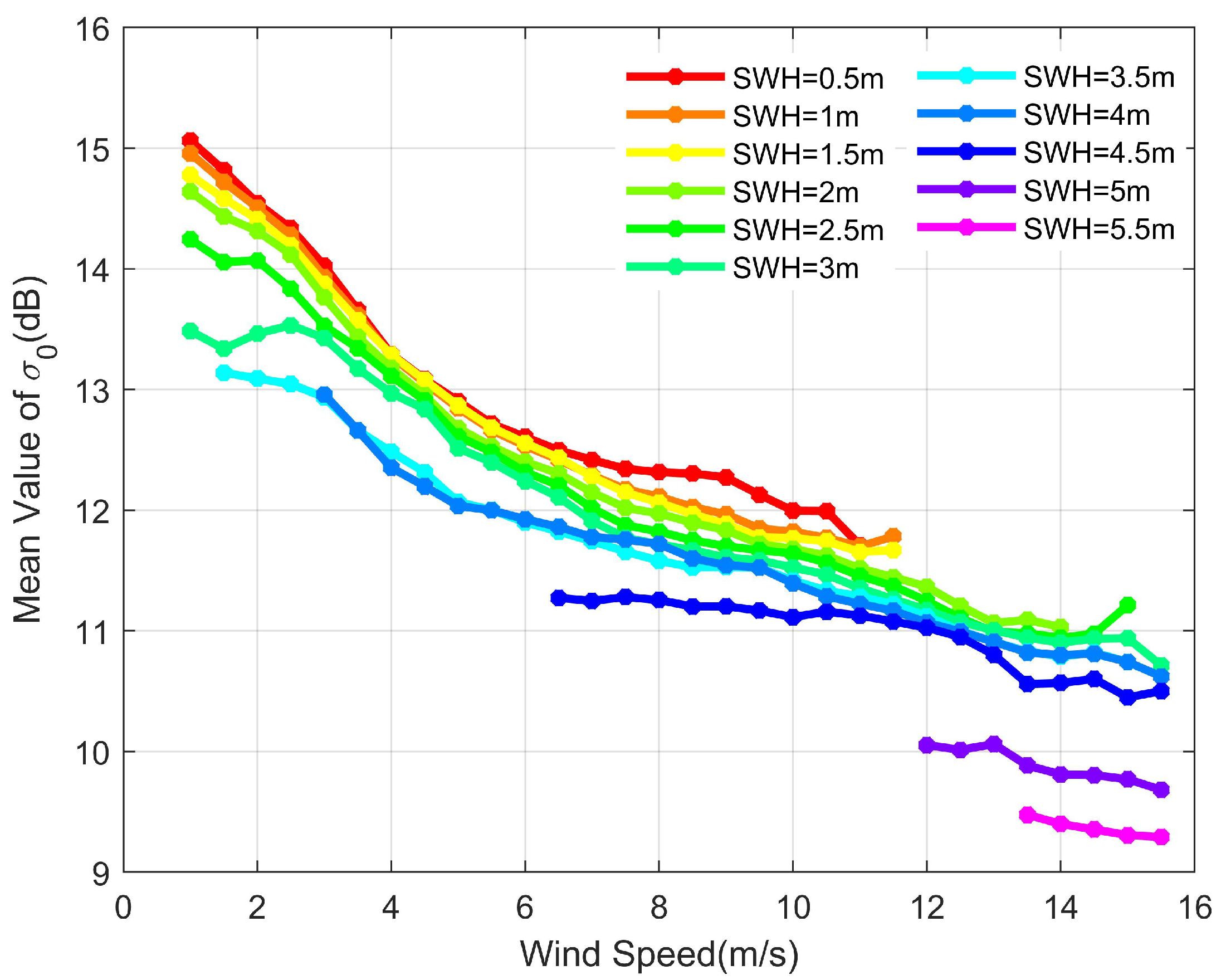
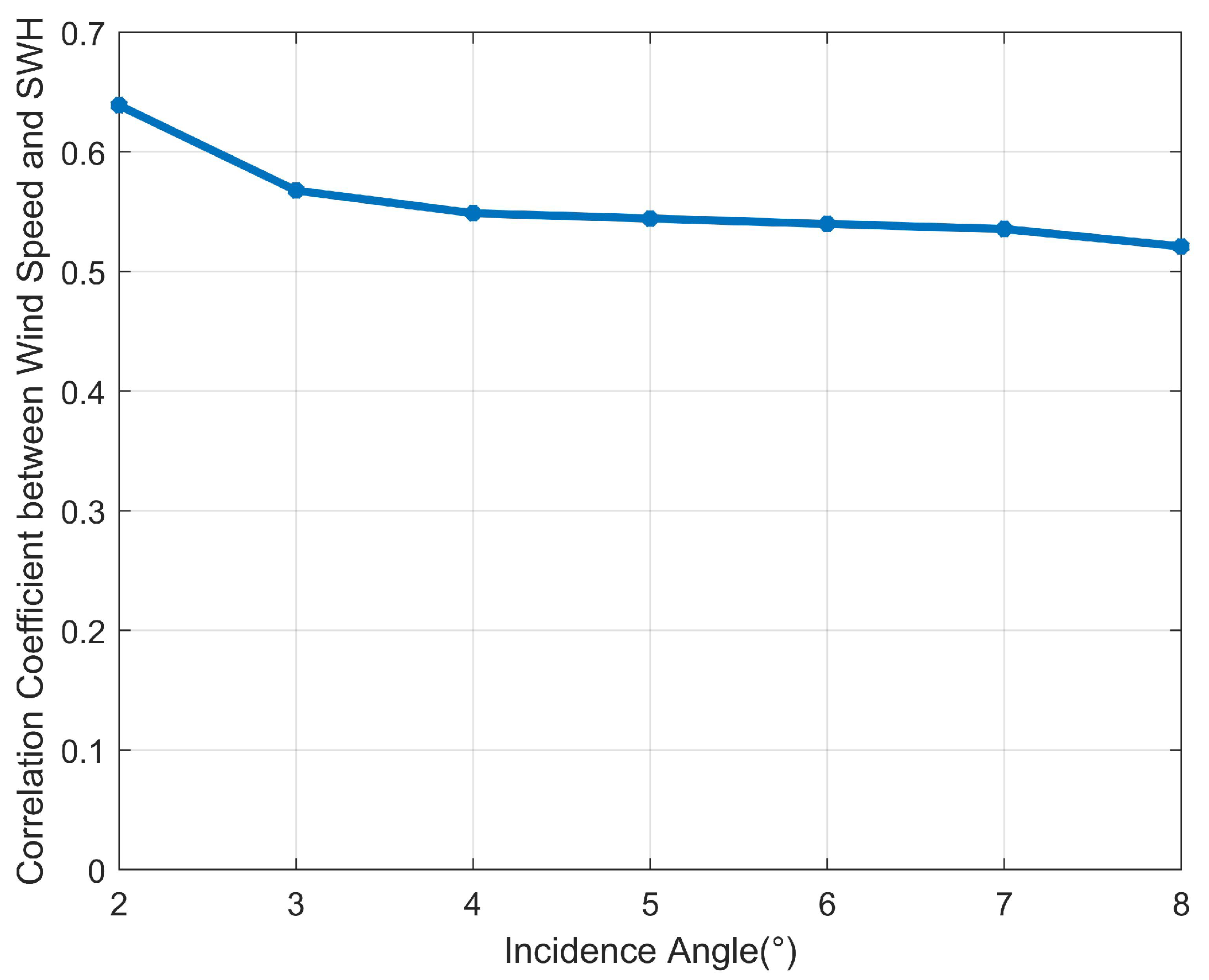
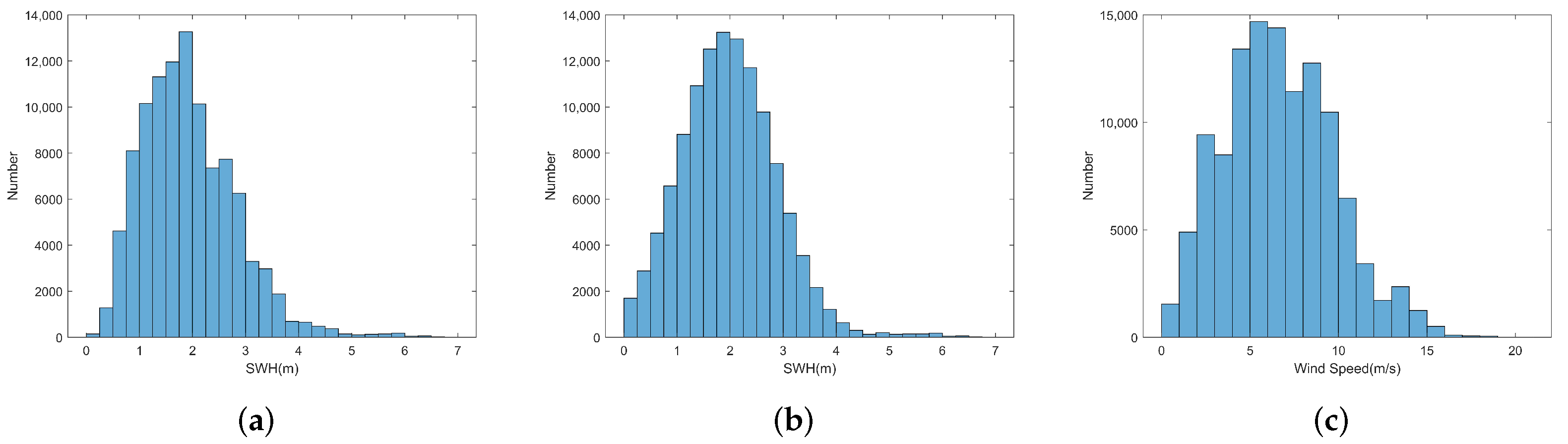
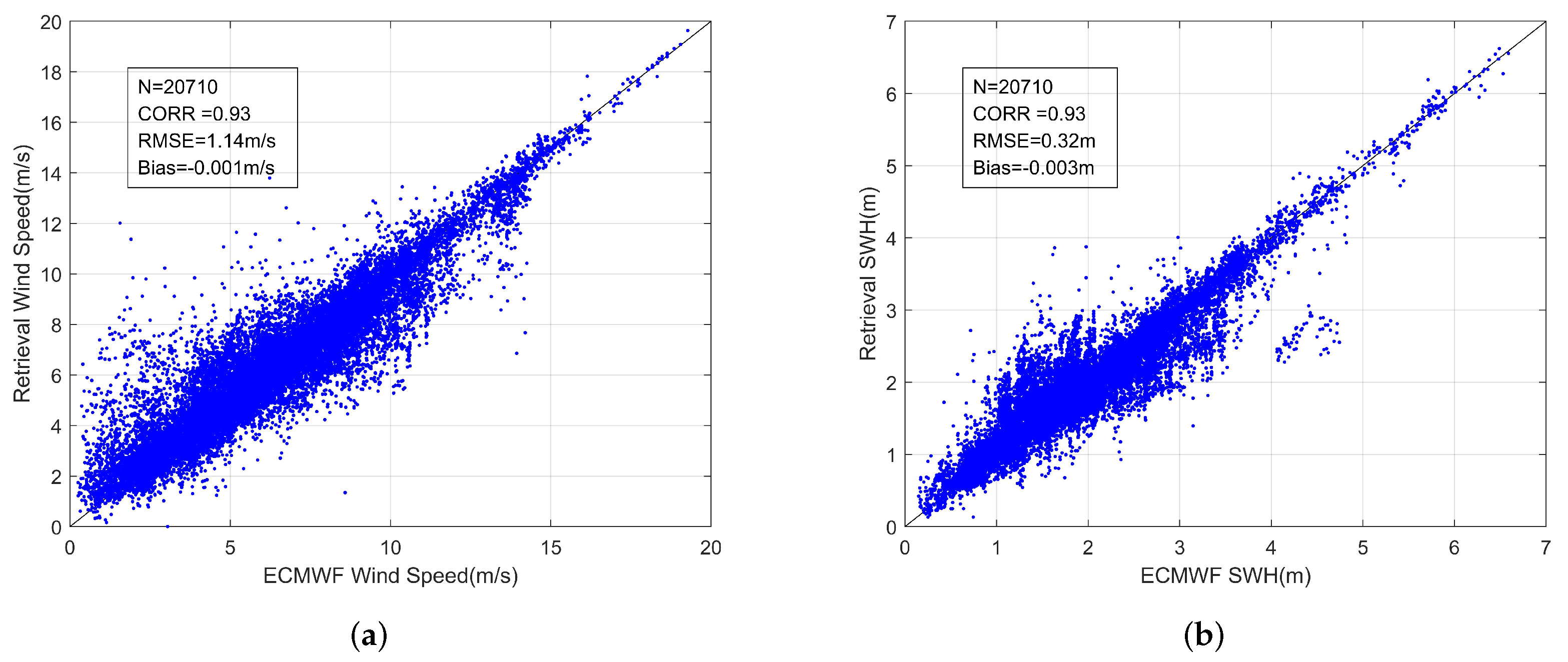

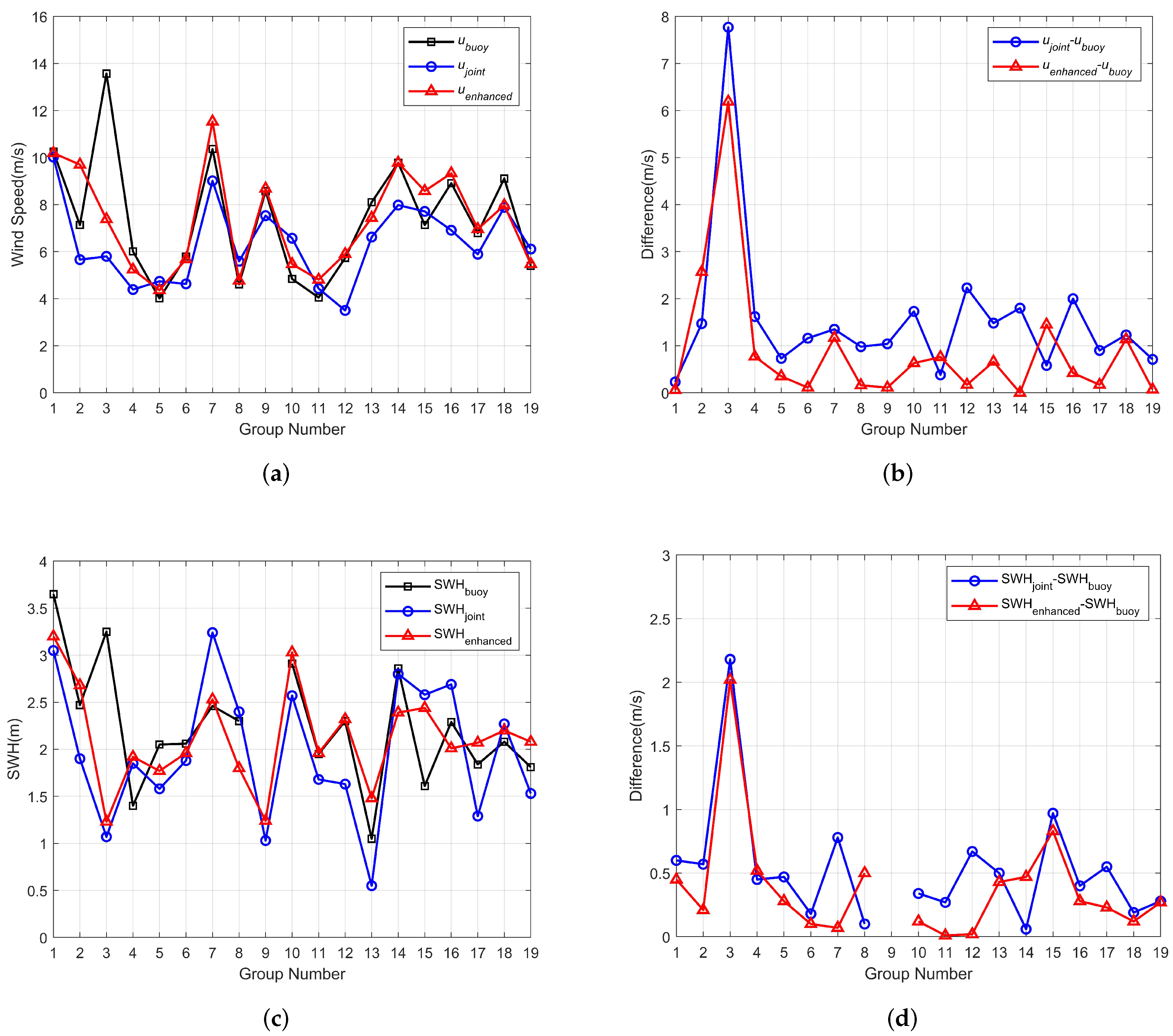
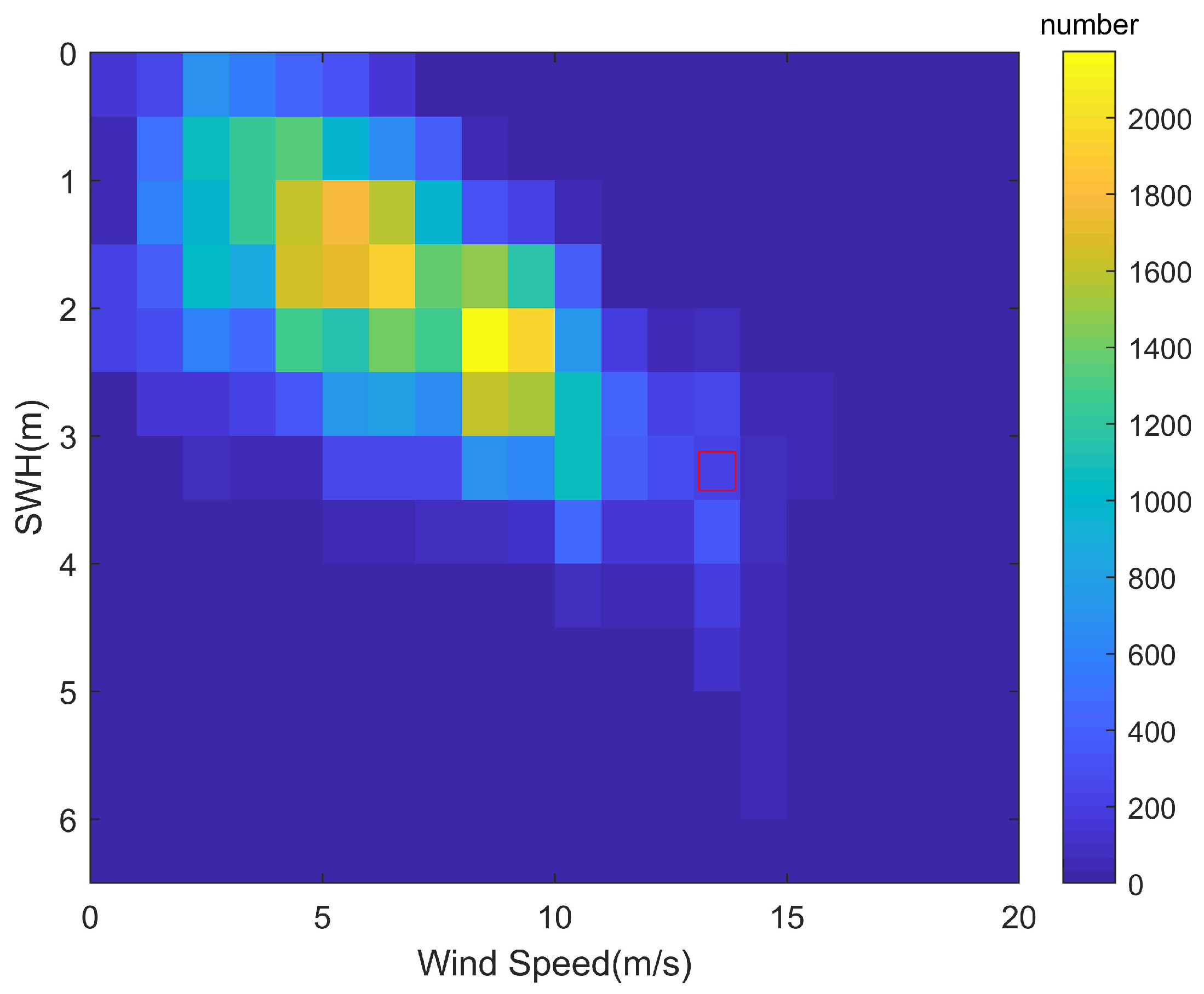
| Model | Whole Dataset | Dataset for Low Sea State (SWHs < 4.0 m) | Dataset for High Sea State (SWHs ≥ 4.0 m) |
|---|---|---|---|
| Enhanced Wind Speed Model | - | 1.12 m/s | 0.73 m/s |
| Model without Data Division | 1.14 m/s | - | - |
| Model | Whole Dataset | Dataset for Wind Speeds < 9 m/s | Dataset for Wind Speeds ≥ 9 m/s |
|---|---|---|---|
| Enhanced SWH Model | - | 0.19 m | 0.16 m |
| Model without Data Division | 0.32 m | - | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, G.; Zhang, Y.; Dong, X. Approaches for Joint Retrieval of Wind Speed and Significant Wave Height and Further Improvement for Tiangong-2 Interferometric Imaging Radar Altimeter. Remote Sens. 2022, 14, 1930. https://doi.org/10.3390/rs14081930
Li G, Zhang Y, Dong X. Approaches for Joint Retrieval of Wind Speed and Significant Wave Height and Further Improvement for Tiangong-2 Interferometric Imaging Radar Altimeter. Remote Sensing. 2022; 14(8):1930. https://doi.org/10.3390/rs14081930
Chicago/Turabian StyleLi, Guo, Yunhua Zhang, and Xiao Dong. 2022. "Approaches for Joint Retrieval of Wind Speed and Significant Wave Height and Further Improvement for Tiangong-2 Interferometric Imaging Radar Altimeter" Remote Sensing 14, no. 8: 1930. https://doi.org/10.3390/rs14081930
APA StyleLi, G., Zhang, Y., & Dong, X. (2022). Approaches for Joint Retrieval of Wind Speed and Significant Wave Height and Further Improvement for Tiangong-2 Interferometric Imaging Radar Altimeter. Remote Sensing, 14(8), 1930. https://doi.org/10.3390/rs14081930






