Detection of Solar Flares from the Analysis of Signal-to-Noise Ratio Recorded by Digisonde at Mid-Latitudes

Abstract

This work proposes a new indirect method to detect the impact of solar flares on ionospheric sounding measurements, i.e., on the signal-to-noise ratio of ionospheric reflected radio signals. The method allows us to detect and characterize the ionospheric absorption of high-frequency radio waves as a product of these energetic events. The detection is based on the estimation of the quiet conditions signal-to-noise ratio (SNR) pattern of the month and the subsequent comparison of this pattern with the SNR for the analyzed day. The method has been tested by using data from Ebro Observatory ionospheric station (DPS4D, EB040), but it can be applied to any other ionospheric station. At EB040, it can provide observational data to the international Service of Rapid Magnetic Variations (SRMV) to help confirm Sfe (Solar Flare Effects). To set up the method, we considered a data set of 262 solar flares that occurred during 2011–2014 and were observed during daylight hours at EB040 (17 X-class, 124 M-class, and 121 C-class). This led to impose a threshold of −20 dB in the SNR for at least four consecutive frequencies to confirm that a solar flare took place. The method is particularly sensitive for the detection of X-class solar flares, performs quite well with M-class events, and is even able to detect some C-class flares with high solar altitude angles. Furthermore, we studied some constraints that affect the detection of solar flares from the analysis of GOES-15 hard X-ray flux data about the considered events. For each flare, we computed its solar altitude angle at the time of the ionospheric sounding to get an estimation of its geoeffective irradiance, which had an effect on the local ionosphere. We can confirm that the method of detection is more effective with flares that present a solar elevation angle higher than 18.94°, a geoeffective hard X-ray irradiance above 3.30 × 10⁻⁶ W/m², and a geoeffective hard X-ray radiant exposure higher than 1.61 × 10⁻³ J/m², computed during the 5 min preceding the ionospheric sounding.

1. Introduction

It is well established that the ionosphere is a stratified medium of the atmosphere placed between 60 and 2000 km of altitude approximately, characterized by a high density of free electrons and free ions, mostly generated by the energetic incident radiation originated in the Sun, and having the capacity to deflect radio waves [1]. The ionosphere acts as an absorbing medium for electromagnetic waves, affecting particularly the strength of high-frequency (HF) radio signals and, consequently, the performance of radio wave communication [2]. Ionospheric absorption has been studied extensively since the 1950s [3]. It is well known that the absorption of radio waves depends on the collision frequency along the propagation path, i.e., on the number of gas molecules and free electrons, but also on the inverse square of their frequency [4], and that the radio waves are predominantly attenuated in the D-region of the ionosphere (50–90 km). However, partially reflecting Sporadic E layers, E_s, can cause multipath and mode interference, resulting in detrimental signal reception of transmission systems [5].

The ionosphere experiences regular and transitory variations that change its shape and its electron density. Regular variations of the ionosphere, such as diurnal, seasonal, and solar cycle variations, can be modeled and predicted at a given location or at a regional/global scale [6]. Such regular variations of the ionosphere also manifest in the ionospheric absorption [7,8], observing diurnal (with higher absorption for local noon), seasonal (with higher absorption for summer and a subsidiary maximum in winter), and solar cycle variations (with higher absorption for larger solar activity). In contrast, transitory variations of the ionosphere are mostly unpredictable. They are usually short in time but produce important changes in the vertical profile of electron density and therefore can significantly affect the propagation of radio waves, among other effects [9,10,11]. The sudden increase of the incident radiation of the Sun due to solar flares, which produces an over-ionization of the ionosphere, plays an important role in the ionospheric transient variation and causes a significant absorption of radio waves [12].

Solar flares are sudden bursts of charged particles and electromagnetic energy at a broad range of wavelengths, particularly in the X-ray and extreme ultraviolet (EUV) bands, coming out of active regions of the Sun [13]. These events are usually classified in a logarithmic scale of five classes, according to their maximum flux measured by satellites with X-ray sensors, such as the Geostationary Operational Environmental Satellite (GOES) series, in the wavelength range of 0.1–0.8 nm, in Watts per square meter units: A (<10⁻⁷ W/m²), B (10⁻⁷–10⁻⁶ W/m²), C (10⁻⁶–10⁻⁵ W/m²), M (10⁻⁵–10⁻⁴ W/m²), and X (>10⁻⁴ W/m²). At the same time, solar flares are organized by a finer logarithmic scale ranging from 0 to 9 within the above-mentioned five classes.

Even though flares are a relatively brief phenomena, i.e., ~30 min to ~1 h [14], they intensify the ionizing radiation when reaching the sunlit Earth hemisphere, thus mainly enhancing the electron density of all ionospheric layers in comparison with the usual values, especially in E and D regions. Consequently, they cause an increase in the absorption of radio waves, especially in the HF band. These episodes are called short-wave fadeouts, which may last tens of minutes or even hours [13,15,16,17]. In addition, polar regions are especially affected by the precipitation of energetic solar protons during these events. Solar flares also contribute to the ionization enhancement process in the D layer, producing the so-called polar cap blackout, which intensifies the HF radio wave attenuation in these regions and generates interferences in LF (low frequency), VLF (very low frequency), and ELF (extremely low frequency) systems that operate in these bands [16,18]. Another consequence of solar flares is the enhancement of the electric conductivity in the upper atmosphere, since electric currents in the ionosphere become more intense, inducing variations in the Earth’s magnetic field, which closely follows the energetic behavior over time of a given solar flare. This phenomenon is designated as the Solar Flare Effect (Sfe) or geomagnetic crochet. In general, Sfes are considered to be caused by the occurrence of solar flares of the M-class or higher [10,16,19,20]. However, it has been reported that Sfes have also occurred due to C-class flares [21].

Therefore, detecting, modeling, and monitoring the transitory variations of the ionosphere caused by solar flares is crucial in an increasingly technological society, since they have a deep impact on our everyday life, causing shortages and blackouts in radio communications and affecting navigation systems, especially in commercial aircraft operations (e.g., [13,16,22,23]).

Ionospheric absorption measurements are mainly carried out by three methods: vertical or oblique incident pulse reflection, cosmic radio noise absorption by using riometers, and the minimum reflection frequency, f_min, from vertical incident ionograms [17]. Recent studies report also ionospheric absorption measurements caused by solar flares based on NVIS propagation [24]. However, Curto et al. [10] have shown that ionospheric absorption caused by solar flares is clearly observed by analyzing the signal-to-noise ratio (SNR) of radio waves obtained from ionograms by comparing the corresponding SNR for flare and no flare conditions.

This manuscript aims at proposing a new indirect method to detect solar flares based, particularly, on the effects that they produce in the signal of the radio waves reflected from the ionosphere as measured by a digisonde. There is also an exhaustive study to set some physical constraints, such as the minimum solar altitude angle or the minimum geoeffective hard X-ray irradiance, that solar flares must accomplish to cause detectable effects in the local ionosphere. The manuscript is organized as follows: Section 2 presents the main data used in this study, describes the method of detection, and discusses the ionospheric data quality with impact in the reliability of the method. Section 3 analyzes which are the physical characteristics that solar flares must present to cause observable effects on the HF radio signals to be detected by the method. Section 4 discusses the solar flare detection rate of the method applied to the Ebro ionospheric station. Finally, Section 5 presents the summary and main conclusions of this study.

2. Data and Method of Detection

To address this work, we used data obtained by the ionograms recorded at Ebro Observatory station (40.82°N, 0.50°E), EB040 according to its URSI code. The station is equipped with a ground-based Digisonde-Portable-Sounder-4D (DPS4D), which has been operating since September 2011. The DPS4D at EB040 routinely performs vertical and oblique ionospheric soundings at different time samplings, usually at 5 or 15 min, depending on the measurement campaign, and produces the well-known ionograms records. The DPS4D ionogram records simultaneously provide measurements of seven observable parameters of reflected radio signals received from the ionosphere: frequency, range (or height for vertical incidence measurements), amplitude, phase, Doppler number (doppler shift and spread), angle of arrival, and wave polarization. We refer the reader to the DPS4D manual for further details (https://digisonde.com/pdf/Digisonde4DManual_LDI-web.pdf, last accessed on 1 February 2022). For this study, we considered amplitudes of the first echo radio wave reflected from the ionosphere, obtained by vertical incidence soundings and with ordinary wave polarization. The latter choice is related to the larger amplitudes of the ordinary polarization echoes compared to the extraordinary polarization echoes (not shown). The latter agrees with the expectations (e.g., [25]) and is especially observed during daytime hours and for low frequencies (below 5 MHz). Under such conditions, the extraordinary polarization echoes observe very weak amplitudes, and this makes it not possible to observe any effect caused by solar flares. The ionogram data are available at the GIRO portal (https://giro.uml.edu/, last accessed on 18 February 2022), and the amplitudes are extracted from ionograms with the Digisonde Ionogram Data Visualization/Editing Tool (SAO-X), which is available from the website of the Center for Atmospheric Research (https://ulcar.uml.edu/SAO-X/SAO-X.html, last accessed on 14 February 2022). A brief description of the SAO-X is shown by Reinisch et al. [26] and references therein, and a short technical description of using SAO-X to obtain echo amplitudes of ionograms measured by digisondes is provided as Supplementary Materials. SAO-X makes it possible to extract amplitudes (AMPs) for each reflected radio signal as well as the most probable amplitude (MPA), both in decibel (dB) units. The MPA refers to the amplitude threshold below the noise level in the Digisonde ionograms (DPS4D manual). Finally, SNRs are computed by subtracting the MPA from the signal amplitude value. Although not shown here, the AMP significantly changes from one frequency to another as well as for different times of the day, according to the ionospheric conditions, whereas the SNR shows a more constant behavior for different frequencies and time. This is because SNR is an indicator of the signal normalized to the noise level in the Digisonde ionograms. That is why this work focuses on the analysis of the SNR.

Solar flares cause significant effects in the SNRs of radio waves reflected in the ionosphere. Witvliet et al. [24] have shown that both the signal amplitude and the ambient electromagnetic noise level drop due to increased ionospheric absorption caused by a solar flare and reported that degradation is larger for the signal amplitude than for the ambient noise, resulting an SNR degradation. Curto et al. [10] have shown that SNRs are strongly reduced in ionograms under solar flare conditions compared to the non-flare conditions, even causing a total wave fadeout. By using this effect, we built a method to detect the solar flare effects in the SNR by comparing the current SNR measurement with an SNR pattern for non-flare conditions. Such an SNR pattern is obtained on a monthly basis to provide a typical daily variation of the SNR in order to remove the seasonal and solar cycle effects in the ionosphere. It is well known that the ionospheric absorption presents diurnal, seasonal, and solar cycle variations [7,8], which is also manifested in the SNR observations.

The quiet pattern for a given month (i.e., season and solar activity level) was obtained by averaging the SNRs around each 0.25 MHz frequency with a frequency window of ±0.5 MHz for the five quietest days of the month. The five quietest days were selected by checking the daily Solar and Geophysical Activity Summary (SGAS) from the data service of the National Oceanic and Atmospheric Administration (NOAA) (ftp://ftp.swpc.noaa.gov/pub/forecasts/SGAS/, last accessed on 17 February 2022), taking those days that presented a geomagnetic field in quiet levels (low Kp index) and no X-, M-, or C-class solar flare, when it was possible. Additionally, a visual inspection of the SNRs belonging to the five selected days was needed to minimize the impact of any punctual anomaly in the ionosphere, especially the presence of an E_s layer, a higher level of deviative absorption between Regions E and F, or a relatively high f_min [10]. It should be noticed here that stratospheric warmings are related to abnormal increases of mid-latitude ionospheric absorption in winter (e.g., [7,8]), and that the presence of an E_s layer can cause detrimental signal reception [5]. Figure 1 shows an example of the SNR quiet pattern for a given month in the winter season (October–March) and summer season (April–September). We selected November 2013 as an example for the winter season (left panel) and July 2014 for the summer season (right panel). Noteworthy differences can be seen between both seasonal periods. Winter season patterns are hat-shaped, so during the daylight hours, they reach higher frequencies (typically 8–9 MHz) than at night, where they show frequencies in the range of 3–4 MHz. In contrast, summer season patterns present a much more regular trend over time, showing frequencies typically in the range of 6–7 MHz. However, during the central hours of the day, the comparison process at low frequencies (2–6 MHz) is made more difficult because of the enhancement of the E_s phenomenon [27] and a usually high f_min. Consequently, in the summer season, the comparison during the central hours of the day can only be made in a quite small range of frequencies.

We established a threshold value of −20 dB in the SNR to consider possible event detection. This threshold was established by an analysis of the daily SNR observed for a given set scenarios with X-class solar flares. The daily SNR is obtained by averaging the current measures of SNRs around each 0.25 MHz frequency with a frequency window of ±0.5 MHz. However, the number of scenarios that lead to SNRs below −20 dB is large because of the presence of an E_s layer, a higher f_min, or a different day-to-day SNR behavior at high frequencies, especially in the summer season. Therefore, we consider an event detection when a degradation of 20 dB occurs for four consecutive frequencies (with 0.25 MHz steps) in the daily SNR compared to the monthly pattern of the SNR, since effects produced by solar flares are usually observed in more than one frequency, when they do not produce a complete absorption. The time of detection corresponds to the time of the first measurement reporting a degradation of 20 dB in the SNR with respect to the monthly pattern of the SNR.

We ran the method for data covering the 2013–2014 period, close to the maximum of Solar Cycle 24. Figure 2 shows an example of two detected events—one for each seasonal period. The effect of a flare on the SNR can be observed as a degradation or even a total extinction for different frequencies at around 10:30 LT and 16:15 LT, respectively.

In order to check if the method was working appropriately, we compared its results with 258 events listed in SGAS which occurred in the period 2013–2014 in daylight hours at EB040 (13 X-class, 124 M-class, and 121 C-class). Additionally, to extend the sample of X-class flares, we added to the event a set of four more X-class flares that occurred during 2011–2012 in daylight hours. After running the method for that period, we faced the problem of false positives; i.e., the method indicates a positive flare detection, but the solar flare did not occur. In winter conditions, we only observed false positives at around 15% of the total number of true detected flare events. These winter events were concentrated in a few specific days: 10, 11 and 17 January 2013. These false positives may be related with other phenomena that affect the ionosphere, such as sudden stratospheric warming (SSW), which takes place very sporadically during winter conditions [28,29] and can be particularly related to the SSW of January 2013 [30]. A sudden increase in ambient electromagnetic noise decreasing the SNR could also lead to false positives. On the other hand, the number of false positives for the summer season was very large—more than 10 times larger than the number of true detected flare events. This is because summer ionograms originate from shorter monthly patterns, and at high frequencies, the day-to-day variability has no signal for comparison with the monthly pattern, causing a false positive. To mitigate this issue, the method was run only for the frequency range from 2.0 to 5.0 MHz for the summer season. This way, the number of false positives could by reduced to less than 5% with respect to the total number of true detected flare events.

As we discussed above, the method is not able to ensure the detection of solar flares under adverse ionospheric conditions, such as the presence of an E_s layer and/or deviative absorption between E and F layers, especially for summer conditions. Figure 3 shows an example of the difficulties in detecting an X-class flare that occurred on a summer day near noon, with the occurrence of the E_s layer causing detrimental signal reception. By checking the SGAS, we noticed 43 events under these adverse conditions. Notwithstanding this situation, the method was able to detect the effect of 77 solar flares that took place in the absence of adverse ionospheric conditions. It has to be remembered that we considered all events that occurred during daylight hours at EB040, so an important fraction of these may have happened with a small solar elevation angle and/or have presented a very low hard X-ray flux, and therefore they were not able to produce significant absorbing effects in the local ionosphere. Thus, one of the aims of this work is to analyze a hypothetical set of physical constraints that solar flares must accomplish to significantly disturb the local ionosphere and, in consequence, produce a significant absorption that is detectable by our method.

3. Analysis of Physical Characteristics of the Solar Flares and Limitations of the Detection Method

In order to explore the role of some parameters that may have an influence on the absorption effects on the local ionosphere and in consequence be detectable by our method, we analyzed in detail the energetic information of the whole set of solar flares furnished by the GOES-15 spacecraft of NOAA, which provides 5 and 1 min averaged flux for the wavelength bands of 0.05–0.4 nm and 0.1–0.8 nm in W/m² units [31]. In this analysis, we used the 1 min averaged long band data, which correspond to hard X-ray flux, F, and can be downloaded from https://sohowww.nascom.nasa.gov/sdb/goes/xray/, last accessed on 15 February 2022.

Since the incident solar radiation on the top of the ionosphere, and consequently the ionospheric wave absorption, varies with the latitude, the time of the day, and day of the year [32], for each flare, we obtained an estimation of its geoeffective hard X-ray irradiance, $E_{eff}$ (Equation (1)), by calculating first its local solar altitude angle or solar elevation angle, ${\alpha }_s$, i.e., the angle between the Sun and the horizontal surface (Equation (2); [33]).

$$E_{eff}=F·\sin {\alpha }_s$$

(1)

$$\sin {\alpha }_s=\sin \delta ·\sin \varphi +\cos \delta ·\cos \varphi ·\cos \left(h\right)$$

(2)

where $\delta$ is the current declination of the Sun, $\varphi$ is the local latitude, and h is the hour angle in the local solar time. In addition, the solar declination can be estimated in terms of the day of the year, n, from Equation (3) [33]:

$$\delta =23.45·\sin \left[2\pi ·\left(\frac{284+n}{365}\right)\right]$$

(3)

The examination of the obtained values for the estimation of the geoeffective hard X-ray irradiances at the time of the peak flux of the events reveals, on average, an energetic reduction of about 52 ± 1% in comparison with the absolute hard X-ray flux measurements provided by the GOES-15 spacecraft. This energetic reduction even exceeds 60% in 36% of the whole set of solar flares.

The analysis of the parameters presented in Section 3.1, Section 3.2 and Section 3.3 determines a set of physical constraints that events must present to cause detectable effects on the local ionosphere. These are the minimum geoeffective hard X-ray irradiance and the minimum geoeffective hard X-ray radiant exposure, as well as the minimum solar altitude angle. Furthermore, we also discuss the results of flare detection for ionospheric soundings recorded a few minutes earlier or later with respect to the peak time of the solar flares. The latter has a special impact on the flare detection when the ionospheric time sampling of measurements is coarse, as is shown later.

3.1. Geoeffective Hard X-ray Irradiance—Solar Altitude Angle Relationship

To determine the minimum geoeffective hard X-ray irradiance and the minimum solar altitude angle for which solar flares can be detected, we plotted in Figure 4 the relationship between the geoeffective hard X-ray irradiance and the corresponding solar altitude angle, computed at the time of the ionospheric sounding (defined as the time in which the temporal mismatch with the peak of the flares is minimum), excluding those flares that occurred under local ionospheric adverse conditions (the 43 events mentioned in Section 2). Flares were classified into two main categories, detected and undetected, according to the detection method results.

Figure 4 can be divided into four distinguishable regions in which events are placed, delimited by the corresponding physical constraints. The main criterion to establish these constraints is to find the limits of the regions to not to exclude more than 10% of the detected events. In the upper-right region, most of the detected events (70 out of 77) can be seen as well as a few undetected events (13 out of 142), which present a geoeffective hard X-ray irradiance equal to or higher than $E_{ef{f}_{min}}=$ 3.30 × 10⁻⁶ W/m² and also a solar altitude angle equal to or higher than ${\alpha }_{s_{min}}$ = 18.94°. In the other three regions, most of the undetected events (129 out of 142) can be seen with a geoeffective hard X-ray irradiance below $E_{ef{f}_{min}}$ and/or a solar altitude angle lower than ${\alpha }_{s_{min}}$. Only 7 detected events are placed in these regions. These 7 detected events out of the upper right region present a very low geoeffective hard X-ray irradiance (6.84 × 10⁻⁷ W/m² at most) or a low solar altitude angle (12.71° at most).

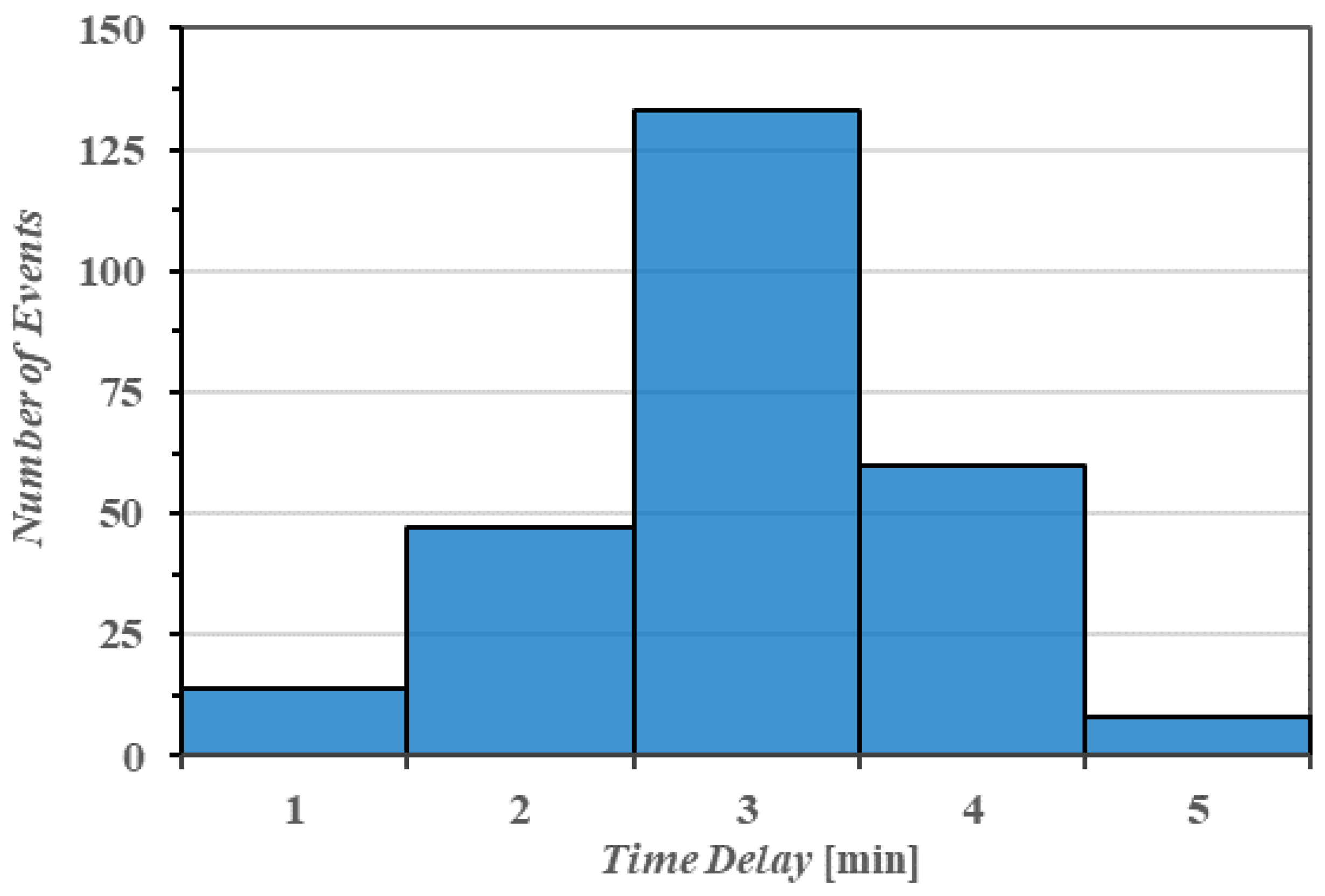
3.2. Asynchronous Measurement: Temporal Window of Detection

Another factor that can limit the detection of solar flares by ground-based ionospheric sounders is an asynchronous occurrence of the peak flare with the time of the ionospheric measurement. As previously mentioned, our ionospheric sounder was working with different time sampling modes for the period of analysis—every 5 or 15 min. Hence, if the sounding were not performed at the same time as the solar flare maximum, as the energy that the ionosphere receives from the flare can change significantly in a very short time, this could prevent the detection of relatively short events or low-energy events.

We are interested in explaining why the method was not able to detect events with a solar altitude angle over ${\alpha }_{s_{min}}$. Hence, we only analyzed this effect for those undetected events with a solar altitude angle higher than ${\alpha }_{s_{min}}$ (76 solar flares out of 142). Notice that there were no events whose solar altitude angle changed enough from their maximum to the time of the sounding to become undetectable.

Figure 5 shows the geoeffective hard X-ray irradiance for each solar flare at two different times: at the peak of the solar flare (the time corresponding to the maximum flux of the events) and at the time of the ionospheric sounding. Events were sorted according to the maximum flux measured by the GOES-15 spacecraft. The consequence of performing the sounding before or after the peak time of the flare can be observed as the vertical downward movement of the geoeffective hard X-ray irradiance corresponding to the peak time of the flares (solid gray triangles) to the geoeffective hard X-ray irradiance corresponding to the time of the sounding (open triangles). A major part of the events show an appreciable difference in their geoeffective hard X-ray irradiance computed at their peak time and at the time of the ionospheric sounding. Actually, this geoeffective hard X-ray irradiance reduction, $\mathsf{\Delta }{E}_{eff}$, is on average $14\pm 2$% for those undetected events that occurred for the 5 min sampling campaign and $33\pm 3$% for those undetected events that took place for the 15 min sampling campaign.

In Figure 5, we also marked with a blue dashed line the energetic constraint $E_{ef{f}_{min}}$, found in Section 3.1. Moreover, it is possible to identify three different regions, roughly marked with green vertical dashed lines. Thus, the left region is mainly characterized by events with a geoeffective X-ray irradiance higher than $E_{ef{f}_{min}}$ in both moments, so they were considered as false negative. The second region, in the center, is mostly composed of events with a geoeffective X-ray irradiance higher than $E_{ef{f}_{min}}$ in the peak time but with a lower value in the ionospheric sounding, so they were considered as undetected–asynchronous. Finally, the third region, on the right, is mainly comprised of events with a geoeffective X-ray irradiance lower than $E_{ef{f}_{min}}$ in both moments, so they were considered as undetected–low irradiance. Nevertheless, we noted that some Undetected-Asynchronous events can also be observed in the left region, and the same occurs with other regions and categories. Finally, after a more carefully examination, the 76 undetected solar flares considered in this section were classified as false negative (13 events), undetected–asynchronous (11 events), and undetected–low irradiance (52 events).

After this analysis, we can explain the reasons why our method was not able to detect all the events now classified as undetected–asynchronous. These events suffer a dramatic reduction of their geoeffective hard X-ray irradiance at sounding time with respect to the maximum value at peak time, reaching decreases up to 96%. Due to an asynchronous measurement, their absorbing effects on the local ionosphere could not be observed in the SNR and could not be detected by our method. This is mainly caused by their short total duration, which in general is under 15 min. Detailed information about these 11 events is summarized in

Table 1. List of undetected–asynchronous solar flares. For each event, the year, day of year (DOY), and class; the total duration of the flare, in minutes; the peak time (PT) of the flare, and the time in which the ionospheric sounding was carried out (IST), both in Local Time (LT); the temporal mismatch (TM) between PT and IST, in minutes; the solar elevation angle at PT (α_S (Max)) and at IST (α_S (IST)), both in degrees; the geoeffective hard X-ray irradiance at PT (E_eff (Max)) and at IST (E_eff (IST)), both in W/m²; and the geoeffective hard X-ray irradiance reduction (ΔE_eff), which presents the energetic difference (in %) between E_eff (IST) and E_eff (Max) are shown.

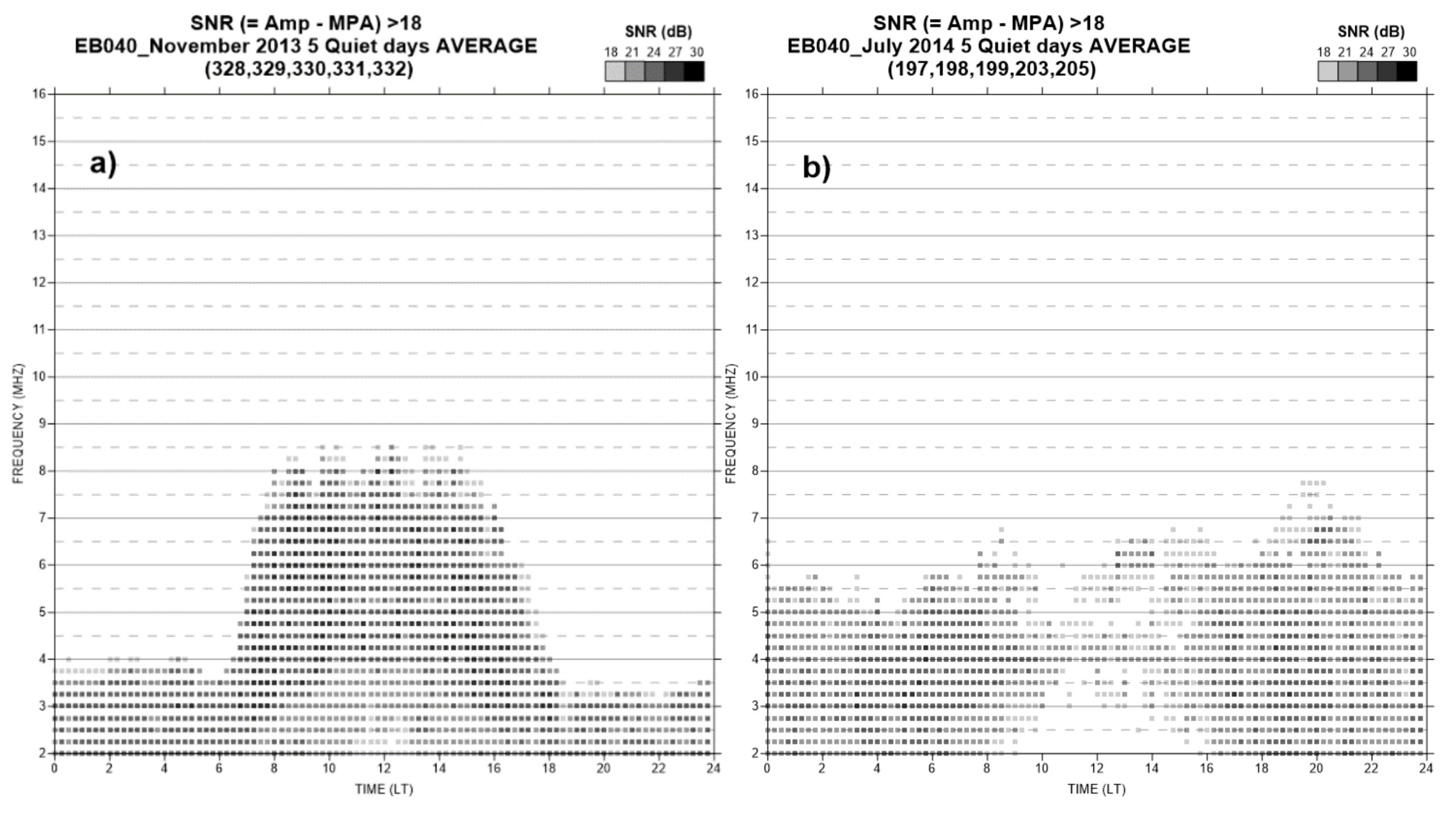
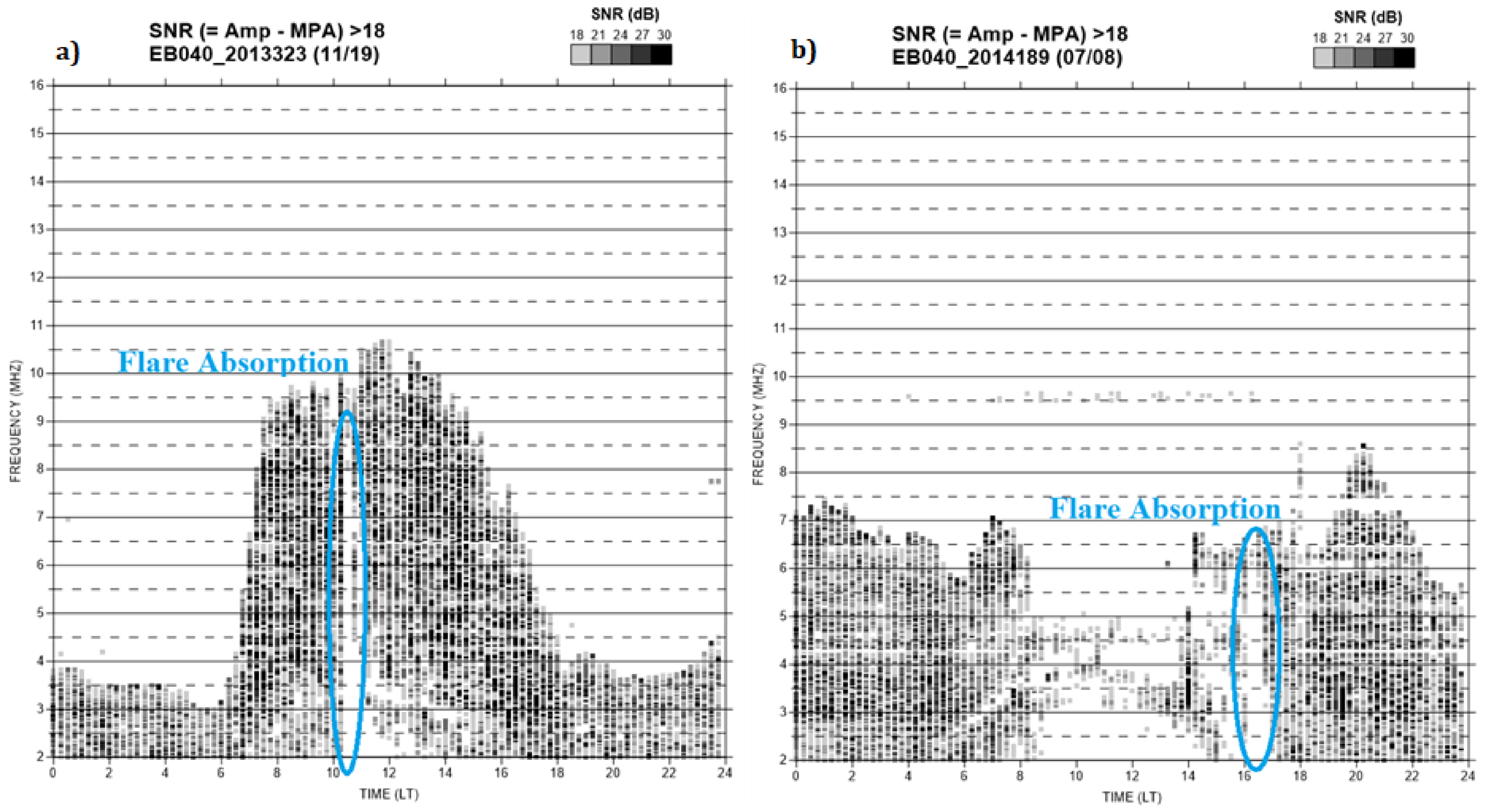
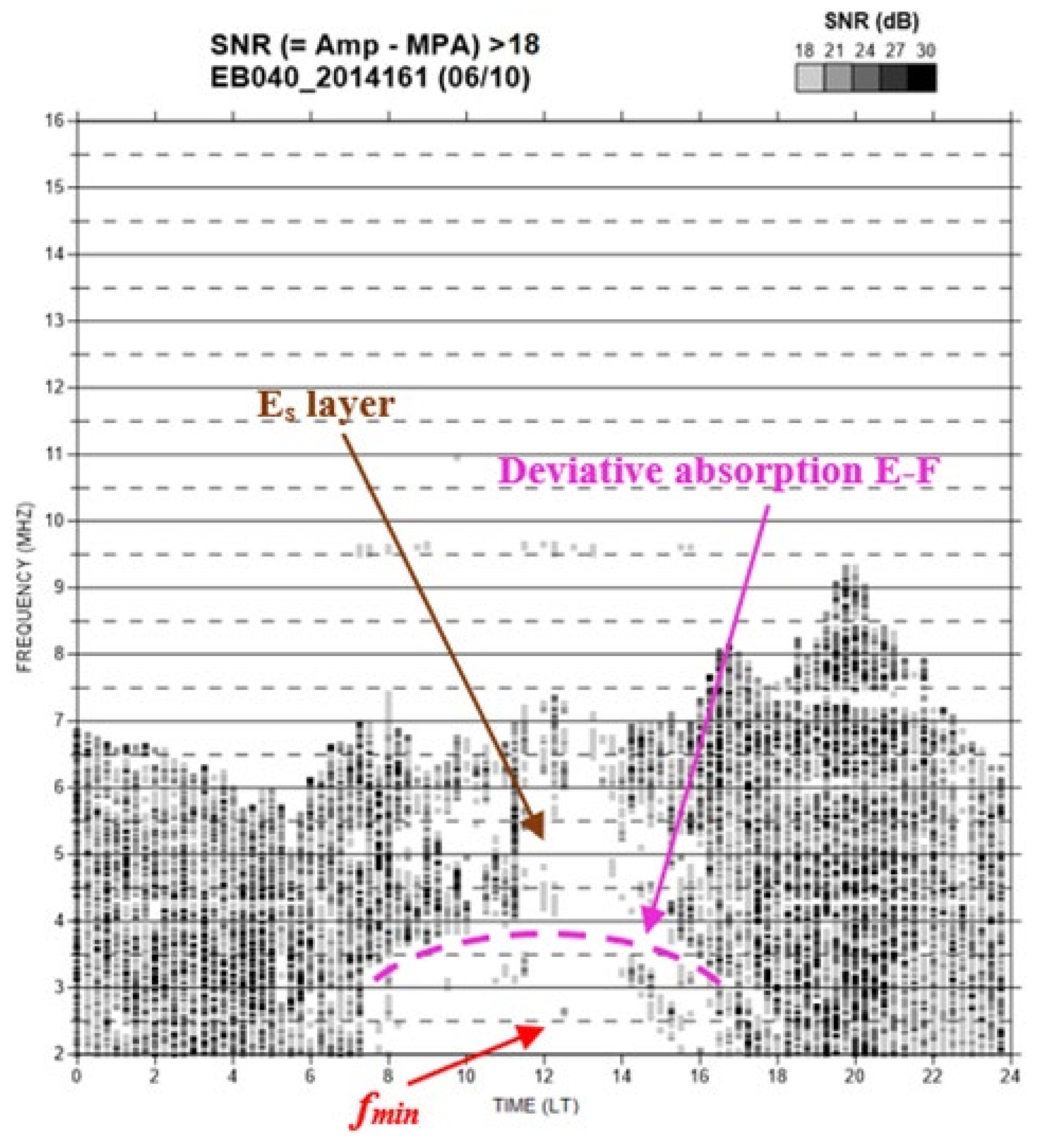
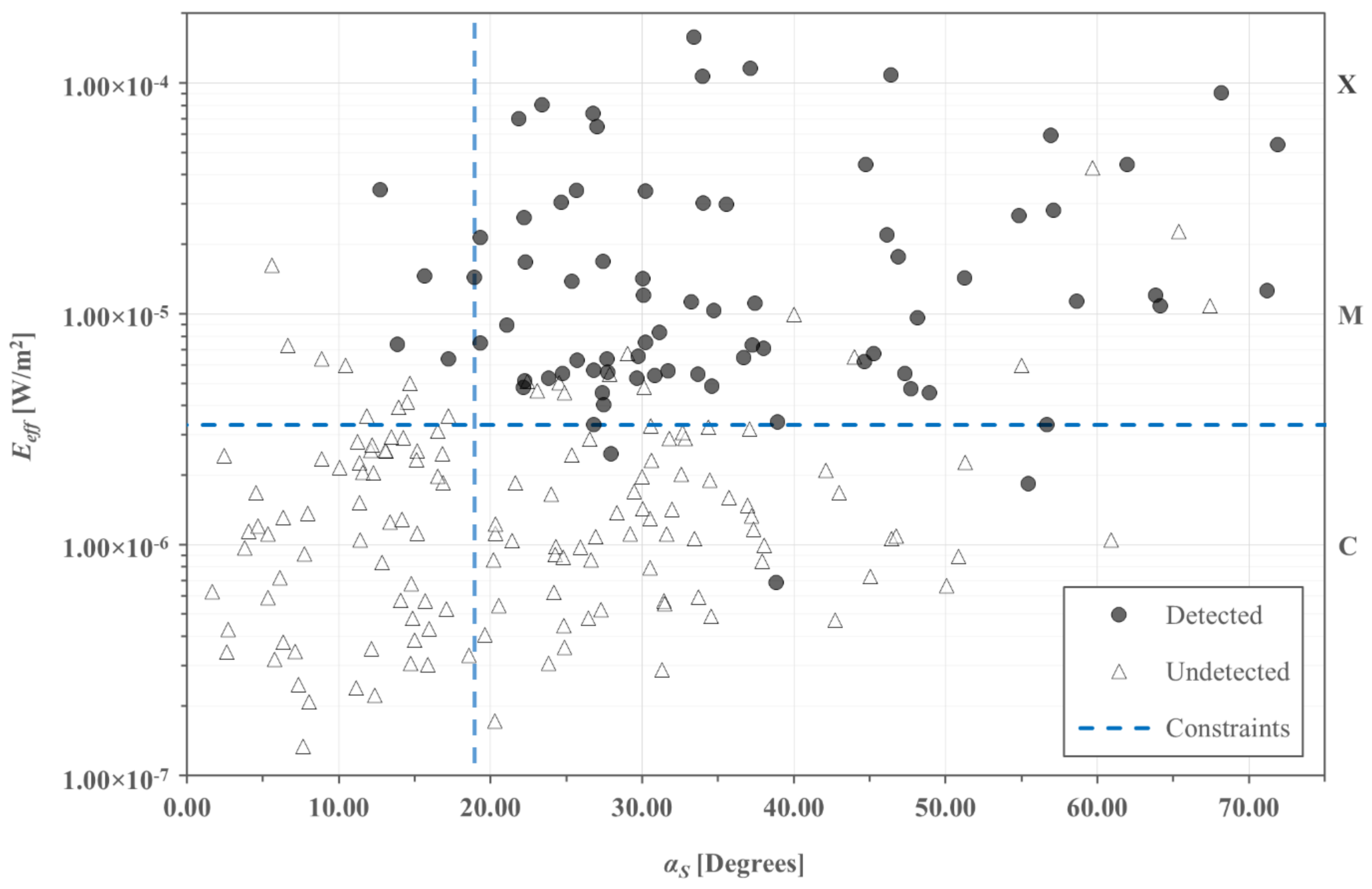
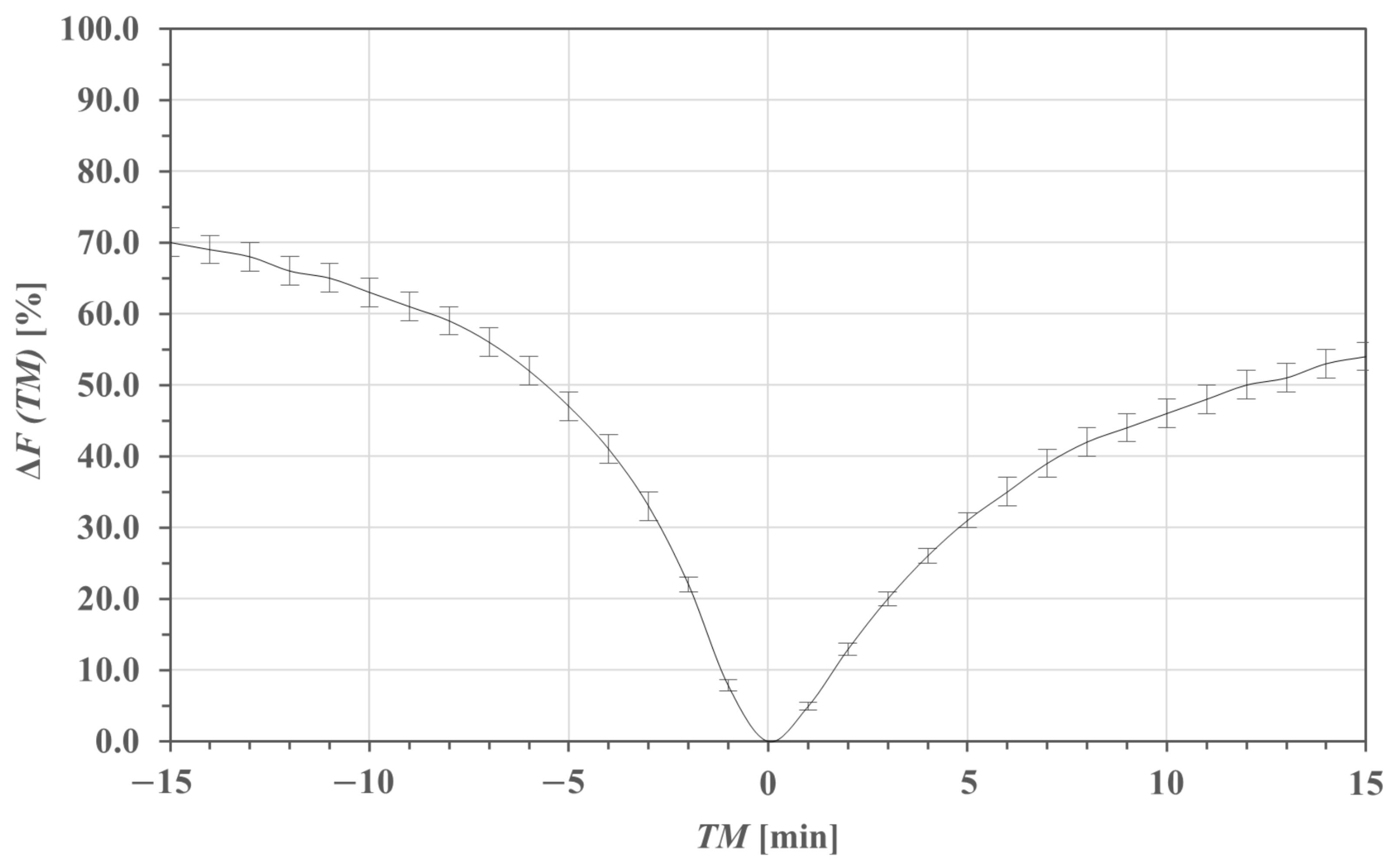
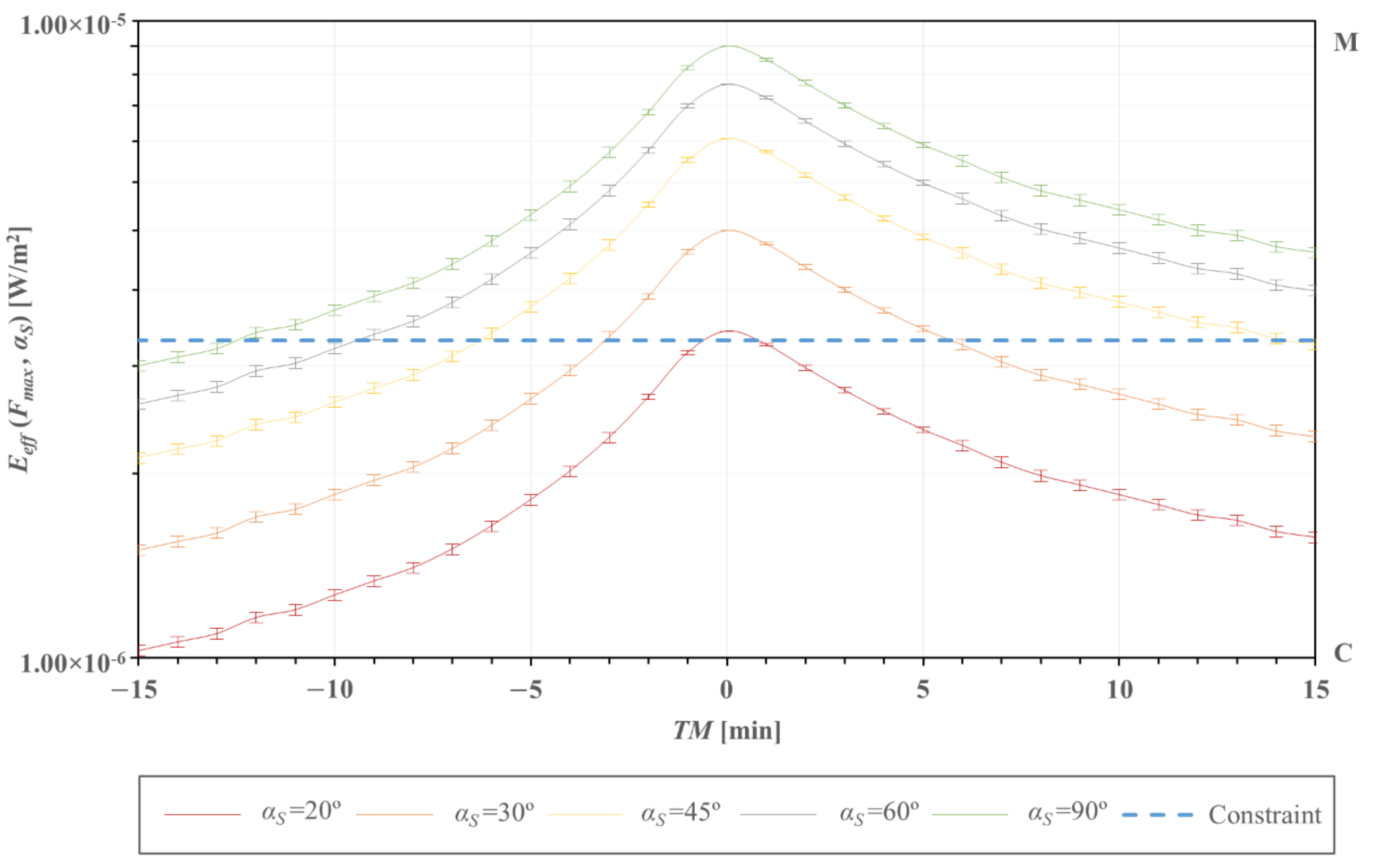
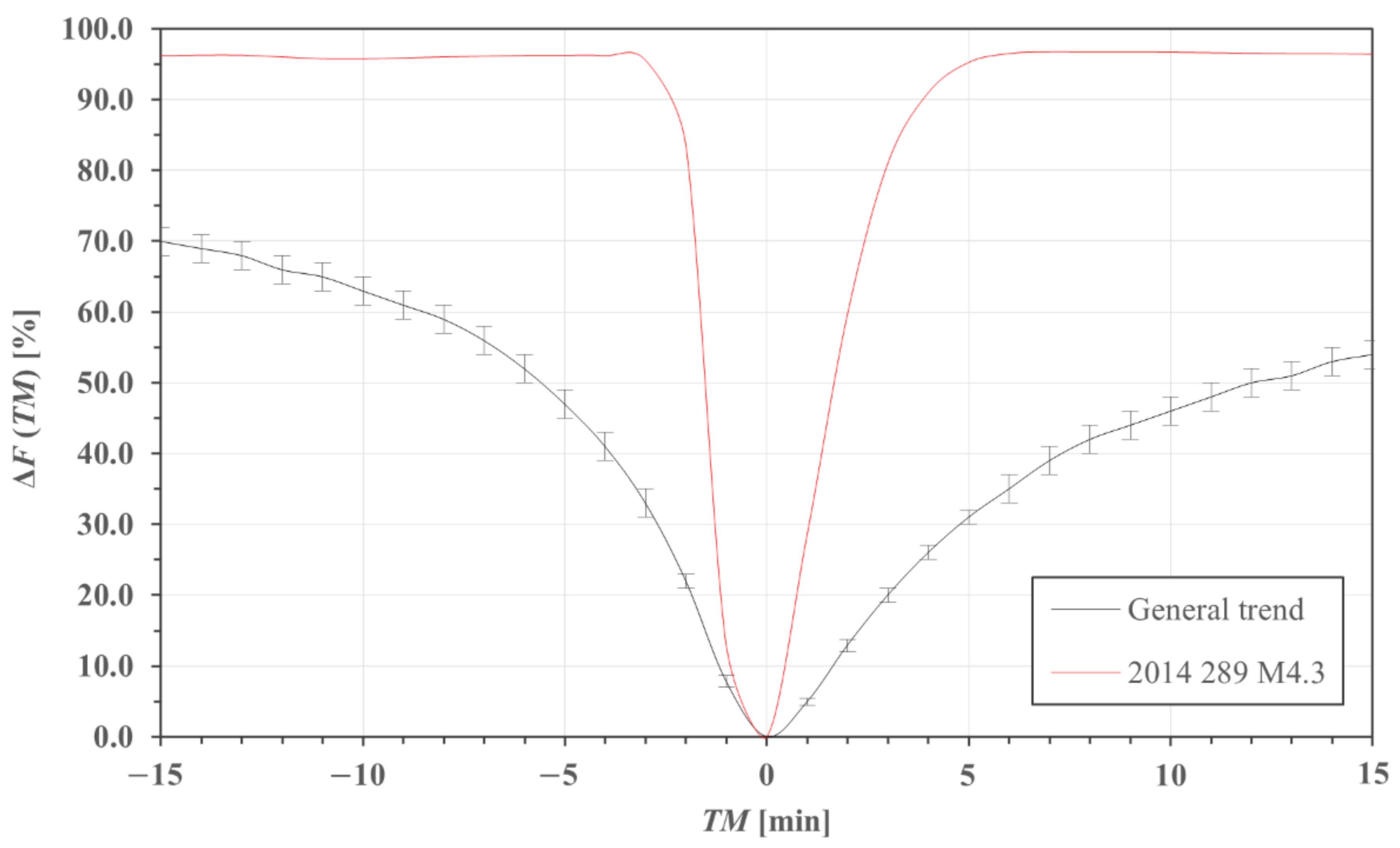
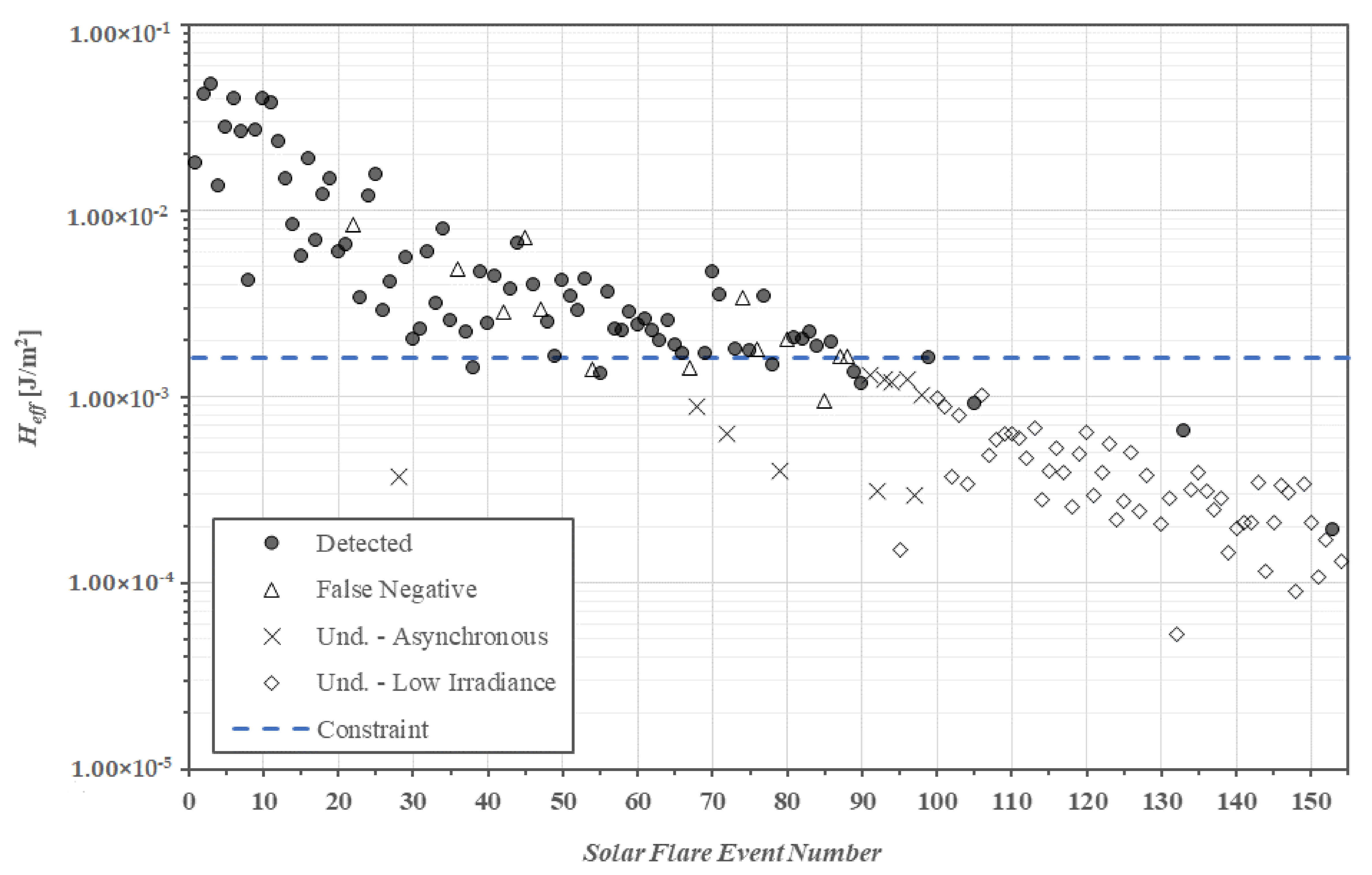
Event [Year-DOY-Class]	Total Duration [min]	PT [LT]	IST [LT]	TM [min]	αS (Max) [°]	αS (IST) [°]	Eeff (Max) [W/m2]	Eeff (IST) [W/m2]	ΔEeff [%]
2013 296 C6.5	0:10	11:17	11:15	−0:02	35.81	35.72	3.84 × 10−6	1.60 × 10−6	58.3
2014 028 M1.4	0:07	11:38	11:45	+0:07	30.41	30.53	7.39 × 10−6	1.29 × 10−6	82.5
2014 033 M1.3	0:08	14:06	14:15	+0:09	24.99	24.02	5.70 × 10−6	1.66 × 10−6	70.9
2014 034 C7.9	0:22	12:54	13:00	+0:06	30.87	30.55	4.08 × 10−6	3.27 × 10−6	19.9
2014 045 C7.2	0:15	10:41	10:45	+0:04	32.57	32.85	3.92 × 10−6	2.88 × 10−6	26.5
2014 110 C6.4	0:11	8:13	8:15	+0:02	32.29	32.66	3.47 × 10−6	3.07 × 10−6	11.5
2014 163 C7.8	0:12	16:03	16:00	−0:03	36.66	37.22	4.70 × 10−6	1.34 × 10−6	71.5
2014 182 C6.6	0:49	7:37	7:45	+0:09	32.86	34.37	3.63 × 10−6	3.21 × 10−6	11.6
2014 289 M4.3	0:07	13:03	13:00	−0:03	37.17	37.36	2.63 × 10−5	1.17 × 10−6	95.6
2014 294 M1.2	0:05	13:38	13:30	−0:08	32.75	33.46	6.87 × 10−6	1.06 × 10−6	84.6
2014 303 C6.9	0:13	13:12	13:15	+0:03	31.98	31.78	3.70 × 10−6	2.87 × 10−6	22.4

.

We also determined the temporal window (TW) in which the method is able to detect an event; i.e., we defined the time sampling of the ionospheric measurements needed to detect a given solar flare. Thus, we modeled the geoeffective hard X-ray irradiance of solar flares, $E_{ef{f}_{TW}}$, as a function of the hard X-ray flux of the events at the peak time, F_max, the general trend of the hard X-ray flux reduction from peak time to time of the ionospheric sounding, $\mathsf{\Delta }F$, and the local solar altitude angle at time of the sounding, ${\alpha }_S$(Equation (4)).

$$E_{ef{f}_{TW}}\left(F_{max},\mathsf{\Delta }F,{\alpha }_S\right)=\left[F_{max}-\left(F_{max}·\frac{\mathsf{\Delta }F}{100}\right)\right]·\sin {\alpha }_S$$

(4)

The general trend of the hard X-ray flux reduction from the peak time to time of the ionospheric sounding can be expressed in terms of the temporal mismatch (TM), i.e., $\mathsf{\Delta }F=\mathsf{\Delta }F\left(TM\right)$. We constructed and adjusted $\mathsf{\Delta }F\left(TM\right)$ by averaging the evolution over the time of the whole set of solar flares (see Figure 6).

Even though each solar flare is unique, they show an evolution over time that is very similar (Figure 6), presenting an asymmetrical pattern. Thus, events tend to increase their energy very quickly just before they reach their maximum, and from then on, they decrease it at a slower pace. Temmer et al. [34] extracted similar conclusions after doing a statistical analysis of 97,894 Hα flare events reported during 1975—1999. They found that for more than 50% of all flares, the decay phase was even more than four times as long as the rising phase, obtaining averaged results of 5.1 and 15.5 min for their rise and decay times, respectively. The latter is coherent with the mean rise and decay times found by Curto et al. [35] in geomagnetic Sfe, which are also clearly connected with the ionospheric effects of solar flares.

To check the goodness of the temporal-window model, we computed the modeled geoeffective hard X-ray irradiance at the time of the ionospheric sounding of the whole solar flare event set by using Equation (4), and then we compared the results obtained by using the estimation from Equation (1). Only 57 out of 262 events present a deviation of more than 35% of their geoeffective hard X-ray irradiance. Figure 7 depicts an example of the variation of the geoeffective hard X-ray irradiance in terms of the temporal mismatch for a hypothetical M1.0 class solar flare. We plotted five different curves related to five different values of the local solar elevation angle $({\alpha }_S=20°, 30°,45°, 60°,$ and $90°$). We also plotted the geoeffective hard X-ray irradiance constraint, $E_{ef{f}_{min}}$, with a blue dashed line. Assuming that the method can detect all the solar flares whose $E_{eff}\ge E_{ef{f}_{min}}$, the time sampling (temporal window) needed for a solar flare detection refers to the interval of time observed between the points where the modeled geoeffective hard X-ray irradiance, in terms of the temporal mismatch (TM), crosses the value of $E_{ef{f}_{min}}$. Figure 7 shows that the larger the elevation angle, the longer the temporal window. Moreover, for a ${\alpha }_S$ equal or higher than 20°, our method is able to detect the event, but only if the temporal mismatch between the peak time of the flare and the time of the ionospheric sounding is relatively short. On the other hand, for higher values of ${\alpha }_S$, we can expect a better performance with our method, because the influence of an asynchronous measurement is reduced as ${\alpha }_S$ is much higher.

We aim to model for how long, regarding the peak time of a flare, the method is able to observe its absorbing effects in the local ionosphere, i.e., the temporal window for a hypothetical solar flare in a certain location. To compute that, the peak flux, F_max, and the local solar altitude angle at time of the ionospheric sounding, ${\alpha }_S$, are needed. Then, by fixing $E_{ef{f}_{TW}}=E_{ef{f}_{min}}$ in Equations (4) and (5) is obtained:

$$\mathsf{\Delta }F\left(TM\right)\le 100\left(1-\frac{E_{ef{f}_{min}}}{F_{max}·\sin {\alpha }_S}\right)$$

(5)

Finally, the temporal window is obtained by inverting $\mathsf{\Delta }F\left(TM\right)$. Main results for the case of the EB040 ionospheric station are shown in

Table 2. Temporal window at the EB040 ionospheric station for different classes of solar flares (from C1.0 to M4.0) and solar altitude angles obtained from Equation (5). Results are shown in minutes and accompanied by their deviation due to the standard error associated with ΔF(TM). Those solar flares whose detection is not affected by the temporal mismatch are indicated by “Always Detected”. Those flares that cannot be detected in any temporal window are indicated by “Undetectable”. M4.0 class solar flares or higher occurring at any solar altitude angle higher than ${\alpha }_{s_{min}}$ are always detected since they are not affected by the temporal mismatch.

Class	${\mathit{\alpha }}_{\mathit{S}}=20°$	${\mathit{\alpha }}_{\mathit{S}}=30°$	${\mathit{\alpha }}_{\mathit{S}}=45°$	${\mathit{\alpha }}_{\mathit{S}}=60°$	${\mathit{\alpha }}_{\mathit{S}}=90°$
C1.0	Undetectable	Undetectable	Undetectable	Undetectable	Undetectable
C2.0	Undetectable	Undetectable	Undetectable	Undetectable	Undetectable
C3.0	Undetectable	Undetectable	Undetectable	Undetectable	Undetectable
C4.0	Undetectable	Undetectable	Undetectable	[0, 0+1]	[−1, 2]
C5.0	Undetectable	Undetectable	[0, 1]	[−2, 3]	[−$3_{-1}$, $5^{+1}$]
C6.0	Undetectable	Undetectable	[−$2^{+1}$, 3]	[−$3$, $6_{-1}$]	[−4, $9_{-1}^{+1}$]
C7.0	Undetectable	[0, 1]	[−$3_{-1}$, $5^{+1}$]	[−$4_{-1}$, $9_{-1}^{+1}$]	[−$6_{-1}$, ${13}_{-1}^{+2}$]
C8.0	Undetectable	[−1, 2]	[−$4_{-1}$, $7^{+1}$]	[−$6^{+1}$, ${13}_{-1}^{+2}$]	[−$7_{-1}$, 15]
C9.0	Undetectable	[−$2$, $4_{-1}$]	[−5+1, ${11}_{-1}^{+1}$]	[−$7_{-1}^{+1}$, 15]	[−${10}_{-1}^{+1}$, 15]
M1.0	0	[−3+1, 5+1]	[−6+1, ${14}_{-1}^{+1}$]	[−$9_{-1}^{+1}$, 15]	[−${12}_{-2}^{+1}$, 15]
M2.0	[−$5_{-1}$, ${13}_{-2}^{+1}$]	[−${12}_{-2}^{+1}$, 15]	Always Detected	Always Detected	Always Detected
M3.0	[−${12}_{-2}^{+1}$, 15]	Always Detected	Always Detected	Always Detected	Always Detected
M4.0	Always Detected	Always Detected	Always Detected	Always Detected	Always Detected

. Numbers expressed in brackets are the minimum and maximum values of the TM in which the method is able to detect a flare of a certain class that occurred with a given ${\alpha }_S$.

Results in Table 2 show that as long as the sampling frequency of the ionospheric sounding is under 15 min, all M4.0 class or higher solar flares occurring at any solar altitude angle (above ${\alpha }_{S_{min}}$) always produce a signature in the ionospheric SNR, making their detection possible. In other words, their detection is not affected by the temporal mismatch. This means that even 15 min before and after their peak time, M4.0 class or higher events present a geoeffective hard X-ray irradiance that is higher than the energetic constraint found in the previous section. In contrast, the detection of M3.0 or lower-class events can be compromised depending on the solar altitude angles they present and the temporal mismatch between the peak time and the ionospheric sounding. Carrying out an ionospheric sounding every 5 min leads to temporal mismatches of 2 min at most, and consequently, it increases the chances of detecting relatively short events or low-energy events. Moreover, the lowest detectable class according to this approximation is C4.0, even at a solar altitude angle of 60°, provided the ionospheric sounding is carried out with a temporal mismatch of 1 min at most. The only event analyzed that is not concordant with the temporal-window model is the M4.3 flare, which occurred on day of the year 289 in 2014. Its main characteristics are listed in Table 1. The evolution over time of its hard X-ray flux strongly deviates from the general trend of the whole set of analyzed solar flares (Figure 8), and consequently, the temporal window to detect it was extremely short. Thus, the very short duration and the sharp shape of this event explain why it was not detected by the method.

3.3. Geoeffective Hard X-ray Radiant Exposure

The electron density in the ionosphere is controlled by the balance between photoionization and recombination processes. Consequently, a time delay can be noted between the geoeffective X-ray irradiance peak and the ionospheric response, which is commonly found to be on the order of minute timescales [36]. Since the absorption effects due to the ionization enhancement process are not instantaneous, an additional energetic constraint can be obtained from analyzing the total amount of energy that the local ionosphere is receiving from a solar flare from the previous 5 min interval ($t=-5 \min$) to the time in which the ionospheric sounding is carried out ($t=0 \min$). This will determine the minimum geoeffective hard X-ray radiant exposure, $H_{eff}{}_{min}$, that a flare must present to disrupt the local electron density at that time and hence, to be detectable. The choice of this 5 min interval is supported by the results of Hayes et al. [36], who find that a great fraction of events show a time delay between their peak time (X-ray flux in the 0.1–0.8 nm channel), and the peak corresponding to the VLF ionospheric measurements amplitude does not exceed 5 min. For this purpose, we analyzed all detected and undetected events with a solar altitude angle above ${\alpha }_{S_{min}}$, excluding those events that were affected by adverse ionospheric conditions. Since we have been working with 1 min GOES-15 averaged hard X-ray flux, in W/m² units, we estimated the geoeffective hard X-ray radiant exposure of the events over the above-mentioned time span, measured in J/m² units, from the sum of each 1 min averaged geoeffective hard X-ray irradiance, $E_{ef{f}_t}$, multiplied by 60 s:

$$H_{eff}=60{\displaystyle \sum }_{t=-5}^0{E}_{ef{f}_t}$$

(6)

Figure 9 depicts the geoeffective hard X-ray radiant exposure of the selected flares. Events were sorted according to their maximum flux measured by the GOES-15 spacecraft and were classified as detected (solid black dots), false negative (open triangles), undetected–asynchronous (black crosses), and undetected–low irradiance (open diamonds). The results allowed us to establish another energetic constraint of $H_{ef{f}_{min}}$ = 1.61 × 10⁻³ J/m² (marked with a blue dashed line) after considering the same criterion adopted in Section 3.1, i.e., finding the threshold in order to not to exclude more than 10% of the detected events. We found that 5 out of the 13 false negative events could be interpreted in terms of the phenomenon described in this section, since they present approximately the same geoeffective hard X-ray radiant exposure as the established constraint, or even a lower value. In other words, these events could not be detected since they did not present a geoeffective hard X-ray radiant exposure that was enough to disrupt the local ionosphere.

We also analyzed the×⁻⁵ time delay between the peak of the geoeffective hard X-ray irradiance of all events and the corresponding geoeffective hard X-ray radiant exposure maximum. We noted that, on average, the geoeffective hard X-ray radiant exposure maximum was always displaced after the geoeffective hard X-ray irradiance peak of the events, and in the majority of flares, this time delay was of 3 min (see Figure 10). This result could complement the temporal window model results in Section 3.2, since a 3 min delayed ionospheric sounding (with respect the peak time of the events) could be helpful in the detection of solar flares, while performing the sounding before the peak time of the events could worsen it. In other words, in an asynchronous measurement situation, the method provides better results in those cases in which the ionospheric sounding is performed after the peak time of solar flares.

4. Solar Flare Detection Rate

After the discussion carried out in Section 3, we found three constraints that a solar flare must accomplish to disturb the local ionosphere and consequently be detectable by the proposed method: a geoeffective hard X-ray irradiance above 3.30 × 10⁻⁶ W/m², a geoeffective hard X-ray radiant exposure above 1.61 × 10⁻³ J/m², and a solar altitude angle higher than 18.94°. Then, considering these values, we can explain the results of the detection method. Therefore, we developed a robust method of solar flare detection that is based on the effects that such transitory events cause in SNRs.

Considering the whole set of 262 events, 77 were detected (29.4%). The remaining events could not be detected due to several reasons: low solar elevation angle (66 events, 25.2%), low geoeffective hard X-ray irradiance (52 events, 19.8%), local ionospheric adverse conditions (especially in summer) (43 events, 16.4%), asynchronous measurement (11 events, 4.2%), false negatives derived from our method (8 events, 3.1%), or low geoeffective X-ray radiant exposure (5 events, 1.9%).

Bearing in mind all the previous statements, the solar flare detection rate of this method applied at the Ebro ionospheric station (EB040), focusing on those events that accomplished all the aforementioned constraints, was 100.0% for the X-class, 82.6% for the M-class, and even 46.2% for the C-class.

Table 3. Solar flare detection rate of the Ebro ionospheric station (EB040) for X-, M- and C-classes, and for the general case (all classes), considering only those events that accomplish all constraints. For each class, the detection rate is described in %, and the number of detected events against the total number of events is given in parentheses. Below this information, the reason why the method is not able to detect each of the undetected events is summarized.

X-Class	M-Class	C-Class	All Classes
100.0% (14/14)	82.6% (57/69)	46.2% (6/13)	80.2% (77/96)
Cause undetected events: ▪ Asynchronous Meas.: 0 events ▪ False Negative: 0 events	Cause undetected events: ▪ Asynchronous Meas.: 4 events ▪ False Negative: 8 events	Cause undetected events: ▪ Asynchronous Meas.: 7 events ▪ False Negative: 0 events	Cause undetected events: ▪ Asynchronous Meas.: 11 events ▪ False Negative: 8 events

shows a complete summary of detection rates for all classes of solar flares. For those undetected events, the reasons why the method was not able to detect them are listed.

5. Summary and Conclusions

In this work, we presented a new ground-based method of detection of the absorbing effects in the local ionosphere caused by solar flares. The method compares the daily variation of the SNR of radio signals reflected in the ionosphere with the monthly pattern under quiet conditions. The method has been developed by the Ebro Observatory and carried out by using the EB040 ionospheric data obtained with a Digisonde-Portable-Sounder-4D (DPS-4D). However, this method could be used at any place with similar ionospheric sounding data.

We applied the method to the period 2013–2014. To assess its goodness, we compared its results with the 258 X-, M-, and C-class events that occurred at daylight hours at EB040, which are listed in the SGAS. In addition, to enlarge the number of X-class events, we also applied the method to four more cases that occurred during 2011–2012. To consider that an event was detected, we set a difference of at least −20 dB in four consecutive frequencies. We also pointed out the difficulties of having a good performance during the summer season, mainly due to the E_s layer, whose appearance is intensified in this period [27,37,38,39], and that the presence of the E_s layer can cause detrimental signal reception [5], but also because of the presence of deviative absorption between E and F layers or a high f_min. The combination of all these adverse conditions on the local ionosphere at central hours of the days led the method to work with a lower range of frequencies in the summer season, and consequently, it was not able to confirm the detection of 43 events. In addition, in the winter season, we observed a few false positives in the detection of solar flares, which caused an abnormal increase of the ionospheric absorption. These cases were concentrated on specific days, coinciding with the SSW event of January 2013 [30]. We also inspected the energetic information corresponding to the full set of solar flares to determine some physical constraints that events must accomplish to cause an evident enhancement in the ionospheric absorption of HF radio waves. Moreover, with the aim of obtaining more realistic results, we computed the geoeffective hard X-ray irradiance of all 262 events (Equation (1)), considering the local solar altitude angle (Equations (2) and (3)).

The analysis of some physical properties such as the geoeffective hard X-ray irradiance–solar altitude angle relationship or the geoeffective hard X-ray radiant exposure and phenomena such as the asynchrony between the peak of the flare and the moment of the ionospheric sounding allowed us to explain why the method cannot reach a more successful detection rate. This allowed us to find the conditions for which the method is sound enough to detect solar flares.

We established three physical constraints that flares must accomplish to produce absorption effects in the ionosphere and in consequence be detectable by the method: the minimum geoeffective hard X-ray irradiance ($E_{ef{f}_{min}}$ = 3.30 × 10⁻⁶ W/m²), the minimum geoeffective hard X-ray radiant exposure ($H_{ef{f}_{min}}$ = 1.61 × 10⁻³ J/m²), and the minimum solar altitude angle (${\alpha }_{S_{min}}=$ 18.94°).

We also studied the effect of the temporal mismatch between the time corresponding to the maximum flux of the events and the time of the ionospheric sounding on the detection of solar flares in our ground-based ionospheric station, which operated with a sampling frequency of 5 or 15 min, depending on the campaign. The temporal mismatch effect arises as a result of carrying out an ionospheric sounding asynchronously with the peak time of the events. In average, this leads to reductions in the geoeffective hard X-ray irradiance of $14\pm 2$% and $33\pm 3$%, respectively (depending on whether the events occurred during the 5 min sampling campaign or during the 15 min sampling campaign) and prevents the detection of relatively short or low-energy events.

Furthermore, we developed a model to evaluate the temporal window in which a given solar flare can produce enough signatures in the SNR to be detected. This approximation was carried out by averaging the hard X-ray flux reduction over the temporal mismatch of all events. We observed that solar flares tend to increase their energy very quickly until they reach their maximum, and from then on, they decrease it at a slower pace. Consequently, this asymmetrical behavior worsens the detection when the ionospheric sounding is carried out before the peak time of the events. Nevertheless, only the detection of M3.0 class events or lower can be compromised due to temporal mismatch effects.

Finally, we estimated the solar flare detection rate, using the method applied at the Ebro ionospheric station (EB040) data, focusing on those events that accomplished all the above-mentioned physical constraints. Thus, the method was able to detect 100.0% of X-class, 82.6% of M-class, and even 46.2% of C-class solar flares that accomplished the three aforementioned physical constraints.

Although a system designed specifically for monitoring solar flare effects in the ionosphere will yield better results, the proposed method provides new product and potential applications resulting from the existing Digisonde ionogram measurements. From all these results, we can conclude that this method applied to the SNR from ionograms recorded by the DPS-4D in the Ebro ionospheric station is robust enough to detect the absorption caused by solar flares. One application of the method is to help the international Service of Rapid Magnetic Variations (SRMV) in the detection of Sfes [10,16]. The lists of Sfes elaborated by the SRMV refer to events detected first on magnetic observations and later confirmed by simultaneous observation of solar activity (flares). Detection is not an easy task because many factors are present in the origin of the Sfe. Thus, additional information of ionospheric disturbances helps to confirm whether a movement in the magnetograms could be assigned as an Sfe (e.g., [19]).

Further research on the absorption of HF radio signals by solar flares could result in more precise constraints and also establish relationships between the different features of solar flares, such as the total duration of the radio fade-out according to the geoeffective hard X-ray irradiance which they present. In future studies, we will improve the detection method to be able to work in near real-time with the aim of creating a warning system of HF communication blackouts. For that, we need to evaluate how to improve the method and make the SNR quiet pattern upgradable. We also plan to improve the method by considering the SNR of extraordinary polarization echoes, which could provide information of additional frequencies to those of the ordinary echoes. This will allow us to increase the frequency range of analysis by half of the gyrofrequency, which could help in improving the detection in the summer season. Moreover, deeper study of the applicability of the method to potentially detect SSW during winter is envisaged considering the long-time duration of the SSW effects in the SNR compared to the duration of the effects on the SNR caused by solar flares.