Exploiting Graph and Geodesic Distance Constraint for Deep Learning-Based Visual Odometry
Abstract
:1. Introduction
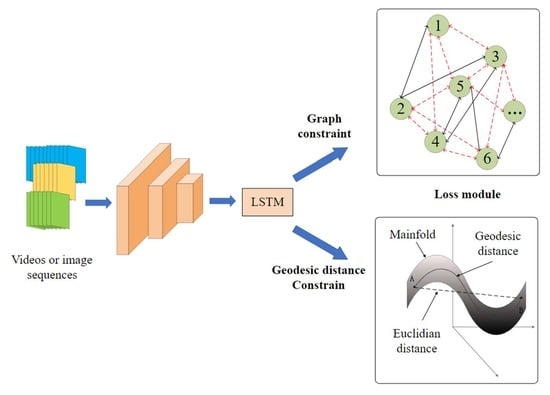
- A graph loss is proposed to fully exploit the constraints of a tiny image sequence to replace the conventional loss module based on two consecutive images, which can alleviate the accumulating errors in visual odometry. Moreover, the proposed graph loss leads to more constraints to regularize the network.
- A new representation of rotation loss is designed based on the geodesic distance, which is more robust than the usual methods that use the angles difference in Euclidean distance.
- Extensive experiments are conducted to demonstrate the superiority of the proposed losses. Furthermore, the effects of different sliding window sizes and sequence overlapping are also analyzed.
2. Related Work
2.1. Geometry-Based Methods
2.2. Deep Learning-Based Methods
3. Deep Learning-Based Visual Odometry with Graph and Geodesic Distance Constraints
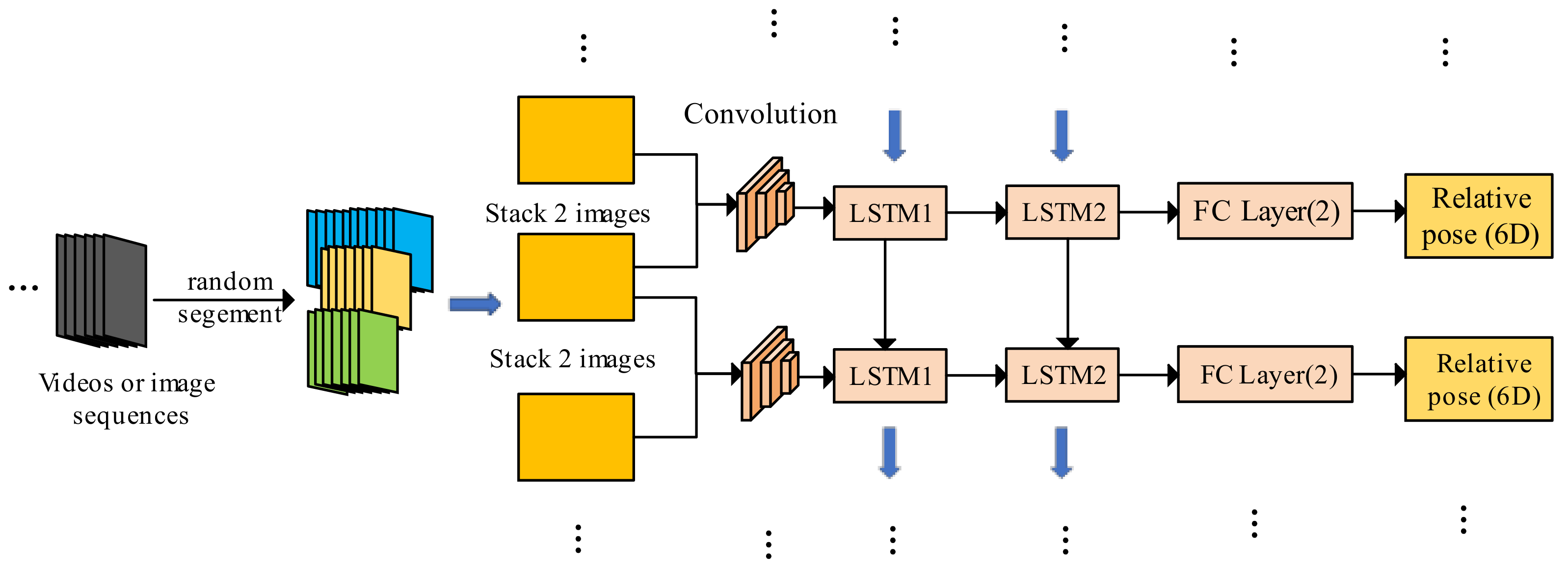
3.1. Deep Learning-Based Visual Odometry
3.2. Network Architecture
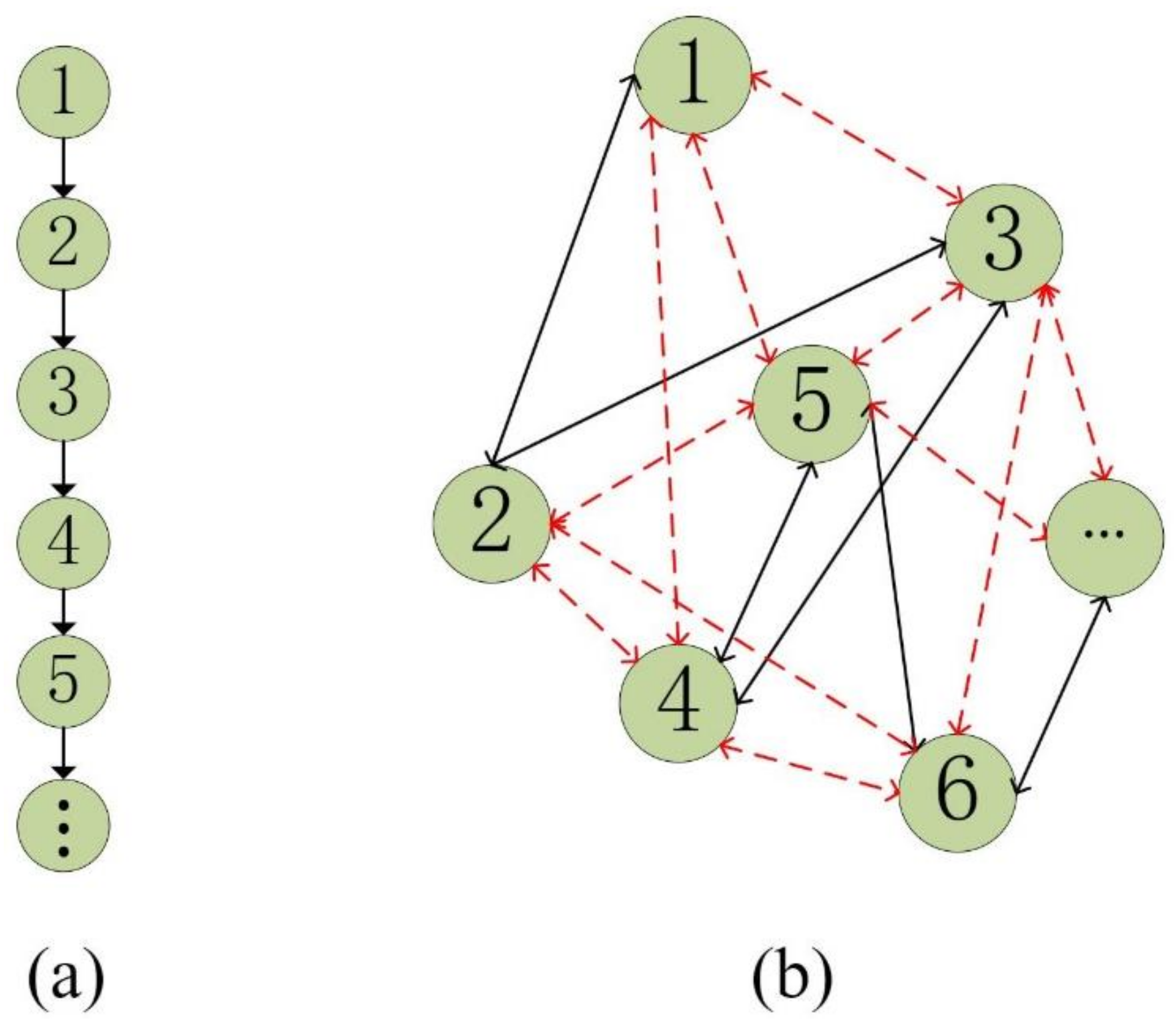
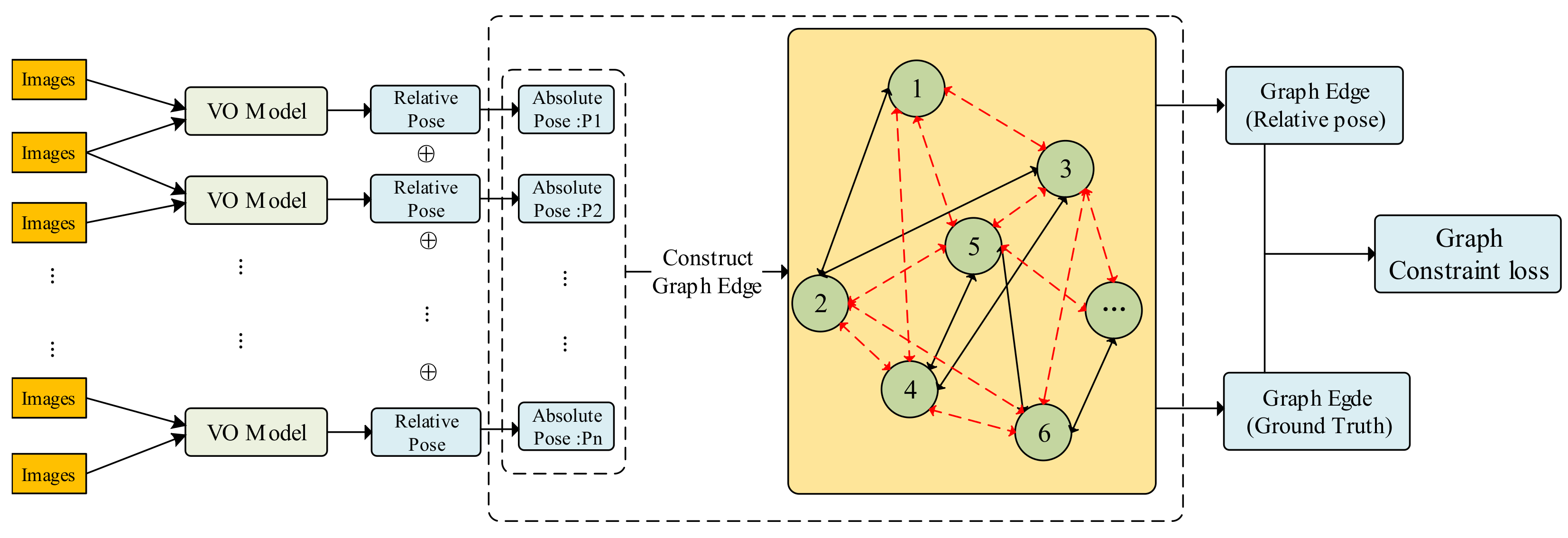
3.3. Graph Loss
3.4. Geodesic Rotation Loss
4. Results
4.1. Dataset
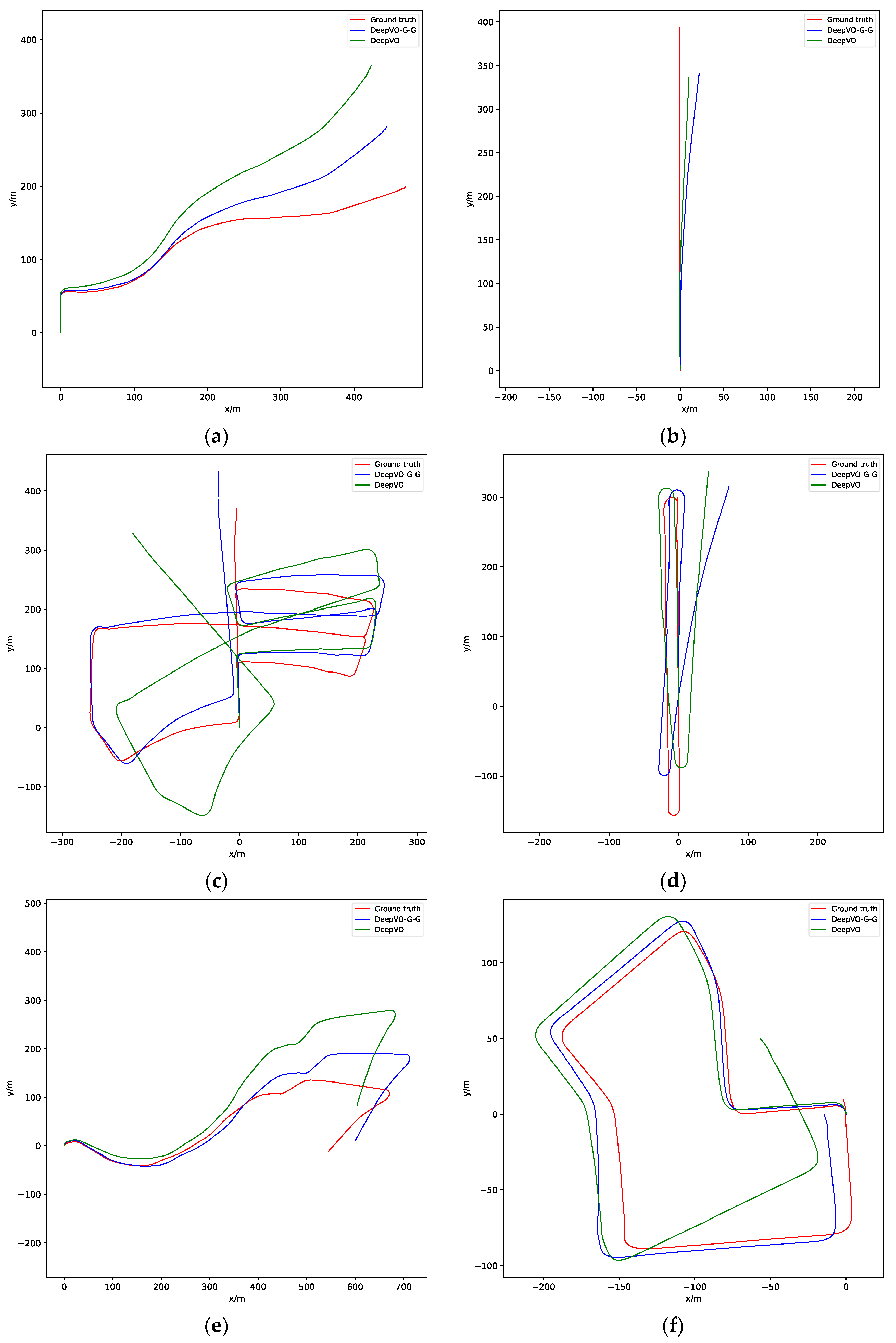
4.2. Experiment on Dataset with Ground Truth
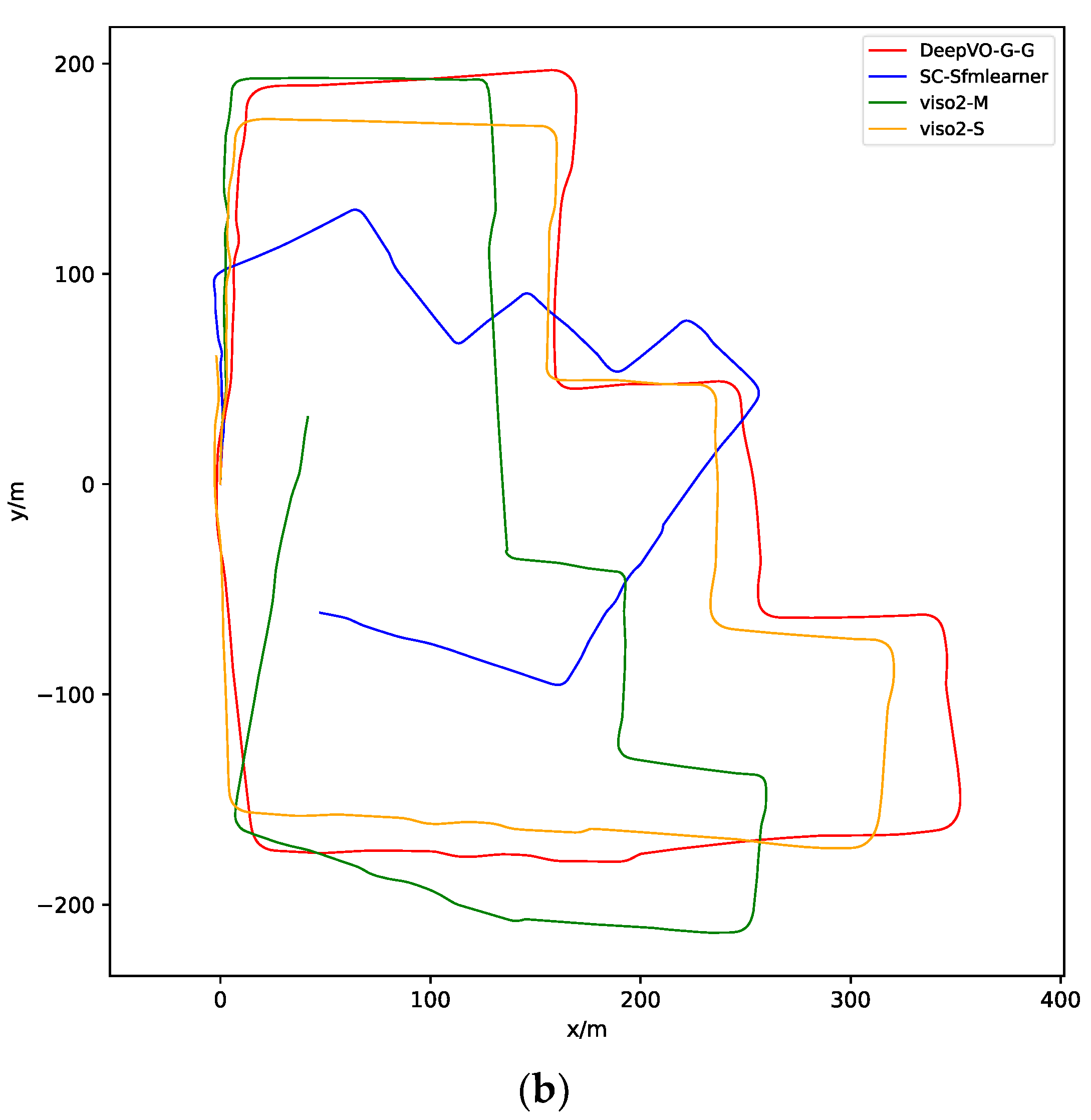
4.3. Experiment on Dataset without Ground Truth
5. Discussion
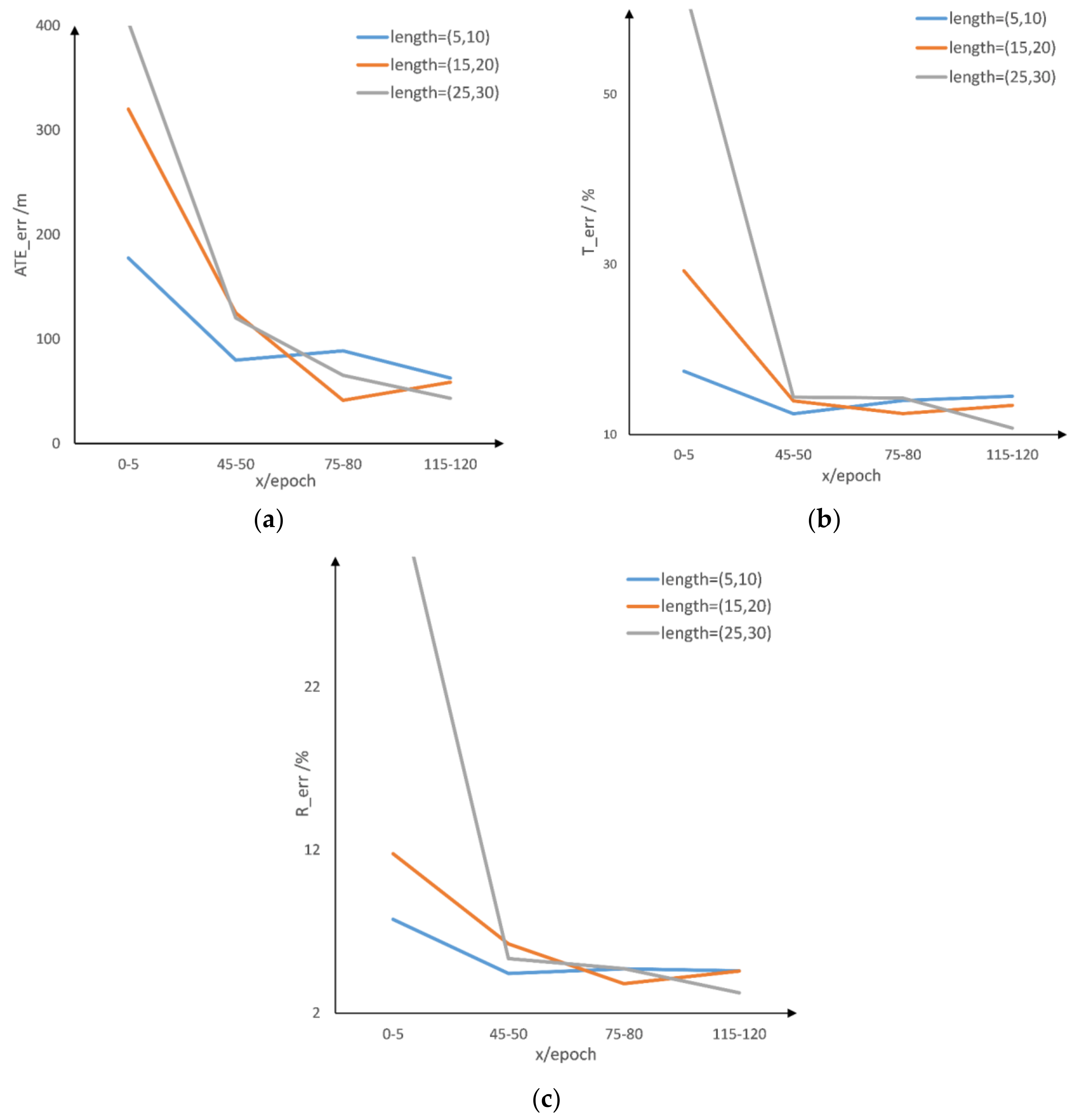
5.1. Effect of Different Sliding Window Sizes
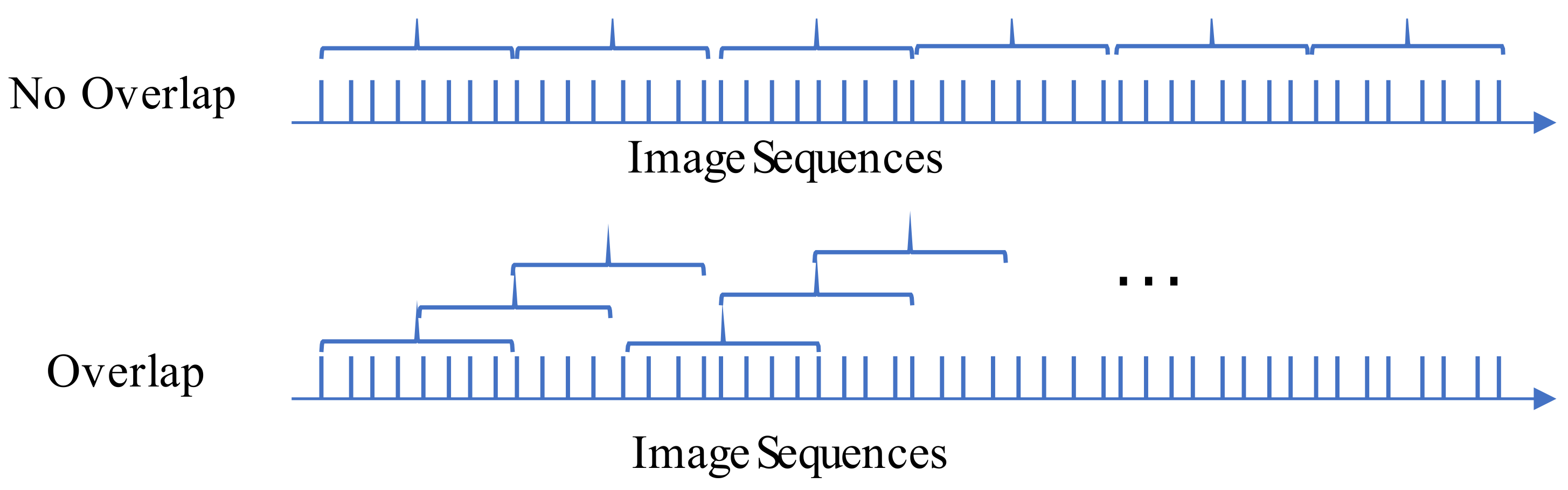
5.2. Effect of Sequence Overlap
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Scaramuzza, D.; Fraundorfer, F. Visual Odometry [Tutorial]. IEEE Robot. Autom. Mag. 2011, 18, 80–92. [Google Scholar] [CrossRef]
- Nister, D.; Naroditsky, O.; Bergen, J. Visual odometry. In Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, CVPR 2004, Washington, DC, USA, 27 June–2 July 2004; Volume 1, pp. 652–659. [Google Scholar] [CrossRef]
- Weiss, S.; Scaramuzza, D.; Siegwart, R. Monocular-SLAM–based navigation for autonomous micro helicopters in GPS-denied environments. J. Field Robot. 2011, 28, 854–874. [Google Scholar] [CrossRef]
- Kröse, B.J.; Vlassis, N.; Bunschoten, R.; Motomura, Y. A probabilistic model for appearance-based robot localization. Image Vis. Comput. 2001, 19, 381–391. [Google Scholar] [CrossRef]
- Wolf, J.; Burgard, W.; Burkhardt, H. Robust vision-based localization by combining an image-retrieval system with Monte Carlo localization. IEEE Trans. Robot. 2005, 21, 208–216. [Google Scholar] [CrossRef]
- Wiseman, Y. Ancillary ultrasonic rangefinder for autonomous vehicles. Int. J. Secur. Its Appl. 2018, 12, 49–58. [Google Scholar] [CrossRef]
- Wang, S.; Clark, R.; Wen, H.; Trigoni, N. DeepVO: Towards End-to-End Visual Odometry with Deep Recurrent Convolutional Neural Networks. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 2043–2050. [Google Scholar] [CrossRef] [Green Version]
- Saputra, M.R.U.; de Gusmao, P.P.; Wang, S.; Markham, A.; Trigoni, N. Learning monocular visual odometry through geometry-aware curriculum learning. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 3549–3555. [Google Scholar]
- Zhan, H.; Weerasekera, C.S.; Bian, J.-W.; Reid, I. Visual odometry revisited: What should be learnt? In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 4203–4210. [Google Scholar]
- Clark, R.; Wang, S.; Markham, A.; Trigoni, N.; Wen, H. Vidloc: A deep spatio-temporal model for 6-dof video-clip relocalization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 6856–6864. [Google Scholar]
- Li, Q.; Zhu, J.; Cao, R.; Sun, K.; Garibaldi, J.M.; Li, Q.; Liu, B.; Qiu, G. Relative Geometry-Aware Siamese Neural Network for 6DOF Camera Relocalization. Neurocomputing 2021, 426, 134–146. [Google Scholar] [CrossRef]
- Xue, F.; Wu, X.; Cai, S.; Wang, J. Learning Multi-View Camera Relocalization With Graph Neural Networks. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 11372–11381. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Zhang, Z. A flexible new technique for camera calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1330–1334. [Google Scholar] [CrossRef] [Green Version]
- Kumar, G.; Bhatia, P.K. A detailed review of feature extraction in image processing systems. In Proceedings of the 2014 Fourth International Conference on Advanced Computing & Communication Technologies, Rohtak, India, 8–9 February 2014; pp. 5–12. [Google Scholar]
- Kummerle, R.; Grisetti, G.; Strasdat, H.; Konolige, K.; Burgard, W. G2O: A general framework for graph optimization. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 3607–3613. [Google Scholar] [CrossRef]
- Dellaert, F.; Kaess, M. Factor Graphs for Robot Perception. Found. Trends Robot. 2017, 6, 1–139. [Google Scholar] [CrossRef]
- Jiang, S.; Jiang, C.; Jiang, W. Efficient structure from motion for large-scale UAV images: A review and a comparison of SfM tools. ISPRS J. Photogramm. Remote Sens. 2020, 167, 230–251. [Google Scholar] [CrossRef]
- Ji, S.; Qin, Z.; Shan, J.; Lu, M. Panoramic SLAM from a multiple fisheye camera rig. ISPRS J. Photogramm. Remote Sens. 2020, 159, 169–183. [Google Scholar] [CrossRef]
- Qin, T.; Li, P.; Shen, S. VINS-Mono: A Robust and Versatile Monocular Visual-Inertial State Estimator. IEEE Trans. Robot. 2018, 34, 1004–1020. [Google Scholar] [CrossRef] [Green Version]
- Campos, C.; Elvira, R.; Rodriguez, J.J.G.; Montiel, J.M.M.; Tardos, J.D. ORB-SLAM3: An Accurate Open-Source Library for Visual, Visual–Inertial, and Multimap SLAM. IEEE Trans. Robot. 2021, 37, 1874–1890. [Google Scholar] [CrossRef]
- Rosinol, A.; Abate, M.; Chang, Y.; Carlone, L. Kimera: An open-source library for real-time metric-semantic localization and mapping. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 1689–1696. [Google Scholar]
- Zhang, G. Towards Optimal 3D Reconstruction and Semantic Mapping. Ph.D. Thesis, University of California, Merced, CA, USA, 2021. [Google Scholar]
- Rosten, E.; Drummond, T. Machine learning for high-speed corner detection. In Proceedings of the European Conference on Computer Vision, Graz, Austria, 7–13 May 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 430–443. [Google Scholar]
- Bay, H.; Ess, A.; Tuytelaars, T.; van Gool, L. Speeded-up robust features (SURF). Comput. Vis. Image Underst. 2008, 110, 346–359. [Google Scholar] [CrossRef]
- Calonder, M.; Lepetit, V.; Strecha, C.; Fua, P. Brief: Binary robust independent elementary features. In Proceedings of the European Conference on Computer Vision, Heraklion, Greece, 5–11 September 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 778–792. [Google Scholar]
- Harris, C.; Stephens, M. A combined corner and edge detector. Alvey Vis. Conf. 1988, 15, 10–5244. [Google Scholar]
- Aguiar, A.; Sousa, A.; Santos, F.N.d.; Oliveira, M. Monocular Visual Odometry Benchmarking and Turn Performance Optimization. In Proceedings of the 2019 IEEE International Conference on Autonomous Robot Systems and Competitions (ICARSC), Porto, Portugal, 24–26 April 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Geiger, A.; Ziegler, J.; Stiller, C. StereoScan: Dense 3d reconstruction in real-time. In Proceedings of the 2011 IEEE Intelligent Vehicles Symposium (IV), Baden-Baden, Germany, 5–9 June 2011; pp. 963–968. [Google Scholar] [CrossRef]
- Mur-Artal, R.; Tardós, J.D. ORB-SLAM2: An Open-Source SLAM System for Monocular, Stereo, and RGB-D Cameras. IEEE Trans. Robot. 2017, 33, 1255–1262. [Google Scholar] [CrossRef] [Green Version]
- Engel, J.; Schöps, T.; Cremers, D. LSD-SLAM: Large-Scale Direct Monocular SLAM. In Proceedings of the Computer Vision—ECCV 2014; Fleet, D., Pajdla, T., Schiele, B., Tuytelaars, T., Eds.; Springer International Publishing: Cham, Switzerland, 2014; Volume 8690, pp. 834–849. [Google Scholar] [CrossRef] [Green Version]
- Engel, J.; Koltun, V.; Cremers, D. Direct sparse odometry. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 40, 611–625. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Redmon, J.; Farhadi, A. YOLOv3: An Incremental Improvement. arXiv 2018, arXiv:1804.02767. Available online: http://arxiv.org/abs/1804.02767 (accessed on 21 April 2021).
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towar ds Real-Time Object Detection with Region Proposal Networks. arXiv 2016, arXiv:1506.01497. Available online: http://arxiv.org/abs/1506.01497 (accessed on 19 February 2021). [CrossRef] [Green Version]
- Kwon, H.; Kim, Y. BlindNet backdoor: Attack on deep neural network using blind watermark. Multimed. Tools Appl. 2022, 81, 6217–6234. [Google Scholar] [CrossRef]
- Kendall, A.; Cipolla, R. Geometric Loss Functions for Camera Pose Regression With Deep Learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Konda, K.R.; Memisevic, R. Learning visual odometry with a convolutional network. In Proceedings of the VISAPP (1), Berlin, Germany, 11–14 March 2015; pp. 486–490. [Google Scholar]
- Vu, T.; van Nguyen, C.; Pham, T.X.; Luu, T.M.; Yoo, C.D. Fast and efficient image quality enhancement via desubpixel convolutional neural networks. In Proceedings of the European Conference on Computer Vision (ECCV) Workshops, Munich, Germany, 8–14 September 2018. [Google Scholar]
- Jeon, M.; Jeong, Y.-S. Compact and Accurate Scene Text Detector. Appl. Sci. 2020, 10, 2096. [Google Scholar] [CrossRef] [Green Version]
- Kendall, A.; Grimes, M.; Cipolla, R. PoseNet: A Convolutional Network for Real-Time 6-DOF Camera Relocalization. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 2938–2946. [Google Scholar] [CrossRef] [Green Version]
- Zhou, L.; Luo, Z.; Shen, T.; Zhang, J.; Zhen, M.; Yao, Y.; Fang, T.; Quan, L. KFNet: Learning Temporal Camera Relocalization using Kalman Filtering. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 4919–4928. [Google Scholar]
- Li, Q.; Zhu, J.; Liu, J.; Cao, R.; Fu, H.; Garibaldi, J.M.; Li, Q.; Lin, B.; Qiu, G. 3D map-guided single indoor image localization refinement. ISPRS J. Photogramm. Remote Sens. 2020, 161, 13–26. [Google Scholar] [CrossRef]
- Costante, G.; Mancini, M.; Valigi, P.; Ciarfuglia, T.A. Exploring Representation Learning With CNNs for Frame-to-Frame Ego-Motion Estimation. IEEE Robot. Autom. Lett. 2016, 1, 18–25. [Google Scholar] [CrossRef]
- Muller, P.; Savakis, A. Flowdometry: An optical flow and deep learning based approach to visual odometry. In Proceedings of the 2017 IEEE Winter Conference on Applications of Computer Vision (WACV), Santa Rosa, CA, USA, 24–31 March 2017; pp. 624–631. [Google Scholar]
- Dosovitskiy, A.; Fischer, P.; Ilg, E.; Hausser, P.; Hazirbas, C.; Golkov, V.; Van Der Smagt, P.; Cremers, D.; Brox, T. Flownet: Learning optical flow with convolutional networks. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 2758–2766. [Google Scholar]
- Wang, S.; Clark, R.; Wen, H.; Trigoni, N. End-to-end, sequence-to-sequence probabilistic visual odometry through deep neural networks. Int. J. Robot. Res. 2018, 37, 513–542. [Google Scholar] [CrossRef]
- Bian, J.; Li, Z.; Wang, N.; Zhan, H.; Shen, C.; Cheng, M.M.; Reid, I. Unsupervised scale-consistent depth and ego-motion learning from monocular video. Adv. Neural Inf. Process. Syst. 2019, 32, 35–45. [Google Scholar]
- Zhao, C.; Tang, Y.; Sun, Q.; Vasilakos, A.V. Deep Direct Visual Odometry. IEEE Trans. Intell. Transp. Syst. 2021, 1–10. [Google Scholar] [CrossRef]
- Clark, R.; Wang, S.; Wen, H.; Markham, A.; Trigoni, N. VINet: Visual-Inertial Odometry as a Sequence-to-Sequence Learning Problem. arXiv 2017, arXiv:1701.08376. [Google Scholar]
- Liu, Q.; Li, R.; Hu, H.; Gu, D. Using Unsupervised Deep Learning Technique for Monocular Visual Odometry. IEEE Access 2019, 7, 18076–18088. [Google Scholar] [CrossRef]
- Jiao, J.; Jiao, J.; Mo, Y.; Liu, W.; Deng, Z. Magicvo: End-to-end monocular visual odometry through deep bi-directional recurrent convolutional neural network. arXiv 2018, arXiv:1811.10964. [Google Scholar]
- Fang, Q.; Hu, T. Euler angles based loss function for camera relocalization with Deep learning. In Proceedings of the 2018 IEEE 8th Annual International Conference on CYBER Technology in Automation, Control, and Intelligent Systems (CYBER), Tianjin, China, 19–23 July 2018. [Google Scholar]
- Li, D.; Dunson, D.B. Geodesic Distance Estimation with Spherelets. arXiv 2020, arXiv:1907.00296. Available online: http://arxiv.org/abs/1907.00296 (accessed on 28 January 2022).



| Layer | Output Size | Kernel Size | Padding | Stride | Channel | Dropout |
|---|---|---|---|---|---|---|
| Input size | 6 × 608 × 184 (image pairs) | |||||
| Conv1 | (304,92) | 7 × 7 | 3 | 2 | 64 | 0.0 |
| Conv2 | (152,46) | 5 × 5 | 2 | 2 | 128 | 0.0 |
| Conv3 | (76,23) | 5 × 5 | 2 | 2 | 256 | 0.0 |
| Conv3_1 | (76,23) | 3 × 3 | 1 | 1 | 256 | 0.1 |
| Conv4 | (38,12) | 3 × 3 | 1 | 2 | 512 | 0.1 |
| Conv4_1 | (38,12) | 3 × 3 | 1 | 2 | 512 | 0.1 |
| Conv5 | (19,6) | 3 × 3 | 1 | 1 | 512 | 0.1 |
| Conv5_1 | (19,6) | 3 × 3 | 1 | 2 | 512 | 0.3 |
| Conv6 | (10,3) | 3 × 3 | 1 | 1 | 1024 | 0.2 |
| LSTM | num_layer = 2, input_size = 30,720 (1024 × 3 × 10), hidden_size = 1024 | |||||
| FC layer1 | Input_feature = 1024, output_feature = 128 | |||||
| FC layer2 | Input_size = 128, output_size = 6 | |||||
| Sequence | VISO2-M [29] | SC-Sfmlearner [48] | DeepVO [7] | DeepVO-Graph (Ours) | DeepVO-G-G (Ours) | |
|---|---|---|---|---|---|---|
| 00 | 37.14 | 9.88 | 4.1 | 2.99 | 3.35 | |
| 15.84 | 3.91 | 1.76 | 1.37 | 1.43 | ||
| ATE | 142.14 | 137.34 | 83.77 | 31.8 | 73.02 | |
| RPE(m) | 0.377 | 0.093 | 0.023 | 0.018 | 0.029 | |
| RPE(°) | 1.161 | 0.134 | 0.209 | 0.105 | 0.198 | |
| 02 | 6.38 | 7.27 | 5.86 | 3.86 | 3.98 | |
| 1.39 | 2.19 | 1.75 | 1.34 | 1.37 | ||
| ATE | 86.73 | 199.27 | 95.05 | 86.98 | 147.13 | |
| RPE(m) | 0.119 | 0.081 | 0.029 | 0.023 | 0.034 | |
| RPE(°) | 0.183 | 0.089 | 0.173 | 0.093 | 0.163 | |
| 08 | 24.46 | 18.26 | 5.59 | 2.65 | 3.38 | |
| 8.03 | 2.01 | 2.26 | 1.08 | 1.54 | ||
| ATE | 132.79 | 133.79 | 180.91 | 28.09 | 128.09 | |
| RPE(m) | 0.312 | 0.244 | 0.026 | 0.019 | 0.030 | |
| RPE(°) | 0.896 | 0.07 | 0.164 | 0.086 | 0.156 | |
| 09 | 4.41 | 11.24 | 4.32 | 4.04 | 3.36 | |
| 1.23 | 3.34 | 1.52 | 1.49 | 1.29 | ||
| ATE | 18.03 | 121.96 | 43.71 | 37.89 | 38.83 | |
| RPE(m) | 0.121 | 0.106 | 0.025 | 0.022 | 0.031 | |
| RPE(°) | 0.121 | 0.106 | 0.142 | 0.08 | 0.137 | |
| Sequence | VISO2-M [29] | SC-Sfmlearner [48] | TrajNet [49] | DeepVO [7] | DeepVO-Graph (Ours) | DeepVO-G-G (Ours) | |
|---|---|---|---|---|---|---|---|
| 03 | 16.88 | 4.45 | - | 15.06 | 9.72 | 10.00 | |
| 5.21 | 2.77 | - | 6.6 | 4.5 | 4.87 | ||
| ATE | 91.92 | 15.67 | - | 87.2 | 46.57 | 41.92 | |
| RPE(m) | 0.101 | 0.055 | - | 0.065 | 0.062 | 0.058 | |
| RPE(°) | 0.423 | 0.062 | - | 0.162 | 0.109 | 0.153 | |
| 04 | 1.73 | 3.28 | - | 8.04 | 8.97 | 7.11 | |
| 1.39 | 0.95 | - | 2.46 | 1.91 | 2.60 | ||
| ATE | 7.62 | 7.15 | - | 16.03 | 17.32 | 15.55 | |
| RPE(m) | 0.106 | 0.069 | - | 0.126 | 0.139 | 0.111 | |
| RPE(°) | 0.098 | 0.049 | - | 0.11 | 0.088 | 0.117 | |
| 05 | 16.8 | 6.02 | - | 7.8 | 7.76 | 6.55 | |
| 5.14 | 1.8 | - | 2.65 | 3.0 | 2.59 | ||
| ATE | 108.02 | 55.91 | - | 83.51 | 55.1 | 36.03 | |
| RPE(m) | 0.296 | 0.069 | - | 0.081 | 0.083 | 0.073 | |
| RPE(°) | 0.29 | 0.063 | - | 0.158 | 0.106 | 0.153 | |
| 06 | 4.57 | 10.73 | - | 9.99 | 9.43 | 8.43 | |
| 1.45 | 2.18 | - | 1.96 | 1.9 | 2.36 | ||
| ATE | 33.81 | 44.5 | - | 43.12 | 42.77 | 39.84 | |
| RPE(m) | 0.09 | 0.135 | - | 0.125 | 0.126 | 0.107 | |
| RPE(°) | 0.119 | 0.167 | - | 0.134 | 0.091 | 0.134 | |
| 07 | 26.15 | 7.13 | 10.93 | 6.97 | 9.01 | 4.87 | |
| 15.11 | 2.38 | 5.15 | 4.79 | 6.78 | 2.82 | ||
| ATE | 48.25 | 22.41 | - | 30.25 | 39.32 | 13.99 | |
| RPE(m) | 0.359 | 0.056 | - | 0.063 | 0.06 | 0.055 | |
| RPE(°) | 0.928 | 0.068 | - | 0.16 | 0.129 | 0.168 | |
| 10 | RPE(°) | 31.99 | 10.07 | 11.9 | 14.17 | 14.02 | 10.91 |
| 9.06 | 4.91 | 2.84 | 4.29 | 4.2 | 3.50 | ||
| ATE | 229.19 | 78.28 | - | 126.45 | 97.3 | 64.08 | |
| RPE(m) | 0.486 | 0.103 | - | 0.122 | 0.121 | 0.111 | |
| RPE(°) | 0.824 | 0.113 | - | 0.205 | 0.147 | 0.198 | |
| Sequence | Number of Frames | Inference Runtime (s) |
|---|---|---|
| 03 | 801 | 4.6 |
| 04 | 271 | 3.6 |
| 05 | 2761 | 7.7 |
| 06 | 1101 | 4.2 |
| 07 | 1101 | 4.2 |
| 10 | 1201 | 4.3 |
| 00 | 08 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ATE | RPE(m) | RPE(°) | ATE | RPE(m) | RPE(°) | |||||
| Overlap | 2.91 | 1.34 | 56.33 | 0.017 | 0.210 | 4.2 | 1.84 | 149.32 | 0.017 | 0.166 |
| No-overlap | 9.51 | 4.37 | 241.77 | 0.020 | 0.215 | 9.74 | 4.21 | 321.38 | 0.020 | 0.171 |
| 09 | 10 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ATE | RPE(m) | RPE(°) | ATE | RPE(m) | RPE(°) | |||||
| Overlap | 13.77 | 4.47 | 111.2 | 0.15 | 0.215 | 13.3 | 5.82 | 80.64 | 0.129 | 0.267 |
| No-overlap | 15.58 | 5.49 | 208.56 | 0.138 | 0.201 | 23.03 | 9.57 | 266.30 | 0.121 | 0.244 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, X.; Li, Q.; Li, Q.; Ding, K.; Zhu, J. Exploiting Graph and Geodesic Distance Constraint for Deep Learning-Based Visual Odometry. Remote Sens. 2022, 14, 1854. https://doi.org/10.3390/rs14081854
Fang X, Li Q, Li Q, Ding K, Zhu J. Exploiting Graph and Geodesic Distance Constraint for Deep Learning-Based Visual Odometry. Remote Sensing. 2022; 14(8):1854. https://doi.org/10.3390/rs14081854
Chicago/Turabian StyleFang, Xu, Qing Li, Qingquan Li, Kai Ding, and Jiasong Zhu. 2022. "Exploiting Graph and Geodesic Distance Constraint for Deep Learning-Based Visual Odometry" Remote Sensing 14, no. 8: 1854. https://doi.org/10.3390/rs14081854
APA StyleFang, X., Li, Q., Li, Q., Ding, K., & Zhu, J. (2022). Exploiting Graph and Geodesic Distance Constraint for Deep Learning-Based Visual Odometry. Remote Sensing, 14(8), 1854. https://doi.org/10.3390/rs14081854