Abstract
Moderate Resolution Imaging Spectroradiometer (MODIS) snow cover product is one of the prevailing datasets for global snow monitoring, but cloud obscuration leads to the discontinuity of ground coverage information in spatial and temporal. To solve this problem, a novel spatial-temporal missing information reconstruction model based on U-Net with partial convolutions (PU-Net) is proposed to recover the cloud gaps in the MODIS Normalized Difference Snow Index (NDSI) products. Taking the Yellow River Source Region as a study case, in which the snow cover is characterized by shallow, fast-changing and complex heterogeneity, the MODIS NDSI product in the 2018–2019 snow season is reconstructed, and the reconstruction accuracy is validated with simulated cloud mask and in situ snow depth (SD) observations. The results show that under the simulated cloud mask scenario, the mean absolute error (MAE) of the reconstructed missing pixels is from 4.22% to 18.81% under different scenarios of the mean NDSI of the patch and the mask ratio of the applied mask, and the coefficient of determination (R) ranges from 0.76 to 0.94. The validation based on in situ SD observations at 10 sites shows good consistency, the overall accuracy is increased by 25.66% to 49.25% compared with the Aqua-Terra combined MODIS NDSI product, and its value exceeds 90% at 60% of observation stations.
1. Introduction
Snow cover, as an important component of the cryosphere, plays an important role in the global climate and heat budget [1,2,3]. High albedo and thermal insulation of snow surface changes energy balance of land surface, affecting global atmospheric circulation [4]. Moreover, snow cover is also a sensitive indicator of climate changes, which directly affects many physical and hydrological processes [5]. As an important freshwater supply, glaciers and snowmelt provides freshwater for about 17% of the world’s population, of which more than 600 million people are nourished by mountain meltwaters [6]. Agriculture and animal husbandry are also largely influenced by snow cover [7,8].
The development and advances in space information technologies enable satellite remote sensing to become an effective means of snow monitoring [9]. The Moderate Resolution Imaging Spectrometer (MODIS) sensor has been widely used in snow monitoring since the launch of Terra satellite in 1999 and Aqua satellite in 2002 [10,11]. Extensive studies have evaluated the quality of MODIS snow cover products over various regions of the world, and the results show that it has good qualified performance under clear sky conditions when compared with in situ observations and snow cover estimated from other higher-resolution remote sensing images [12,13,14,15].
However, the MODIS snow product is long suffered from cloud obscuration [11], which leads to the discontinuity in space and time and severely limits its application in the fields of hydrological cycle, climate change, etc. [16,17]. In order to derive cloud-free snow cover products, several methods have been developed to eliminate the cloud pixels in the MODIS snow cover products, which can be classified into spatial methods, temporal methods, spatial-temporal methods, and multi-source fusion methods [18]. Spatial methods assign the value of cloud pixels based on spatially selected non-cloudy pixels [19,20,21]. However, if the fraction of cloud cover is high, spatial methods always leads to unsatisfactory cloud removal effect [22]. Temporal methods such as Terra and Aqua combination [23,24], seasonal filter [25], and multi-day combination [26] recover cloudy pixels using information within a time window. Unluckily, the reconstruction accuracy in snow-transitional periods tends to be hampered since temporal methods assumes that the snow cover remains constant or experiences simple linear or non-linear changes in a given temporal interval [27]. The spatial-temporal methods are essentially successive or alternate combinations of spatial and temporal methods, which utilize their complementary advantages [28]. Multi-source fusion methods entail the optical, microwave, and/or in situ observations, which can completely remove all cloud contaminations, but the performance is severely affected by the spatial resolution, complementarity, and accuracy of the input data [29]. As reported by Wang et al. [30], the performance of multi-source fusion methods using MODIS and AMSR-E is more dependent on the accuracy of AMSR-E itself.
The cloud removal methods mentioned above aim classically at the MODIS collection 5 (C5) product, which provides the fraction snow cover (FSC) and the binary snow cover data. However, in 2016, the MODIS collection 6 (C6) product was published, in which only the Normalized Difference Snow Index (NDSI) snow cover data were provided. Therefore, it is urgent to develop new cloud removal methods based on the MODIS C6 product. Jing et al. [22] proposed a Gaussian-kernel-function-based two-stage fusion framework to eliminate cloud gaps in the MODIS NDSI product, and the accuracy had been validated over the Tibetan Plateau. Chen et al. [31] developed a spatial and temporal adaptive reflectance fusion model to generate cloud-free MODIS NDSI products. Their model was tested in Northeast China and proved to be effective in cloud removal. The above-mentioned approaches can directly recover NDSI without converting it to FSC in advance, but when the cloud fraction is high, the limited ground information can influence the accuracy of the predicted result.
Deep neural networks, which learn meaningful hidden representations and semantic priors in an end-to-end fashion, have been used in image inpainting in recent studies [32]. Several studies have applied deep neural networks to reconstruct missing pixels in satellite remote sensing products, such as soil moisture [33] and land surface temperature [34]. However, as far as we know, deep learning networks have not been explored in the reconstruction of missing information in snow cover products. This might be because, when compared with other surface variables such as land surface temperature and soil moisture, the spatial-temporal variation in snow cover is more complex, which is not only affected by environmental factors but also includes a series of complex physical and chemical processes of the snow cover itself. Convolutional neural network (CNN), which is one of the most popular deep learning algorithms, has shown strong power in image processing and inpainting [35]. However, traditional CNN cannot deal with images with missing regions directly, which needs pre-processing steps, such as the initial missing pixels with a fixed value [36] or through interpolation methods using the value of adjacent or nearby pixels [37], and this will inevitably introduce new error sources. Thus, his paper presents an innovative spatial and temporal information fusion framework for filling the cloud gaps in MODIS NDSI product based on U-Net, i.e., a type of CNN, with partial convolutions, which do not need any missing region initialization method and utilizes both spatial and temporal information of the ground.
The rest of this paper is organized as follows. Section 2 gives descriptions of our study area and the relevant data used in this study. The detailed model design and validation methodology are presented in Section 3. Section 4 gives the results of our model. The choice of time window and loss function is discussed in Section 5. Finally, the conclusions and directions for possible improvements are given in Section 6.
2. Study Area and Data
2.1. Study Area
The Qinghai–Tibetan Plateau is surrounded by the Earth’s highest mountains and is known as the roof of the world [38]. Studies have shown that the thermal and dynamical effects of its unique terrain directly or indirectly affect the atmospheric circulation and climate systems in the Northern Hemisphere [39,40,41]. The study area (Figure 1), i.e., the Yellow River Source Region (955326E–1032443E, 32931N–363333N), is located in the northeast of the Qinghai–Tibet Plateau, covering an area of about 1.36 × 10 km. Most of the study area is above 3000 m, and the elevation decreases from west to east, with the highest being 6212 m and the lowest being 1961 m. The study area consists of a variety of landforms such as mountains, basins, valleys, meadows, lakes, glaciers, and permafrost areas. Alpine vegetation is widely distributed in this region, such as alpine meadow, alpine swamp meadow, and alpine grassland, which accounts for more than 70% of the total area [42,43]. The study area has a drainage area of 123,700 km [44] and makes outstanding contributions to the water resources of the Yellow River Basin, among which snow melt water is an important water supply. The snow cover in study area is fast-changing and exhibits significant spatiotemporal heterogeneity [45]. The permanent snow cover and glaciers are mainly distributed in the northern Qilian Mountains, Bayankala, and southern A’nyêmaqên [46]. To sum up, the complex conditions of regional climate and underlying surface makes the snow cover in the study area highly heterogeneous and changes rapidly, which makes it difficult to be accurately estimated.
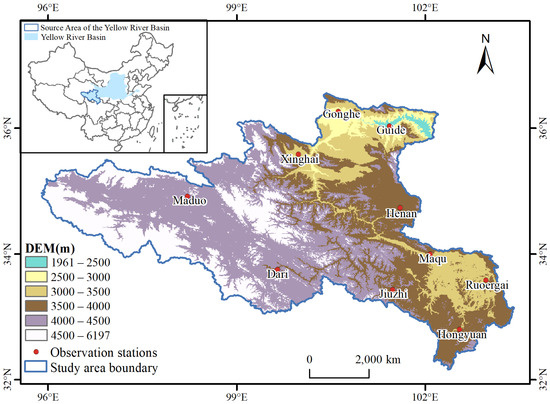
Figure 1.
Elevation of the Yellow River Source Region and position of meteorological stations.
2.2. Data
2.2.1. MODIS C6 Snow Cover Products
The MODIS C6 snow cover products (MOD10A1 and MYD10A1) are acquired from the Terra and Aqua satellites. Compared with previous versions, C6 has great improvements including better handling of confusion between cloud and snow, an improved atmospheric calibration and restoration of band 6 of Aqua [31]. The MODIS C6 snow cover products include raw NDSI data, NDSI snow cover, snow albedo, and quality control flags, among which the NDSI snow cover is used in this study. The NDSI snow cover data are coded as integers, which have valid pixels with values ranging from 0 to 100(%), as well invalid pixels indicating missing data, no decision, night, inland water, ocean, cloud, detector saturated, and fill. The tiling system of the MODIS C6 snow cover products are integerized sinusoidal grids with a total of 36 horizontal tiles and 18 vertical tiles. The spatial resolution is 500 m, and the temporal resolution is 1 day.
In this study, two tiles, i.e., tile horizontal 25 vertical 5 (h25v05) and horizontal 26 vertical 5 (h26v05), during the 2018–2019 snow season (1 November 2018 to 31 March 2019) were collected from NASA’s EOSDIS “Earthdata” (https://earthdata.nasa.gov/ accessed on 21 September 2021). First, two tiles were moisaicked to cover the entire study area. Second, the mosaic images were projected to the ellipsoid WGS84 geographic coordinates. After that, we reclassified all of the invalid pixels (i.e., missing data, no decision, night, inland water, ocean, cloud, detector saturated, and fill) as cloud cover and assigned a value of 250, while leaving the valid pixels unchanged.
2.2.2. Meteorological Snow Depth (SD) Data
Daily SD observations of 10 meteorological stations from 1 November 2018 to 31 March 2019 are collected from China Meteorological Data Service Centre (http://data.cma.cn accessed on 6 August 2021). The in situ SD was measured automatically at the station at 8 a.m. The locations of the stations are depicted in Figure 1.
3. Methodology
In this study, we built a U-Net with partial convolutions (PU-Net) which utilizes both spatial and temporal information to reconstruct the cloud gaps in the MODIS NDSI product. The following section gives descriptions on U-Net, partial convolution, our model structure, the model training procedure, as well as the validation methodology.
3.1. U-Net
U-Net, which stems from the so-called “fully convolutional network”, was first introduced by Ronneberger et al. [47] for biomedical image segmentation. In the original papaer, U-Net is expressed as an expansion of traditional CNN, which has a u-shaped architecture and consists of a contracting path followed with an expansion path, and do not have any fully connected layers. The contracting path consists of repeated convolutions followed by a rectified linear unit (ReLU) and a max pooling operation for downsampling. In the expansion path, every step includes an upsampling of the feature map, a 2 × 2 up convolution to halve the number of feature channels, a concatenation with corresponding feature map from the contracting path, and convolution operations followed by ReLU [47]. The structure of a U-Net, although not typical, can be found in Figure 2.
3.2. Partial Convolution
CNN has been widely used in image inpainting [36,37] and satellite imagery recovery [48] scenarios. However, the traditional convolution operation requires the input pixels to be all valid, which needs a ‘hole-initialization’ method to initialize the invalid pixels in the input images with appropriate values [32]. This preprocessing procedure introduces extra error sources. To deal with this negative effect, we use partial convolution layers [32] in our model to utilize only the information of valid pixels.
The partial convolution layer consists of a partial convolution operation and a mask update function. Different from the traditional convolution operation, partial convolution uses a binary mask matrix M to mark the invalid pixels. This mask matrix should have the same size with the input patches, and at each location, 1 means this pixel is valid and 0 stands for invalid. The partial convolution at every location can be expressed as:
where ⊙ denotes the element-wise multiply operation, X is the matrix of the input patch, 1 is the matrix with same shape as M and all elements being 1, W is the weights of the convolution filter, and b is the corresponding bias. The sum(1)/sum(M) is a scaling factor according to the valid pixel fraction. Obviously, the output of partial convolution operation only depends on the valid pixels.
After each partial convolution operation, the mask matrix M should be updated in the following way: If the convolution can generate its output using at least one valid input value, the mask value at this location is marked as valid. This procedure is expressed as:
and through the successive implementation of the partial convolution layers, the mask will eventually become all ones.
3.3. MODIS NDSI Gap-Filling Framework Based on PU-Net
3.3.1. Preprocessing for Gap-Filling
Prior to building our PU-Net reconstruction model, preprocessing methods for MODIS NDSI product can be applied to remove parts of the cloud gaps. This includes two procedures, namely, the Aqua–Terra combination method and Adjacent Temporal Filter (ATF). In the Aqua–Terra combination procedure, daily MODIS NDSI products from Aqua and Terra were combined and the priority was assigned to Terra, as validation results have shown it has better retrievals than Aqua [49]. ATF is a widely accepted temporal method for snow cover recovering, which rests on the assumption that the snow cover will persist on land surface for a certain period of time [28], and its accuracy has been confirmed by researchers through applying different option on composition days [25,50]. After Aqua–Terra combination and ATF, more snow information can be delivered to PU-Net for NDSI reconstruction. In this study, the Aqua–Terra combination and ATF method were carried out before PU-Net. However, using PU-Net itself directly is capable of reconstructing the NDSI for all gap pixels.
3.3.2. Gap-Filling Framework
A new MODIS NDSI missing pixel reconstruction model based on PU-Net is proposed in this study. The PU-Net was built through replacing all convolution layers with partial convolution layers in a traditional U-Net. Our U-Net consists of four encoder layers and four decoder layers, with skip-links between corresponding layers. Each encoder layer includes a partial convolution operation (PConv), a mask update operation, and a batch normalization operation. The kernel size of each partial convolution operation is 3 × 3, the stride is 2, the activation function is ReLU, and the optimizer used in our PU-Net is Adam (for readers not familiar with these terms, please refer to reference [51,52,53]). The detailed architecture of the proposed PU-Net is depicted in Figure 2.
If the current day is date T, the input of the proposed PU-Net is the spatiotemporal MODIS NDSI patches from date 3 to date T + 3 and the corresponding mask patches. The patch size in this study was 64 × 64 (which means a region of 32 km × 32 km), so the shapes of the input NDSI and input mask were all 64 × 64 × 7. The model output was the reconstructed NDSI patch at date T, with shape of 64 × 64.
The loss function used in our model consisted of three parts: the ‘inside-mask’ loss , the ‘outside-mask’ loss , and the mask boundary loss .
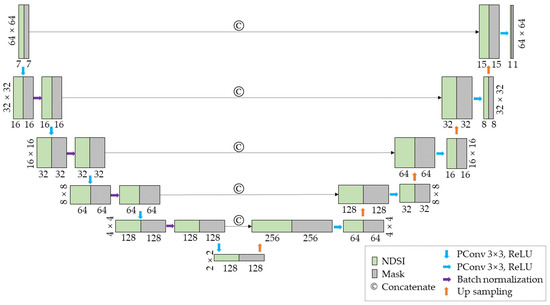
Figure 2.
The structure of proposed PU-Net NDSI reconstruction model.
The ‘inside-mask’ loss refers to the L2 paradigm penalty for the difference between the reconstructed NDSI gap pixels and that of the reference truth values inside a patch. This is the major criterion for evaluation because our ultimate goal is to reconstruct the NDSI value of gap pixels. However, the prediction of our NDSI reconstruction model should also not disturb the original valid pixels. Thus, the ‘outside-mask’ loss’ gives the model this restriction, which is the L2 paradigm penalty for the disturbance of valid pixels in a patch:
The final part of the loss function introduces smoothing factor to the prediction at boundaries between valid and invalid pixels. The is expressed as:
where and are adjacent pixels inside and outside a gap area within a patch, respectively, P is the one-pixel margin inside masked region, Q is the one-pixel margin outside masked region, and N is the total number of pixels inside P and Q.
The total loss is the linearly weighted combination of , , and with their corresponding weights. The value of , , and are 10, 1, and 0.1, respectively, which are determined through the trial-and-error method:
3.4. Model Training and Application
In the training procedure, large numbers of MODIS NDSI patches need to be generated to train the reconstruction model. The generation of training data included two steps: patch selection and mask simulation. The purpose of the patch selection step was to pick out complete MODIS NDSI patches as the reference truth scenes, which were later also applied with a simulated mask in the mask simulation step. In this way, we obtained both the masked incomplete patches and their corresponding unmasked complete patches, which were used as training samples for the proposed model. The flow chart of the proposed PU-Net is shown in Figure 3. In this study, the time window for the spatial-temporal NDSI patch group was 7 days (from date 3 to date T + 3), thus i was set to 3.
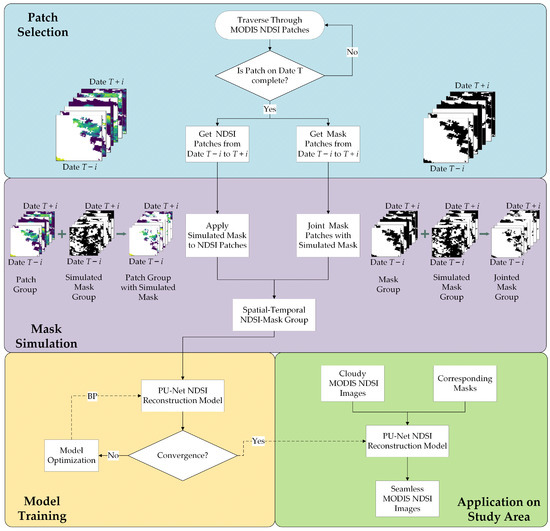
Figure 3.
Flow chart of proposed PU-Net NDSI reconstruction model.
In the patch selection step, we traversed the MODIS NDSI image over the entire 2018–2019 snow season in the study area to obtain the complete NDSI patches. After a complete patch on date T was found, we picked out the NDSI patches at this corresponding location from date 3 to date T + 3 to form the spatial-temporal NDSI patch group. Moreover, the corresponding spatial-temporal mask group between date 3 to date T + 3 of this spatial-temporal NDSI patch group was also generated according to its pixel value. After traversing from the 2018–2019 snow season, 2695 complete patches with mean NDSI value no less than 10, 500 complete patches with mean NDSI value between 0 to 10, and 500 complete patches with mean NDSI equals to 0 were selected to form the training set. The purpose of this was to ensure that all types of snow cover pixels were included in the training sample and that all types were balanced as much as possible. In total, 3695 spatial-temporal NDSI patch groups along with their corresponding spatial-temporal mask patch groups are selected after the patch selection step. In this study, the patch size was 64 × 64 for both NDSI and mask patches.
In the mask simulation step, we also traversed the MODIS NSDI images of the entire study area and selected incomplete patches with a size of 64 × 64 as mask patches. From these mask patches, we randomly chose 1000 with mask ratio from 0 to 0.1, …, and 0.9 to 1.0, respectively. After a mask patch on date T was chosen, the mask patches at this corresponding location from date 3 to date T + 3 were also generated and picked out. After this, we obtained 10,000 mask patches groups in total for mask simulation. These simulated mask groups were randomly selected and applied to the spatial-temporal NDSI patch groups, and were jointed with the corresponding mask groups (Figure 3). After finishing mask simulation, the spatial-temporal mask patch groups and NDSI patch groups corresponding to date 3 to date T + 3 for the target patch groups on the given date T were generated.
In this study, the proposed PU-Net model for MODIS NDSI missing information reconstruction is built on Keras-Tensorflow platform. The batch size was set to 40 for each training step. The training epoch was 200, and the learning rate was set to 0.0002. For readers not familiar with these terms, their descriptions can be found in reference [54].
3.5. Validation Methodology
To validate the reconstruction accuracy of our model, the most appropriate approach is to use the meteorological station observed SD as ground truth. However, the SD observed by meteorological stations cannot depict the snow information over the entire study area because most stations locate in valleys with low elevation (Figure 1), which results in the sparse distribution of observed SD, and there is no record for some high-mountain, inaccessible regions. Thus, in addition to the validation with in situ SD observation, another validation methodology based on simulated cloud masks was adopted. The cloud masks from some cloudy MODIS NDSI images are extracted and applied to the cloud-free MODIS NDSI images, which is regarded as the ground truth [23,28].
3.5.1. Simulated Cloud Mask
To validate our model accuracy on patch scale, similar to the generation of training dataset in Section 3.4, we generated the validation patch dataset which consisted of 34,491 spatial-temporal NDSI patch groups from date 3 to T + 3 (where the patch on date T is complete and 2449 with mean NDSI larger than 10 on date T, 500 from 0 to 10 on date T, and 500 equal to 0 on date T), as well as their corresponding spatial-temporal mask patch groups. Similarly, the 10,000 randomly chosen mask patches groups (1000 with mask ratio from 0 to 0.1, …, and 0.9 to 1, respectively) in Section 3.4 were randomly selected and applied to the validation patches. The training dataset and the validation dataset were independent and have no intersections.
To testify the accuracy of our model on the entire study region, the MODIS NDSI images after 5-day ATF from date to date + 3 over the entire study area were chosen to be applied with simulated mask, where the was selected to have no or least cloud cover among the 2018–2019 snow season. The corresponding simulated mask was extracted from the 5-day ATF-ed MODIS NDSI images at from date to date + 3, where the was at the day as of the previous year, i.e., .
The performance evaluation criteria for simulated mask scenario are the mean absolute error (MAE) and coefficient of determination (R) over the masked region, which is defined as:
where M is the mask matrix, 1 is the matrix with same shape as M and all elements being 1, is the reconstructed MODIS NDSI, is the Aqua–Terra combined MODIS NDSI (ground truth), is the reconstructed NDSI at the i-th cloud pixel, is the ground truth NDSI at corresponding pixel, is the standard deviation of the reconstructed NDSI over the masked region, and is the standard deviation of the ground truth NDSI over the masked region.
3.5.2. Validation with In-Situ SD Observation
The Aqua–Terra combined NDSI, MODIS NDSI after 5-day ATF, and PU-Net reconstructed MODIS NDSI are compared with the in situ observed SD at 10 meteorological stations among the Yellow River Source Region (Figure 1). The validation strategy of the confusion matrix [55] (Table 1) were applied to evaluate our results.

Table 1.
Confusion matrix for validating MODIS NDSI with in situ SD observations.
In the table, pixels are classified into four categories: correctly rejected, omission error, commission error, and correctly hit. Their pixels numbers are represented by a, b, c, and d, respectively. e and f are the number of pixels regarded as cloud in MODIS NDSI images when the meteorological station considers no snow and snow. and are thresholds for SD and NDSI to distinguish a pixel between covered by snow or not. In our study, and are set to 3 and 40%, respectively.
Four validation indices based on confusion matrix are expressed as follows:
where OA is the overall accuracy, which stands for the partition of MODIS pixels being correctly classified. MU and MO indicate number of snow events which are underestimated and overestimated, respectively. In perfect condition, the validation indices should be OA = 1, MU = 0, and MO = 0.
4. Experiment Results
In this section, we give the results of PU-Net reconstructed NDSI and its validation during the 2018–2019 snow season. The results are shown in the following three aspects: visual results of reconstruction, validation with simulated mask, and validation with in situ SD observations.
4.1. Visual Results of Reconstruction
4.1.1. Results on Patches
To directly show the visual reconstruction results of PU-Net, several NDSI patches from validation dataset are chosen to be reconstructed by our model. The applied simulated mask, the masked Aqua–Terra combined NDSI patch, the PU-Net reconstructed NDSI patch, the complete Aqua–Terra combined NDSI patch (reference truth), and the elevation patch from digital elevation model (DEM) are presented in Figure 4. The applied masks have mask ratio ranges from 11% to 45%, which is in accordance with the cloud fraction of the Aqua–Terra combined MODIS NDSI data in the study area.
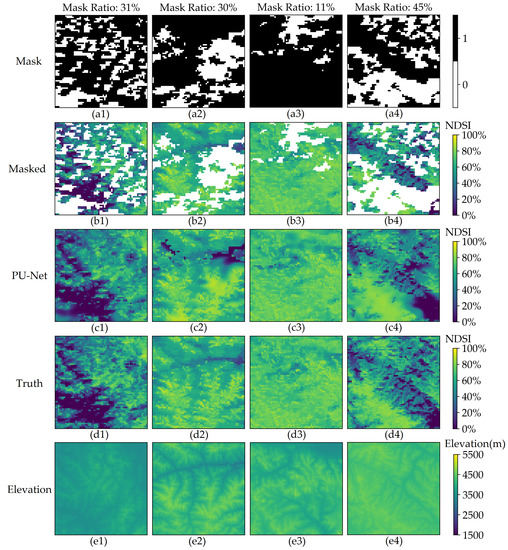
Figure 4.
Examples of reconstruction results on single patches randomly chosen from 2018–2019 snow season. The applied mask (Mask, (a1–a4)), masked NDSI patch (Masked, (b1–b4)), PU-Net reconstructed NDSI patch (PU-Net, (c1–c4)), reference truth NDSI patch (Truth, (d1–d4)), and the corresponding elevation patch (Elevation, (e1–e4)) are presented.
From Figure 4, we can clearly see that PU-Net can completely remove all cloud gaps in the NDSI patches. The reconstructed patches can well preserve the spatial distribution of snow on the reference truth NDSI patches, and the distribution of reconstructed pixels have spatial continuity with merely no abrupt changes. Compared with the elevation data, the reconstructed patches can restore the shape of ridges and mountains well, which proves that the spatial distribution of snow on the reconstructed patches is reasonable. The difference between reconstructed and reference truth NDSI mainly located in the area with large gradients in NDSI. PU-Net tends to smoothen these change processes. This is because the strong spatial heterogeneity of snow makes drastic and frequent changes in NDSI difficult to predict. In addition, the introduction of mask boundary loss also adds a smoothing term to the prediction.
4.1.2. Results on Study Area
To further show the visual results of our reconstruction model on entire study area, the Aqua NDSI image, Terra NDSI image, Aqua–Terra combined NDSI image, MODIS NDSI image after 5-day ATF, and PU-Net reconstructed MODIS NDSI image at 6 March 2019 are presented, which is shown in Figure 5. The cloud fractions of Aqua NDSI image, Terra NDSI image, Aqua–Terra combined NDSI image, MODIS NDSI image after 5-day ATF, and the PU-Net reconstructed NDSI image are 95.7%, 91.4%, 88.7%, 38.9%, and 0%, respectively. The ATF method can remove parts of the cloud gaps, but it still left us with large areas of cloud in the middle of the study area. Our reconstruction model can remove all cloud gaps, and the reconstructed NDSI shows good continuity. From Figure 5, it is clear that PU-Net can be applied to areas with a large scale. Compared with Figure 1, the reconstructed snow cover mainly distributes in high-altitude areas and mountain ridges, which is consistent with the expected distribution characteristics of snow. These results prove that the spatial distribution of NDSI reconstructed by our model is reasonable.
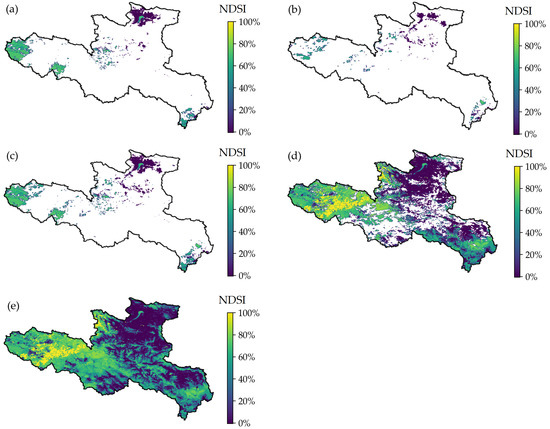
Figure 5.
NDSI over the study area at 6 March 2019. Subplots are (a) Aqua NDSI, (b) Terra NDSI, (c) Aqua–Terra combined NDSI, (d) NDSI after 5-day ATF, and (e) reconstructed NDSI from PU-Net.
4.2. Validation with Simulated Mask
4.2.1. Validation on Patches
To evaluate the reconstruction accuracy, all patches in the validation dataset with date from 1 November 2018 to 31 March 2019 are used for validation. Simulated masks are randomly selected to be applied to these patches, and the MAE, as well as the R, of the masked region between the reconstructed patch and the corresponding complete Aqua–Terra combined patch are collected. The results are categorized according to the mask ratio of the simulated mask, and the mean NDSI of the complete Aqua–Terra combined patch, which are listed in Table 2 and Table 3.

Table 2.
MAE of the masked region between reconstructed NDSI patch and corresponding complete NDSI patch during the 2018–2019 snow season. The results are categorized according to the mask ratio of applied mask and the mean NDSI of the corresponding complete NDSI patch.

Table 3.
R of the masked region between reconstructed NDSI patch and corresponding complete NDSI patch during the 2018–2019 snow season. Results are categorized according to the mask ratio of applied mask and the mean NDSI of the complete Aqua–Terra combined NDSI patch.
Table 2 indicates the following: (1) Generally, PU-Net show good performance when the mean NDSI of the complete Aqua–Terra combined patch is less than 50%, where the MAE of the reconstructed regions are kept below 13%. (2) With the increase in patch mean NDSI, the MAE of the reconstructed area first increases then decreases. Our model performs slightly worse when the mean NDSI is from 50% to 70%, but the MAE under this condition could be limited to no more than 18.81%. When the mean NDSI is larger than 70%, the MAE of the reconstructed region decreases to values between 9.59% and 13.53%. This is because when the mean NDSI is close to 100%, the snow cover on this patch is more likely to be dense and stable, which is easier to be reconstructed. On the other hand, when the mean NDSI is around 60%, the heterogeneity of snow cover is more obvious, thus affecting the accuracy of our model. (3) The reconstruction accuracy slightly decreases with the increase in the mask ratio. This is reasonable because the higher the mask ratio, the less spatial information we can obtain directly from the patch on date T, which means the model has to rely more on the spatial and temporal information from the patch on date 3 to date T + 3 (exclude date T) to reconstruct the masked area.
The results of R in Table 3 also indicate that PU-Net has good reconstruction accuracy. (1) Overall, the R is larger than 0.8 when the mean NDSI of the complete Aqua–Terra combined patch is less than 50% or larger than 70%. Particularly, when the mean NDSI of the complete Aqua–Terra combined patch is between 0 and 10%, the R exceeds 90%. These show that the reconstructed NDSI of PU-Net has good consistency with the Aqua–Terra combined MODIS NDSI. (2) When the mean NDSI of the complete Aqua–Terra combined patch is fixed, our model performs best when the mask ratio is under 10%. This is because the less area that is being masked, the more available snow information can our model have. With the increase in the mask ratio, the R has no significant increasing or decreasing trend, which indicates that our model can make use of temporal information on date 3 to date T + 3 (exclude date T); thus, it is not very sensitive to the mask ratio. (3) Similar to the results of the MAE, the R is better for both small and large values of NDSI than for the intermediate values, which indicates our model gives more reliable reconstruction results when the patch shows less snow heterogeneity.
4.2.2. Validation on Entire Study Area
To examine our reconstruction performance under the scenario of simulated mask over the entire study area, we choose the MODIS NDSI products after 5-day ATF on 10 October 2018, 29 November 2018, and 30 March 2019 as ground truth because the MODIS NDSI products after 5-day ATF on these days have no or the least clouds among the 2018–2019 snow season. The mask ratios for the MODIS NDSI products after 5-day ATF on these 3 dates are 0.27%, 0.34%, and 0%, respectively. To simulate the real cloud state over the entire study area, the cloud masks on 10 October 2017, 29 November 2017, and 30 March 2018 are extracted for mask simulation, and their mask ratios are 29.0%, 40.7%, and 18.4%, respectively, which can represent the cloud fraction of the MODIS NDSI product after 5-day ATF. After reconstructed by PU-Net reconstruction model, the output MODIS NDSI gap-filled images are compared to the unmasked MODIS NDSI at the corresponding date, with the MAE and R of the masked region being calculated. The results are shown in Table 4 and Table 5.

Table 4.
MAE of reconstructed MODIS NDSI at chosen date with simulated mask.

Table 5.
R of reconstructed MODIS NDSI at chosen date with simulated mask.
From Table 4, we can see that the MAE of the reconstructed cloud regions is less than 15% for all three simulated mask scenarios. Our model performs best on 30 March 2019, with an MAE of 12.106%. This is partly because the mask on 30 March 2018 has the smallest mask ratio compared to the others. The reconstruction accuracy for 27 November 2018 is a little worse, but the MAE can be still kept less than 15%. This is because the cloud mask on 27 November 2017 forms large blocks and gathers in the east side of the study area, where the elevation is lower and the snow cover changes fast. The MAE of the reconstructed NDSI on 10 October 2018 is 12.906%. The R in Table 5 show similar characteristics, with 30 March 2019 having the best accuracy and 27 November 2018 having the worst. Overall, the R is larger than 0.8 on all 3 days, which also indicates the reconstructed NDSI is consistent with the MODIS NDSI product.
To give a direct visual result, Figure 6 shows the reconstruction performance on 30 March 2019 with a simulated mask on 30 March 2018. From the figure, we can see that PU-Net can completely remove all clouds and gaps in the MODIS NDSI product, and the snow patterns under cloud gaps can be successfully recovered. In addition, the areas with high NDSI corresponds well to the regions with elevation higher than 4500 m in Figure 1. Subplot (e) in Figure 6 depicts the PU-Net reconstructed NDSI minus NDSI after 5-day ATF (Diff), from which we can see the absolute difference is kept below 10% over most reconstructed regions. In the regions to the west border of the study area, compared with the NDSI after 5-day ATF, PU-Net tends to overestimate NDSI. Since these regions are located in mountainous areas with elevation higher than 4500 m (Figure 1), it is reasonable for PU-Net to fill these regions with higher NDSI values.
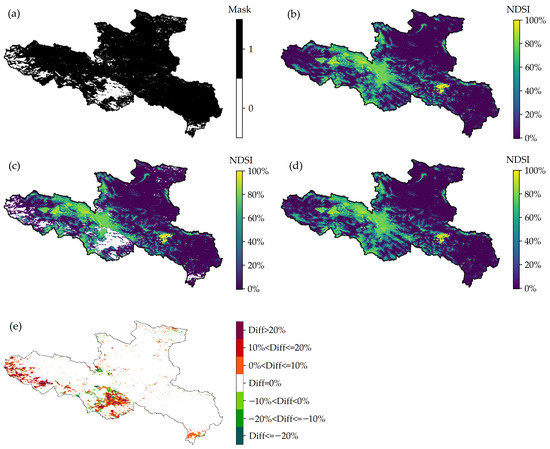
Figure 6.
Reconstruction performance on 30 March 2019 with simulated mask on 30 March 2018. The subplots correspond to (a) mask, (b) NDSI after 5-day ATF, (c) masked NDSI, (d) PU-Net reconstructed NDSI, and (e) PU-Net reconstructed NDSI minus NDSI after 5-day ATF (Diff).
4.3. Validation with In Situ SD Observation
To further evaluate the performance of PU-Net, we validate the reconstructed NDSI with in situ observed SD of 10 meteorological stations among the Yellow River Source Region. Table 6 lists the results of three performance quantitative validation indices over 10 meteorological stations during the 2018–2019 snow season.

Table 6.
Validation indices for MODIS NDSI and observed SD from meteorological stations. Results using Aqua–Terra combined MODIS NDSI product (MYOD), MODIS NDSI product after 5-day ATF (ATF), and MODIS NDSI reconstructed by our model (PU-Net) are listed.
From Table 6, we can see that compared with the Aqua–Terra combined NDSI product, the NDSI product generated by 5-day ATF has significantly higher OA, but the MU is slightly increased. This indicates that the ATF method can remove part of cloud gaps with good reconstruction accuracy. After being reconstructed by PU-Net, the OA witnesses an obvious increase at all 10 sites, while the value of MU and MO could be reduced, compared with the NDSI product generated by 5-day ATF. Thus, it is clear that the pixels reconstructed by PU-Net have good accuracy. At the Gonghe, Guide, Maduo, Henan, Ruoergai, and Hongyuan sites, the OA of our final reconstructed NDSI is higher than 90%, which increases up to 49.25% compared to the Aqua–Terra combined MODIS NDSI product (at site Maduo). Even when the Aqua–Terra combined MODIS NDSI product is not very consistent with the observed SD (at site Maqu), our reconstruction model could still improve the OA to 79.17%.
Figure 7 gives the reconstructed MODIS NDSI as well as the observed SD at site Maqu and Maduo. It can be seen that, affected by cloud gaps, for both sites, the Aqua–Terra combined NDSI (in red stars) has no valid NDSI on many dates (the dates of green and blue stars). After applying the 5-day ATF method, the NDSI on some dates can be recovered (in green stars), but there are still many remaining dates that cannot be restored (the date of the blue stars). Finally, through PU-Net, the NDSIs of the dates where the blue stars are located can be successfully restored, and the temporal variation in NDSI during the whole snow season can be completely obtained. Maqu and Maduo represent two different types of snow cover: the transient, fast changing snow cover and the continuous snow cover through the whole snow season. The reconstructed NDSI at Maqu shows the characteristics of violent oscillation, which is consistent with the observed SD. Maduo has a non-zero SD observation during the whole snow season, and the reconstructed NDSI remains stable between 60% and 80%. To sum up, Figure 7 show that at both Maqu and Maduo, the reconstructed NDSI has good consistency with the observed SD, which indicates that our model has good reconstruction accuracy.
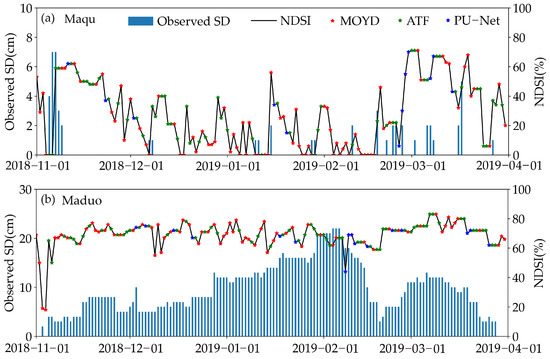
Figure 7.
Reconstructed NDSI and observed SD at site (a) Maqu and (b) Maduo. The Aqua–Terra combined NDSI (MOYD) points are drawn in red stars, the NDSI points recovered by 5-day ATF method (ATF) are drawn in green stars, and the NDSI points reconstructed by PU-Net (PU-Net) are drawn in blue stars. Black line shows the final reconstructed NDSI. The observed SD are shown with blue bars.
5. Discussion
5.1. The Impact of Time Window on Reconstruction Accuracy
In former parts of this paper, we use the NDSI patches from date 3 to date T + 3 to generate the spatial-temporal NDSI patch group at date T; thus, our time window is 7 days. However, since the snow cover in the Yellow River Source Region has strong spatial-temporal heterogeneity, its characteristics of fast-changing requires us to be very careful in the selection of time window. On the one hand, a longer time window captures more temporal information, but it may also introduce a large amount of misleading information inconsistent with the actual situation, i.e., snow information on a non-snow pixel and vice versa. On the other hand, as the time window shortens, the amount of misleading information could be decreased, but a too short time window may also lead to the fact that the temporal information is not effectively used. Thus, an appropriate time window should be considered.
In this section, we test the reconstruction accuracy under 3 time window options: 5 days (from 2 to T + 2), 7 days (from 3 to T + 3), and 9 days (from 4 to T + 4). For each time window option, MAE of the masked region between reconstructed NDSI patch and reference truth Aqua–Terra combined NDSI patch during the 2018–2019 snow season are calculated and collected, which are shown in Figure 8. It is clear that among the three different time window scenarios, the results from time window 7 days are the best. The results from time window at 5 days are always the worst, which indicates that the too-small time window cannot obtain enough snow information for reconstruction. The option with a time window at 9 days can generate some better results when the mean NDSI of the patch is larger than 60%, but overall, it underperforms in the option with the time window at 7 days. This is partly because when mean NDSI is high, the snow on this patch is more likely to be stable and last for a longer time. Therefore, a larger time window can better capture this information. On the other hand, when there is no snow or the snow cover is unstable, a too-large time window will introduce more misleading information and results in larger error, so the overall accuracy of 9-day time window is not very satisfactory. The results show that too-small or too-large time window will all lead to lower reconstruction accuracy and the performance under the option of a 7-day time window is relatively better. Thus, the final setting of the time window in our PU-Net is 7 days. It should be noted that the setting of the time window is dependent on the inherent characteristics of snow cover and cloudiness of the study area; thus, for other regions, the time window should be reconsidered, i.e., persistent snow cover and persistent cloudiness likely favors the use of a longer time window (and vice versa).
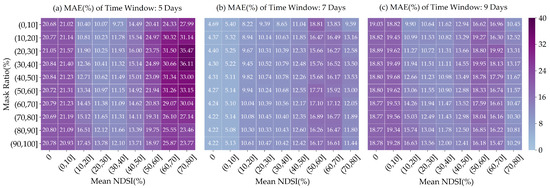
Figure 8.
MAE between reconstructed NDSI value and reference true value of the masked pixels during the 2018–2019 snow season for (a) 5-day time windows, (b) 7-day time windows, and (c) 9-day time windows.
5.2. The Impact of Loss Function on Reconstruction Accuracy
The loss function controls the optimization of the learning parameters in the back propagation step, thus is crucial to the performance of our reconstruction model. In Section 3.3, we introduce the loss function in our model as the combination of L2 paradigm penalty inside mask, L2 paradigm penalty outside mask, and mask boundary loss. In most data reconstruction or regression approaches based on deep learning, the L1 or L2 penalty is employed in the loss function, such as image inpainting for irregular holes [32], satellite product retrieval [56], and the reconstruction of soil moisture [33]. Thus, which one is more suitable for our model should be discussed. The mask boundary loss introduces smooth factors into the loss function, which gives the reconstructed NDSI a better spatial continuity and less sudden changes. However, this loss factor is seldom used in the reconstruction of snow products. Thus, the impact of mask boundary loss on the reconstruction accuracy is also discussed.
In this section, we present four loss functions with different combinations:
- : L1 penalty with mask boundary loss;
- : L1 penalty without mask boundary loss;
- : L2 penalty with mask boundary loss;
- : L2 penalty without mask boundary loss.
Their expressions are listed as follows. The values of , , and are set equal to the same setting in Section 3.3, and the loss function used in Section 3.3 is the following :
where
Similarly, to compare the performance of the reconstruction model itself, we apply the evaluation on patches of the 2018–2019 snow season with simulated mask, which is described in Section 4.2. The MAE of the reconstructed MODIS NDSI using different loss functions are listed in Figure 9.
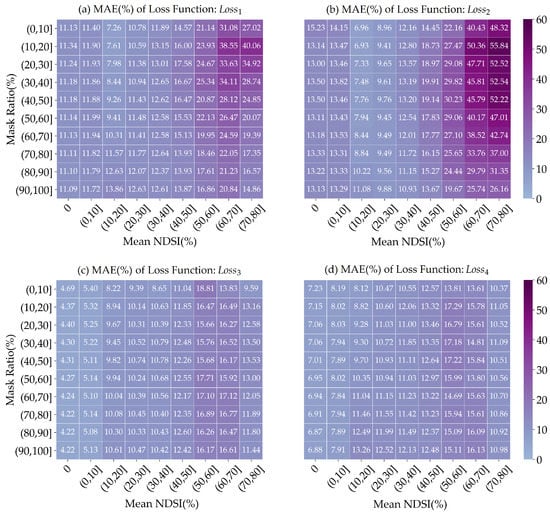
Figure 9.
MAE between reconstructed NDSI value and reference true value of the masked pixels during the 2018–2019 snow season for (a) : L1 penalty with mask boundary loss, (b) : L1 penalty without mask boundary loss, (c) : L2 penalty with mask boundary loss, and (d) : L2 penalty without mask boundary loss.
It is clear that the MAE under loss function and is significantly larger than that of and , which indicates that the L2 penalty is more suitable for our PU-Net model. The reason for this might be that the L2 loss function is more sensitive than the L1 loss function to outliers in the estimation. Since our goal is to reconstruct NDSI, we do not want the predicted pixels to have too large differences with the target, and more punitive losses should be given to these kinds of predictions. Thus, the L2 paradigm loss suits our PU-Net model better. As for the mask boundary loss, obviously, the MAE under loss function and is smaller than that of and , respectively, which shows that the introduction of the mask boundary loss can effectively improve the reconstruction accuracy. When the mean NDSI of the patch is larger than 50, the loss function outperforms under certain conditions of the mask ratio, but overall, the performance of is better than . Thus, the final loss function chosen for our model is , as described in Section 3.3.
6. Conclusions
The MODIS NDSI product suffers from a large percentage of cloud contamination, which is the main limitation to the wide use of this product. In addition, traditional deep learning methods for image recovery cannot solve the problem of invalid regions without ’hole-initialization’ methods. Thus, to address the temporal discontinuity and spatial incompleteness, we proposed a novel spatial-temporal NDSI reconstruction model based on U-Net with partial convolutions, namely, PU-Net. To evaluate the accuracy of PU-Net reconstructed NDSI, (1) visual results of reconstruction, (2) validation with simulated mask, and (3) validation with in situ SD observations are presented. The determination of the time window for our reconstruction model as well as the appropriate loss function are also discussed. The validation results show that the reconstructed NDSI from our model show high accuracy and reliability through validation with simulated mask and has good consistency with in situ observations.
Although the proposed PU-Net reconstruction model performs well, there are still limitations and drawbacks that need to be improved. Possible improvement could be achieved through (1) introducing auxiliary information into the model, such as terrain, land use, surface temperature, etc.; (2) adaptively selecting time windows according to the characteristics of the snow cover; and (3) further optimizing the model’s structure and parameters. This work could be further applied to other satellite observations other than snow cover, such as land surface temperature and vegetation fraction.
Author Contributions
D.X. and J.H. conceived and designed the experiments; D.X. performed the experiments and wrote the paper; D.X. and J.H. analyzed the data; C.H. and W.Z. contributed to discussions and revisions. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the National Natural Science Foundation of China (Grant No. 42130113, 41971326, and 41871251) and the Basic Research Innovative Groups of Gansu province, China (Grant 21JR7RA068).
Data Availability Statement
The data that support the findings of this study are available from the website given in the manuscript.
Acknowledgments
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Dietz, A.J.; Kuenzer, C.; Gessner, U.; Dech, S. Remote sensing of snow—A review of available methods. Int. J. Remote Sens. 2012, 33, 4094–4134. [Google Scholar] [CrossRef]
- Robinson, D.A.; Dewey, K.F.; Heim, R.R., Jr. Global snow cover monitoring: An update. Bull. Am. Meteorol. Soc. 1993, 74, 1689–1696. [Google Scholar] [CrossRef] [Green Version]
- Brown, R.D. Northern Hemisphere snow cover variability and change, 1915–1997. J. Clim. 2000, 13, 2339–2355. [Google Scholar] [CrossRef]
- Brown, R.D.; Mote, P.W. The response of Northern Hemisphere snow cover to a changing climate. J. Clim. 2009, 22, 2124–2145. [Google Scholar] [CrossRef]
- Robock, A. The seasonal cycle of snow cover, sea ice and surface albedo. Mon. Weather. Rev. 1980, 108, 267–285. [Google Scholar] [CrossRef]
- Barnett, T.P.; Adam, J.C.; Lettenmaier, D.P. Potential impacts of a warming climate on water availability in snow-dominated regions. Nature 2005, 438, 303–309. [Google Scholar] [CrossRef]
- Wang, W.; Liang, T.; Huang, X.; Feng, Q.; Xie, H.; Liu, X.; Chen, M.; Wang, X. Early warning of snow-caused disasters in pastoral areas on the Tibetan Plateau. Nat. Hazards Earth Syst. Sci. 2013, 13, 1411–1425. [Google Scholar] [CrossRef]
- Mijinyawa, Y.; Dlamini, S.S. Impact Assessment of Water Scarcity at Somntongo in the Lowveld Region of Swaziland. Sci. Res. Essays 2008, 3, 61. [Google Scholar]
- Hall, D. Remote Sensing of Ice and Snow; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Hall, D.K.; Riggs, G.A.; Salomonson, V.V.; DiGirolamo, N.E.; Bayr, K.J. MODIS snow-cover products. Remote Sens. Environ. 2002, 83, 181–194. [Google Scholar] [CrossRef] [Green Version]
- Hall, D.K.; Riggs, G.A. Accuracy assessment of the MODIS snow products. Hydrol. Process. Int. J. 2007, 21, 1534–1547. [Google Scholar] [CrossRef]
- Parajka, J.; Blöschl, G. Validation of MODIS snow cover images over Austria. Hydrol. Earth Syst. Sci. 2006, 10, 679–689. [Google Scholar] [CrossRef] [Green Version]
- Huang, X.; Liang, T.; Zhang, X.; Guo, Z. Validation of MODIS snow cover products using Landsat and ground measurements during the 2001–2005 snow seasons over northern Xinjiang, China. Int. J. Remote Sens. 2011, 32, 133–152. [Google Scholar] [CrossRef]
- Klein, A.G.; Barnett, A.C. Validation of daily MODIS snow cover maps of the Upper Rio Grande River Basin for the 2000–2001 snow year. Remote Sens. Environ. 2003, 86, 162–176. [Google Scholar] [CrossRef]
- Flueraru, C.; Stancalie, G.; Craciunescu, V.; Savin, E. A validation of MODIS snowcover products in Romania: Challenges and future directions. Trans. GIS 2007, 11, 927–941. [Google Scholar] [CrossRef]
- Ciancia, E.; Coviello, I.; Di Polito, C.; Lacava, T.; Pergola, N.; Satriano, V.; Tramutoli, V. Investigating the chlorophyll-a variability in the Gulf of Taranto (North-western Ionian Sea) by a multi-temporal analysis of MODIS-Aqua Level 3/Level 2 data. Cont. Shelf Res. 2018, 155, 34–44. [Google Scholar] [CrossRef]
- Li, X.; Shen, H.; Zhang, L.; Zhang, H.; Yuan, Q.; Yang, G. Recovering quantitative remote sensing products contaminated by thick clouds and shadows using multitemporal dictionary learning. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7086–7098. [Google Scholar]
- Li, X.; Jing, Y.; Shen, H.; Zhang, L. The recent developments in cloud removal approaches of MODIS snow cover product. Hydrol. Earth Syst. Sci. 2019, 23, 2401–2416. [Google Scholar] [CrossRef] [Green Version]
- Tong, J.; Déry, S.; Jackson, P. Topographic control of snow distribution in an alpine watershed of western Canada inferred from spatially-filtered MODIS snow products. Hydrol. Earth Syst. Sci. 2009, 13, 319–326. [Google Scholar] [CrossRef] [Green Version]
- Parajka, J.; Pepe, M.; Rampini, A.; Rossi, S.; Blöschl, G. A regional snow-line method for estimating snow cover from MODIS during cloud cover. J. Hydrol. 2010, 381, 203–212. [Google Scholar] [CrossRef]
- López-Burgos, V.; Gupta, H.V.; Clark, M. Reducing cloud obscuration of MODIS snow cover area products by combining spatio-temporal techniques with a probability of snow approach. Hydrol. Earth Syst. Sci. 2013, 17, 1809–1823. [Google Scholar] [CrossRef] [Green Version]
- Jing, Y.; Shen, H.; Li, X.; Guan, X. A two-stage fusion framework to generate a spatio–temporally continuous MODIS NDSI product over the Tibetan Plateau. Remote Sens. 2019, 11, 2261. [Google Scholar] [CrossRef] [Green Version]
- Parajka, J.; Blöschl, G. Spatio-temporal combination of MODIS images–potential for snow cover mapping. Water Resour. Res. 2008, 44, 1–13. [Google Scholar] [CrossRef]
- Chen, S.; Yang, Q.; Xie, H.; Zhang, H.; Lu, P.; Zhou, C. Spatiotemporal variations of snow cover in northeast China based on flexible multiday combinations of moderate resolution imaging spectroradiometer snow cover products. J. Appl. Remote Sens. 2014, 8, 084685. [Google Scholar] [CrossRef]
- Paudel, K.P.; Andersen, P. Monitoring snow cover variability in an agropastoral area in the Trans Himalayan region of Nepal using MODIS data with improved cloud removal methodology. Remote Sens. Environ. 2011, 115, 1234–1246. [Google Scholar] [CrossRef]
- Wang, X.; Zheng, H.; Chen, Y.; Liu, H.; Liu, L.; Huang, H.; Liu, K. Mapping snow cover variations using a MODIS daily cloud-free snow cover product in northeast China. J. Appl. Remote Sens. 2014, 8, 084681. [Google Scholar] [CrossRef] [Green Version]
- Gao, Y.; Xie, H.; Yao, T.; Xue, C. Integrated assessment on multi-temporal and multi-sensor combinations for reducing cloud obscuration of MODIS snow cover products of the Pacific Northwest USA. Remote Sens. Environ. 2010, 114, 1662–1675. [Google Scholar] [CrossRef]
- Hou, J.; Huang, C.; Zhang, Y.; Guo, J.; Gu, J. Gap-filling of modis fractional snow cover products via non-local spatio-temporal filtering based on machine learning techniques. Remote Sens. 2019, 11, 90. [Google Scholar] [CrossRef] [Green Version]
- Li, M.; Zhu, X.; Li, N.; Pan, Y. Gap-Filling of a MODIS Normalized Difference Snow Index Product Based on the Similar Pixel Selecting Algorithm: A Case Study on the Qinghai–Tibetan Plateau. Remote Sens. 2020, 12, 1077. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Xie, H.; Liang, T.; Huang, X. Comparison and validation of MODIS standard and new combination of Terra and Aqua snow cover products in northern Xinjiang, China. Hydrol. Process. Int. J. 2009, 23, 419–429. [Google Scholar] [CrossRef]
- Chen, S.; Wang, X.; Guo, H.; Xie, P.; Sirelkhatim, A.M. Spatial and temporal adaptive gap-filling method producing daily cloud-free ndsi time series. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 2251–2263. [Google Scholar] [CrossRef]
- Liu, G.; Reda, F.A.; Shih, K.J.; Wang, T.C.; Tao, A.; Catanzaro, B. Image inpainting for irregular holes using partial convolutions. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 85–100. [Google Scholar]
- Zhang, Q.; Yuan, Q.; Li, J.; Wang, Y.; Sun, F.; Zhang, L. Generating seamless global daily AMSR2 soil moisture (SGD-SM) long-term products for the years 2013–2019. Earth Syst. Sci. Data 2021, 13, 1385–1401. [Google Scholar] [CrossRef]
- Wu, P.; Yin, Z.; Yang, H.; Wu, Y.; Ma, X. Reconstructing geostationary satellite land surface temperature imagery based on a multiscale feature connected convolutional neural network. Remote Sens. 2019, 11, 300. [Google Scholar] [CrossRef] [Green Version]
- Yu, J.; Lin, Z.; Yang, J.; Shen, X.; Lu, X.; Huang, T.S. Generative image inpainting with contextual attention. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 5505–5514. [Google Scholar]
- Russakovsky, O.; Deng, J.; Su, H.; Krause, J.; Satheesh, S.; Ma, S.; Huang, Z.; Karpathy, A.; Khosla, A.; Bernstein, M.; et al. Imagenet large scale visual recognition challenge. Int. J. Comput. Vis. 2015, 115, 211–252. [Google Scholar] [CrossRef] [Green Version]
- Song, Y.; Yang, C.; Lin, Z.; Liu, X.; Huang, Q.; Li, H.; Kuo, C.C.J. Contextual-based image inpainting: Infer, match, and translate. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 3–19. [Google Scholar]
- Liu, X.; Chen, B. Climatic warming in the Tibetan Plateau during recent decades. Int. J. Climatol. J. R. Meteorol. Soc. 2000, 20, 1729–1742. [Google Scholar] [CrossRef]
- Ye, D.; Gao, Y. The Meteorology of the Qinghai-Xizang (Tibet) Plateau; Science Press: Beijing, China, 1979; pp. 1–278. (In Chinese) [Google Scholar]
- Yanai, M.; Li, C.; Song, Z. Seasonal heating of the Tibetan Plateau and its effects on the evolution of the Asian summer monsoon. J. Meteorol. Soc. Jpn. Ser. II 1992, 70, 319–351. [Google Scholar] [CrossRef] [Green Version]
- Kutzbach, J.; Prell, W.; Ruddiman, W.F. Sensitivity of Eurasian climate to surface uplift of the Tibetan Plateau. J. Geol. 1993, 101, 177–190. [Google Scholar] [CrossRef]
- Zheng, H.; Zhang, L.; Liu, C.; Shao, Q.; Fukushima, Y. Changes in stream flow regime in headwater catchments of the Yellow River basin since the 1950s. Hydrol. Process. Int. J. 2007, 21, 886–893. [Google Scholar] [CrossRef]
- Sato, Y.; Ma, X.; Xu, J.; Matsuoka, M.; Zheng, H.; Liu, C.; Fukushima, Y. Analysis of long-term water balance in the source area of the Yellow River basin. Hydrol. Process. Int. J. 2008, 22, 1618–1629. [Google Scholar] [CrossRef]
- Qin, Y.; Yang, D.; Gao, B.; Wang, T.; Chen, J.; Chen, Y.; Wang, Y.; Zheng, G. Impacts of climate warming on the frozen ground and eco-hydrology in the Yellow River source region, China. Sci. Total Environ. 2017, 605, 830–841. [Google Scholar] [CrossRef] [Green Version]
- Li, C.; Su, F.; Yang, D.; Tong, K.; Meng, F.; Kan, B. Spatiotemporal variation of snow cover over the Tibetan Plateau based on MODIS snow product, 2001–2014. Int. J. Climatol. 2018, 38, 708–728. [Google Scholar] [CrossRef]
- Hu, Y.; Maskey, S.; Uhlenbrook, S. Trends in temperature and rainfall extremes in the Yellow River source region, China. Clim. Change 2012, 110, 403–429. [Google Scholar] [CrossRef] [Green Version]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In International Conference on Medical Image Computing and Computer-Assisted Intervention; Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- Zhang, Q.; Yuan, Q.; Li, J.; Yang, Z.; Ma, X. Learning a dilated residual network for SAR image despeckling. Remote Sens. 2018, 10, 196. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.; Jiang, L.; Ménard, C.B.; Luojus, K.; Lemmetyinen, J.; Pulliainen, J. Evaluation of snow products over the Tibetan Plateau. Hydrol. Process. 2015, 29, 3247–3260. [Google Scholar] [CrossRef]
- Gao, Y.; Xie, H.; Yao, T. Developing snow cover parameters maps from MODIS, AMSR-E, and blended snow products. Photogramm. Eng. Remote Sens. 2011, 77, 351–361. [Google Scholar] [CrossRef]
- Albawi, S.; Mohammed, T.A.; Al-Zawi, S. Understanding of a convolutional neural network. In Proceedings of the 2017 International Conference on Engineering and Technology (ICET), Antalya, Turkey, 21–23 August 2017; pp. 1–6. [Google Scholar]
- Schmidt, R.M.; Schneider, F.; Hennig, P. Descending through a crowded valley-benchmarking deep learning optimizers. In Proceedings of the International Conference on Machine Learning, Virtual Event, 18–24 July 2021; pp. 9367–9376. [Google Scholar]
- Li, Z.; Liu, F.; Yang, W.; Peng, S.; Zhou, J. A survey of convolutional neural networks: Analysis, applications, and prospects. IEEE Trans. Neural Netw. Learn. Syst. 2021, 1, 1–21. [Google Scholar] [CrossRef]
- Bernico, M. Deep Learning Quick Reference: Useful Hacks for Training and Optimizing Deep Neural Networks with TensorFlow and Keras; Packt Publishing Ltd.: Birmingham, UK, 2018. [Google Scholar]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences; Academic Press: Cambridge, MA, USA, 2011; Volume 100. [Google Scholar]
- Lee, C.S.; Sohn, E.; Park, J.D.; Jang, J.D. Estimation of soil moisture using deep learning based on satellite data: A case study of South Korea. GISci. Remote Sens. 2019, 56, 43–67. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).