A Shrink-Branch-Bound Algorithm for eLoran Pseudorange Positioning Initialization
Abstract
:1. Introduction
2. Materials and Methods
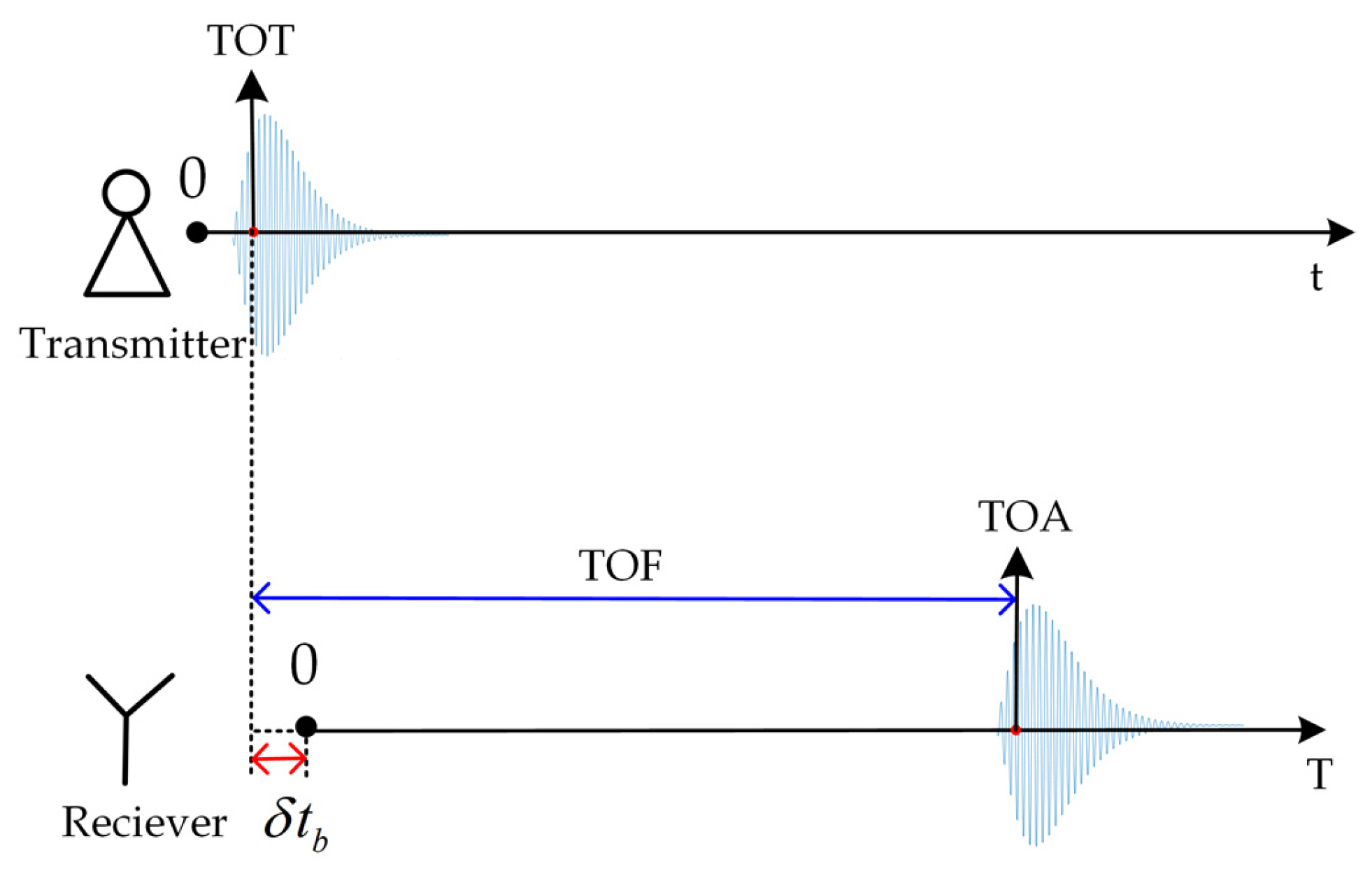
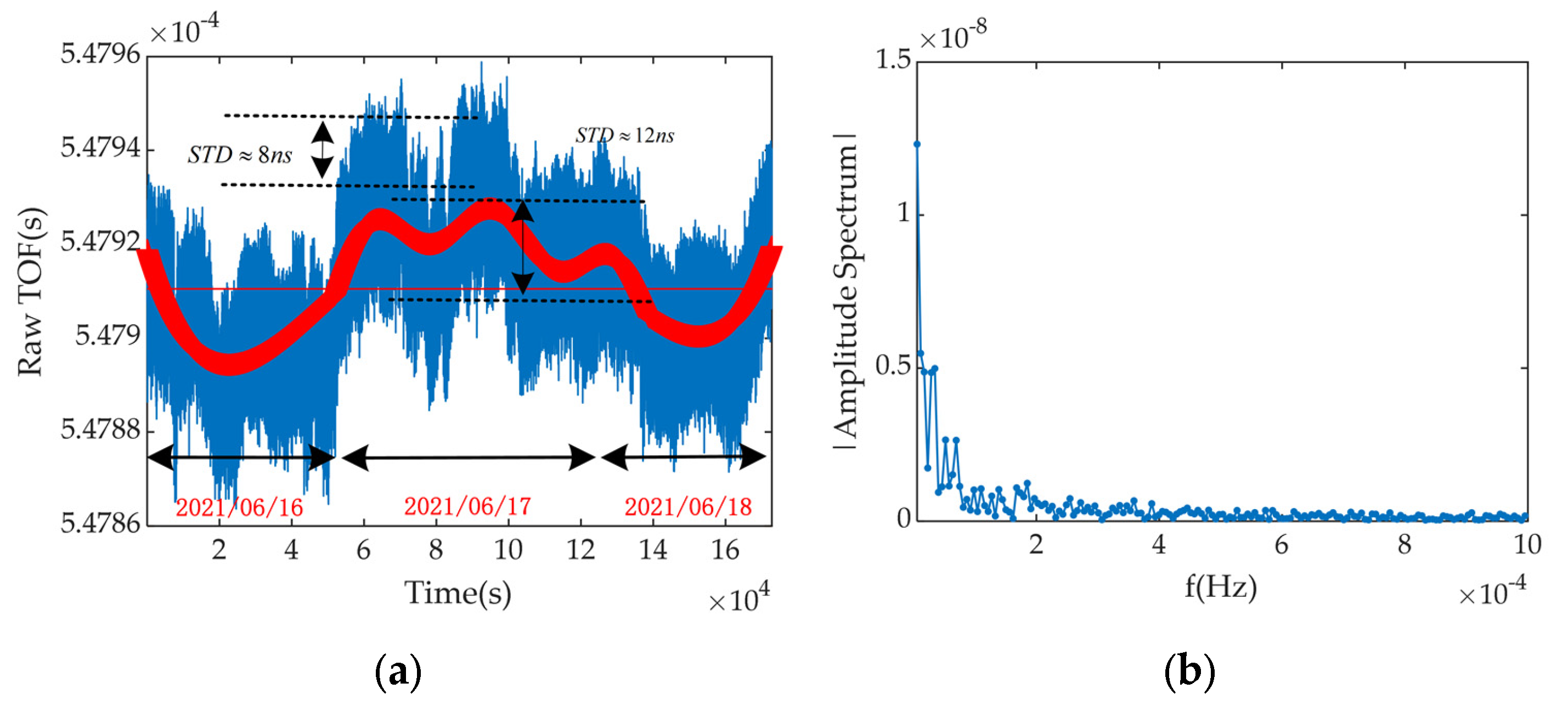
2.1. Principle of eLoran’s Pseudorange Measurement and Error Analysis
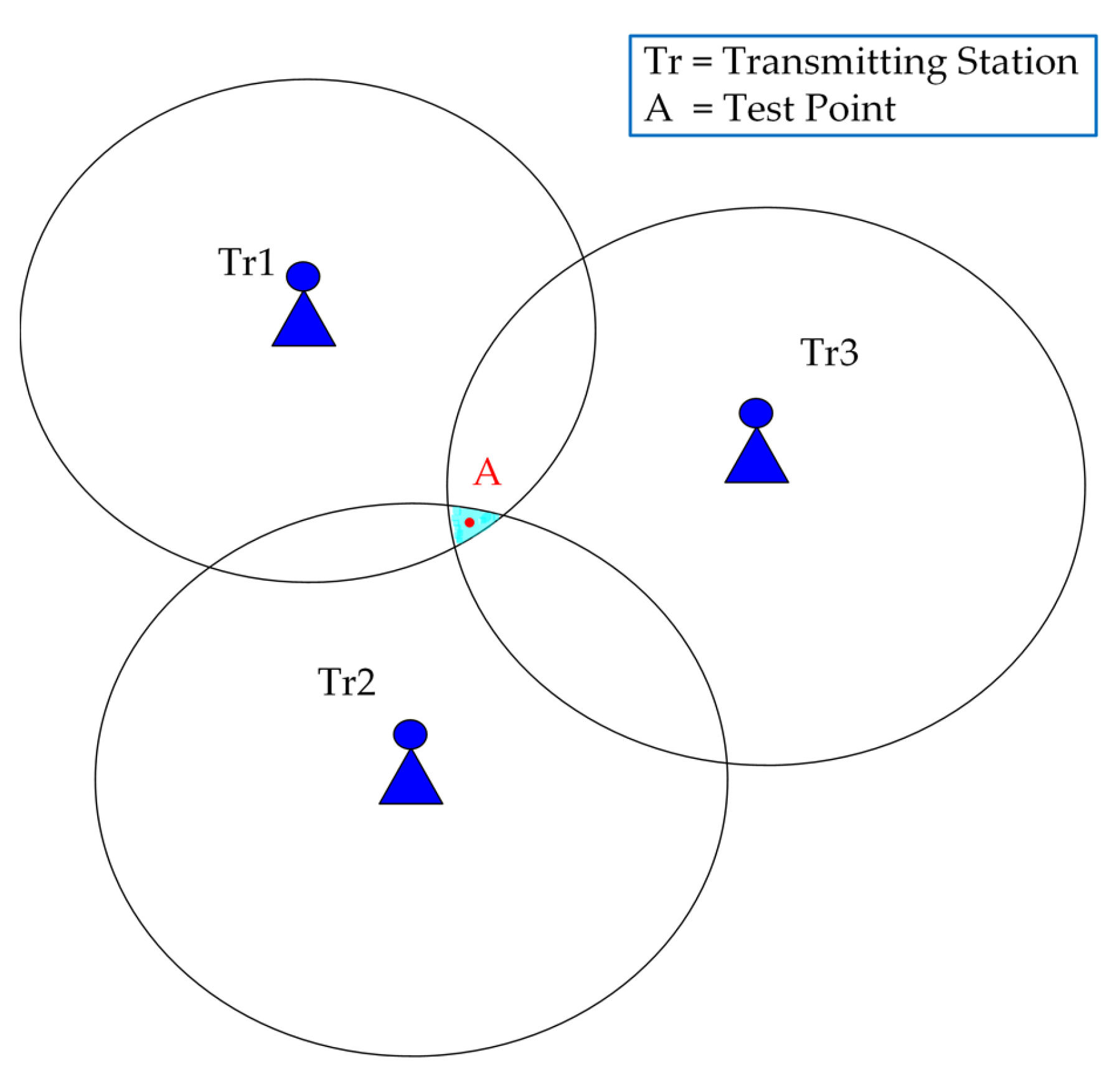
2.2. eLoran Pseudorange Positioning Model and Conventional Positioning Algorithm
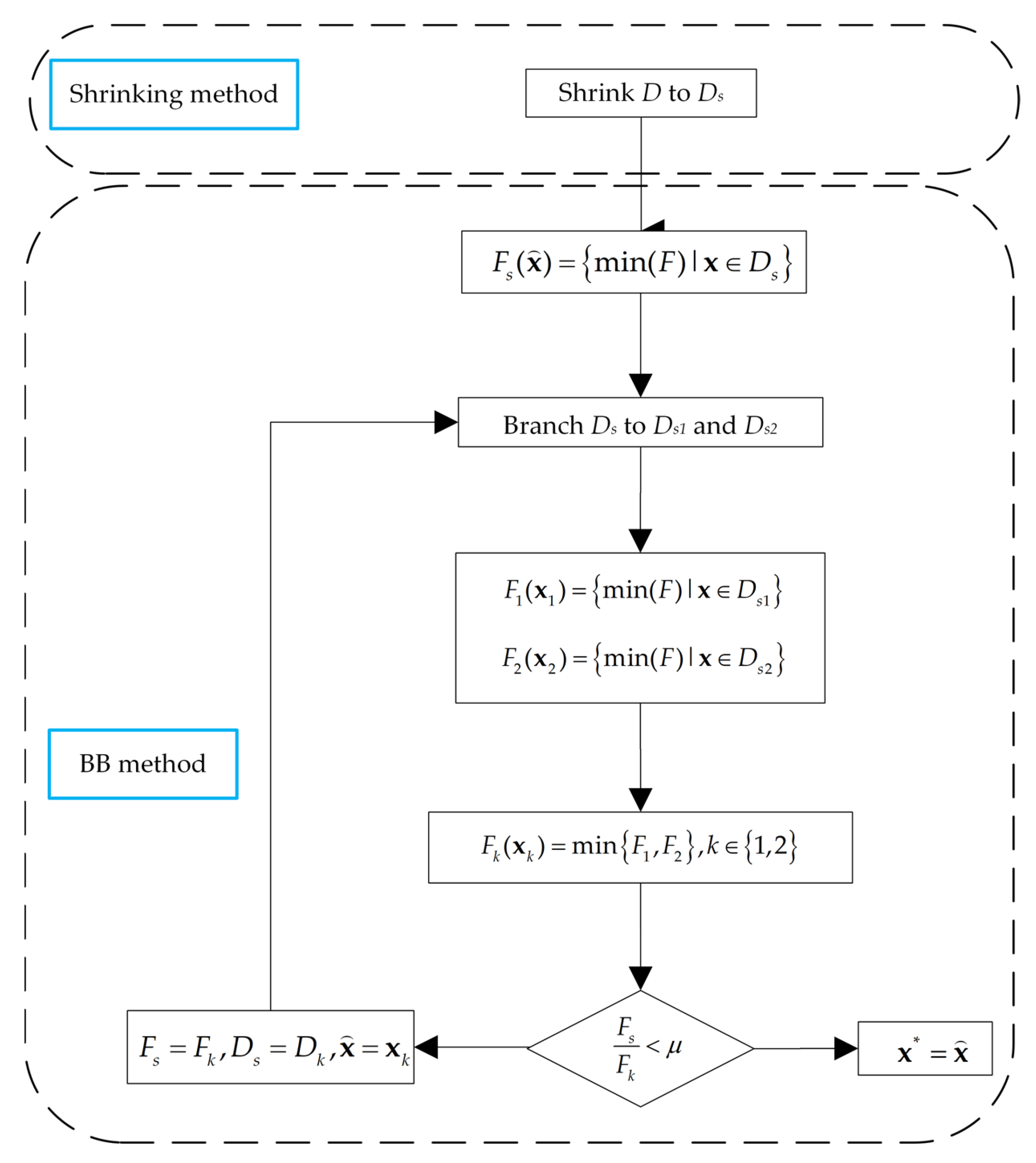
2.3. The Shrink-Branch-Bound Algorithm
| Algorithm 1 Generic Branch-and-Bound |
| 1. Set L = {D}, initial x∗ = |
| 2. While L ≠ Ø |
| 3. Select a subproblem Ds from L to explore |
| 4. if a solution can be found, then = x1 |
| 5. if Ds cannot be pruned: |
| 6. Partition Ds into Ds1, Ds2,…, Dsn |
| 7. Insert Ds1, Ds2,…, Dsn into L |
| 8. Remove Ds from L |
| 9. Return |
2.3.1. The Shrink Method
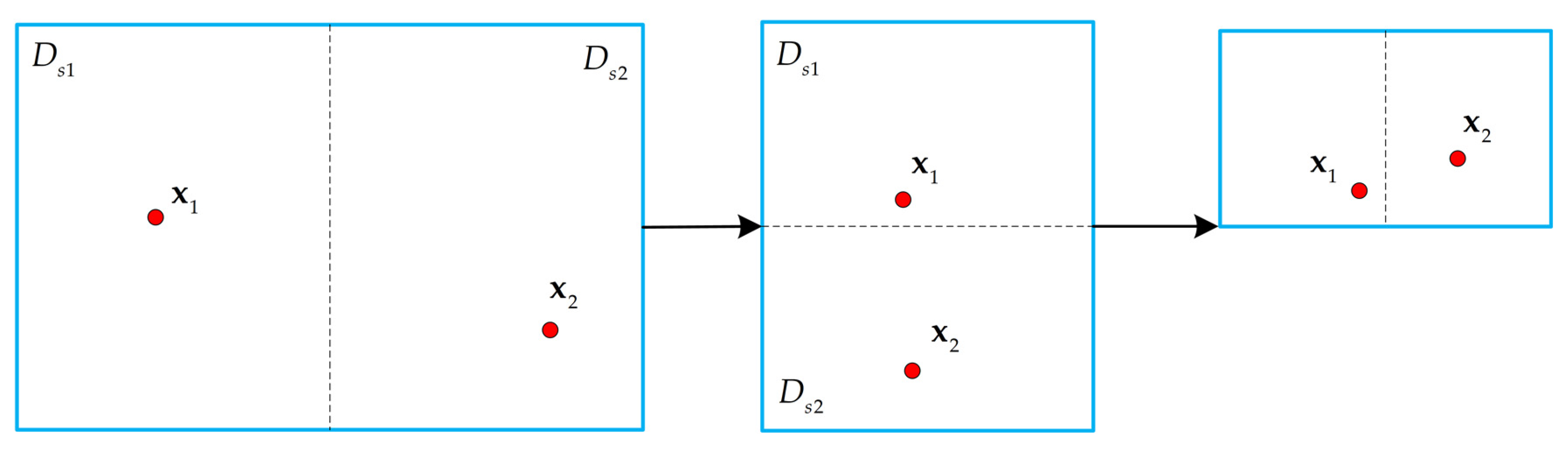
2.3.2. The Branch and Bound Method in SBB Algorithm
| Algorithm 2 SBB Algorithm |
| 1. Shrinking to Ds, using Equation (20) |
| 2. Take the initial value , use TRR algorithm to calculate |
| 3. Branch Ds into and. |
| 4. Calculate and and their corresponding solutions and . |
| 5. and, where , |
| 6. If , Then , the iteration ends; |
| 7. If , Then , and repeat steps 3–5. |
| Algorithm 3 TRR Algorithm |
| 1. and μ |
| 2. |
| 3. |
| 4. Solve the trust region subproblem, |
| 5. |
| 6. |
| 7. |
| 8. |
2.3.3. Complexity Analysis
3. Results
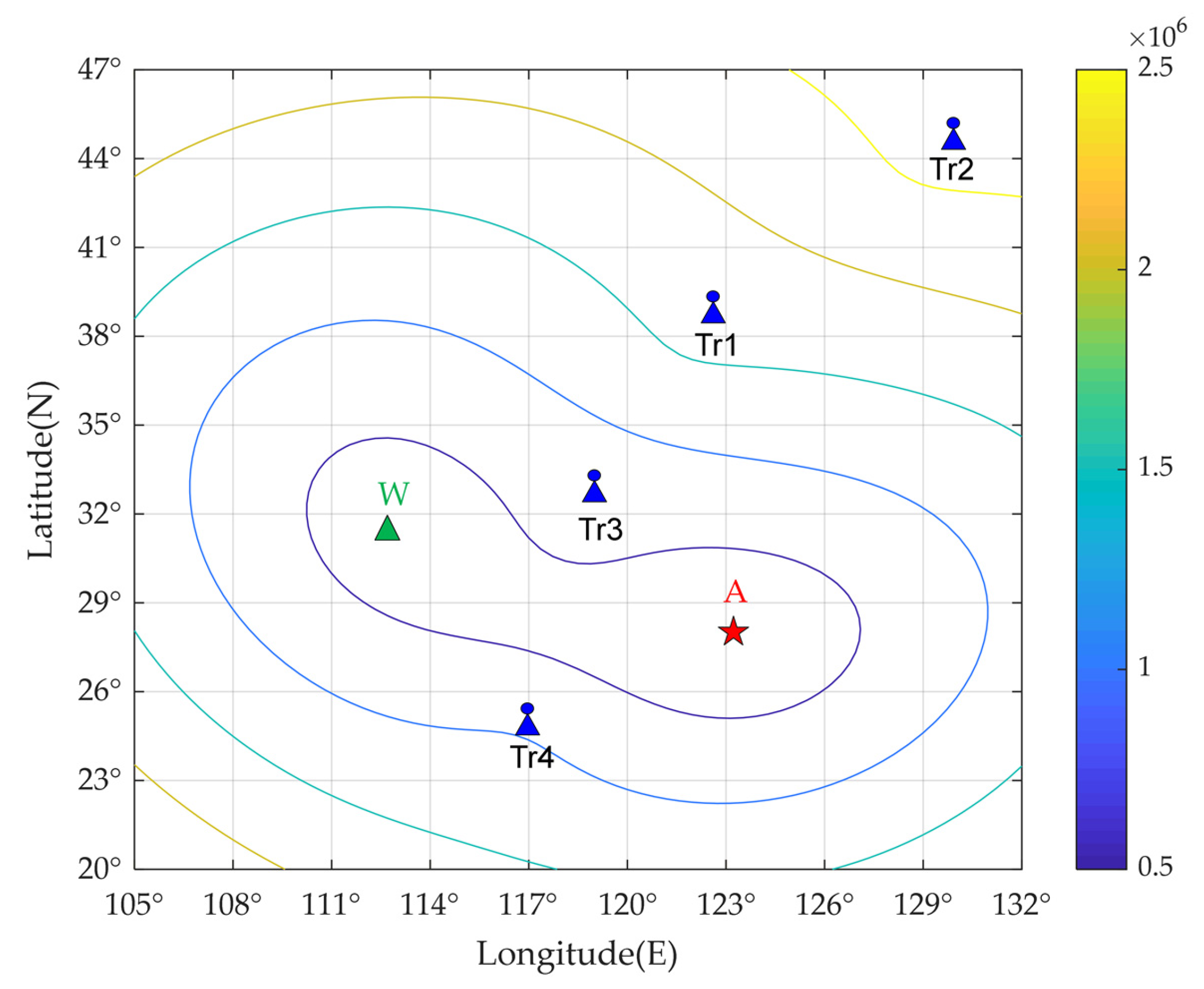
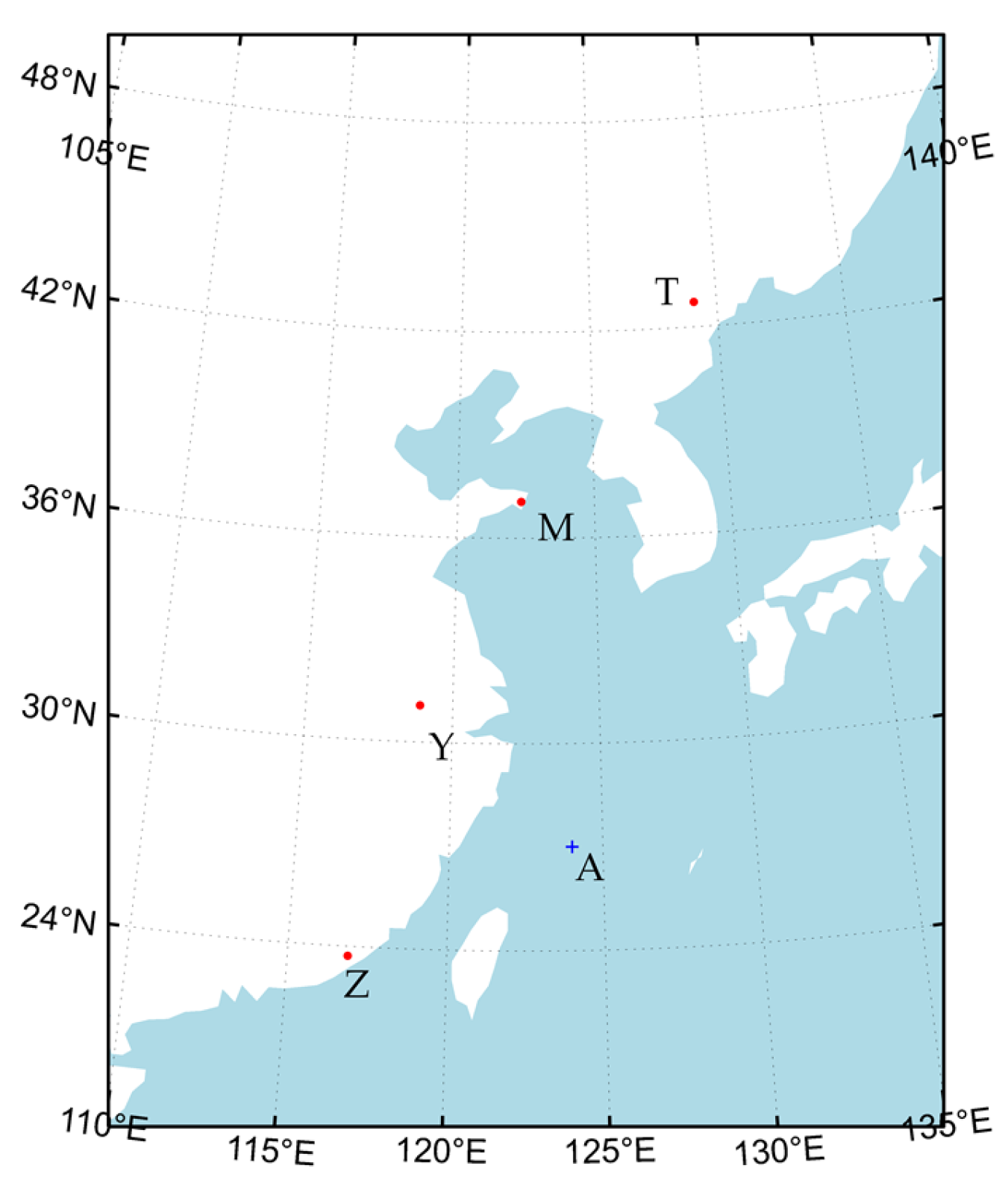
3.1. Simulation Parameter Settings
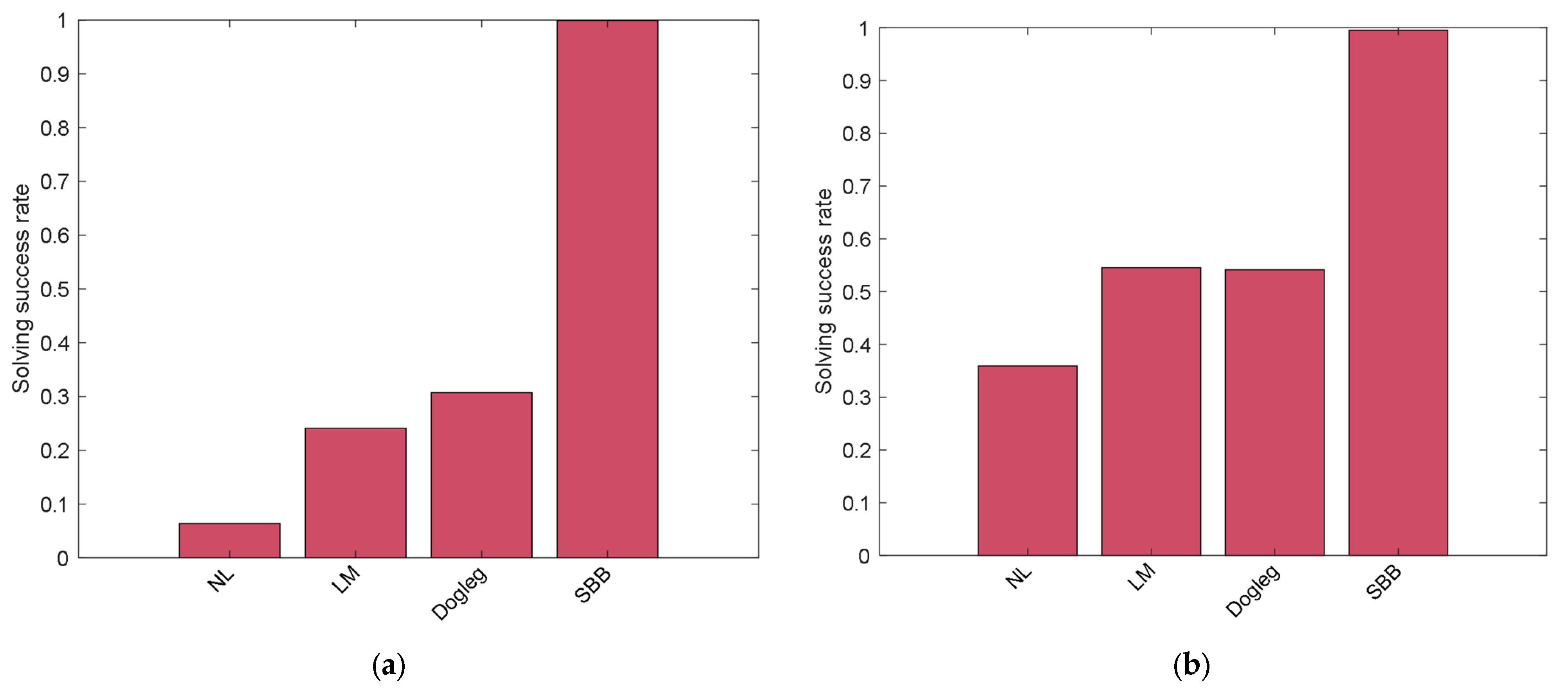
3.2. Analysis and Comparison of Simulation Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hussain, A.; Akhtar, F.; Khand, Z.H.; Rajput, A.; Shaukat, Z. Complexity and Limitations of GNSS Signal Reception in Highly Obstructed Enviroments. Eng. Technol. Appl. Sci. Res. 2021, 11, 6864–6868. [Google Scholar] [CrossRef]
- Lu, D.; Jiang, S.; Cai, B.; Shangguan, W.; Liu, X.; Luan, J. Quantitative analysis of GNSS performance under railway obstruction environment. In Proceedings of the 2018 IEEE/ION Position, Location and Navigation Symposium (PLANS), Monterey, CA, USA, 23–26 April 2018; pp. 1074–1080. [Google Scholar] [CrossRef]
- Wang, L.; Groves, P.D.; Ziebart, M.K. Multi-Constellation GNSS Performance Evaluation for Urban Canyons Using Large Virtual Reality City Models. J. Navig. 2012, 65, 459–476. [Google Scholar] [CrossRef] [Green Version]
- Zhao, X.; Zhan, X.-Q.; Liu, X.; Li, S.-J. GNSS Vulnerability Analysis and Assessment. J. Aeronaut. Astronaut. Aviat. 2014, 46, 11–19. [Google Scholar] [CrossRef]
- Dinesh, S. Globle Navigation Satellite System (GNSS) Spoofing: A Review of Growing Risks and Mitigation Steps. Def. ST Tech. Bull. 2013, 6, 42–61. [Google Scholar]
- Panagiotis, P.; Jovanovic, A. Protection and Fundamental Vulnerability of GNSS. In Proceedings of the the 2008 IEEE International Workshop on Satellite and Space Communications 2008, Toulouse, France, 1–3 October 2008. [Google Scholar] [CrossRef] [Green Version]
- Fascista, A.; Coluccia, A.; Ricci, G. A Pseudo Maximum likelihood approach to position estimation in dynamic multipath environments. Signal Process. 2020, 181, 107907. [Google Scholar] [CrossRef]
- Lesouple, J.; Robert, T.; Sahmoudi, M.; Tourneret, J.-Y.; Vigneau, W. Multipath Mitigation for GNSS Positioning in an Urban Environment Using Sparse Estimation. IEEE Trans. Intell. Transp. Syst. 2018, 20, 1316–1328. [Google Scholar] [CrossRef]
- Cheng, L.; Wang, K.; Ren, M.; Yan, G. Adaptive Filter Approach for Gps Multipath Estimation under Correntropy Criterion in Dynamic Multipath Environment. IEEE Trans. Signal Process. 2019, 67, 5798–5810. [Google Scholar] [CrossRef]
- Cheng, C.; Tourneret, J.-Y. An EM-based multipath interference mitigation in GNSS receivers. Signal Process. 2019, 162, 141–152. [Google Scholar] [CrossRef] [Green Version]
- Ferrigno, L.; Laracca, M.; Milano, F.; Cerro, G.; Bellitti, P.; Serpelloni, M.; Piedrafita, O.C. Magnetic Localization System for Short-Range Positioning: A Ready-to-Use Design Tool. IEEE Trans. Instrum. Meas. 2020, 70, 1–9. [Google Scholar] [CrossRef]
- Wang, T.; Sui, T.; Liu, X.; Yuan, M.; Sun, G.; Gao, Z. WiFi positioning algorithm in tunnel based on Fuzzy C-means clustering and KNN algorithm. In Proceedings of the the 2019 Chinese Automation Congress (CAC), Hangzhou, China, 22–24 November 2019; pp. 567–571. [Google Scholar] [CrossRef]
- Halili, R.; BniLam, N.; Yusuf, M.; Tanghe, E.; Joseph, W.; Weyn, M.; Berkvens, R. Vehicle Localization Using Doppler Shift and Time of Arrival Measurements in a Tunnel Environment. Sensors 2022, 22, 847. [Google Scholar] [CrossRef]
- Sheng, C.; Gan, X.; Yu, B.; Zhang, J. Precise Point Positioning Algorithm for Pseudolite Combined with GNSS in a Constrained Observation Environment. Sensors 2020, 20, 1120. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Griffioen, J.W.; Oonincx, P.J. Suitability of Low-Frequency Navigation Systems for Artillery Positioning in a GNSS Denied Environment. J. Navig. 2012, 66, 35–48. [Google Scholar] [CrossRef] [Green Version]
- Johnson, G.W.; Swaszek, P.F.; Hartnett, R.J.; Shalaev, R.; Wiggins, M. An Evaluation of Eloran as a Backup to GPS. In Proceedings of the 2007 IEEE Conference on Technologies for Homeland Security, Woburn, MA, USA, 16–17 May 2007. [Google Scholar] [CrossRef]
- Offermans, G.; Bartlett, S.; Schue, C. Providing a Resilient Timing and UTC Service Using eLoran in the United States. Navigation 2017, 64, 339–349. [Google Scholar] [CrossRef]
- Son, P.-W.; Park, S.G.; Han, Y.; Seo, K. eLoran: Resilient Positioning, Navigation, and Timing Infrastructure in Maritime Areas. IEEE Access 2020, 8, 193708–193716. [Google Scholar] [CrossRef]
- Narkus-Kramer, M.; Scales, W.; Calle, E. Evaluating Eloran as a Backup for Surveillance and Navigation: A Comparative Cost Analysis. In Proceedings of the the 2009 IEEE/AIAA 28th Digital Avionics Systems Conference, Orlando, FL, USA, 23–29 October 2009. [Google Scholar] [CrossRef]
- Pierce, J.A. An Introduction to Loran. IEEE Aerosp. Electron. Syst. Mag. 1990, 5, 16–33. [Google Scholar] [CrossRef]
- Peterson, B.; Hartnett, R.; Bruckner, D.; Heatherington, R.; Fiedler, R. Integrated GPS/LORAN: Structures and Issues. Navigation 1998, 45, 183–193. [Google Scholar] [CrossRef]
- Peterson, B.B.; Lo, S.; Enge, P. Integrating Loran and Gnss for Safety of Life Applications. In Proceedings of the Institute of Navigation GNSS Conference, Savannah, GA, USA, 16–19 September 2008. [Google Scholar]
- Groves, P.D. Principles of GNSS, Inertial, and Multisensor Integrated Navigation Systems; Boston Artech House: Norwood, MA, USA, 2013. [Google Scholar]
- Yan, B.; Li, Y.; Guo, W.; Hua, Y. High-Accuracy Positioning Based on Pseudo-Ranges: Integrated Difference and Performance Analysis of the Loran System. Sensors 2020, 20, 4436. [Google Scholar] [CrossRef]
- Kim, Y.; Fang, T.H.; Kim, D.; Seo, K.; Park, S.H. Loran-C Multiple Chain Positioning Using Toa Measurements. J. Navig. Port Res. 2019, 43, 23–32. [Google Scholar] [CrossRef]
- Fang, T.H.; Kim, Y.; Park, S.G.; Seo, K.; Park, S.H. GPS and eLoran Integrated Navigation for Marine Applications Using Augmented Measurement Equation Based on Range Domain. Int. J. Control. Autom. Syst. 2020, 18, 2349–2359. [Google Scholar] [CrossRef]
- Coleman, T.F.; Li, Y. A Reflective Newton Method for Minimizing a Quadratic Function Subject to Bounds on Some of the Variables. SIAM J. Optim. 1996, 6, 1040–1058. [Google Scholar] [CrossRef]
- Morrison, D.R.; Jacobson, S.; Sauppe, J.J.; Sewell, E.C. Branch-and-bound algorithms: A survey of recent advances in searching, branching, and pruning. Discret. Optim. 2016, 19, 79–102. [Google Scholar] [CrossRef]
- Shapiro, L.D. Time synchronization from Loran-C. IEEE Spectr. 1968, 5, 46–55. [Google Scholar] [CrossRef]
- Yan, W.; Dong, M.; Li, S.; Yang, C.; Yuan, J.; Hu, Z.; Hua, Y. An eLoran Signal Cycle Identification Method Based on Joint Time–Frequency Domain. Remote Sens. 2022, 14, 250. [Google Scholar] [CrossRef]
- Johler, J. Propagation of the Low-Frequency Radio Signal. Proc. IRE 1962, 50, 404–427. [Google Scholar] [CrossRef]
- Samaddar, S.N. The Theory of Loran-C Ground Wave Propagation—A Review. Navigation 1979, 26, 173–187. [Google Scholar] [CrossRef]
- Yang, S.H.; Lee, C.B.; Lee, Y.K.; Lee, J.K.; Kim, Y.J.; Lee, S.J. Accuracy Improvement Technique for Timing Application of Loran-C Signal. IEEE Trans. Instrum. Meas. 2011, 60, 2648–2654. [Google Scholar] [CrossRef]
- Li, Y.; Hua, Y.; Yan, B.; Guo, W. Research on the eLoran Differential Timing Method. Sensors 2020, 20, 6518. [Google Scholar] [CrossRef]
- Son, P.-W.; Rhee, J.H.; Hwang, J.; Seo, J. Universal Kriging for Loran Asf Map Generation. IEEE Trans. Aerosp. Electron. Syst. 2018, 55, 1828–1842. [Google Scholar] [CrossRef]
- Kim, Y.; Park, S.H.; Fang, T.H.; Seo, K. A Test of a Loran-C Multi-Chain Positioning Method Using Asf Estimates. In Proceedings of the the 2019 European Navigation Conference (ENC), Warsaw, Poland, 9–12 April 2019. [Google Scholar] [CrossRef]
- Felski, A.; Jaskólski, K.; Zwolak, K.; Piskur, P. Analysis of Satellite Compass Error’s Spectrum. Sensors 2020, 20, 4067. [Google Scholar] [CrossRef]
- Wang, L.-L.; Liang, Z.-C.; Pu, Y.-R.; Xi, X.-L. Method for Loran-C Additional Secondary Factor Correction Based on Neural Network and Transfer Learning. IEEE Antennas Wirel. Propag. Lett. 2021, 21, 332–336. [Google Scholar] [CrossRef]
- Pu, Y.; Zheng, X.; Wang, D.-D.; Xi, X. Accuracy Improvement Model for Predicting Propagation Delay of Loran-C Signal Over a Long Distance. IEEE Antennas Wirel. Propag. Lett. 2021, 20, 582–586. [Google Scholar] [CrossRef]
- Li, Y.; Hua, Y.; Yan, B.; Guo, W. Experimental Study on a Modif I Ed Method for Propagation Delay of Long Wave Signal. IEEE Antennas Wirel. Propag. Lett. 2019, 18, 1716–1720. [Google Scholar] [CrossRef]
- Fisikopoulos, V. Geodesic Algorithms: An Experimental Study. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, 42, 45–47. [Google Scholar] [CrossRef] [Green Version]
- Tseng, W.-K.; Guo, J.-L.; Liu, C.-P. A Comparison of Great Circle, Great Ellipse, and Geodesic Sailing. J. Mar. Sci. Technol. 2013, 21, 7. [Google Scholar] [CrossRef]
- Kornerup, P.; Muller, J.-M. Choosing starting values for certain Newton–Raphson iterations. Theor. Comput. Sci. 2005, 351, 101–110. [Google Scholar] [CrossRef] [Green Version]
- Moré, J.J. The Levenberg-Marquardt algorithm: Implementation and theory. In Numerical Analysis; Springer: Berlin, Germany, 1978; pp. 105–116. [Google Scholar]
- Land, A.H.; Doig, A.G. An Automatic Method of Solving Discrete Programming Problems. Econometrica 1960, 28, 497. [Google Scholar] [CrossRef]
- Steihaug, T. The Conjugate Gradient Method and Trust Regions in Large Scale Optimization. SIAM J. Numer. Anal. 1983, 20, 626–637. [Google Scholar] [CrossRef] [Green Version]
- Byrd, R.H.; Schnabel, R.B.; Shultz, G.A. Approximate Solution of the Trust Region Problem by Minimization over Two-Dimensional Subspaces. Math. Program. 1988, 40, 247–263. [Google Scholar] [CrossRef]
- Gratton, S.; Sartenaer, A.; Toint, P.L. Recursive Trust-Region Methods for Multiscale Nonlinear Optimization. SIAM J. Optim. 2008, 19, 414–444. [Google Scholar] [CrossRef]
- Battiti, R. First- and Second-Order Methods for Learning: Between Steepest Descent and Newton’s Method. Neural Comput. 1992, 4, 141–166. [Google Scholar] [CrossRef]
- Ueda, K.; Yamashita, N. On a Global Complexity Bound of the Levenberg-Marquardt Method. J. Optim. Theory Appl. 2010, 147, 443–453. [Google Scholar] [CrossRef]



| Algorithms | Computional Complexity |
|---|---|
| NR [49] | |
| LM [50] | |
| Dogleg/TTR [48] | |
| SBB |
| Transmitting Station Mark | Position | Longitude (E) | Latitude (N) |
|---|---|---|---|
| M | Rongcheng | 122.3228 | 37.0644 |
| T | Helong | 129.1075 | 42.7199 |
| Y | Xuancheng | 118.886 | 31.0689 |
| Z | Raoping | 116.8958 | 23.7239 |
| Test Point | Transmitting Station | Distance (Rd/m) | PF (μs) | Pseudorange |
|---|---|---|---|---|
| A (27, 124) | M | 1,128,758 | 3766.316 | 1,130,278 |
| T | 1,806,302 | 6027.074 | 1,807,799 | |
| Y | 672,027 | 2242.348 | 673,547 | |
| Z | 801,620 | 2674.758 | 803,112 |
| Point | Initial Points | NR Results | LM Results | Dogleg Results | SBB Results |
|---|---|---|---|---|---|
(N, E) | (N, E) | (N, E) | (N, E) | (N, E) | (N, E) |
| A (27, 124) | 0, 0 | 23.7162, 148.7832 | 31.2167, 103.7164 | 31.2167, 103.7164 | 27.0001, 124.0001 |
| 28, 125 | 27.0001, 124.0001 | 27.0001, 124.0001 | 27.0001, 124.0001 | 27.0001, 124.0001 | |
| 40.1, 97.4 | 31.7164, 103.2167 | 31.21671, 03.7164 | 31.2167, 103.7164 | 27.0001, 124.0001 | |
| 32, 148.8 | 30.2167, 10.7162 | 27.0001, 124.0001 | 27.0001, 124.0001 | 27.0001, 124.0001 | |
| 28, 100 | 31.2167, 103.7164 | 31.2167, 103.7164 | 31.2167, 103.7164 | 27.0000, 123.9998 | |
| 15, 128 | 31.2195, 16.7159 | 26.9991, 124.0011 | 26.9991, 124.0011 | 26.9991, 124.0011 |
| Feasible Region | Fmin | |
|---|---|---|
| D | 3.5 × 109 | 31.2174, 103.7183, −2480 |
| 63.7 | 27.0001, 124.0001, 5.091 | |
| 3.5 × 109 | 31.2174, 103.7183, −2480 | |
| 63.7 | 27.0001, 124.0001, 5.091 |
| Feasible Region | ||
|---|---|---|
| D | 3.5 × 109 | 31.2147, 103.7225, −2480 |
| 3.5 × 109 | 31.2147, 103.7225, −2480 | |
| 3.5 × 109 | 31.2147, 103.7225, −2480 | |
| 99.8 | 26.9998, 124.0009, 4.933 | |
| 99.8 | 31.2147, 103.7225, −2480 | |
| 1.5 × 109 | 26.9998, 124.0009, 4.933 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, K.; Yuan, J.; Yan, W.; Yang, C.; Guo, W.; Li, S.; Hua, Y. A Shrink-Branch-Bound Algorithm for eLoran Pseudorange Positioning Initialization. Remote Sens. 2022, 14, 1781. https://doi.org/10.3390/rs14081781
Liu K, Yuan J, Yan W, Yang C, Guo W, Li S, Hua Y. A Shrink-Branch-Bound Algorithm for eLoran Pseudorange Positioning Initialization. Remote Sensing. 2022; 14(8):1781. https://doi.org/10.3390/rs14081781
Chicago/Turabian StyleLiu, Kaiqi, Jiangbin Yuan, Wenhe Yan, Chaozhong Yang, Wei Guo, Shifeng Li, and Yu Hua. 2022. "A Shrink-Branch-Bound Algorithm for eLoran Pseudorange Positioning Initialization" Remote Sensing 14, no. 8: 1781. https://doi.org/10.3390/rs14081781
APA StyleLiu, K., Yuan, J., Yan, W., Yang, C., Guo, W., Li, S., & Hua, Y. (2022). A Shrink-Branch-Bound Algorithm for eLoran Pseudorange Positioning Initialization. Remote Sensing, 14(8), 1781. https://doi.org/10.3390/rs14081781






