Study of Coastal Effects Relevant for Offshore Wind Energy Using Spaceborne Synthetic Aperture Radar (SAR)
Abstract
:1. Introduction
2. Data and Methods
2.1. Synthetic Aperture Radar (SAR) Derived Wind Field
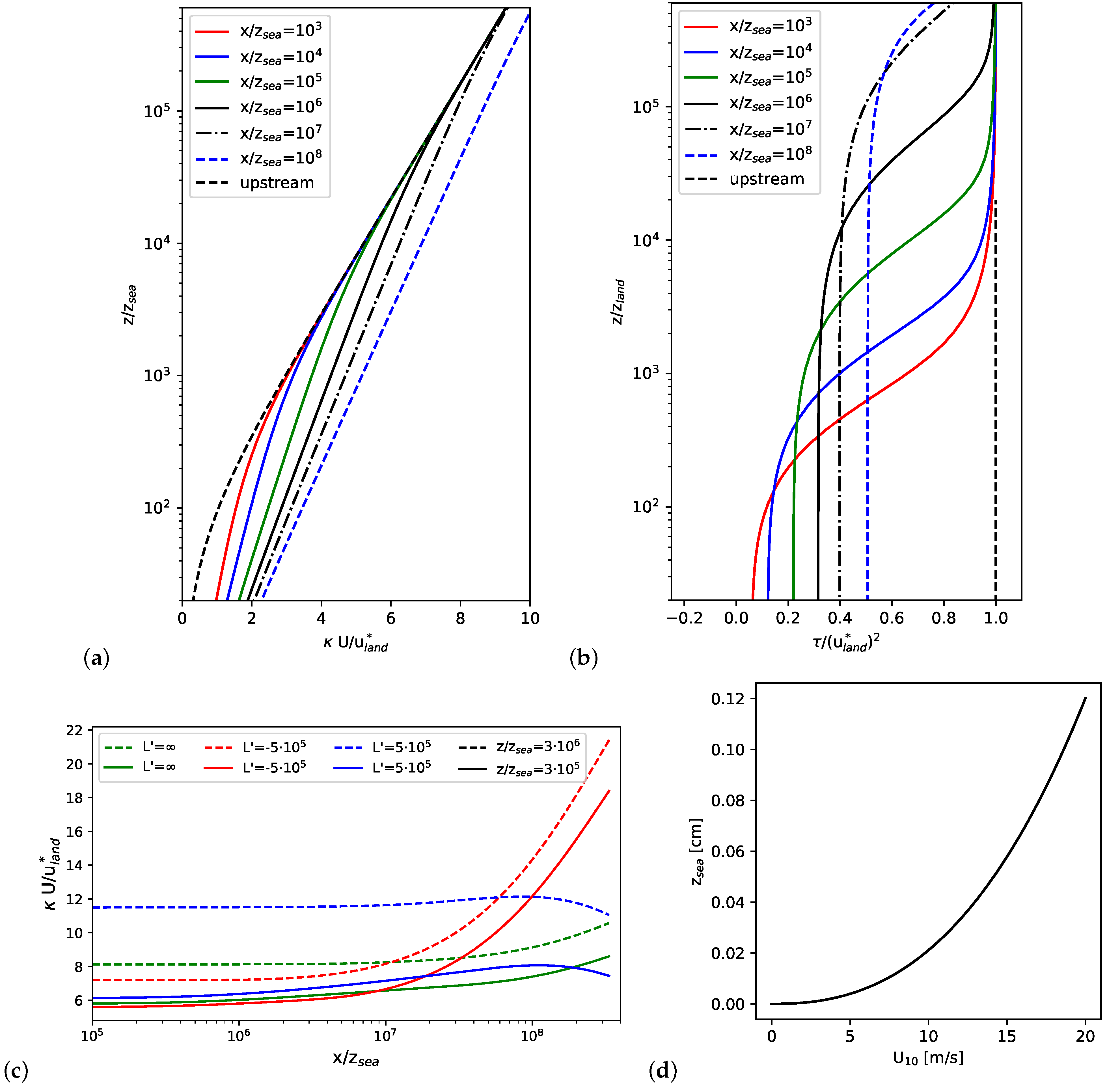
2.2. Theoretical Background of Coastal Effects
2.3. Downwind Horizontal Wind Speed Gradient Estimations
- the absolute wind speed ,
- the wind speed increase ,
- the normalised wind speed increase .
2.4. Empirical Model for Horizontal Wind Speed Gradients
2.5. Auxiliary Data Sets
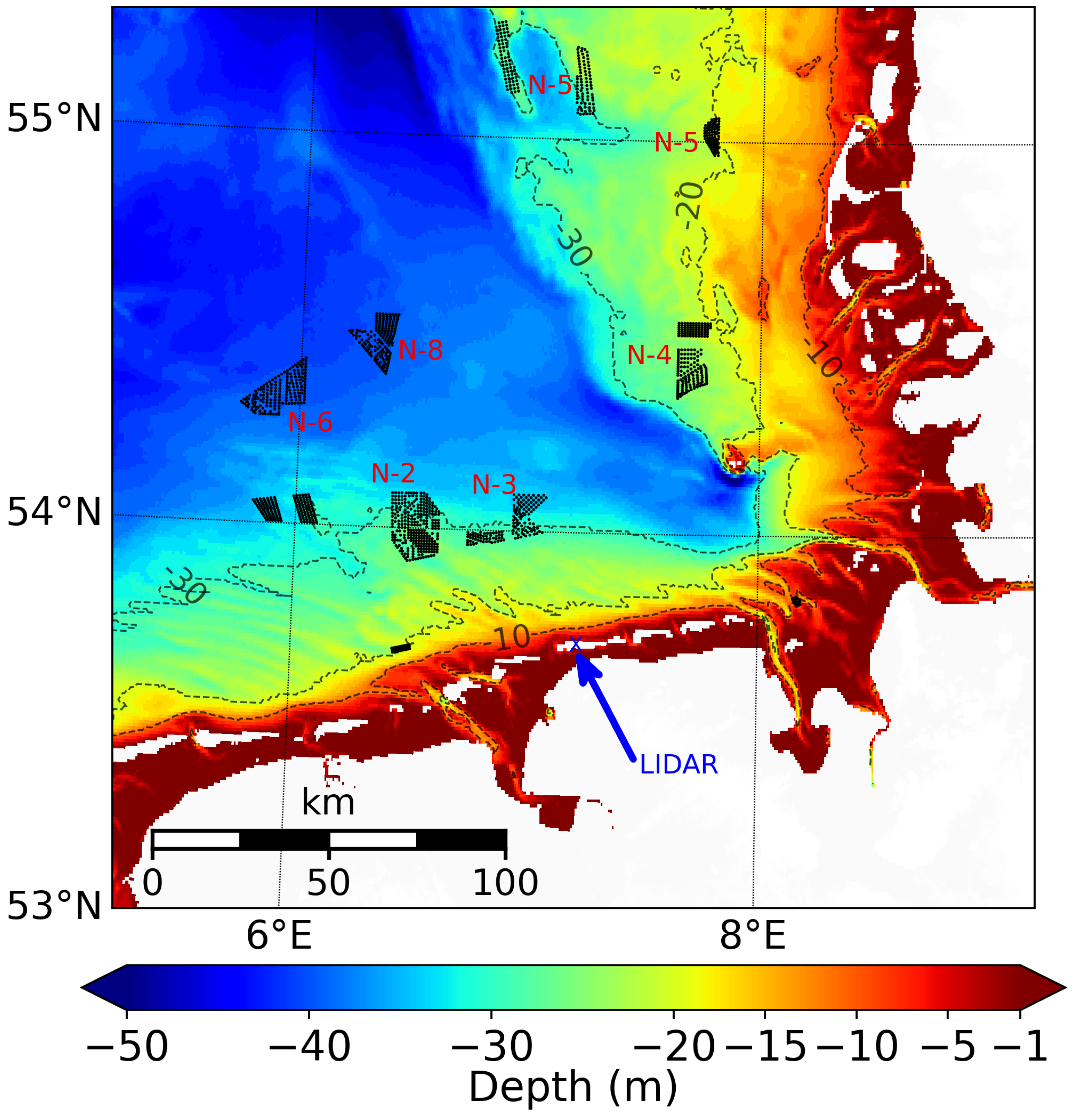
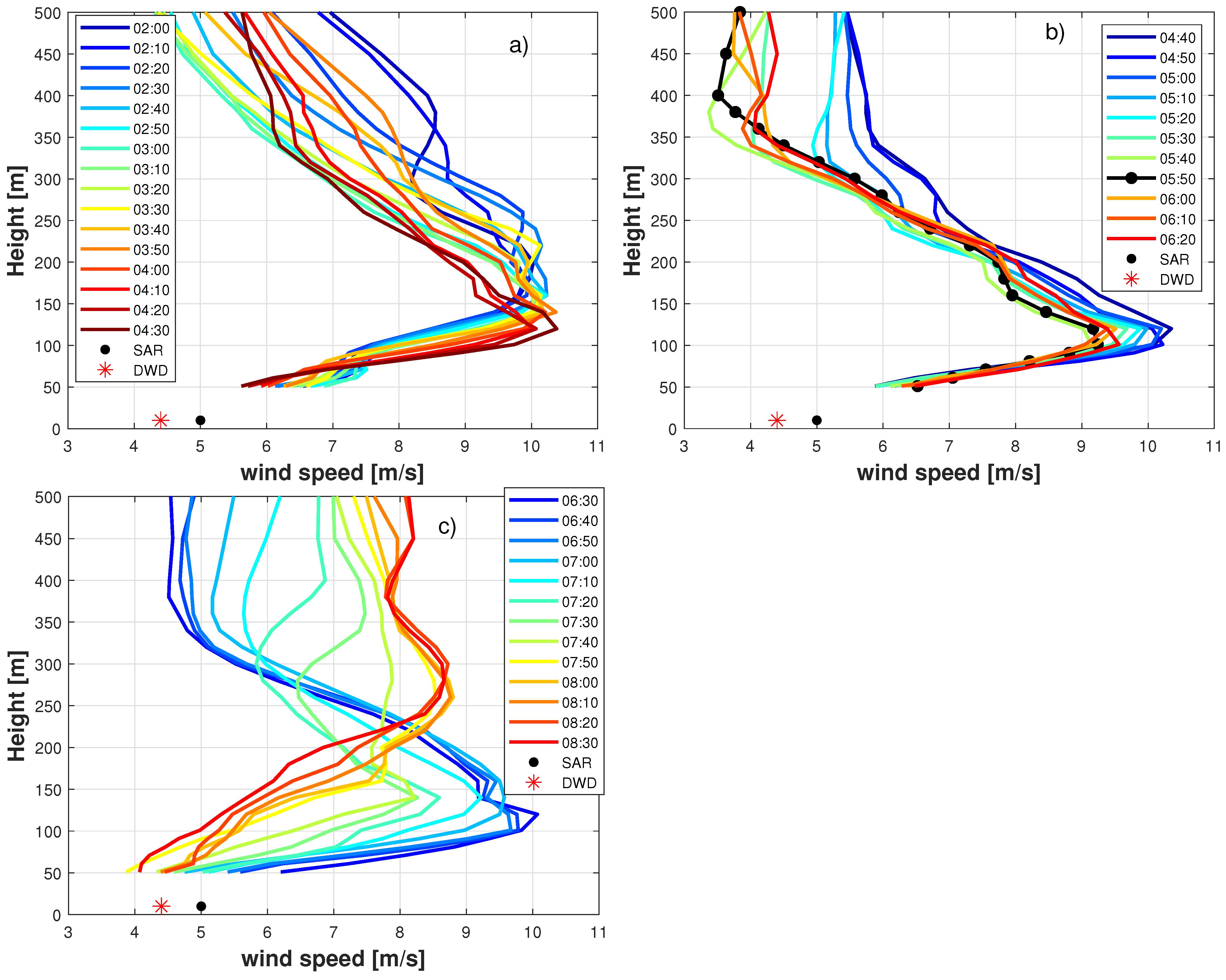
2.5.1. LIDAR Wind Profile
2.5.2. Weather Forecast Data
3. Results
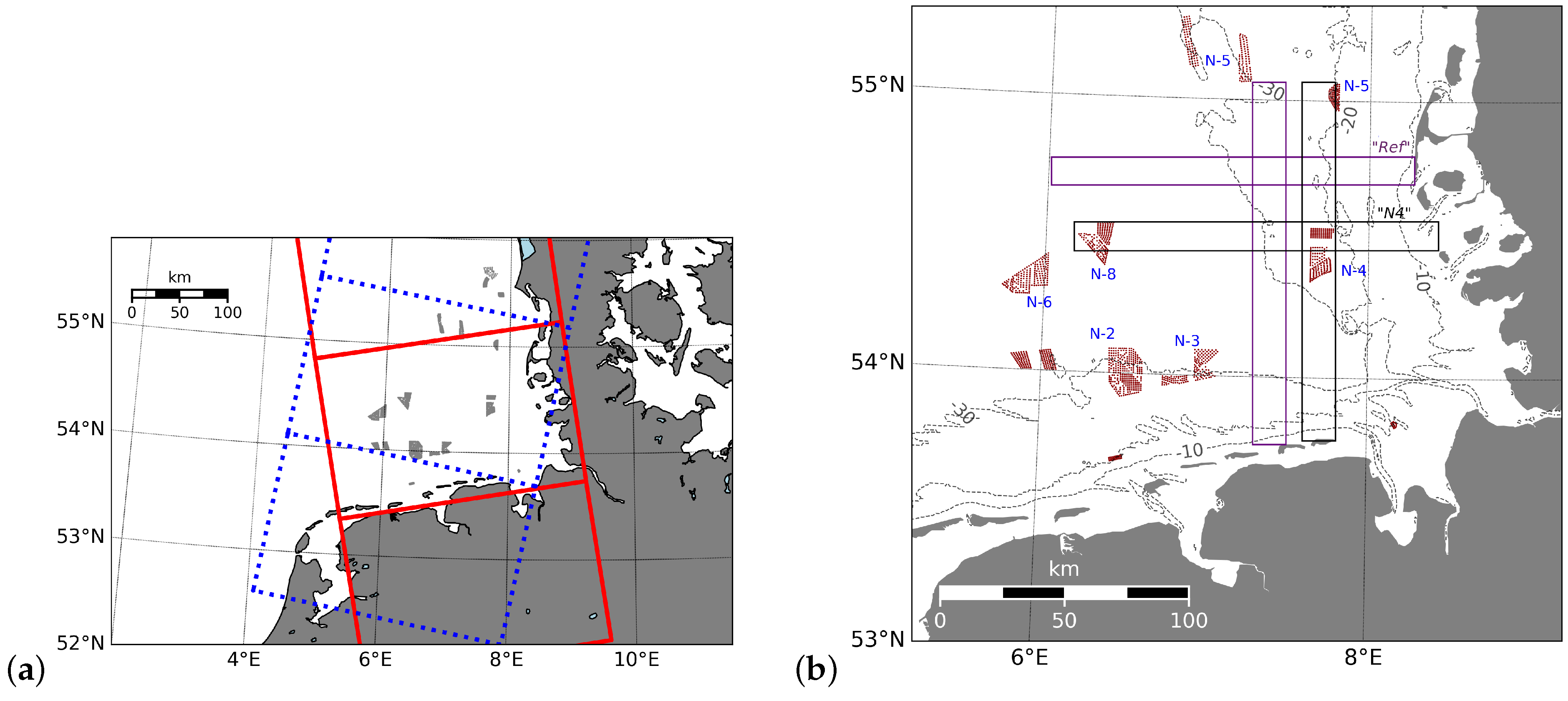
3.1. Coastal Effects in the German Bight
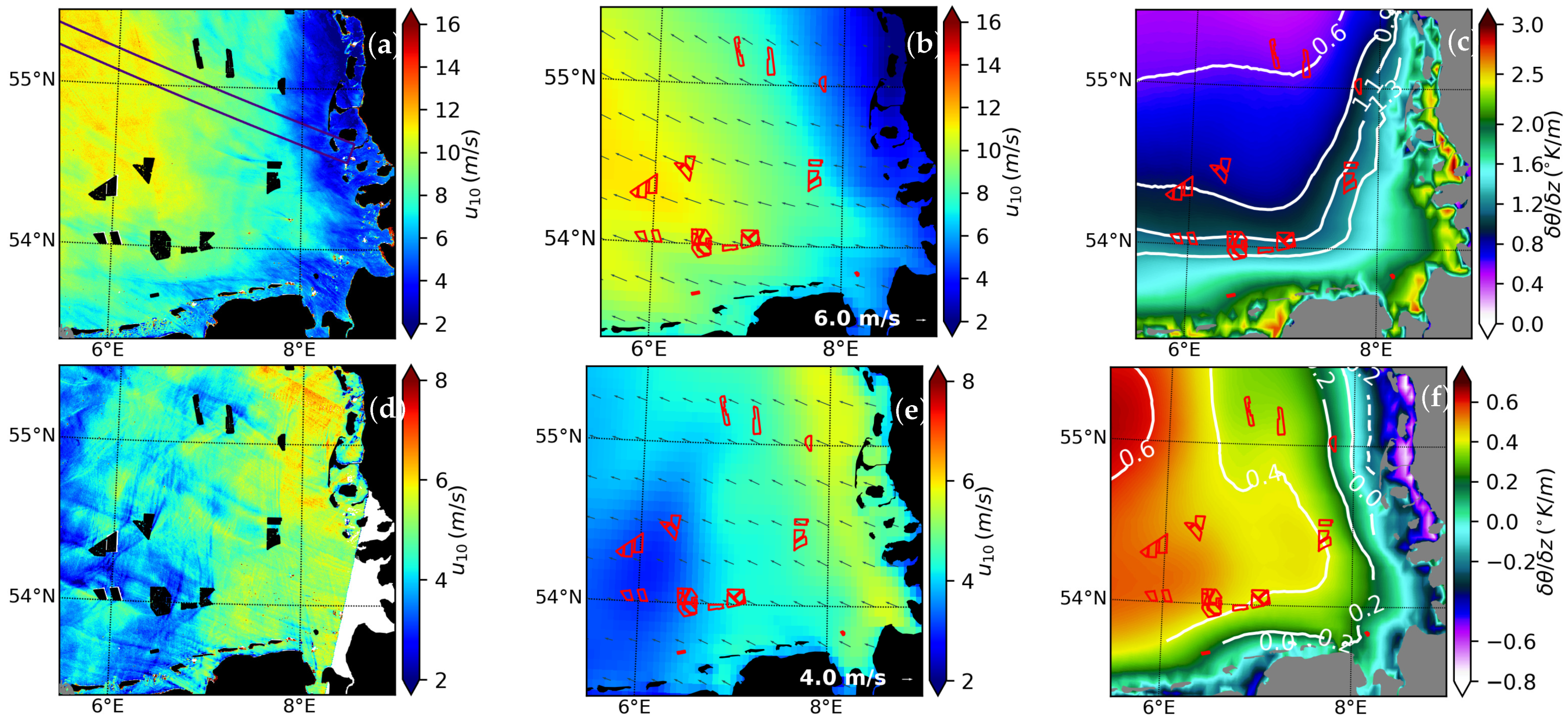
3.2. Example of Horizontal Wind Speed Gradient on 6 April 2018
3.3. Example of Horizontal Wind Speed Gradient on 25 August 2019
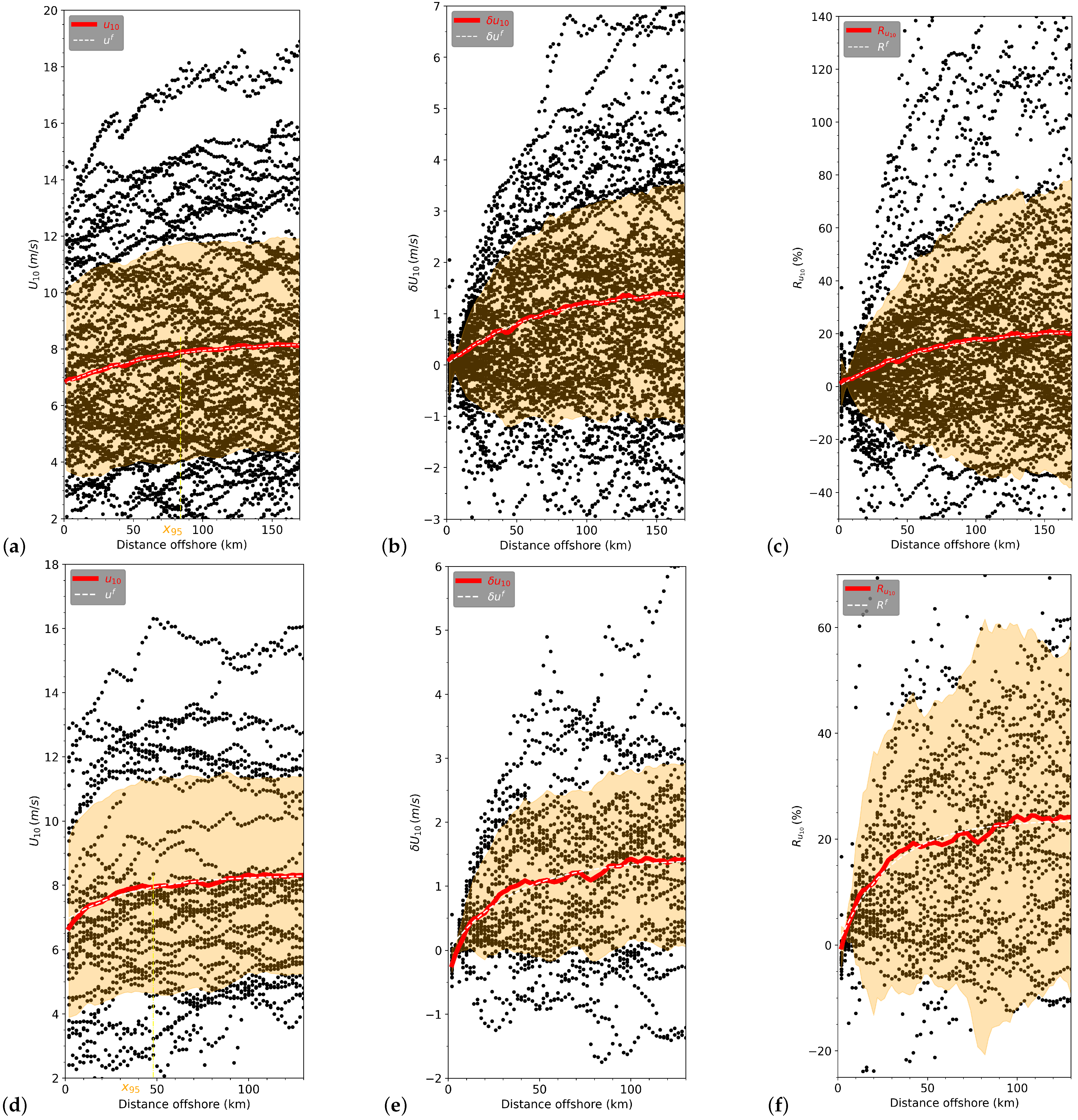
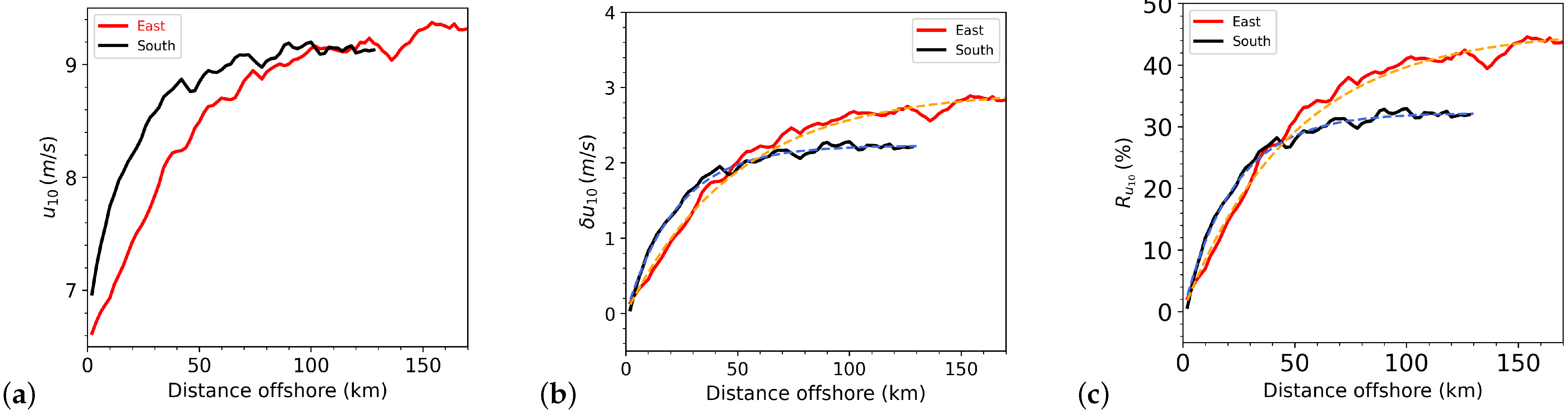
3.4. Statistical Analysis: Horizontal Wind Speed Gradients
3.5. Classification of Shape of Wind Speed Gradients
- The horizontal wind speed transects of that increase with distance to the land (Figure 10a). They are hereafter referred to as “INCS”.
- From the coast to offshore, the horizontal wind speed transects of that show a wind speed decrease with growing distance to land (Figure 10b). In the following these cases will be called “DECS”.
- Some horizontal wind speed transects of display a delay in the wind speed increase, which begins further offshore (Figure 10c). These types are hereafter referred to as “LINCS” (Late INCreasing Samples).
3.6. Distribution of the Parameters , , and , and Atmospheric Stability Dependence
3.7. Influence of the Atmospheric Stability on Wind Speed Gradients
3.7.1. “Undisturbed” Horizontal Wind Speed Gradients
3.7.2. Interaction of Coastal Wind Speed Gradients with OWF Wakes
4. Discussion
5. Summary–Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Deutsche WindGuard GmbH. Status des Offshore—Windenergieausbaus Deutschland—Status 2020; Deutsche WindGuard GmbH: Varel, Germany, 2020. [Google Scholar]
- IEA. Offshore Wind Outlook; Technical Report; IEA: Paris, France, 2019. [Google Scholar]
- Lee, J.; Zhao, F. Global Wind Report 2021; Technical Report; Global Wind Energy Council (GWEC): Brussels, Belgium, 2021. [Google Scholar]
- Ramírez, L.; Fraile, D.; Brindley, G. Offshore Wind in EuropeKey Trends and Statistics 2019; Technical Report; WindEurope: Brussels, Belgium, 2020. [Google Scholar]
- Van Der Laan, M.; Pena, A.; Volker, P.; Hansen, K.S.; Sørensen, N.N.; Ott, S.; Hasager, C.B. Challenges in simulating coastal effects on an offshore wind farm. J. Phys. Conf. Ser. IOP Pub. 2017, 854, 012046. [Google Scholar] [CrossRef] [Green Version]
- Schulz-Stellenfleth, J.; Emeis, S.; Dörenkämper, M.; Bange, M.; Canadillas, B.; Neumann, T.; Schneemann, J.; Weber, I.; zum Berge, K.; Platis, A.; et al. Coastal impacts on offshore wind farms—A review focussing on the German Bight area. Meteorol. Z. 2022; accepted for Publication. [Google Scholar]
- Lange, B.; Larsen, S.; Højstrup, J.; Barthelmie, R. Importance of thermal effects and sea surface roughness for offshore wind resource assessment. J. Wind Eng. Ind. Aerodyn. 2004, 92, 959–988. [Google Scholar] [CrossRef] [Green Version]
- Taylor, P.A. A model of airflow above changes in surface heat flux, temperature and roughness for neutral and unstable conditions. Bound.-Layer Meteorol. 1970, 1, 18–39. [Google Scholar] [CrossRef]
- Taylor, P. On wind and shear stress profiles above a change in surface roughness. Q. J. R. Meteorol. Soc. 1969, 95, 77–91. [Google Scholar] [CrossRef]
- Dörenkämper, M.; Optis, M.; Monahan, A.; Steinfeld, G. On the Offshore Advection of Boundary-Layer Structures and the Influence on Offshore Wind Conditions. Bound.-Layer Meteorol. 2015, 155, 459–482. [Google Scholar] [CrossRef]
- Dörenkämper, M.; Witha, B.; Steinfeld, G.; Heinemann, D.; Kühn, M. The impact of stable atmospheric boundary layers on wind-turbine wakes within offshore wind farms. J. Wind Eng. Ind. Aerodyn. 2015, 144, 146–153. [Google Scholar] [CrossRef] [Green Version]
- Lehner, S.; Horstmann, J.; Koch, W.; Rosenthal, W. Mesoscale wind measurements using recalibrated ERS SAR images. J. Geophys. Res. Oceans 1998, 103, 7847–7856. [Google Scholar] [CrossRef]
- Djath, B.; Schulz-Stellenfleth, J. Wind speed deficits downstream offshore wind parks—A new automised estimation technique based on satellite synthetic aperture radar data. Meteorol. Z. 2019, 28, 499–515. [Google Scholar] [CrossRef]
- Ahsbahs, T.; Badger, M.; Volker, P.; Hansen, K.S.; Hasager, C.B. Applications of satellite winds for the offshore wind farm site Anholt. Wind Energy Sci. 2018, 3, 573–588. [Google Scholar] [CrossRef] [Green Version]
- Hasager, C.B.; Badger, M.; Peña, A.; Larsén, X.G.; Bingöl, F. SAR-based wind resource statistics in the Baltic Sea. Remote Sens. 2011, 3, 117–144. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Lehner, S. Observation of TerraSAR-X for studies on offshore wind turbine wake in near and far fields. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 1757–1768. [Google Scholar] [CrossRef] [Green Version]
- Djath, B.; Schulz-Stellenfleth, J.; Canadillas, B. Impact of atmospheric stability on X-band and C-band Synthetic Aperture Radar imagery of offshore windpark wakes. J. Sustain. Renew. Energy 2018, 10, 043301. [Google Scholar] [CrossRef] [Green Version]
- Ahsbahs, T.; Maclaurin, G.; Draxl, C.; Jackson, C.R.; Monaldo, F.; Badger, M. US East Coast synthetic aperture radar wind atlas for offshore wind energy. Wind Energy Sci. 2020, 5, 1191–1210. [Google Scholar] [CrossRef]
- Barthelmie, R.; Badger, J.; Pryor, S.; Hasager, C.B.; Christiansen, M.B.; Jørgensen, B. Offshore coastal wind speed gradients: Issues for the design and development of large offshore windfarms. Wind Eng. 2007, 31, 369–382. [Google Scholar] [CrossRef]
- Becker, G.A.; Dick, S.; Dippner, J.W. Hydrography of the German Bight. Mar. Ecol. Progress Ser. 1992, 91, 9–18. [Google Scholar] [CrossRef]
- Schulz-Stellenfleth, J.; Stanev, E.V. Analysis of the upscaling problem—A case study for the barotropic dynamics in the North Sea and the German Bight. Ocean Model. 2016, 100, 109–124. [Google Scholar] [CrossRef]
- Torres, R.; Snoeij, P.; Geudtner, D.; Bibby, D.; Davidson, M.; Attema, E.; Potin, P.; Rommen, B.; Floury, N.; Brown, M.; et al. GMES Sentinel-1 mission. Remote Sens. Environ. 2012, 120, 9–24. [Google Scholar] [CrossRef]
- Peter, H.; Jaggi, A.; Fernández, J.; Escobar, D.; Ayuga, F.; Arnold, D.; Wermuth, M.; Hackel, S.; Otten, M.; Simons, W.; et al. Sentinel-1A—First precise orbit determination results. Adv. Space Res. 2017, 60, 879–892. [Google Scholar] [CrossRef]
- GEBCO Compilation Group. GEBCO 2020 Grid; GEBCO Compilation Group: Paris, France, 2020. [Google Scholar]
- Koch, W. Directional Analysis of SAR images aiming at wind direction. IEEE Trans. Geosci. Remote Sens. 2004, 42, 702–710. [Google Scholar] [CrossRef]
- Koch, W.; Feser, F. Relationship between SAR-Derived Wind Vectors and Wind at 10 m Height Represented by a Mesoscale Model. Mon. Weather Rev. 2006, 134, 1505–1517. [Google Scholar] [CrossRef] [Green Version]
- Chapron, B.; Fouhaily, T.; Kerbaol, V. Calibration and Validation of ERS Wave Mode Products. Document DRO/OS/95-02; Institut Français de Recherche pour l’Exploitation de la Mer: Brest, France, 1995. [Google Scholar]
- Kerbaol, V.; Chapron, B.; Vachon, P.W. Analysis of ERS-1/2 synthetic aperture radar wave mode imagettes. J. Geophys. Res. Oceans 1998, 103, 7833–7846. [Google Scholar] [CrossRef]
- Benassai, G.; Di Luccio, D.; Corcione, V.; Nunziata, F.; Migliaccio, M. Marine spatial planning using high-resolution synthetic aperture radar measurements. IEEE J. Ocean. Eng. 2018, 43, 586–594. [Google Scholar] [CrossRef]
- Zou, Q.; He, Y.; Perrie, W.; Vachon, P.W. Wind-vector estimation for RADARSAT-1 SAR images: Validation of wind-direction estimates based upon geometry diversity. IEEE Geosci. Remote Sens. Lett. 2007, 4, 176–180. [Google Scholar] [CrossRef]
- Portabella, M.; Stoffelen, A.; Johannessen, J.A. Toward an optimal inversion method for synthetic aperture radar wind retrieval. J. Geophys. Res. Oceans 2002, 107, 1–13. [Google Scholar] [CrossRef]
- Zuhlke, M.; Fomferra, N.; Brockmann, C.; Peters, M.; Veci, L.; Malik, J.; Regner, P. SNAP (Sentinel Application Platform) and the ESA Sentinel 3 Toolbox. In Proceedings of the Sentinel-3 for Science Workshop, Venice, Italy, 2–5 June 2015; Volume 734, p. 21. [Google Scholar]
- Verhoef, A.; Portabella, M.; Stoffelen, A.; Hersbach, H. CMOD5. n-the CMOD5 GMF for Neutral Winds; Technical Report SAF/OSI/CDOP/KNMI/TEC/TN/3, 165; KNMI: De Bilt, The Netherlands, 2008. [Google Scholar]
- Leelössy, Á.; Molnár, F.; Izsák, F.; Havasi, Á.; Lagzi, I.; Mészáros, R. Dispersion modeling of air pollutants in the atmosphere: A review. Open Geosci. 2014, 6, 257–278. [Google Scholar] [CrossRef]
- Rodrigo, J.S.; Cantero, E.; García, B.; Borbón, F.; Irigoyen, U.; Lozano, S.; Fernande, P.; Chávez, R. Atmospheric stability assessment for the characterization of offshore wind conditions. J. Phys. Conf. Ser. IOP Publ. 2015, 625, 012044. [Google Scholar] [CrossRef] [Green Version]
- Charnock, H. Wind stress on a water surface. Q. J. R. Meteorol. Soc. 1955, 81, 639–640. [Google Scholar] [CrossRef]
- Alpers, W.; Hennings, I. A theory of the imaging mechanism of underwater bottom topography. J. Geophys. Res. 1984, 89, 1029–10546. [Google Scholar]
- Christiansen, M.B.; Hasager, C.B. Using Airborne and Satellite SAR for Wake Mapping Offshore. Wind Energy 2006, 9, 437–455. [Google Scholar] [CrossRef]
- Sjöholm, M.; Wagner, R.; Lindelöw, P. Commercial lidar profilers for wind energy. A comparative guide. In Proceedings of the European Wind Energy Conference and Exhibition 2008, Brussels, Belgium, 31 March–3 April 2008; Volume 6. [Google Scholar]
- Courtney, M.; Wagner, R.; Lindelöw, P. Testing and comparison of LIDARs for profile and turbulence measurements in wind energy. IOP Conf. Ser. Earth Environ. Sci. 2008, 1, 012021. [Google Scholar] [CrossRef]
- Canadillas, B.; Westerhellweg, A.; Neumann, T. Testing the performance of a ground-based wind LiDAR system: One year intercomparison at the offshore platform FINO1. DEWI Mag. 2011, 38, 58–64. [Google Scholar]
- Goit, J.; Shimada, S.; Kogaki, T. Can LiDARs Replace Meteorological Masts in Wind Energy? Energies 2019, 12, 3680. [Google Scholar] [CrossRef] [Green Version]
- Rausch, T.; Schuchard, M.; Ca nadillas, B.; Lampert, A. One Year Measurements of Vertical Profiles of Wind Speed and Wind Direction from 40 to 500 m at Heligoland, German Bight, North Sea, Germany; Technische Universität Braunschweig, PANGAEA: Braunschweig, Germany, 2020. [Google Scholar] [CrossRef]
- Schulz-Stellenfleth, J.; Lampert, A.; Emeis, S.; Dörenkämper, M.; Bange, J.; Ca nadillas, B.; Neumann, T.; Schneemann, J.; Weber, I.; zum Berge, K.; et al. Coastal impacts on offshore wind farms. Meteorol. Z. (Contrib. Atmosph. Sci.), 2021; submitted. [Google Scholar]
- Wan, H.; Giorgetta, M.A.; Zängl, G.; Restelli, M.; Majewski, D.; Bonaventura, L.; Fröhlich, K.; Reinert, D.; Rípodas, P.; Kornblueh, L.; et al. The ICON-1.2 hydrostatic atmospheric dynamical core on triangular grids–Part 1: Formulation and performance of the baseline version. Geosci. Model Dev. 2013, 6, 735–763. [Google Scholar] [CrossRef] [Green Version]
- Zängl, G.; Reinert, D.; Rípodas, P.; Baldauf, M. The ICON (ICOsahedral Non-hydrostatic) modelling framework of DWD and MPI-M: Description of the non-hydrostatic dynamical core. Q. J. R. Meteorol. Soc. 2015, 141, 563–579. [Google Scholar] [CrossRef]
- Stark, J.D.; Donlon, C.J.; Martin, M.J.; McCulloch, M.E. OSTIA: An operational, high resolution, real time, global sea surface temperature analysis system. In Proceedings of the OCEANS 2007—Europe, Aberdeen, UK, 18–21 June 2007; pp. 1–4. [Google Scholar] [CrossRef]
- Fino123 Homepage. FINO—Forschungsplattformen in Nord- und Ostsee; Fino123: Kiel, Germany, 2021. [Google Scholar]
- Borsche, M.; Kaiser-Weiss, A.K.; Kaspar, F. Wind speed variability between 10 and 116 m height from the regional reanalysis COSMO-REA6 compared to wind mast measurements over Northern Germany and the Netherlands. Adv. Sci. Res. 2016, 13, 151–161. [Google Scholar] [CrossRef] [Green Version]
- Platis, A.; Bange, J.; Bärfuss, K.; Canadillas, B.; Hundhausen, M.; Djath, B.; Lampert, A.; Schulz-Stellenfleth, J.; Siedersleben, S.; Neumann, T.; et al. Long-range modifications of the wind field by offshore wind parks—Results of the project WIPAFF. Meteorol. Z. 2020, 29, 355–376. [Google Scholar] [CrossRef]
- Emeis, S.; Siedersleben, S.; Lampert, A.; Platis, A.; Bange, J.; Djath, B.; Schulz-Stellenfleth, J.; Neumann, T. Exploring the wakes of large offshore wind farms. J. Phys. Conf. Ser. IOP Pub. 2016, 753, 092014. [Google Scholar] [CrossRef] [Green Version]
- Platis, A.; Siedersleben, S.K.; Bange, J.; Lampert, A.; Bärfuss, K.; Hankers, R.; Cañadillas, B.; Foreman, R.; Schulz-Stellenfleth, J.; Djath, B.; et al. First in situ evidence of wakes in the far field behind offshore wind farms. Sci. Rep. 2018, 8, 2163. [Google Scholar] [CrossRef]
- Cañadillas, B.; Foreman, R.; Barth, V.; Siedersleben, S.; Lampert, A.; Platis, A.; Djath, B.; Schulz-Stellenfleth, J.; Bange, J.; Emeis, S.; et al. Offshore wind farm wake recovery: Airborne measurements and its representation in engineering models. Wind Energy 2020, 23, 1249–1265. [Google Scholar] [CrossRef]
- Wagner, D.; Steinfeld, G.; Witha, B.; Wurps, H.; Reuder, J. Low Level Jets over the Southern North Sea. Meteorol. Z. 2019, 28, 389–415. [Google Scholar] [CrossRef]
- Zou, Z.; Zhao, D.; Liu, B.; Zhang, J.A.; Huang, J. Observation-based parameterization of air-sea fluxes in terms of wind speed and atmospheric stability under low-to-moderate wind conditions. J. Geophys. Res. Oceans 2017, 122, 4123–4142. [Google Scholar] [CrossRef]
- Takeyama, Y.; Ohsawa, T.; Kozai, K.; Hasager, C.B.; Badger, M. Comparison of geophysical model functions for SAR wind speed retrieval in Japanese coastal waters. Remote Sens. 2013, 5, 1956–1973. [Google Scholar] [CrossRef] [Green Version]
- Mulhearn, P. On the formation of a stably stratified internal boundary-layer by advection of warm air over a cooler sea. Bound.-Layer Meteorol. 1981, 21, 247–254. [Google Scholar] [CrossRef]
- Garratt, J.; Ryan, B. The structure of the stably stratified internal boundary layer in offshore flow over the sea. Bound.-Layer Meteorol. 1989, 47, 17–40. [Google Scholar] [CrossRef]
- Barthelmie, R.; Palutikof, J. Coastal wind speed modelling for wind energy applications. J. Wind Eng. Ind. Aerodyn. 1996, 62, 213–236. [Google Scholar] [CrossRef]
- Garratt, J. The internal boundary layer—A review. Bound.-Layer Meteorol. 1990, 50, 171–203. [Google Scholar] [CrossRef]
- Platis, A.; Hundhausen, M.; Lampert, A.; Emeis, S.; Bange, J. The Role of Atmospheric Stability and Turbulence in Offshore Wind-Farm Wakes in the German Bight. Bound.-Layer Meteorol. 2021, 182, 441–469. [Google Scholar] [CrossRef]
- Pryor, S.; Barthelmie, R. Analysis of the effect of the coastal discontinuity on near-surface flow. Ann. Geophys. 1998, 16, 882–888. [Google Scholar] [CrossRef]
- Emeis, S. A simple analytical wind park model considering atmospheric stability. Wind Energy 2010, 13, 459–469. [Google Scholar] [CrossRef]
- Christiansen, M.B.; Hasager, C.B. Wake effects of large offshore wind farms identified from satellite SAR. Remote Sens. Environ. 2005, 98, 251–268. [Google Scholar] [CrossRef]
- Platis, A.; Hundhausen, M.; Siedersleben, S.; Lampert, A.; Bärfuss, K.; Schulz-Stellenfleth, J.; Djath, B.; Emeis, S.; Neumann, T.; Canadillas, B.; et al. Evaluation of a simple analytical model for offshore wind farm wake recovery by in-situ data and Forecasting simulations. Wind Energy 2020, 24, 212–228. [Google Scholar] [CrossRef]
- Meyers, J.; Meneveau, C. Optimal turbine spacing in fully developed wind farm boundary layers. Wind Energy 2012, 15, 305–317. [Google Scholar] [CrossRef] [Green Version]
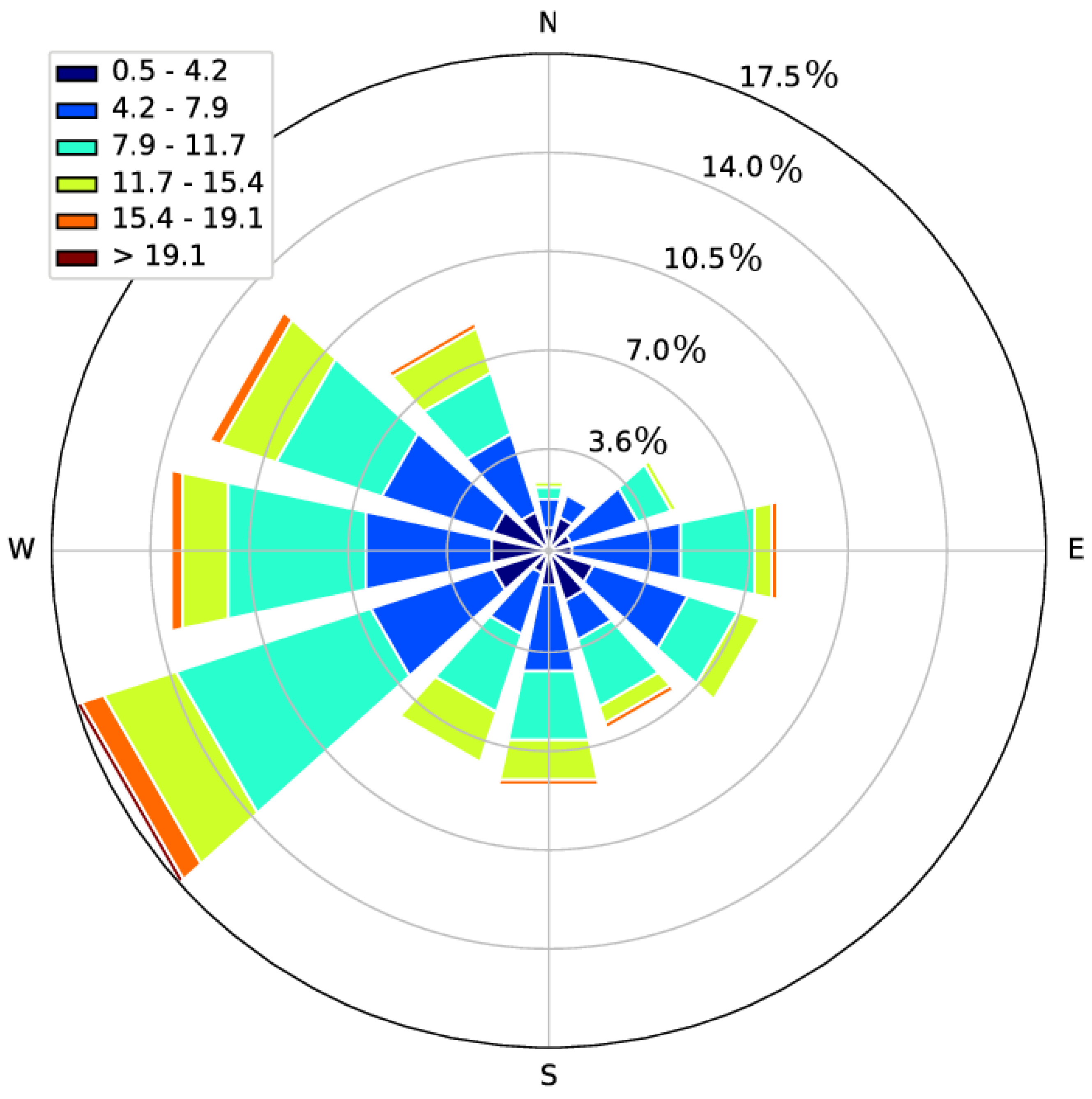






| Offshore Winds | Wind Direction Range (°) | Samples |
|---|---|---|
| Easterly | 60 120 | 70 |
| Southerly | 160 200 | 47 |
| All wind directions | 447 |
| Shape Types | Samples (Percentage) | (m/s) |
|---|---|---|
| Easterly wind | ||
| Increasing (“INCS”) | 60% | ∼3 |
| Decreasing (“DECS”) | 22% | ∼−2 |
| Late increasing (“LINCS”) | 15% | ∼2 |
| Southerly wind | ||
| Increasing (“INCS”) | 62% | ∼2 |
| Decreasing (“DECS”) | 19% | ∼−1 |
| Late increasing (“LINCS”) | 15% | ∼2 |
| Atmospheric Stability | (m/s) | (km) | (%) | (m/s) | (m/s) |
|---|---|---|---|---|---|
| Easterly wind | |||||
| Unstable | 3.2 | 72 | 37 | 8.6 | 11.9 |
| Stable | 2.8 | 115 | 78 | 3.7 | 6.5 |
| Southerly wind | |||||
| Unstable | 2.3 | 30 | 31 | 7.5 | 9.8 |
| Stable | 2.4 | 50 | 43 | 5.4 | 7.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Djath, B.; Schulz-Stellenfleth, J.; Cañadillas, B. Study of Coastal Effects Relevant for Offshore Wind Energy Using Spaceborne Synthetic Aperture Radar (SAR). Remote Sens. 2022, 14, 1688. https://doi.org/10.3390/rs14071688
Djath B, Schulz-Stellenfleth J, Cañadillas B. Study of Coastal Effects Relevant for Offshore Wind Energy Using Spaceborne Synthetic Aperture Radar (SAR). Remote Sensing. 2022; 14(7):1688. https://doi.org/10.3390/rs14071688
Chicago/Turabian StyleDjath, Bughsin’, Johannes Schulz-Stellenfleth, and Beatriz Cañadillas. 2022. "Study of Coastal Effects Relevant for Offshore Wind Energy Using Spaceborne Synthetic Aperture Radar (SAR)" Remote Sensing 14, no. 7: 1688. https://doi.org/10.3390/rs14071688
APA StyleDjath, B., Schulz-Stellenfleth, J., & Cañadillas, B. (2022). Study of Coastal Effects Relevant for Offshore Wind Energy Using Spaceborne Synthetic Aperture Radar (SAR). Remote Sensing, 14(7), 1688. https://doi.org/10.3390/rs14071688






