Unsupervised Infrared Small-Object-Detection Approach of Spatial–Temporal Patch Tensor and Object Selection

Abstract

In this study, an unsupervised infrared object-detection approach based on spatial–temporal patch tensor and object selection is proposed to fully use effective temporal information and maintain a balance between object-detection performance and computation time. Initially, a spatial–temporal patch tensor is proposed by performing median pooling function on patch tensors generated from consecutive frames to suppress sky or cloud clutter. Then, a contrast-boosted approach that incorporates morphological operations is proposed to improve the contrast between objects and background. Finally, an object-selection approach is proposed based on the cluster center derived from clustering locations and gray values, thereby decreasing the search scope of objects in the detection process. The experiments of five infrared sequence frames confirm that the proposed framework can obtain better results than most previous methods when handling heterogeneous scenes in terms of gray values. Experimental results of five real sequence frames also demonstrate that the spatial–temporal patch tensor, the contrast-boosted approach, and object-selection approach can increase the recall ratio by 6.7, 2.21, and 1.14 percentage units and the precision ratio by 1.61, 3.44, and 11.79 percentage units, respectively. Moreover, the proposed framework can achieve an average F1 score of 0.9804 with about 1.85 s of computation time, demonstrating that it can obtain satisfactory object-detection performance with relatively low computation time.

1. Introduction

Infrared search-and-track systems (ISTS) have been widely applied to military applications such as missile warning, precision guidance, and space surveillance [1,2,3]. Infrared small-object detection is one of the most important techniques that can influence the performance of ISTS [4]. Infrared small-object detection aims to detect objects including ships, airplanes, and vehicles on backgrounds of sea, sky, and land [5,6]. 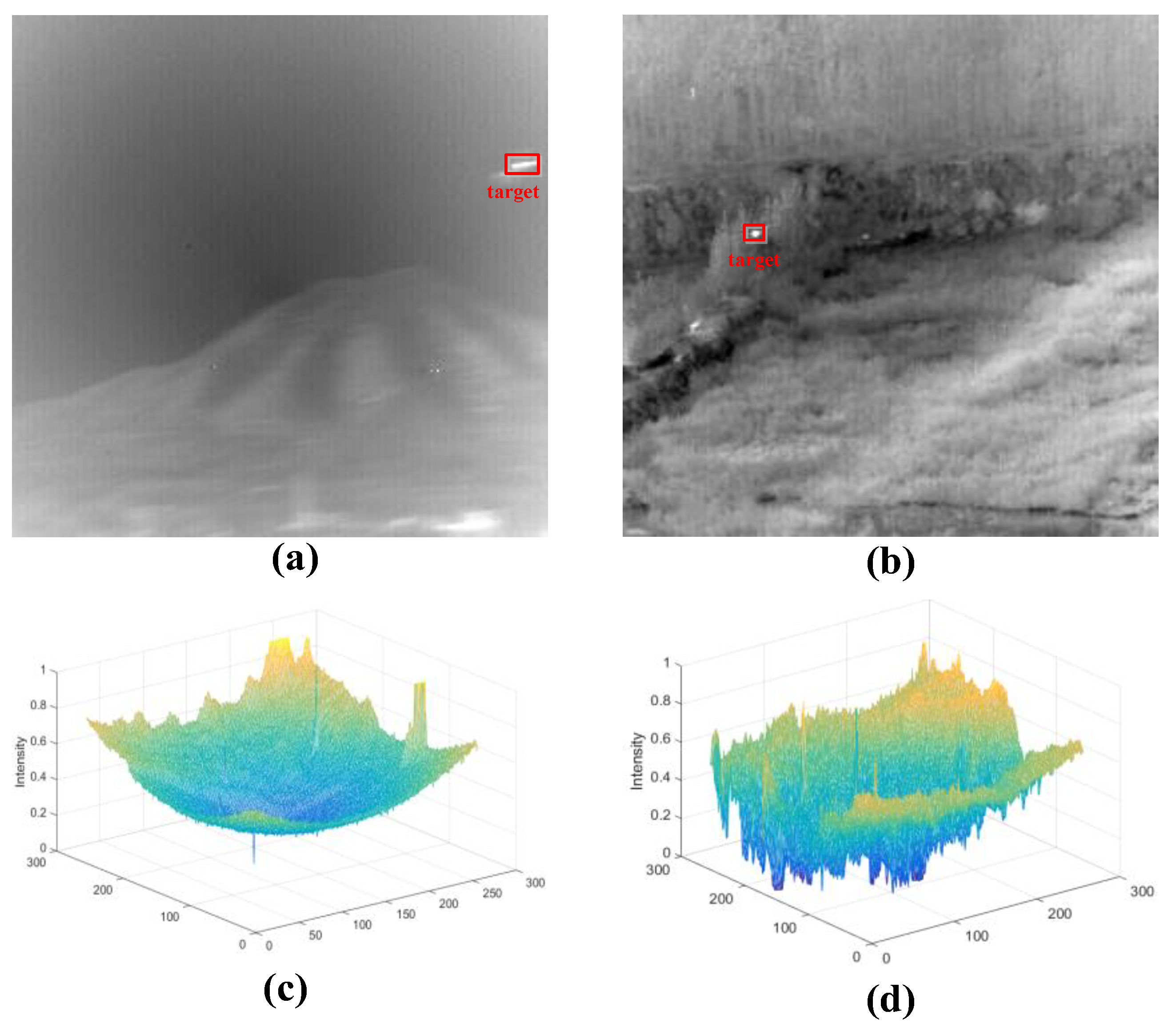However, as shown in Figure 1, unmanned aerial vehicle (UAV) objects in infrared images may take up only several pixels, with little structural or texture information because they are far from the imaging sensor [7,8]; thus, they may reduce the detection robustness. Moreover, complex backgrounds, such as cloud clutter and sea clutter, may lead to low signal-to-clutter ratio (SCR) [9,10], which may increase the difficulty of detecting small objects in infrared images. For example, artificial heat sources and heavy clouds may increase the false-alarm rates [11]. Therefore, detecting objects with infrared image sequences is still a difficult problem.

Figure 1. UAV objects in infrared images and their intensity distributions. (a) UAV object under the sky background. (b) UAV object under the ground background. (c) Intensity distribution of infrared image (a). (d) Intensity distribution of infrared image (b).

Infrared object-detection methods usually consist of single-frame-based methods and sequence-based methods according to the number of frames used for detecting objects in infrared images [12]. Sequence-based methods including 3D matched filter [13], dynamic programming [14], pipeline filter [15], and Kalman filter [16], assume that the background is static between adjacent frames of the same image sequence. Nevertheless, the background usually changes rapidly in military applications because sensor platforms used for ISTS move fast even though the objects to be detected may remain static [17]. Therefore, sequence-based approaches are unsuitable for potential applications. Single-frame-based methods that detect objects in each frame by exploring the consistency between background pixels are investigated because they can represent the background information more accurately.

The prior information is one of the most important components in single-frame-based infrared object-detection methods [18]. The infrared object-detection approaches can be categorized into two types based on the type of prior information used, namely, local prior-based methods and nonlocal prior-based methods [19].

Local prior-based approaches exploit a local background consistent prior that assumes the background is slowly transitional and close background pixels are highly correlated [20]. However, real objects may break the local correlation hidden in the background pixels. Under this assumption, traditional local prior-based approaches include 2D least-mean-square filter [21], morphological filter [22], max-median filter [23], and their improved methods. Unfortunately, traditional filters improve the edges of objects as well as the sky–sea surface or heavy cloud clutter because these background structures also break the local correlation. Approaches based on the saliency map that computes the difference between objects and their neighborhood have been proposed to better distinguish objects and background structures [24]. Multiscale patch-based contrast measure [25], local contrast measure (LCM) [26], laplacian of Gaussian filter [27], multiscale gray difference weighted image entropy [28], nonnegativity constrained variational mode decomposition [29], and saliency in the Fourier domain [30] are used to obtain saliency maps. The local prior-based methods may suffer from a nonuniform or heterogeneous background that ruins the spatial consistency, thereby leading to a high false-alarm rate [31].

Different from local priors, nonlocal priors explore the nonlocal self-correlation property of background patches by taking advantage of target sparsity and low-rank of background pixels in infrared images [32]. Essentially, these types of methods model objects in infrared images as a sparse representation of the input data. A classical nonlocal prior-based approach called the infrared patch image (IPI) model [33] is proposed by taking advantage of the nonlocal relation between background images. However, it suffers from over-shrinking of targets and noise residual due to the nuclear norm of the low-rank regularization term. Therefore, some improved versions of IPI are proposed by better reconstructing a low-rank matrix. The patch tensor model [34] can explore the nonlocal information on the assumption of low-rank unfolding matrices. Dictionary learning and principal component pursuit approaches can separate the background and target matrix from the original image. However, they cannot effectively handle infrared images with complex background. Total variation should be combined with principal component pursuit to address this problem [35]. However, the result may be a local minimum because it approximates the $l_0-norm$ [36] that represents the total number of nonzero elements as the $l_1-norm$ [37], representing the sum of the magnitudes. Moreover, $l_p-norm=({\displaystyle \sum _{\mathrm{i}=1}^n|x_i{|}^p}{)}^{\frac{1}{p}}$ [38] is used to optimize the infrared small-object detection approaches to better reach the global minimum [39]. To accurately detect the small target located in a highly heterogeneous background, a low-rank and sparse representation model is proposed under the multi-subspace cluster assumption [40]. The nonlocal priors are more powerful and fit the real scenes effectively, but still suffer from sparse edges and noise [41]. Moreover, existing approaches are faced with two drawbacks, namely, target edges highlighted along with background edges, as shown in Figure 2a, and no clear edges, as shown in Figure 2b.

Figure 2. Drawbacks of existing prior-based methods. (a) Target edges highlighted along with background edges. (b) No clear edges but the target is similar to the background.

A novel infrared object-detection approach based on spatial–temporal patch tensor and object selection is proposed to fully use effective information in the temporal domain and to maintain a balance between the object-detection performance and computation time. Using the spatial–temporal patch tensor, color-boosted and object selection approach, UAV targets under sky or cloud background can be detected in target images reconstructed from original infrared images. The major contributions of this study are as follows:

• The proposed framework is an unsupervised infrared object-detection method which can provide effective means for infrared small-object detection when no labeled information of true UAV targets is acquired.
• The proposed spatial–temporal patch tensor can dig out the spatial and temporal evidence hidden in infrared image sequences by performing median pooling operations on three adjacent frames to further suppress the sky or cloud clutter and enable a better target-detection performance.
• An object-selection approach is proposed to automatically extract objects from infrared images based on the cluster center derived from unsupervised clustering, which can decrease the search scope of objects and the false-alarm rates.

This paper is organized as follows. Section 2 introduces the proposed framework for infrared small-object detection consisting of constructing spatial–temporal patch tensor, contrast-boosted, and object-selection approach. Then, the dataset description and experimental setup are depicted in Section 3. Experimental results and their analysis are shown in Section 4. Section 5 concludes the study, and is then followed by future directions.

2. Materials and Methods

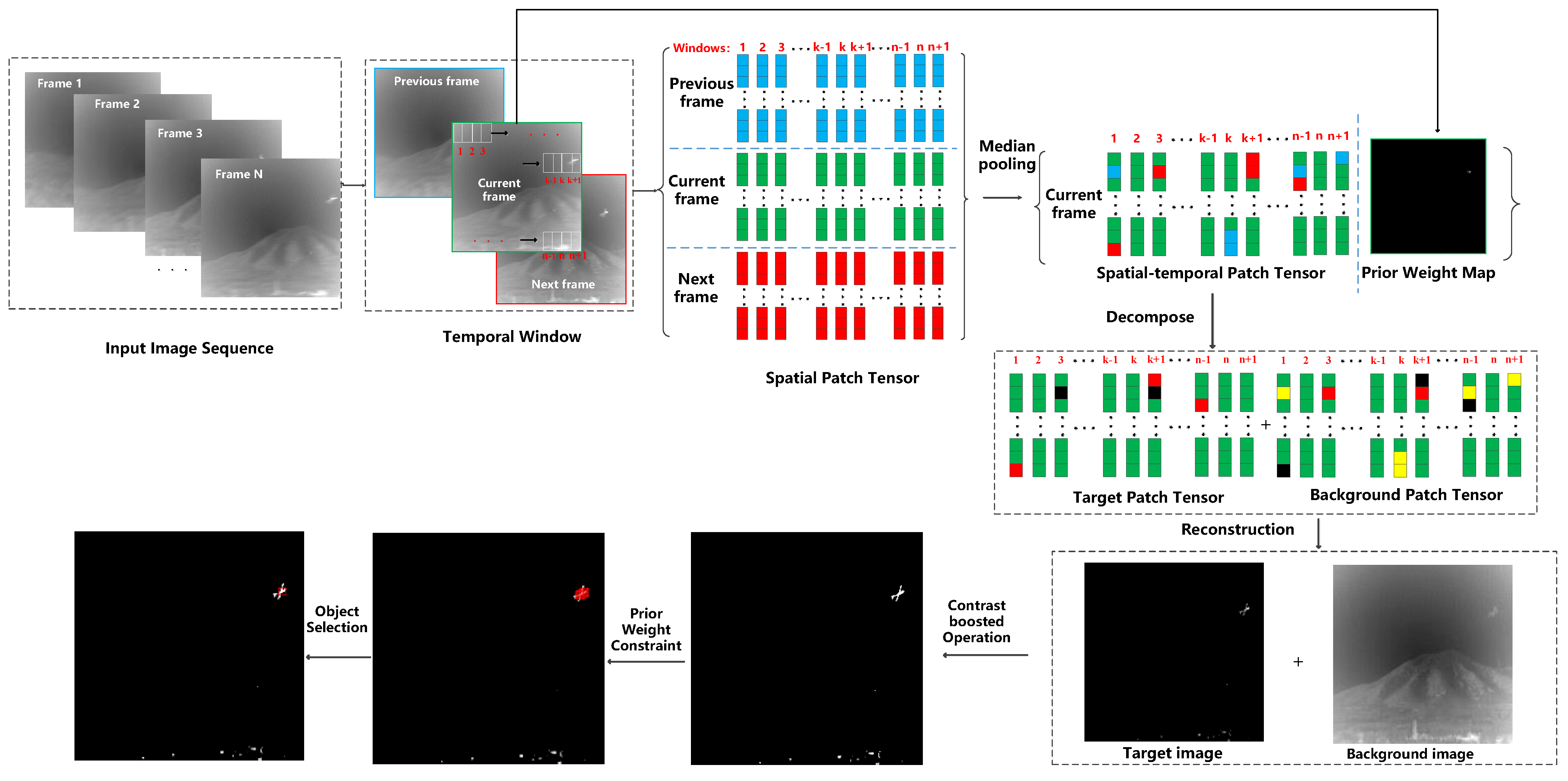
An unsupervised infrared UAV target-detection method based on spatial–temporal patch tensor and object selection is proposed in this study. Figure 3 shows that the proposed method can be divided into the following steps.

Figure 3. The overall architecture of the proposed framework.

• Constructing spatial–temporal patch tensor for each frame of infrared image sequences. For each frame of the infrared image sequence, its temporal window is constructed with three adjacent frames. Patch tensor is constructed for each frame of the temporal window with t sliding windows whose size is $k\times k$. Median pooling is applied to the patch tensor of all frames in the temporal window to obtain the spatial–temporal patch tensor $P\in R^{k\times k\times t}$.
• Calculating prior weight map and its patch tensor. The prior weight maps that can reflect the background and object information in infrared images to some extent are calculated for each temporal frame by combining local and nonlocal priors. Patch tensor of prior weight map $W_P\in R^{k\times k\times t}$ is constructed for each temporal frame with t sliding windows with a size of $k\times k$.
• Decomposing background and target patch tensor from the spatial–temporal patch tensor $P$ and patch tensor of prior weight map $W_P$. The patch tensor of temporal frame $P\in R^{k\times k\times t}$ is separated into a sparse patch tensor $T\in R^{k\times k\times t}$ and a low-rank patch tensor $B\in R^{k\times k\times t}$ with the constraint of $W_P$, which can be considered a target and background patch tensor.
• Reconstructing background and target images from background and target patch tensors. Background image $I_B$ and target image $I_T$ are reconstructed from the background patch tensor $B$ and target patch tensor $T$.
• Performing the proposed contrast-boosted method on reconstructed target images. To enhance the contrast between gray values of background pixels and target pixels, the contrast-boosted approach that combines Tophat operations with Bothat operations are performed on reconstructed target images to obtain enhanced target images.
• Segmenting UAV targets from the enhanced target images by the object-selection approach based on the cluster center. Candidate pixels that satisfy the threshold of prior weight map are obtained for each frame. Then, the object-selection approach is proposed to determine the optimal object number by clustering the candidate object pixels. Each cluster center is considered a detected object.

2.1. Construction of Spatial–Temporal Patch Tensor and Prior Weight Map

Construction of spatial–temporal patch tensor: The existing infrared object-detection methods are usually based on the spatial patch tensor, which may ignore the temporal information hidden in infrared image sequences. Therefore, a spatial–temporal patch tensor is proposed to solve this problem.

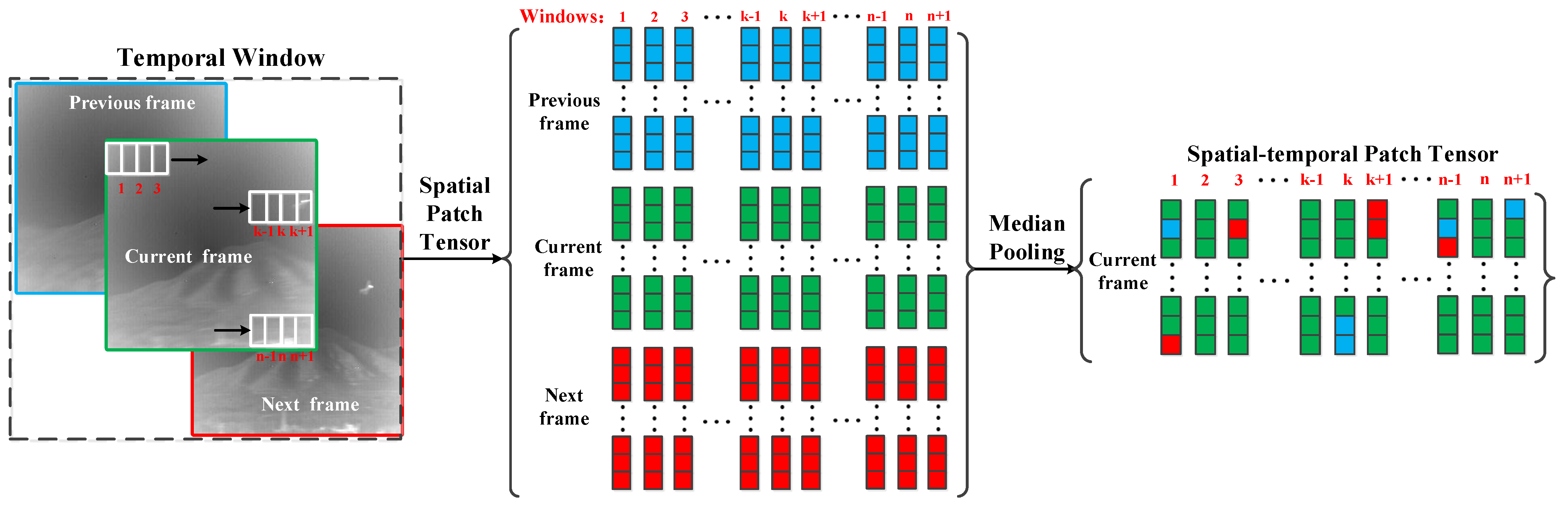
The main idea of spatial–temporal patch tensor is shown in Figure 4. Given an infrared image sequence consisting of three frames $I_{k-1},I_k,I_{k+1}$ in a sliding window $\omega \times h\times 3$, a temporal window is initially constructed for each frame, namely, $I_{k-1},I_k,I_{k+1}$. Then, a spatial patch tensor is constructed for each frame of the temporal window. Finally, median pooling is performed on all spatial patch tensors to obtain the spatial–temporal patch tensor.

Figure 4. Sketch map of constructing spatial–temporal patch tensor.

The idea of constructing a spatial patch tensor should be explained prior to illustrating a spatial–temporal patch tensor. Overlapped local patches may contain spatial information hidden in pixels because different patches may include the same pixel in one image. Therefore, a spatial patch tensor from generated overlapped local patches in infrared images is constructed. The procedure can be illustrated as follows. Initially, overlapped local patches are generated from left to right and top to bottom in each frame of infrared image sequences. Then, gray values of each pixel in the overlapped local patches are vectorized as a column of a tensor. Finally, vectors of all local patches in the frame form the spatial patch tensor.

The details of constructing a spatial–temporal patch tensor can be illustrated as follows. A temporal window $I_{k-1},I_k,I_{k+1}$ is constructed for frame $I_k$ to fully use the temporal information. For each frame in the temporal windows, spatial patch tensors $P_{k-1},P_k,P_{k+1}$ are constructed. Three patch tensors in the temporal window that are generated by the local patch located in the same place of image are highly correlated because adjacent frames are usually highly correlated in image sequences. Therefore, the spatial patch tensors in the temporal may be redundant. To reduce the redundancy of the spatial patch tensor and fully use temporal information, median pooling is performed on three spatial patch tensors, as shown in Equation (1), as follows:

$$P_{median}=median(P_{k-1},P_k,P_{k+1}),$$

(1)

where the median value of corresponding elements of three spatial patch tensors is considered the value of the spatial–temporal patch tensor.

The size of the spatial–temporal patch tensor is the same as that of the spatial patch tensor for each frame but with richer temporal information. The spatial–temporal patch tensor can enrich the temporal information and better represent each frame of infrared image sequences.

Construction of prior weight map: Existing prior weight-based methods use structure tensors [42] to distinguish between image boundaries and real objects. Structure tensors are widely used in many partial differential equation (PDE)-based methods [43] to estimate the local structure information in the image, including edge orientation. To integrate the local information, the structure tensor is constructed based on a local regularization of a tensorial product, which is defined in Equation (2), as follows:

$$J_{\alpha }(\nabla I_{\sigma })=G_{\alpha }\ast (\nabla I_{\sigma }\otimes I_{\sigma })=\left(\begin{array}{l}{J}_{11} J_{12}\\ J_{21} J_{22}\end{array}\right)$$

(2)

where $I_{\sigma }$ is a Gaussian-smoothed version of a given image I. $\sigma >0$ is the standard deviation of the Gaussian kernel; it denotes the noise scale, making the edge detector ignorant of small details. $J_{\alpha }$ is a symmetric and positive semi-definite matrix.

Two highest eigenvalues ${\lambda }_1$ and ${\lambda }_2$ of the structure tensor can be used as two feature descriptors of the local geometry structure, which can be calculated as Equation (3).

$${\lambda }_1,{\lambda }_2=(J_{11}+J_{22})\pm \sqrt{{(J_{22}-J_{11})}^2+4J_{12}^2}$$

(3)

A combination of eigenvalues can enhance image boundaries, which can distinguish image boundaries similar to those of targets. The existing local prior is designed in Equation (4).

$$W_{LP}=\exp (h\times \frac{(L_1-L_2)-d_{\min }}{d_{\max }-d_{\min }})$$

(4)

where $L_1$ and $L_2$ can be calculated by applying Equations (2) and (3) to every pixel in the input image I, h is a weight-stretching parameter, $d_{\max }$ and $d_{\min }$ are the maximum and minimum of eigenvectors $L_1$ and $L_2$, respectively.

However, ${\lambda }_1-{\lambda }_2$ operator cannot identify whether image boundaries are background or targets. As a result, objects located at corner regions disappear or over-shrink.

To address these problems, the prior weight map $W_P$ improves the corner strength function $W_{cs}$ [44], as shown in Equations (5) and (6).

$$W_P(x,y)=\max ({\lambda }_1,{\lambda }_2)W_{cs}$$

(5)

$$W_{cs}=\frac{{\lambda }_1{\lambda }_2}{{\lambda }_1+{\lambda }_2}$$

(6)

where $(x,y)$ represents the location of pixel. The prior weight map $W_P$ consists of two parts. The first part $\max ({\lambda }_1,{\lambda }_2)$ replaces the ${\lambda }_1-{\lambda }_2$ operator with the maximum operator $\max ({\lambda }_1,{\lambda }_2)$ to suppress the problem in the ${\lambda }_1-{\lambda }_2$ operator to some extent. In the second part, ${\lambda }_1+{\lambda }_2$ and ${\lambda }_1{\lambda }_2$ denote the trace and determinant of the structure tensor, respectively. The second part, namely, $W_{\mathit{cs}}$ can not only highlight object information as expected, but also identify the objects located at corner regions.

Then, the prior weight map $W_P$ is normalized with Equation (7).

$$W_P=\frac{W_P-W_{\min }}{W_{\max }-W_{\min }},$$

(7)

where $W_{\min }$ and $W_{\max }$ represent the minimum and the maximum of the prior weight map $W_P$, respectively.

2.2. Reconstructing Background and Target Images from Spatial–Temporal Patch Tensor

Reconstructing background and target patch tensor: Existing methods impose tensor robust principal component analysis [45] to separate sparse and low-rank tensors, as shown in Equation (8).

$$\underset{B,T}{\min } rank(B)+\lambda {\Vert T\Vert }_0 s.t.D=B+T,$$

(8)

where D, B and T represent the input, background, and target patch tensor, respectively; $\lambda$ represents the tradeoff parameter between the background patch tensor and target patch tensor. ${\Vert \Vert }_0$ represents the number of nonzero elements. However, the low-rank of tensors cannot be evaluated in a mathematical approach.

To approximate the rank of the patch tensor more accurately and to incorporate prior information into the model that separates low-rank and sparse matrices, the objective function is modified in Equation (9), as follows:

$$\underset{B,T}{\min }{\displaystyle \sum _{i=1}^{n_3}{\displaystyle \sum _{i=N+1}^{\min (n_1,n_2)}{\sigma }_i(B)}}+\lambda {\Vert T\otimes W_{rec}\Vert }_1,B\in R^{n_1\times n_2\times n_3}$$

(9)

where $\otimes$ represents the Hadamard product [46], and ${\Vert \Vert }_1$ represents the sum of absolute values of all elements in the tensor. Each element in $W_{rec}$ represents the reciprocals of the corresponding element in $W_P$. N represents the preserved target rank, and ${\sigma }_i(B)$ is the i-th largest singular value of B. The objective function Equation (9) can be solved with alternating direction method of multiplier (ADMM) solver [47] whose procedure is shown in Algorithm 1.

Algorithm 1.ADMM solver

Input: Patch tensor of original image D, prior weight map $W_p$, tradeoff parameter $\lambda$, penalty factor ${\mu }_0$, preserved target rank N, stopping threshold $\xi$, and learning rate of penalty factor $\rho$.

Output: Patch tensor of target and background images $T_k$ and $B_k$.

Initialize:$B_k$ = $T_k$ = 0, ${\mu }_0=3\times {10}^{-3}$, $\rho =1.1$, k = 0.

(1)    Calculate the Langrangian function of Equations (9) with Equation (10). $$L(B,T,W,M)={\displaystyle \sum _{i=1}^{n_3}{\Vert B\Vert }_{p=N}+\lambda {\Vert T\otimes W_{rec}\Vert }_1+(B+T-D)\oplus y+\frac{\mu }{2}}{\Vert B+T-D\Vert }_F^2$$ (10)     where $y$ represents the langrangian multiplier. $\oplus$ is the inner product of two tensors and ${\Vert \Vert }_F$ is the Frobenius norm.

(2)    While not end of convergence do

(3)      Calculate $T_{k+1}$ when fixing other parameters by solving Equation (11). $$T_{k+1}=\underset{T}{\arg \min }\lambda \Vert T\otimes W_{rec}\Vert +\frac{{\mu }_k}{2}{\Vert B_k+T-D+\frac{y_k}{{\mu }_k}\Vert }_F^2$$ (11)

(4)      Calculate $B_{k+1}$ when fixing other parameters by solving Equation (12). $$B_{k+1}=\underset{B}{\arg \min }{\displaystyle \sum _{i=1}^{n_3}{\Vert B\Vert }_{p=N}}+\frac{{\mu }_k}{2}{\Vert B+T_{k+1}-D+\frac{y_k}{{\mu }_k}\Vert }_F^2$$ (12)

(5)      Calculate $y_{k+1}$ and ${\mu }_{k+1}$ with Equations (13) and (14), respectively. $$y_{k+1}=y_k+{\mu }_k(D-B_{k+1}-T_{k+1})$$ (13) $${\mu }_{k+1}=\rho {\mu }_k$$ (14)

(6)      Check the stopping criterion shown in Equation (15). $$\frac{{\Vert T_{k+1}\Vert }_0-{\Vert T_k\Vert }_0}{{\Vert T_k\Vert }_0}\prec \xi$$ (15)

(7)      k = k + 1

(8)    End while

(9)  Return: background and target patch tensor $B_{k+1}$ and $T_{k+1}$

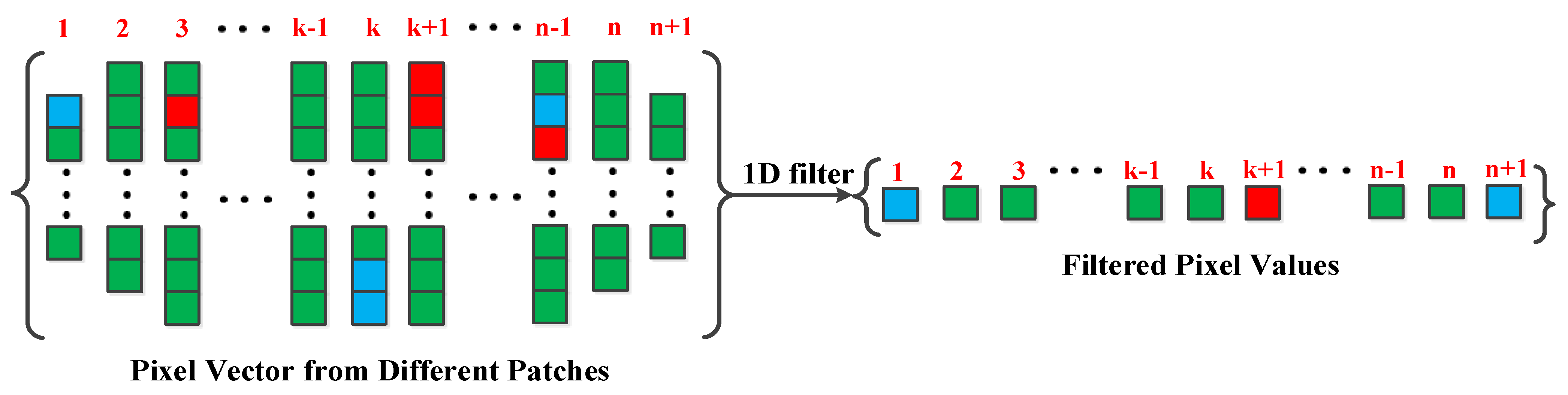
As shown in Figure 5, diverse types of patches may include the same pixel because local patches generated by the spatial patch tensor are usually overlapped. As a result, a pixel in infrared images may have several pixel values due to overlapped local patches. To determine pixel values from overlapped patches, a median function is introduced to reconstruct each pixel value as the median values of pixel values from overlapped patches, as shown in Equation (16).

$$v=median(x)$$

(16)

where $v\in R$ and $x\in R^p$ are vectors including pixel gray values from p local patches.

Figure 5. Reconstruction of pixel values from patch tensor.

Contrast-boosted approach for target images: When reconstructing target and background images from original images, gray values of objects are lost in the background image to some extent because parts of objects are similar to the backgrounds. Therefore, target images should be enhanced in terms of the contrast between object and background to better distinguish between target and background pixels. Therefore, a contrast-boosted approach that combines Tophat [48] with Bothat [49] operations is proposed.

The contrast-boosted approach is performed to achieve an enhanced target image $T_E$, as shown in Equation (17), as follows:

$$T_E=T+T_{tophat}-T_{bothat}$$

(17)

where $T_{tophat}$ and $T_{bothat}$ can be computed as Equations (18) and (19).

$$T_{tophat}=T-(T\ast b)÷b,$$

(18)

$$T_{bothat}=(T÷b)\times b-T,$$

(19)

where b represents the structure elements, $\times$ represents the dilation operation, and $÷$ represents the erosion operation.

As shown in Figure 6, the gray values of objects are improved after performing the contrast-boosted method shown in Equation (17) on target images. The enhanced target images can better distinguish between background pixels and object pixels, thereby decreasing the false-alarm rate.

Figure 6. Target image and enhanced target images.

2.3. Object-Selection Approach Based on the Cluster Center

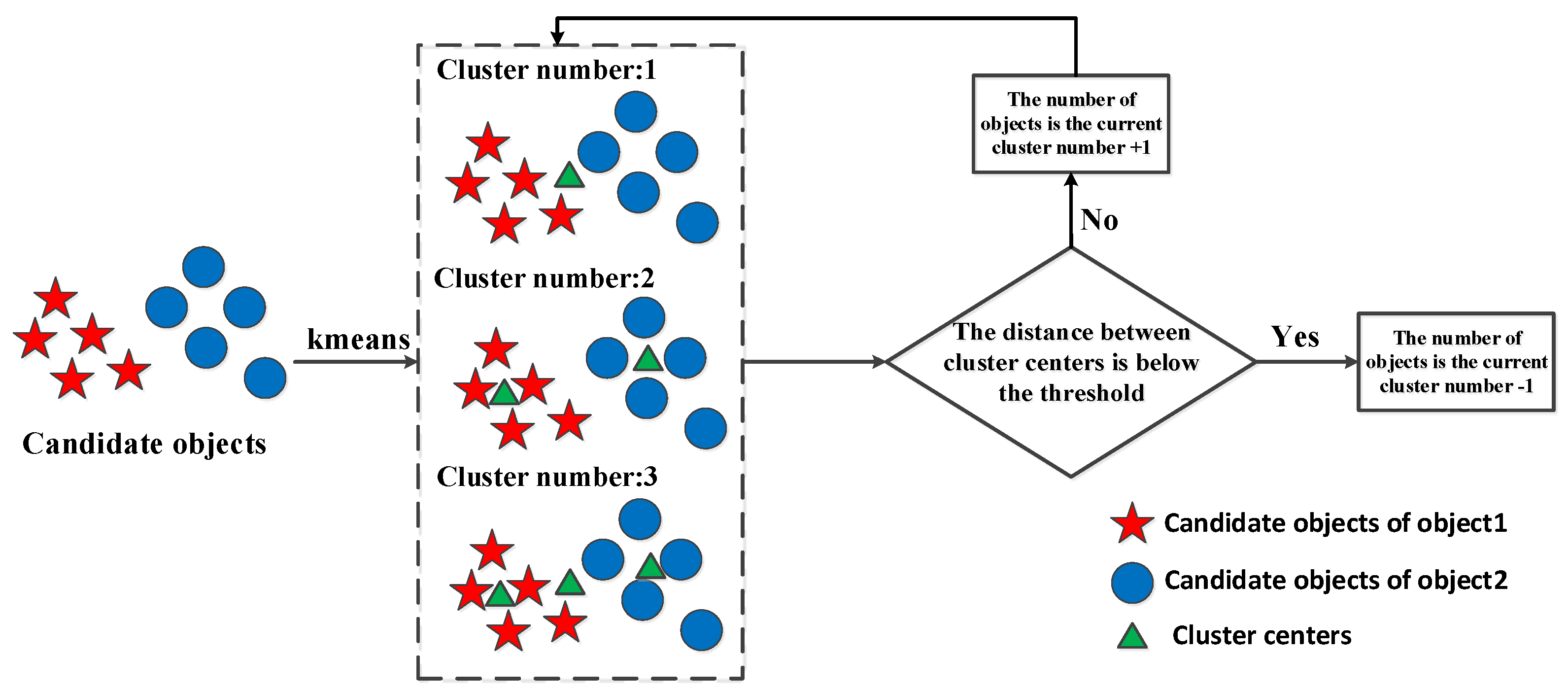
After obtaining enhanced target images, objects should be detected. When detecting objects in target images, the number of objects should be determined. Therefore, an object-selection approach is proposed for improving target images based on the cluster center derived from clustering locations and gray values. The main idea of determining the optimal number of objects is shown in Figure 7. The object selection approach can be divided into the following steps:

Figure 7. Determination of object number from candidate objects.

A predefined threshold $\tau$ is used to select candidate object pixels because the prior weight maps calculated can reflect the possibility that one pixel belongs to the target.

Then, the optimal number of objects is determined by clustering candidate object pixels in terms of locations and gray values with k-means based on the assumption that close candidate object pixels are likely to belong to the same object. The procedure of determining the optimal number of objects is shown in Algorithm 2.

Algorithm 2.Determination of optimal object number

Input: Locations and gray values of candidate objects $L_c$ and $G_c$, the stopping threshold ${\tau }_1$ and ${\tau }_2$.

Output: The optimal object number $O_k$.

Initialize: Cluster number k = 1.

(1)   Cluster locations and gray values of candidate object pixels with k-means and cluster number k, respectively.

(2)    While not end of convergence do

(3)       k = k + 1.

(4)        Calculate the distance between each cluster center derived from clustering locations and locations, respectively, with Equations (20) and (21). $$D_c^l={\Vert c_i^l-c_j^l\Vert }_2$$ (20) $$D_c^g={\Vert c_i^g-c_j^g\Vert }_2$$ (21)

where $c_i^l$ and $c_i^g$ represent the i-th cluster center derived from locations and gray values of candidate object pixels, respectively.

(5)         Check the stopping criterion shown in Equation (22). $$\Vert D_c^l\Vert \le {\tau }_1 \& \Vert D_c^g\Vert \le {\tau }_2$$ (22)

(6)     End while

(7)    Return: optimal object number k − 1

Finally, cluster locations of candidate object pixels with the determined optimal object number. Each cluster is considered a detected object.

The object-selection approach can decrease the false-alarm rate and the search scope of objects to obtain satisfactory object-detection performance with relatively low computation time.

3. Results

3.1. Description of the Datasets and Experimental Setup

3.1.1. Description of the Datasets

Five infrared approaches are employed to evaluate the performance of the proposed infrared UAV target-detection method. The first dataset [50] is aimed at detecting and tracking small UAV targets under the ground or sky background. This dataset is denoted as dataset 1. Four representative image sequences are selected from 22 image sequences to evaluate the proposed method under various scenes, namely, Sequence 3, Sequence 4, Sequence 16, and Sequence 18. Dataset 1 can be downloaded at the web address of http://www.dx.doi.org/10.11922/sciencedb.902 (accessed on 6 March 2022). Table 1 describes the detailed information about all five infrared image sequences, and Figure 8 shows the examples and ground truth of four infrared image sequences in dataset 1. All thermal images have the same size of 256 × 256. The spatial resolution of this dataset ranges from 10 m to 100 m. The distance to targets ranges from 50 m to 500 m. The object in this dataset ranges from 3 pixels to 10 pixels due to diverse distances to targets. The ground truth of the dataset provides each image frame with its number of objects and the center of object.

Table 1. Details of five representative infrared image sequences.

Sequences	Number of Frames	Average SCR Values	Description of Scenes
3	100	2.17	Single object, close imaging distance, mixed sky and ground background, no objects in some scenes.
4	399	3.75	Two objects, close imaging distance, sky background, cross flight
16	499	2.98	Single extended object, fast moving speed of objects, from close to far imaging distance, ground background,
18	500	3.32	Single mobile object, from close to far imaging distance, ground background
1	70	5.11	Single mobile object, sky background, cloud clutter

Figure 8. Image samples of four infrared image sequences in dataset 1. Frames without objects contain no red rectangles.

Another infrared image sequence that contains airplane targets under a complex sky background has been experimented on to evaluate the robustness of the proposed method. This sequence is denoted as dataset 2. All images in this dataset have a size of 256 × 200. All images have the same spatial resolution, and the object size is 6 pixels. Examples of the sequence along with their ground truth are shown in Figure 9.

Figure 9. Image sample of one infrared image sequence in dataset 2.

3.1.2. Experimental Setup

To prove the superiority of the proposed unsupervised infrared small-object detection method, it is compared with seven publicly available infrared object-detection approaches that reconstruct the background and the target from original infrared images and two deep-learning-based approaches. The compared approaches include sequence-based approaches, mixture of Gaussians (MOG) [51], nonlocal prior weight-based approaches IPI model [33], non-convex rank approximation minimization (NRAM) [39], local prior weight-based approaches tri-layer local contrast measure (TLLCM) [52], weighted scale local contrast measure (WSLCM) [53], generalized structure tensor (GST) [54], and partial sum of the tensor nuclear norm (PSTNN) [55] that combines local and nonlocal prior weights and deep-learning-based approaches, you only look once (YOLO), and single-shot detector (SSD). The target images obtained from seven methods not based on deep-learning approaches and the proposed framework are used to detect objects by using Algorithm 2. A window with size of $5\times 5$ is used after ADMM is solved.

Table 2 describes the computer settings of the proposed framework and compared methods. All experiments are implemented under MATLAB 2016a on a PC (Core i7-6700 CPU @ 3.40 GHz, 16.0 GB of memory) with Windows 7 x64 operating system.

Table 2. Parameter settings of state-of-the-art infrared small-object-detection approaches.

Type	State-of-the-Art Methods	Abbreviations	Parameter Settings
Nonlocal prior weight	Infrared Patch-Image	IPI	Patch size 50, slide step 10, $\lambda =\frac{1}{\sqrt{\min (m,n)}}$$, \epsilon ={10}^{-7}$
	Non-Convex Rank Approximation Minimization	NRAM	Patch size 50, slide step 10, $\lambda =\frac{1}{\sqrt{\min (m,n)}}$
Sequence based approaches	Mixture of Gaussians	MOG	Temporal step 3, patch step 5, patch size 50, component number 3, maximum iterations 300
Local prior weight	Tri-Layer Local Contrast Measure	TLLCM	Gaussian kernel $\frac{\left[\begin{array}{l}1 2 1\\ 2 4 2\\ 1 2 1\end{array}\right]}{16}$
	Weighted Scale Local Contrast Measure	WSLCM	Gaussian kernel $\frac{\left[\begin{array}{l}1 2 1\\ 2 4 2\\ 1 2 1\end{array}\right]}{16}$
	Generalized Structure Tensor	GST	${\sigma }_1=0.6$$, {\sigma }_2=1.1$, boundary width 5, filter size 5
Deep learning	You Look Only Once	YOLO	Batch size 32,initial learning rate 0.001,weight decreases 50% every 2000 iterations, maximum iterations = 12,000, momentum = 0.9, weight decay = 0.0005
	Single-Shot Detector	SSD	Batch size 32, initial learning rate 0.0005, weight decreased by 10% every 500 iterations, 2000 max iterations
Local and nonlocal prior weights	Partial Sum of the Tensor Nuclear Norm	PSTNN	Patch size 40, slide step 40, $\lambda =0.7$
	The proposed framework	-	Patch size 40, slide step 40, temporal size 3, $\lambda =0.7$$, {\tau }_1=3.85$$, {\tau }_2=4.2$$, \tau =0.5$

The precision ratio, recall ratio, F1 score, and average computation time are used to evaluate the performance of infrared object-detection performance. The recall ratio (RR), precision ratio (PR), and F1 score can be calculated according to Equations (23)–(25).

$$RR=\frac{TP}{TP+FN},$$

(23)

$$PR=\frac{TP}{TP+FP},$$

(24)

$$F1=\frac{2TP}{2TP+FN+FP}$$

(25)

where TP represents the number of objects that are correctly classified, FP represents the number of background objects that is classified as objects, and FN represents the number of undetected objects.

3.2. Comparison with State-of-the-Art Methods in Five Sequences

Table 3 and Table 4 show the recall ratio and precision ratio of the proposed framework compared with competitive infrared object detection approaches. As shown in Table 3 and Table 4, the proposed framework achieves the highest precision ratio and relatively high recall ratio, demonstrating that it is suitable for heterogeneous scenes, where the background can be distinguished from the targets. The proposed framework can improve the recall ratio by the proposed spatial–temporal patch tensor or the contrast-boosted approach and increase the precision ratio by the object-selection method. SSD and YOLO achieve higher recall ratio and lower precision ratio in most sequences because they do not have clutter samples. The MOG algorithm achieves the highest recall ratio in four sequences but the lowest precision ratio in sequences 3, 16, and 18, demonstrating that it is more suitable for scenes, where background is different from objects in gray values. The MOG approach delivers poor precision ratio because it considers the temporal information hidden in adjacent frames, which may enhance the background information and cause false alarms. PSTNN and GST approaches deliver poorer performance in terms of recall and precision ratio because they lose object information when suppressing background information. IPI and NRAM methods perform worse than the proposed framework in sequences 3, 4, and 16 but better than the proposed framework in sequence 18, demonstrating that they are more suitable for sequences, where each frame contains only one object, and unsuitable for scenes, where multiple objects or no object exists. TLLCM and WSLCM deliver acceptable object detection performance in sequences 3, 16, and 18 but unsatisfactory performance in sequence 4, demonstrating that they cannot handle scenes, where multiple objects exist.

Table 3. The recall ratio compared with state-of-the-art infrared object detection approaches.

Method	Dataset 1				Dataset 2
	Sequence 3	Sequence 4	Sequence 16	Sequence 18
IPI	0.8235	0.9925	0.9879	0.942	0.986
NRAM	0.84	0.9013	0.9212	0.858	0.8861
GST	0.92	0.6875	0.9454	0.928	0.986
MOG	1	1	0.9919	0.99	0.7778
TLLCM	0.9867	0.7775	0.9798	0.906	0.875
WSLCM	0.8267	0.7488	0.9697	0.926	0.9589
PSTNN	0.9730	0.9525	0.9615	0.868	0.986
SSD	0.9941	0.9782	0.9580	0.9539	0.9857
YOLO	0.9962	0.9887	0.9639	0.9633	0.9929
The proposed framework	0.9865	0.9988	0.9838	0.938	1

Table 4. The precision ratio compared with state-of-the-art infrared object detection approaches.

Method	Dataset 1				Dataset 2
	Sequence 3	Sequence 4	Sequence 16	Sequence 18
IPI	0.8046	0.9975	0.8989	0.9058	0.6863
NRAM	0.9843	0.9986	0.8686	0.8597	0.7527
GST	0.6330	0.9667	0.8014	0.7669	0.6863
MOG	0.4310	1	0.4630	0.4778	0.7778
TLLCM	0.8314	1	0.9291	0.8580	0.6667
WSLCM	0.7126	0.9967	0.9143	0.8820	0.986
PSTNN	1	0.9987	0.9327	0.9061	0.729
SSD	0.9902	0.9913	0.9194	0.9266	0.9929
YOLO	0.9773	0.9945	0.9266	0.9129	0.9857
The proposed framework	1	1	0.9898	0.938	0.986

Table 5 shows the comprehensive evaluation metric F1 score of the proposed framework compared with state-of-the-art infrared object-detection approaches. The proposed framework achieves an F1 score comparable or even higher than deep-learning-based approaches SSD and YOLO, demonstrating that it can adapt to sequences when faced with multiple objects and complex background. SSD and YOLO can achieve an F1-score comparable to the proposed framework because object samples are used to train the object-detection model. The MOG achieves the highest F1 score in sequence 4 and the lowest F1 score in other sequences, indicating that it is suitable for scenes, where objects are highly different from the background. PSTNN performs effectively in sequences 3, 4, and 16 but delivers poor performance in sequence 18, indicating that PSTNN is unsuitable for scenes, where objects are similar to backgrounds to some extent. The IPI approach delivers satisfactory performance in sequences 4, 16, and 18 but unsatisfactory performance in sequence 3. This condition is caused by the nonexistence of objects in some frames of sequence 3. NRAM achieves a relatively high precision ratio at the sacrifice of the recall ratio in five sequences. TLLCM and WSLCM are more appropriate for scenes, where only one object exists, and these methods may suffer from multiple objects and no objects in some frames of image sequences.

Table 5. The F1 score compared with state-of-the-art infrared object detection approaches.

Method	Dataset 1				Dataset 2
	Sequence 3	Sequence 4	Sequence 16	Sequence 18
IPI	0.8140	0.9950	0.9413	0.9235	0.8092
NRAM	0.9065	0.9474	0.8941	0.9060	0.8139
GST	0.75	0.8035	0.8675	0.8398	0.8092
MOG	0.6	1	0.6033	0.6445	0.7778
TLLCM	0.9024	0.8748	0.9538	0.8813	0.7568
WSLCM	0.7654	0.8551	0.9412	0.9251	0.9722
PSTNN	0.9863	0.9750	0.9469	0.8866	0.838
SSD	0.9921	0.9854	0.9316	0.9374	0.9893
YOLO	0.9887	0.9921	0.9471	0.9415	0.9893
The proposed framework	0.9932	0.9994	0.9789	0.938	0.9929

3.3. Ablation Experiments

Table 6 and Table 7 show the recall and precision ratio of ablation experiments. Table 6 shows that the spatial–temporal tensor, the contrast-boosted, and the object-selection approach can increase average recall ratio by 6.7, 2.21, and 1.14 percentage units, respectively, in five sequences. The spatial–temporal patch tensor increases the recall ratio the most because it considers the temporal information hidden in adjacent frames. The contrast-boosted approach increases the recall ratio the second most in 3, 4, and 16 and dataset 2 but reduces the recall ratio in sequence 18 because it may enhance the object and background information. Thus, the possibility of detecting objects may increase. The object-selection approach increases the recall ratio the least because it does not increase the possibility of detecting objects.

Table 6. The recall ratio of the ablation experiments.

Method	Dataset 1				Dataset 2
	Sequence 3	Sequence 4	Sequence 16	Sequence 18
Without spatial–temporal patch tensor	0.9067	0.9362	0.9313	0.888	0.9091
Without the contrast-boosted approach	0.9467	0.97	0.9757	0.958	0.9459
Without the object selection approach	0.9733	0.9812	0.9676	0.932	0.986
The proposed method	0.9865	0.9988	0.9838	0.938	1

Table 7. The precision ratio of the ablation experiments.

Method	Dataset 1				Dataset 2
	Sequence 3	Sequence 4	Sequence 16	Sequence 18
Without spatial–temporal patch tensor	1	1	0.9527	0.9217	0.9589
Without the contrast-boosted approach	1	0.9987	0.9306	0.8772	0.9333
Without object selection approach	0.869	0.9033	0.8615	0.8258	0.8642
The proposed method	1	1	0.9898	0.938	0.986

Table 7 indicates that the spatial–temporal tensor, the contrast-boosted approach, and the object-selection approach can improve an average precision ratio by 1.61, 3.44, and 11.79 percentage units, respectively. The object-selection approach can increase the precision ratio the most because it predicts the most suitable number of objects, thereby decreasing the possibility of detecting background pixels as objects. The contrast-boosted approach can increase the precision ratio because they can increase the possibility of detecting objects by enhancing the gray value of objects. The spatial–temporal tensor slightly increases precision ratio because more temporal information may enhance the object and background information, thereby increasing the possibility of detecting background as objects.

3.4. Computation Cost

Table 8 shows the computation cost of the proposed framework along with other state-of-the-art infrared object-detection methods. The computation time of deep-learning-based methods only consists of time for testing each frame in the image sequence without the time for training an object-detection model. Table 8 shows that the proposed framework achieves a relatively balanced computation time of 1.85 s compared with existing approaches. GST and PSTNN obtain lower computation time than the proposed framework but delivers unsatisfactory object-detection performance. The MOG, IPI, and WSLCM require higher computation time, which cannot satisfy the requirements of real-time object detection. NRAM and TLLCM have computation time comparable to the proposed framework, but their object-detection performance is worse. Although deep-learning-based approaches require less than 1 s to test, the training time is thousands of seconds.

Table 8. The average computation time compared with state-of-the-art infrared object-detection approaches.

Method	Dataset 1				Dataset 2
	Sequence 3	Sequence 4	Sequence 16	Sequence 18
IPI	28.10 s	79.76 s	84.68 s	79.14 s	55.99 s
NRAM	1.32 s	1.57 s	1.10 s	1.15 s	1.21 s
GST	0.05 s	0.04 s	0.02 s	0.03 s	0.02 s
MOG	81.26 s	33.21 s	60.25 s	111.81 s	263.86 s
TLLCM	1.49 s	1.62 s	1.54 s	1.57 s	2.22 s
WSLCM	7.16 s	6.79 s	7.13 s	7.25 s	9.54 s
PSTNN	0.37 s	0.26 s	0.39 s	0.48 s	0.31 s
YOLO	0.921 s	0.421 s	0.755 s	0.589 s	0.673 s
SSD	0.04 s	0.04 s	0.02 s	0.03 s	0.04 s
The proposed framework	1.74 s	1.46 s	1.38 s	1.41 s	3.23 s

4. Discussion

Figure 10 shows the performance comparison in the 27th frame of sequence 3 between the proposed framework and other existing methods. The proposed framework can detect the actual UAV objects because the contrast-boosted approach can enhance the object information when parts of object information are lacking. Figure 9 shows that NRAM, IPI, GST, and WSLCM approaches fail to detect UAV targets because they cannot effectively handle scenes, where part of UAV targets is missing. TLLCM MOG and PSTNN approaches can detect UAV targets but the MOG algorithm detects some background pixels as objects.

Figure 10. Performance of the proposed method compared with state-of-the-art infrared object detection methods in the 27th frame of sequence 3. (a) Original image along with its ground truth, (b) proposed method, (c) IPI, (d) NRAM, (e) GST, (f) MOG, (g) TLLCM, (h) WSLCM, (i) and PSTNN.

Figure 11 shows the performance of the proposed framework in the 165th frame of sequence 4 compared with other existing infrared object-detection methods. Figure 10 shows that the proposed framework can detect two true UAV targets because the object-selection approach can determine the number of objects accurately, even though two objects are close in images. NRAM, GST, TLLCM, WSLCM, and PSTNN approaches may miss one UAV target because two UAV targets are very close in the 165th frame. The proposed framework, MOG, and IPI approaches can accurately detect two UAV targets, whereas the IPI method detects one background object as object.

Figure 11. Performance of the proposed method compared with state-of-the-art infrared object detection methods in the 165th frame from sequence 4. (a) Original image along with its ground truth, (b) proposed method, (c) IPI, (d) NRAM, (e) GST, (f) MOG, (g) TLLCM, (h) WSLCM, and (i) PSTNN.

Figure 12 shows the performance of the proposed framework along with other existing infrared object detection approaches in the 28th frame of sequence 16. Figure 11 shows that all methods including the proposed framework can detect true UAV targets because the background can be suppressed effectively in this scene. However, IPI, MOG, and PSTNN approaches detect some background pixels as objects because they do not suppress background information effectively.

Figure 12. Performance of the proposed method compared with state-of-the-art infrared object detection methods in the 28th frame from sequence 16. (a) Original image along with its ground truth, (b) proposed method, (c) IPI, (d) NRAM, (e) GST, (f) MOG, (g) TLLCM, (h) WSLCM, Additionally, (i) PSTNN.

Figure 13 shows the error of the proposed framework in five sequences; it is caused by different reasons. For (a), part of UAV objects is missing, leading to incomplete object shape information. Objects of (b) are close in infrared images, which may lead to missing detection of UAV targets. For (c)–(f), objects and background are highly similar in gray values and may cause confusion between objects and background.

Figure 13. Major confusion of the proposed framework. (a) 28th frame in sequence 3, (b) 164th frame in sequence 4, (c) 207th frame in sequence 16, (d) 297th frame in sequence 16, (e) 25th frame in sequence 18, and (f) 321st frame in sequence 18.

5. Conclusions

An unsupervised infrared object-detection framework based on a spatial–temporal patch tensor and object-selection approach is proposed to address the problems of ignoring the temporal information hidden in infrared image sequences, the low contrast between objects and background, and the imbalance between real-time processing and satisfactory detection results. The proposed framework mainly consists of three contributions, namely, the spatial–temporal patch tensor, the contrast-boosted, and the object-selection approach. The following conclusions can be drawn from experiments performed on five image sequences.

• The proposed framework outperforms most previous infrared object-detection approaches that reconstruct the background and the target from original infrared images when handling scenes, where the background is heterogeneous compared with objects in terms of gray values.
• Spatial–temporal patch tensor and the contrast-boosted approach can increase the possibility of detecting real objects by utilizing temporal information hidden in adjacent frames and enhancing the contrast between objects and background. The object-selection approach can decrease the possibility of detecting background as objects by determining the appropriate number of objects.
• The proposed framework can achieve the average F1 score of 0.9804 with computation time of approximately 1.85 s, demonstrating that it can obtain satisfactory object-detection performance with relatively low computation time.

Section 4 shows that the proposed framework may cause confusion when part of UAV objects is missing, objects are too close in infrared images or objects are highly similar to background. More studies are required in the future to address the above-mentioned problems.