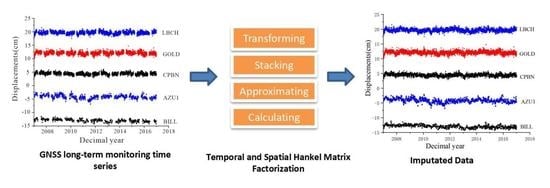
Missing Data Imputation in GNSS Monitoring Time Series Using Temporal and Spatial Hankel Matrix Factorization
Abstract
:1. Introduction
2. Materials and Methods
2.1. Problem Definiton
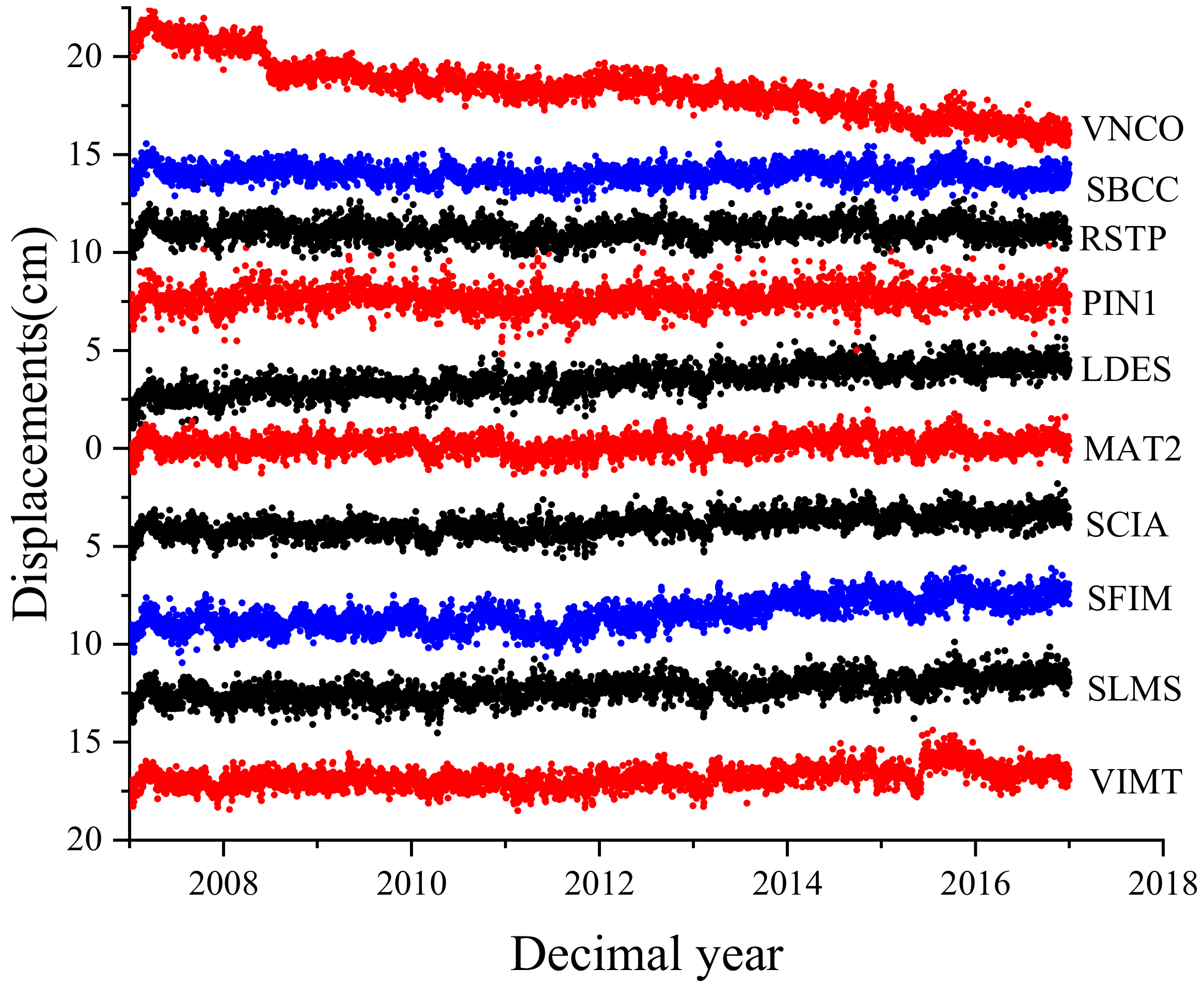
2.2. Datasets
2.3. Methods
2.3.1. Matrix Factorization-Based Approach
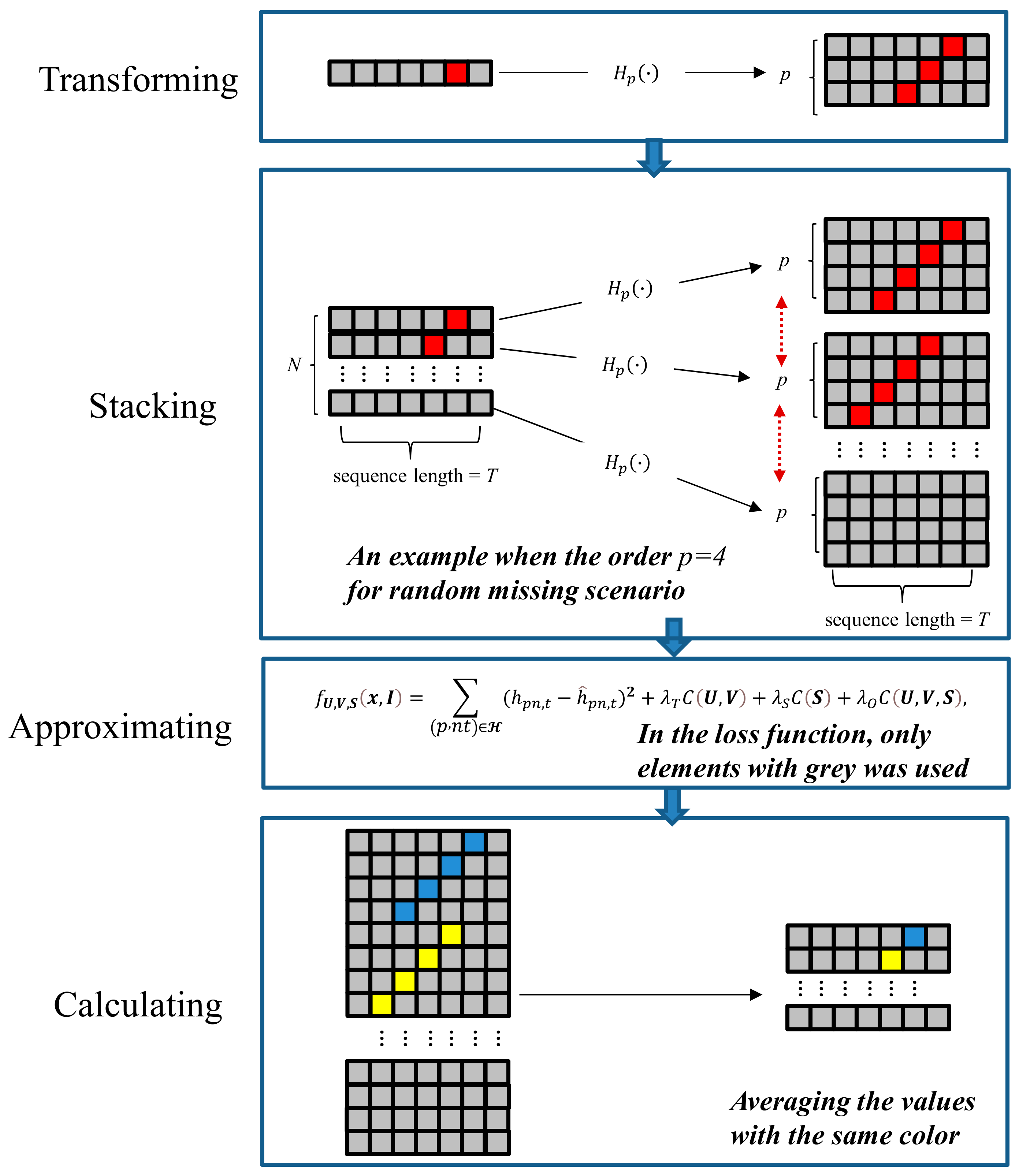
2.3.2. Temporal and Spatial Hankel Matrix Factorization
- (1)
- Main term: The main term in the objective function is used to estimate the error of the imputation during the optimization process; that is, measures the error of approximating with , where .
- (2)
- Temporal correlation: The second term is used to capture the temporal correlations among the GNSS time series, defined asThis term can restrict the solution of to remain as the temporal correlations of the raw data.
- (3)
- Spatial correlation: The third term is implemented to capture the spatial correlations among the regional GNSS time series, defined as
- (4)
- Avoiding overfitting: The final term is implemented to control the balance of the spatial and temporal correlations by avoiding and , defined as
2.3.3. Solution of Factorization
| Algorithm 1 Missing data imputation for regional GNSS time series using TSHMF |
| Input: Regional GNSS time series with missing values the station index of the times series, the indicator matrix, , and the stop condition. |
| Output: The missing values in the Hankel matrix 1: Obtain the longest duration of time-continuous missing and set |
| 2: Obtain the Hankel matrix as demonstrated in the paper and Figure 2 |
| 3: Initial , , and |
| 4: repeat |
| 5: for all do |
| 6: Update following the equation |
| 7: Update following the equation |
| 8: Update following the equation |
| 9: end for |
| 10: until stop condition is reached |
| 11: return the imputation of all missing values |
3. Results and Discussion
3.1. Experimental Design and Evaluation Criteria
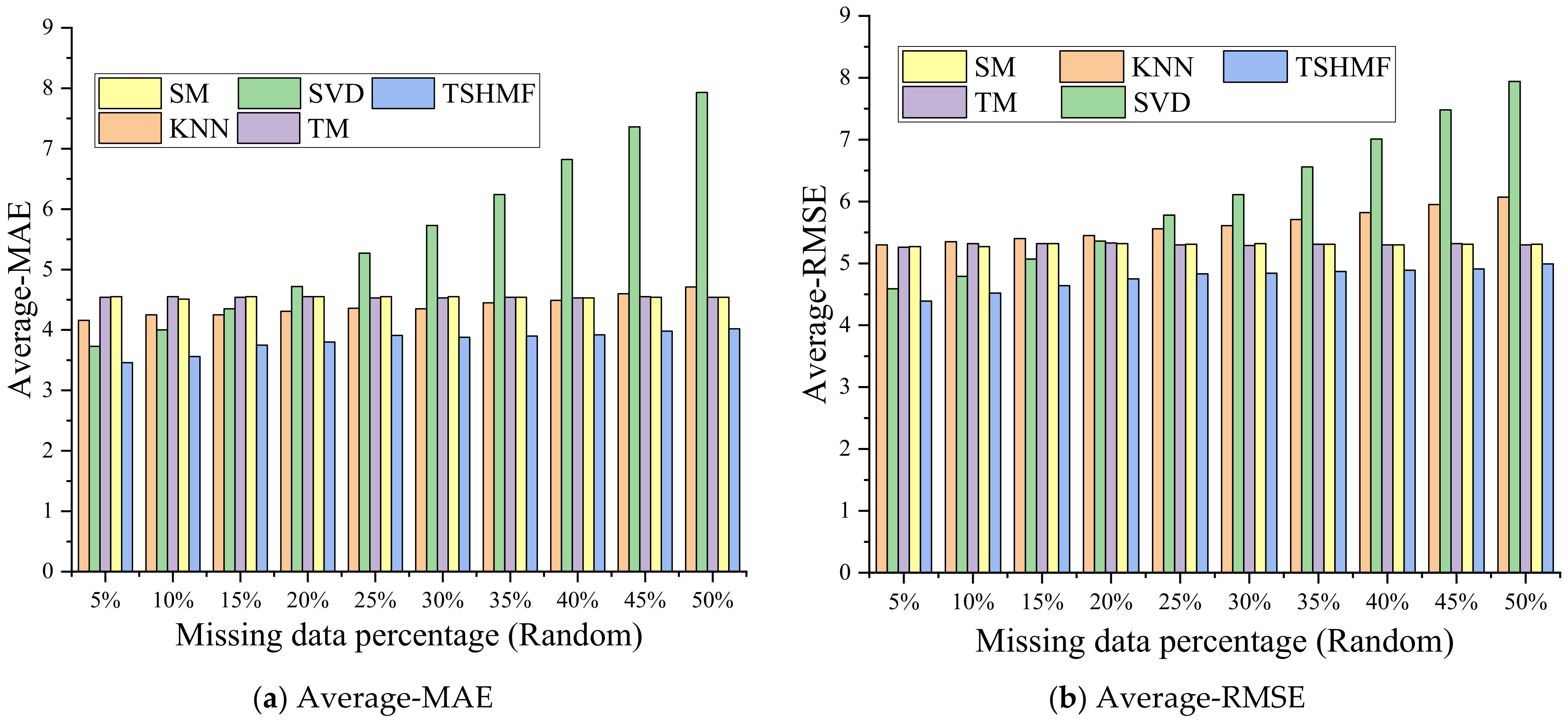
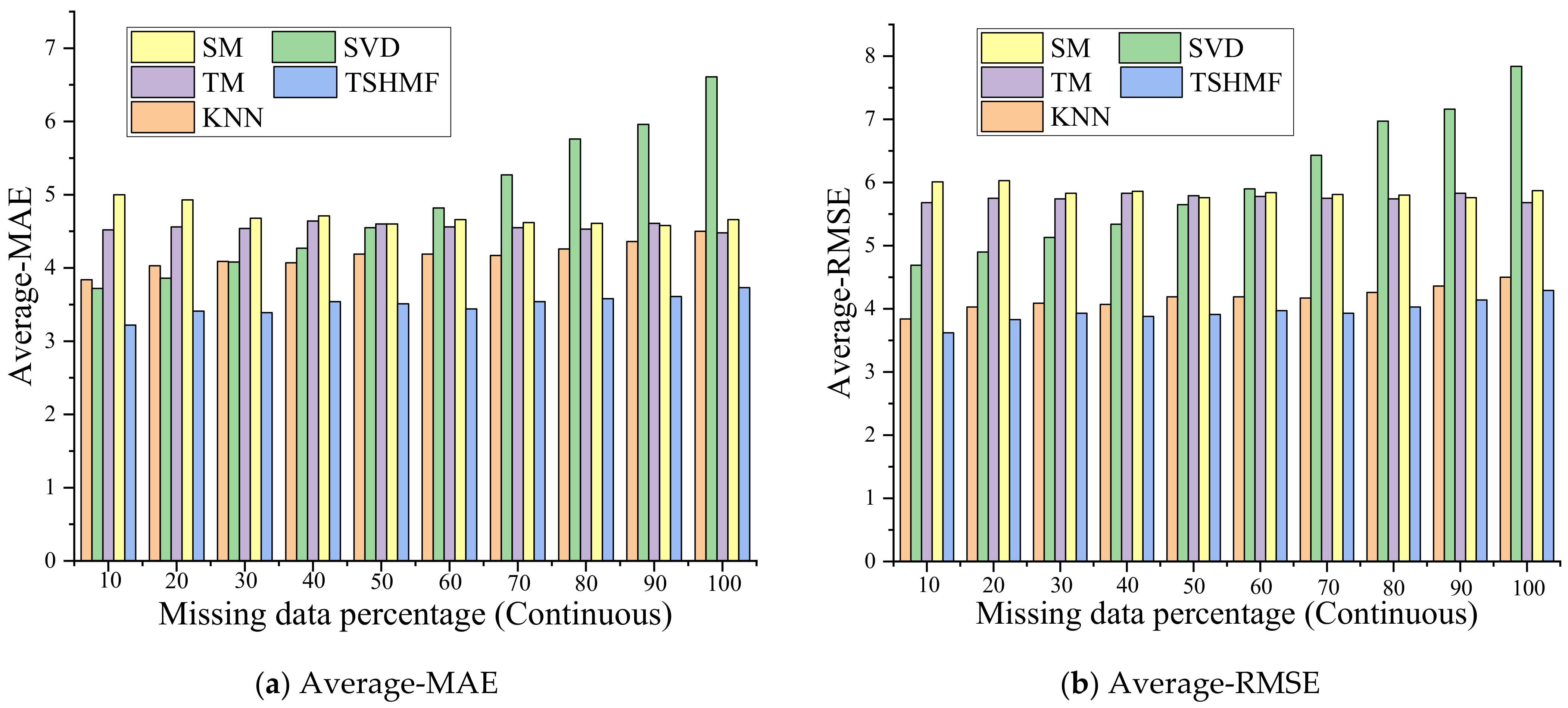
3.1.1. Generation of Missing Values
- (1)
- Totally random missing scenario: This means that the missing observations are independent and randomly missing. This scenario usually shows isolated missing observations, resulting from the solutions removed, sudden satellite signal interruption, etc. In the random missing scenario, we manually extracted the random missing data in each stations. The random missing ratios in this model were manually removed from 5 to 50%, with an increasing interval of 5% in each matrix.
- (2)
- Continuous missing scenario: This means that the missing data are detected with a small group of sequential points lost at one station, resulting from a power cut, device replacements, etc. In this scenario, we divided all ten-year periods of data into a single year, and the missing part was randomly scattered in each station within each year. The number of consecutive missing points ranges from 10 to 100, with 10 as the interval.
3.1.2. Evaluation Criteria
3.1.3. Benchmark Models
3.2. Random Missing Data Scenario
3.3. Continuous Missing Data Scenario
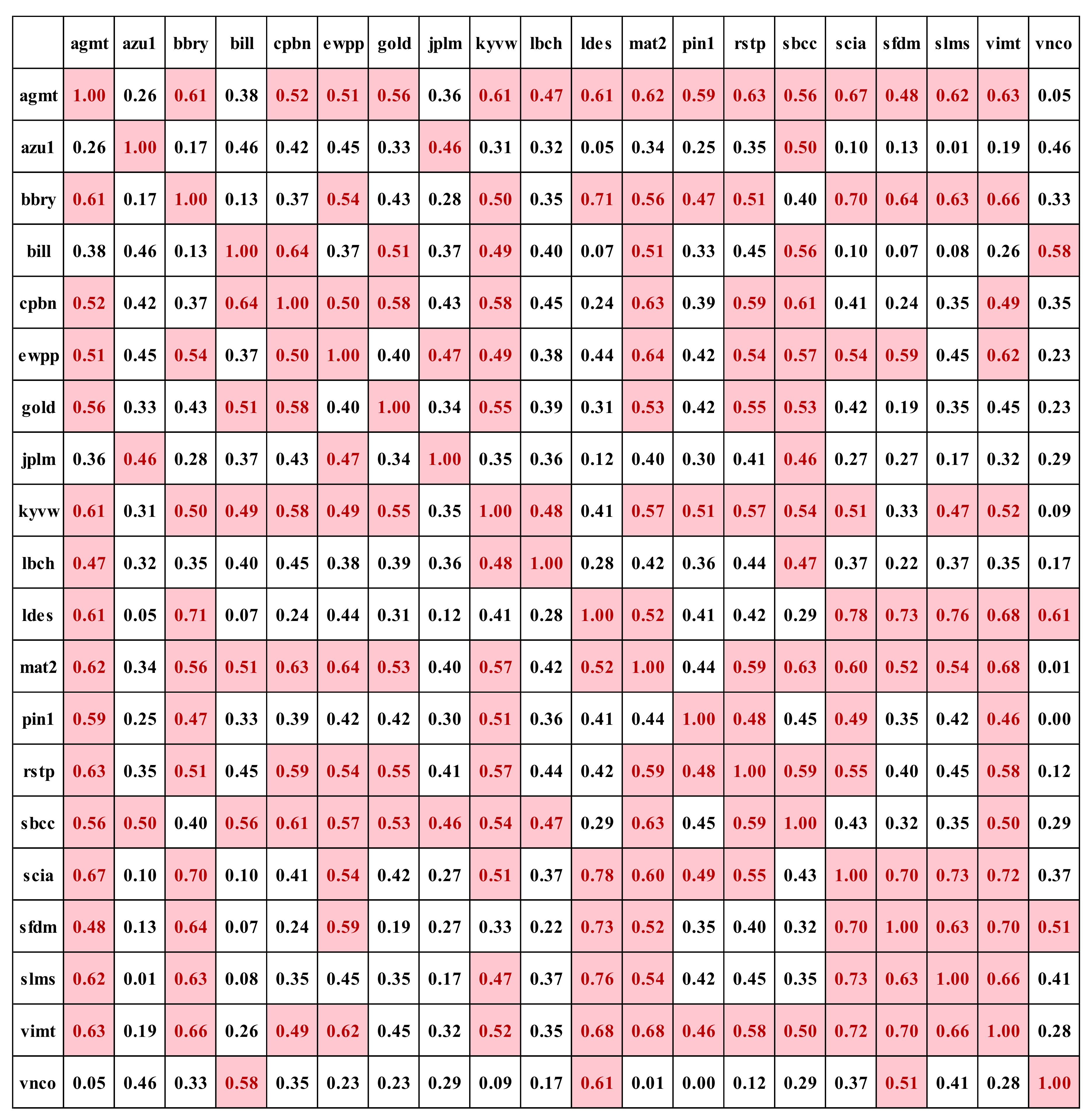
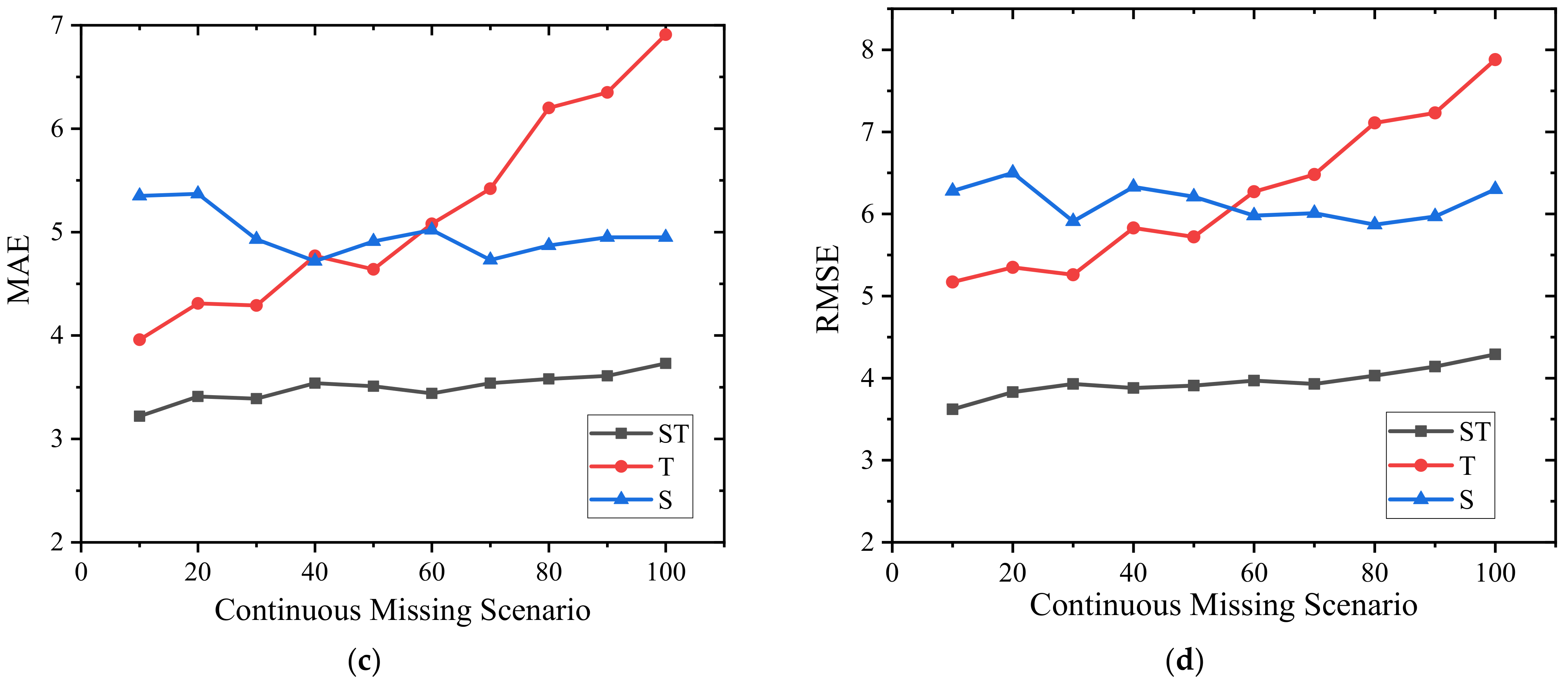
3.4. The Impact of Temporal and Spatial Correlations
4. Conclusions
- (1)
- In real-world long-term tectonic monitoring missing data imputation, the method shows the best applicability in stable local regions. The TSHMF method considers both the long-term stable and moving monitoring time series with respect to the regional area. The result shows the highest accuracy in long-term deformation monitoring when compared with the benchmark models (TM, SM, KNN, and SVD). The proposed method could be used in various geodetic long-term monitoring applications.
- (2)
- The results show the robust performance of the proposed method, which enrolled various ratios of missing data in the random missing scenario and continuous missing scenario. Both temporal correlation and spatial correlation can contribute to the accuracy of missing value imputation, further proving that the simultaneous consideration of temporal and spatial correlations is necessary in regional GNSS time series modeling.
- (3)
- The present paper proves the limitation of only considering a single monitoring station in geoscience long-term time series analysis. To achieve a high-accuracy analysis, not only did the raw data from the station need to be post-processed, but also, the results from a nearby station, which was installed in a rigid area, were also needed for the post-processing method. Regional analysis would further improve the accuracy of single long-term monitoring time series results.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ALLSSA | Anti-Leakage Least-Squares Spectral Analysis |
| BDS | BeiDou Navigation Satellite System |
| CMONC | Crustal Movement Observation Network of China |
| CORS | Continuously Operating Reference Station |
| CME | Common Mode Error |
| GNSS | Global navigation satellite system |
| GPS | Global Positioning System |
| ILSP | Improved Lomb–Scargle Periodogram |
| InSAR | Interferometric Synthetic Aperture Radar |
| IPCA | Incremental principal component analysis |
| KKF | Kriged Kalman Filter |
| KNN | K-nearest neighbor |
| LSWA | Least-squares wavelet analysis |
| MAE | Mean Absolute Error |
| MTLS | Multivariate Total Least-Squares |
| PCA | Principal component analysis |
| RMS | Root Mean Square |
| S | Spatial correlation |
| SCIGN | Southern California Integrated GPS Network |
| SM | Station mean |
| ST | Spatial and temporal correlations |
| SOPAC | Scripps Orbit and Permanent Array Center |
| SVD | Singular value decomposition |
| T | Temporal correlation |
| TM | Time mean |
| TSHMF | Temporal and Spatial Hankel Matrix Factorization |
| VBPCA | Variational Bayesian principal component analysis |
References
- Pourghasemi, H.R.; Kariminejad, N.; Gayen, A.; Komac, M. Statistical functions used for spatial modelling due to assessment of landslide distribution and landscape-interaction factors in Iran. Geosci. Front. 2020, 11, 1257–1269. [Google Scholar] [CrossRef]
- Liu, H.; Yang, L.; Li, L. Analyzing the Impact of Climate Factors on GNSS-Derived Displacements by Combining the Extended Helmert Transformation and XGboost Machine Learning Algorithm. J. Sens. 2021, 3, 2256. [Google Scholar] [CrossRef]
- Li, L.; Lin, X.; Liu, H.; Lu, W.; Zhou, B.; Zhu, J. Displacement Data Imputation in Urban Internet of Things System Based on Tucker Decomposition with L2 Regularization. IEEE Internet Things J. 2022, 38, 2782. [Google Scholar] [CrossRef]
- Shi, K.; Liu, X.; Guo, J.; Liu, L.; You, X.; Wang, F. Pre-Earthquake and Co-seismic Ionosphere Disturbances of the Mw 6.6 Lushan Earthquake on 20 April 2013 Monitored by CMONOC. Atmospheres 2019, 10, 216. [Google Scholar] [CrossRef] [Green Version]
- Dong, D.; Fang, P.; Bock, Y.; Webb, F.; Prawirodirdjo, L.; Kedar, S.; Jamason, P. Spatiotemporal filtering using principal component analysis and Karhunen–Loeve expansion approaches for regional GPS network analysis. J. Geophys. Res. 2006, 111, 1581–1600. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Wang, G. Relative motion between St. Croix and the Puerto Rico-Northern Virgin Islands block derived from continuous GPS observations (1995–2014). Int. J. Geophys. 2015, 37, 2671. [Google Scholar] [CrossRef] [Green Version]
- Wang, G.; Liu, H.; Mattioli, G.S.; Miller, M.M.; Feaux, K.; Braun, J. CARIB18: A stable geodetic reference frame for geological hazard monitoring in the Caribbean region. Remote Sens. 2019, 11, 680. [Google Scholar] [CrossRef] [Green Version]
- Mendez-Astudillo, J.; Lau, L.; Tang, Y.T.; Moore, T. A new Global Navigation Satellite System (GNSS) based method for urban heat island intensity monitoring. Int. J. Appl. Earth Obs. Geoinf. 2021, 94, 102222. [Google Scholar] [CrossRef]
- Kaloop, M.R.; Li, H. Sensitivity and analysis GPS signals based bridge damage using GPS observations and wavelet transform. Measures 2011, 44, 927–937. [Google Scholar] [CrossRef]
- Liu, B.; Dai, W.; Liu, N. Extracting seasonal deformations of the Nepal Himalaya region from vertical GPS position time series using independent component analysis. Adv. Space Res. 2017, 60, 2910–2917. [Google Scholar] [CrossRef]
- Yan, J.; Dong, D.; Bürgmann, R.; Materna, K.; Tan, W.; Peng, Y.; Chen, J. Separation of sources of seasonal uplift in China using independent component analysis of GNSS time series. J. Geophys. Res. Solid Earth 2019, 124, 11951–11971. [Google Scholar] [CrossRef]
- Herring, T.A.; King, R.W.; McClusky, S.C. Introduction to Gamit/Globk; Massachusetts Institute of Technology: Cambridge, MA, USA, 2010. [Google Scholar]
- Williams, S.D. CATS: GPS coordinate time series analysis software. GPS Solut. 2008, 12, 147–153. [Google Scholar] [CrossRef]
- Bos, M.S.; Fernandes, R.M.S.; Williams, S.D.P.; Bastos, L. Fast error analysis of continuous GNSS observations with missing data. J. Geod. 2013, 87, 351–360. [Google Scholar] [CrossRef] [Green Version]
- Tian, Y. iGPS: IDL tool package for GPS position time series analysis. GPS Solut. 2011, 15, 299–303. [Google Scholar] [CrossRef]
- Goudarzi, M.A.; Cocard, M.; Santerre, R.; Woldai, T. GPS interactive time series analysis software. GPS Solut. 2013, 17, 595–603. [Google Scholar] [CrossRef]
- Wu, D.; Yan, H.; Shen, Y. TSAnalyzer, a GNSS time series analysis software. GPS Solut. 2017, 21, 1389–1394. [Google Scholar] [CrossRef]
- Didova, O.; Gunter, B.; Riva, R.; Klees, R.; Roese-Koerner, L. An approach for estimating time-variable rates from geodetic time series. J. Geod. 2016, 90, 1207–1221. [Google Scholar] [CrossRef] [Green Version]
- He, X.; Yu, K.; Montillet, J.P.; Xiong, C.; Lu, T.; Zhou, S.; Ma, X.; Cui, H.; Ming, F. GNSS-TS-NRS: An Open-source MATLAB-Based GNSS time series noise reduction software. Remote Sens. 2020, 12, 3532. [Google Scholar] [CrossRef]
- Ghaderpour, E. Least-squares wavelet and cross-wavelet analyses of VLBI baseline length and temperature time series: Fortaleza–Hartebeesthoek–Westford–Wettzell. Publ. Astron. Soc. Pac. 2021, 133, 014502. [Google Scholar] [CrossRef]
- Ghaderpour, E. JUST: MATLAB and python software for change detection and time series analysis. GPS Solut. 2021, 25, 1–7. [Google Scholar] [CrossRef]
- Shen, Y.; Li, W.; Xu, G.; Li, B. Spatiotemporal filtering of regional GNSS network’s position time series with missing data using principle component analysis. J. Geod. 2014, 88, 1–12. [Google Scholar] [CrossRef]
- Ren, Y.; Wang, H.; Lian, L.; Wang, J.; Cheng, Y.; Zhang, Y.; Zhu, W.; Zhang, S. A method based on MTLS and ILSP for GNSS coordinate time series analysis with missing data. Adv. Space Res. 2021, 68, 3546–3561. [Google Scholar] [CrossRef]
- Li, W.; Jiang, W.; Li, Z.; Chen, H.; Chen, Q.; Wang, J.; Zhu, G. Extracting Common Mode Errors of Regional GNSS Position Time Series in the Presence of Missing Data by Variational Bayesian Principal Component Analysis. Sensors 2020, 20, 2298. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Krypiak-Gregorczyk, A.; Wielgosz, P.; Borkowski, A. Ionosphere model for European region based on multi-GNSS data and TPS interpolation. Remote Sens. 2017, 9, 1221. [Google Scholar] [CrossRef] [Green Version]
- Ansari, K.; Sharma, S.K. Ionospheric TEC variation based on GNSS data over the Arabian Peninsula and validation with the cubic spline interpolated GIM model. Adv. Space Res. 2021, 68, 3814–3820. [Google Scholar] [CrossRef]
- Balogun, A.L.; Rezaie, F.; Pham, Q.B.; Gigović, L.; Drobnjak, S.; Aina, Y.A.; Panahi, M.; Yekeen, T.S.; Lee, S. Spatial prediction of landslide susceptibility in western Serbia using hybrid support vector regression (SVR) with GWO, BAT and COA algorithms. Geosci. Front. 2021, 12, 101104. [Google Scholar] [CrossRef]
- Liu, N.; Dai, W.; Santerre, R.; Kuang, C. A MATLAB-based Kriged Kalman Filter software for interpolating missing data in GNSS coordinate time series. GPS Solut. 2018, 22, 1–8. [Google Scholar] [CrossRef]
- Benoist, C.; Collilieux, X.; Rebischung, P.; Altamimi, Z.; Jamet, O.; Métivier, L.; Chanard, K.; Bel, L. Accounting for spatiotemporal correlations of GNSS coordinate time series to estimate station velocities. J. Geodyn. 2020, 135, 101693. [Google Scholar] [CrossRef]
- Zhang, S.; Li, X.; Zong, M.; Zhu, X.; Cheng, D. Learning k for knn classification. ACM Trans. Intell. Syst. Technol. 2017, 8, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S. Nearest neighbor selection for iteratively kNN imputation. J. Syst. Softw. 2012, 85, 2541–2552. [Google Scholar] [CrossRef]
- Zhang, S.; Cheng, D.; Deng, Z.; Zong, M.; Deng, X. A novel kNN algorithm with data-driven k parameter computation. Pattern Recognit. Lett. 2018, 109, 44–54. [Google Scholar] [CrossRef]
- Ma, Z.F.; Tian, H.P.; Liu, Z.C.; Zhang, Z.W. A new incomplete pattern belief classification method with multiple estimations based on KNN. Appl. Softw. Comput. 2020, 90, 106175. [Google Scholar] [CrossRef]
- Li, L.; Liu, H.; Zhou, H.; Zhang, C. Missing data estimation method for time series data in structure health monitoring systems by probability principal component analysis. Adv. Eng. Softw. 2020, 149, 102901. [Google Scholar] [CrossRef]
- Bao, Z.; Chang, G.; Zhang, L.; Chen, G.; Zhang, S. Filling missing values of multi-station GNSS coordinate time series based on matrix completion. Measures 2021, 183, 109862. [Google Scholar] [CrossRef]
- Li, Y.; Xu, C.; Yi, L.; Fang, R. A data-driven approach for denoising GNSS position time series. J. Geod. 2018, 92, 905–922. [Google Scholar] [CrossRef]
- Kwon, O.W.; Chan, K.; Lee, T.W. Speech feature analysis using variational Bayesian PCA. IEEE Signal Process. Lett. 2003, 10, 137–140. [Google Scholar] [CrossRef]
- Wang, L.; Wu, S.; Wu, T.; Tao, X.; Lu, J. HKMF-T: Recover from Blackouts in Tagged Time Series with Hankel Matrix Factorization. IEEE Trans. Knowl. Data Eng. 2020, 33, 3582–3593. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, Y.; Cui, W. Spectrally sparse signal recovery via Hankel matrix completion with prior information. IEEE Trans. Signal Process. 2021, 69, 2174–2187. [Google Scholar] [CrossRef]
- Jin, K.H.; Lee, D.; Ye, J.C. A general framework for compressed sensing and parallel MRI using annihilating filter based low-rank Hankel matrix. IEEE Trans. Comput. Imaging 2016, 2, 480–495. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Zhang, D.; Jin, Z.; Chen, X.; Zu, S.; Huang, W.; Gan, S. Simultaneous denoising and reconstruction of 5-D seismic data via damped rank-reduction method. Geophys. J. Int. 2016, 206, 1695–1717. [Google Scholar] [CrossRef] [Green Version]
- Dokht, R.M.; Gu, Y.J.; Sacchi, M.D. Singular spectrum analysis and its applications in mapping mantle seismic structure. Geophys. J. Int. 2017, 208, 1430–1442. [Google Scholar] [CrossRef]
- Chen, B.; Bian, J.; Ding, K.; Wu, H.; Li, H. Extracting Seasonal Signals in GNSS Coordinate Time Series via Weighted Nuclear Norm Minimization. Remote Sens. 2020, 12, 2027. [Google Scholar] [CrossRef]
- Nikolaidis, R. Observation of Geodetic and Seismic Deformation with the Global Positioning System; University of California: San Diego, CA, USA, 2002. [Google Scholar]
- Jamason, P.; Bock, Y.; Fang, P.; Gilmore, B.; Malveaux, D.; Prawirodirdjo, L.; Scharber, M. SOPAC Web site (http://sopac.ucsd.edu). GPS Solut. 2004, 8, 272–277. [Google Scholar] [CrossRef]
- Aragón, E.; Fernando, D.; Cuffaro, M.; Doglioni, C.; Ficini, E.; Pinotti, L.; Nacif, S.; Demartis, M.; Hernando, I.; Fuentes, T. The westward lithospheric drift, its role on the subduction and transform zones surrounding Americas: Andean to cordilleran orogenic types cyclicity. Geosci. Front. 2020, 11, 1219–1229. [Google Scholar] [CrossRef]
- Martha, T.R.; Govindharaj, K.B.; Kumar, K.V. Damage and geological assessment of the 18 September 2011 Mw 6.9 earthquake in Sikkim, India using very high resolution satellite data. Geosci. Front. 2015, 6, 793–805. [Google Scholar] [CrossRef] [Green Version]



| MAE | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Index | Method | 5% | 10% | 15% | 20% | 25% | 30% | 35% | 40% | 45% | 50% |
| STD | KNN | 0.76 | 0.84 | 0.81 | 0.78 | 0.82 | 0.70 | 0.80 | 0.77 | 0.82 | 0.88 |
| SVD | 0.91 | 1.39 | 1.86 | 2.38 | 2.99 | 3.67 | 4.26 | 4.98 | 5.62 | 6.24 | |
| TM | 1.72 | 1.64 | 1.64 | 1.62 | 1.64 | 1.64 | 1.65 | 1.64 | 1.66 | 1.65 | |
| SM | 1.75 | 1.65 | 1.66 | 1.64 | 1.68 | 1.63 | 1.65 | 1.66 | 1.65 | 1.66 | |
| TSHMF | 0.61 | 0.75 | 0.81 | 0.83 | 0.80 | 0.78 | 0.83 | 0.84 | 0.92 | 0.96 | |
| RMSE | |||||||||||
| Index | Method | 5% | 10% | 15% | 20% | 25% | 30% | 35% | 40% | 45% | 50% |
| STD | KNN | 0.97 | 0.95 | 0.92 | 0.93 | 1.01 | 1.01 | 1.03 | 1.04 | 1.09 | 1.16 |
| SVD | 0.93 | 1.45 | 1.97 | 2.50 | 3.15 | 3.78 | 4.44 | 5.07 | 5.65 | 6.32 | |
| TM | 2.21 | 2.11 | 2.11 | 2.09 | 2.11 | 2.12 | 2.13 | 2.11 | 2.14 | 2.13 | |
| SM | 2.23 | 2.13 | 2.14 | 2.12 | 2.17 | 2.12 | 2.13 | 2.15 | 2.14 | 2.14 | |
| TSHMF | 0.92 | 0.93 | 0.94 | 1.05 | 1.10 | 1.11 | 1.13 | 1.19 | 1.28 | 1.37 | |
| MAE | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Index | Method | 5% | 10% | 15% | 20% | 25% | 30% | 35% | 40% | 45% | 50% |
| STD | KNN | 0.62 | 0.73 | 0.73 | 0.73 | 0.81 | 0.73 | 0.71 | 0.68 | 0.69 | 0.85 |
| SVD | 0.69 | 0.87 | 1.22 | 1.47 | 1.99 | 2.23 | 2.93 | 3.63 | 3.84 | 4.54 | |
| TM | 1.62 | 1.71 | 1.61 | 1.70 | 1.64 | 1.62 | 1.65 | 1.67 | 1.67 | 1.51 | |
| SM | 1.73 | 1.96 | 1.57 | 1.76 | 1.56 | 1.75 | 1.56 | 1.68 | 1.70 | 1.68 | |
| TSHMF | 0.55 | 0.68 | 0.59 | 0.76 | 0.65 | 0.63 | 0.66 | 0.75 | 0.61 | 0.78 | |
| RMSE | |||||||||||
| Index | Method | 5% | 10% | 15% | 20% | 25% | 30% | 35% | 40% | 45% | 50% |
| STD | KNN | 0.62 | 0.73 | 0.73 | 0.73 | 0.81 | 0.73 | 0.71 | 0.68 | 0.69 | 0.85 |
| SVD | 0.84 | 1.05 | 1.43 | 1.63 | 2.20 | 2.37 | 3.20 | 3.97 | 4.13 | 4.86 | |
| TM | 2.04 | 2.16 | 2.08 | 2.16 | 2.09 | 2.14 | 2.09 | 2.17 | 2.15 | 1.97 | |
| SM | 2.15 | 2.43 | 2.09 | 2.19 | 2.03 | 2.24 | 2.01 | 2.16 | 2.18 | 2.21 | |
| TSHMF | 0.60 | 0.76 | 0.71 | 0.67 | 0.74 | 0.66 | 0.72 | 0.68 | 0.72 | 0.81 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Li, L. Missing Data Imputation in GNSS Monitoring Time Series Using Temporal and Spatial Hankel Matrix Factorization. Remote Sens. 2022, 14, 1500. https://doi.org/10.3390/rs14061500
Liu H, Li L. Missing Data Imputation in GNSS Monitoring Time Series Using Temporal and Spatial Hankel Matrix Factorization. Remote Sensing. 2022; 14(6):1500. https://doi.org/10.3390/rs14061500
Chicago/Turabian StyleLiu, Hanlin, and Linchao Li. 2022. "Missing Data Imputation in GNSS Monitoring Time Series Using Temporal and Spatial Hankel Matrix Factorization" Remote Sensing 14, no. 6: 1500. https://doi.org/10.3390/rs14061500
APA StyleLiu, H., & Li, L. (2022). Missing Data Imputation in GNSS Monitoring Time Series Using Temporal and Spatial Hankel Matrix Factorization. Remote Sensing, 14(6), 1500. https://doi.org/10.3390/rs14061500