Next Article in Journal
Range Gate Pull-Off Mainlobe Jamming Suppression Approach with FDA-MIMO Radar: Theoretical Formalism and Numerical Study
Previous Article in Journal
MLCRNet: Multi-Level Context Refinement for Semantic Segmentation in Aerial Images
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 14
Issue 6
10.3390/rs14061497
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Elevation Regimes Modulated the Responses of Canopy Structure of Coastal Mangrove Forests to Hurricane Damage

by
Qiong Gao
and
Mei Yu
*
Department of Environmental Sciences, University of Puerto Rico, Rio Piedras, San Juan, PR 00926, USA
*
Author to whom correspondence should be addressed.
Remote Sens. 2022, 14(6), 1497; https://doi.org/10.3390/rs14061497
Submission received: 9 February 2022 / Revised: 10 March 2022 / Accepted: 18 March 2022 / Published: 20 March 2022
Browse Figures
Versions Notes

Abstract

:
Mangrove forests have unique ecosystem functions and services, yet the coastal mangroves in tropics are often disturbed by tropical cyclones. Hurricane Maria swept Puerto Rico and nearby Caribbean islands in September 2017 and caused tremendous damage to the coastal mangrove systems. Understanding the vulnerability and resistance of mangrove forests to disturbances is pivotal for future restoration and conservation. In this study, we used LiDAR point clouds to derive the canopy height of five major mangrove forests, including true mangroves and mangrove associates, along the coast of Puerto Rico before and after the hurricanes, which allowed us to detect the spatial variations of canopy height reduction. We then spatially regressed the pre-hurricane canopy height and the canopy height reduction on biophysical factors such as the elevation, the distance to rivers/canals within and nearby, the distance to coast, tree density, and canopy unevenness. The analyses resulted in the following findings. The pre-hurricane canopy height increased with elevation when elevation was low and moderate but decreased with elevation when elevation was high. The canopy height reduction increased quadratically with the pre-hurricane canopy height, but decreased with elevation for the four sites dominated by true mangroves. The site of Palma del Mar dominated by Pterocarpus, a mangrove associate, experienced the strongest wind, and the canopy height reduction increased with elevation. The canopy height reduction decreased with the distance to rivers/canals only for sites with low to moderate mean elevation of 0.36–0.39 m. In addition to the hurricane winds, the rainfall during hurricanes is an important factor causing canopy damage by inundating the aerial roots. In summary, the pre-hurricane canopy structures, physical environment, and external forces brought by hurricanes interplayed to affect the vulnerability of coastal mangroves to major hurricanes.

1. Introduction

Growing under multiple physiological stresses, coastal mangroves possess unique ecosystem functions to maintain high carbon sequestration [1,2], to purify coastal water, to host a number of vertebrate and invertebrate species [3], to offset the sea level rise via vertical accretion [4,5], and to protect societal properties of coastal communities during tropical storms [6]. However, the canopies of coastal mangroves are likely to be severely damaged by tropical storms, thus greatly reducing the functions of mangrove forests [7,8,9]. Understanding the vulnerability and resistance of mangroves under storm disturbance is vital to restore and to conserve coastal wetlands.
In addition to the great wind speed of storms, several biophysical features may elucidate the vulnerability of tropical forests to disturbance; emergent trees or higher canopy, smaller tree diameter, lower tree density, and lower soil-root anchorage may incur more canopy damage [10,11]. Mangroves with higher canopy tend to intercept more wind force, trees with smaller dimeter have a small shear modulus, a lower tree density makes the wind easier to traverse the canopy, and a lower soil-root anchorage makes the coastal forest easier to fall or slant under storm wind [11]. In addition, storms often bring a great amount of rainfall and sea water surge [12], which may flood coastal mangroves and immerse their aerial roots, and the prolonged immersion may lead to delayed death of mangrove trees [13].
Canopy height, stem density, and tree diameter are likely to be shaped by the physical environment, as well as tropical storms [14]. For mangroves in the tropics, salinity is a major limiting factor in most circumstances [15,16,17]. Although mangrove roots can exclude and leaves can excrete variable amounts of salts, the canopy height was found to decrease with soil salinity, which is a result of interplay between salt brought by the sea tides or groundwater and the hydrological processes [18,19]. Ample rainfall, overland flow, and river discharge may carry salt away or dilute the salt concentration in soil, whereas tides bring the salt to mangrove forest, and evapotranspiration removes mostly pure water and lets salt accumulate within the soil. Hence, the soil salinity depends on both the climate region and the frequency of tides [20]. In addition to salinity, mangrove growth may also be threatened by deficiency of nutrients, which depends not only on the parent materials and mineralization, but also on external sources such as urban processes.
The impact of human activities may also affect the mangrove growth and the vulnerability during tropical storms. Most of the world population lives near coasts and often compete for habitat with mangroves. Mangrove forests and neighborhood urban areas may be connected via aerodynamics and hydrology, and the connections via sewage canals/pipes provide freshwater and nutrients to mangrove forests, thus affecting their growth [21]. This is especially important for coastal mangrove forests in heavily populated islands, where mangroves are in close distance to urban communities and were historically drained for agriculture and urban development [22].
The effects of salinity and nutrients on mangrove growth depend on the species salt tolerance and nutrient budget [15,23]. Three major species of true mangroves [24] are found on Caribbean islands: red mangrove (Rhizophora mangle) with stilt roots growing in the coastal water, black mangrove (Avicennia germinans) often found in shallow water or muddy soil with pneumatophores growing from horizontal cable roots, and white mangrove (Laguncularia racemosa) growing in slightly drier conditions than black mangrove. Red and black mangroves have a high tolerance to salt, whereas white mangroves have moderate tolerance [15]. In addition to the above true mangrove species, there are mangrove associates which were once classified as mangroves in history [25]. Buttonwood mangrove (Conocarpus erectus) is occasionally found in relatively dry spots, and Pterocarpus officinalis as a hardwood is also found in brackish water. These species have relatively lower tolerance to salinity and often grow together with true mangroves. Therefore, when we mention mangrove forests, we imply both true mangroves and mangrove associates.
The impact of tropical storms on coastal mangroves can be assessed by ground inventory, as well as remote sensing [26,27]. Ground inventory is often limited by scales [28]. Remote sensing, using aerial photos and satellite-based multispectral images as 2D tools, is often limited to the assessment of greenness and falls short in the assessment of the vertical dimension [7,29,30,31]. Airborne LiDAR (light detection and ranging) provides an ideal tool to measure the 3D changes in the mangrove canopy at landscape scales. A LiDAR instrument onboard an aircraft emits near-infrared laser beams which hit the leaves, branches, trunks, and ground, resulting in multiple returns of the laser beams [32]. The height of the returns is recorded by the LiDAR instruments as a measurement of the top and internal canopy structure.
Two major hurricanes in September 2017 impacted the Caribbean region, especially the island of Puerto Rico [7,33]. Hurricane Irma passed by on 6 September as a Category 5, while Hurricane Maria traversed Puerto Rico on 20 September as a high-end Category 4, which resulted in tremendous damage to the coastal mangrove ecosystems. Trees were defoliated and stems were ruptured or slanted (photos in Appendix A), thus largely reducing the canopy height. LiDAR-based assessment of the hurricanes damage on coastal mangroves is vital to understand their vulnerability at landscape scales. The application of LiDAR data to the largest basin mangroves in Puerto Rico showed that elevation, tree density, and distance to freshwater or sewage canals are important to explain the spatial variations of the pre-hurricane canopy height, as well as the canopy height reduction by the hurricanes [34]. However, it is unknown whether these findings can be generalized to the mangroves of various types with diverse environmental settings.
The objective of this study was to explore the spatial variation of the pre-hurricane canopy structure of multiple mangrove forests along the Puerto Rico coast, as well as the damage to the canopy due to the major hurricanes in 2017. We hypothesized that the pre-hurricane canopy height of coastal mangrove forests is a function of the topography, the distance to the rivers/canals within and nearby, and the distance to the coast, as these variables may modify the hydrology, salinity, and nutrient supply. We also hypothesized that the canopy height reduction by hurricanes is also a function of the above factors, but more importantly determined by the pre-hurricane canopy structure.

2. Materials and Methods

2.1. Site Description

Puerto Rico lies to the east end of the Great Antilles islands (Figure 1, upper panel) with a central latitude of 18.22°N. Rainfall in Puerto Rico varies greatly from ~1000 mm in the southwest to ~4000 mm in the east mountain peak, which shields the rainfall brought by the easterly trade winds. In general, the northern and eastern coasts receive more rainfall than the southern and western coasts. Ample rainfall on the north coast tends to produce more stream discharge and overland flow than the south coast, which dilute the salinity. The difference between the northern and southern coasts also arises from bathymetry. The northern coast is bounded by the Atlantic Ocean with the deepest trench, whereas the southern coast faces the much shallower Caribbean Sea. Thus, the tidal energy on the northern coast is higher than that on the southern coast. The consequence is that the northern coast has developed more and large fluvial plains and sandy beaches than the southern coast. Basin and riverine mangrove forests are mostly found on the northern coast, whereas fringe and over-washed mangrove forests are usually found on the southern coast. Historically, Puerto Rico once had about 11,000 ha of mangroves in 1800s, which declined to about 6000 ha in 1960s due to the expansion of agriculture and urban development [22]. The conservation of wetlands guided by international and national laws led to the recovery to about 8000 ha in large, aggregated patches [5,22,35,36]. Puerto Rico has all three true mangrove species, as well as the mangrove associates, found in the Caribbean.
This study analyzed five mangrove forests, including true mangroves and mangrove associates, along the Puerto Rico coast, four of which were in the east and northeast, along with one site in the southwest (Figure 1, the lower panel). These sites were selected mostly on the basis of data availability. The four sites in the east and northeast (Palma del Mar, Fajardo, Caño Martín Peña, and Toa Baja) were also closer to the path of Hurricane Maria than La Parguera in the southwest. The forest in Palma del Mar is dominated by Pterocarpus officinalis, a mangrove associate, whereas the other four are dominated by true mangroves.

2.2. Data Source

To investigate the spatial patterns of the mangrove canopy and to assess the hurricanes damage, we used airborne LiDAR data provided by two campaigns before and after the hurricanes. In March 2017, the campaign of Goddard’s LiDAR, Hyperspectral, and Thermal Imager (G-LiHT) [37] by the National Aeronautics and Space Administration (NASA) covered a number of transect strips in Puerto Rico. After the hurricanes in September 2017, USGS LiDAR campaigns in 2018 (https://nationalmap.gov/3DEP/, accessed on 15 March 2022) covered most of the island. Both campaigns provided data in the form of point clouds. Hence, the boundaries of the five sites were derived on the basis of the intersections of coverage of G-LiHT and USGS LiDAR and the forested wetland delineated by the NOAA 2010 C-CAP (Coastal Change Analysis Program) land-cover map, and then were shrunk for simplicity [38]. The LiDAR data of the G-LiHT transects (Table 1) were used to derive the canopy height before the hurricanes, which we hereafter refer to as the ‘pre-hurricane canopy height’, while the USGS data were used to derive the canopy height after the hurricanes (Table 1), which we hereafter refer to as the ‘post-hurricane canopy height’. For G-LiHT data, the normal point spacing of the point cloud is 0.24 m with horizontal and vertical accuracies of 1 m (https://glihtdata.gsfc.nasa.gov/, accessed on 15 March 2022), whereas the normal point spacing, vertical accuracy, and horizontal accuracy of USGS LiDAR point cloud are 0.34, 0.1, and 1 m, respectively.
Each G-LiHT transect consists of a few tiles, and each tile is approximately 80 m by 500 m; only those tiles within the sites were analyzed. The USGS LiDAR tiles for the post-hurricane analyses are also listed in Table 1. In addition to the LiDAR point clouds, we used the digital elevation model (DEM) of 1 m resolution provided by the USGS 3D Elevation Program (https://www.usgs.gov/3d-elevation-program, accessed on 15 March 2022), which has a vertical accuracy of 10 cm (RMSEz, Root Mean Square Error in z).

2.3. Analysis of Pre-Hurricane Canopy Height and Canopy Height Reduction by the Hurricanes

Mangrove forest canopies were derived as follows: We first clipped the LiDAR tiles according to the boundary of each site. The canopy height before and after the hurricanes were derived at 1 m resolution from the G-LiHT and USGS point clouds, respectively, using the grid_canopy() and normalize_height() functions provided by the ‘lidR’ package version 3.1.3 [39]. To help explain the canopy height reduction, we also tried to detect trees and tree heights using the find_trees() function using local maximum algorithm. This algorithm may not be able to identify small trees with crowns overlapping with the adjacent trees. However, the parameters set in a previous study allowed us to verify the density derived against a ground survey for trees with stem diameter greater than 10 cm [34]. We named the tree density derived using this method as ‘algorithm-derived tree density’. The reduction in canopy height by hurricanes was further computed as the pre-hurricane canopy height minus the post-hurricane canopy height.
Considering the salinity and nutrient availability which are affected by the rivers, the freshwater or sewage canals within or nearby, as well as the coastal water, we calculated the distance to the rivers/canals and the distance to the coast at 1 m resolution. Average gust wind speed and hurricane rainfall for each site were estimated on the basis of ground measurements and kriging interpolations [31,40].
To test our hypotheses and to explain the spatial variation in pre-hurricane canopy height, as well as the canopy height reduction by the hurricanes, we applied spatial regression to model the response of pre-hurricane canopy height and canopy height reduction to the abovementioned covariates for each site. The spatial error model took the following form:
y = x β + u ,                     u = λ W u + ϵ ,
where y is the dependent variable represented as an n × 1 matrix (n, number of records in the dataset), x is one or multiple (m) independent variables (covariates) represented by an n × (m + 1) matrix, β is an (m + 1) × 1 coefficient matrix to be estimated, and u is an n × 1 spatial error matrix. W is an n × n weight matrix determined by the neighborhood structure, λ is the spatial autocorrelation coefficient, and ε is the normal i.i.d. (independent and identically distributed) residual.
To apply the spatial error model, all the spatial variables were aggregated into 20 m grids to obtain the mean quantities. In addition, we computed the standard deviation of the pre-hurricane canopy height for the 20 m grid to reflect the unevenness of the pre-hurricane canopy height. The variables at 20 m resolution were normalized in the range of 0 to 1, so that we could compare the coefficients estimated by the regressions.
To explore the spatial responses of the mangroves across sites, we also pooled the data of all sites for the same set of spatial regression. This was done by sampling 150 grid cells of 20 m × 20 m from each site in three strata defined as 0–33, 33–67, and 67–100 percentiles of the pre-hurricane canopy height. The spatial regressions were then conducted for the pooled datasets.
The covariates included in the regression of the pre-hurricane canopy height were the elevation, the distance to within or nearby rivers/canals, the distance to coastal saltwater, and the algorithm-derived tree density. The additional covariates for the regression of the canopy height reduction by the hurricanes were the pre-hurricane canopy height and the canopy roughness. The pooled regression also incorporated the mean gust windspeed and total rainfall during the hurricane to explain the difference across sites. All the data analyses and mapping were done with R [41] and ArcGIS Pro (ESRI, Redlands, CA, USA).

3. Results

3.1. Spatial Variation and Summary Statistics of the Canopy Heights before and after the Hurricanes

Elevation was found to be the most important environmental variable explaining the pre-hurricane canopy height, as well as the canopy height reduction by the hurricanes [34]. The elevation profiles of the five forests (Figure 2, Table 2) showed great variations across the sites. The Fajardo site had the highest elevation with a mean ± SD of 1.61 ± 1.07 m, followed by Palma Del Mar with 1.03 ± 0.38 m. La Parguera (fringe mangroves) in the southwest had the lowest elevation with a mean ± SD of 0.16 ± 0.07 m. Caño Martín Peña and Toa Baja had moderate elevations with means ± SD of 0.36 ± 0.32 and 0.39 ± 0.31 m, respectively.
The pre-hurricane canopy height (CHM_2017, Figure 3) shows that there were wide variations in mangrove canopy height within and between sites (Table 2). The mean canopy height of Caño Martín Peña, Palma del Mar, and Toa Baja were in the range of 9.3–11.7 m, higher than that in Fajardo and La Parguera (6.7 and 6.2 m, respectively). Compared to the pre-hurricane canopy height, the mean post-hurricane canopy height (CHM_2018) was more even both within and across the sites (Figure 3 and Figure 4). The mean height varied from 4.2 m in Palma del Mar to 6.1 m in Caño Martín Peña. We found a pattern that a higher pre-hurricane canopy led to a greater reduction by the hurricanes (Figure 5). Toa Baja with the highest mean pre-hurricane canopy showed the greatest reduction of 6.1 m, whereas La Parguera with the lowest pre-hurricane canopy experienced the smallest reduction of 0.5 m (Table 2). The mean algorithm-derived pre-hurricane tree density reached the greatest level in Caño Martín Peña and Toa Baja (2135 ha−1 and 2132 ha−1, respectively), but was lower in La Parguera and Palma del Mar (1674 ha−1 and 1682 ha−1, respectively).
The forests in Palma del Mar and Fajardo are the closest to rivers/canals with mean distance of 57.8 ± 55.3 and 83.8 ± 60.8 m (Table 2), respectively, whereas the forest in La Parguera does not have any rivers or canals nearby and the nearest rivers/canals are 948.1 ± 157.9 m away. The forest near Caño Martín Peña has the closest mean distance to coastal water (101.2 m) because we treated the water in the Channel of Martín Peña as salty. The Pterocarpus forest in Palma del Mar grows inward to the land and is connected to the coast by channels and a river, such that the forest has the farthest mean distance to the coast (710.3 m). The great mean distance of 516.9 m to the coast and the medium distance of 341.5 m to the river/canals of the Toa Baja Forest are largely because of its large area of 71.1 ha.
Windspeed and rainfall interpolated from the ground observations during the hurricane [31,40] showed that the mean gust windspeed was the highest at Palma del Mar (49.5 m·s−1, Table 2), the site closest to the landfall of Hurricane Maria, whereas La Parguera in the southwest farthest from the hurricane path had the lowest mean gust windspeed (34.1 m·s−1). The other three sites in between also had gust speeds of more than 44 m·s−1. The hurricane-brought rainfall showed more variation across sites than gust windspeed. Toa Baja and Caño Martín Peña experienced the highest rainfall of 497.2 and 427.8 mm, respectively, whereas the forest at La Parguera received only 91.1 mm. Palma del Mar, even closer to the landfall of Maria, only received 286.5 mm rainfall.

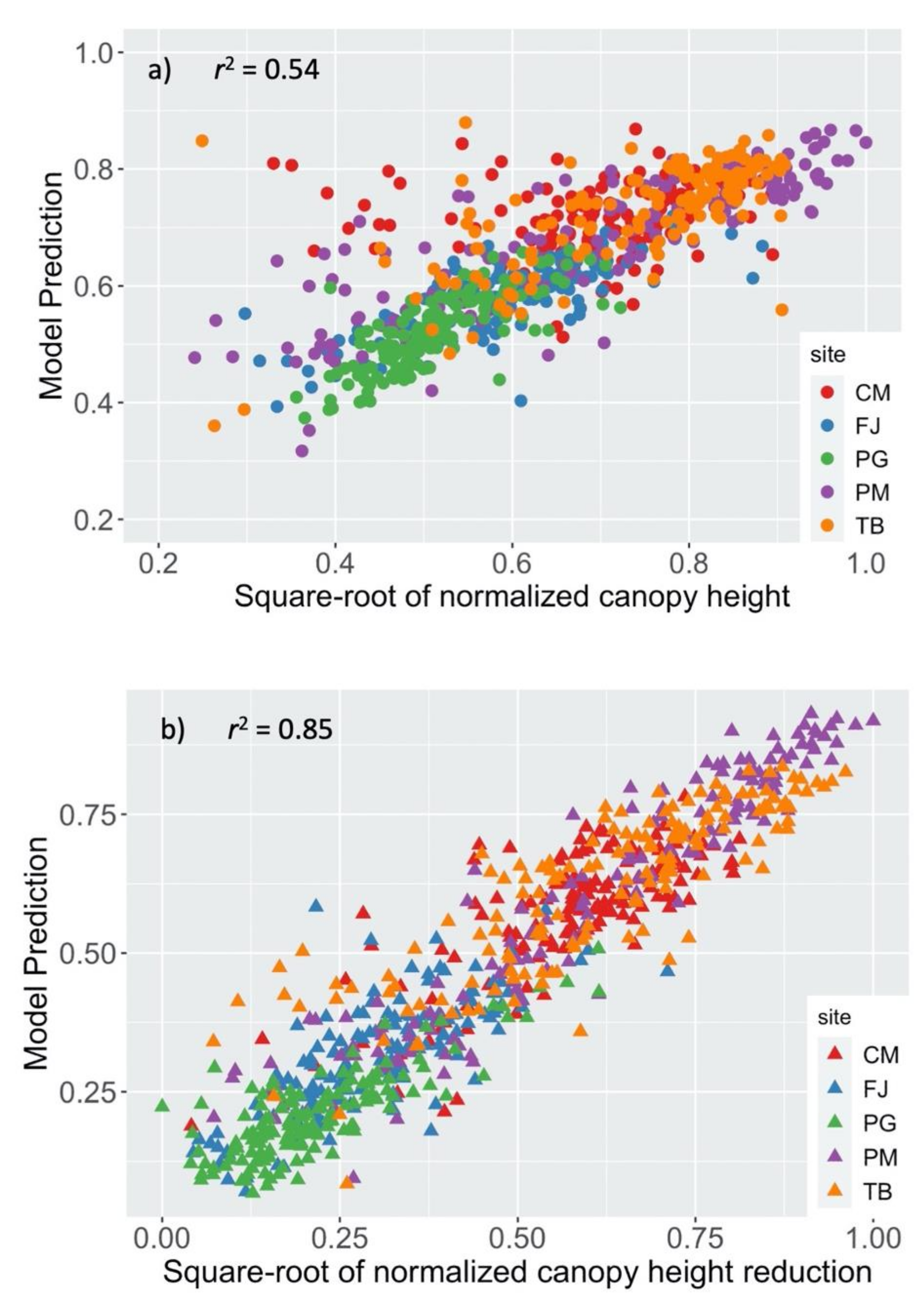
3.2. Spatial Regression Models of the Pre-Hurricane Canopy Height and the Canopy Height Reduction by the Hurricanes

The spatial regression of the pre-hurricane canopy height yielded equations with significant coefficients listed in Table 3. For example, the equation for Palma del Mar was
h = 0.803 − 0.785 z + 0.467 z 2 − 0.646 d ,
where h is the normalized pre-hurricane canopy height, z is the normalized elevation, and d is the normalized algorithm-derived tree density. For symbols in Table 3, sc is the normalized distance to coast, and λ is the spatial autocorrelation coefficient. The spatial error model for Palma del Mar had a λ of 0.90 and r2 of 0.68. Except for the forest in Fajardo, the pre-hurricane canopy height depended significantly on the elevation, but this dependence differed across sites (Table 3). For La Parguera, the pre-hurricane canopy height increased linearly with elevation. Similarly, the pre-hurricane canopy height of the forests in Caño Martín Peña and Toa Baja increased with elevation when elevation was low, but then decreased with elevation when elevation was higher as the absolute value of the z2 coefficient was greater than that of z. The pre-hurricane canopy height of these three sites also significantly decreased with the distance to the coast. The pre-hurricane canopy height in Palma del Mar decreased quadratically with elevation.
The dependence of the pre-hurricane canopy height on the algorithm-derived tree density differed across sites; three sites (La Parguera, Palma del Mar, and Fajardo) had pre-hurricane canopy height decreases with density, whereas the pre-hurricane canopy height increased with density in Toa Baja. The density was not a significant explanator of the pre-hurricane canopy height in Caño Martín Peña.
The equations of the spatial error model for the canopy height reduction with significant coefficients are shown in Table 4 and could be expressed as follows for the Toa Baja site:
Δ h = 0.097 + 0.331   h + 0.536 h 2 − 0.426   z + 0.360 z 2 + 0.112 s h − 0.126 s
where Δh is the normalized canopy height reduction, sh is the normalized standard deviation of pre-hurricane canopy height within the 20 m grid, and s is the distance to rivers/canals.
The canopy height reduction of all sites increased linearly or quadratically with the pre-hurricane canopy height (Table 4). The reduction at all sites except Palma del Mar decreased quadratically with the elevation. For Palma del Mar, the canopy height reduction increased with elevation where the Pterocarpus forest occupied a higher elevation compared to other sites. The canopy height reduction in Palma del Mar and Fajardo was significantly cut back by the high tree density, while that in Toa Baja was significantly promoted by the unevenness of the pre-hurricane canopy height (sh). The canopy height reduction at Toa Baja and Caño Martín Peña was lowered by the distance to the rivers/canals such that a farther distance from rivers/canals led to less canopy height reduction. The canopy height reduction at Caño Martín Peña was also cut back by the distance to the coast water.
Pooling the data of all sites, we found that the pooled pre-hurricane canopy height had the following equation:
h = 1.052 − 1.352 z + 0.956 z 2 − 0.477 d − 0.211 s
Hence, the pooled canopy height decreased quadratically with the elevation and linearly with the algorithm-derived tree density and the distance to rivers/canals. The regression had a λ of 0.48 and r2 of 0.54. The model fit to the data is shown in Figure 6a.
The regression of the pooled canopy height reduction resulted in
Δ h = − 0.067 + 1.147 h − 0.401 h 2 − 0.256 z + 0.095 p + 0.226 w 2
where p is the normalized rainfall, and w is the normalized gust windspeed. The regression had a λ as 0.51 and r2 as 0.85. Hence, the prevailing pattern across the five sites is that the canopy height reduction increased with the pre-hurricane canopy height but decreased with elevation. Large rainfall and gust speed incurred more canopy height reduction; however, the impact of the windspeed was greater than that of rainfall as indicated by the bigger coefficient before windspeed. The model prediction versus LiDAR-derived canopy height reduction is depicted in Figure 6b.

4. Discussion

4.1. Canopy Height before Hurricanes

Our analyses supported our hypothesis that the canopy height reduction significantly depends on the pre-hurricane canopy height, as a higher canopy before hurricanes means more interception of the wind force to damage the canopy [42,43]. The effect of pre-hurricane canopy height has been identified as the primary parameter in several models that simulate the risk of wind damage to forest stands.
The dependence of the canopy height reduction on the pre-hurricane canopy height was quadratic, rather than linear, which implies that the slope decreased as the pre-hurricane canopy height increased. Moreover, the pre-hurricane canopy height was the most important factor determining the hurricane damage to mangrove forest as the coefficients of the normalized canopy height in the equations (Table 4, Equation (5)) were largest compared to other factors.

4.2. Elevation

Our analyses both at a site level and across sites using pooled data supported our hypothesis that both the pre-hurricane mangrove canopy height and the canopy height reduction by the hurricanes depend on elevation, but only partly on the distance to rivers/canals and the distance to coast. The responses of canopy height and the canopy height reduction to elevation and distance to rivers/canals and coast water depended heavily on the regimes of these variables.
The responses of the pre-hurricane canopy height of Toa Baja and Caño Martín Peña to elevation were similar (Table 3) as these two sites had the same elevation regime with a mean elevation in the range of 0.36~0.39 m (Table 2). The quadratic feature implies that the pre-hurricane canopy height increased with elevation when elevation was lower and then decreased with elevation at a higher elevation range. The maximum pre-hurricane canopy height occurred at a moderate elevation around 1 m according to our model and data. The places with lowest elevation were closer to the coast with red mangrove. As elevation went from low to moderate, the species shifted to black or white mangroves. As elevation continued to increase beyond the moderate range, the freshwater supply decreased and salinity increased [44,45], thereby decreasing the pre-hurricane canopy height. It seems that this pattern can be extrapolated across sites with different elevation regimes. La Parguera had the lowest elevation range with a mean of 0.16 m and maximum of 0.2 m, such that the pre-hurricane canopy height increased with elevation. The Pterocarpus growing in brackish water at Palma del Mar had a mean elevation greater than 1 m such that the pre-hurricane canopy height decreased with the elevation.
The canopy height reduction of all sites except Palma del Mar decreased with elevation mostly because the areas with lower elevation were muddier and the stems of the mangroves were easier to fall down or be slanted by the wind [11]. In addition, the lower elevation was more likely to be inundated to cause additional damage [13]. When elevation increased, the lower pre-hurricane canopy height and the stronger root-soil anchorage allowed the system to resist and reduce the wind damage to the canopy. The forest at Palma del Mar had greater than 1 m mean elevation and was closest to the rivers/canals (Table 2), which both helped to drain the hurricane water and, thus, reduced the risk of prolonged inundation. However, this site was closest to the hurricane landing point and experienced the strongest gust wind. With the increase in elevation, the dominant Pterocarpus with high canopy was exposed to stronger wind and, thus, suffered more damage.

4.3. Distance to Rivers/Canals and to Coast

Rivers and canals supply freshwater, and canals of sewage purposes deliver nutrients and freshwater to the mangrove ecosystems to alleviate the salinity and nutrient stresses, especially for places with low elevation. Our analysis supported the hypothesis that the pre-hurricane canopy height and the canopy height reduction decrease with the distance to rivers/canals. However, this hypothesis was only applicable to pre-hurricane canopy height with pooled data and to the canopy height reduction at sites with moderate elevation. La Parguera had the lowest elevation, but no rivers or canals passing through, and the nearest canals were about 1 km away. For Fajardo and Palma del Mar, the elevation regimes were too high to retain the freshwater and nutrients derived by the rivers/canals. Hence, the distance to rivers/canals did not appear significant in the equations for these three sites. The distance to rivers/canals only appeared in the equations for Toa Baja and Caño Martín Peña, where the elevation range was low to moderate. Furthermore, the mean distances to rivers/canals are in the moderate range, and within-site variations of the distance to rivers/canals were the greatest at these two sites (Table 2). It seems that the conditions for the distance to rivers/canals to come into play are at least low or moderate elevation and large within-site variation of the distance to rivers/canals. These conditions did not concurrently exist for other sites.
Our equations show that areas with a shorter distance to rivers/canals were associated with higher pre-hurricane canopy (Equation (4)) and more canopy height reduction (Table 4). Soils near rivers/canals may be associated with lower salinity or better nutrient status, which not only support better mangrove growth, but also change the allocation pattern [4,46,47,48]. The changed allocation pattern would increase the shoot/root ratio so that the mangroves would intercept more wind force during hurricanes but have less soil-root anchorage. The consequence is that the trees would be easier to fall or to slant. The better nutrient supply may also change the leaf traits of plants such that the leaves may grow thinner. Thinner leaves are easier to be torn by hurricane winds, thus incurring more defoliation [49]. The flooding map detected from radar images showed greater inundation along the rivers/canals (unpublished data). These facts explain why the areas with closer distance to rivers/canals suffered more canopy height reduction, whereas those with farther distance were associated with less canopy height reduction.
The distance to coast may be associated with the elevation and salinity gradients. For coastal wetlands with riverine mangroves, the salinity generally increases with the distance to the coast [44,50]. The higher salinity at farther distances allows more root growth than shoot growth to resist wind damage. The farther distance to the coast was also associated with lower pre-hurricane canopy height in Caño Martín Peña, Toa Baja, and La Parguera, as well as lower canopy height reduction in Caño Martín Peña. In addition, places with farther distance to the coast may be less prone to inundation from storm surges.

4.4. Tree Density and Unevenness of Canopy

The algorithm-derived tree density appeared in the equations for Palma del Mar and Fajardo to alleviate the canopy height reduction. However, the relationship between the pre-canopy height and the tree density was not consistent across all sites. Larger and taller trees may be associated with lower tree density due to self-thinning. However, higher tree density may also make the trees grow taller to compete for light so that higher canopy height may be associated higher tree density or may not be significantly related to the tree density [11].
Tree density has been identified as a factor that modulates the wind damage to forests in several studies: Trees growing together can support each other mechanically [8] by increasing the interaction among neighboring trees through friction of leaves and branches in dissipating the wind energy. High tree density is especially important for mangroves with low stem diameters. Theoretical and practical studies of windbreak systems have indicated that density is one of the major parameters for effective wind reduction [51]. On the other hand, forests with lower tree density often experience more dead trees and bent trunks after major hurricanes [52]. A hybrid model of ForestGales developed for simulation of wind damage risk of forests used a series of important parameters including spacing among trees, which is the inverse of the tree density. The sensitivity analysis found that the critical wind speed of stem rupture is inversely proportional to the average spacing among trees so that higher windspeed is needed to rupture closely spaced (high density) trees [10,53].
A closely related concept is the unevenness of the canopy, which appeared in our equation for Toa Baja to enlarge the canopy height reduction (Table 4). Boundary-layer theory indicates that rough surfaces associated with unevenness of canopies can make the boundary thinner to facilitate vertical convections [54] such that the wind can more easily traverse the forest canopy and cause more damage. Unevenness of canopy height is also related to the tree density. In addition to the heterogeneous salinity/nutrient conditions and the competition among trees that gives different canopy growth, the spatial heterogeneity of tree density is likely to create the unevenness of the canopy as low tree densities are likely associated with gaps in the canopy to increase the unevenness of the canopy height.

4.5. Hurricane Winds and Rainfall

Hurricane wind is the most important force damaging the canopy. The forest at Palmar del Mar experienced the strongest gust wind and consequently encountered the most severe canopy damage, i.e., 55% relative canopy height reduction (Table 2). In addition, for the coastal mangroves distributed in a low elevation profile and, thus, susceptible to various flooding drivers (coastal surge, fluvial, or pluvial), rainfall during the hurricanes appeared to be an important driver of canopy height reduction (Equation (5)). The drainage capacity of mangrove ecosystems can, thus, play an important role in rainfall-driven inundation. Our ongoing work on radar-detected inundation showed inundations along the coast, along the rivers/canals, and in low-lying areas after the hurricane which lasted around 10 days. The forests at Caño Martín Peña and Toa Baja experienced strong gust winds and the heaviest hurricane rainfall (Table 2). These two sites had low to moderate elevation with close distance to the coast or the rivers/canals, thus being prone to coastal surge and fluvial or pluvial flooding. The inundation caused by the downpour, storm surge, and river overflow is an important factor resulting in additional damage.
Wetland recovery from hurricane damage will be a future subject. Airborne LiDAR data from campaigns after 2018 should be incorporated with multispectral and hyperspectral images to fulfil this task. In addition to airborne LiDAR, spaceborne LiDAR data are becoming available recently. For example, GEDI (Global Ecosystem Dynamics Investigation) on board the International Space Station provides an alternative data source with longer-term data at a larger scale [55]. Vertical canopy structure and complexity play an important role in providing microhabitats for other species such as insects and birds [56,57]. Therefore, the assessment of canopy height using LiDAR might have implications in biodiversity studies, especially for those species relying on forests as part of their habitats.

5. Conclusions

Using LiDAR point-cloud data before and after the hurricanes in September 2017, we analyzed the pre-hurricane canopy height, as well as the canopy height reduction, during the hurricanes for five coastal mangrove sites. There were three groups of variables that might have interplayed to affect the vulnerability of mangrove forests under tropical storm disturbance: (1) pre-hurricane canopy structure including canopy height and its unevenness, tree density, and allometry pattern, (2) the physical environment including elevation, rivers/canals within or passing through the forests, and distance to coast, and (3) the external forces such as windspeed and rainfall during the hurricanes. Mangrove forests with higher, unevener canopy and lower tree density tend to experience more canopy damage than those with lower, evener canopy and higher tree density. This biological group is shaped by the second factor, i.e., the physical environment. Spatial variation of elevation, climate, and distance to rivers/canals and to coast tend to modify the canopy structure, the allometry, and the leaf traits as these physical environmental variables control the spatial distribution of the soil salinity. Among these physical environments, elevation is the most determinative as its regime governs the significance of the distance to rivers/canals and to the coast. In addition to windspeed, we found rainfall to also be an important factor affecting the mangrove canopy damage by the hurricanes, especially in lowland prone to inundation.
The estimate of canopy height by LiDAR point clouds is based on the returned signals by the source. Thus, the canopy height reduction mostly reflects the defoliation and raptures of branches, but, to a lesser extent, the fall and rapture of the trunks. The significance of the covariates in the equations seemed also dependent on the scales. For example, the distance to rivers/canals was not significant in the equation of pre-hurricane canopy height for any site. However, it was significant in the equation for the pooled equation (Equation (4)). Correlation among covariates may also cause differences in response equations among sites. Future efforts should be made on ground field measurements and scaling from plot to landscape so that LiDAR-based analysis can offer a more certain and complete mechanistic understanding of mangrove vulnerability to hurricane disturbance.

Author Contributions

Conceptualization, Q.G. and M.Y.; methodology, Q.G. and M.Y.; formal analysis, Q.G. and M.Y.; writing—original draft preparation, Q.G.; writing—review and editing, Q.G. and M.Y. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the NOAA Puerto Rico Sea Grant NA18OAR4170089.

Data Availability Statement

All the datasets are publicly available at the USGS 3D Elevation Program (3DEP) data portal (https://nationalmap.gov/3DEP/, accessed on 15 March 2022) and the NASA G-LiHT data portal (https://glihtdata.gsfc.nasa.gov/, accessed on 15 March 2022).

Acknowledgments

We acknowledge USGS for providing the LiDAR after the hurricanes, publicly available at the USGS 3D Elevation Program (3DEP) data portal (https://nationalmap.gov/3DEP/, accessed on 15 March 2022), and NASA for providing the LiDAR data before the hurricanes, publicly accessible at NASA G-LiHT (https://glihtdata.gsfc.nasa.gov/, accessed on 15 March 2022).

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.

Appendix A

The aerial photos of riverine mangroves taken before and after the hurricanes (https://glihtdata.gsfc.nasa.gov/puertorico/index.html, accessed on 15 March 2022).
Remotesensing 14 01497 i001

References

  1. Alongi, D.M. Carbon Cycling and Storage in Mangrove Forests. Annu. Rev. Mar. Sci. 2014, 6, 195–219. [Google Scholar] [CrossRef] [PubMed]
  2. Atwood, T.B.; Connolly, R.M.; Almahasheer, H.; Carnell, P.E.; Duarte, C.M.; Ewers Lewis, C.J.; Irigoien, X.; Kelleway, J.J.; Lavery, P.S.; Macreadie, P.I.; et al. Global patterns in mangrove soil carbon stocks and losses. Nat. Clim. Chang. 2017, 7, 523. [Google Scholar] [CrossRef]
  3. Cannicci, S.; Burrows, D.; Fratini, S.; Smith, T.J.; Offenberg, J.; Dahdouh-Guebas, F. Faunal impact on vegetation structure and ecosystem function in mangrove forests: A review. Aquat. Bot. 2008, 89, 186–200. [Google Scholar] [CrossRef]
  4. Krauss, K.W.; McKee, K.L.; Lovelock, C.E.; Cahoon, D.R.; Saintilan, N.; Reef, R.; Chen, L. How mangrove forests adjust to rising sea level. New Phytol. 2014, 202, 19–34. [Google Scholar] [CrossRef] [Green Version]
  5. Yu, M.; Rivera-Ocasio, E.; Heartsill-Scalley, T.; Davila-Casanova, D.; Rios-López, N.; Gao, Q. Landscape-Level Consequences of Rising Sea-Level on Coastal Wetlands: Saltwater Intrusion Drives Displacement and Mortality in the Twenty-First Century. Wetlands 2019, 39, 1343–1355. [Google Scholar] [CrossRef]
  6. Badola, R.; Hussain, S.A. Valuing ecosystem functions: An empirical study on the storm protection function of Bhitarkanika mangrove ecosystem, India. Environ. Conserv. 2005, 32, 85–92. [Google Scholar] [CrossRef]
  7. Cartier, K. Hurricanes Hit Puerto Rico’s Mangroves Harder Than Florida’s. EOS 2019, 100. [Google Scholar] [CrossRef]
  8. Duryea, M.L.; Kamp, E. Wind and Trees: Lessons Learned from Hurricanes; School of Forest Resources and Conservation, University of Florida FAS Extension: Gainesville, FL, USA, 2017. [Google Scholar]
  9. Smith, T.J.; Anderson, G.H.; Balentine, K.; Tiling, G.; Ward, G.A.; Whelan, K.R.T. Cumulative impacts of hurricanes on Florida mangrove ecosystems: Sediment deposition, storm surges and vegetation. Wetlands 2009, 29, 24. [Google Scholar] [CrossRef]
  10. Gardiner, B.; Byrne, K.; Hale, S.; Kamimura, K.; Mitchell, S.J.; Peltola, H.; Ruel, J.-C. A review of mechanistic modelling of wind damage risk to forests. For. Int. J. For. Res. 2008, 81, 447–463. [Google Scholar] [CrossRef] [Green Version]
  11. Mitchell, S.J. Wind as a natural disturbance agent in forests: A synthesis. For. Int. J. For. Res. 2012, 86, 147–157. [Google Scholar] [CrossRef] [Green Version]
  12. Ye, F.; Huang, W.; Zhang, Y.J.; Moghimi, S.; Myers, E.; Pe'eri, S.; Yu, H.C. A cross-scale study for compound flooding processes during Hurricane Florence. Nat. Hazards Earth Syst. Sci. 2021, 21, 1703–1719. [Google Scholar] [CrossRef]
  13. Choy, S.C.; Booth, W.E. Prolonged inundation and ecological changes in an Avicennia mangrove: Implications for conservation and management. Hydrobiologia 1994, 285, 237–247. [Google Scholar] [CrossRef]
  14. Krauss, K.W.; Osland, M.J. Tropical cyclones and the organization of mangrove forests: A review. Ann. Bot. 2019, 125, 213–234. [Google Scholar] [CrossRef] [PubMed]
  15. Lovelock, C.E.; Krauss, K.W.; Osland, M.J.; Reef, R.; Ball, M.C. The Physiology of Mangrove Trees with Changing Climate. In Tropical Tree Physiology: Adaptations and Responses in a Changing Environment; Goldstein, G., Santiago, L.S., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 149–179. [Google Scholar] [CrossRef]
  16. Peel, J.R.; Sanchez, M.C.M.; Lopez-Portillo, J.; Golubov, J. Stomatal density, leaf area and plant size variation of Rhizophora mangle (Malpighiales: Rhizophoraceae) along a salinity gradient in the Mexican Caribbean. Rev. Biol. Trop. 2017, 65, 701–712. [Google Scholar] [CrossRef] [Green Version]
  17. Kodikara, K.A.S.; Jayatissa, L.P.; Huxham, M.; Dahdouh-Guebas, F.; Koedam, N. The effects of salinity on growth and survival of mangrove seedlings changes with age. Acta Bot. Bras. 2018, 32, 37–46. [Google Scholar] [CrossRef] [Green Version]
  18. Waisel, Y.; Eshel, A.; Agami, M. Salt balance of leaves of the mangrove Avicennia marina. Physiol. Plant. 2006, 67, 67–72. [Google Scholar] [CrossRef]
  19. Reef, R.; Lovelock, C.E. Regulation of water balance in mangroves. Ann.Bot. 2015, 115, 385–395. [Google Scholar] [CrossRef] [Green Version]
  20. Lugo, A.E.; Medina, E. Mangrove Forests. In Encyclopedia of Natural Resources–Land; Wang, Y., Ed.; Taylor & Francis Group: New York, NY, USA, 2014; Volume 1. [Google Scholar]
  21. Branoff, B. Urban Mangrove Biology and Ecology: Emergent Patterns and Management Implications; University of Puerto Rico: San Juan, PR, USA, 2018. [Google Scholar]
  22. Martinuzzi, S.; Gould, W.A.; Lugo, A.E.; Medina, E. Conversion and recovery of Puerto Rican mangroves: 200 years of change. For. Ecol. Manag. 2009, 257, 75–84. [Google Scholar] [CrossRef]
  23. Lugo, A.E.; Medina, E.; Cuevas, E.; Cintrón, G.; Nieves, E.N.L.; Novelli, Y.S. Ecophysiology of a Mangrove Forest in Jobos Bay, Puerto Rico. Caribb. J. Sci. 2007, 43, 200–219. [Google Scholar] [CrossRef] [Green Version]
  24. Quadros, A.F.; Zimmer, M. Dataset of “true mangroves” plant species traits. Biodivers. Data J. 2017, 5, e22089. [Google Scholar] [CrossRef] [Green Version]
  25. Miller, G.L.; Lugo, A.E. Guide to the Ecological Systems of Puerto Rico; U.S. Department of Agriculture, Forest Service, International Institute of Tropical Forestry: San Juan, PR, USA, 2009; p. 437. [Google Scholar]
  26. Castañeda-Moya, E.; Rivera-Monroy, V.H.; Chambers, R.M.; Zhao, X.; Lamb-Wotton, L.; Gorsky, A.; Gaiser, E.E.; Troxler, T.G.; Kominoski, J.S.; Hiatt, M. Hurricanes fertilize mangrove forests in the Gulf of Mexico (Florida Everglades, USA). Proc. Natl. Acad. Sci. USA 2020, 117, 4831–4841. [Google Scholar] [CrossRef]
  27. Taillie, P.J.; Roman-Cuesta, R.; Lagomasino, D.; Cifuentes-Jara, M.; Fatoyinbo, T.; Ott, L.E.; Poulter, B. Widespread mangrove damage resulting from the 2017 Atlantic mega hurricane season. Environ. Res. Lett. 2020, 15, 064010. [Google Scholar] [CrossRef]
  28. Branoff, B.; Martinuzzi, S. Mangrove forest structure and composition along urban gradients in Puerto Rico. bioRxiv 2018, 504928. [Google Scholar] [CrossRef] [Green Version]
  29. Field, C.; Osborn, J.; Hoffman, L.; Polsenberg, J.; Ackerly, D.; Berry, J.; BjÖRkman, O.; Held, A.; Matson, P.; Mooney, H. Mangrove biodiversity and ecosystem function. Glob. Ecol. Biogeogr. Lett. 1998, 7, 3–14. [Google Scholar] [CrossRef]
  30. Giri, C.; Ochieng, E.; Tieszen, L.L.; Zhu, Z.; Singh, A.; Loveland, T.; Masek, J.; Duke, N. Status and distribution of mangrove forests of the world using earth observation satellite data. Glob. Ecol. Biogeogr. 2011, 20, 154–159. [Google Scholar] [CrossRef]
  31. Yu, M.; Gao, Q. Topography, drainage capability, and legacy of drought differentiate tropical ecosystem response to and recovery from major hurricanes. Environ. Res. Lett. 2020, 15, 104046. [Google Scholar] [CrossRef]
  32. Huang, W.; Sun, G.; Dubayah, R.; Cook, B.; Montesano, P.; Ni, W.; Zhang, Z. Mapping biomass change after forest disturbance: Applying LiDAR footprint-derived models at key map scales. Remote Sens. Environ. 2013, 134, 319–332. [Google Scholar] [CrossRef]
  33. Eisemann, E.; Dunkin, L.; Hartman, M.; Wozencraft, J. JALBTCX/NCMP emergency-response airborne Lidar coastal mapping & quick response data products for 2016/2017/2018 hurricane impact assessments. Shore Beach 2019, 87, 31–40. [Google Scholar] [CrossRef]
  34. Gao, Q.; Yu, M. Elevation and Distribution of Freshwater and Sewage Canals Regulate Canopy Structure and Differentiate Hurricane Damages to a Basin Mangrove Forest. Remote Sens. 2021, 13, 3387. [Google Scholar] [CrossRef]
  35. Kennaway, T.; Helmer, E.H. The forest types and ages cleared for land development in Puerto Rico. Gisci. Remote Sens. 2007, 44, 356–382. [Google Scholar] [CrossRef]
  36. Gao, Q.; Yu, M. Discerning Fragmentation Dynamics of Tropical Forest and Wetland during Reforestation, Urban Sprawl, and Policy Shifts. Plos ONE 2014, 9, e113140. [Google Scholar] [CrossRef]
  37. Cook, B.; Corp, L.; Nelson, R.; Middleton, E.; Morton, D.; McCorkel, J.; Masek, J.; Ranson, K.; Ly, V.; Montesano, P. NASA Goddard’s LiDAR, Hyperspectral and Thermal (G-LiHT) Airborne Imager. Remote Sens. 2013, 5, 4045–4066. [Google Scholar] [CrossRef] [Green Version]
  38. Office for Coastal Management. C-CAP Land Cover, Puerto Rico. 2010. Available online: https://www.fisheries.noaa.gov/inport/item/48301 (accessed on 15 March 2022).
  39. Roussel, J.-R.; Auty, D.; Boissieu, F.D.; Meador, A.S. lidR: Airborne LiDAR Data Manipulation and Visualization for Forestry Applications. 2019. Available online: https://cran.r-project.org/package=lidR (accessed on 24 August 2021).
  40. Pasch, R.J.; Penny, A.B.; Berg, R. National Hurricane Center Tropical Cyclone Report–Hurricane Maria (AL152017) September 16–30, 2017; National Hurricane Center: Miami, FL, USA, 2019; pp. 1–48. [Google Scholar]
  41. R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2021; Available online: https://www.R-project.org/ (accessed on 15 March 2022).
  42. Angelou, N.; Dellwik, E.; Mann, J. Wind load estimation on an open-grown European oak tree. For. Int. J. For. Res. 2019, 92, 381–392. [Google Scholar] [CrossRef]
  43. Peterson, C.J.; Ribeiro, G.H.P.d.M.; Negrón-Juárez, R.; Marra, D.M.; Chambers, J.Q.; Higuchi, N.; Lima, A.; Cannon, J.B. Critical wind speeds suggest wind could be an important disturbance agent in Amazonian forests. For. Int. J. For. Res. 2019, 92, 444–459. [Google Scholar] [CrossRef]
  44. Wang, H.; Hsieh, Y.P.; Harwell, M.A.; Huang, W. Modeling soil salinity distribution along topographic gradients in tidal salt marshes in Atlantic and Gulf coastal regions. Ecol. Model. 2007, 201, 429–439. [Google Scholar] [CrossRef]
  45. Jiang, J.; Gao, D.; DeAngelis, D.L. Towards a theory of ecotone resilience: Coastal vegetation on a salinity gradient. Theor. Popul. Biol. 2012, 82, 29–37. [Google Scholar] [CrossRef]
  46. Chen, Y.; Ye, Y. Effects of Salinity and Nutrient Addition on Mangrove Excoecaria agallocha. PLoS ONE 2014, 9, e93337. [Google Scholar] [CrossRef]
  47. Nguyen, H.T.; Stanton, D.E.; Schmitz, N.; Farquhar, G.D.; Ball, M.C. Growth responses of the mangrove Avicennia marina to salinity: Development and function of shoot hydraulic systems require saline conditions. Ann. Bot. 2015, 115, 397–407. [Google Scholar] [CrossRef] [PubMed]
  48. Peters, R.; Vovides, A.G.; Luna, S.; Gruters, U.; Berger, U. Changes in allometric relations of mangrove trees due to resource availability—A new mechanistic modelling approach. Ecol. Model. 2014, 283, 53–61. [Google Scholar] [CrossRef]
  49. Reich, P.B.; Walters, M.B.; Ellsworth, D.S. Leaf Life-Span in Relation to Leaf, Plant, and Stand Characteristics among Diverse Ecosystems. Ecol. Monogr. 1992, 62, 365–392. [Google Scholar] [CrossRef]
  50. Yang, S.-C.; Shih, S.-S.; Hwang, G.-W.; Adams, J.B.; Lee, H.-Y.; Chen, C.-P. The salinity gradient influences on the inundation tolerance thresholds of mangrove forests. Ecol. Eng. 2013, 51, 59–65. [Google Scholar] [CrossRef]
  51. Talkkari, A.; Peltola, H.; Kellomäki, S.; Strandman, H. Integration of component models from the tree, stand and regional levels to assess the risk of wind damage at forest margins. For. Ecol. Manag. 2000, 135, 303–313. [Google Scholar] [CrossRef]
  52. Jimenez-Rodríguez, D.L.; Alvarez-Añorve, M.Y.; Pineda-Cortes, M.; Flores-Puerto, J.I.; Benítez-Malvido, J.; Oyama, K.; Avila-Cabadilla, L.D. Structural and functional traits predict short term response of tropical dry forests to a high intensity hurricane. For. Ecol. Manag. 2018, 426, 101–114. [Google Scholar] [CrossRef]
  53. Hale, S.E.; Gardiner, B.; Peace, A.; Nicoll, B.; Taylor, P.; Pizzirani, S. Comparison and validation of three versions of a forest wind risk model. Environ. Model. Softw. 2015, 68, 27–41. [Google Scholar] [CrossRef] [Green Version]
  54. Krogstadt, P.Å.; Antonia, R.A. Surface roughness effects in turbulent boundary layers. Exp. Fluids 1999, 27, 450–460. [Google Scholar] [CrossRef]
  55. Patterson, P.L.; Healey, S.P.; Ståhl, G.; Saarela, S.; Holm, S.; Andersen, H.-E.; Dubayah, R.O.; Duncanson, L.; Hancock, S.; Armston, J.; et al. Statistical properties of hybrid estimators proposed for GEDI—NASA’s global ecosystem dynamics investigation. Environ. Res. Lett. 2019, 14, 065007. [Google Scholar] [CrossRef]
  56. Monmany Garzia, A.C.; Yu, M.; Zimmerman, J.K. Effects of vegetation structure and landscape complexity on insect parasitism across an agricultural frontier in Argentina. Basic Appl. Ecol. 2018, 29, 69–78. [Google Scholar] [CrossRef]
  57. Mccormack, J.J.; Cotoras, D.D. Beetle Diversity Across Micro-habitats on Lizard Island Group (Great Barrier Reef, Australia). Zool. Stud. 2021, 60, 12. [Google Scholar] [CrossRef]
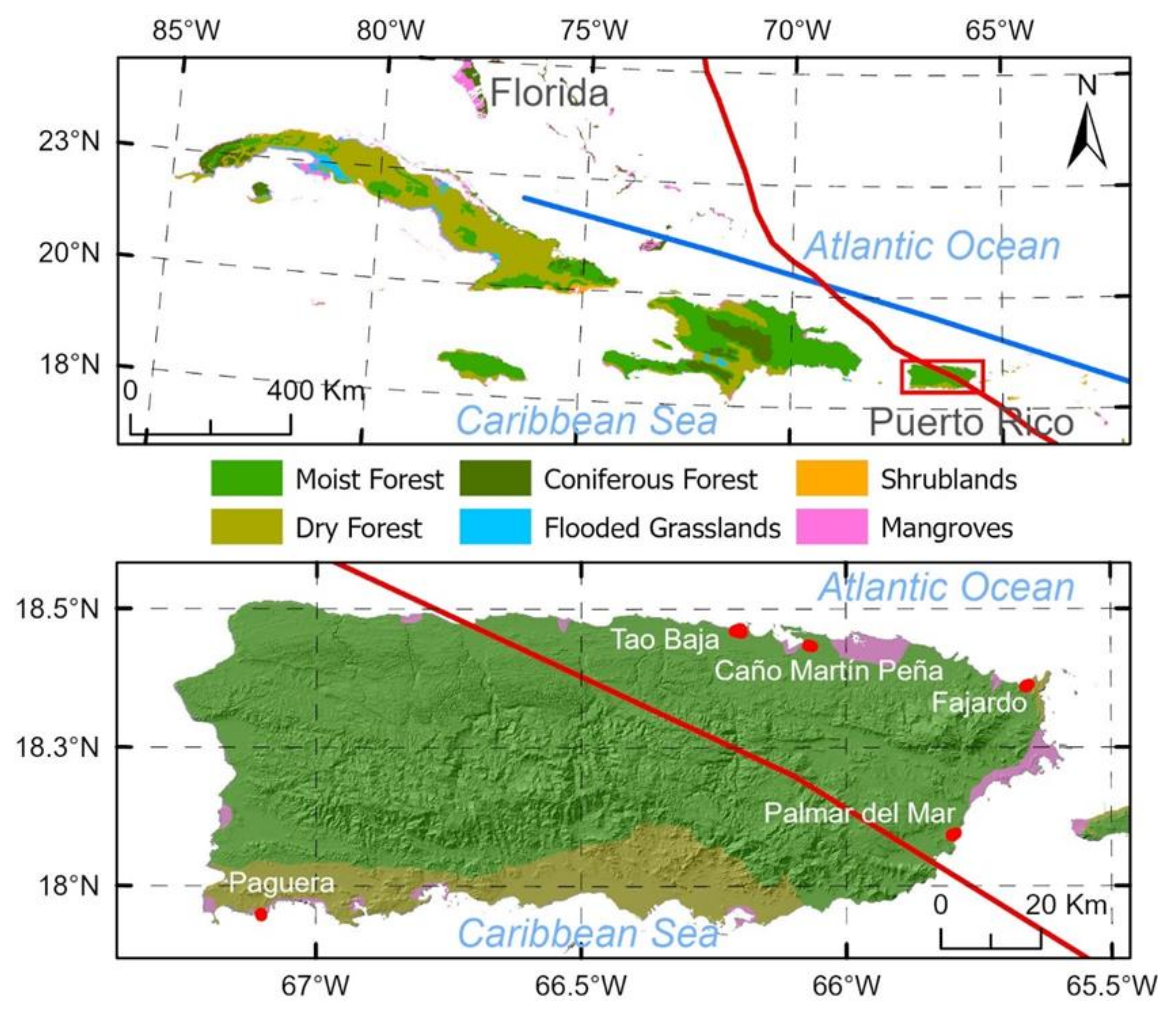
Remotesensing 14 01497 g001 550
Figure 1. Puerto Rico geographical location (up) and location of five sites along its coast (low). Red and blue lines depict the paths of Hurricane Maria and Hurricane Irma, respectively.
Figure 1. Puerto Rico geographical location (up) and location of five sites along its coast (low). Red and blue lines depict the paths of Hurricane Maria and Hurricane Irma, respectively.
Remotesensing 14 01497 g001
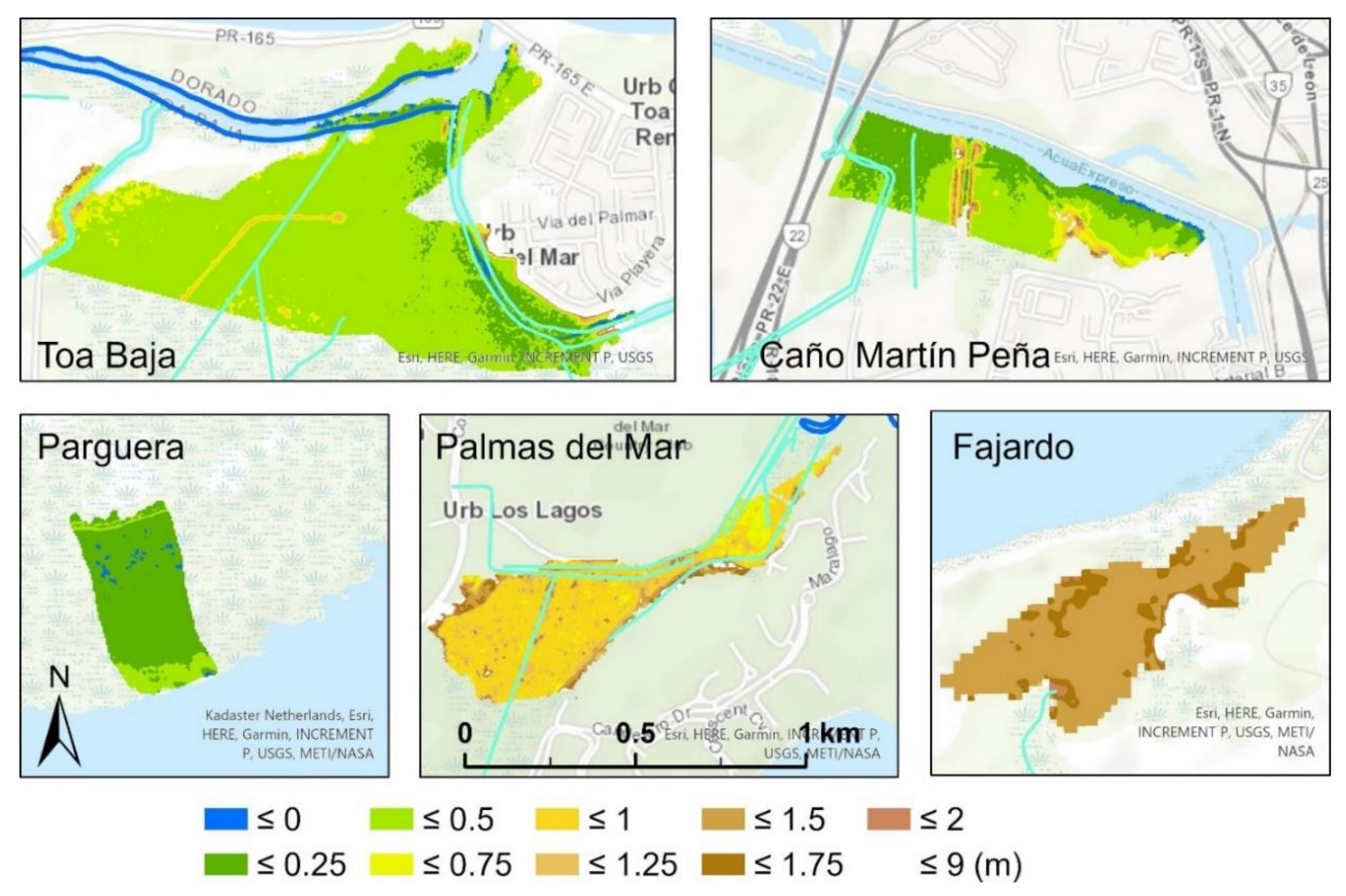
Remotesensing 14 01497 g002 550
Figure 2. DEM of the five mangrove forests. Blue and light-green lines depict rivers and canals of freshwater/sewage, respectively.
Figure 2. DEM of the five mangrove forests. Blue and light-green lines depict rivers and canals of freshwater/sewage, respectively.
Remotesensing 14 01497 g002
Remotesensing 14 01497 g003 550
Figure 3. The pre-hurricane canopy height, derived from the G-LiHT point-cloud data.
Figure 3. The pre-hurricane canopy height, derived from the G-LiHT point-cloud data.
Remotesensing 14 01497 g003
Remotesensing 14 01497 g004 550
Figure 4. The post-hurricane canopy height, derived from the USGS LiDAR point clouds.
Figure 4. The post-hurricane canopy height, derived from the USGS LiDAR point clouds.
Remotesensing 14 01497 g004
Remotesensing 14 01497 g005 550
Figure 5. Canopy height reduction calculated as the pre-hurricane canopy height minus the post-hurricane canopy height.
Figure 5. Canopy height reduction calculated as the pre-hurricane canopy height minus the post-hurricane canopy height.
Remotesensing 14 01497 g005
Remotesensing 14 01497 g006 550
Figure 6. (a) Model-predicted versus LiDAR-derived pre-hurricane canopy height, and (b) model-predicted versus LiDAR-derived canopy height reduction. Codes for the five sites: CM—Caño Martín Peña, FJ—Fajardo, PG—La Parguera, PM—Palma del Mar, TB—Toa Baja.
Figure 6. (a) Model-predicted versus LiDAR-derived pre-hurricane canopy height, and (b) model-predicted versus LiDAR-derived canopy height reduction. Codes for the five sites: CM—Caño Martín Peña, FJ—Fajardo, PG—La Parguera, PM—Palma del Mar, TB—Toa Baja.
Remotesensing 14 01497 g006
Table
Table 1. Pre- and post-hurricane LiDAR point-cloud images provided by the NASA G-LiHT and the USGS 3D Elevation Program.
Table 1. Pre- and post-hurricane LiDAR point-cloud images provided by the NASA G-LiHT and the USGS 3D Elevation Program.
SitePre-Hurricane GLiHT TransectsPost-Hurricane USGS Tiles
Caño Martín PeñaPR_10March2017_118E_2018_19QHA37506600, E_2018_19QHA39006600
FajardoPR_15March2017_75H_2018_20QKF81005700, H_2018_20QKF81005850
Palma del MarPR_12March2017_58a, PR_12March2017_58bH_2018_20QKF66002850, H_2018_20QKF67502700, H_2018_20QKF67502850
La PargueraPR_8March2017_114A_2018_19QFV28001200
Toa BajaPR_10March2017_117, PR_17March2017_199G_2018_19QGA22506750, G_2018_19QGA22506900, G_2018_19QGA24006900, G_2018_19QGA25506900
Table
Table 2. Summary of the canopy heights before (CHM_2017) and after the hurricanes (CHM_2018), canopy height reduction, algorithm-derived tree density, and the covariates of DEM, distance to rivers/canals and to coast, and hurricane rainfall and gust wind based on the 20 m grid maps.
Table 2. Summary of the canopy heights before (CHM_2017) and after the hurricanes (CHM_2018), canopy height reduction, algorithm-derived tree density, and the covariates of DEM, distance to rivers/canals and to coast, and hurricane rainfall and gust wind based on the 20 m grid maps.
SiteToa BajaCaño Martín PeñaLa PargueraPalma del MarFajardo
Area (ha)71.122.813.924.022.0
CHM_2017 (m)11.7 ± 4.310.8 ± 3.76.2 ± 1.89.3 ± 5.66.7 ± 2.8
CHM_2018 (m)5.5 ± 3.16.1 ± 3.35.7 ± 1.14.2 ± 2.26.0 ± 2.2
Reduction (m)6.1 ± 4.4
(52%)		4.8 ± 3.4
(44%)		0.5 ± 1.4
(8%)		5.1 ± 4.2
(55%)		0.7 ± 1.8
(10%)
Tree density (ha−1)2132 ± 9382135 ± 8631674 ± 14101682 ± 7181988 ± 585
DEM (m)0.39 ± 0.310.36 ± 0.320.16 ± 0.071.03 ± 0.381.61 ± 1.07
To river/canal (m)341.5 ± 173.6294.9 ± 201.0948.1 ± 157.957.8 ± 55.383.8 ± 60.8
To coast(m)516.9 ± 209.2101.2 ± 67.7247.9 ± 151.4710.3 ± 188.0291.1 ± 98.5
Gust speed (m·s−1)44.745.034.149.544.3
Rainfall (mm)497.2427.891.1286.5148.2
Table
Table 3. Spatial regression of normalized pre-hurricane canopy height (h) on normalized covariates. z, the elevation; d, the normalized algorithm-derived tree density; sc, the distance to the coast; λ, the spatial autocorrelation coefficient; r2, the coefficient of determination. All coefficients were significant at α = 0.05.
Table 3. Spatial regression of normalized pre-hurricane canopy height (h) on normalized covariates. z, the elevation; d, the normalized algorithm-derived tree density; sc, the distance to the coast; λ, the spatial autocorrelation coefficient; r2, the coefficient of determination. All coefficients were significant at α = 0.05.
SiteInterceptzz2dscλr2
Toa Baja0.2940.377−0.4900.700−0.0800.790.80
Caño Martín Peña0.5850.539−1.191 −0.2120.870.43
La Parguera0.1830.762 −0.623−0.2950.910.62
Palma del Mar0.803−0.7850.467−0.646 0.900.68
Fajardo0.684 −0.684 0.640.58
Table
Table 4. Spatial regression of normalized canopy height reduction (Δh) on normalized covariates: h, pre-hurricane canopy height; z, elevation; d, algorithm-derived tree density; sh, standard deviation of pre-hurricane canopy height; s, distance to rivers/canals; sc, distance to coast; λ, spatial autocorrelation coefficient; r2, coefficient of determination. All coefficients were significant at α = 0.05.
Table 4. Spatial regression of normalized canopy height reduction (Δh) on normalized covariates: h, pre-hurricane canopy height; z, elevation; d, algorithm-derived tree density; sh, standard deviation of pre-hurricane canopy height; s, distance to rivers/canals; sc, distance to coast; λ, spatial autocorrelation coefficient; r2, coefficient of determination. All coefficients were significant at α = 0.05.
SiteIntercepthh2zz2dshsscλr2
Toa Baja0.0970.3310.536−0.4260.360 0.112−0.126 0.750.78
Caño Martín Peña0.1821.101−0.328−0.7680.947 −0.088−0.1670.690.60
La Parguera0.267−0.4511.076 −0.316 0.750.69
Palma del Mar0.0220.884 0.161 −0.151 0.840.91
Fajardo0.1660.440 −0.238−0.255 0.540.57
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Gao, Q.; Yu, M. Elevation Regimes Modulated the Responses of Canopy Structure of Coastal Mangrove Forests to Hurricane Damage. Remote Sens. 2022, 14, 1497. https://doi.org/10.3390/rs14061497

AMA Style

Gao Q, Yu M. Elevation Regimes Modulated the Responses of Canopy Structure of Coastal Mangrove Forests to Hurricane Damage. Remote Sensing. 2022; 14(6):1497. https://doi.org/10.3390/rs14061497

Chicago/Turabian Style

Gao, Qiong, and Mei Yu. 2022. "Elevation Regimes Modulated the Responses of Canopy Structure of Coastal Mangrove Forests to Hurricane Damage" Remote Sensing 14, no. 6: 1497. https://doi.org/10.3390/rs14061497

APA Style

Gao, Q., & Yu, M. (2022). Elevation Regimes Modulated the Responses of Canopy Structure of Coastal Mangrove Forests to Hurricane Damage. Remote Sensing, 14(6), 1497. https://doi.org/10.3390/rs14061497

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop