Flood Monitoring Using Enhanced Resolution Passive Microwave Data: A Test Case over Bangladesh
Abstract
:1. Introduction and Background
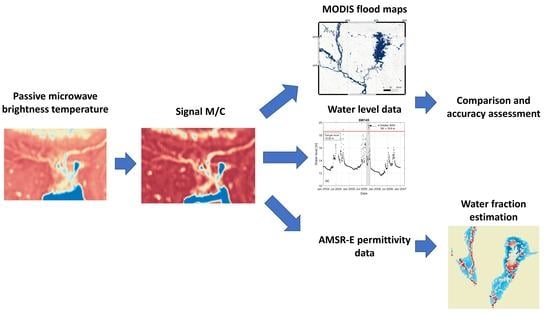
2. Materials and Methods
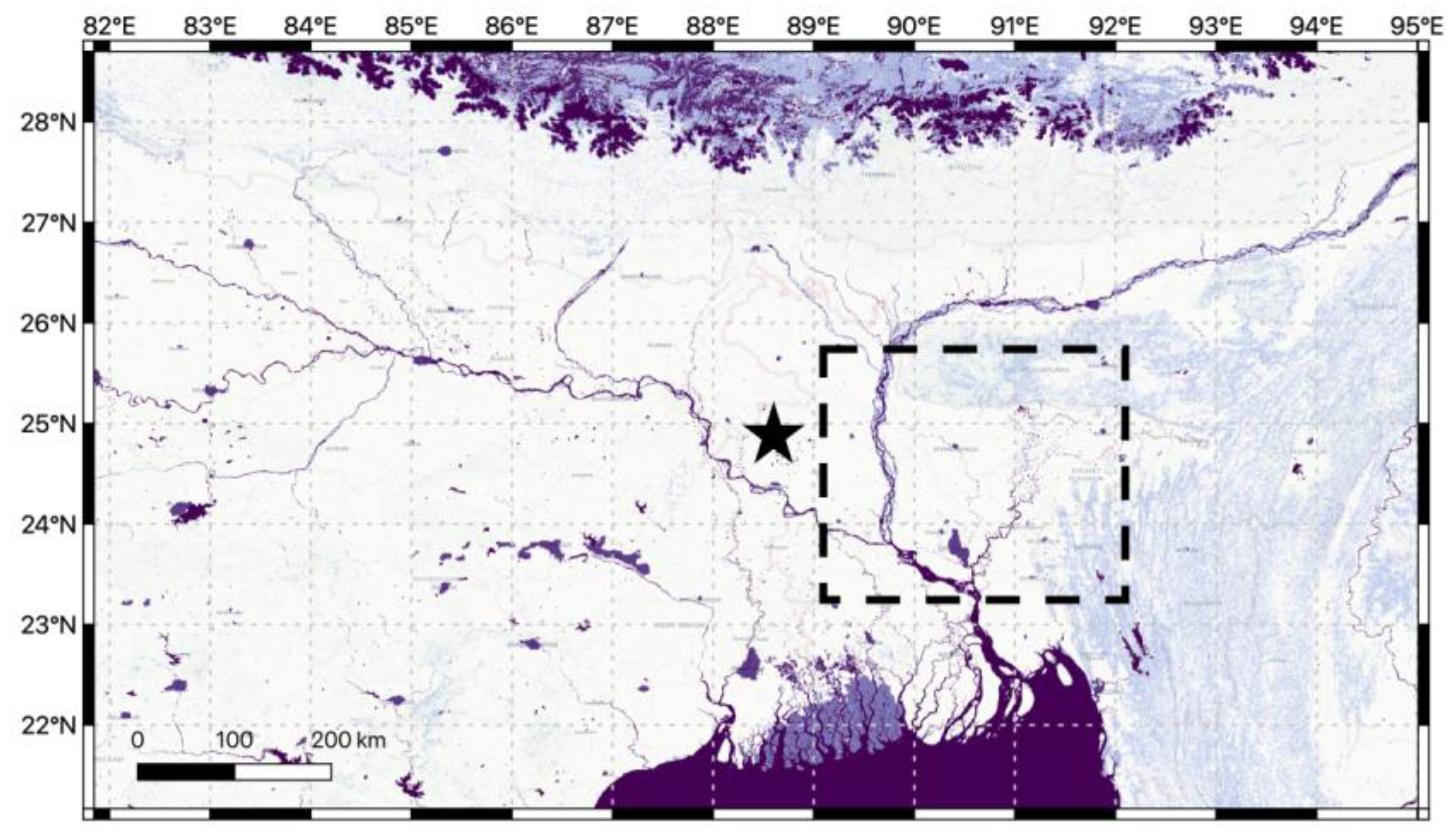
2.1. Study Area
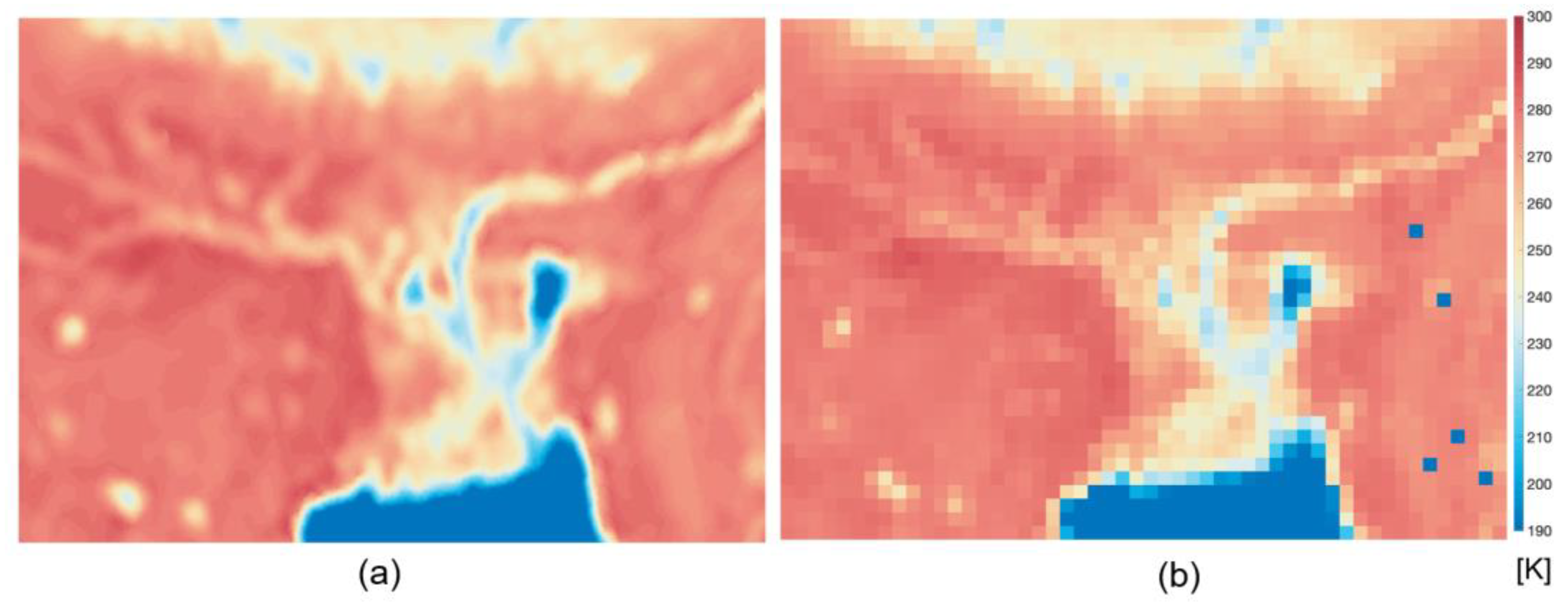
2.2. Passive Microwave Data
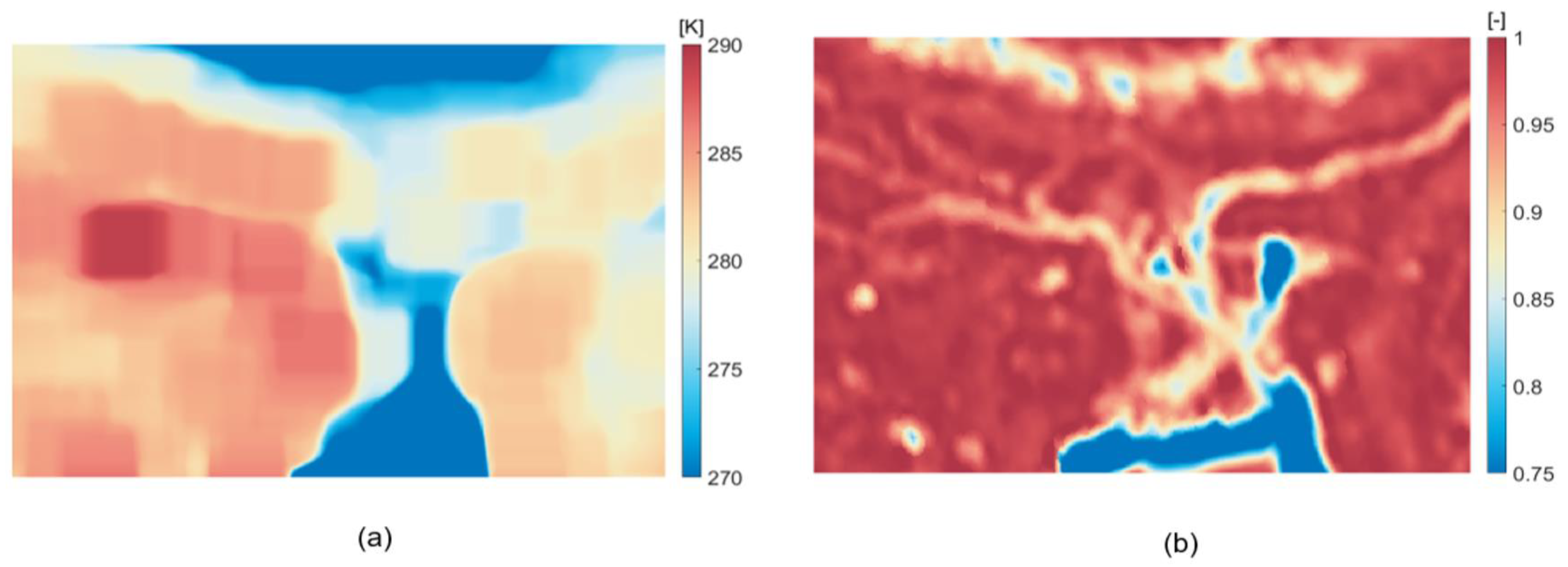
2.3. Passive Microwave Flood Detection Method
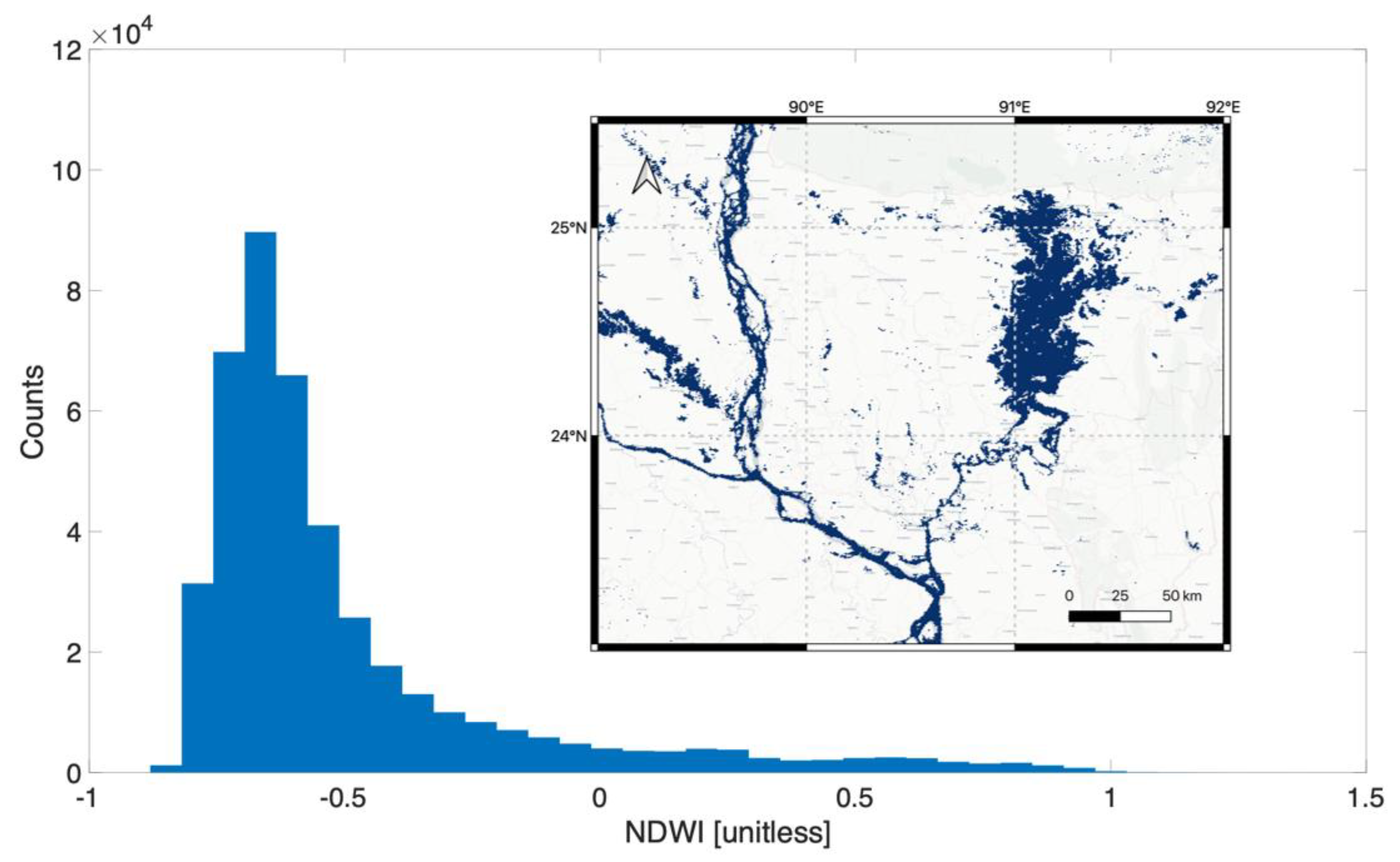
2.4. MODIS Data and the Normalized Difference Water Index
2.5. Water Level Data
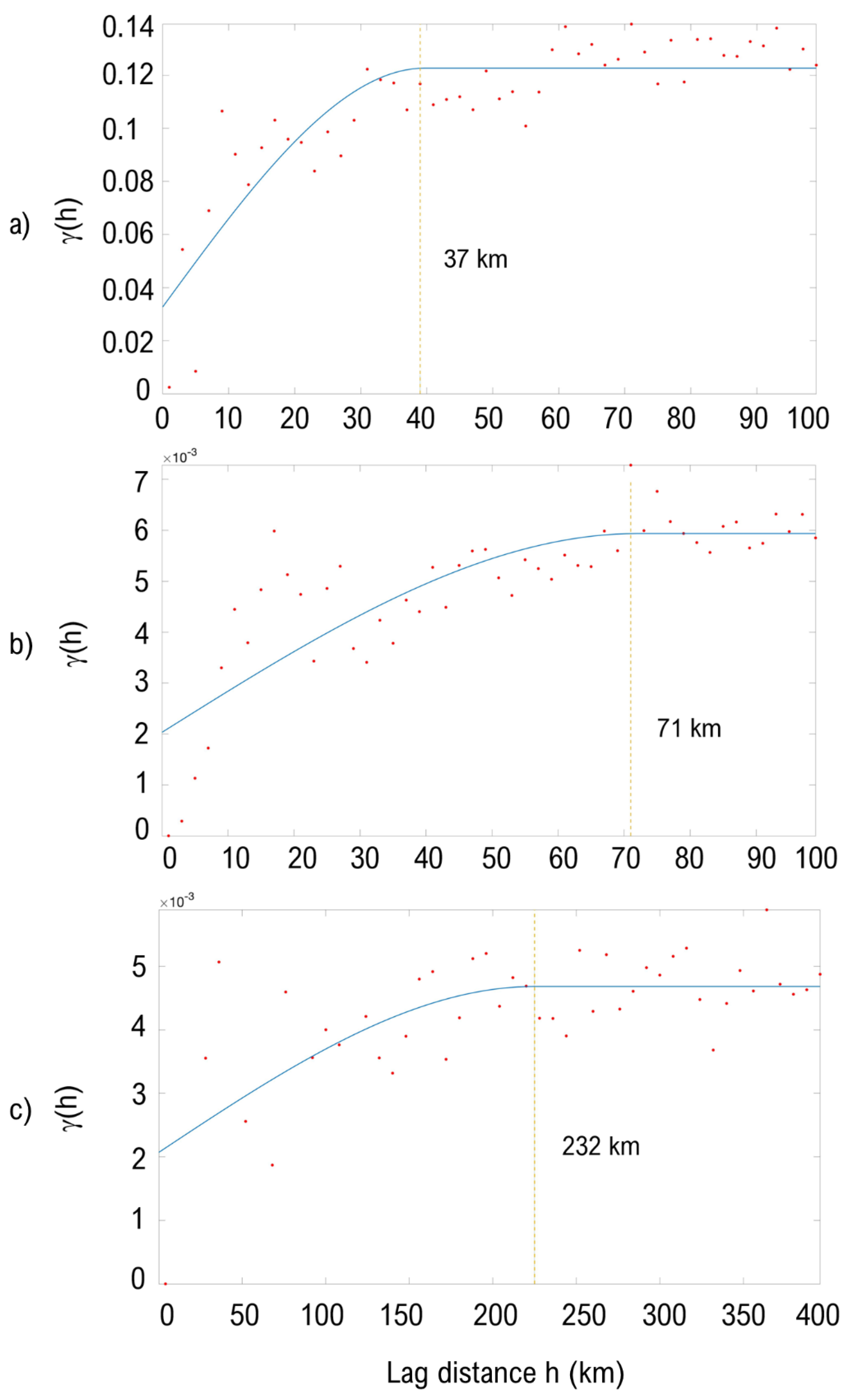
2.6. Spatial Scale analysis and Semi-Variograms
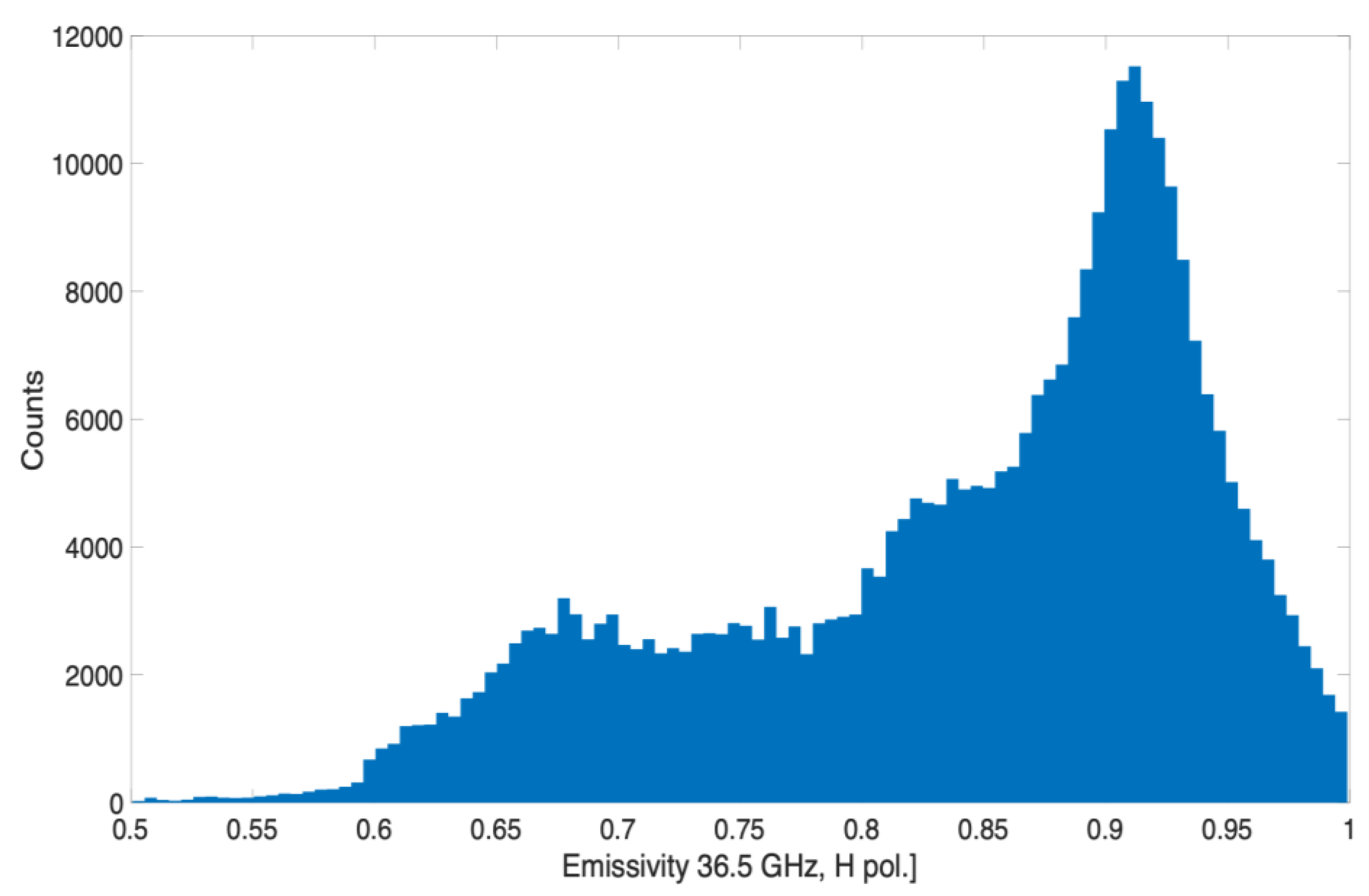
2.7. AMSR-E Emissivity Data and Water Fraction Extraction
3. Results and Discussion
3.1. Spatial Coverage
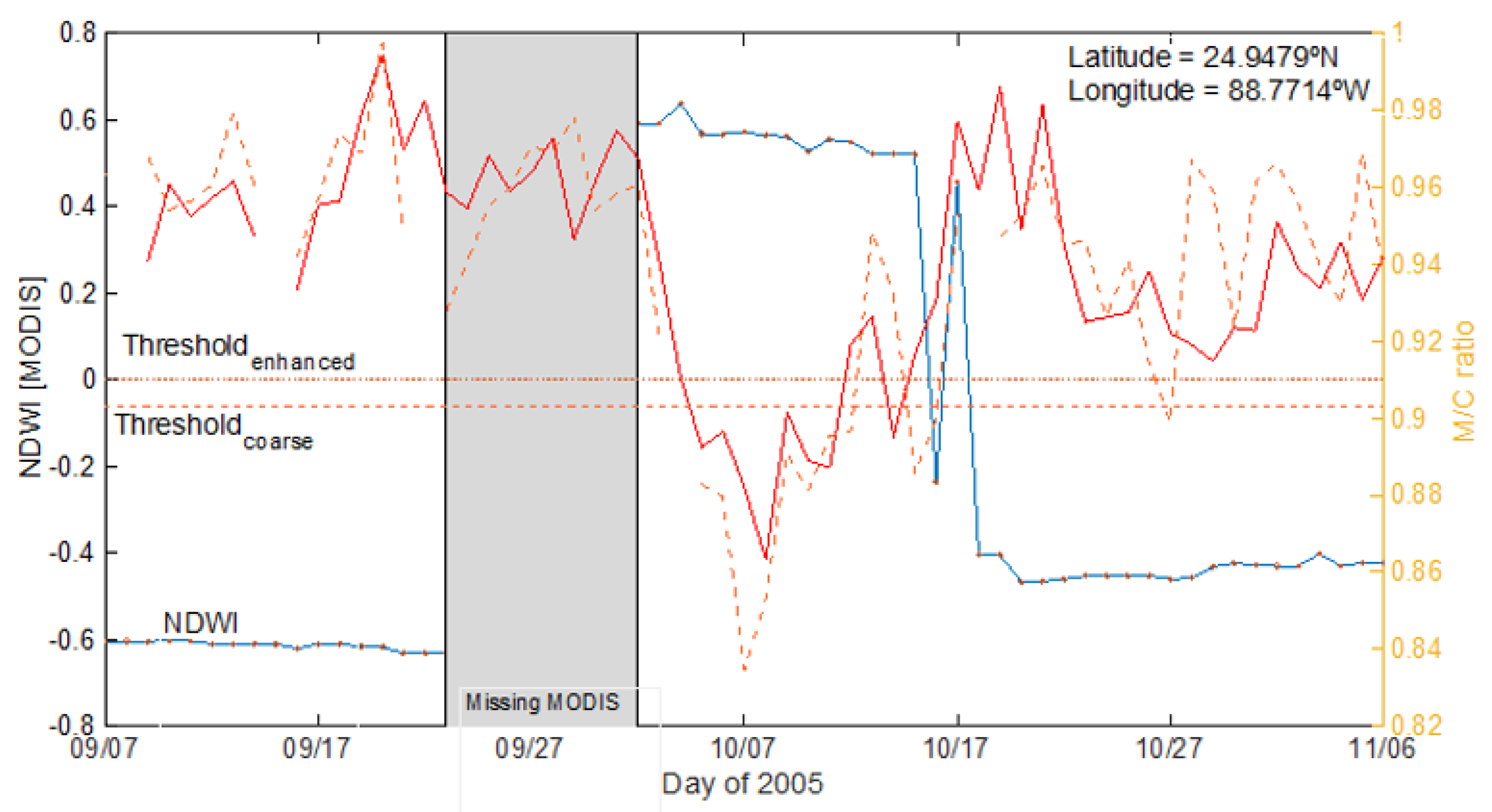
3.2. Time series Analysis
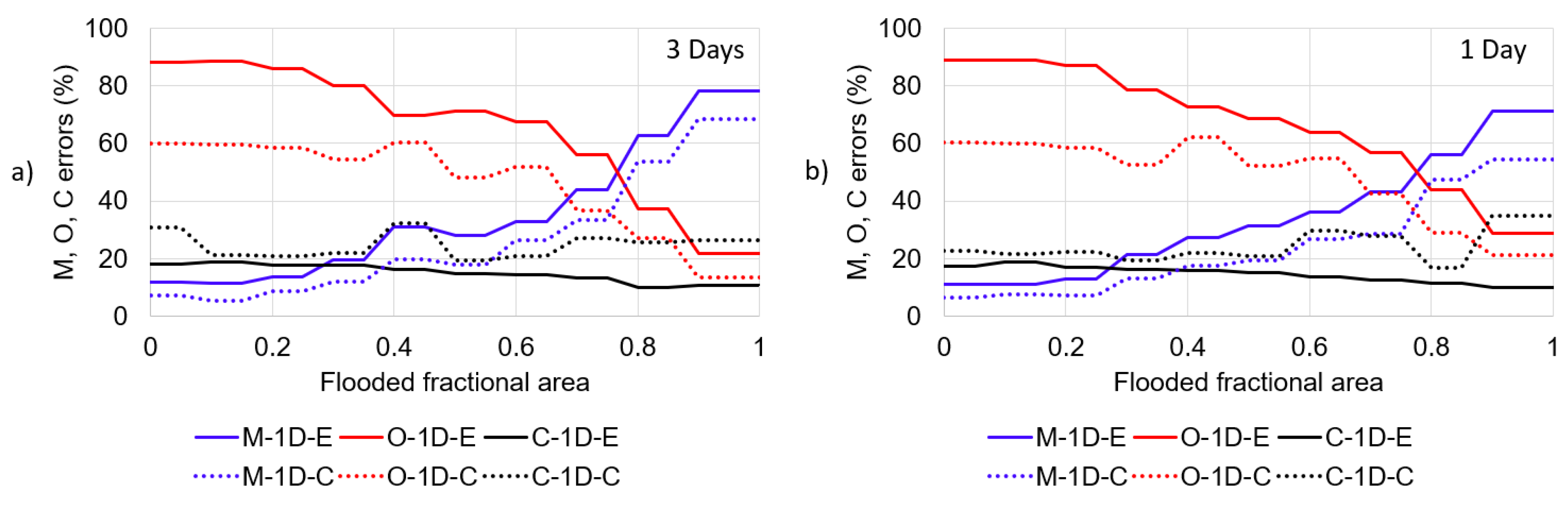
3.3. Commission, Omission, and Matching Analysis
3.4. Spatial Autocorrelation Analysis
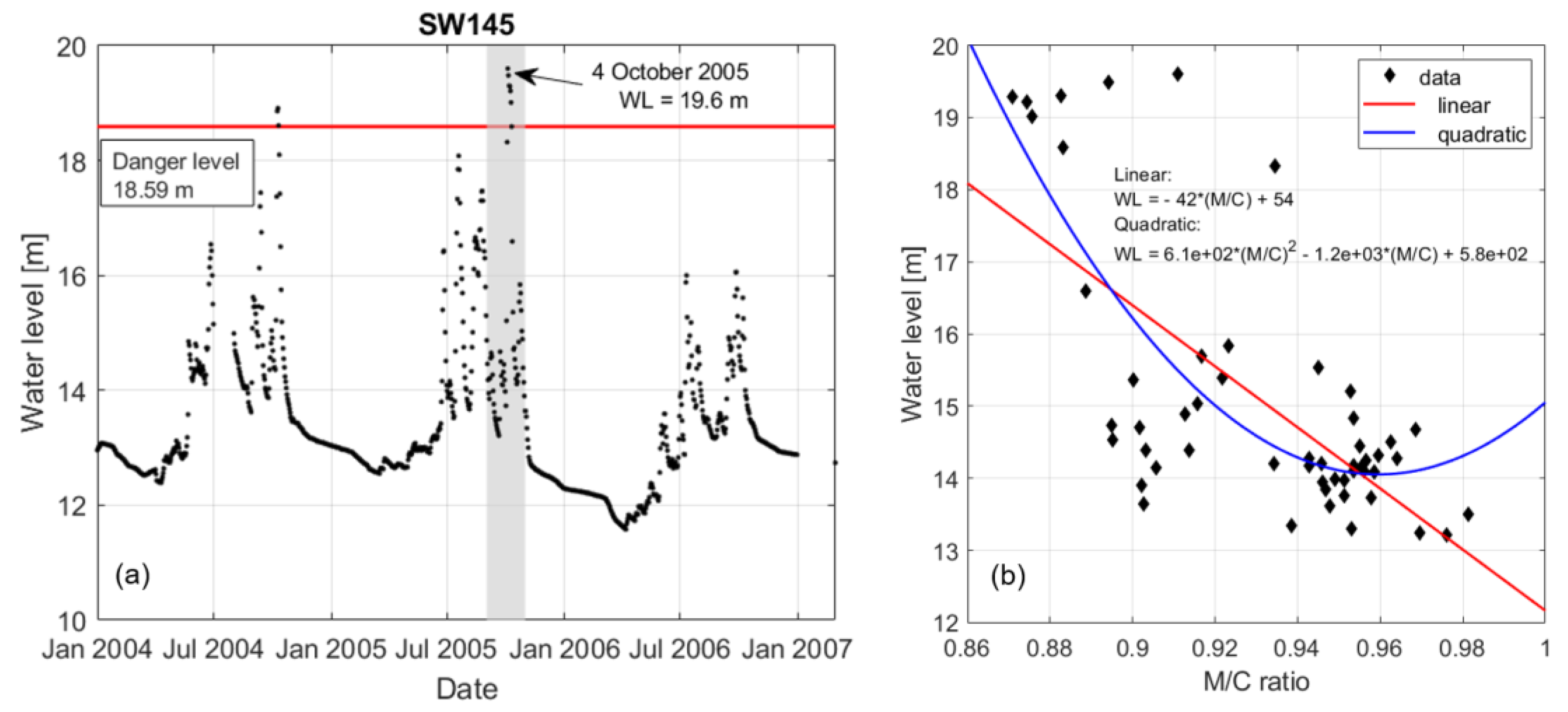
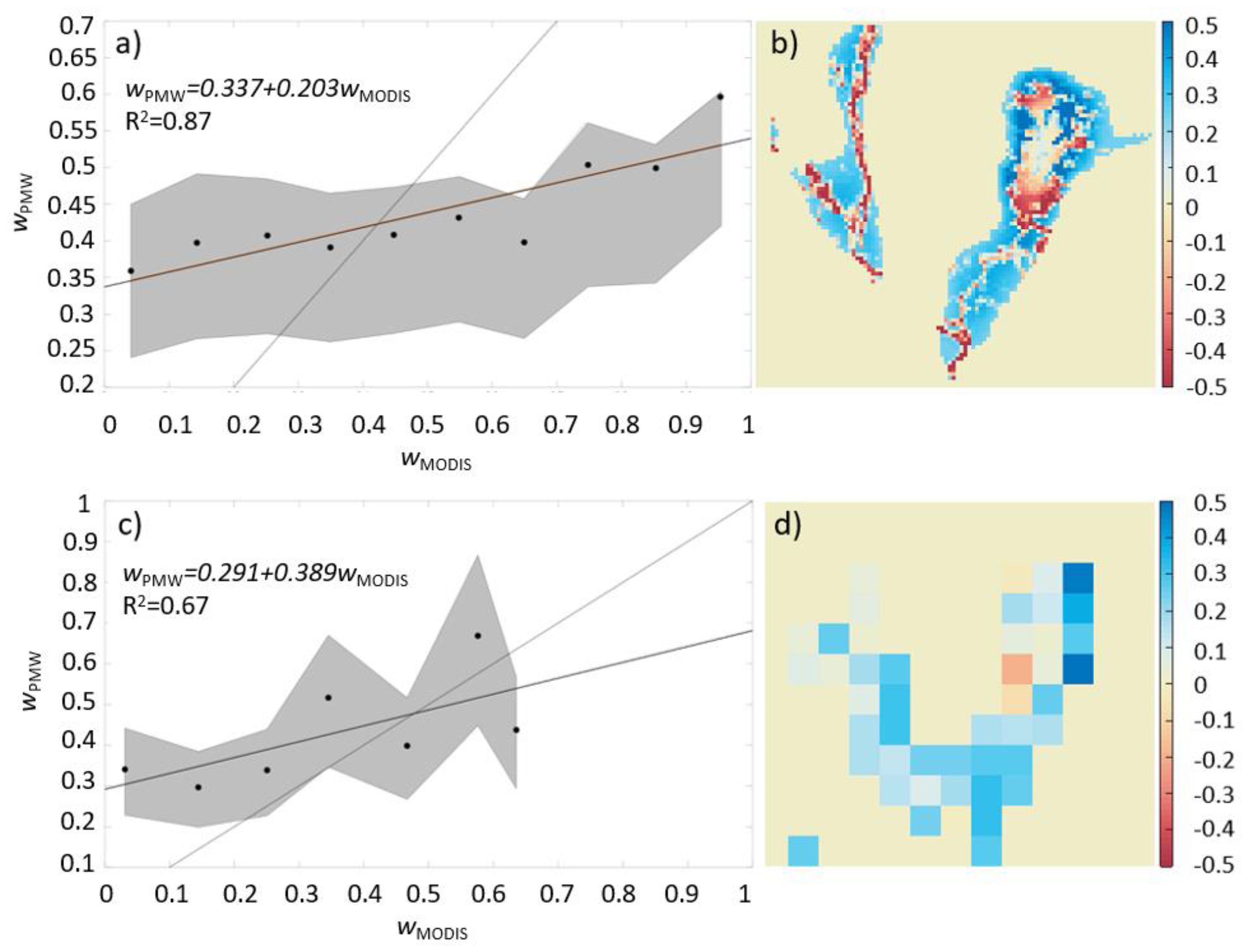
3.5. Water Fraction Estimation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Boni, G.; Ferraris, L.; Pulvirenti, L.; Squicciarino, G.; Pierdicca, N.; Candela, L.; Pisani, A.R.; Zoffoli, S.; Onori, R.; Proietti, C.; et al. A Prototype System for Flood Monitoring Based on Flood Forecast Combined With COSMO-SkyMed and Sentinel-1 Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 2794–2805. [Google Scholar] [CrossRef]
- Twele, A.; Cao, W.; Plank, S.; Martinis, S. Sentinel-1-based flood mapping: A fully automated processing chain. Int. J. Remote Sens. 2016, 37, 2990–3004. [Google Scholar] [CrossRef]
- Amitrano, D.; Martino, G.D.; Iodice, A.; Riccio, D.; Ruello, G. Unsupervised Rapid Flood Mapping Using Sentinel-1 GRD SAR Images. IEEE Trans. Geosci. Remote Sens. 2018, 56, 3290–3299. [Google Scholar] [CrossRef]
- Ulaby, F.T.; Moore, R.K.; Fung, A.K. Microwave Remote Sensing: Active and Passive—3: From Theory to Applications; Artech House: Dedham, MA, USA, 1986. [Google Scholar]
- Groeve, T.D. Flood monitoring and mapping using passive microwave remote sensing in Namibia. Geomat. Nat. Hazards Risk 2010, 1, 19–35. [Google Scholar] [CrossRef]
- Sippel, S.J.; Hamilton, S.K.; Melack, J.M.; Choudhury, B.J. Determination of inundation area in the Amazon River floodplain using the SMMR 37 GHz polarization difference. Remote Sens. Environ. 1994, 48, 70–76. [Google Scholar] [CrossRef]
- Galantowicz, J. High-resolution flood mapping from low-resolution passive microwave data. IEEE Int. Geosci. Remote Sens. Symp. 2002, 3, 1499–1502. [Google Scholar]
- Schroeder, R.; Mcdonald, K.; Chapman, B.; Jensen, K.; Podest, E.; Tessler, Z.; Bohn, T.; Zimmermann, R. Development and Evaluation of a Multi-Year Fractional Surface Water Data Set Derived from Active/Passive Microwave Remote Sensing Data. Remote Sens. 2015, 7, 16688–16732. [Google Scholar] [CrossRef] [Green Version]
- Du, J.; Kimball, J.S.; Galantowicz, J.; Kim, S.-B.; Chan, S.K.; Reichle, R.; Jones, L.A.; Watts, J.D. Assessing global surface water inundation dynamics using combined satellite information from SMAP, AMSR2 and Landsat. Remote Sens. Environ. 2018, 213, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Zeng, Z.; Gan, Y.; Kettner, A.J.; Yang, Q.; Zeng, C.; Brakenridge, G.R.; Hong, Y. Towards high resolution flood monitoring: An integrated methodology using passive microwave brightness temperatures and Sentinel synthetic aperture radar imagery. J. Hydrol. 2020, 582, 124377. [Google Scholar] [CrossRef]
- Allison, L.J.; Schmugge, T.J.; Byrne, G. A hydrological analysis of East Australian floods using Nimbus-5 electrically scanning radiometer data. Bull. Am. Meteorol. Soc. 1979, 60, 1414–1427. [Google Scholar] [CrossRef] [Green Version]
- Giddings, L.; Choudhury, B. Observation of hydrological features with Nimbus-7 37 GHz data, applied to South America. Int. J. Remote Sens. 1989, 10, 1673–1686. [Google Scholar] [CrossRef]
- Choudhury, B.J. Monitoring global land surface using Nimbus-7 37 GHz data theory and examples. Int. J. Remote Sens. 1989, 10, 1579–1605. [Google Scholar] [CrossRef]
- Prigent, C.; Matthews, E.; Aires, F.; Rossow, W.B. Remote sensing of global wetland dynamics with multiple satellite data sets. Geophys. Res. Lett. 2001, 28, 4631–4634. [Google Scholar] [CrossRef] [Green Version]
- Fluet-Chouinard, E.; Lehner, B.; Rebelo, L.-M.; Papa, F.; Hamilton, S.K. Development of a global inundation map at high spatial resolution from topographic downscaling of coarse-scale remote sensing data. Remote Sens. Environ. 2015, 158, 348–361. [Google Scholar] [CrossRef]
- Brodzik, M.J.; Long, D.G.; Hardman, M.A.; Paget, A.; Armstrong, R.L. MEaSUREs Calibrated Enhanced-Resolution Passive Microwave Daily EASE-Grid 2.0 Brightness Temperature ESDR, Version 1; Digital Media; National Snow and Ice Data Center: Boulder, CO, USA, 2018. [Google Scholar] [CrossRef]
- Colosio, P.; Tedesco, M.; Ranzi, R.; Fettweis, X. Surface melting over the Greenland ice sheet derived from enhanced resolution passive microwave brightness temperatures (1979–2019). Cryosphere 2020, 15, 2623–2646. [Google Scholar] [CrossRef]
- Chowdhury, M.R.; Ward, N. Hydro-meteorological variability in the greater Ganges-Brahmaputra-Meghna basins. Int. J. Climatol. 2004, 24, 1495–1508. [Google Scholar] [CrossRef]
- Williams, B.A.; Long, D.G. Reconstruction from Aperture-Filtered Samples with Application to Scatterometer Image Reconstruction. IEEE Trans. Geosci. Remote Sens. 2011, 49, 1663–1676. [Google Scholar] [CrossRef] [Green Version]
- Rees, W.G. Physical Principles of Remote Sensing; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- MODIS Web. Available online: https://modis.gsfc.nasa.gov/data/dataprod/mod09.php (accessed on 17 January 2022).
- Gao, B.-C. NDWI—A normalized difference water index for remote sensing of vegetation liquid water from space. Remote Sens. Environ. 1996, 58, 257–266. [Google Scholar] [CrossRef]
- Webster, R.; Oliver, M.A. Geostatistics for Environmental Scientists; John Wiley & Sons: New York, NY, USA, 2001. [Google Scholar]
- Deems, J.S.; Fassnacht, S.R.; Elder, K.J. Fractal Distribution of Snow Depth from Lidar Data. J. Hydrometeorol. 2006, 7, 285–297. [Google Scholar] [CrossRef]
- Norouzi, H.; Temimi, M.; Rossow, W.B.; Pearl, C.; Azarderakhsh, M.; Khanbilvardi, R. The sensitivity of land emissivity estimates from AMSR-E at C and X bands to surface properties. Hydrol. Earth System Sci. 2011, 15, 3577–3589. [Google Scholar] [CrossRef] [Green Version]
- Bonafilia, D.; Tellman, B.; Anderson, T.; Issenberg, E. Sen1Floods11: A georeferenced dataset to train and test deep learning flood algorithms for Sentinel-1. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Seattle, WA, USA, 14–19 June 2020; pp. 210–211. [Google Scholar]
- Jensen, K.; Mcdonald, K. Surface water microwave product series Version 3: A near-real time and 25-year historical global inundated area fraction time series from active and passive microwave remote sensing. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1402–1406. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Colosio, P.; Tedesco, M.; Tellman, E. Flood Monitoring Using Enhanced Resolution Passive Microwave Data: A Test Case over Bangladesh. Remote Sens. 2022, 14, 1180. https://doi.org/10.3390/rs14051180
Colosio P, Tedesco M, Tellman E. Flood Monitoring Using Enhanced Resolution Passive Microwave Data: A Test Case over Bangladesh. Remote Sensing. 2022; 14(5):1180. https://doi.org/10.3390/rs14051180
Chicago/Turabian StyleColosio, Paolo, Marco Tedesco, and Elizabeth Tellman. 2022. "Flood Monitoring Using Enhanced Resolution Passive Microwave Data: A Test Case over Bangladesh" Remote Sensing 14, no. 5: 1180. https://doi.org/10.3390/rs14051180
APA StyleColosio, P., Tedesco, M., & Tellman, E. (2022). Flood Monitoring Using Enhanced Resolution Passive Microwave Data: A Test Case over Bangladesh. Remote Sensing, 14(5), 1180. https://doi.org/10.3390/rs14051180