Analysis of the Periodic Component of Vertical Land Motion in the Po Delta (Northern Italy) by GNSS and Hydrological Data
Abstract
:1. Introduction
2. Po Delta Area (Northern Italy)
3. Data Presentation
3.1. Geodetic Time Series
3.2. Hydro-Meteorological, Hydrogeological and Climate Datasets
4. Application of the Multi-Component and Multi-Source Approach
- Step 1—once removed the permanent trend, moving average and wavelet analyses are applied to geodetic data for individuating the periodicity of the seasonal oscillations;
- Step 2—comparative analyses, performed through statistic and wavelet techniques, are used to correlate the geodetic time series with datasets of different nature (e.g., hydro-meteorological and climate data). The purpose of this step is to find relations between land and hydrologic systems, and to infer the relevant sources among all those likely responsible for the observed land motion;
- Step 3—the relevant processes are validated through physically based models.
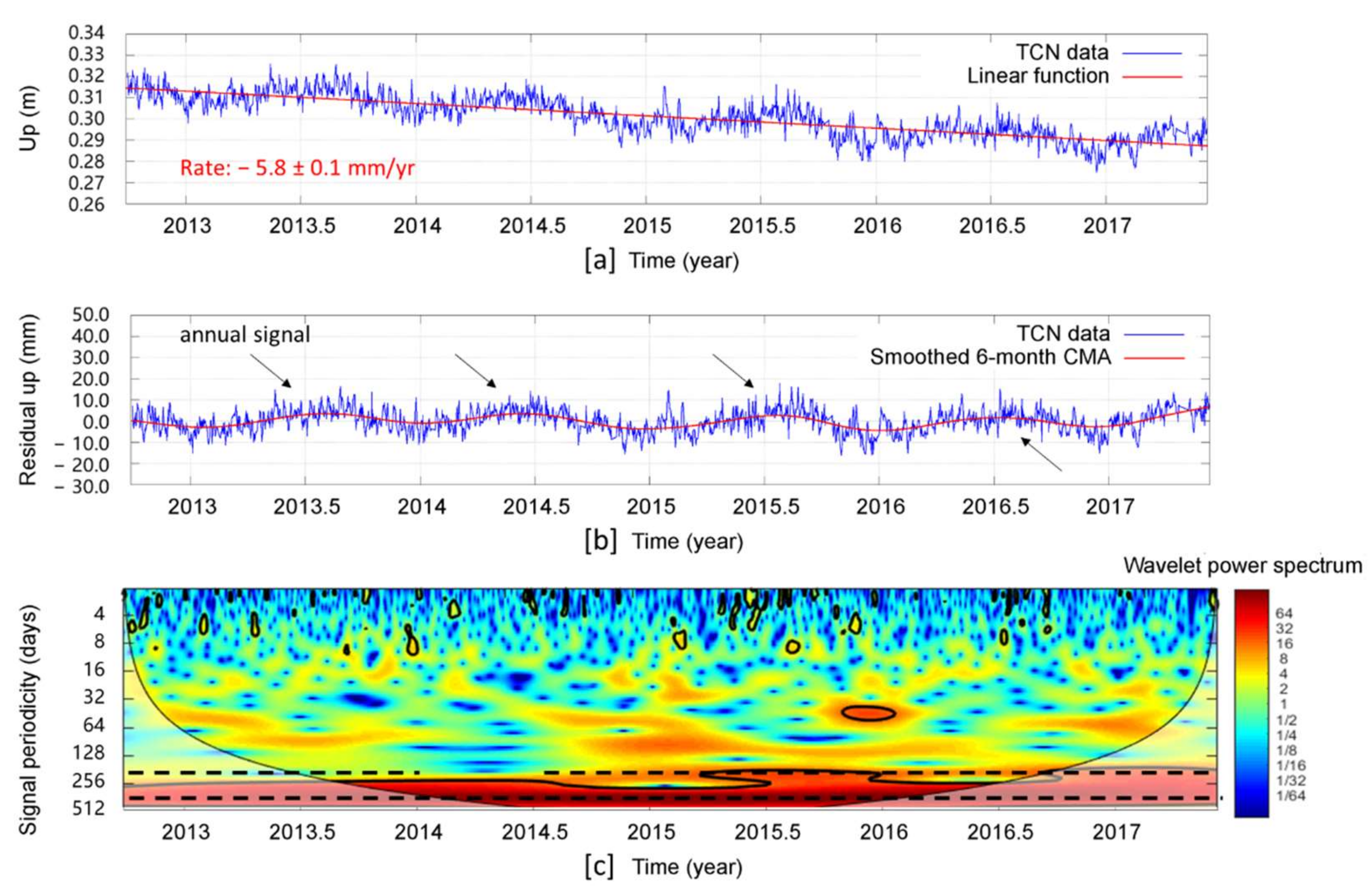
4.1. Step 1: Component Recognition of Geodetic Datasets
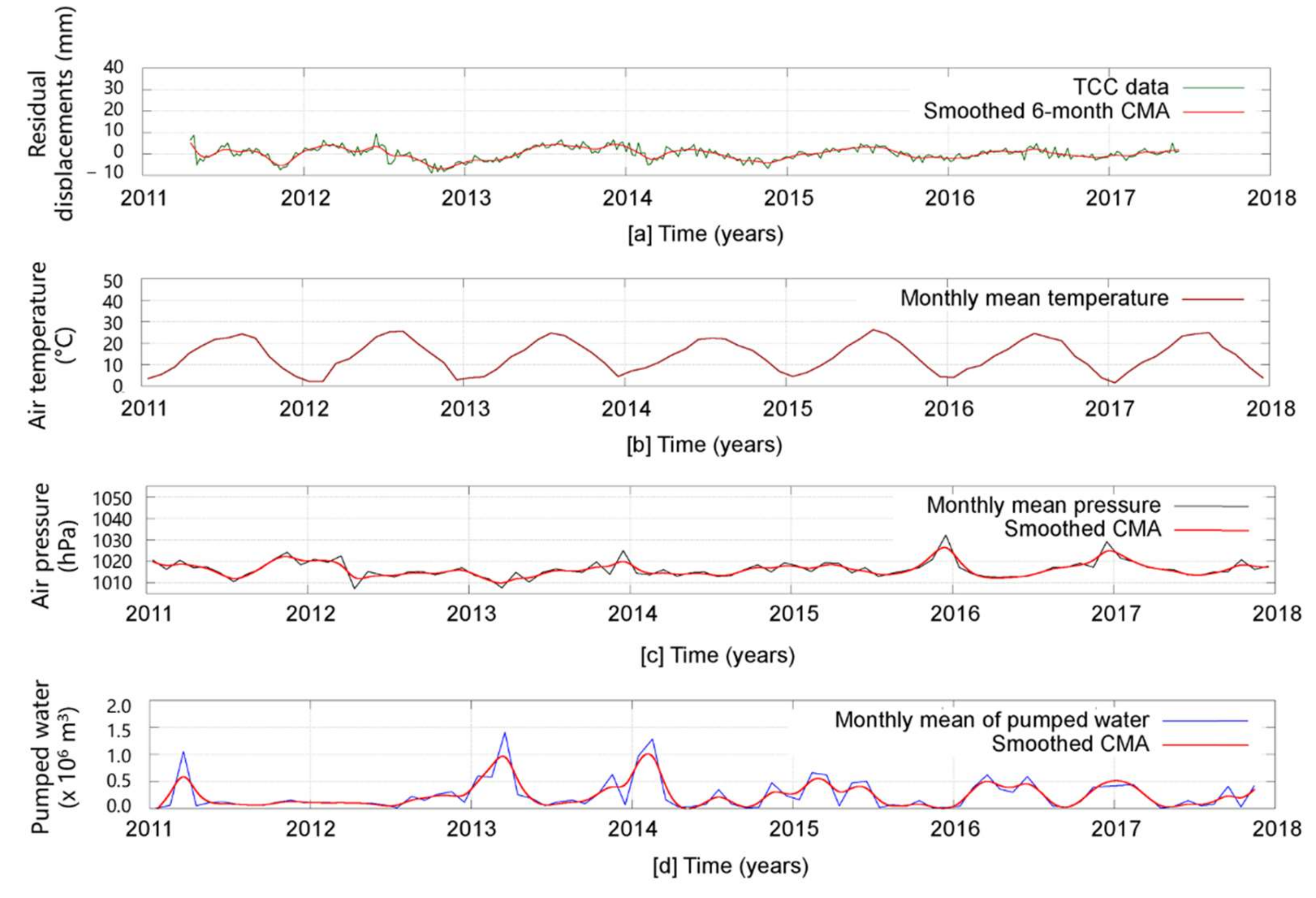
4.2. Step 2: Source Selection
4.3. Step 3: Source Validation
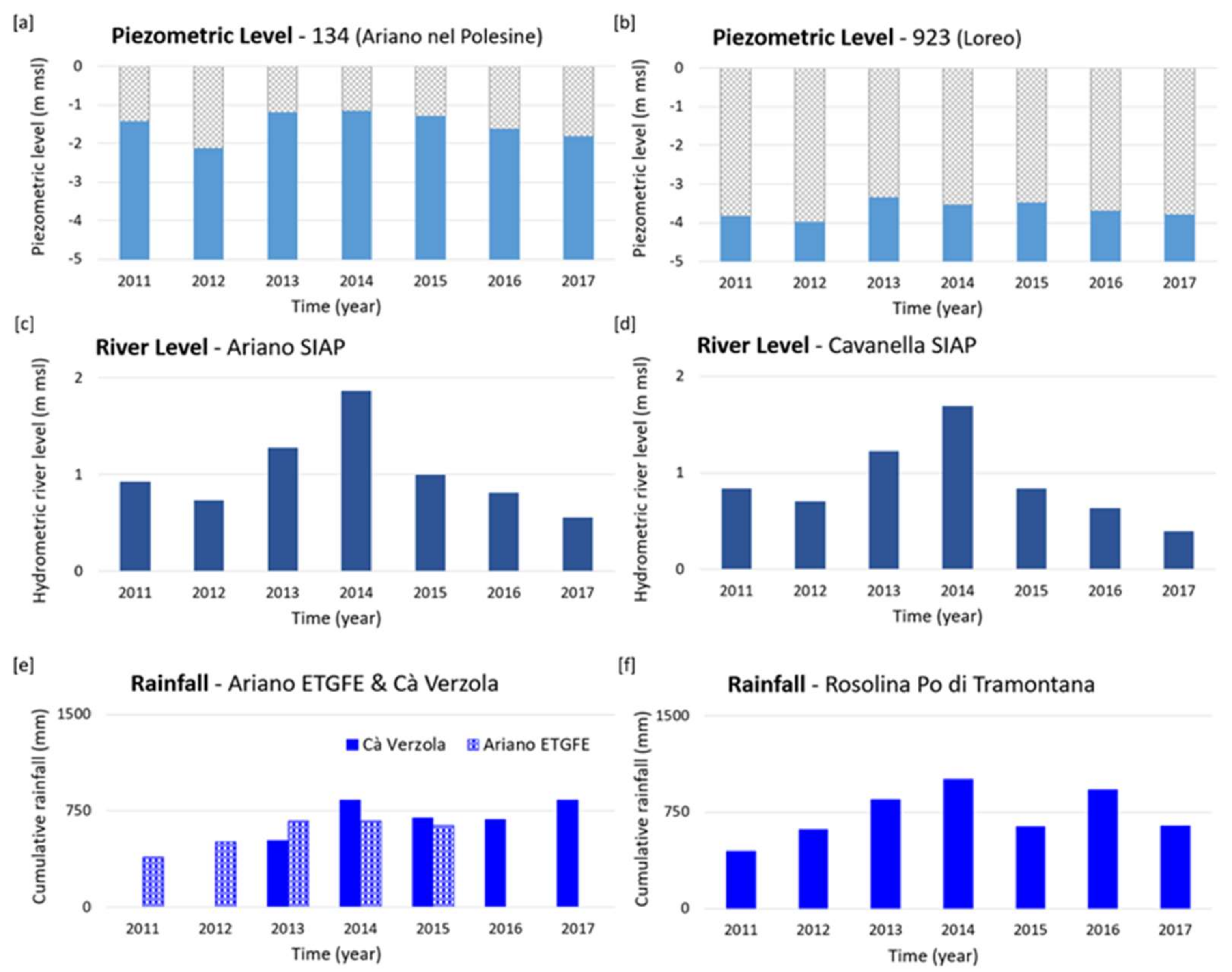
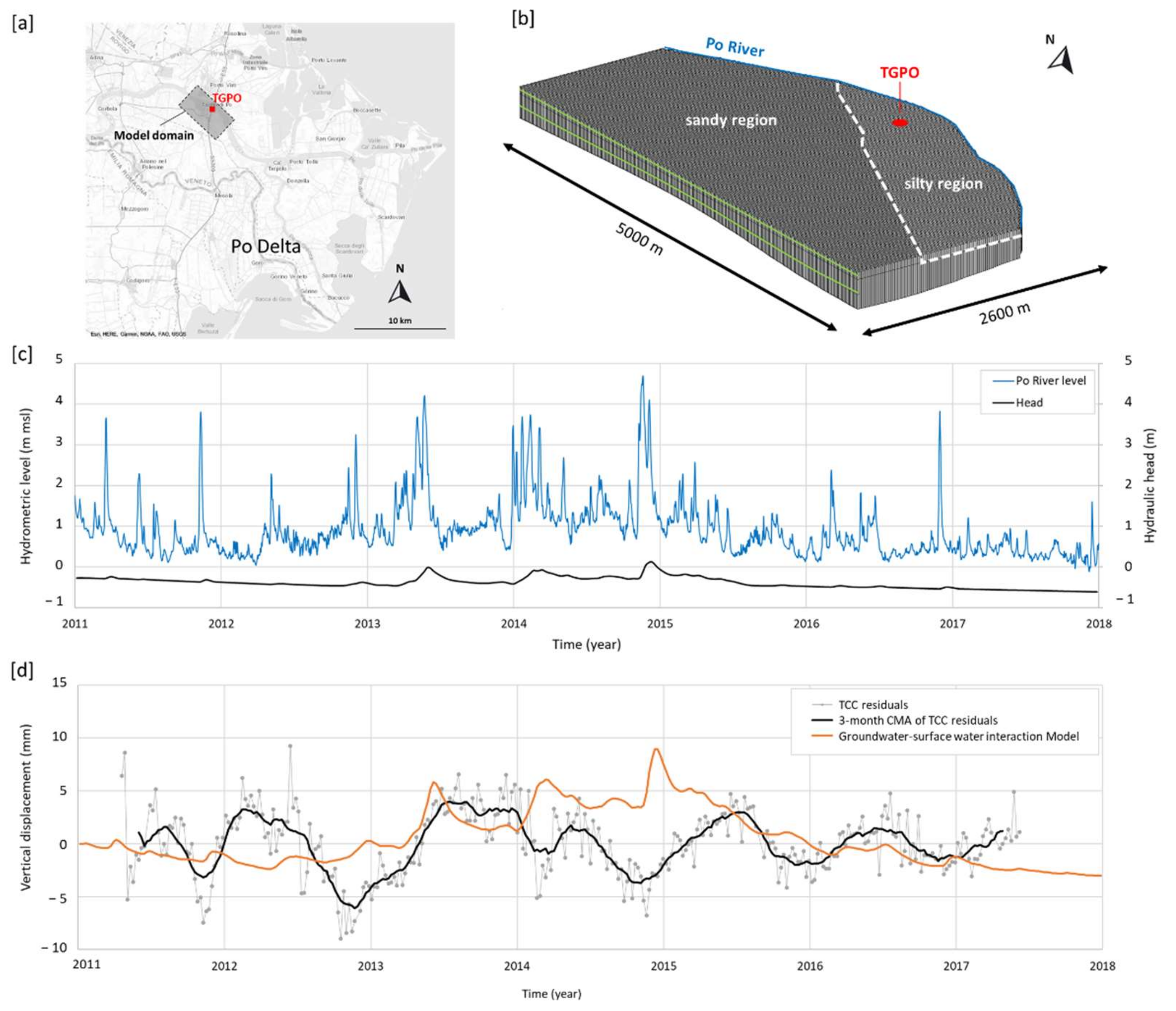
4.3.1. Groundwater–Surface Water Interaction
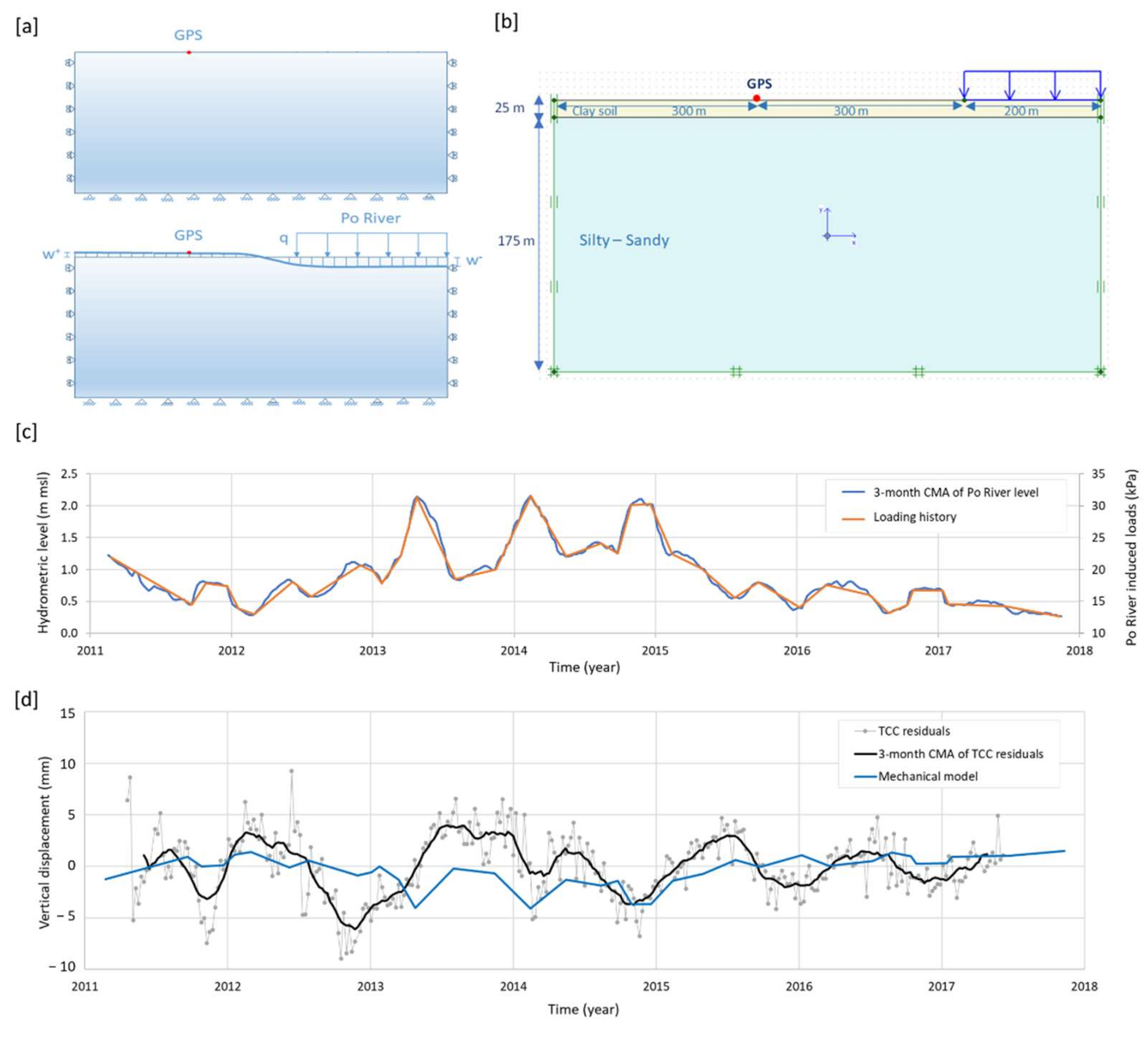
4.3.2. Mechanical Modelling via FEM
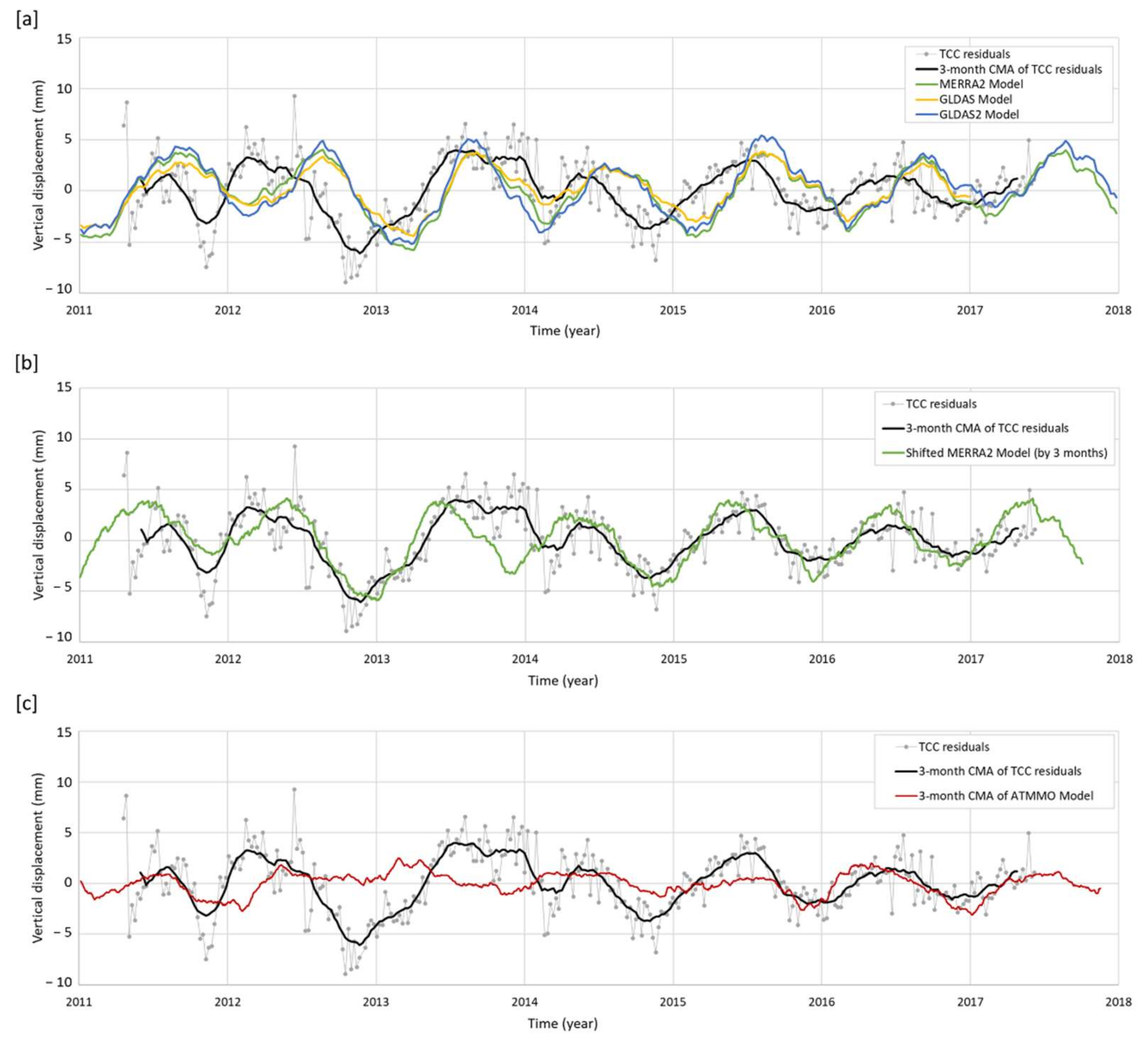
4.3.3. Models of Global Mass Variability in Atmosphere, Ocean and Continental Hydrology
5. Joint Contribution of the Proposed Sources
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bitelli, G.; Bonsignore, F.; Pellegrino, I.; Vittuari, L. Evolution of the techniques for subsidence monitoring at regional scale: The case of Emilia-Romagna region (Italy). Proc. IAHS 2015, 372, 315–321. [Google Scholar] [CrossRef] [Green Version]
- Bock, Y.; Melgar, D. Physical applications of GPS geodesy: A review. Rep. Prog. Phys 2016, 79, 106801. [Google Scholar] [CrossRef] [PubMed]
- Webb, F.H.; Zumberge, J.F. An introduction to GIPSY/OASIS II. JPL Publ. 1997, D-11088. [Google Scholar]
- Dach, R.; Lutz, S.; Walser, P.; Fridez, P. (Eds.) Bernese GNSS Software Version 5.2; User Manual; Astronomical Institute, University of Bern, Bern Open Publishing: Bern, Switzerland, 2015; ISBN 978-3-906813-05-9. [Google Scholar] [CrossRef]
- Herring, T.; King, R.; McClusky, S. Introduction to Gamit/Globk Technical Report Version 1050; Massachusetts Institute of Technology: Cambridge, MA, USA, 2008. [Google Scholar]
- Klos, A.; Bogusz, J.; Bos, M.S.; Gruszczynska, M. Modelling the GNSS time series: Different approaches to extract seasonal signals. In Geodetic Time Series Analysis in Earth Science; Montillet, J.-P., Bos, M.S., Eds.; Springer: Cham, Switzerland, 2019; pp. 211–237. [Google Scholar] [CrossRef]
- Nikolaidis, R. Observation of Geodetic and Seismic Deformation with the Global Positioning System. Ph.D. Thesis, University of California, La Jolla, CA, USA, 2002. [Google Scholar]
- Teferle, F.N.; Williams, S.D.P.; Kierulf, H.P.; Bingley, R.M.; Plag, H.-P. A continuous GPS coordinate time series analysis strategy for high-accuracy vertical land movements. Phys. Chem. Earth 2008, 33, 205–216. [Google Scholar] [CrossRef] [Green Version]
- Masson, C.; Mazzotti, S.; Vernant, P. Precision of continuous GPS velocities from statistical analysis of synthetic time series. Solid Earth 2019, 10, 329–342. [Google Scholar] [CrossRef] [Green Version]
- Klos, A.; Bos, M.S.; Bogusz, J. Detecting time-varying seasonal signal in GPS position time series with different noise levels. GPS Solut. 2018, 22, 21. [Google Scholar] [CrossRef] [Green Version]
- Chen, Q.; van Dam, T.; Sneeuw, N.; Collilieux, X.; Weigelt, M.; Rebischung, P. Singular spectrum analysis for modeling seasonal signals from GPS time series. J. Geodyn. 2013, 72, 25–35. [Google Scholar] [CrossRef]
- Davis, J.L.; Wernicke, B.P.; Tamisiea, M.E. On seasonal signals in geodetic time series. J. Geophys. Res. 2012, 117, B01403. [Google Scholar] [CrossRef] [Green Version]
- Didova, O.; Gunter, B.; Riva, R.; Klees, R.; Roese-Koerner, L. An approach for estimating time-variable rates from geodetic time series. J. Geod. 2016, 90, 1207–1221. [Google Scholar] [CrossRef] [Green Version]
- Xu, C.; Yue, D. Monte Carlo SSA to detect time-variable seasonal oscillations from GPS-derived site position time series. Tectonophysics 2015, 665, 118–126. [Google Scholar] [CrossRef]
- Bennett, R.A. Instantaneous deformation from continuous GPS: Contributions from quasi-per iodic loads. Geophys. J. Int. 2008, 174, 1052–1064. [Google Scholar] [CrossRef] [Green Version]
- van Dam, T.; Wahr, J.; Milly, P.C.D.; Shmakin, A.B.; Blewitt, G.; Lavallée, D.; Larson, K.M. Crustal displacements due to continental water loading. Geophys. Res. Lett. 2001, 28, 651–654. [Google Scholar] [CrossRef] [Green Version]
- Tregoning, P.; Watson, C.; Ramillien, G.; McQueen, H.; Zhang, J. Detecting hydrologic deformation using GRACE and GPS. Geophys. Res. Lett. 2009, 36, L15401. [Google Scholar] [CrossRef] [Green Version]
- Prawirodirdjo, L.; Ben-Zion, Y.; Bock, Y. Observation and modeling of thermoelastic strain in Southern California Integrated GPS Network daily position time series. J. Geophys. Res. 2006, 111, B02408. [Google Scholar] [CrossRef] [Green Version]
- King, N.E.; Argus, D.; Langbein, J.; Agnew, D.C.; Bawden, G.; Dollar, R.S.; Liu, Z.; Galloway, D.; Reichard, E.; Yong, A.; et al. Space geodetic observation of expansion of the San Gabriel Valley California aquifer system during heavy rainfall in winter 2004–2005. J. Geophys. Res. 2007, 112, B03409. [Google Scholar] [CrossRef]
- Yan, H.; Chen, W.; Zhu, Y.; Zhang, W.; Zhong, M. Contributions of thermal expansion of monuments and nearby bedrock to observed GPS height changes. Geophys. Res. Lett. 2009, 36, L13301. [Google Scholar] [CrossRef] [Green Version]
- Bell, J.; Amelung, F.; Ramelli, A.; Blewitt, G. Land subsidence in Las Vegas Nevada 1935–2000: New geodetic data show evolution revised spatial patterns and reduced rates. Environ. Eng. Geosci. 2002, 8, 155–174. [Google Scholar] [CrossRef]
- Shirzaei, M.; Burgmann, R. Global climate change and local land subsidence exacerbate inundation risk to the San Francisco Bay Area. Sci. Adv. 2018, 4, eaap9234. [Google Scholar] [CrossRef] [Green Version]
- Fernández-Torres, E.; Cabral-Cano, E.; Solano-Rojas, D.; Havazli, E.; Salazar-Tlaczani, L. Land Subsidence risk maps and InSAR based angular distortion structural vulnerability assessment: An example in Mexico City. Proc. IAHS 2020, 382, 583–587. [Google Scholar] [CrossRef] [Green Version]
- Vitagliano, E.; Riccardi, U.; Piegari, E.; Boy, J.-P.; Di Maio, R. Multi-Component and Multi-Source Approach for Studying Land Subsidence in Deltas. Remote Sens. 2020, 12, 1465. [Google Scholar] [CrossRef]
- Caputo, M.; Folloni, G.; Gubellini, A.; Pieri, L.; Unguendoli, M. Survey and geometric analysis of the phenomena of subsidence in the region of Venice and its hinterland. Riv. Ital. Geofis. 1972, 21, 19–26. (In Italian) [Google Scholar]
- Baldi, P.; Casula, G.; Cenni, N.; Loddo, F.; Pesci, A. GPS-based monitoring of land subsidence in the Po Plain (Northern Italy). Earth Planet Sci. Lett. 2009, 288, 204–212. [Google Scholar] [CrossRef]
- Fabris, M.; Achilli, V.; Menin, A. Estimation of Subsidence in Po Delta Area (Northern Italy) by Integration of GPS Data High-Precision Leveling and Archival Orthometric Elevations. Int. J. Geosci. 2014, 5, 571–585. [Google Scholar] [CrossRef] [Green Version]
- Fiaschi, S.; Fabris, M.; Floris, M.; Achilli, V. Estimation of land subsidence in deltaic areas through differential SAR interferometry: The Po River Delta case study (Northeast Italy). Int. J. Remote Sens. 2018, 39, 8724–8745. [Google Scholar] [CrossRef]
- MAB Program UNESCO. Available online: https://enunescoorg/mab (accessed on 23 May 2020).
- Corbau, C.; Simeoni, U.; Zoccarato, C.; Mantovani, G.; Teatini, P. Coupling land use evolution and subsidence in the Po Delta Italy: Revising the past occurrence and prospecting the future management challenges. Sci. Total Environ. 2019, 654, 1196–1208. [Google Scholar] [CrossRef] [PubMed]
- Stefani, M.; Vincenzi, S. The interplay of eustasy climate and human activity in the Late Quaternary depositional evolution and sedimentary architecture of the Po Delta system. Mar. Geol. 2005, 222–223, 19–48. [Google Scholar] [CrossRef]
- Correggiari, A.; Cattaneo, A.; Trincardi, F. The modern Po Delta system Lobe switching and asymmetric prodelta growth. Mar. Geol. 2005, 222–223, 49–74. [Google Scholar] [CrossRef]
- Correggiari, A.; Cattaneo, A.; Trincardi, F. Depositional patterns in the Late-Holocene Po delta system. In River Deltas—Concepts Models and Examples; Giosan, L., Bhattacharya, J.P., Eds.; SEPM Special Publication: Tulsa, Oklahoma, 2005; pp. 365–392. [Google Scholar] [CrossRef]
- Amorosi, A.; Maselli, V.; Trincardi, F. Onshore to offshore anatomy of a late Quaternary source-to-sink system (Po Plain–Adriatic Sea Italy). Earth-Sci. Rev. 2016, 153, 212–237. [Google Scholar] [CrossRef]
- Braga, F.; Zaggia, L.; Bellafiore, D.; Bresciani, M.; Giardino, C.; Lorenzetti, G.; Maicu, F.; Manzo, C.; Riminucci, F.; Ravaioli, M.; et al. Mapping turbidity patterns in the Po river prodelta using multi-temporal Landsat 8 imagery. Estuar. Coast. Mar. Sci. 2017, 198, 555–567. [Google Scholar] [CrossRef]
- Trampe, A. The Detection of Turbidity Plumes in the Po River Prodelta Using Multispectral Landsat 8 and Sentinel-2 Imagery. M.Sc. Thesis, Kiel University, Kiel, Germany, 2018. [Google Scholar] [CrossRef]
- Pecora, S.; Ricciardi, G. Runoff fluctuations of Po River and its tributaries. In Proceedings of the Eu.watercenter Annual Conference, Parma, Italy, 28 September 2018. (In Italian). [Google Scholar]
- Marabini, F. The Po river delta evolution. Geo-Eco-Marina 1997, 2, 47–55. [Google Scholar]
- Syvitski, J.; Kettner, A.J. On the flux of water and sediment into the Northern Adriatic Sea. Cont. Shelf Res. 2007, 27, 296–308. [Google Scholar] [CrossRef]
- Besset, M.; Anthony, E.J.; Sabatier, F. River delta shoreline reworking and erosion in the Mediterranean and Black Seas: The potential roles of fluvial sediment starvation and other factors. Elem. Sci. Anthr. 2017, 5, 54. [Google Scholar] [CrossRef] [Green Version]
- Fabris, M. Coastline evolution of the Po River Delta (Italy) by archival multi-temporal digital photogrammetry. Geomat. Nat. Hazards Risk 2019, 10, 1007–1027. [Google Scholar] [CrossRef] [Green Version]
- Salvioni, G. Land motions in Central and Northern Italy. Boll. Geod. Sci. Affin. 1957, 16, 325–366. (In Italian) [Google Scholar]
- Puppo, A. Po Delta subsidence: Early outlines of a cinematic phenomenon. Metano Petrol. Nuove Energ. 1957, 10, 567–575. (In Italian) [Google Scholar]
- Borgia, G.; Brighenti, G.; Vitali, D. Water-methane production in the Polesano and Ferrarese Basins Critical review. Inarcos 1982, 425, 13–23. (In Italian) [Google Scholar]
- Barbarella, M.; Pieri, L.; Russo, P. Study of soil lowering in the Bolognese area through repeated leveling: Analysis of movements and statistical considerations. Inarcos 1990, 506, 1–19. (In Italian) [Google Scholar]
- Teatini, P.; Tosi, L.; Strozzi, T.; Carbognin, L.; Wegmüller, U.; Rizzetto, F. Mapping regional land displacements in the Venice coastland by an integrated monitoring system. Remote Sens. Environ. 2005, 98, 403–413. [Google Scholar] [CrossRef]
- Teatini, P.; Tosi, L.; Strozzi, T. Quantitative evidence that compaction of Holocene sediments drives the present land subsidence of the Po Delta Italy. J. Geophys. Res. 2011, 116, B08407. [Google Scholar] [CrossRef]
- Tosi, L.; Teatini, P.; Strozzi, T.; Carbognin, L.; Brancolini, G.; Rizzetto, F. Ground Surface Dynamics in the Northern Adriatic Coastland over the Last Two Decades. Rend. Lincei 2010, 21, 115–129. [Google Scholar] [CrossRef]
- Tosi, L.; Da Lio, C.; Strozzi, T.; Teatini, P. Combining L- and X-Band SAR Interferometry to Assess Ground Displacements in Heterogeneous Coastal Environments: The Po River Delta and Venice Lagoon Italy. Remote Sens. 2016, 8, 308. [Google Scholar] [CrossRef] [Green Version]
- Cenni, N.; Viti, M.; Baldi, P.; Mantovani, E.; Bacchetti, M.; Vannucchi, A. Present vertical movements in Central and Northern Italy from GPS data: Possible role of natural and anthropogenic causes. J. Geodyn. 2013, 71, 74–85. [Google Scholar] [CrossRef]
- Zambon, M. Subsidence of the Ground for Water and Gas Extractions: Deductions and Addresses Logically Consequent for the Settlement of the Po River Delta. In Proceedings of the 23nd National Conference on “Remediation”, Rome, Italy, 20 May 1967; pp. 345–370. (In Italian). [Google Scholar]
- Colombo, C.; Tosini, L. Sixty Years of Land Reclamation in Po Delta Area Padua (Italy); Papergraf Spa: Padua, Italy, 2010; ISBN 978-88-87264-70-8. (In Italian) [Google Scholar]
- Blewitt, G.; Hammond, W.C.; Kreemer, C. Harnessing the GPS data explosion for interdisciplinary science. Eos 2018, 99. [Google Scholar] [CrossRef]
- Altamimi, Z.; Rebischung, P.; Métivier, L.; Collilieux, X. ITRF2014: A new release of the International Terrestrial Reference Frame modeling nonlinear station motions. J. Geophys. Res. 2016, 121, 6109–6131. [Google Scholar] [CrossRef] [Green Version]
- Caporali, A.; Neubauer, F.; Ostini, L.; Stangl, G.; Zuliani, D. Modeling surface GPS velocities in the Southern and Eastern Alps by finite dislocations at crustal depths. Tectonophysics 2013, 590, 136–150. [Google Scholar] [CrossRef]
- Grinsted, A.; Moore, J.C.; Jevrejeva, S. Application of the cross wavelet transform and wavelet coherence to geophysical time series. Nonlinear Proc. Geophys. 2004, 11, 561–566. [Google Scholar] [CrossRef]
- Smith, S.W. Moving Average Filters. In Digital Signal Processing: A Practical Guide for Engineers and Scientists; Smith, S.W., Ed.; Elsevier: New York, NY, USA, 2013; pp. 277–284. [Google Scholar]
- Barbarella, M.; Cenni, N.; Gandolfi, S.; Ricucci, L.; Zanutta, A. Technical and Scientific Aspects Derived by the Processing of GNSS Networks using Different Approaches and Software. In Proceedings of the 22nd Intern Tech Meeting of the Satellite Division of the Inst of Navigation (ION GNSS 2009), Savannah, GA, USA, 22–25 September 2009; pp. 2677–2688. [Google Scholar]
- Montanari, A. Hydrology of the Po River: Looking for changing patterns in river discharge. Hydrol. Earth Syst. Sci. 2012, 16, 3739–3747. [Google Scholar] [CrossRef] [Green Version]
- Kendall, M.G. Rank Correlation Methods, 4th ed.; Griffin: London, UK, 1970. [Google Scholar]
- Buck, J.R.; Daniel, M.M.; Singer, A.C. Computer Explorations in Signals and Systems Using MATLAB® Upper Saddle River, 2nd ed.; Prentice Hall Publishing: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Rashvand, M.; Li, J.; Liu, Y. Coupled Stress-Dependent Groundwater Flow-Deformation Model to Predict Land Subsidence in Basins with Highly Compressible Deposits. Hydrology 2019, 6, 78. [Google Scholar] [CrossRef] [Green Version]
- Jafari, F.; Javadi, S.; Golmohammadi, G.; Karimi, N.; Mohammadi, K. Numerical simulation of groundwater flow and aquifer-system compaction using simulation and InSAR technique: Saveh basin Iran. Environ. Earth Sci. 2016, 75, 833. [Google Scholar] [CrossRef]
- Romagnoli, C.; Zerbini, S.; Lago, L.; Richter, B.; Simon, D.; Domenichini, F.; Elmi, C.; Ghirotti, M. Influence of soil consolidation and thermal expansion effects on height and gravity variations. J. Geodyn. 2003, 35, 521–539. [Google Scholar] [CrossRef]
- Hoffmann, J.; Galloway, D.L.; Zebker, H.A. Inverse modeling of interbed storage parameters using land subsidence observations Antelope Valley California. Water Resour Res 2003, 39, 1–13. [Google Scholar] [CrossRef]
- Harbaugh, A.W. MODFLOW-2005 the US Geological Survey Modular Ground-Water Model—The Ground-Water Flow Process; US Geological Survey Techniques and Methods USGS Numbered Series 6-A16; U.S. Geological Survey: Reston, VA, USA, 2005. [CrossRef] [Green Version]
- Geological Survey of Italy. Geological Map of Italy 1:50,000 Sheet 187 Codigoro; ISPRA: Rome, Italy, 2009. (In Italian) [Google Scholar]
- Moriasi, D.N.; Arnold, J.G.; van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models: Part 1 A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Anderson, M.P.; Woessner, W.W.; Hunt, R.J. Applied Groundwater Modeling, 2nd ed.; Academic Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Memin, A.; Boy, J.-P.; Santamaria-Gomez, A. Correcting GPS measurements for non-tidal loading. GPS Solut. 2020, 24, 45. [Google Scholar] [CrossRef]
- Rodell, M.; Houser, P.R.; Jambor, U.; Gottschalck, J.; Mitchell, K.; Meng, C.J.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M.; et al. The Global Land Data Assimilation System. Bull. Amer. Meteor. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef] [Green Version]
- Gelaro, R.; McCarty, W.; Suárez, M.J.; Todling, R.; Molod, A.; Takacs, L.; Randles, C.A.; Darmenov, A.; Bosilovich, M.G.; Reichle, R.; et al. The Modern-Era Retrospective Analysis for Research and Applications Version 2 (MERRA-2). J. Clim. 2017, 30, 5419–5454. [Google Scholar] [CrossRef]
- Reichle, R.H.; Draper, C.S.; Liu, Q.; Girotto, M.; Mahanama, S.P.P.; Koster, R.D.; De Lannoy, G.J.M. Assessment of MERRA-2 Land Surface Hydrology Estimates. J. Clim. 2017, 30, 2937–2960. [Google Scholar] [CrossRef] [Green Version]
- Carrère, C.; Lyard, F. Modelling the barotropic response of the global ocean to atmospheric wind and pressure forcing—comparisons with observations. Geophys. Res. Lett. 2003, 30, 1275. [Google Scholar] [CrossRef] [Green Version]
- Hou, D.; Li, D.; Xu, G.; Zhang, Y. Superposition model for analyzing the dynamic ground subsidence in mining area of thick loose layer. Int. J. Min. Sci. Technol. 2018, 28, 663–668. [Google Scholar] [CrossRef]
- Orellana-Rovirosa, F.; Richards, M. Emergence/subsidence histories along the Carnegie and Cocos Ridge sand their bearing upon biological speciation in the Galápagos. Geochem. Geophys. Geosyst. 2018, 19, 4099–4129. [Google Scholar] [CrossRef]
- Jayeoba, A.; Mathias, S.A.; Nielsen, S.; Vilarrasa, V.; Bjørnarå, T.I. Closed-form equation for subsidence due to fluid production from a cylindrical confined aquifer. J. Hydrol. 2019, 573, 964–969. [Google Scholar] [CrossRef] [Green Version]
- Zhu, X.; Guo, G.; Liu, H.; Yang, X. Surface subsidence prediction method of backfill-strip mining in coal mining. Bull. Eng. Geol. Environ. 2019, 78, 6235–6248. [Google Scholar] [CrossRef]
- Lasdon, L.S.; Fox, R.; Ratner, M. Nonlinear Optimization Using the Generalized Reduced Gradient Method. Rev. Franç. D’automat. Inform. Rech. Opér. Rech. Opérationnelle 1974, 8, 73–103. [Google Scholar] [CrossRef] [Green Version]
- Bogawski, P.; Bednorz, E. Comparison and Validation of Selected Evapotranspiration Models for Conditions in Poland (Central Europe). Water Resour. Manag. 2014, 28, 5021–5038. [Google Scholar] [CrossRef] [Green Version]
- Elci, A. Calibration of groundwater vulnerability mapping using the generalized reduced gradient method. J. Contam. Hydrol. 2017, 207, 39–49. [Google Scholar] [CrossRef] [PubMed]
- Rodgers, J.L.; Nicewander, W.A. Thirteen ways to look at the correlation coefficient. Am. Stat. 1988, 42, 59–66. [Google Scholar] [CrossRef]
- Rosat, S.; Gillet, N.; Boy, J.-P.; Couhert, A.; Dumberry, M. Inter-annual variations of degree 2 from geodetic observations and surface processes. Geophys. J. Intern. 2021, 225, 200–221. [Google Scholar] [CrossRef]




| Data Type | Sampling Rate | Source (Website) | Station Name | Time Span | Analytical Technique |
|---|---|---|---|---|---|
| Rainfall | Daily | www.bonificadeltadelpo.it | Cà Giustiniani; Cà Verzola | January 2011–December 2017 June 2012–December 2017 | Mean (1-, 6-, 7.5-, 9-, 12-month period) |
| www.scia.isprambiente.it www.arpa.veneto.it | Pradon Porto Tolle; Rosolina Po di Tramontana; Adria Bellombra | January 2011–December 2017 | CMA (12-, 6- and 3- month period) | ||
| www.scia.isprambiente.it | Ariano ETGFE | January 2011–December 2015 | |||
| Monthly | https://cloud.consorziocer.it /FaldaNET | 26FE | August 2011–December 2017 | ||
| River hydrometric level | Hourly | www.agenziapo.it | Cavanella SIAP; Ariano SIAP; Pila SIAP | January 2011–December 2017 | Daily mean |
| September 2012–December 2017 | Mean (12- and 7.5- month period) Annual CMA; WA; XWT; WTC | ||||
| Piezometric level | 4 values/year | http://dati.veneto.it | Loreo 923; Porto Viro 143; Adria 138; Villanova Marchesana 133 Ariano nel Polesine 134 | January 2011–December 2017 | Annual mean Semi-annual CMA |
| 12–36 values/year | https://cloud.consorziocer.it /FaldaNET | 26FE | August 2011–December 2017 | Annual mean Annual and semi-annual CMA | |
| Pumped water volumes | Monthly | www.bonificadeltadelpo.it | Cà Zen; Cà Verzola; Conca Pisana | January 2011–October 2017 | Semi-annual CMA |
| Air temperature Air humidity | Monthly | www.scia.isprambiente.it | Adria Bellombra; Rosolina Po di Tramontana; Pradon Porto Tolle | January 2011–December 2017 | Annual mean |
| Air pressure | Monthly | www.scia.isprambiente.it | Pradon Porto Tolle; Rovigo | January 2011–December 2017 | Semi-annual CMA |
| Dataset | Function Used for Fitting Data | Goodness of Fit |
|---|---|---|
| TCN data | Linear equation: f(x) = a × (x − 2012.74) + b Coefficients and Asymptotic Standard Error: a = −0.00581235 ± 0.0001 (1.721%) b = 0.314595 ± 0.0002699 (0.0858%) | SSE: 0.04936 R-squared: 0.6744 Adjusted R-squared: 0.6742 RMSE: 0.005501 |
| TCC data | Linear equation: f(x) = a × (x − 2011.29) + b Coefficients and Asymptotic Standard Error: a = −0.00909587 ± 0.0001467 (1.613%) b = 49.3513 ± 0.0005187 (0.001051%) | SSE: 0.006615 R-squared: 0.9247 Adjusted R-squared: 0.9244 RMSE: 0.004597 |
| Quadratic equation: f(x) = p1 × x2 + p2 × x + p3 (x is normalized by mean 2014 and std 1.768) Coefficients (with 95% confidence bounds): p1 = 3.819 (3.439, 4.199) p2 = −0.02619 (−0.3668, 0.3145) p3 = −3.806 (−4.316, −3.297) | SSE: 2936 R-squared: 0.5561 Adjusted R-squared: 0.5533 RMSE: 3.068 |
| GNSS vs. Air Pressure | GNSS vs. Air Temperature | GNSS vs. Pumped Water | |
|---|---|---|---|
| Linear correlation coefficient (rho) | −0.29 < −0.07 < 0.16 | 0.12 < 0.34 < 0.53 | −0.41 < −0.20 < 0.03 |
| Linear correlation p-value | 0.56 | 0.003 | 0.09 |
| Cross-correlation index with no lag | 0.02 | 0.16 | −0.14 |
| Best cross-correlation index | 0.03 (with 12-month lag) | 0.23 (with 2-month lag) | 0.18 (with 5-month lag) |
| Zone | Layer | K (m/s) | Sy | n | Ss (1/m) | Sfe |
|---|---|---|---|---|---|---|
| Silty aquitard | 1 | 1 × 10−5 | 0.05 | 0.05 | 6.67 × 10−4 | 3.33 × 10−3 |
| Sandy aquifer | 1 | 1 × 10−4 | 0.10 | 0.10 | 6.71 × 10−5 | 3.33 × 10−4 |
| Sandy aquifer | 2 | 1 × 10−4 | 0.10 | 0.10 | 6.71 × 10−5 | 1.00 × 10−3 |
| Parameter | Description | Unit | Layer 1 (Silty Sand Deposits) | Layer 2 (Sandy Deposits) |
|---|---|---|---|---|
| Material Model | Constitutive model | - | Linear elastic | Linear elastic |
| Soil unit weight | γsat | kN/m3 | 19 | 20 |
| Young’s modulus | E | kN/m2 | 15,000 | 150,000 |
| Poisson’s ratio | ν | - | 0.3 | 0.3 |
| Hydrological Model | RMSE (mm) | NRMSE (%) | NSE |
|---|---|---|---|
| MERRA2 | 2.92 | 29.03 | −0.65 |
| GLDAS2 | 3.15 | 31.39 | −0.93 |
| MERRA2 (phase-shifted) | 1.85 | 18.40 | 0.34 |
| GLDAS2 (phase-shifted) | 2.23 | 22.17 | 0.04 |
| ATMMO | 2.42 | 24.12 | −0.14 |
| Computed Joint Displacements vs. Observed Displacements | RMS (mm) | NRMS (%) | NSE | R |
|---|---|---|---|---|
| First scenario: superposition principle | 2.94 | 29.22 | −0.67 | 0.62 |
| Second scenario: time-constant weights | 1.56 | 0.16 | 0.53 | 0.73 |
| Third scenario: time-variable weights | 0.63 | 6.25 | 0.92 | 0.97 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vitagliano, E.; Vitale, E.; Russo, G.; Piccinini, L.; Fabris, M.; Calcaterra, D.; Di Maio, R. Analysis of the Periodic Component of Vertical Land Motion in the Po Delta (Northern Italy) by GNSS and Hydrological Data. Remote Sens. 2022, 14, 1126. https://doi.org/10.3390/rs14051126
Vitagliano E, Vitale E, Russo G, Piccinini L, Fabris M, Calcaterra D, Di Maio R. Analysis of the Periodic Component of Vertical Land Motion in the Po Delta (Northern Italy) by GNSS and Hydrological Data. Remote Sensing. 2022; 14(5):1126. https://doi.org/10.3390/rs14051126
Chicago/Turabian StyleVitagliano, Eleonora, Enza Vitale, Giacomo Russo, Leonardo Piccinini, Massimo Fabris, Domenico Calcaterra, and Rosa Di Maio. 2022. "Analysis of the Periodic Component of Vertical Land Motion in the Po Delta (Northern Italy) by GNSS and Hydrological Data" Remote Sensing 14, no. 5: 1126. https://doi.org/10.3390/rs14051126
APA StyleVitagliano, E., Vitale, E., Russo, G., Piccinini, L., Fabris, M., Calcaterra, D., & Di Maio, R. (2022). Analysis of the Periodic Component of Vertical Land Motion in the Po Delta (Northern Italy) by GNSS and Hydrological Data. Remote Sensing, 14(5), 1126. https://doi.org/10.3390/rs14051126









