Abstract
As the first in-orbit formation satellites equipped with a Laser Ranging Interferometer (LRI) instrument, Gravity Recovery and Climate Experiment Follow-on (GRACE-FO) satellites are designed to evaluate the effective ability of the new LRI ranging system applied to satellite-to-satellite tracking. To evaluate the application of LRI in GRACE-FO, a relative kinematic orbit determination scheme for formation satellites integrating Kalman filters and GPS/LRI is proposed. The observation equation is constructed by combining LRI and spaceborne GPS data, and the intersatellite baselines of GRACE-FO formation satellites are calculated with Kalman filters. The combination of GPS and LRI techniques can limit the influence of GPS observation errors and improve the stability of orbit determination of the GRACE-FO satellites formation. The linearization of the GPS/LRI observation model and the process of the GPS/LRI relative kinematic orbit determination are provided. Relative kinematic orbit determination is verified by actual GPS/LRI data of GRACE-FO-A and GRACE-FO-B satellites. The quality of relative kinematic orbit determination is evaluated by reference orbit check and K-Band Ranging (KBR) check. The result of the reference orbit check indicates that the accuracy of GRACE-FO relative kinematic orbit determination along X, Y, and Z (components of the baseline vector) directions is better than 2.9 cm. Compared with the relative kinematic orbit determination by GPS only, GPS/LRI improves the accuracy of the relative kinematic orbit determination by approximately 1cm along with X, Y and Z directions, and by about 1.8 cm in 3D directions. The overall accuracy of relative kinematic orbit determination is improved by 25.9%. The result of the KBR check indicates that the accuracy of the intersatellite baseline determination is about +/−10.7 mm.
1. Introduction
Gravity Recovery and Climate Experiment Follow-on (GRACE-FO) is regarded as a new mission of gravity formation satellites launched jointly by the National Aeronautics and Space Administration (NASA) and Helmholtz-Centre Potsdam, German Research Centre for Geosciences (GFZ), with a design life of 5 years. Having been launched successfully at Vandenberg Air Force Base in California on May 22, 2018, GRACE-FO satellites attempt to replace GRACE satellites that had orbited for 15 years and retired in June, 2017 [1,2,3]. GRACE-FO satellites carry the same equipment as GRACE, including GPS, a K-Band Ranging (KBR) System, a satellite accelerometer, and star sensor [4,5]. Similarly, GRACE-FO satellites also adopt an orbit design similar to that of GRACE satellites, with an orbit height of about 500 10 km, an orbit eccentricity of less than 0.005, and an orbit inclination of about 89 [5,6]. GRACE-FO satellites, mainly used to accurately measure and invert the time-varying Earth’s gravitational field, are regarded as an important mission for collecting Earth’s gravitational field data of high resolution [2]. The high quality satellite orbit and relative position can ensure the high quality processing of gravity data, which contributes to the estimation of gravity field models with a monthly resolution [7,8]. Therefore, the study of the precise orbit determination of GRACE-FO satellites is considered crucial. To ensure a stable relative distance in formation flight, GRACE satellites are equipped with a KBR system. In addition, GRACE-FO satellites have on-board a Laser Ranging Interferometer (LRI) [9,10,11,12]. LRI can accurately measure the intersatellite distance of GRACE-FO formation satellites and provide distance data of high quality [13].
At present, several formation satellites have been performing in orbit, including GRACE, GRACE-FO, TanDEM-X, PRISMA, SJ-9 and TechSat21 [14,15,16,17,18,19,20,21]. The existing formation satellites mainly realize relative positioning based on a GPS technique [19]. Generally, the relative kinematic orbit determination of LEO satellites is based on carrier-phase differential observations (CDGPS) [14]. The differential technique promises to eliminate and weaken some common observation errors, such as receiver clock bias, satellite clock bias and ionospheric delay errors [19,20,21,22,23,24,25,26,27,28,29,30]. Gu et al. [31] combined single and double differential techniques to jointly solve the orbit of formation satellites. A comparison with satellite laser ranging (SLR) indicates that the accuracy of the orbit was improved by 25%. Van Barneveld [32] analyzed the influence of ionospheric delay on the calculation of intersatellite long baselines (>100 km) and compared existing ionospheric delay models.
The new generation GRACE-FO satellites are equipped with an LRI system, which makes it possible to use LRI observations to enhance the quality and stability of formation satellites orbit. Currently, the intersatellite distance are generally used to verify the intersatellite baseline, and to maintain the relative state of formation satellites. GRACE-FO satellites can be equipped with dual ranging system (LRI and KBR). Concerning the LRI ranging system, this manuscript describes the following activities: firstly, the inter-satellite distance observed by LRI is combined with the GPS observation data of the GRACE-FO satellites to form the GPS/LRI observations. Secondly, the estimated orbits are compared to reference orbits and KBR measurements. Thirdly, this study analyzed the relative kinematic orbit determination results of GPS/LRI and GPS only.
2. Mathematical Model of GPS and LRI
LEO satellites’ orbit determination generally takes pseudo range and carrier phase of GPS as the main observed values. The pseudo range and carrier phase observation models are as follows:
where is the observed code pseudo range; is the geometric distance between the GRACE-FO satellite to the GPS satellite; is the velocity of light; and are receivers and satellite clock offsets, respectively; is the ionospheric delay; is the observed value of carrier phase; is the ambiguity; and and are observation noise. To eliminate ionospheric delay, ionospheric-free combinations are usually adopted:
where is the pseudo range of ionospheric-free combinations; is the carrier phase of ionospheric-free combinations; is the wavelength of carrier phase , is the ambiguity of ionospheric-free combinations, and and are observation noise of pseudo range and carrier phase ionospheric-free combinations. The equations of ionospheric-free combinations are as follows:
where and are the frequencies of carrier phases and . Ionospheric-free combinations can eliminate most of the ionospheric delay, and loses integer characteristic.
To build double-difference observation equations, inter-satellite single-difference equations should first be constructed. The single-difference models are as follows:
where and are single-difference observed values of the carrier phase and pseudo range. The satellite with the largest altitude angle is selected as the reference satellite. The double-difference models are as follows:
where double-difference observed values of , and are double-difference pseudo range, carrier phase and ambiguity, respectively.
For the first time, GRACE-FO formation satellites are equipped with a LRI ranging system. The model of LRI is as follows [5]:
where is the LRI measurement (unit: m), is the observed phase value of LRI at , is the time delay correction of the LRI acquisition system, is the time of signal transmission of LRI, and is the LRI-frequency of the observed phase. The ground nominal value of in GRACE-FO-A is 2.81616393e14 Hz, and the ground nominal value of in GRACE-FO-B is 2.81615684e14 Hz. The original phase observed values (LRI1A) of LRI have glitches [33]. Glitches of LRI mainly occurs during thruster firings. JPL laboratory detects glitches of LRI by three methods. Firstly, differences in phase observed values are performed, and then glitches of LRI are detected by comparing the observed differential values with the tolerance. Secondly, small glitches of LRI are fitted by a phase filter model [33]. Thirdly, glitches are further detected by residuals of Two-Way Range [11]. In order to simplify experiments, this study adopts secondary-treated Level-1B data of JPL laboratory, and all glitches of LRI were detected and repaired.
Based on the principle of LRI and product description published by GFZ, LRI observations deliver a biased distance . To obtain the actual intersatellite distance, the biased distance must be gained in advance. This study proposes a simple and feasible calculation process for the biased LRI distance.
(1) The intersatellite distance is resolved by using relative kinematic orbit determination from spaceborne GPS data. Assuming that there are n epochs, the intersatellite distance between two LEO satellites is obtained according to the relative kinematic orbit determination of spaceborne GPS;
(2) LRI range minus the intersatellite distance at the corresponding epoch, and the initial value of LRI biased distance can be introduced;
(3) The mean value of should be calculated;
(4) The difference between the initial value () and the mean value () is calculated, and epochs with a difference greater than a threshold are marked as outliers. This threshold is defined as follows:
where is the precision of relative kinematic orbit determination of spaceborne GPS. For the convenience of the experiment, was set to 0.15 m ();
(5) The marked observed values of LRI should be eliminated, and then steps from 2 to 4 are repeated until all pass the inspection formula;
(6) Taking into account the LRI bias, ranging values of each epoch are corrected to obtain the intersatellite distance of LEO satellites based on LRI ranging.
To evaluate the precision of LRI (actually LRI biased), the LRI biased distances for 4 months (days 121 to 242 of 2019) are calculated. The statistical results are shown in Table 1, confirming the good quality of LRI distances. More than 98.5% of LRI observations can be used to solve LRI bias.

Table 1.
RMS of LRI bias (unit: m) and percentage of LRI outliers (unit: %).
3. GPS/LRI Observation Equation and Linearization
As observed distance values, LRI can establish the observation of the LEO satellite by combining with GPS. The GPS/LRI observation equation in matrix form reads as follows:
where is obtained by subtracting the calculated values from actual observed values, is the correction of observed values, and is the linearized parameter coefficient matrix to be solved. is expressed as follows:
After the observation equation is linearized, a Kalman filter process can be used for iterative processing.
4. Kalman Filter Theory Applied to Relative Kinematic Orbit Determination of LEO Satellites
Relative Kinematic orbit determination of LEO satellites aims to obtain coordinates of satellites. Under the condition of double-difference orbit determination, the parameters to be obtained not only include the coordinates of satellites, but also the ambiguities of double-difference carrier observed values. The parameters of LEO satellites are to be calculated by setting double-difference carrier observed values:
where are components of the baseline vector between the GRACE-FO satellites (Earth-fixed reference frame) and are ambiguities of the observed carrier values. The Kalman filter equations of LEO satellites are as follows:
where is the prior variance matrix of parameters; is the observation variance matrix; is the gain matrix; and are the prior value and calculated value of parameters to be solved, respectively; is the observed minus computed (O-C); and is the posterior variance matrix of parameters.
Pseudo-range single point positioning is used to replace the state-transition matrix to generate prior coordinates of LEO satellites (prediction coordinates), with an accuracy of about 10 m, which requires continuous refinement of LEO satellites’ coordinates according to observed carrier values and their corresponding variance information. The variance processing of parameters is regarded as an important basis for Kalman filter calculation. Therefore, this manuscript provides the detailed settings for the corresponding parameter variance matrix and observation variance matrix in the Kalman filter. The variance matrix formula of observed values is as follows:
and are the phase prior variances and pseudo-range prior variances, is the elevation angle of GPS satellites, and are the error factors of phase observation (unit: m), and are the error factors of pseudo-range observation (unit: m), and is the variance of LRI’s observed values. In the experiment of this manuscript, (unit: m2).
In this work, Kalman filter orbit determination does not take dynamic information into consideration, and pseudo-range single point positioning is used to generate a priori coordinate . The prior value of the ambiguity parameter adopts the floating-point value resolved in the previous epoch. The initial-state parameter variance matrix of LEO satellites is assigned as follows:
where the variance corresponding to the coordinate parameter is reset as (unit: m2) in the next epoch, while the variance corresponding to the ambiguity parameter directly adopts the posterior variance of previous epochs.
5. Relative Kinematic Orbit Determination Process of GPS/LRI
The essence of relative kinematic orbit determination of spaceborne GPS/LRI is to regard LRI as a directly observed value, and build the observation equation with GPS double-difference observations for resolving the intersatellite baseline. The relative kinematic orbit determination process of GPS/LRI is shown in Figure 1.
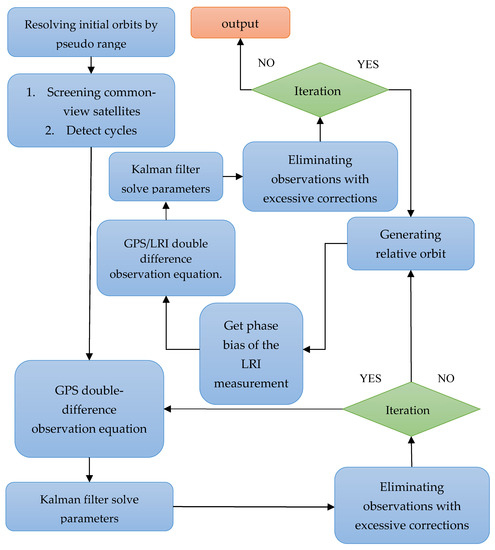
Figure 1.
Orbit determination process.
The specific process of kinematic orbit determination is shown below:
(1) Resolving initial coordinates of orbits by the ionospheric-free pseudo range;
(2) Screening common-view satellites of GRACE-FO-A and GRACE-FO-B;
(3) Detecting cycle slips according to Melbourne–Wübbena (MW) and geometry-free (GF) combination [34,35]. The models of MW and GF are provided below:
Equations (19) and (20) are usually used to jointly detect cycle slips. In this paper, the threshold of cycle slips detection between epochs (i and i + 1) is set as:
The detection for cycle slips is regarded as data preprocessing;
(4) Constructing double-difference observation equation according to Equations (1) to (7);
(5) Updating the parameters to be resolved by Kalman filter;
(6) Correcting phase center offsets (PCO) and Sensor Offsets of LEO satellite. Taking GRACE-FO-A and GRACE-FO-B as examples, Table 2 and Table 3 show the three components of PCO and Sensor Offsets in the body- fixed coordinate of GRACE-FO satellites. As for LEO satellites, their solar panel must always aim at the sun, so the satellite gesture will change according to time. Therefore, several steps should be taken in calculating PCO and Sensor Offsets correction of LEO satellites with spaceborne GPS:

Table 2.
PCO of GRACE-FO satellites (unit: mm).

Table 3.
Sensor Offset of GRACE-FO satellites (unit: mm).
(a) The coordinates of LEO satellites without being corrected by PCO and Sensor Offset are converted from Earth-fixed coordinate system to inertial coordinate system.
(b) According to the attitude of LEO satellites, the three components of PCO and Sensor offset in the body- fixed coordinate system are transferred to the inertial coordinate system.
(c) The corrections of PCO and Sensor Offset in the inertial system are added to the coordinates of LEO satellites.
(d) The coordinates of LEO satellites are transferred from the inertial coordinate system to the Earth-fixed coordinate system;
(7) The intersatellite baseline is recalculated according to the correction of mass center, and the relative kinematic orbit determination results are generated.
6. Case Study and Analysis
To verify the influence of LRI on the relative kinematic orbit determination of GRACE-FO formation satellites, a control experiment is designed according to actual observation data of GRACE-FO satellites. The experimental group achieves relative kinematic orbit determination by adopting GPS/LRI combinations, and the control group only uses GPS. The paper adopts reference orbit comparison and KBE check to analyze and compare the experimental results. The observation data of GPS/LRI and KBR in GRACE-FO satellites are provided by GFZ (https://isdc.gfz-potsdam.de/, accessed on 9 June 2020), collected from day 121 to day 242 in 2019, a total of 121 days. Samples of GPS data are collected at the interval of 10 s, and those of LRI and KBR data are collected at the interval of 2 s and 5 s, respectively. Then, synchronous GPS, LRI and KBR data should be used for check. The precise ephemeris, satellite clock offsets and Earth rotation parameter files are provided by the Center for Orbit Determination in Europe (CODE), and broadcast ephemeris are provided by the International GNSS Service (IGS). More details about these data are listed in Table 4.

Table 4.
Data description.
6.1. Reference Orbit Check
The orbit published by GFZ is regarded as the reference value. The relative orbit determination results of GPS/LRI and GPS are separately compared with the reference orbit. Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6 show the comparison results of days 121–242’s reference orbits. As is shown, there are no systematic errors in the GRACE-FO satellites’ relative kinematic orbit determination. The main reason is that the relative kinematic orbit determination method used in this paper essentially belongs to a geometric orbit determination without being affected by the dynamic satellite model. However, the residual errors of GPS/LRI joint relative kinematic orbit determination result in X, Y, and Z (components of the baseline vector) directions are obviously smaller than those of GPS only. Compared with relative kinematic orbit determination by GPS only, the distribution of orbit residuals calculated by GPS/LRI is closer, and the obvious spikes in the figure are weakened. The main reason is that on-board GPS is quite different from ground stations in that the number of satellites observed by the on-board GPS receiver in some arcs is smaller than five. Meanwhile, the travel speed of LEO satellites can reach 6–7 km per second, so the observed GPS satellites change frequently. Usually, a satellite can be observed for only 10 to 30 min. Therefore, the observation data quality is poor for a small part of the arc, reducing the stability of the geometric method for relative kinematic orbit determination. The Geometric Dilution Precision (GDOP) is related to the orbit determination accuracy. We analyzed the GDOP of GRACE-FO satellites for 121 to 242 days. When the value of GDOP increases, the orbit accuracy will decrease. However, GPS / LRI can limit the impact of GDOP increase on the orbit accuracy. Therefore, combined GPS/LRI observations can better eliminate GPS observations of poor quality and reduce the impact of GPS observation quality on relative kinematic orbit determination. Additionally, the results of 121 days’ relative kinematic orbit determination show that introducing GPS/LRI observations is obviously better than using GPS only.
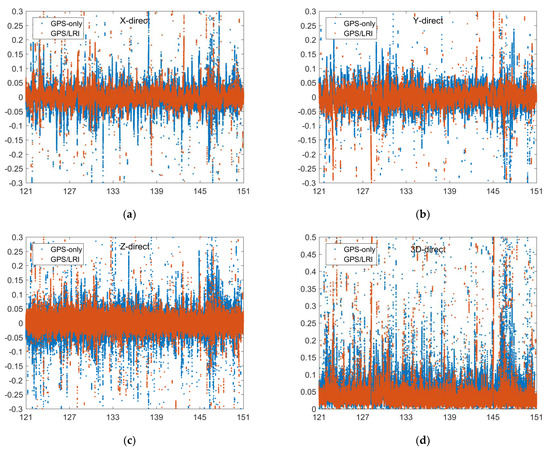
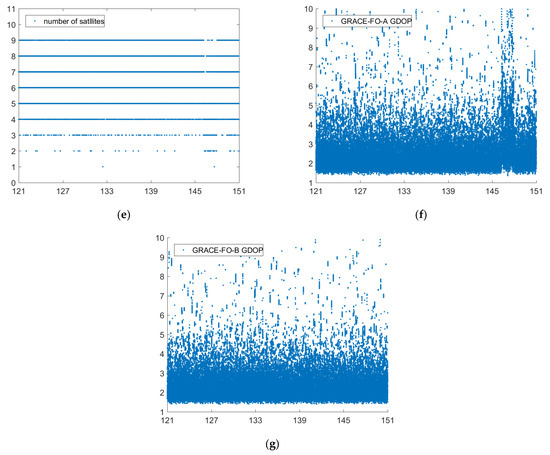
Figure 2.
Reference orbit check for GRACE-FO in the X, Y, Z, 3D (X, Y, Z are components of the baseline vector, unit: m, (a–d)) directions (days 121–151), number of satellites for each epoch (e) and GDOP (f,g).
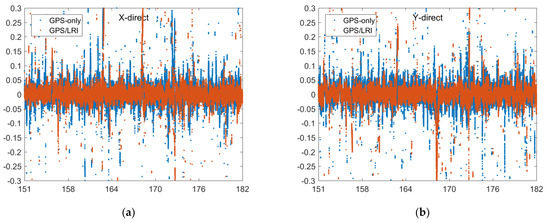
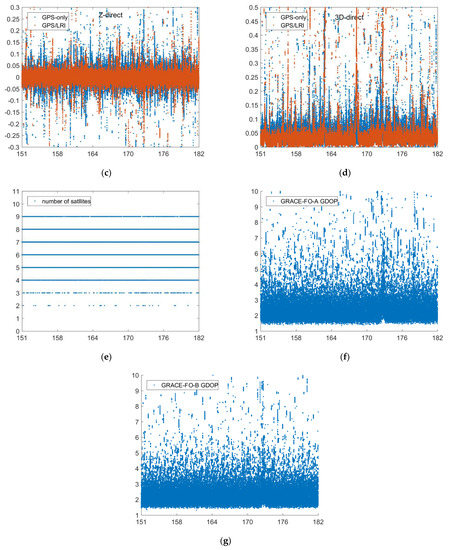
Figure 3.
Reference orbit check for GRACE-FO in the X, Y, Z, 3D (X, Y, Z are components of the baseline vector, unit: m, (a–d)) directions (days 151–182), number of satellites for each epoch (e) and GDOP (f,g).
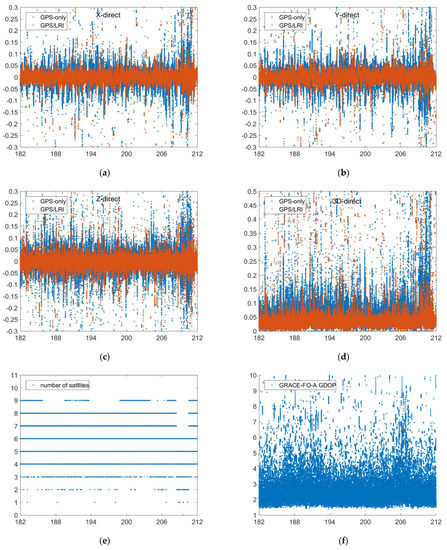
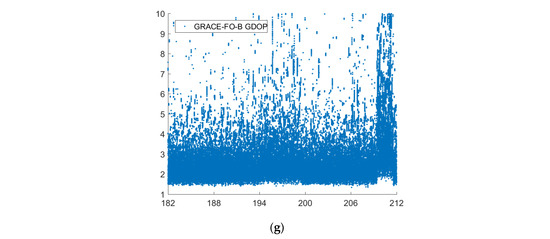
Figure 4.
Reference orbit check for GRACE-FO in the X, Y, Z, 3D (X, Y, Z are components of the baseline vector, unit: m, (a–d)) directions (days 182–212), number of satellites for each epoch (e) and GDOP (f,g).
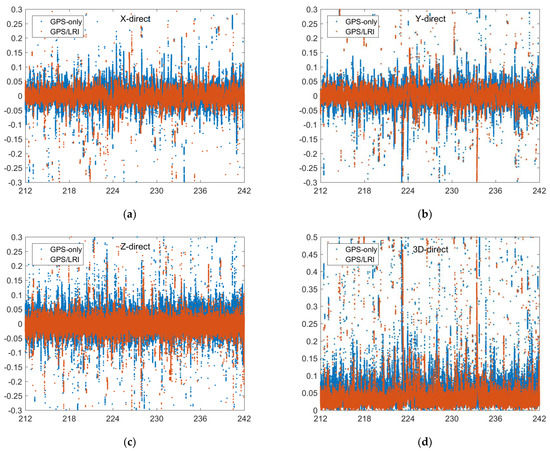
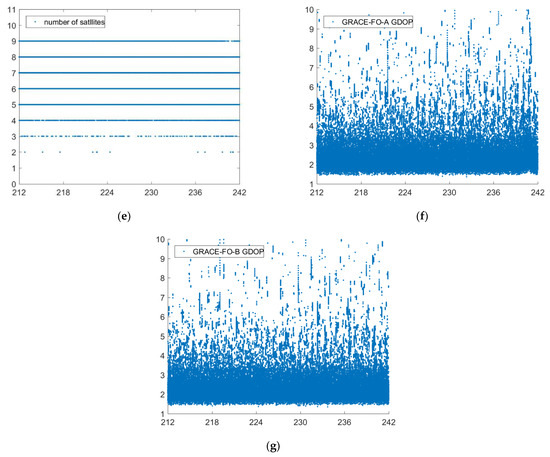
Figure 5.
Reference orbit check for GRACE-FO in the X, Y, Z, 3D (X, Y, Z are components of the baseline vector, unit: m, (a–d)) directions (days 212–242), number of satellites for each epoch (e) and GDOP (f,g).
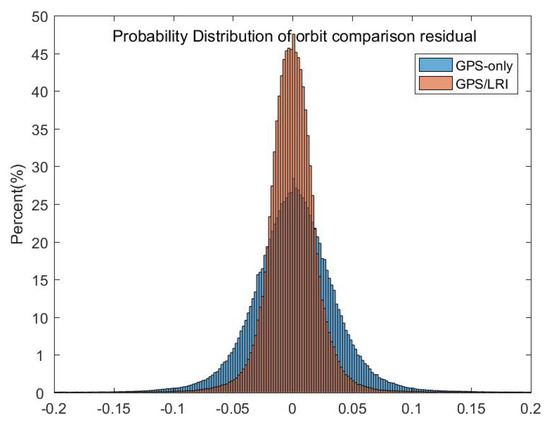
Figure 6.
Days 121–242 orbit comparison residuals (in the X, Y and Z directions, unit: m) probability distribution for the GPS/LRI and GPS relative orbit.
To obtain more specific results of relative kinematic orbit determination, statistics over 121 days are carried out in this part. X, Y, and Z refer to the baseline vectors of the two satellites in Earth-fixed coordinates. It is shown in Table 5 that along the X direction, the 121 days accuracy of GPS/LRI relative kinematic orbit determination is improved by 12.4 mm, and the relative kinematic orbit determination accuracy along the X direction reaches 25.4 mm, with an accuracy increase of 32.8%; along the Y direction, the accuracy of GPS/LRI relative kinematic orbit determination is improved by 8.5 mm, and the accuracy along the Y direction reaches 28.6 mm, with an accuracy increase of 22.9%; along the Z direction, the accuracy of GPS/LRI relative kinematic orbit determination is improved by 15.2 mm, and the accuracy along the Z direction reaches 21.9 mm, with an accuracy increase of 41.0%; along the 3D direction, the accuracy of GPS/LRI relative kinematic orbit determination is improved by 17.5 mm, and the accuracy along the 3D direction reaches 50.1 mm, with an accuracy increase of 25.9%. LRI observed values are added to increase the number of redundant observations, enhancing the geometric strength of observed values, so the accuracy of GPS/LRI is greatly improved compared with that of only GPS for formation orbit determination. Statistical results show that the joint GPS/LRI data can effectively improve the overall accuracy of relative kinematic orbit determination of GRACE-FO formation satellites and limit orbit determination errors due to GPS observation quality, improving the stability of relative kinematic orbit determination.

Table 5.
Statistics of reference orbit check (days 121–242) in Earth-fixed coordinate (unit: m).
To analyze the orbital residual, we set GRACE-FO-B as the reference orbit and solve the orbit of GRACE-FO-A according to the relative kinematic orbit determination results. The orbit of the GRACE-FO-A satellite and the orbit released by GFZ are compared by using the ORBCMP module of Bernese 5.2 software. Under the radial, along–track and out–of–plane (RSW) decomposition, we analyze the residual results. Figure 7, Figure 8, Figure 9 and Figure 10 show the comparison results of day 121–242’s reference orbits. Figure 11 shows the probability distribution of satellite orbit residuals. In the R and W directions, the residual distributions of GPS-only and GPS/LRI are similar. However, in the S direction, GPS/LRI can significantly improve the relative kinematic orbit determination accuracy of GRACE-FO-A satellite. For further analysis, we calculated the MEAN, MEDIAN and RMS of orbital residuals in R, S and W directions. It is shown in Table 6 that along the R direction, the 121 days accuracy of GPS/LRI relative kinematic orbit determination is improved by 10.0 mm, and the relative kinematic orbit determination accuracy along the R direction reaches 29.0 mm, with an accuracy increase of 34.48%; along the S direction, the accuracy of GPS/LRI relative kinematic orbit determination is improved by 31.7 mm, and the accuracy along the S direction reaches 8.9 mm, with an accuracy increase of 78.8%; along the W direction, the accuracy of GPS/LRI relative kinematic orbit determination is not significantly improved. The RMS of the 3D vector is decreased by 18 mm which corresponds to an improvement of 26.3%.
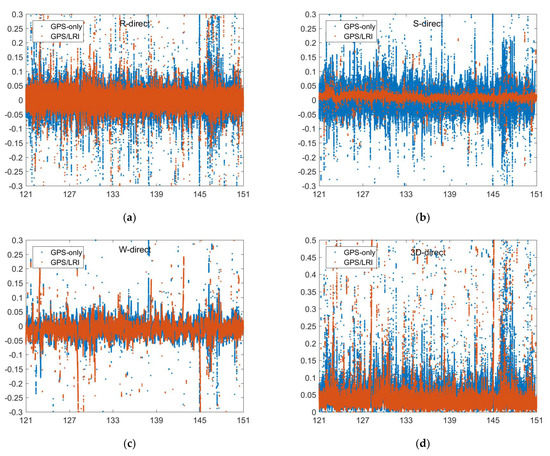
Figure 7.
Reference orbit check for GRACE-FO-A in the R, S, W, 3D directions (days 121–151, (a–d)).
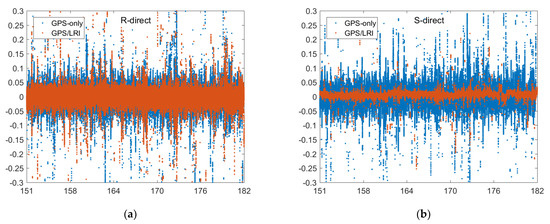
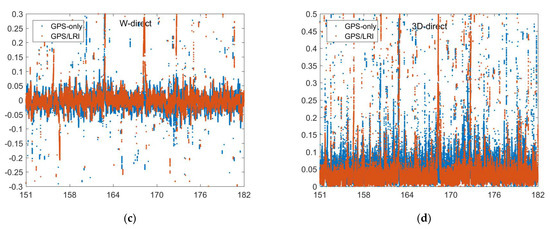
Figure 8.
Reference orbit check for GRACE-FO-A in the R, S, W, 3D directions (days 151–182, (a–d)).
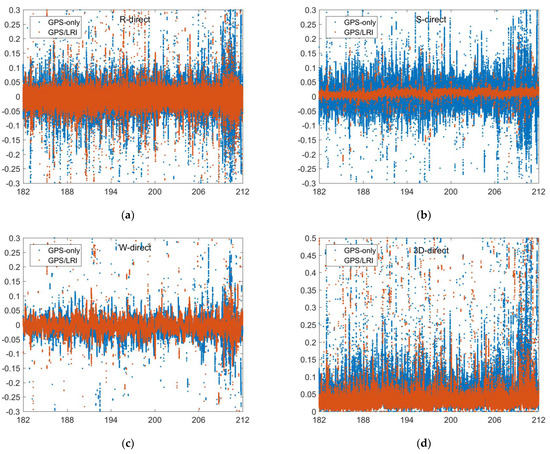
Figure 9.
Reference orbit check for GRACE-FO-A in the R, S, W, 3D directions (days 182–212, (a–d)).
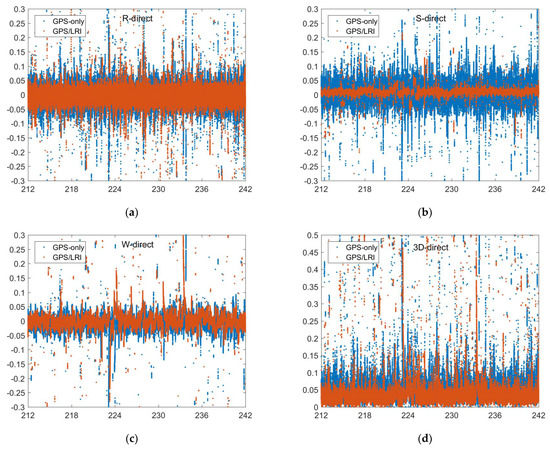
Figure 10.
Reference orbit check for GRACE-FO-A in the R, S, W, 3D directions (days 212–242, (a–d)).
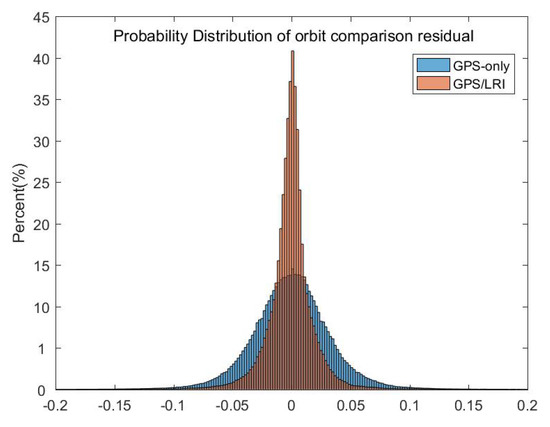
Figure 11.
Days 121–242 orbit comparison residuals (in the R, S and W directions, unit: m) probability distribution for the GPS/LRI and GPS relative orbit.

Table 6.
Statistics of reference orbit check (days 121–242) in RSW (unit: m).
To evaluate the GPS/LRI under sunlight and solar eclipse, we use the ORBGEN module of Bernese 5.2 software to mark the epochs in solar eclipse. GRACE-FO satellites were under solar eclipse for 25% of the total period. Figure 12 show the comparison results of day 121–242’s reference orbits in the sunlight and solar eclipse. In the case of sunlight and solar eclipse, there is no significant difference in GPS/LRI orbit residuals. In both cases, the accuracy of GPS/LRI orbit determination is higher than the GPS-only. To further analyze the impact of solar eclipse on GPS/LRI, we calculated the RMS, MEAN and MEDIAN of orbital residuals. It is shown in Table 7 and Table 8 that the RMS values differ by 2.2 mm and 2.1 mm in the 3D-directions. Along the X, Y, Z and 3D direction the 121-days accuracy of GPS/LRI relative kinematic orbit determination, under the conditions of sunlight and solar eclipse, is not a significant difference.
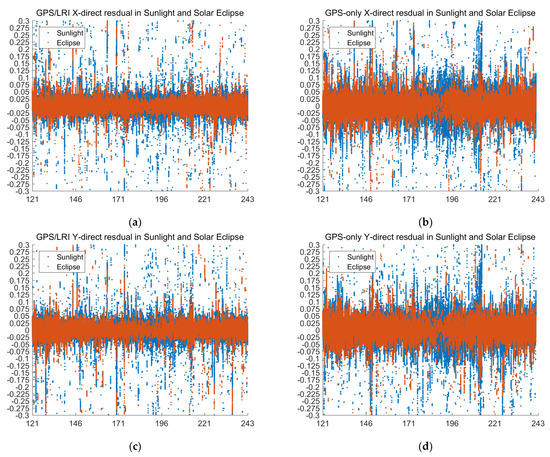
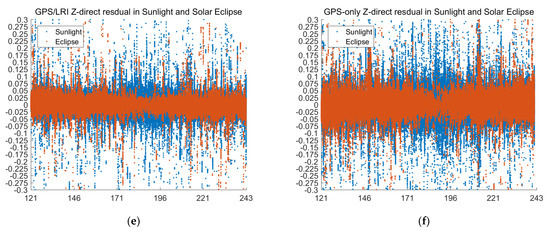
Figure 12.
D (X, Y, Z are components of the baseline vector, unit: m, (a–d)) directions (days 121–242).

Table 7.
Statistics of X, Y, Z and 3D residual (unit: m, days 121–242) in Sunlight and Solar eclipse.

Table 8.
Statistics of X, Y, Z and 3D residual (unit: m, days 121–242) in Sunlight and Solar eclipse.
To evaluate the GPS/LRI in satellite orbit maneuver, we analyzed the orbit eccentricity of GRACE-FO satellites for 121 days. Landerer points out that regular orbit maintenance maneuvers will be performed throughout the GRACE-FO mission duration [36]. Figure 13 shows the orbital eccentricity of GRACE-FO satellites and their hourly variation. We marked the time of orbital maneuver in the figure with circles. Table 9 shows the date of the satellite orbit maneuver. Figure 14 shows the comparison results of reference orbits in the orbit maneuver. Table 10 shows the RMS, MEAN and MEDIAN of orbital residuals during orbital maneuver.
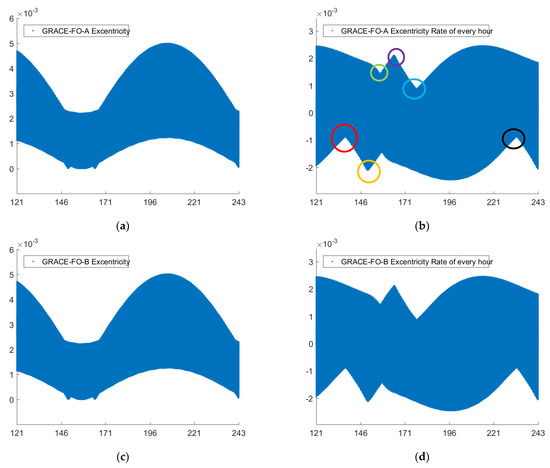
Figure 13.
Eccentricity and eccentricity variation of GRACE-FO satellites (hourly variation).

Table 9.
Days of Orbital Maneuver.
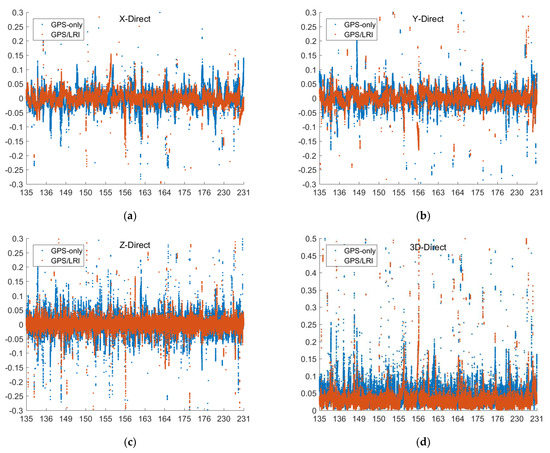
Figure 14.
Reference orbit check for Orbital Maneuver in the X, Y, Z, 3D (X, Y, Z are components of the baseline vector, unit: m, (a–d)) directions (days 121–242).

Table 10.
Statistics of X, Y, Z and 3D residual (unit: m, days 121–242) in Orbital Maneuver.
6.2. KBR Validation
The KBR system is one of the key scientific instruments carried by GRACE-FO satellites with a sampling interval of 5 s, ranging accuracy of 10 um, and range-changing rate accuracy of 1 um/s [37]. Actually, KBR and LRI are distinctly separate intersatellite ranging systems. Therefore, KBR can be used as an important external condition to verify GPS/LRI relative kinematic orbit determination results. The basic principle of KBR check is to obtain the difference between KBR-observed values and intersatellite baseline, and then evaluate the quality of the orbit difference between LEO satellites. Figure 15, Figure 16, Figure 17, Figure 18 and Figure 19 show the residual distribution of KBR from day 121 to 242 in 2019. It shows that the relative kinematic orbit determination residuals by GPS only are mainly distributed within m, and the fluctuation of orbit determination residuals presents random distribution with some residual spikes. The residual values of a few epochs exceed m. However, the relative kinematic orbit determination results of joint GPS/LRI are quite smooth with the residual fluctuation range within m, and only very few epochs have KBR residual values greater than m. Compared with relative kinematic orbit determination by GPS, relative kinematic orbit determination by joint GPS/LRI reduces the orbital spikes of relative kinematic orbit determination caused by GPS observation quality, and improves the orbital accuracy of relative kinematic orbit determination.
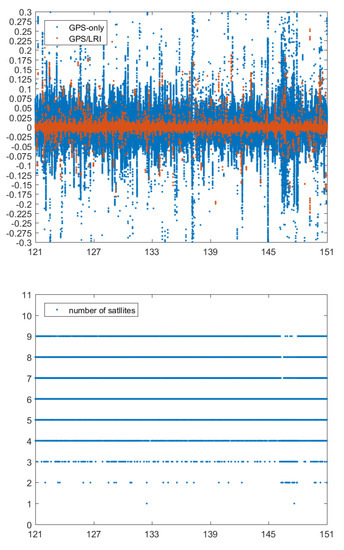
Figure 15.
Day 121–151 KBR residuals (unit: m) for the GPS/LRI and GPS-only relative orbit and number of satellites.
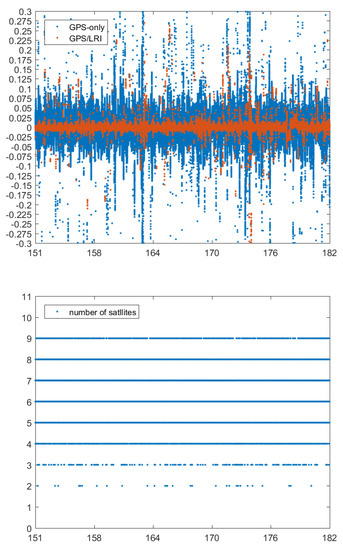
Figure 16.
Day 151–182 KBR residuals (unit: m) for the GPS/LRI and GPS-only relative orbit and number of satellites.
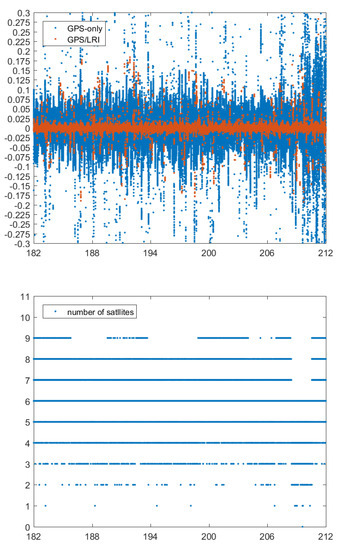
Figure 17.
Day 182–212 KBR residuals (unit: m) for the GPS/LRI and GPS-only relative orbit and number of satellites.
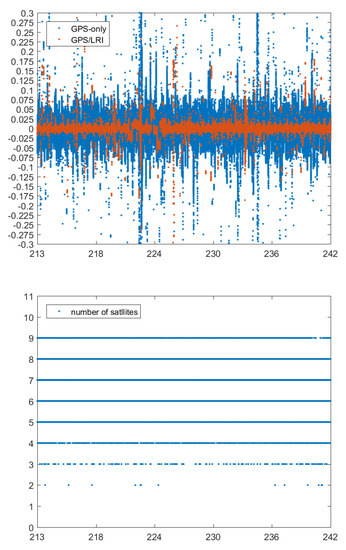
Figure 18.
Day 213–242 KBR residuals (unit: m) for the GPS/LRI and GPS-only relative orbit and number of satellites.
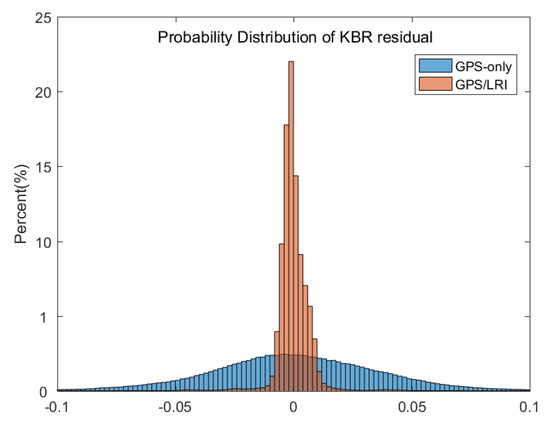
Figure 19.
Day 121–242 KBR residuals (unit: m) probability distribution for the GPS/LRI and GPS-only relative orbit.
To obtain more detailed statistical information, we have conducted for all 121 days a comparison between KBR ranges and the relative kinematic orbit determination results. RMS, MEAN and MEDIAN values of 121 days KBR residuals are listed in Table 11. The accuracy of 121 days’ relative kinematic orbit determination based on GPS only approximates 42.8 mm while that calculated from joint GPS/LRI data approximates 10.7 mm. It indicates that joint GPS/LRI improves the quality of relative kinematic orbit determination, and confirms the results of reference orbit verification. The mean value of KBR residuals in 121 days is less than 0.5 mm, indicating no obvious systematic errors in joint GPS/LRI and GPS relative kinematic orbit determination, and the results of relative kinematic orbit determination comply with the statistical law.

Table 11.
Statistics of KBR check (unit: m).
KBR can be used to evaluate the ability of GPS/LRI under sunlight and eclipse conditions. Figure 20 shows the KBR residuals of GPS/LRI and GPS-only relative kinematic orbit determination. There is no significant difference in the KBR residuals of GPS/LRI relative kinematic orbit determination under sunlight and solar eclipse. Table 12 shows the RMS, MEAN and MEDIAN of KBR residuals for GPS/LRI and GPS-only. Under the sunlight and solar eclipse, the KBR residuals RMS corresponding to GPS/LRI are 9.3 mm and 9.7 mm, and their differences are very slight. The RMS values of KBR residuals corresponding to GPS-only are 42.4 mm and 42.2 mm. Their differences are also small.
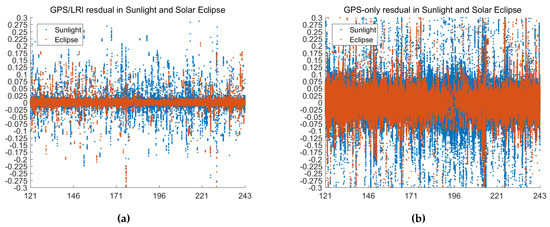
Figure 20.
Days 121–242 KBR residuals (unit: m) for the GPS/LRI (a) and GPS-only (b) relative orbit in the Sunlight and Solar eclipse).

Table 12.
Statistics of KBR residual (unit: m, days 121–242) in Sunlight and Solar eclipse.
7. Conclusions
In this manuscript, we studied the LRI ranging system carried by GRACE-FO formation satellites, achieving high-quality relative kinematic orbit determination based on joint GPS/LRI data and the Kalman filter. Additionally, we introduced the LRI ranging systems as well as the LRI observation equation, and described the process of relative kinematic orbit determination of GPS/LRI in detail. Ultimately, relative kinematic orbit determination results of GPS/LRI were verified and analyzed by comparing to a reference orbit and verifying KBR. Accordingly, we draw two conclusions: 1. Compared with relative kinematic orbit determination by GPS only, kinematic orbit determination by GPS/LRI achieves more robust results, which can weaken some orbits’ error and significantly improve the accuracy of relative kinematic orbit determination. The accuracy of relative kinematic orbit determination by GPS/LRI is improved by 17.5 mm in 3D directions, and the accuracy of relative kinematic orbit determination is improved by 25.9%, reaching 50.1 mm (compared with the reference orbit released by GFZ). 2. The results of KBR validation are ideal. The residual distribution of KBR is smooth without obvious fluctuation. The consistency between the relative kinematic orbit determination and the KBR measurements is at the +/−10.7 mm level.
Author Contributions
Conceptualization, writing—original draft preparation, writing—review and editing, and methodology, Z.Y., X.L. and J.G.; software, Z.Y.; validation, H.G., G.L. and Q.K.; data curation, X.C.; formal analysis, H.G.; funding acquisition, J.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by The National Natural Science Foundation of China (42174041, 41774001), the Independent and Controllable Project of National Surveying and Mapping (816-517) and the SDUST Research Fund (2014TDJH101).
Institutional Review Board Statement
Not applicable for studies not involving humans or animals.
Informed Consent Statement
Not applicable for studies not involving humans.
Data Availability Statement
Our sincere thanks go to the German Research Centre Geosciences(GFZ) for providing space-borne GPS data for GRACE-FO (ftp://isdcftp.gfz-potsdam.de/grace-fo, accessed on 9 June 2020); CODE and IGS for providing GPS satellite orbits, clocks and Earth rotation parameters; the GFZ for providing precise orbits, KBR and LRI data for GRACE-FO.
Acknowledgments
This research is supported by National Natural Science Foundation of China (grant numbers 42174041, 41774001) and SDUST Research Fund (grant number2014TDJH101).
Conflicts of Interest
The authors declare no conflict interest.
References
- Dragon, K. GRACE Follow-On Mission Plan; NASA Jet Propulsion Laboratory/California Institute of Technology: Pasadena, CA, USA, 2015. [Google Scholar]
- Kornfeld, R.P.; Arnold, B.W.; Gross, M.A.; Dahya, N.T.; Klipstein, W.M.; Gath, P.F.; Bettadpur, S. GRACE-FO: The Gravity Recovery and Climate Experiment Follow-On Mission. J. Spacecr. Rocket. 2019, 56, 931–951. [Google Scholar] [CrossRef]
- Xia, Y.; Liu, X.; Guo, J.; Yang, Z.; Qi, L.; Ji, B.; Chang, X. On GPS data quality of GRACE-FO and GRACE satellites: Effects of phase center variation and satellite attitude on precise orbit determination. Acta Geod. Geophys. 2020, 56, 93–111. [Google Scholar] [CrossRef]
- Case, K.; Kruizinga, G.; Wu, S.-C. GRACE Level 1B Data Product User Handbook; JPL Publication D-22027; NASA Jet Propulsion Laboratory/California Institute of Technology: Pasadena, CA, USA, 2002. [Google Scholar]
- Wen, H.Y.; Kruizinga, G.; Paik, M.; Landerer, F.; Bertiger, W.; Sakumura, C.; Bandikova, T.; Mccullough, C. Gravity Recovery and Climate Experiment Follow-On (GRACE-FO) Level-1 Data Product User Handbook; NASA Jet Propulsion Laboratory/California Institute of Technology: Pasadena, CA, USA, 2019. [Google Scholar]
- Bertiger, W.; Desai, S.D.; Haines, B.; Harvey, N.; Moore, A.W.; Owen, S.; Weiss, J.P. Single receiver phase ambiguity resolution with GPS data. J. Geodesy 2010, 84, 327–337. [Google Scholar] [CrossRef]
- Allende-Alba, G.; Montenbruck, O. Robust and precise baseline determination of distributed spacecraft in LEO. Adv. Space Res. 2015, 57, 46–63. [Google Scholar] [CrossRef]
- Bettadpur, S. Gravity Recovery and Climate Experiment Product Specification Document (Rev 4.5–February 20, 2007); The University of Texas at Austin, Center for Space Research: Austin, TX, USA, 2007. [Google Scholar]
- Dubovitsky, S. Definition of Time Specification Relevant to LRI Operations; NASA Jet Propulsion Laboratory/California Institute of Technology: Pasadena, CA, USA, 2016. [Google Scholar]
- Bertiger, W.; Harvey, N.; Spero, R. An Alternate Formulation of The LRI Measurement; NASA Jet Propulsion Laboratory/California Institute of Technology: Pasadena, CA, USA, 2019. [Google Scholar]
- Abich, K.; Abramovici, A.; Amparan, B.; Baatzsch, A.; Okihiro, B.B.; Barr, D.C.; Bize, M.P.; Bogan, C.; Braxmaier, C.; Burke, M.J.; et al. In-Orbit Performance of the GRACE Follow-on Laser Ranging Interferometer. Phys. Rev. Lett. 2019, 123, 031101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sodnik, Z.; Cugny, B.; Karafolas, N.; Nicklaus, K.; Herding, M.; Baatzsch, A.; Dehne, M.; Diekmann, C.; Voss, K.; Heinzel, G.; et al. Laser ranging interferometer on Grace follow-on. In International Conference on Space Optics—ICSO 2016; International Society for Optics and Photonics: Bellingham, DC, USA, 2017. [Google Scholar]
- Turyshev, S.; Sazhin, M.V.; Toth, V. General relativistic laser interferometric observables of the GRACE-Follow-On mission. Phys. Rev. D 2014, 89, 105029. [Google Scholar] [CrossRef] [Green Version]
- Kroes, R.; Montenbruck, O.; Bertiger, W.; Visser, P. Precise GRACE baseline determination using GPS. GPS Solut. 2005, 9, 21–31. [Google Scholar] [CrossRef]
- Jäggi, A.; Hugentobler, U.; Bock, H.; Beutler, G. Precise orbit determination for GRACE using undifferenced or doubly differenced GPS data. Adv. Space Res. 2007, 39, 1612–1619. [Google Scholar] [CrossRef]
- Krieger, G.; Moreira, A.; Fiedler, H.; Hajnsek, I.; Werner, M.; Younis, M.; Zink, M. TanDEM-X: A Satellite Formation for High-Resolution SAR Interferometry. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3317–3341. [Google Scholar] [CrossRef] [Green Version]
- Van Barneveld, P. Orbit Determination of Satellite Formations; Delft University of Technology: Delft, The Netherlands, 2012. [Google Scholar] [CrossRef]
- D’Amico, S.; Ardaens, J.-S.; De Florio, S. Autonomous formation flying based on GPS—PRISMA flight results. Acta Astronaut. 2013, 82, 69–79. [Google Scholar] [CrossRef]
- Chen, P.; Shu, L.; Ding, R.; Han, C. Kinematic single-frequency relative positioning for LEO formation flying mission. GPS Solut. 2014, 19, 525–535. [Google Scholar] [CrossRef]
- Ju, B.; Gu, D.; Herring, T.A.; Allende-Alba, G.; Montenbruck, O.; Wang, Z. Precise orbit and baseline determination for maneuvering low earth orbiters. GPS Solut. 2015, 21, 53–64. [Google Scholar] [CrossRef] [Green Version]
- Guo, H.; Guo, J.; Yang, Z.; Wang, G.; Qi, L.; Lin, M.; Peng, H.; Ji, B. On Satellite-Borne GPS Data Quality and Reduced-Dynamic Precise Orbit Determination of HY-2C: A Case of Orbit Validation with Onboard DORIS Data. Remote Sens. 2021, 13, 4329. [Google Scholar] [CrossRef]
- Blewitt, G. Carrier phase ambiguity resolution for the Global Positioning System applied to geodetic baselines up to 2000 km. J. Geophys. Res. Earth Surf. 1989, 94, 10187–10203. [Google Scholar] [CrossRef] [Green Version]
- Maosheng, Z.; Liu, X.; Guo, J.; Qinghua, Z.; Zhimin, L.; Ji, B.; Yongzhong, O. Epoch-by-epoch phase difference method to evaluate GNSS single-frequency phase data quality. Rev. Int. Métodos Numér. Cálc. Diseño Ing. 2020, 36, 42. [Google Scholar] [CrossRef]
- Qi, L.; Guo, J.; Xia, Y.; Yang, Z. Effect of Higher-Order Ionospheric Delay on Precise Orbit Determination of GRACE-FO Based on Satellite-Borne GPS Technique. IEEE Access 2021, 9, 29841–29849. [Google Scholar] [CrossRef]
- Shi, J.; Huang, Y.; Ouyang, C. A GPS relative positioning quality control algorithm considering both code and phase observation errors. J. Geodesy 2019, 93, 1419–1433. [Google Scholar] [CrossRef]
- Montenbruck, O.; Kroes, R. In-flight performance analysis of the CHAMP BlackJack GPS Receiver. GPS Solut. 2003, 7, 74–86. [Google Scholar] [CrossRef]
- Montenbruck, O.; Gill, E. Ionospheric Correction for GPS Tracking of LEO Satellites. J. Navig. 2002, 55, 293–304. [Google Scholar] [CrossRef] [Green Version]
- Banville, S.; Langley, R.B. Mitigating the impact of ionospheric cycle slips in GNSS observations. J. Geod. 2012, 87, 179–193. [Google Scholar] [CrossRef]
- Hwang, C.; Tseng, T.-P.; Lin, T.-J.; Švehla, D.; Hugentobler, U.; Chao, B.F. Quality assessment of FORMOSAT-3/COSMIC and GRACE GPS observables: Analysis of multipath, ionospheric delay and phase residual in orbit determination. GPS Solut. 2009, 14, 121–131. [Google Scholar] [CrossRef]
- Kim, J.; Lee, Y.J. Using ionospheric corrections from the space-based augmentation systems for low earth orbiting satellites. GPS Solut. 2014, 19, 423–431. [Google Scholar] [CrossRef]
- Gu, D.; Ju, B.; Liu, J.; Tu, J. Enhanced GPS-based GRACE baseline determination by using a new strategy for ambiguity resolution and relative phase center variation corrections. Acta Astronaut. 2017, 138, 176–184. [Google Scholar] [CrossRef]
- Van Barneveld, P.; Montenbruck, O.; Visser, P. Epochwise prediction of GPS single differenced ionospheric delays of formation flying spacecraft. Adv. Space Res. 2009, 44, 987–1001. [Google Scholar] [CrossRef]
- Grace, S.R. Follow-On Laser Ranging Interferometer Phase Jump Removal; NASA Jet Propulsion Laboratory/California Institute of Technology: Pasadena, DC, USA, 2018. [Google Scholar]
- Blewitt, G. An Automatic Editing Algorithm for GPS data. Geophys. Res. Lett. 1990, 17, 199–202. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z. A new automated cycle slip detection and repair method for a single dual-frequency GPS receiver. J. Geodesy 2010, 85, 171–183. [Google Scholar] [CrossRef]
- Landerer, F.W.; Flechtner, F.M.; Save, H.; Webb, F.H.; Bandikova, T.; Bertiger, W.I.; Bettadpur, S.V.; Byun, S.H.; Dahle, C.; Dobslaw, H.; et al. Extending the Global Mass Change Data Record: GRACE Follow-On Instrument and Science Data Performance. Geophys. Res. Lett. 2020, 47. [Google Scholar] [CrossRef]
- Kang, Z.; Tapley, B.; Bettadpur, S.; Ries, J.; Nagel, P.; Pastor, R. Precise orbit determination for the GRACE mission using only GPS data. J. Geodesy 2006, 80, 322–331. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).