Inversion of Groundwater Storage Variations Considering Lag Effect in Beijing Plain, from RadarSat-2 with SBAS-InSAR Technology
Abstract
1. Introduction
2. Study Area and Datasets
2.1. Study Area
2.2. Datasets
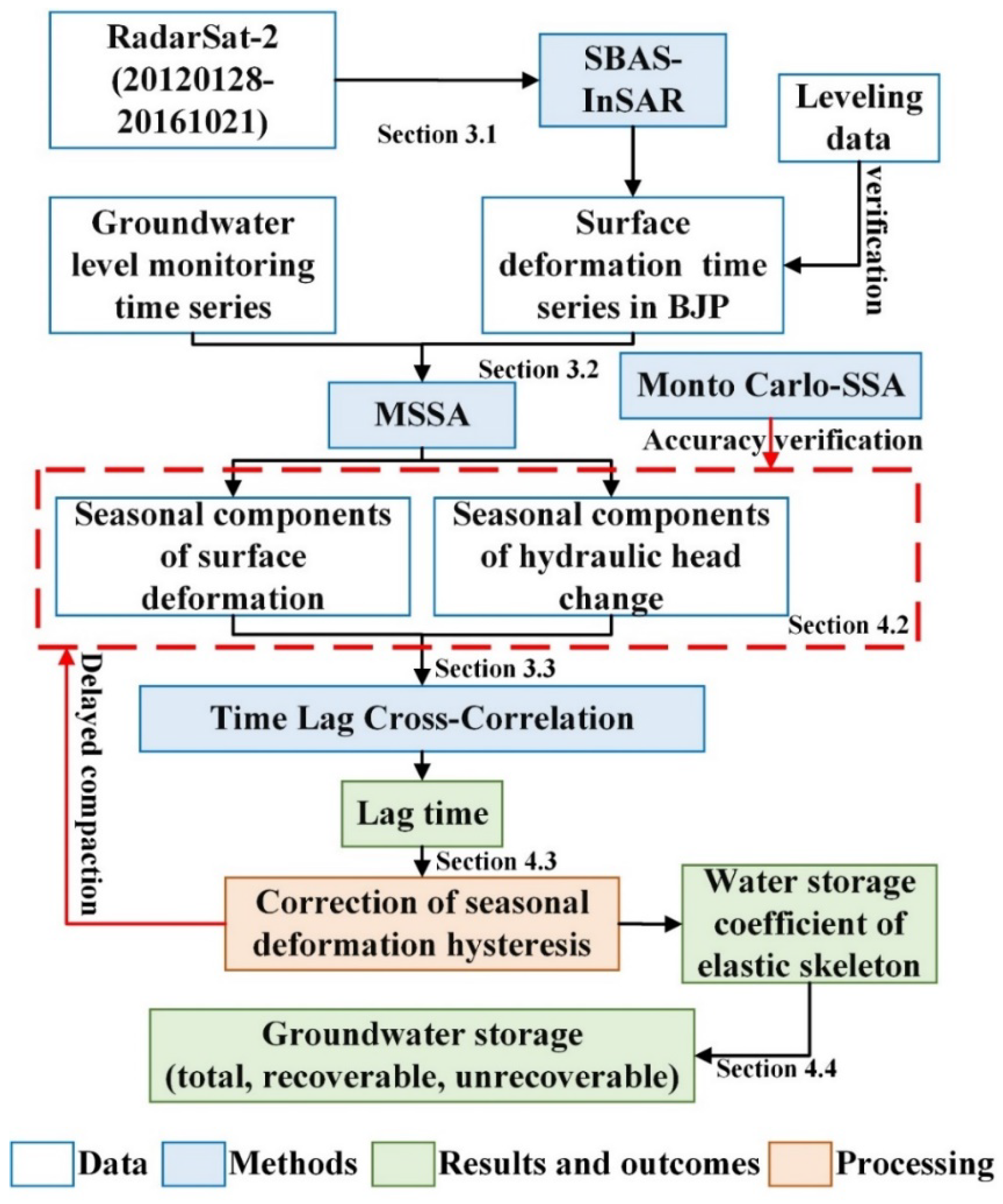
3. Methods
3.1. SBAS-InSAR Processing
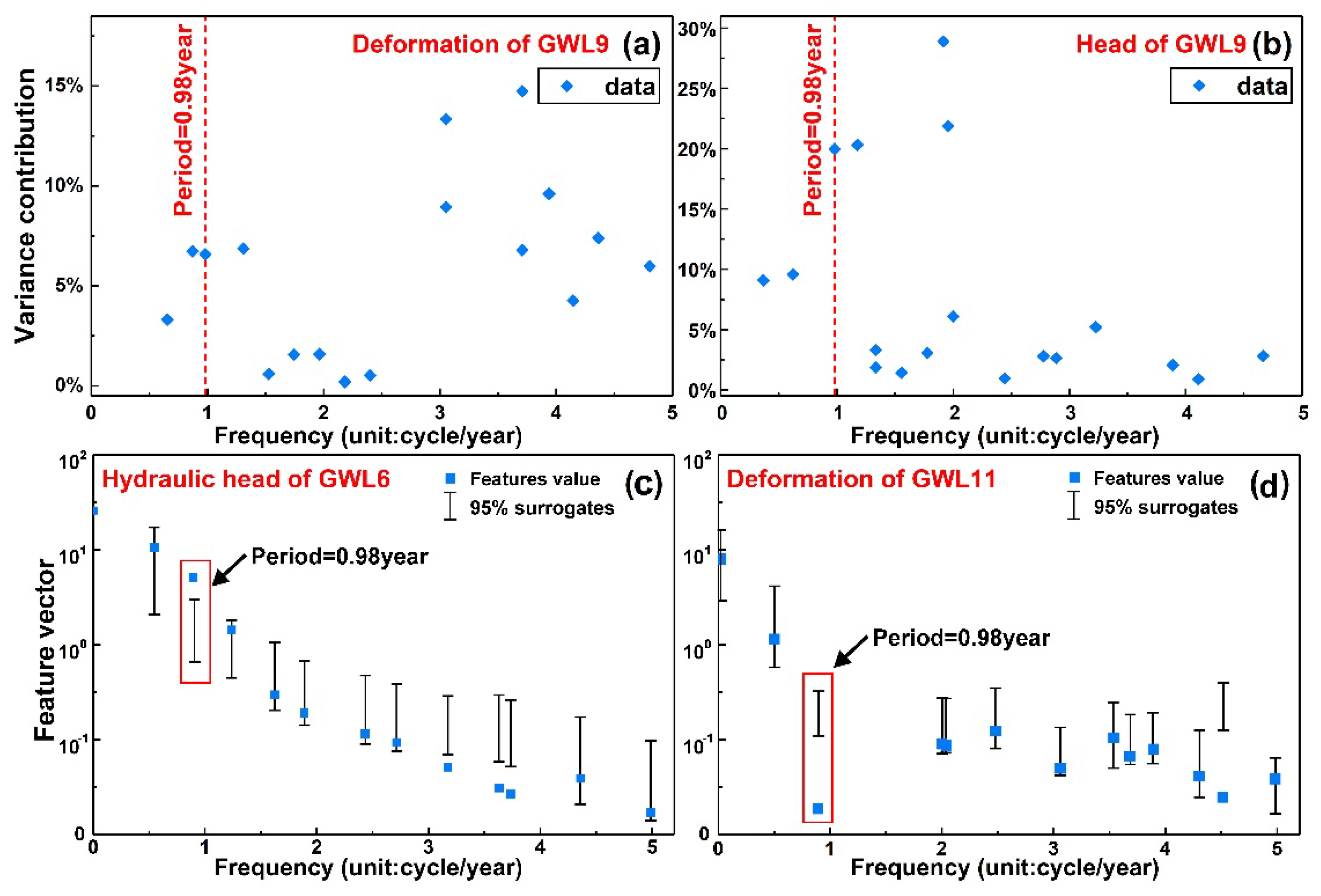
3.2. MSSA and MC-SSA
3.3. TLCC Analysis
3.4. Estimation of Aquifer Storage Properties and GWS Loss
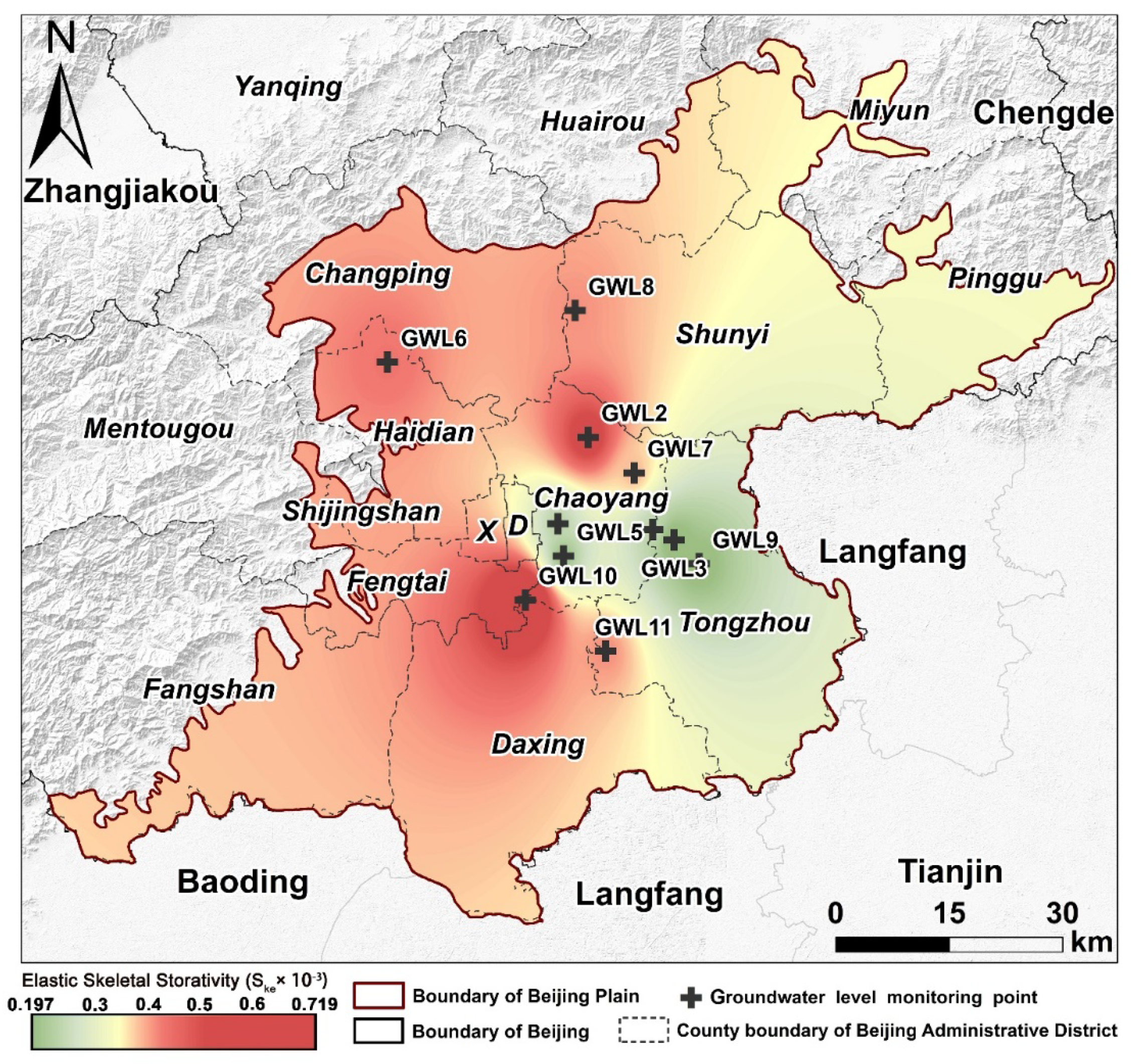
3.4.1. Estimation of Aquifer Skeletal Storativity Coefficient
3.4.2. Quantization of GWS Depletion
4. Results
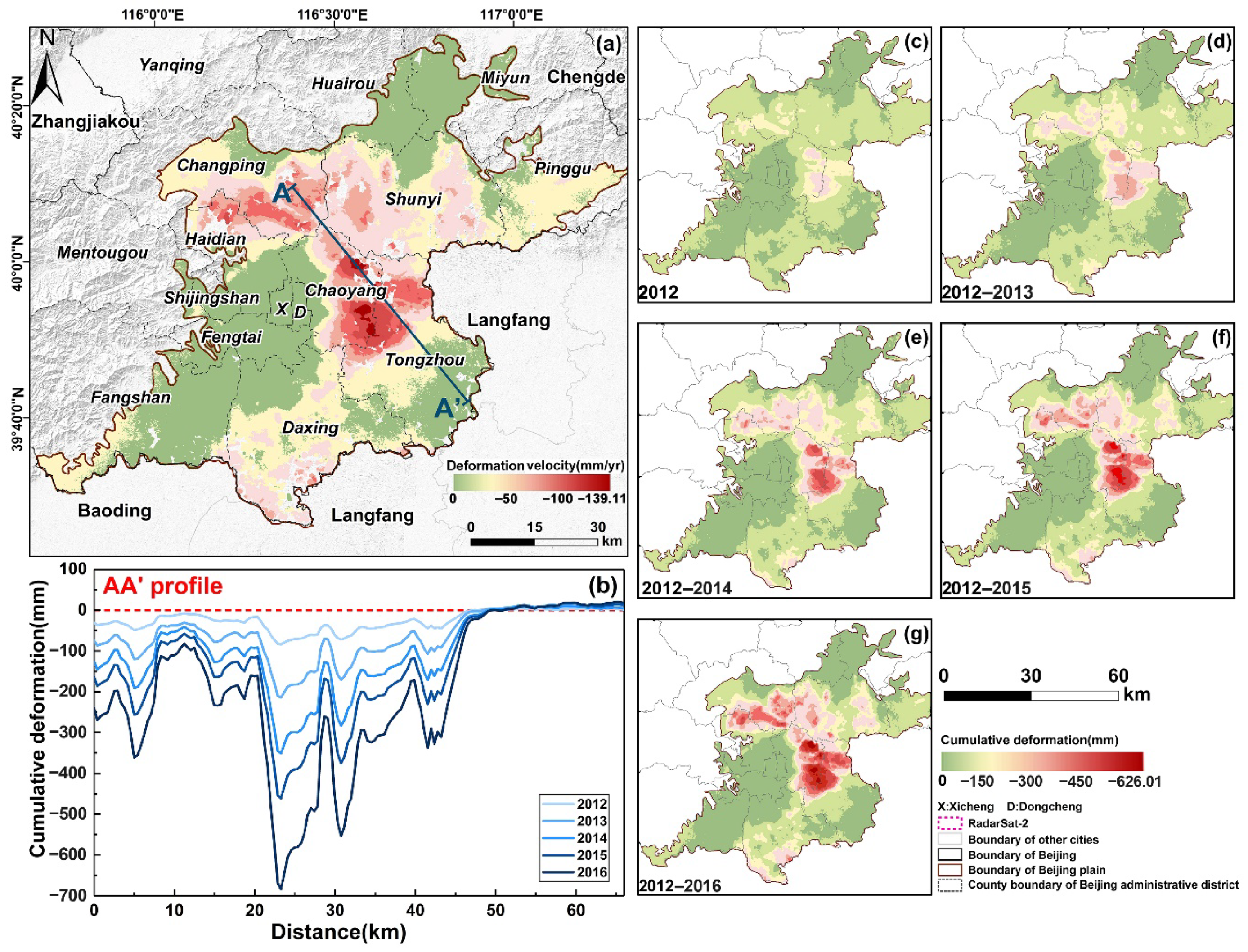
4.1. Evolution Analysis of Deformation Characteristics
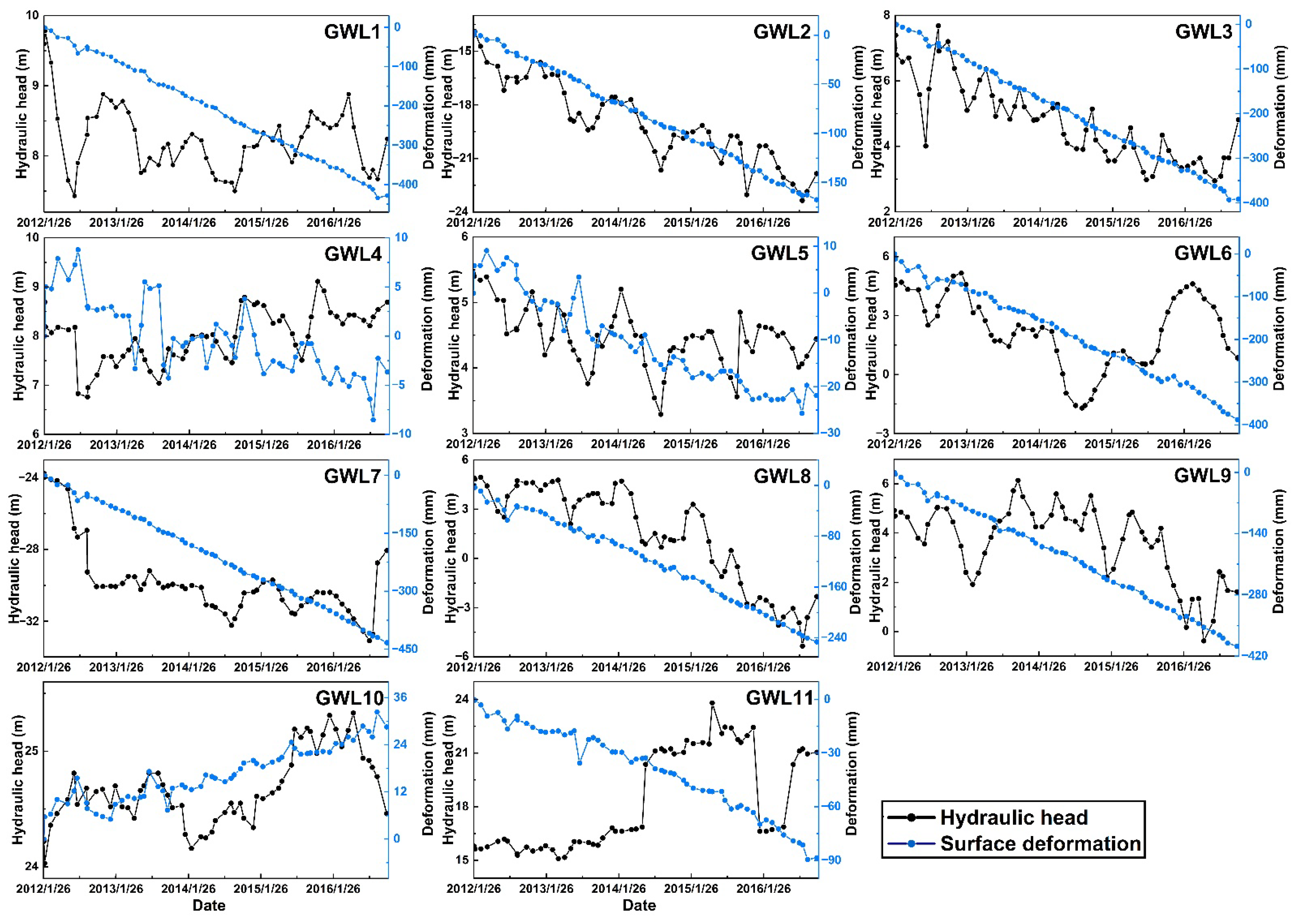
4.2. Separation of Seasonal Surface Deformation and Hydraulic Head Variation Components
4.3. Hysteresis Correction and Estimation of Elastic Skeletal Storativity Coefficient
4.4. Quantization of GWS Depletion
5. Discussion
5.1. Temporal Relationship between Deformation and UGWS Loss
5.2. Spatial Relationship between Deformation and UGWS Loss
5.3. Uncertainty Analysis and Future Work
- As is shown in the study, if the aquifer system has significant horizontal deformation, without considering the horizontal deformation and its contribution to skeleton storage, the estimated elastic skeletal storativity coefficient may well show a deviation which is less than the theoretical value.
- The uncertainty error is connected with the precision of deformation velocity obtained by the SBAS-InSAR technique. This is mainly caused by the atmospheric latency phase, decoloration and registration errors, according to previous research.
- There may be errors caused by human factors with respect to the monitored groundwater level and the real groundwater level.
- As the time series of surface deformation needs to be matched against the head change, the linear interpolation method of supplementing the vacancy value will also produce some errors.
- For coherent points, which are characteristic of significant surface deformation, the long-term trend and the random noise using MSSA may not be able to be completely eliminated from the time series of surface deformation and head change. Although a 95% confidence interval was constructed for verification by means of MC-SSA, there may still be uncertain noise in the seasonal component obtained by separation. Although we have adjusted the lag of the seasonal surface deformation, it is a fact that more frequent InSAR and hydraulic head data sampling (daily or weekly) time series over longer periods are required to obtain more accurate lag times. Other errors may be caused by the fact that the lag time of surface deformation and head change cannot be completely accurately corrected.
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Number | SAR Sensor | Image Acquisition Date | Track | Orbit | Orbit Direction |
|---|---|---|---|---|---|
| 1 | Radarsat-2 | 20120128 | 62-26D | 21528 | Descending |
| 2 | Radarsat-2 | 20120221 | 63-26D | 21871 | Descending |
| 3 | Radarsat-2 | 20120409 | 65-26D | 22557 | Descending |
| 4 | Radarsat-2 | 20120527 | 67-26D | 23243 | Descending |
| 5 | Radarsat-2 | 20120831 | 71-26D | 24615 | Descending |
| 6 | Radarsat-2 | 20121018 | 73-26D | 25301 | Descending |
| 7 | Radarsat-2 | 20121111 | 74-26D | 25644 | Descending |
| 8 | Radarsat-2 | 20121229 | 76-26D | 26330 | Descending |
| 9 | Radarsat-2 | 20130122 | 77-26D | 26673 | Descending |
| 10 | Radarsat-2 | 20130428 | 81-26D | 28045 | Descending |
| 11 | Radarsat-2 | 20130522 | 82-26D | 28388 | Descending |
| 12 | Radarsat-2 | 20130615 | 83-26D | 28731 | Descending |
| 13 | Radarsat-2 | 20130802 | 85-26D | 29417 | Descending |
| 14 | Radarsat-2 | 20130826 | 86-26D | 29760 | Descending |
| 15 | Radarsat-2 | 20130919 | 87-26D | 30103 | Descending |
| 16 | Radarsat-2 | 20131013 | 88-26D | 30446 | Descending |
| 17 | Radarsat-2 | 20131106 | 89-26D | 30789 | Descending |
| 18 | Radarsat-2 | 20131130 | 90-26D | 31132 | Descending |
| 19 | Radarsat-2 | 20131224 | 91-26D | 31475 | Descending |
| 20 | Radarsat-2 | 20140210 | 93-26D | 32161 | Descending |
| 21 | Radarsat-2 | 20140306 | 94-26D | 32504 | Descending |
| 22 | Radarsat-2 | 20140330 | 95-26D | 32847 | Descending |
| 23 | Radarsat-2 | 20140423 | 96-26D | 33190 | Descending |
| 24 | Radarsat-2 | 20140610 | 98-26D | 33876 | Descending |
| 25 | Radarsat-2 | 20140728 | 100-26D | 34562 | Descending |
| 26 | Radarsat-2 | 20140914 | 102-26D | 35248 | Descending |
| 27 | Radarsat-2 | 20141101 | 104-26D | 35934 | Descending |
| 28 | Radarsat-2 | 20141125 | 105-26D | 36277 | Descending |
| 29 | Radarsat-2 | 20141219 | 106-26D | 36620 | Descending |
| 30 | Radarsat-2 | 20150205 | 108-26D | 37306 | Descending |
| 31 | Radarsat-2 | 20150325 | 110-26D | 37992 | Descending |
| 32 | Radarsat-2 | 20150512 | 112-26D | 38678 | Descending |
| 33 | Radarsat-2 | 20150629 | 114-26D | 39364 | Descending |
| 34 | Radarsat-2 | 20150816 | 116-26D | 40050 | Descending |
| 35 | Radarsat-2 | 20150909 | 117-26D | 40393 | Descending |
| 36 | Radarsat-2 | 20151003 | 118-26D | 40736 | Descending |
| 37 | Radarsat-2 | 20151027 | 119-26D | 41079 | Descending |
| 38 | Radarsat-2 | 20151120 | 120-26D | 41422 | Descending |
| 39 | Radarsat-2 | 20160107 | 122-26D | 42108 | Descending |
| 40 | Radarsat-2 | 20160131 | 123-26D | 42451 | Descending |
| 41 | Radarsat-2 | 20160506 | 127-26D | 43823 | Descending |
| 42 | Radarsat-2 | 20160530 | 128-26D | 44166 | Descending |
| 43 | Radarsat-2 | 20160623 | 129-26D | 44509 | Descending |
| 44 | Radarsat-2 | 20160810 | 131-26D | 45195 | Descending |
| 45 | Radarsat-2 | 20160903 | 132-26D | 45538 | Descending |
| 46 | Radarsat-2 | 20161021 | 134-26D | 46224 | Descending |
Appendix A.1. This Part Includes the Processing Flow of SBAS-InSAR Technology and the Selection Method of Stable Slow Filter Phase (SFP) Pixels

- The selection method of stable slow filter phase (SFP) pixels:
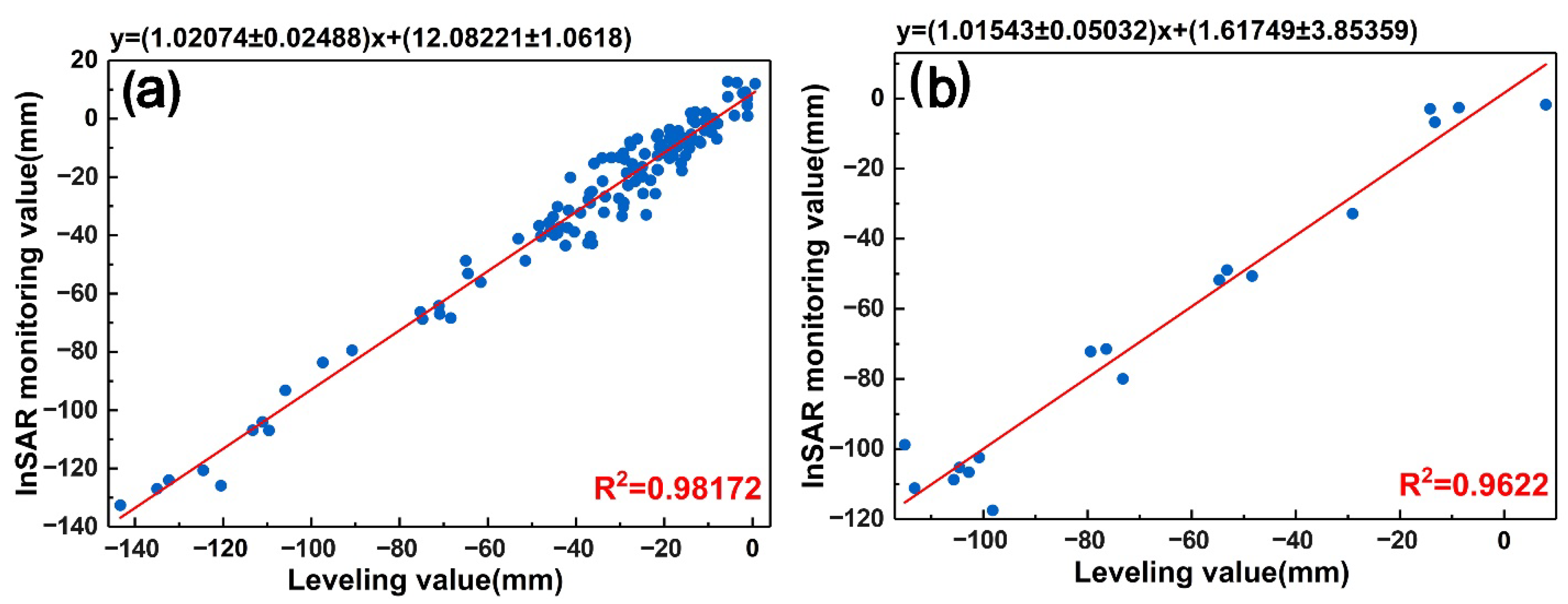
Appendix A.2. Linear Regression Fitting for Leveling Data and InSAR Deformation Verification
- Linear regression is a statistical analysis method that uses regression analysis in mathematical statistics to determine the interdependent quantitative relationship between two or more variables. The linear regression model is expressed in the following form:where is the error term, and the total sum of squares (SST) is expressed as follows:
| Year | 2012 | 2013 | 2014 | 2015 | 2016 |
|---|---|---|---|---|---|
| Annual deformation rate (mm/yr) | 0~−127.74 | 0~−144.44 | 0~−166.98 | 0~−127.72 | 0~−177.06 |
| The maximum cumulative settlement year by year (mm) | −127.74 | −270.82 | −403.12 | −511.81 | −626.01 |
| Area with annual deformation velocity greater than 60 mm/yr (km2) | 220.48 | 273.75 | 300.33 | 246.92 | 349.22 |
References
- Hoffman, J.; Galloway, D.L.; Zebker, H.A. Inverse modeling of interbed storage parameters using land subsidence observations, Antelope Valley, California. Water. Resour. Res. 2003, 39, 1031. [Google Scholar] [CrossRef]
- Abidin, H.Z.; Andreas, H.; Gumilar, I.; Fukuda, Y.; Deguchi, T. Land subsidence of Jakarta (Indonesia) and its relation with urban development. Nat. Hazards 2011, 59, 1753–1771. [Google Scholar] [CrossRef]
- Tomás, R.; Herrera, G.; Delgado, J.; Lopez-Sanchez, J.M.; Mallorquí, J.J.; Mulas, J. A ground subsidence study based on DInSAR data: Calibration of soil parameters and subsidence prediction in Murcia City (Spain). Eng. Geol. 2010, 111, 19–30. [Google Scholar] [CrossRef]
- Zhao, Q.; Lin, H.; Gao, W.; Zebker, H.; Albert, C.; Yeung, K. InSAR detection of residual settlement of an ocean reclamation engineering project: A case study of Hong Kong International Airport. J. Oceanogr. 2011, 67, 415–426. [Google Scholar] [CrossRef]
- Figueroa-Miranda, S.; Tuxpan-Vargas, J.; Ramos-Leal, J.A.; Hernández-Madrigal, V.M.; Villaseñor-Reyes, C.I. Land subsidence by groundwater over-exploitation from aquifers in tectonic valleys of Central Mexico: A review. Eng. Geol. 2018, 246, 91–106. [Google Scholar] [CrossRef]
- Galloway, D.L.; Burbey, T.J. Review: Regional land subsidence accompanying groundwater extraction. Hydrogeol. J. 2011, 19, 1459–1486. [Google Scholar] [CrossRef]
- Gambolati, G.; Teatini, P. Geomechanics of subsurface water withdrawal and injection. Water. Resour. Res. 2015, 51, 3922–3955. [Google Scholar] [CrossRef]
- Gu, K.; Shi, B.; Liu, C.; Jiang, H.; Li, T.; Jinghong, W. Investigation of land subsidence with the combination of distributed fiber optic sensing techniques and microstructure analysis of soils. Eng. Geol. 2018, 240, 34–47. [Google Scholar] [CrossRef]
- Hayashi, T.; Tokunaga, T.; Aichi, M.; Shimada, M.; Taniguchi, M. Effects of human activities and urbanization on groundwater environments: An example from the aquifer system of Tokyo and the surrounding area. Sci. Total Environ. 2009, 407, 3165–3172. [Google Scholar] [CrossRef]
- Mahmoudpour, M.; Khamehchiyan, M.; Nikudel, M.R.; Ghassemi, M.R. Numerical simulation and prediction of regional land subsidence caused by groundwater exploitation in the southwest plain of Tehran, Iran. Eng. Geol. 2016, 201, 6–28. [Google Scholar] [CrossRef]
- Rezaei, A.; Mousavi, Z. Characterization of land deformation, hydraulic head, and aquifer properties of the Gorgan confined aquifer, Iran, from InSAR observations. J. Hydrol. 2019, 579, 124196. [Google Scholar] [CrossRef]
- Simeoni, U.; Tessari, U.; Corbau, C.; Tosatto, C.; Polo, P.; Teatini, P. Impact of land subsidence due to residual gas production on surficial infrastructures: The Dosso degli Angeli field study (Ravenna, Northern Italy). Eng. Geol. 2017, 229, 1–12. [Google Scholar] [CrossRef]
- Thoang, T.T.; Giao, P.H. Subsurface characterization and prediction of land subsidence for HCM City, Vietnam. Eng. Geol. 2015, 199, 107–124. [Google Scholar] [CrossRef]
- Uchida, Y. Recent trends of land subsidence and groundwater management in Chikugo-Saga Plain. J. Groundw. Hydrol. 2015, 57, 19–27. [Google Scholar] [CrossRef]
- Döll, P.; Hoffmann-Dobrev, H.; Portmann, F.T.; Siebert, S.; Eicker, A.; Rodell, M.; Strassberg, G.; Scanlon, B.R. Impact of water withdrawals from groundwater and surface water on continental water storage variations. J. Geodyn. 2012, 59–60, 143–156. [Google Scholar] [CrossRef]
- Famiglietti, J.S. The global groundwater crisis. Nat. Clim. Chang. 2014, 4, 945–948. [Google Scholar] [CrossRef]
- Chaussard, E.; Bürgmann, R.; Shirzaei, M.; Fielding, E.J.; Baker, B. Predictability of hydraulic head changes and characterization of aquifer-system and fault properties from InSAR-derived ground deformation. J. Geophys. Res. Solid Earth 2014, 119, 6572–6590. [Google Scholar] [CrossRef]
- Chen, B.; Gong, H.; Li, X.; Lei, K.; Zhang, Y. Spatial-temporal characteristics of land subsidence corresponding to dynamic groundwater funnel in Beijing Municipality, China. Chin. Geogr. Sci. 2011, 21, 753–764. [Google Scholar] [CrossRef]
- Chen, B.; Gong, H.; Lei, K.; Li, J.; Zhou, C.; Gao, M.; Guan, H.; Lv, W. Land subsidence lagging quantification in the main exploration aquifer layers in Beijing plain, China. Int. J. Appl. Earth Obs. Geoinf. 2019, 75, 54–67. [Google Scholar] [CrossRef]
- Gao, M.; Gong, H.; Chen, B.; Zhou, C.; Shi, M. Mapping and characterization of land subsidence in Beijing Plain caused by groundwater pumping using the Small Baseline Subset (SBAS) InSAR technique. Proc. Int. Assoc. Hydrol. Sci. 2015, 372, 347–349. [Google Scholar] [CrossRef]
- Gong, H.; Pan, Y.; Zheng, L.; Li, X.; Zhou, C. Long-term groundwater storage changes and land subsidence development in the North China Plain (1971–2015). Hydrogeol. J. 2018, 26, 1417–1427. [Google Scholar] [CrossRef]
- Zhang, Y.; Gong, H.; Gu, Z.; Rong, W.; Zhao, W. Characterization of land subsidence induced by groundwater withdrawals in the plain of Beijing City, China. Hydrogeol. J. 2014, 22, 397–409. [Google Scholar] [CrossRef]
- Zhu, L.; Gong, H.; Li, X.; Rong, W.; Chen, B.; Dai, Z.; Teatini, P. Land subsidence due to groundwater withdrawal in the northern Beijing plain, China. Eng. Geol. 2015, 193, 243–255. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhu, Y.; Lin, Z.; Lin, Z.; Wang, J.; He, G.; Li, H.; Li, L.; Wang, H.; Jiang, S.; et al. Energy Reduction Effect of the South-to-North Water Diversion Project in China. Sci. Rep. 2017, 7, 15956. [Google Scholar] [CrossRef] [PubMed]
- Siles, G.; Trudel, M.; Peters, D.L. Hydrological monitoring of high-latitude shallow water bodies from high-resolution space-borne D-InSAR. Remote Sens. Environ. 2020, 236, 111444. [Google Scholar] [CrossRef]
- Lang, M.W.; Kasischke, E.S. Using C-band synthetic aperture radar data to monitor forested wetland hydrology in Maryland’s coastal plain, USA. IEEE Trans. Geosci. Remote Sens. 2008, 46, 535–546. [Google Scholar] [CrossRef]
- Jefriza, Y.I.M.; Abir, I.A. The applications of InSAR technique for natural hazard detection in smart society. J. Phys. Conf. Ser. 2020, 1572, 12067. [Google Scholar] [CrossRef]
- Orhan, O. Monitoring of land subsidence due to excessive groundwater extraction using small baseline subset technique in Konya, Turkey. Environ. Monit. Assess. 2021, 193, 174. [Google Scholar] [CrossRef]
- Rezaei, A.; Zhan, H.; Zare, M. Impact of thin aquitards on two-dimensional solute transport in an aquifer. J. Contam. Hydrol. 2013, 152, 117–136. [Google Scholar] [CrossRef]
- Rezaei, A.; Zare, M.; Zhan, H. Aquitard Horizontal Dispersion on Reactive Solute Transport in an Aquifer–Aquitard System. Transp. Porous Media 2016, 113, 695–716. [Google Scholar] [CrossRef]
- Bell, J.W.; Amelung, F.; Ferretti, A.; Bianchi, M.; Novali, F. Permanent scatterer InSAR reveals seasonal and long-term aquifer-system response to groundwater pumping and artificial recharge. Water. Resour. Res. 2008, 44, 94–111. [Google Scholar] [CrossRef]
- Bonì, R.; Cigna, F.; Bricker, S.; Meisina, C.; McCormack, H. Characterisation of hydraulic head changes and aquifer properties in the London Basin using Persistent Scatterer Interferometry ground motion data. J. Hydrol. 2016, 540, 835–849. [Google Scholar] [CrossRef]
- Chen, J.; Knight, R.; Zebker, H.A.; Schreüder, W.A. Confined aquifer head measurements and storage properties in the San Luis Valley, Colorado, from spaceborne InSAR observations. Water Resour. Res. 2016, 52, 3623–3636. [Google Scholar] [CrossRef]
- Hoffmann, J.; Zebker, H.A.; Galloway, D.L.; Amelung, F. Seasonal subsidence and rebound in Las Vegas Valley, Nevada, observed by Synthetic Aperture Radar Interferometry. Water. Resour. Res. 2001, 37, 1551–1566. [Google Scholar] [CrossRef]
- Miller, M.M.; Shirzaei, M. Spatiotemporal characterization of land subsidence and uplift in Phoenix using InSAR time series and wavelet transforms. J. Geophys. Res. Solid Earth 2015, 120, 5822–5842. [Google Scholar] [CrossRef]
- Reeves, J.A.; Knight, R.; Zebker, H.A. An Analysis of the Uncertainty in InSAR Deformation Measurements for Groundwater Applications in Agricultural Areas. IEEE. J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2992–3001. [Google Scholar] [CrossRef]
- Reeves, J.A.; Knight, R.; Zebker, H.A.; Kitanidis, P.K.; Schreüder, W.A. Estimating temporal changes in hydraulic head using InSAR data in the San Luis Valley, Colorado. Water. Resour. Res. 2014, 50, 4459–4473. [Google Scholar] [CrossRef]
- Béjar-Pizarro, M.; Ezquerro, P.; Herrera, G.; Tomás, R.; Guardiola-Albert, C.; Ruiz Hernández, J.M.; Fernández Merodo, J.A.; Marchamalo, M.; Martínez, R. Mapping groundwater level and aquifer storage variations from InSAR measurements in the Madrid aquifer, Central Spain. J. Hydrol. 2017, 547, 678–689. [Google Scholar] [CrossRef]
- Chaussard, E.; Milillo, P.; Bürgmann, R.; Perissin, D.; Fielding, E.J.; Baker, B. Remote Sensing of Ground Deformation for Monitoring Groundwater Management Practices: Application to the Santa Clara Valley During the 2012–2015 California Drought. J. Geophys. Res. Solid Earth 2017, 122, 8566–8582. [Google Scholar] [CrossRef]
- Miller, M.M.; Shirzaei, M.; Argus, D. Aquifer Mechanical Properties and Decelerated Compaction in Tucson, Arizona. J. Geophys. Res. Solid Earth 2017, 122, 8402–8416. [Google Scholar] [CrossRef]
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms. IEEE. Trans. Geosci. Remote Sens. 2002, 40, 2375–2383. [Google Scholar] [CrossRef]
- Hooper, A.; Zebker, H.; Segall, P.; Kampes, B. A new method for measuring deformation on volcanoes and other natural terrains using InSAR persistent scatterers. Geophys. Res. Lett. 2004, 31, L23611. [Google Scholar] [CrossRef]
- Hooper, A.; Segall, P.; Zebker, H. Persistent scatterer interferometric synthetic aperture radar for crustal deformation analysis, with application to Volcán Alcedo, Galápagos. J. Geophys. Res. Solid Earth 2007, 112, B07407. [Google Scholar] [CrossRef]
- Qu, F.; Zhang, Q.; Lu, Z.; Zhao, C.; Yang, C. Land subsidence and ground fissures in Xi’an, China 2005–2012 revealed by multi-band InSAR time-series analysis. Remote Sens. Environ. 2014, 155, 366–376. [Google Scholar] [CrossRef]
- Neely, W.R.; Borsa, A.A.; Burney, J.A.; Levy, M.C.; Silverii, F.; Sneed, M. Characterization of Groundwater Recharge and Flow in California’s San Joaquin Valley from InSAR-Observed Surface Deformation. Water. Resour. Res. 2021, 57, e2020WR028451. [Google Scholar] [CrossRef] [PubMed]
- Hu, X.; Lu, Z.; Wang, T. Characterization of Hydrogeological Properties in Salt Lake Valley, Utah, using InSAR. J. Geophys. Res. Earth Surf. 2018, 123, 1257–1271. [Google Scholar] [CrossRef]
- Chaussard, E.; Farr, T.G. A New Method for Isolating Elastic from Inelastic Deformation in Aquifer Systems: Application to the San Joaquin Valley, CA. Geophys. Res. Lett. 2019, 46, 10800–10809. [Google Scholar] [CrossRef]
- Jiang, L.; Bai, L.; Zhao, Y.; Cao, G.; Wang, H.; Sun, Q. Combining InSAR and Hydraulic Head Measurements to Estimate Aquifer Parameters and Storage Variations of Confined Aquifer System in Cangzhou, North China Plain. Water. Resour. Res. 2018, 54, 8234–8252. [Google Scholar] [CrossRef]
- Ireland, R.L.; Poland, J.F.; Riley, F.S. Land Subsidence in the San Joaquin Valley, California, As of 1980; US Geological Survey: Reston, VA, USA, 1984. [Google Scholar] [CrossRef]
- Ng, A.H.; Ge, L.; Li, X.; Zhang, K. Monitoring ground deformation in Beijing, China with persistent scatterer SAR interferometry. J. Geod. 2012, 86, 375–392. [Google Scholar] [CrossRef]
- Hu, B.; Wang, H.S.; Sun, Y.L.; Hou, J.G.; Liang, J. Long-Term Land Subsidence Monitoring of Beijing (China) Using the Small Baseline Subset (SBAS) Technique. Remote Sens. 2014, 6, 3648–3661. [Google Scholar] [CrossRef]
- Gao, M.; Gong, H.; Chen, B.; Zhou, C.; Chen, W.; Liang, Y.; Shi, M.; Si, Y. InSAR time-series investigation of long-term ground displacement at Beijing Capital International Airport, China. Tectonophysics 2016, 691, 271–281. [Google Scholar] [CrossRef]
- Beijing Bureau of Geology and Mineral Exploration and Development. Groundwater in Beijing; Land Press of China: Beijing, China, 2008. [Google Scholar]
- Zhu, L.; Franceschini, A.; Gong, H.; Ke, Y.; Pan, Y. The 3-D Facies and Geomechanical Modeling of Land Subsidence in the Chaobai Plain, Beijing. Water. Resour. Res. 2020, 56, e2019WR027026. [Google Scholar] [CrossRef]
- Zhu, L.; Dai, Z.; Gong, H.; Gable, G.; Teatini, P. Statistic inversion of multi-zone transition probability models for aquifer characterization in alluvial fans. Stoch. Environ. Res. Risk Assess. 2016, 30, 1005–1016. [Google Scholar] [CrossRef][Green Version]
- He, G.P.; Zhou, D.; Yang, Z.S.; Zhao, H.Y.; Li, C.J. Current status and evaluation of groundwater resources exploitation in the plain area of Beijing. Hydrogeol. Eng. Geol. 2005, 2, 45–48. (In Chinese) [Google Scholar]
- Tian, F.; Luo, Y.; Zhou, Y.; Yu, L.; Kou, W.J.; Jiang, Y.; Wang, R. Contrastive analysis of spatial-temporal evolution between land subsidence and groundwater exploitation in Beijing. South-to-North Water Transf. Water Sci. Technol. 2017, 15, 163–169. (In Chinese) [Google Scholar]
- Massonnet, D.; Feigl, K.L. Radar interferometry and its application to changes in the Earth’s surface. Rev. Geophys. 1998, 36, 441–500. [Google Scholar] [CrossRef]
- Kampes, B.M. Radar Interferometry: Persistent Scatterer Technique; Springer: Dordrecht, The Netherlands, 2006. [Google Scholar] [CrossRef]
- Gabriel, A.K.; Goldstein, R.M.; Zebker, H.A. Mapping small elevation changes over large areas: Differential radar interferometry. J. Geophys. Res. Solid Earth 1989, 94, 9183–9191. [Google Scholar] [CrossRef]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent scatterers in SAR interferometry. IEEE. Trans. Geosci. Remote Sens. 2001, 39, 8–20. [Google Scholar] [CrossRef]
- Ferretti, A.; Prati, C.; Rocca, F. Nonlinear subsidence rate estimation using permanent scatterers in differential SAR interferometry. IEEE. Trans. Geosci. Remote Sens. 2000, 38, 2202–2212. [Google Scholar] [CrossRef]
- Hooper, A. A multi-temporal InSAR method incorporating both persistent scatterer and small baseline approaches. Geophys. Res. Lett. 2008, 35, L16302. [Google Scholar] [CrossRef]
- Plaut, G.; Vautard, R. Spells of Low-Frequency Oscillations and Weather Regimes in the Northern Hemisphere. J. Atmos. Sci. 1994, 51, 210–236. [Google Scholar] [CrossRef]
- Groth, A.; Ghil, M. Multivariate singular spectrum analysis and the road to phase synchronization. Phys. Rev. E Stat. Nonlinear Biol. Soft Matter Phys. 2011, 84, 036206. [Google Scholar] [CrossRef]
- Ghil, M.; Allen, M.R.; Dettinger, M.D.; Ide, K.; Kondrashov, D.; Mann, M.E.; Robertson, A.W.; Saunders, A.; Tian, Y.; Varadi, F.; et al. Advanced spectral methods for climatic time series. Rev. Geophys. 2002, 40, 1003–1043. [Google Scholar] [CrossRef]
- Allen, M.R.; Robertson, A.W. Distinguishing modulated oscillations from coloured noise in multivariate datasets. Clim. Dyn. 1996, 12, 775–784. [Google Scholar] [CrossRef]
- Chen, Q.; van Dam, T.; Sneeuw, N.; Collilieux, X.; Weigelt, M.; Rebischung, P. Singular spectrum analysis for modeling seasonal signals from GPS time series. J. Geodyn. 2013, 72, 25–35. [Google Scholar] [CrossRef]
- Papoulis, A. The Fourier Integral and Its Applications, Reissued.; McGraw-Hill: New York, NY, USA, 1987. [Google Scholar]
- Bracewell, R.N. The Fourier Transform and Its Applications, 3rd ed.; WCB/McGraw Hill: Boston, MA, USA, 2000. [Google Scholar]
- Wiest, R.J.M. On the storage coefficient and the equations of groundwater flow. J. Geophys. Res. Solid Earth 1966, 71, 1117–1122. [Google Scholar] [CrossRef]
- Saar, M.O.; Manga, M. Seismicity induced by seasonal groundwater recharge at Mt. Hood, Oregon. Earth Planet. Sci. Lett. 2003, 214, 605–618. [Google Scholar] [CrossRef]
- Rhoads, G.H.; Robinson, E.S. Determination of aquifer parameters from well tides. J. Geophys. Res. Solid Earth 1979, 84, 6071. [Google Scholar] [CrossRef]
- Jacob, C.E. Flow of groundwater. In Engineering Hydraulics; John Wiley: Hoboken, NJ, USA, 1950; pp. 321–386. [Google Scholar]
- Jacob, C.E. On the flow of water in an elastic artesian aquifer. Eos Trans. Am. Geophys. Union 1940, 21, 574–586. [Google Scholar] [CrossRef]
- Hantush, M.S. Hydraulics of Wells. In Advances in Hydroscience, 2nd ed.; Yen, B.C., Ed.; Academic Press: New York, NY, USA, 1964; Volume 1, pp. 281–432. [Google Scholar] [CrossRef]
- Green, D.H.; Wang, H.F. Specific storage as a poroelastic coefficient. Water. Resour. Res. 1990, 26, 1631–1637. [Google Scholar] [CrossRef]
- Cooper, H.H. The equation of groundwater flow in fixed and deforming coordinates. J. Geophys. Res. Solid Earth 1966, 71, 4785–4790. [Google Scholar] [CrossRef]
- Bredehoeft, J.D. Response of well-aquifer systems to Earth tides. J. Geophys. Res. Solid Earth 1967, 72, 3075–3087. [Google Scholar] [CrossRef]
- Bear, J. Hydraulics of Groundwater; McGraw-Hill: New York, NY, USA, 1979. [Google Scholar]
- Bear, J. Dynamics of Fluids in Porous Media. Soil Sci. 1975, 120, 162–163. [Google Scholar] [CrossRef]
- Smith, R.G.; Knight, R.; Chen, J.; Reeves, J.A.; Zebker, H.A.; Farr, T.; Liu, Z. Estimating the permanent loss of groundwater storage in the southern San Joaquin Valley, California. Water. Resour. Res. 2017, 53, 2133–2148. [Google Scholar] [CrossRef]
- Castellazzi, P.; Martel, R.; Rivera, A.; Huang, J.; Pavlic, G.; Calderhead, A.I.; Chaussard, E.; Garfias, J.; Salas, J. Groundwater depletion in Central Mexico: Use of GRACE and InSAR to support water resources management. Water. Resour. Res. 2016, 52, 5985–6003. [Google Scholar] [CrossRef]



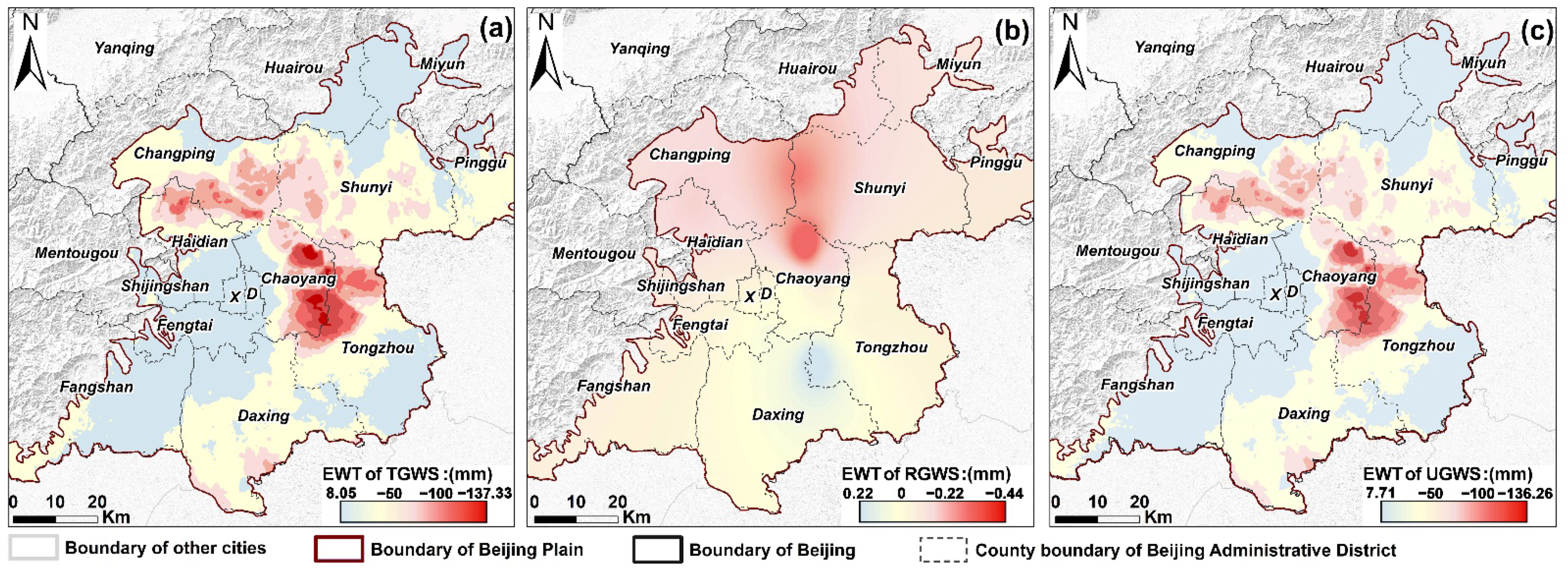
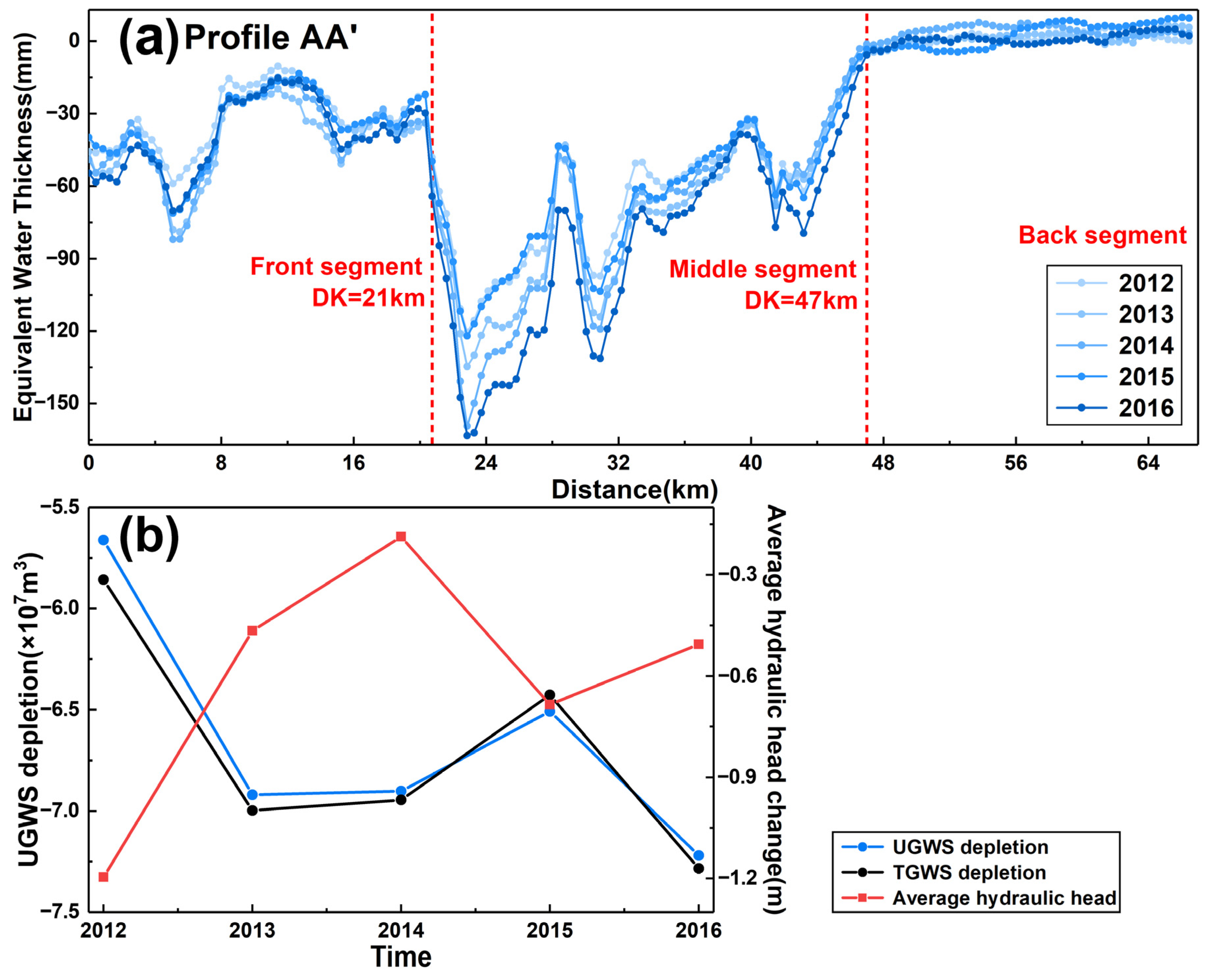
| Aquifer Group | Lithology | Thickness (m) | Depth of Bottom (m) |
|---|---|---|---|
| The first aquifer group (Unconfined aquifer) | silt, silty sandy, and sandy clay | 15–120 | 0–50 |
| The second aquifer group | multiple types of gravel, sand, and clay soil | 60–95 | 80–100 |
| The third aquifer group | multiple types of gravel, sand, and clay soil | 65–120 | 100–180 |
| The fourth aquifer group | mainly sand | 200–300 | 180–300 |
| SAR Sensor | RadarSat-2 | Polarization Mode | VV |
|---|---|---|---|
| Orbit direction | Descending | External DEM | SRTM |
| Band (wavelength) | C band (5.63 cm) | Spatial resolution of SRTM | 90 m |
| Spatial resolution | 30 m | Width range | 150 km × 150 km |
| Return period | 24 days | Temporal baseline | <300 d |
| Average incidence angle | 27.10° | Spatial baseline | <300 m |
| Number of images | 46 | ||
| Temporal period | January 2012–October 2016 | ||
| Point Number | Elastic Skeletal Storativity (Ske) | Lag Time (Unit: Days) | Thickness of Compressible Layer (Unit: m) |
|---|---|---|---|
| GWL1 | 0.249 × 10−3 | 60 | 150–200 |
| GWL2 | 0.563 × 10−3 | 152 | 150–200 |
| GWL3 | 0.169 × 10−3 | 91 | 100–150 |
| GWL4 | 0.241 × 10−3 | 244 | 100–150 |
| GWL5 | 0.201 × 10−3 | 182 | 100–150 |
| GWL6 | 0.442 × 10−3 | 0 | 150–200 |
| GWL7 | 0.395 × 10−3 | 31 | 200–250 |
| GWL8 | 0.420 × 10−3 | 60 | 150–200 |
| GWL9 | 0.179 × 10−3 | 213 | 100–150 |
| GWL10 | 0.719 × 10−3 | 0 | 50–100 |
| GWL11 | 0.423 × 10−3 | 31 | 100–150 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Chen, B.; Gong, H.; Lei, K.; Zhou, C.; Lu, Z.; Zhao, D. Inversion of Groundwater Storage Variations Considering Lag Effect in Beijing Plain, from RadarSat-2 with SBAS-InSAR Technology. Remote Sens. 2022, 14, 991. https://doi.org/10.3390/rs14040991
Zhang X, Chen B, Gong H, Lei K, Zhou C, Lu Z, Zhao D. Inversion of Groundwater Storage Variations Considering Lag Effect in Beijing Plain, from RadarSat-2 with SBAS-InSAR Technology. Remote Sensing. 2022; 14(4):991. https://doi.org/10.3390/rs14040991
Chicago/Turabian StyleZhang, Xin, Beibei Chen, Huili Gong, Kunchao Lei, Chaofan Zhou, Zhaozhao Lu, and Danni Zhao. 2022. "Inversion of Groundwater Storage Variations Considering Lag Effect in Beijing Plain, from RadarSat-2 with SBAS-InSAR Technology" Remote Sensing 14, no. 4: 991. https://doi.org/10.3390/rs14040991
APA StyleZhang, X., Chen, B., Gong, H., Lei, K., Zhou, C., Lu, Z., & Zhao, D. (2022). Inversion of Groundwater Storage Variations Considering Lag Effect in Beijing Plain, from RadarSat-2 with SBAS-InSAR Technology. Remote Sensing, 14(4), 991. https://doi.org/10.3390/rs14040991





