Abstract
Compressed sensing (CS)-based frequency agile radar (FAR) is attractive due to its superior data rate and target measurement performance. However, traditional frequency strategies for CS-based FAR are not cognitive enough to adapt well to the increasingly severe active interference environment. In this paper, we propose a cognitive frequency design method for CS-based FAR using reinforcement learning (RL). Specifically, we formulate the frequency design of CS-based FAR as a model-free partially observable Markov decision process (POMDP) to cope with the non-cooperation of the active interference environment. Then, a recognizer-based belief state computing method is proposed to relieve the storage and computation burdens in solving the model-free POMDP. This method is independent of the environmental knowledge and robust to the sensing scenario. Finally, the double deep Q network-based method using the exploration strategy integrating the CS-based recovery metric into the ϵ-greedy strategy (DDQN-CSR-ϵ-greedy) is proposed to solve the model-free POMDP. This can achieve better target measurement performance while avoiding active interference compared to the existing techniques. A number of examples are presented to demonstrate the effectiveness and advantage of the proposed design.
1. Introduction
In electronic warfare scenarios, hostile jammers emit active interference by intercepting and imitating radar signals [1,2], having a significant negative effect on radar functioning. Hence, it is necessary to equip radar systems with anti-jamming techniques. In addition, since an ever-growing number of electromagnetic systems require access to the limited frequency resource, especially after the wide deployment of the fifth generation (5G), minimizing the active co-frequency interference between different radiators becomes an attractive consideration. Frequency agile radar (FAR), which transmits pulses with different carrier frequencies in a coherent processing interval (CPI), possesses anti-jamming capabilities and has the potential to realize spectrum compatibility [3,4]. Random frequency is a common strategy for FAR with the thumbtack-type ambiguity function, but it cannot avoid active interference flexibly due to the lack of utilization of environmental information. Sense-and-avoid (SAA) techniques can be employed to select unoccupied frequency bands automatically [5,6], but the selection is based on the active interference knowledge sensed in the previous time. This cannot handle the anti-interference design in a dynamically changing environment. Therefore, it is of great significance to learn the interference dynamics and design a more cognitive frequency strategy for FAR.
Reinforcement learning (RL) is a branch of machine learning that aims at making the agent learn a control strategy through interaction with the environment [7,8,9]. It has been widely studied in the cognitive communication field to learn spectrum sense and access strategies [10,11]. Inspired by these investigations, some researchers have attempted to employ RL in radar frequency designs [12,13,14,15,16,17,18]. In [12,13], the frequency control problem was modeled as a Markov decision process (MDP), and RL was employed to find an optimal frequency strategy to mitigate co-frequency interference between the radar and communication systems. In [12], the transition probability of the state in the MDP model was estimated during the training phase where the emission frequencies are random. This does not make full use of the learned experience and is unsuitable for decision problems with large state spaces. To overcome these problems, the deep Q-network (DQN)-based method was developed in [13]. This method introduces experience replay and can be used in scenarios with large state spaces. However, similar to the design in [12], the method in [13] ignores the target measurement capability of the designed pulses. In [14,15], fast Fourier transform (FFT)-based moving target detection (MTD) was employed as the target measurement method, and the design attempted to maintain consistent frequencies while avoiding active interference to achieve satisfactory target measurement performance. Obviously, the FFT-based MTD technique considered in [14,15] wastes some degrees of freedom (DOF) since it only coherently integrates the target returns of subpulses with the same carrier frequency. Furthermore, similar to [12,13], the frequency control problem in [14,15] was modeled as an MDP, which is impractical in the non-cooperative active interference environment since the state cannot be obtained directly.
Facilitated by the fact that the target scene is always sparse, the compressed sensing (CS)-based recovery method to estimate the range and Doppler of moving targets in a coarse range bin is suggested, which improves the data rate of FAR and saves more DOF to counter active interference [19,20,21]. Hence, in this paper, we develop a cognitive frequency design method for countering active interference on CS-based FAR. At each time slot, since the true state of active interference is uncertain, we formulate the anti-interference problem as a model-free partially observable MDP (POMDP). In POMDPs, actions are determined based on historical observations and actions, which places large burdens on storage and computation. To overcome this obstacle, we propose a recognizer-based belief state computing method to represent the historical information of the model-free POMDP. After that, the POMDP is transformed to a belief-state-based MDP, and the double DQN (DDQN)-based solution method using the exploration strategy integrating the CS-based recovery (CSR) metric into the ϵ-greedy strategy (DDQN-CSR-ϵ-greedy) is proposed. The key contributions of this work are summarized as follows.
(1) To the best of our knowledge, this is the first study to develop a cognitive frequency strategy based on CS-based FAR using RL to improve target measurement performance in the presence of active interference. The closest to our study is the design of the random sparse step-frequency radar waveform (RaSSteR) [16]. However, the RaSSteR design only points out the potential capability of CS-based FAR to skip the occupied spectrum and realize target recovery but does not provide a specific implementation method. In contrast, our work gives a full description of the cognitive frequency design technique for CS-based FAR. Further, it provides a demonstration of the target measurement performance of the designed frequency strategy in different active interference scenarios by comparing different anti-interference and target measurement techniques.
(2) Compared to prior RL-based radar frequency strategy designs in active interference, our work provides a more realistic modeling method. Specifically, in contrast to the MDP formulated in [12,13,14,15], the model formulated in this paper does not require the environmental knowledge. In addition, both agent and environment states are denoted in the formulation to cope with signal-dependent and signal-independent active interference.
(3) In the conventional POMDP formulation, the belief state is updated with the known environment transition model [22], which is unavailable in non-cooperative active interference scenarios. To overcome this, a model-free method for computing the belief state is proposed in this paper. In more detail, we construct an NN-softmax-based active interference recognizer, the input and output of which are the observation and posterior probability, respectively. With the obtained posterior probability, the belief state of the POMDP can be derived using probability theory. Clearly, it only requires observations to implement the proposed recognizer-based belief state computing method. This avoids dependence on environmental knowledge. Moreover, the proposed recognizer-based method has superior robustness to the sensing scenario. This is verified by the numerical results.
(4) We propose the DDQN-CSR-ϵ-greedy method to solve the model-free POMDP. This is able to achieve better target measurement performance in active interference than the state-of-art methods. Concretely, the DDQN-CSR-ϵ-greedy method takes actions based on the agent state and output posterior probability, which is independent of the environmental model. In addition, this method uses the CSR metric to guide both anti-interference action exploration and exploitation phases. Consequently, the target measurement performance can be optimized while avoiding active interference.
The rest of the paper is organized as follows. Section 2 presents the signal model of CS-based FAR in active interference. Section 3 formulates and solves the problem of transmit frequency design for CS-based FAR in active interference. Section 4 presents the results and corresponding analyses. Section 5 provides the conclusion.
2. Signal Model
In this section, we introduce the signal model of CS-based FAR in active interference. Figure 1 presents a simplified working scenario where clutter is negligible and radar returns are not subject to multipath. The scenario contains a hostile jammer and a communication system that shares frequency channels with the CS-based FAR. The hostile jammer transmits intentional active interference by imitating intercepted radar signals. The communication equipment generates unintentional electromagnetic interference to the radar system. Consider that the targets of interest are measured by the CS-based FAR within the CPI consisting of N pulses. The pulse width and the pulse repetition interval are and , respectively. As shown in Figure 2, the N pulses are transmitted with the agile frequency
where is the lowest carrier frequency, is the frequency hopping interval of the nth pulse, and B is the maximum value of . The nth transmit pulse is defined as
where , and
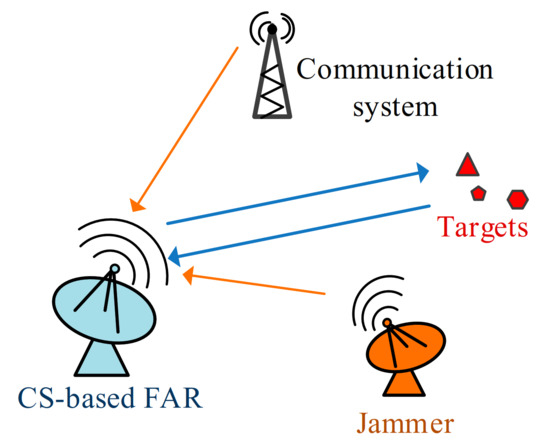
Figure 1.
Working scenario.
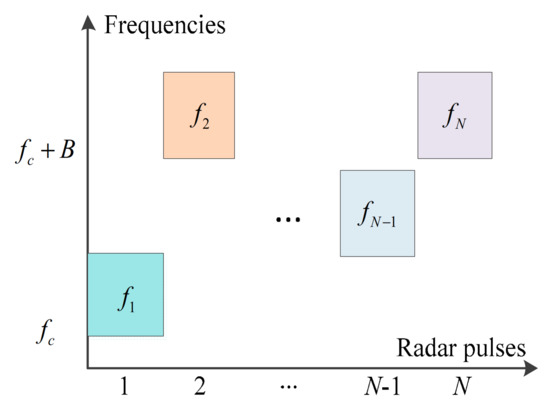
Figure 2.
Emission frequencies of the CS-based FAR.
Considering K targets in a coarse range and sampling each received pulse once, the nth received target echo can be represented by
where , , and are the scattering intensity, range, and velocity of the kth target, respectively. As seen in Equation (4), the phase of the received signal is discontinuous due to the agile frequency, which will degrade the performance of the conventional FFT-based MTD method. Since the target distribution is usually sparse within a coarse range, the CSR technique can be employed to realize moving target measurement [19,20,21]. To do so, uniformly divide the coarse range and interesting velocity scope into P and Q grids, respectively. Define the measurement matrix as . The elements of are given by
where , , denotes the transpose, and denotes the Hadamard product. Then, the target echo can be written as
where is a K-sparse vector, and the position of the nonzero in corresponds to the range-Doppler of the targets. Given the received target echo , the vector can be reconstructed using l1 minimization CSR algorithms such as orthogonal matching pursuit (OMP) [23], and correspondingly, the target range-Doppler measurement can be finished. In the numerical experiments later, we adopt OMP for sparse recovery.
In practice, the received signal is contaminated by noise and active interference. Uniformly dividing the available frequency band into M channels , the signal received in the mth frequency channel can be classified into the following four cases.
where is an independent and identically distributed Gaussian noise vector, is the target echo, is the active interference signal, and and represent the hypotheses of the absence and presence of active interference, respectively. In Equation (7), the second and fourth cases appear in the frequency channel used for target measurement at the receiver. Obviously, the presence of active interference in the measured channel, i.e., the fourth case in Equation (7), will degrade the target measurement performance significantly. Therefore, the transmit frequency should satisfy to guarantee target measurement performance in the active interference environment, where is the index set of the frequency channels occupied by the active interference.
3. Problem Formulation and Solution Method
In this section, we present a model-free POMDP model for designing frequency strategies in active interference and provide a recognizer-based belief state computing method to relieve the storage and computation burdens in solving the POMDP. Then, the DDQN-CSR-ϵ-greedy method is proposed to solve the model-free POMDP to obtain the transmit frequency strategy of the CS-based FAR.
3.1. Model-Free Partially Observable Markov Decision Process
As analyzed in Section 2, the transmit frequency should satisfy to protect the CS-based FAR against active interference. To this end, SAA-based transmit design techniques have been studied. In the SAA framework, radar senses environmental knowledge first. Then, the anti-interference strategy is designed based on the sensed information. We can learn from the working process above that the SAA-based method will perform poorly in the dynamically changing interference scenario where the sensed interference information is inconsistent with the current one. Hence, the frequency design should be carried out based on learning the dynamics of the interference. For the CS-based FAR, the received contaminated signal is the only information that can be used to complete the learning process. POMDP is a well-studied mathematical framework for learning dynamic environments and making decisions by an agent under imperfect observations. Therefore, following the scenario in Figure 1, we formulate the frequency design for anti-interference as a POMDP by regarding the CS-based FAR as an autonomous agent working in the dynamic interference environment consisting of a hostile jammer and a communication system. Furthermore, due to the non-cooperation of the active interference environment, the environmental model is hard to obtain. Hence, we formulate the design as a model-free POMDP specified by the tuple :
- is the action space of the agent. Here, the action is assigned within to denote the transmit frequency channel selected by the CS-based FAR.
- S is the state space. In our case, the state is represented bywhere is an -dimensional vector denoting the agent state and composed of the recent actions of the CS-based FAR, is an -dimensional binary vector showing the frequency channels occupied by the active interference. As an example, with and , denotes that the last two actions taken by the CS-based FAR are to select the first and third frequency channels for emission and that the second frequency channel is occupied in the nth step. In practice, the value of is determined by balancing the computational complexity and the ability of to represent the agent state. Since the agent state is known, the number of underlying states is under a given observation.
- is the reward obtained by the agent. Our work aims to avoid active interference from other electromagnetic equipment, so the reward function we adopt has the form
- denotes the observation space where the observation
- is the discount parameter used to put weights on future rewards.
As shown in Figure 3, the CS-based FAR takes action at first. Then, the state is transformed into the next state , and the CS-based FAR obtains the observation and the reward . After that, the new action will be taken. The loop above is performed until the target measurement task is finished.
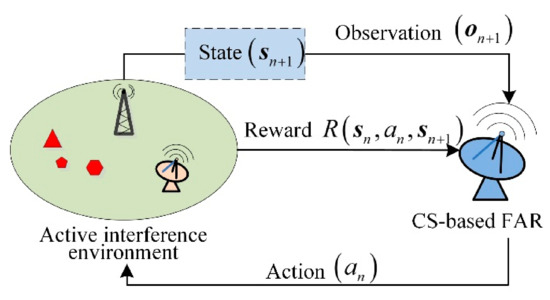
Figure 3.
Model-free POMDP of the frequency design for CS-based FAR working in active interference.
3.2. Recognizer-Based Belief State Computing Method
In the POMDP, we do not have direct access to the state, so the next action must be determined according to historical observations and actions [22]. This places heavy burdens on storage and computation. To overcome this, the belief state is introduced in the POMDP to represent historical information. The belief state is the posterior probabilities of underlying states under a given observation. In light of the Bayesian rule, the updating expression for the belief state is defined as
where is the probability of receiving observation under state , is the probability of the transition from state to state under action , is a normalizing constant, and
In Equation (11), the values of and are hard to obtain in the non-cooperative active interference environment. This makes the implementation of the updating expression to be intractable. Here, we propose a model-free recognizer-based method for calculating the belief state. The framework of the recognizer-based belief state computing method is presented in Figure 4. Specifically, we use the classification algorithm combining a neural network and softmax regression (NN-softmax) to construct the active interference recognizer. The input of the neural network is the contaminated observation , and the output features of the neural network are addressed by softmax regression to obtain the probability of the presence of active interference in the observation, i.e.,
where and denote the weight and bias for the output , respectively, and and denote the weight and bias for the output , respectively. Assume that the signals received by different channels are independent. According to probability theory, the belief state can be computed by
where is the index set of the occupied channels for the ith underlying state .
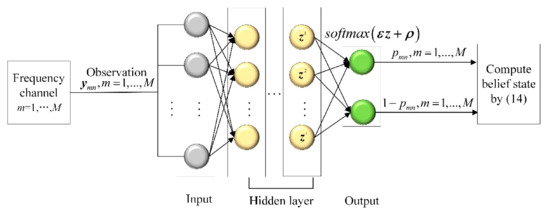
Figure 4.
Recognizer-based belief state computing method.
Thus, the proposed recognizer-based belief state computing method avoids the requirement of environmental knowledge, which makes it more suitable for application in a non-cooperative environment.
Given the belief state, the reward function of the POMDP can be derived as
According to Equation (9), the value of the reward depends only on whether the frequency channel used for emission is occupied. Considering that the th frequency channel is used for emission, the probabilities of the presence and absence of active interference in the emission channel are and , respectively. Hence, by substituting Equations (9) and (14) into Equation (15), the derived reward function is
where .
3.3. Transmit Frequency Strategy Design Using the DDQN-CSR-ϵ-Greedy Method
In this subsection, the model-free POMDP is solved by the proposed DDQN-CSR-ϵ-greedy method to obtain the transmit frequency strategy of the CS-based FAR.
First, the formulated POMDP is transformed into a belief-state-based MDP so that the solution method for MDP can be employed in the solving stage. As shown in Equation (14), the belief state can be determined by the output posterior probability vector . Therefore, we specify the belief-state-based MDP by the tuple , where the state space contains states defined as
The belief-state-based MDP aims to obtain the optimal solution that yields the highest expected discounted reward. The DDQN-based solution method, which can mitigate estimation bias in the learning process, is developed to find an approximate solution by learning the value function through the loss function as follows:
where is the weight of the main network used for selecting actions, and is the weight of the target network used for evaluating actions. The advantages of using the quadratic loss function mainly include reasonable penalties for errors and easy computation of gradients. Associating the step and episode of RL with the transmit pulse and CPI of the CS-based FAR, the flow chart of the DDQN-based transmit frequency design for CS-based FAR is given in Figure 5, and the corresponding learning details are given in Algorithm 1. Note that ‘%’ in Algorithm 1 denotes the remainder operator.
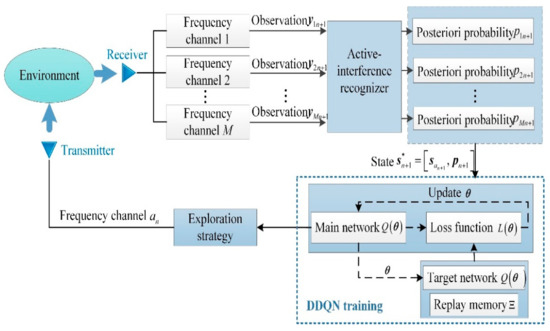

Figure 5.
DDQN-based transmit frequency design for CS-based FAR in the active interference environment.
| Algorithm 1. DDQN-based frequency design for CS-based FAR in active interference. |
| Input: the maximum number of episodes , the maximum number of steps for each episode, the number of transitions used for training the main network, the updating interval of the main network, the updating interval of the target network, the dimension of the agent state and the number of the divided frequency channels M. Observation phase: Select the transmit frequency channel randomly, transform the state into the state compute the reward , and select the transmit frequency channel randomly again. Perform the loop above and store the generated transitions in the replay memory . Interaction phase: . Repeat (for each episode):
|
As shown in Algorithm 1, the exploration strategy plays a significant connecting role in the learning loop. Conventional DDQN adopts the ϵ-greedy strategy to explore and exploit anti-interference actions, which is insufficient to achieve good target measurement performance. In this paper, we develop the CSR-ϵ-greedy exploration strategy, the main idea of which is to use the target measurement metric to guide the exploration and exploitation of the anti-interference action.
The recovery performance of the l1-minimization-based CSR algorithms is guaranteed by the restricted isometry property (RIP) and mutual coherence of the measurement matrix [19,20,21]. The coherence of is defined as follows:
where denotes the conjugate transpose. The smaller the coherence is, the better the sparse recovery performance will be [19,20,21]. Therefore, to achieve better CSR capability, the action can be obtained by solving the following optimization problem using the exhaustive search or other numerical methods [24]:
where is a vector consisting of previous transmit frequencies.
In the exploration phase of the traditional ϵ-greedy strategy, the action is selected randomly to realize action exploration. This strategy can explore the anti-interference action effectively but cannot guarantee the sparse recovery capability of the transmit pulses. Since the transmit frequency sequence possesses randomness to achieve a high sparse recovery probability [21], it is feasible to use the CSR metric to conduct anti-interference action exploration. Therefore, as described in Algorithm 2, the action is selected using Equation (20) in the exploration phase. In addition, the CSR metric can be used in the exploitation phase to achieve better target measurement performance while avoiding active interference. According to the definition of the reward function, the frequency channels corresponding to the lower output Q values are more likely to have interference and vice versa. Therefore, the set of unoccupied frequency channels can be obtained by performing the following clustering method on the outputs of the main Q network for different frequency channels. Specifically, rank the output Q values as
where . Next, the occupied and unoccupied frequency channels can be divided by clustering the lower and higher Q values in , respectively. In detail, compute the difference between the adjacent Q values in and obtain the vector
The clustering boundary can be obtained by
The set of the high Q values is defined as
Correspondingly, the set can be obtained by
Finally, the action of the CS-based FAR can be selected from using Equation (20) in the exploitation phase. The process of the CSR-ϵ-greedy exploration method is summarized in Algorithm 2.
| Algorithm 2. CSR-ϵ-greedy exploration strategy. |
Input: the state , main network , and previous transmit frequency vector .
|
4. Numerical Results
In this section, experimental results are presented to show the effectiveness and advantage of the design. Section 4.1 and 4.2 first analyze the proposed recognizer-based belief state computing method and the developed CSR-ϵ-greedy exploration strategy. Section 4.3 and 4.4 present the comparisons between different anti-interference strategies and different target measurement methods to demonstrate the superiority of the proposed DDQN-CSR-ϵ-greedy method. Unless otherwise stated, the experimental conditions are set as follows:
- (1)
- The parameters used to define the radar environment and characterize the DDQN-based cognitive frequency design are given in Table 1. To eliminate the limitation brought by the pulse width on the frequency step, the linear frequency modulated (LFM) signal is transmitted in the pulse.
- (2)
- A fully connected feedforward neural network is employed to be the Q network. The parameters of the Q network are given in Table 2.
- (3)
- Based on the related works [12,13,14,15,16,17], several active interference dynamics are employed to evaluate the performance of the proposed design. The interference strategies are detailed in Table 3.
- (4)
- For the recognizer-based belief state computing method, to balance the computation complexity and recognition performance, the NN-softmax with two hidden layers is used to construct the active interference recognizer. The network parameters are given in Table 4.
- (5)
- For the CSR-ϵ-greedy and ϵ-greedy exploration strategies, the exploration probability ϵ is linearly reduced from 1 to 0.

Table 1.
Summary of main parameters.
Table 1.
Summary of main parameters.
| Parameter | Value |
|---|---|
| Memory Buffer Size | 2000 transitions |
| Batch Size | 64 |
| Shared Channel Bandwidth | 100 MHz |
| Sub-Channel Bandwidth | 20 MHz |
| The updating interval of the main network | 1 |
| The updating interval of the target network | 3 |
| The maximum number of episodes | 100 |
| Discount factor | 0.9 |

Table 2.
Q network parameters.
Table 2.
Q network parameters.
| Layer | Hidden Layer 1 | Hidden Layer 2 | Output Layer |
|---|---|---|---|
| Neuron number | 40 | 40 | 1 |
| Transfer function | linear | ||
| Training method | gradient descent | ||

Table 3.
Active interference dynamics.
Table 3.
Active interference dynamics.
| Interference | Strategy |
|---|---|
| Constant−1 | Always occupies the first frequency channel |
| Constant−2 | Always occupies the first two frequency channels |
| Triangular sweep | Sweeps over the available frequency bands with triangular behavior |
| Pseudorandom sweep | Sweeps over the available frequency bands with pseudorandom behavior |
| Signal−dependent | Occupies the frequency channel consistent with the intercepted radar signal |
| Stochastic | Occupies the five frequency channels with probabilities (0, 0.05, 0.05, 0.3, 0.6) |

Table 4.
Network parameters of the active interference recognizer.
Table 4.
Network parameters of the active interference recognizer.
| Layer | Hidden Layer 1 | Hidden Layer 2 | Output Layer |
|---|---|---|---|
| Neuron number | 40 | 40 | 1 |
| Transfer function | softmax | ||
| Training method | gradient descent | ||
4.1. Analysis of the Recognizer-Based Belief State Computing Method
The belief state computing formula in Equation (14) is strictly derived based on probability theory, and the output posterior probability is the only variable in the computing formula. In addition, we can see in Figure 5 that the output posterior probability plays a key role in implementing the RL-based radar strategy design. Therefore, in this subsection, we analyze the output posterior probability of the designed active interference recognizer under different scenarios to verify the effectiveness of the proposed recognizer-based method.
In the following examples, the active interference data are from the jammer, and the target echo is simulated by modulating the transmit signal in the range-Doppler domain. We train the active interference recognizer with 79 active interference signals and test the recognizer with 100 noise signals, 100 target echoes, and 100 active interference signals. Figure 6 plots the output posterior probabilities for different observation cases in Equation (7). In Figure 6a, the noise-only environment is considered. In Figure 6b–d, white Gaussian noise of power 0 dBW is added, and a signal-to-noise ratio (SNR) of 0 dB is assumed in Figure 6d.
As Figure 6 shows, the output posterior probabilities are less than 0.01 and 0.04 for the noise-only and target scenarios, respectively. When the interference-to-noise ratio (INR) is greater than 0 dB, the values of the output posterior probability exceed 0.96 and 0.7 for the interference and coexisting cases, respectively. We can observe that the value of the output posterior probability is low in both noise-only and target scenarios and increases significantly in the presence of active interference. This illustrates that the output posterior probability can well reflect the state of the channel, and the reflection is robust to the sensing scenarios. In [17], the energy detector is used to connect the observation and state of the POMDP, which will make an incorrect judgment in the presence of high-powered noise and target echoes. As presented in Figure 6a,b, the proposed recognizer-based belief state computing method can maintain good performance in this case. Furthermore, as Figure 6c,d shows, the value of the output posterior probability increases with increasing interference energy, which illustrates that the output posterior probability can not only predict the presence of interference but also reflect the degree of interference. This capability contributes to the success of the DDQN-based solution method for avoiding active interference, which can be understood through the expression of the reward function in Equation (16).
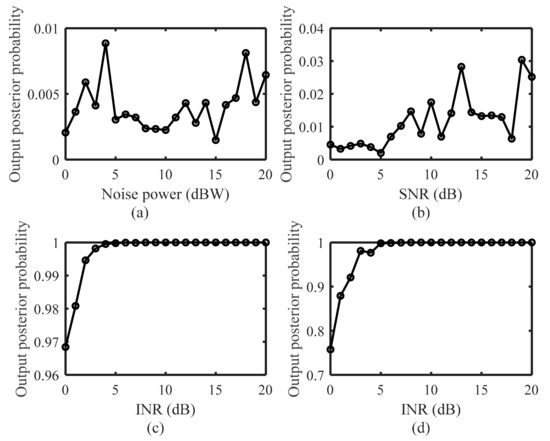
Figure 6.
Output posterior probabilities in (a) noise−only scenario; (b) target scenario; (c) interference scenario; and (d) interference and target coexisting scenario.
4.2. Analysis of the CSR-ϵ-Greedy Exploration Strategy
In this subsection, we examine the effectiveness of the proposed CSR-ϵ-greedy exploration strategy by presenting the convergence, anti-interference performance, and coherence achieved by the method.
Figure 7 plots the convergence curves of the average rewards versus episodes for different interference scenarios. All curves rise in the early stage of the interaction and reach stabilized values quickly. This means that anti-interference strategies have been learned efficiently by the CS-based FAR agents with the two exploration strategies. We can observe in Figure 7 that the learning speed of the developed CSR-ϵ-greedy exploration strategy is similar to that of the ϵ-greedy exploration strategy. In fact, due to the improved action selection process, the CSR-ϵ-greedy strategy has better convergence performance of target measurement capability than the ϵ-greedy strategy, which is demonstrated in the next subsection.
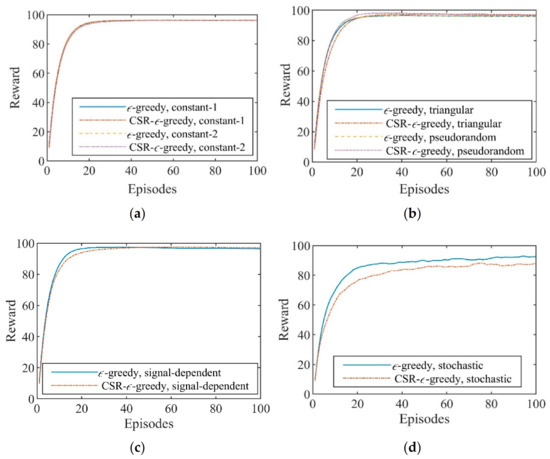
Figure 7.
Average rewards versus episodes for (a) constant interference; (b) sweep interference; (c) signal−dependent interference; and (d) stochastic interference.
To see how well the CS-based FAR agent has learned, we test the anti-interference performance of the learned frequency strategy. As shown in Figure 8a–e, the CS-based FAR can totally avoid constant, sweep, and signal-dependent active interference. In Figure 8f, we test the proposed method in the stochastic interference environment. As presented, the CS-based FAR cannot predict the frequency of stochastic interference accurately, but it can learn the probability of the interference and select the frequency channel with the low probability of being occupied to avoid active interference.
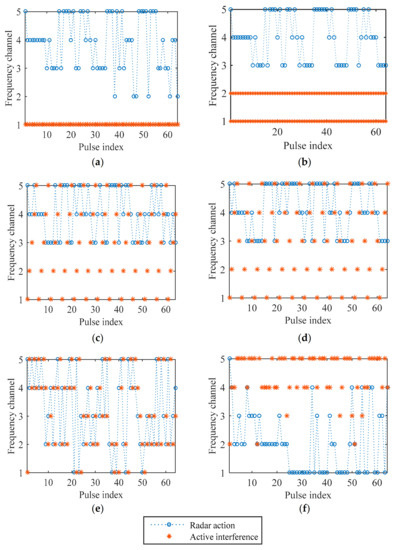
Figure 8.
Interference and anti−interference strategies for (a) constant−1 interference; (b) constant−2 interference; (c) triangular sweep interference; (d) pseudorandom sweep interference; (e) signal−dependent interference; (f) stochastic interference.
To quantify and highlight the performance of the developed CSR-ϵ-greedy exploration method, the anti-interference probability and coherence achieved after 100 episodes are given in Table 5. In all active interference scenarios, the proposed CSR-ϵ-greedy exploration strategy can achieve lower coherence than the ϵ-greedy strategy while obtaining anti-interference probabilities comparable to the ones obtained by the ϵ-greedy strategy. Specifically, both exploration strategies can achieve 100% anti-interference probabilities in the constant, sweep, and signal-dependent interference scenarios. For the stochastic case, since the CSR-ϵ-greedy strategy considers the target measurement metric in the action selection, it obtains a slightly lower anti-interference probability than the ϵ-greedy strategy. Nevertheless, due to the lower coherence, the developed method can achieve better target measurement performance than the ϵ-greedy strategy in the active interference environment. This is illustrated in the following subsection.

Table 5.
Anti-interference probability (%)/coherence.
4.3. Target Measurement Comparison between Different Anti-Interference Frequency Strategies in Active Interference
In this subsection, we compare the proposed DDQN-CSR-ϵ-greedy method with other anti-interference frequency control techniques, including the random frequencies, the SAA method, and the DDQN with the ϵ-greedy exploration strategy (DDQN-ϵ-greedy). For the random strategy, the frequency channels are selected with uniform probabilities. For the SAA method, the CS-based FAR senses the active interference frequency first and then picks an unoccupied frequency channel randomly. The OMP method [23] is used at the receiver to measure target parameters. To evaluate the target measurement performance, we define the correct measurement probability as
where is the total number of target measurement experiments, and is the number of correct measurements. When both the range and velocity of the target are measured correctly, the value of is increased by 1. Consider that the INR is 10 dB, the SNR is -5 dB, and 64 pulses (one CPI) are used for measuring target parameters. Figure 9 plots the convergence curves of Cr versus episode for different exploration strategies under 100 Monte Carlo experiments. As Figure 9 presents, the proposed DDQN-CSR-ϵ-greedy outperforms the DDQN-ϵ-greedy method in terms of convergence speed, stability, and the average value of Cr upon convergence due to the improved learning process in which the CSR-ϵ-greedy strategy can optimize CSR compatibility while exploring and exploiting anti-interference actions compared to the ϵ-greedy strategy.
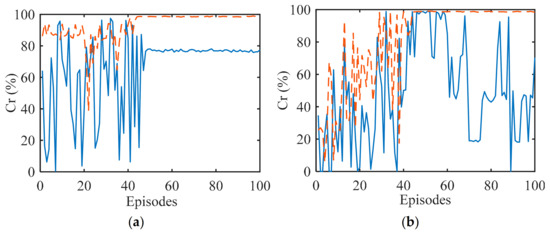
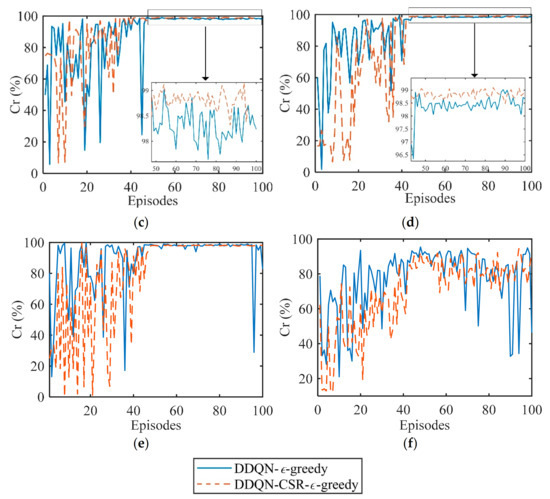
Figure 9.
Cr versus episode for (a) constant−1 interference; (b) constant−2 interference; (c) triangular sweep interference; (d) pseudorandom sweep interference; (e) signal−dependent interference; (f) stochastic interference.
Considering that the number of episodes in the DDQN-CSR-ϵ-greedy and DDQN-ϵ-greedy methods is 100, Figure 10 plots the value of Cr achieved by different anti-interference strategies under 100 Monte Carlo experiments. As shown, the value of Cr increases with the increasing SNR, and the proposed method can achieve better target measurement performance than other techniques. Specifically, the random strategy performs poorly in all interference scenarios due to the absence of environmental knowledge. The SAA method is suitable for countering constant interference but cannot handle dynamic interference scenarios. The DDQN-ϵ-greedy method can learn the dynamics of the active interference. However, due to the lack of consideration of measurement performance in the action selection, the DDQN-ϵ-greedy method obtains a target measurement performance that is even worse than the random strategy in some interference scenarios. In contrast, the proposed DDQN-CSR-ϵ-greedy method can achieve better target measurement performance in all interference scenarios since it optimizes the CSR performance while learning the interference behaviors. In detail, the value of achieved by the proposed method is approximately 100% when the SNR is greater than −2 dB for all interference scenarios.
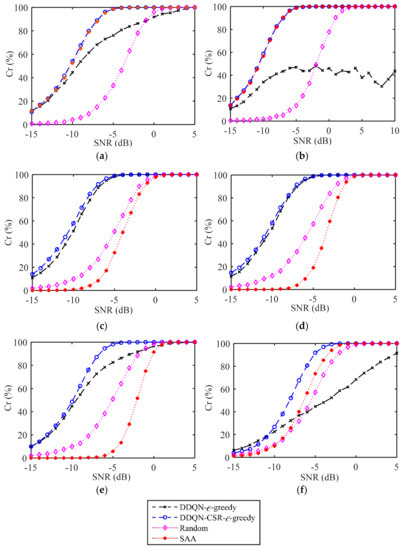
Figure 10.
Target measurement performance for different anti-interference strategies in (a) constant−1 interference; (b) constant−2 interference; (c) triangular sweep interference; (d) pseudorandom sweep interference; (e) signal−dependent interference; (f) stochastic interference.
4.4. Target Measurement Comparison between Different Target Measurement Techniques in Active Interference
To further illustrate the superiority of the proposed method, we compare the DDQN-CSR-ϵ-greedy-based CSR method with other moving target measurement techniques, including the FFT-based MTD and the min-coherence-based CSR. The FFT-based MTD technique chooses the LFM signal with a bandwidth of 100 MHz for emission and uses pulse compression and FFT-based MTD for signal processing at the receiver. For the min-coherence-based CSR, the carrier frequency of the transmit pulse is determined by Equation (20), and other parameters are the same as the DDQN-CSR-ϵ-greedy-based CSR. As Figure 11 illustrates, the DDQN-CSR-ϵ-greedy-based CSR method can achieve a significant shift of the performance curve to the left compared to the FFT-based MTD and min-coherence-based CSR techniques. This demonstrates a considerable improvement in target measurement in the presence of active interference.
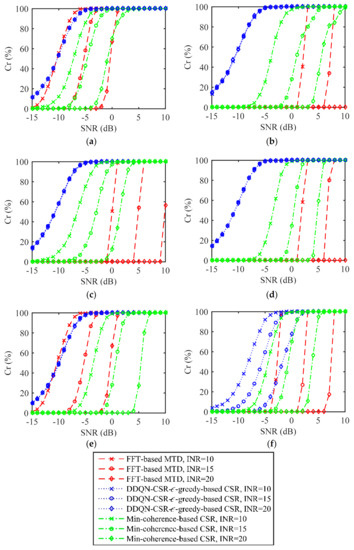
Figure 11.
Target measurement performance for different target measurement techniques in (a) constant−1 interference; (b) constant−2 interference; (c) triangular sweep interference; (d) pseudorandom sweep interference; (e) signal−dependent interference; (f) stochastic interference.
5. Conclusions
This work presented and validated an effective cognitive frequency design method for CS-based FAR in the presence of non-cooperative active interference.
As the problem formulation shows, the developed model does not require the environmental knowledge compared to the previous decision model of radar frequency strategy design. Hence, it is more applicable in the non-cooperative interference environment. In addition, both agent and environment states are denoted in the model to cope with the signal-dependent and signal-independent interference. In addition to the superiority of not relying on environmental knowledge, the results illustrate that the proposed recognizer-based belief state computing method for the model-free POMDP can well reflect the state of the environment and is robust to sensing scenarios. In the solution stage, the proposed DDQN-CSR-ϵ-greedy-based solution method can find a frequency strategy that achieves good target measurement performance while avoiding active interference. As the simulation results show, the proposed DDQN-CSR-ϵ-greedy method achieves considerable target measurement performance improvement in the presence of active interference over existing anti-interference and target measurement techniques.
In addition to the advantages above, the proposed designs can be flexibly extended to other fields. For example, the proposed recognizer-based method can be employed in other control problems to relate the observation with the state of the control model to solve the difficulties caused by non-cooperation. Additionally, the developed DDQN-CSR-ϵ-greedy-based design method can be employed in other tasks involving active interference by substituting the CSR metric with other metrics.
This work assumes that observations in different frequency channels can be obtained at the same time, which increases the complexity of CS-based FAR receivers. Future work can focus on how to design a cognitive frequency strategy by observing only the frequency channel used for target measurement at each step. Perhaps some RL-based methods for spectrum sensing in the communication field can be used to solve this problem. In addition, the designed method is based on a single agent, i.e., CS-based FAR. Extending the design to multi-agent scenarios is also a research direction. Due to the incomplete information in the considered model, combining the proposed method with Bayesian game theory [25,26] may be an approach.
Author Contributions
Conceptualization, S.W.; methodology, Z.L. and S.W.; software, S.W.; validation, S.W., L.R. and R.X.; formal analysis, S.W.; investigation, S.W. and L.R.; writing—original draft preparation, S.W.; writing—review and editing, L.R.; supervision, Z.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant number 62001346.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Li, N.; Zhang, Y. A survey of radar ECM and ECCM. IEEE Trans. Aerosp. Electron. Syst. 1995, 31, 1110–1120. [Google Scholar]
- Govoni, M.A.; Li, H.; Kosinski, J.A. Low probability of interception of an advanced noise radar waveform with Linear-FM. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 1351–1356. [Google Scholar]
- Wehner, D.R. High Resolution Radar; Artech House Publisher: London, UK, 1987. [Google Scholar]
- Aubry, A.; Carotenuto, V.; de Maio, A.; Farina, A.; Pallotta, L. Optimization theory-based radar waveform design for spectrally dense environments. IEEE Aerosp. Electron. Syst. Mag. 2016, 31, 14–25. [Google Scholar] [CrossRef]
- Carotenuto, V.; Aubry, A.; de Maio, A.; Pasquino, N.; Farina, A. Assessing agile spectrum management for cognitive radar on measured data. IEEE Aerosp. Electron. Syst. Mag. 2020, 35, 20–32. [Google Scholar] [CrossRef]
- Haykin, S. Cognitive radar: A way of the future. IEEE Signal Process. Mag. 2006, 23, 30–40. [Google Scholar] [CrossRef]
- Van Hasselt, H.; Guez, A.; Silver, D. Deep reinforcement learning with double Q-Learning. In Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence (AAAI’16), Phoenix, AZ, USA, 12–17 February 2016; pp. 2094–2100. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Graves, A.; Antonoglou, I.; Wierstra, D.; Riedmiller, M. Playing Atari with Deep Reinforcement Learning. Comput. Sci. 2013, 21, 351–362. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Yan, Z.; Cheng, P.; Chen, Z.; Li, Y.; Vucetic, B. Gaussian process reinforcement learning for fast opportunistic spectrum access. IEEE Trans. Signal Process. 2020, 68, 2613–2628. [Google Scholar] [CrossRef]
- Li, Z.; Guo, C. Multi-agent deep reinforcement learning based spectrum allocation for D2D underlay communications. IEEE Trans. Veh. Technol. 2020, 69, 1828–1840. [Google Scholar] [CrossRef] [Green Version]
- Selvi, E.; Buehrer, R.M.; Martone, A.; Sherbondy, K. Reinforcement learning for adaptable bandwidth tracking radars. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 3904–3921. [Google Scholar] [CrossRef]
- Thornton, C.E.; Kozy, M.A.; Buehrer, R.M.; Martone, A.F.; Sherbondy, K.D. Deep reinforcement learning control for radar detection and tracking in congested spectral environments. IEEE Trans. Cogn. Commun. Netw. 2020, 6, 1335–1349. [Google Scholar] [CrossRef]
- Kang, L.; Bo, J.; Hongwei, L.; Siyuan, L. Reinforcement learning based anti-jamming frequency hopping strategies design for cognitive radar. In Proceedings of the IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Qingdao, China, 14–16 September 2018; pp. 1–5. [Google Scholar]
- Li, K.; Jiu, B.; Liu, H. Deep Q-Network based anti-Jamming strategy design for frequency agile radar. In Proceedings of the International Radar Conference (RADAR), Toulon, France, 23–27 September 2019; pp. 1–5. [Google Scholar]
- Mishra, K.V.; Mulleti, S.; Eldar, Y.C. Range-Doppler Decoupling and Interference Mitigation using Cognitive Random Sparse Stepped Frequency Radar. In Proceedings of the 2020 IEEE Radar Conference, Florence, Italy, 21–25 September 2020; pp. 1–6. [Google Scholar]
- Ak, S.; Brüggenwirth, S. Avoiding Jammers: A reinforcement learning approach. In Proceedings of the IEEE International Radar Conference (RADAR), Chongqing City, China, 4–6 November 2020; pp. 321–326. [Google Scholar]
- Li, K.; Jiu, B.; Liu, H.; Pu, W. Robust Antijamming Strategy Design for Frequency-Agile Radar against Main Lobe Jamming. Remote Sens. 2021, 13, 3043. [Google Scholar] [CrossRef]
- Eldar, Y.C.; Kutyniok, G. Compressed Sensing: Theory and Applications; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Huang, T.; Liu, Y.; Meng, H.; Wang, X. Cognitive random stepped frequency radar with sparse recovery. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 858–870. [Google Scholar] [CrossRef]
- Huang, T.; Liu, Y.; Xu, X.; Eldar, Y.C.; Wang, X. Analysis of frequency agile radar via compressed sensing. IEEE Trans. Signal Process. 2018, 66, 6228–6240. [Google Scholar] [CrossRef] [Green Version]
- Astrom, K.J. Optimal control of Markov decision process with incomplete state estimation. J. Math. Anal. Appl. 1965, 10, 174–205. [Google Scholar] [CrossRef] [Green Version]
- Tropp, J.A.; Gilbert, A.C. Signal recovery from random measurements via orthogonal matching pursuit. IEEE Trans. Inf. Theory 2007, 53, 4655–4666. [Google Scholar] [CrossRef] [Green Version]
- Gill, P.E.; Murray, W.; Wright, M.H. Practical optimization. Math. Gaz. 1981, 104, 180. [Google Scholar]
- Deligiannis, A.; Lambotharan, S. A Bayesian game theoretic framework for resource allocation in multistatic radar networks. In Proceedings of the 2017 IEEE Radar Conference (RadarConf), Seattle, WA, USA, 8–12 May 2017; pp. 546–551. [Google Scholar]
- Garnaev, A.; Petropulu, A.; Trappe, W.; Poor, H.V. A power control problem for a dual communication-radar system facing a jamming threat. In Proceedings of the 2020 IEEE Radar Conference (RadarConf20), Florence, Italy, 21–25 September 2020; pp. 1–6. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).