Comprehensive Study on the Tropospheric Wet Delay and Horizontal Gradients during a Severe Weather Event
Abstract
1. Introduction
2. Materials and Methods
2.1. ERA5 Data
2.2. TRMM Data
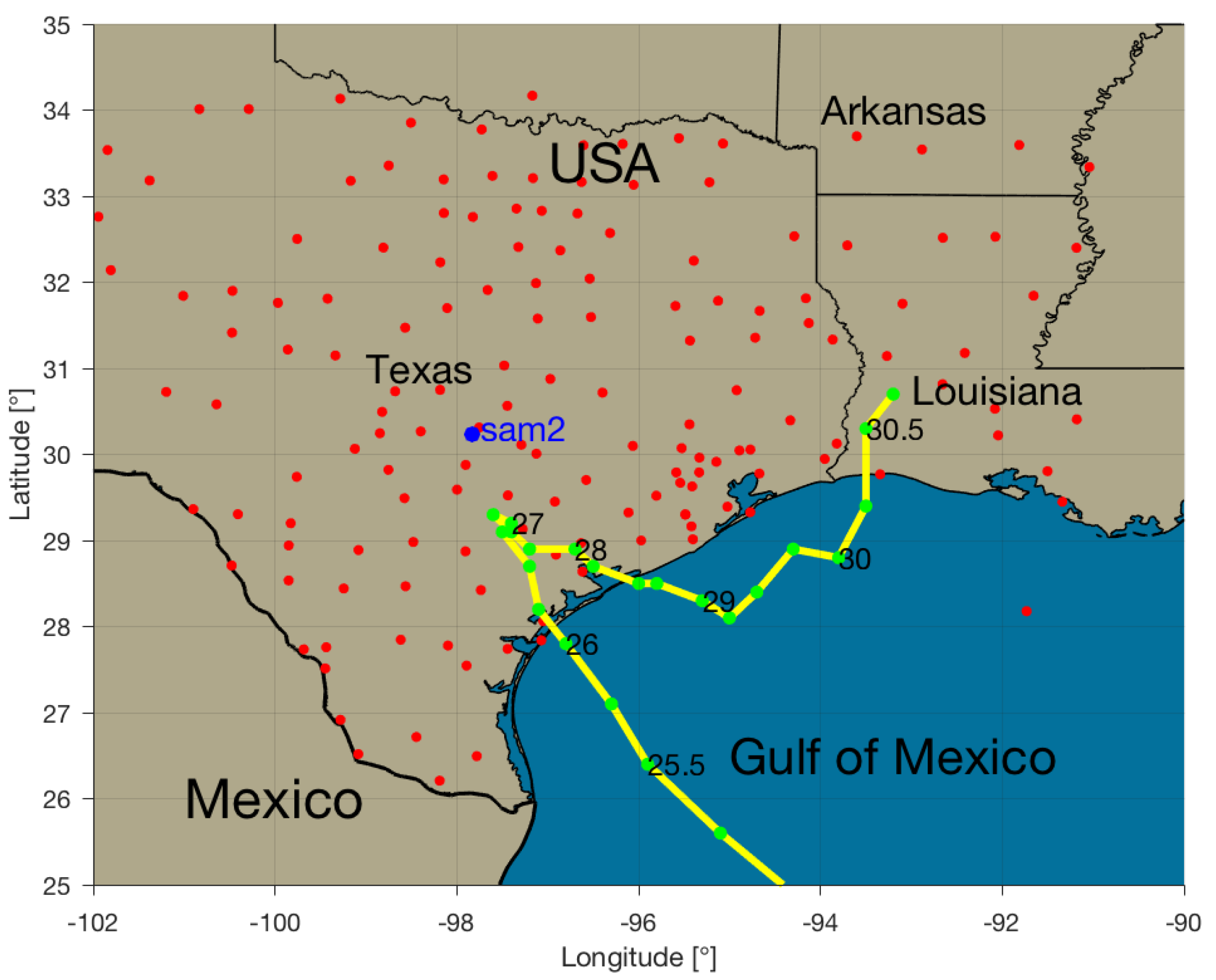
2.3. GPS Data
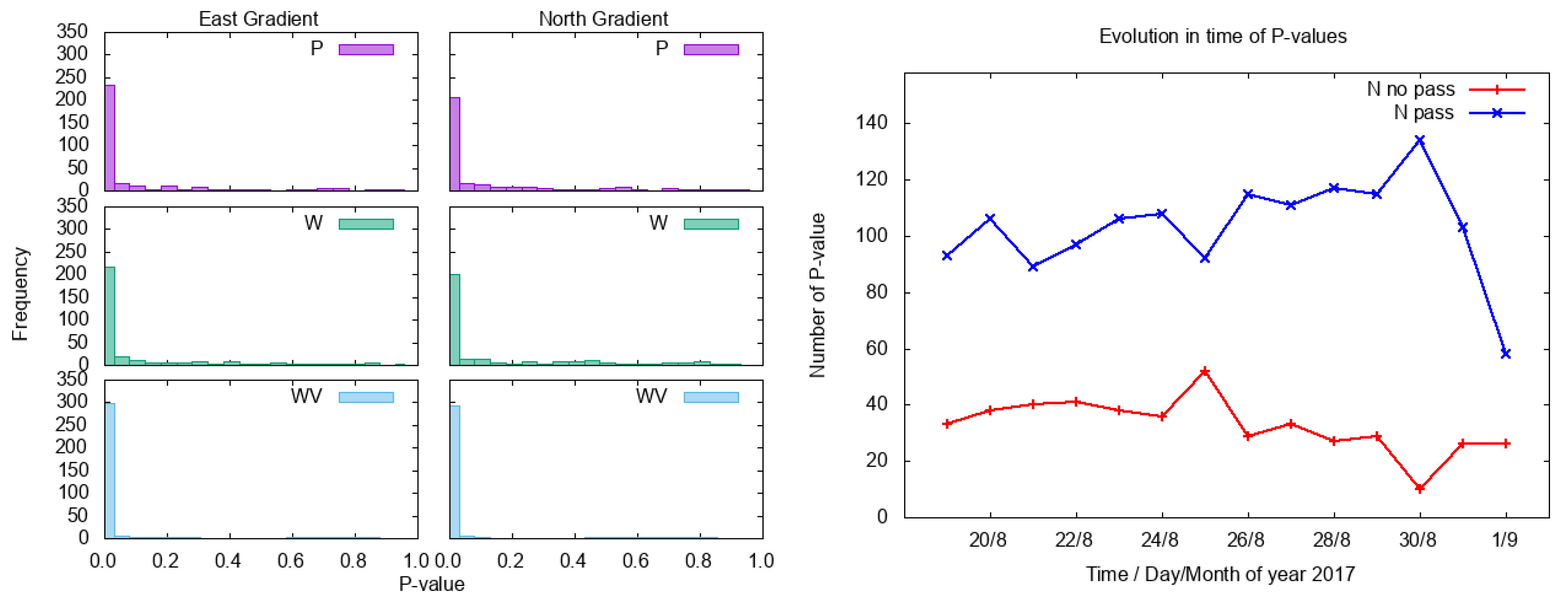
3. Results
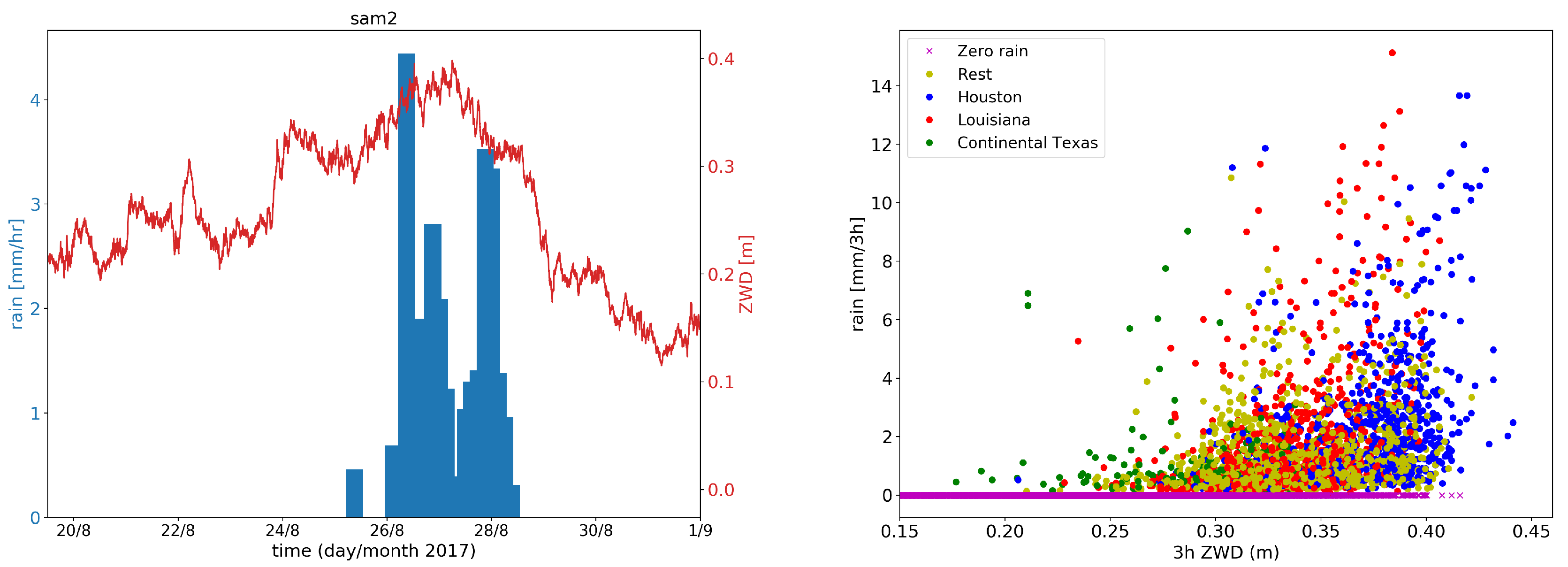
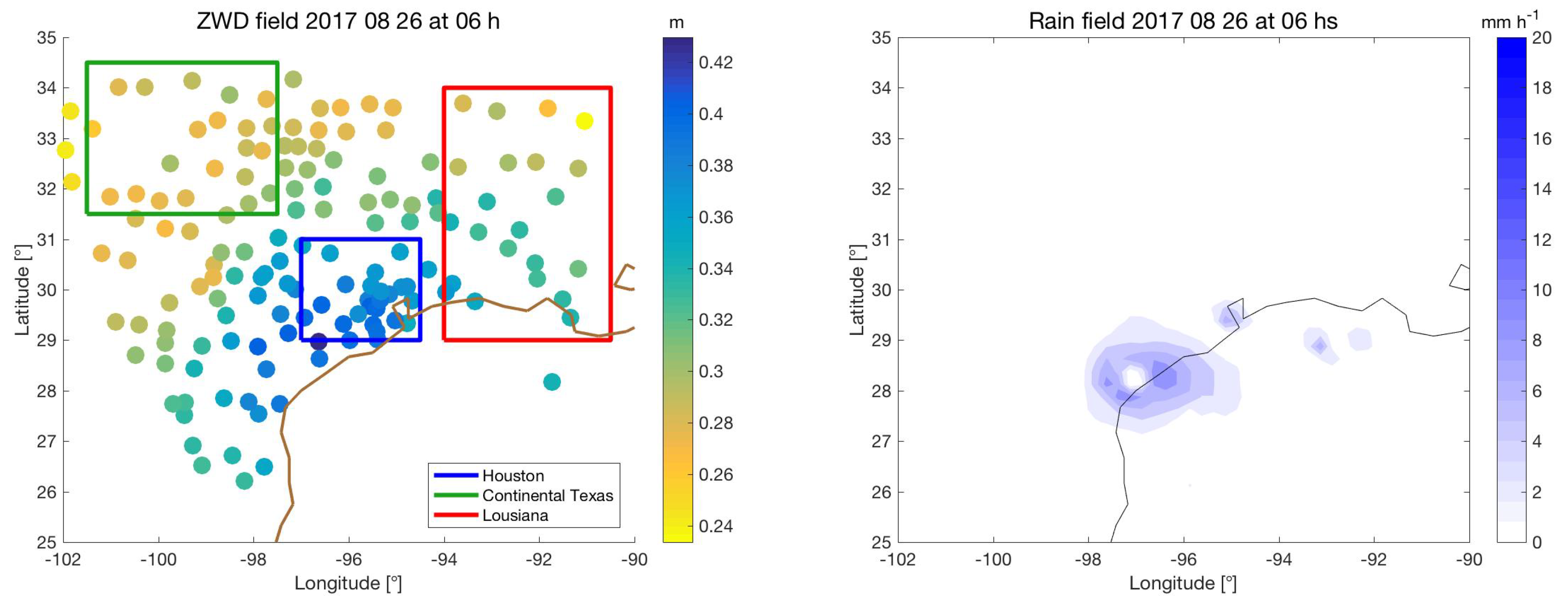
3.1. Relationship between ZWD and Rain Rate
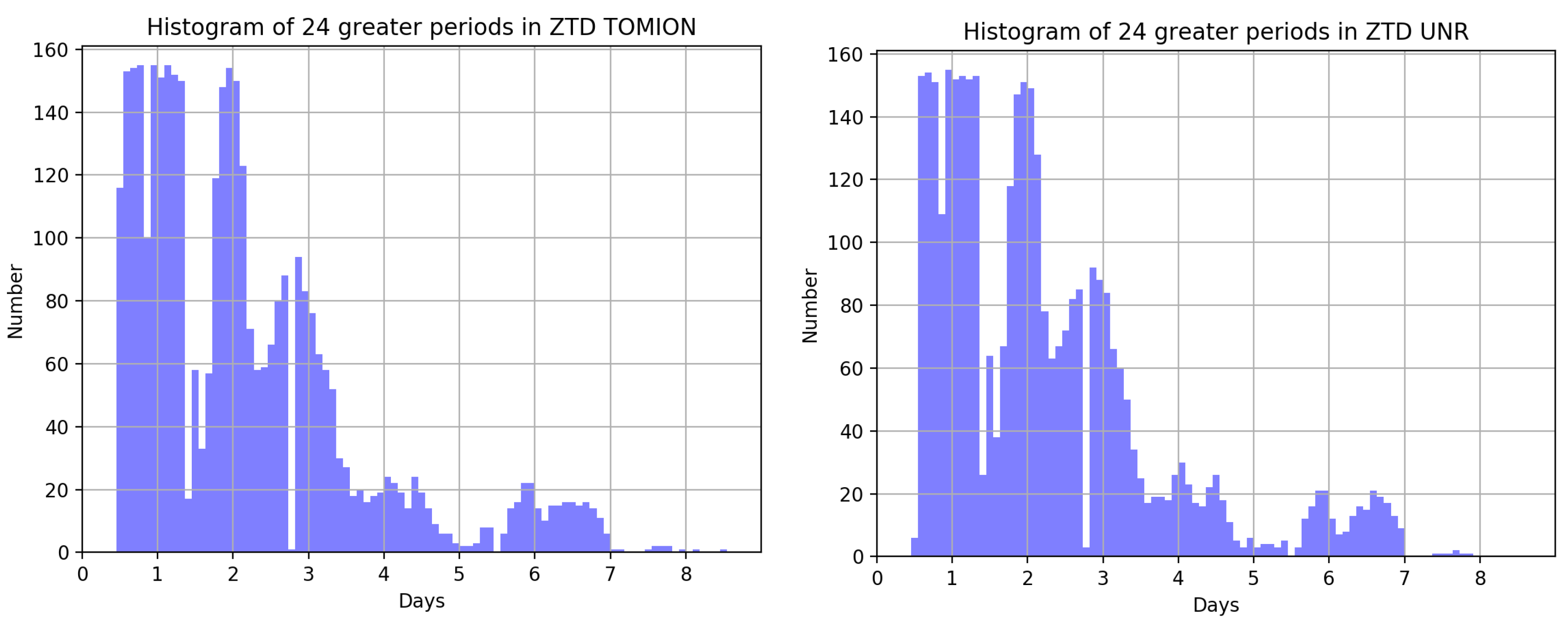
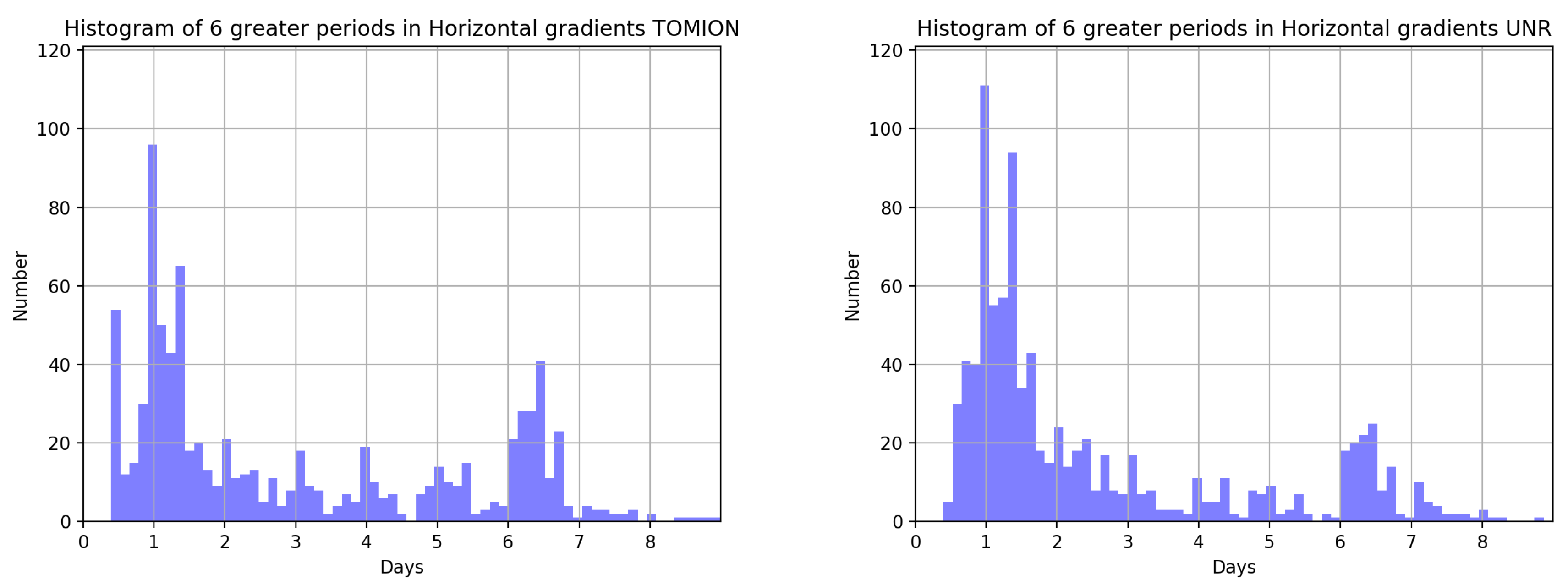
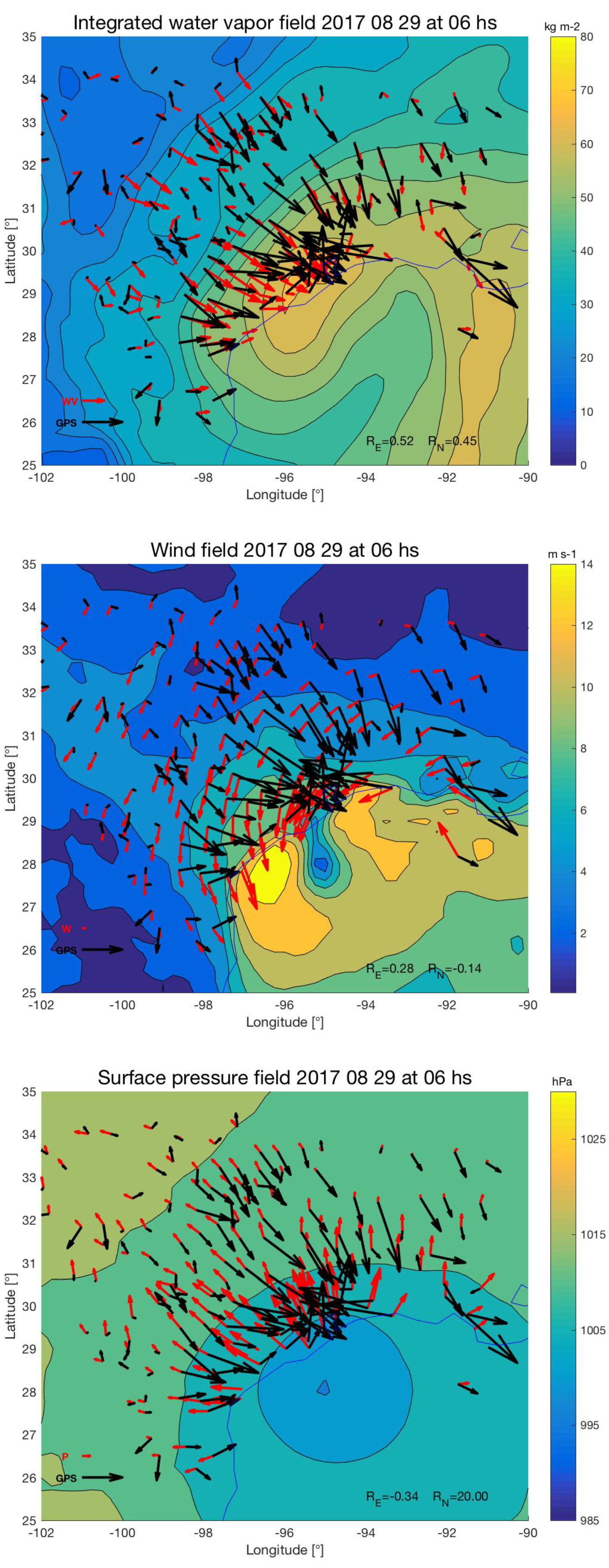
3.2. Diurnal Cycle of the Tropospheric Delay and Horizontal Gradients
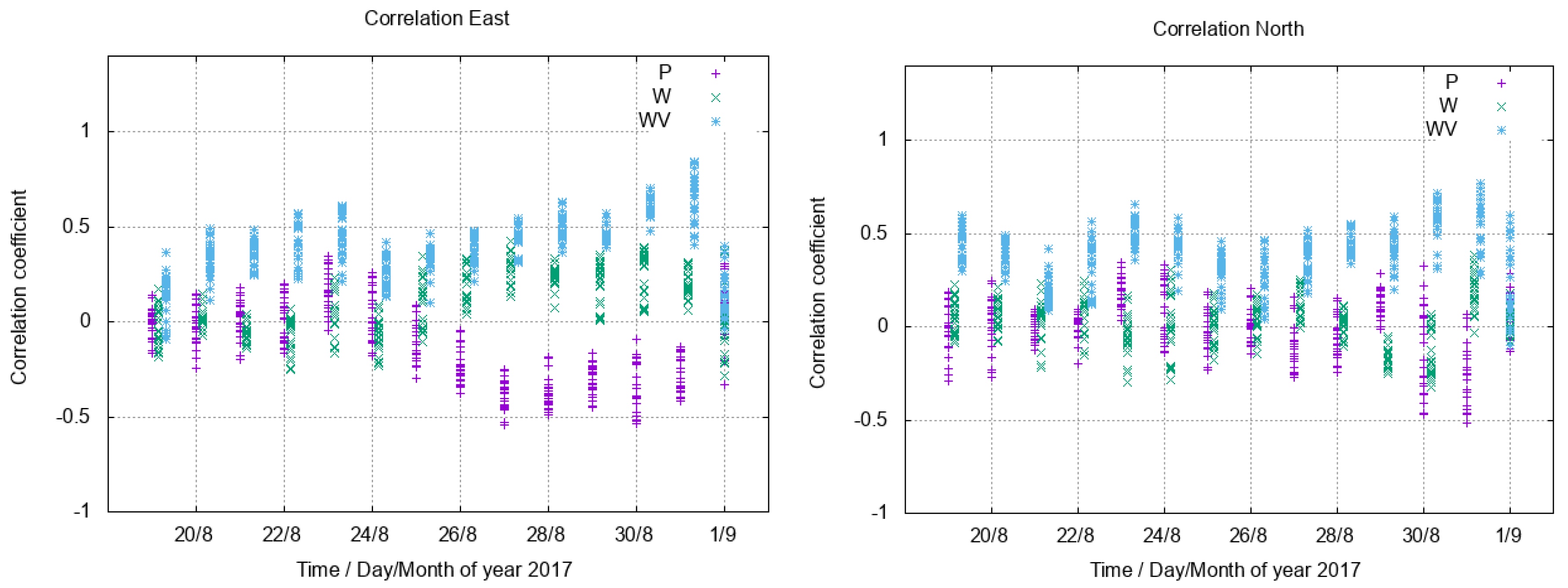
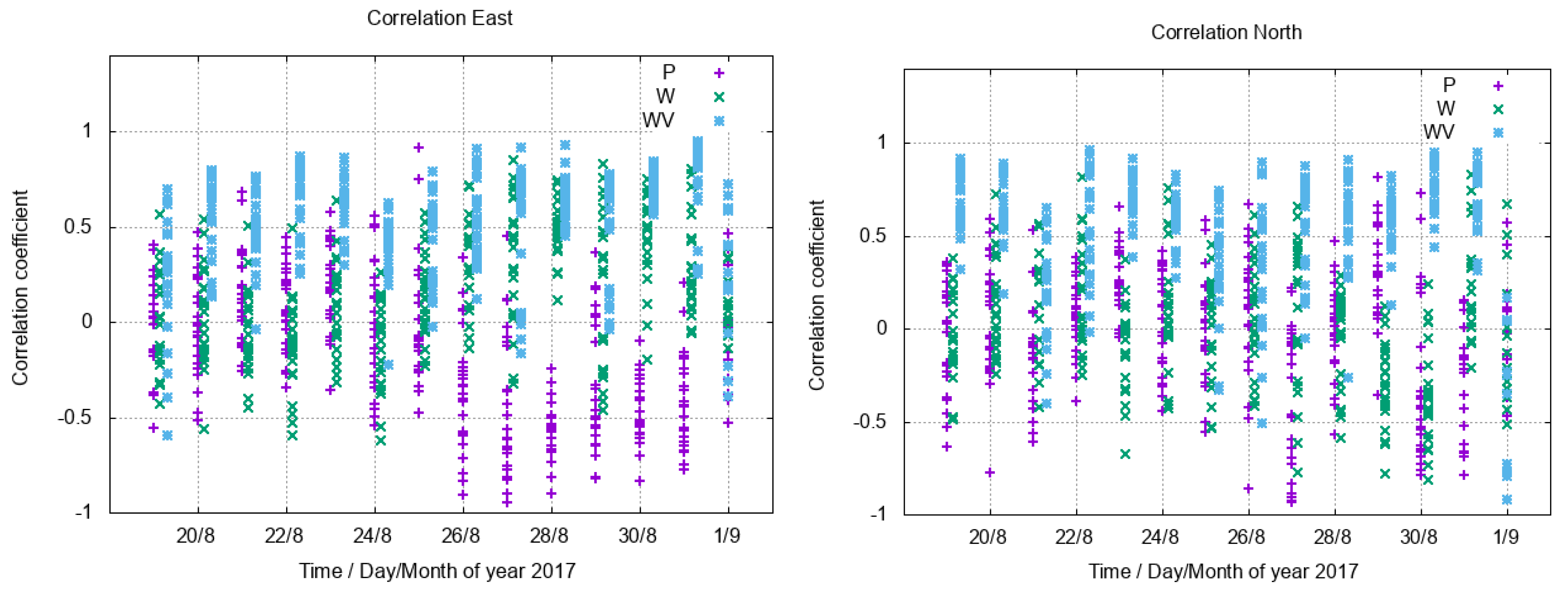
3.3. Correlations with ERA5
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Abbreviations
| MDPI | Multidisciplinary Digital Publishing Institute |
| DOAJ | Directory of open access journals |
| TLA | Three letter acronym |
| LD | Linear dichroism |
References
- Bevis, M.; Businger, S.; Herring, T.A.; Rocken, C.; Anthes, R.A.; Ware, R.H. GPS meteorology: Remote sensing of atmospheric water vapor using the Global Positioning System. J. Geophys. Res. Atmos. 1992, 97, 15787–15801. [Google Scholar] [CrossRef]
- Dick, G.; Gendt, G.; Reigber, C. First experience with near real-time water vapor estimation in a German GPS network. J. Atmos. Sol.-Terr. Phys. 2001, 63, 1295–1304. [Google Scholar] [CrossRef]
- Gendt, G.; Reigber, C.; Dick, G. Near real-time water vapor estimation in a German GPS network-first results from the ground program of the HGF GASP project. Phys. Chem. Earth Part A Solid Earth Geod. 2001, 26, 413–416. [Google Scholar] [CrossRef]
- Nykiel, G.; Figurski, M.; Baldysz, Z. Analysis of GNSS sensed precipitable water vapour and tropospheric gradients during the derecho event in Poland of 11th August 2017. J. Atmos. Sol.-Terr. Phys. 2019, 193, 105082. [Google Scholar] [CrossRef]
- Ejigu, Y.G.; Teferle, F.N.; Klos, A.; Bogusz, J.; Hunegnaw, A. Tracking Hurricanes Using GPS Atmospheric Precipitable Water Vapor Field. In International Association of Geodesy Symposia; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar] [CrossRef]
- Dousa, J.; Dick, G.; Kačmařík, M.; Brožková, R.; Zus, F.; Brenot, H.; Stoycheva, A.; Möller, G.; Kaplon, J. Benchmark campaign and case study episode in central Europe for development and assessment of advanced GNSS tropospheric models and products. Atmos. Meas. Tech. 2016, 9, 2989–3008. [Google Scholar] [CrossRef]
- Guerova, G.; Jones, J.; Douša, J.; Dick, G.; Haan, S.D.; Pottiaux, E.; Bock, O.; Pacione, R.; Elgered, G.; Vedel, H.; et al. Review of the state of the art and future prospects of the ground-based GNSS meteorology in Europe. Atmos. Meas. Tech. 2016, 9, 5385–5406. [Google Scholar] [CrossRef]
- Van Baelen, J.; Reverdy, M.; Tridon, F.; Labbouz, L.; Dick, G.; Bender, M.; Hagen, M. On the relationship between water vapour field evolution and the life cycle of precipitation systems. Q. J. R. Meteorol. Soc. 2011, 137, 204–223. [Google Scholar] [CrossRef]
- Graham, E.; Koffi, E.N.; Mätzler, C. An observational study of air and water vapour convergence over the Bernese Alps, Switzerland, during summertime and the development of isolated thunderstorms. Meteorol. Z. 2012, 21, 561–574. [Google Scholar] [CrossRef]
- Elosegui, P.; Davis, J.; Gradinarsky, L.; Elgered, G.; Johansson, J.; Tahmoush, D.; Rius, A. Sensing atmospheric structure using small-scale space geodetic networks. Geophys. Res. Lett. 1999, 26, 2445–2448. [Google Scholar] [CrossRef]
- Zhang, K.; Manning, T.; Wu, S.; Rohm, W.; Silcock, D.; Choy, S. Capturing the signature of severe weather events in Australia using GPS measurements. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 1839–1847. [Google Scholar] [CrossRef]
- Riccardi, U.; Tammaro, U.; Capuano, P. Tropospheric Delay in the Neapolitan and Vesuvius Areas (Italy) by Means of a Dense GPS Array: A Contribution for Weather Forecasting and Climate Monitoring. Atmosphere 2021, 12, 1225. [Google Scholar] [CrossRef]
- Shoji, Y. Retrieval of water vapor inhomogeneity using the Japanese nationwide GPS array and its potential for prediction of convective precipitation. J. Meteorol. Soc. Jpn. Ser. II 2013, 91, 43–62. [Google Scholar] [CrossRef][Green Version]
- Elgered, G.; Tong, N.; Forkman, P.; Haas, R. On the information content in linear horizontal delay gradients estimated from space geodesy observations. Atmos. Meas. Tech. 2019, 12, 3805–3823. [Google Scholar] [CrossRef]
- Graffigna, V.; Hernández-Pajares, M.; Gende, M.; Azpilicueta, F.; Antico, P. Interpretation of the tropospheric gradients estimated with GPS during hurricane Harvey. Earth Space Sci. 2019, 6, 1348–1365. [Google Scholar] [CrossRef]
- Ning, T.; Elgered, G. High temporal resolution wet delay gradients estimated from multi-GNSS and microwave radiometer observations. Atmos. Meas. Tech. Discuss. 2021, 14, 5593–5605. [Google Scholar] [CrossRef]
- Chen, G.; Herring, T. Effects of atmospheric azimuthal asymmetry on the analysis of space geodetic data. J. Geophys. Res. Solid Earth 1997, 102, 20489–20502. [Google Scholar] [CrossRef]
- Bar-Sever, Y.E.; Kroger, P.M.; Borjesson, J.A. Estimating horizontal gradients of tropospheric path delay with a single GPS receiver. J. Geophys. Res. Solid Earth 1998, 103, 5019–5035. [Google Scholar] [CrossRef]
- Meindl, M.; Schaer, S.; Hugentobler, U.; Beutler, G. Tropospheric gradient estimation at CODE: Results from global solutions. J. Meteorol. Soc. Jpn. Ser. II 2004, 82, 331–338. [Google Scholar] [CrossRef]
- Kačmařík, M.; Douša, J.; Zus, F.; Václavovic, P.; Balidakis, K.; Dick, G.; Wickert, J. Sensitivity of GNSS tropospheric gradients to processing options. Ann. Geophys. Discuss. 2018, 2018, 1–19. [Google Scholar] [CrossRef]
- Olivares-Pulido, G.; Hernández-Pajares, M.; Lyu, H.; Gu, S.; García-Rigo, A.; Graffigna, V.; Tomaszewski, D.; Wielgosz, P.; Rapiński, J.; Krypiak-Gregorczyk, A.; et al. Ionospheric tomographic common clock model of undifferenced uncombined GNSS measurements. J. Geod. 2021, 95, 1–13. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM multisatellite precipitation analysis (TMPA): Quasi-global, multiyear, combined-sensor precipitation estimates at fine scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Graffigna, V. Validation of Real-Time Zenith Tropospheric Delay Estimation with TOMION Software within WAGNSS Networks. Master’s Thesis, Universitat Politècnica de Catalunya, Barcelona, Spain, 2017. [Google Scholar]
- Zumberge, J.; Heflin, M.; Jefferson, D.; Watkins, M.; Webb, F.H. Precise point positioning for the efficient and robust analysis of GPS data from large networks. J. Geophys. Res. Solid Earth 1997, 102, 5005–5017. [Google Scholar] [CrossRef]
- Dach, R.; Schaer, S.; Arnold, D.; Orliac, E.; Prange, L.; Susnik, A.; Villiger, A.; Jäggi, A. CODE Final Product Series for the IGS. 2016. Available online: https://boris.unibe.ch/75876/1/AIUB_AFTP.TXT (accessed on 21 December 2021).
- Saastamoinen, J. Atmospheric correction for the troposphere and stratosphere in radio ranging satellites. Use Artif. Satell. Geod. 1972, 15, 247–251. [Google Scholar]
- Askne, J.; Nordius, H. Estimation of tropospheric delay for microwaves from surface weather data. Radio Sci. 1987, 22, 379–386. [Google Scholar] [CrossRef]
- Böhm, J.; Schuh, H. Vienna mapping functions in VLBI analyses. Geophys. Res. Lett. 2004, 31, 277. [Google Scholar] [CrossRef]
- Milliner, C.; Materna, K.; Bürgmann, R.; Fu, Y.; Moore, A.W.; Bekaert, D.; Adhikari, S.; Argus, D.F. Tracking the weight of Hurricane Harvey’s stormwater using GPS data. Sci. Adv. 2018, 4, eaau2477. [Google Scholar] [CrossRef]
- Miyazaki, S.; Iwabuchi, T.; Heki, K.; Naito, I. An impact of estimating tropospheric delay gradients on precise positioning in the summer using the Japanese nationwide GPS array. J. Geophys. Res. Solid Earth 2003, 108, 4315. [Google Scholar] [CrossRef]
- Jin, S.; Luo, O.; Gleason, S. Characterization of diurnal cycles in ZTD from a decade of global GPS observations. J. Geod. 2009, 83, 537–545. [Google Scholar] [CrossRef]
- Blewitt, G.; Hammond, W.C.; Kreemer, C. Harnessing the GPS data explosion for interdisciplinary science. Eos 2018, 99, 485. [Google Scholar] [CrossRef]
- Tu, M.; Zhang, W.; Bai, J.; Wu, D.; Liang, H.; Lou, Y. Spatio-Temporal Variations of Precipitable Water Vapor and Horizontal Tropospheric Gradients from GPS during Typhoon Lekima. Remote Sens. 2021, 13, 4082. [Google Scholar] [CrossRef]
- Arief, S.; Heki, K. GNSS Meteorology for Disastrous Rainfalls in 2017–2019 Summer in SW Japan: A New Approach Utilizing Atmospheric Delay Gradients. Front. Earth Sci. 2020, 8, 182. [Google Scholar] [CrossRef]
- Zus, F.; Douša, J.; Kačmařík, M.; Václavovic, P.; Dick, G.; Wickert, J. Estimating the Impact of Global Navigation Satellite System Horizontal Delay Gradients in Variational Data Assimilation. Remote Sens. 2019, 11, 41. [Google Scholar] [CrossRef]
- Press, W.H.; Teukolsky, S.A.; Flannery, B.P.; Vetterling, W.T. Numerical Recipes in Fortran 77: Volume 1 of Fortran Numerical Recipes: The Art of Scientific Computing; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
| Item | Description |
|---|---|
| Sampling rate | 30 s |
| Observables | GPS |
| Strategy | Ionospheric-free combination |
| Troposphere delay modeling | VMF1 |
| Receiver clock | white noise |
| A priori sigma of observations | m y m. |
| Satellite orbits and clocks | CODE high rate |
| Elevation weighting | (S: Elevation weighting scale factor) |
| Elevation cutoff angle | 7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Graffigna, V.; Hernández-Pajares, M.; Azpilicueta, F.; Gende, M. Comprehensive Study on the Tropospheric Wet Delay and Horizontal Gradients during a Severe Weather Event. Remote Sens. 2022, 14, 888. https://doi.org/10.3390/rs14040888
Graffigna V, Hernández-Pajares M, Azpilicueta F, Gende M. Comprehensive Study on the Tropospheric Wet Delay and Horizontal Gradients during a Severe Weather Event. Remote Sensing. 2022; 14(4):888. https://doi.org/10.3390/rs14040888
Chicago/Turabian StyleGraffigna, Victoria, Manuel Hernández-Pajares, Francisco Azpilicueta, and Mauricio Gende. 2022. "Comprehensive Study on the Tropospheric Wet Delay and Horizontal Gradients during a Severe Weather Event" Remote Sensing 14, no. 4: 888. https://doi.org/10.3390/rs14040888
APA StyleGraffigna, V., Hernández-Pajares, M., Azpilicueta, F., & Gende, M. (2022). Comprehensive Study on the Tropospheric Wet Delay and Horizontal Gradients during a Severe Weather Event. Remote Sensing, 14(4), 888. https://doi.org/10.3390/rs14040888






