Stripe Noise Detection of High-Resolution Remote Sensing Images Using Deep Learning Method
Abstract
:1. Introduction
2. Related Work
2.1. Deep Learning
2.2. Object Detection Based on Deep Neural Networks
3. Methods Used in Linear Object Detection
3.1. Stripe Noise Simulation Method
3.2. Linear Object Detection Algorithm for Stripe Noise
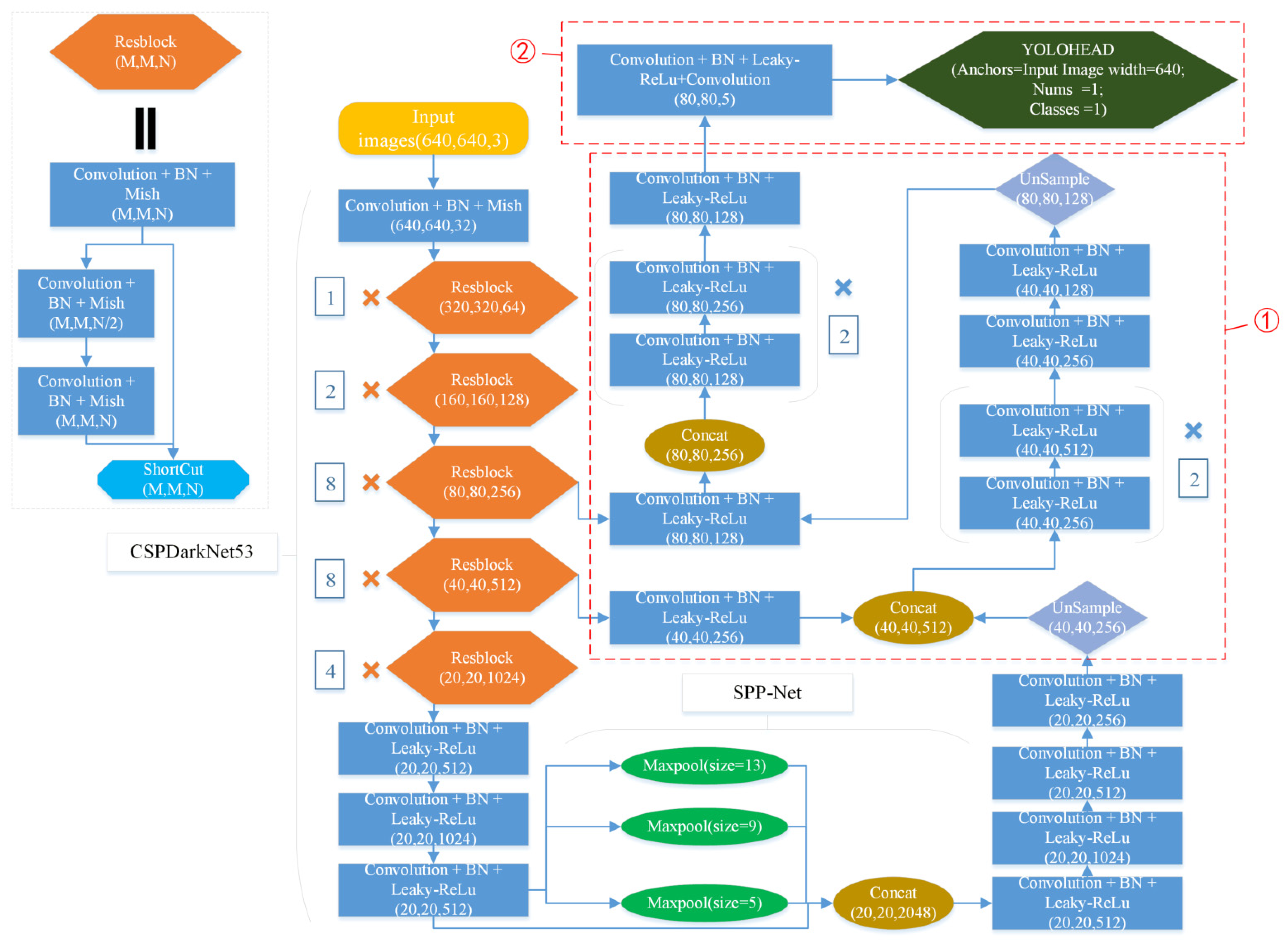
3.2.1. Network Structure Framework
3.2.2. Loss Function
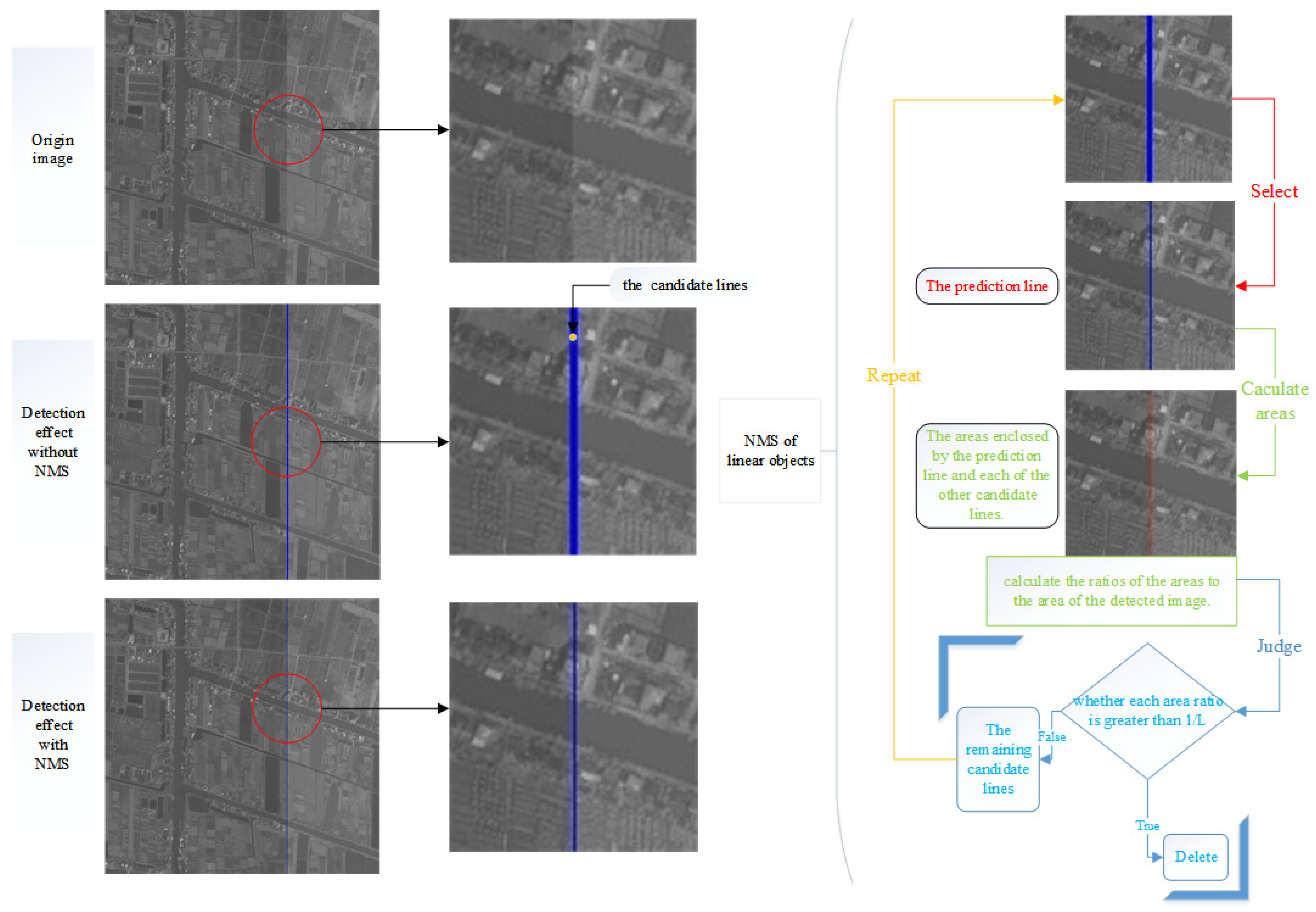
3.2.3. Non-Maximum Suppression of Linear Objects
3.3. Large-Scale Image Stripe Noise Detection Method
4. Experiment and Analysis
4.1. Dataset
4.2. Training
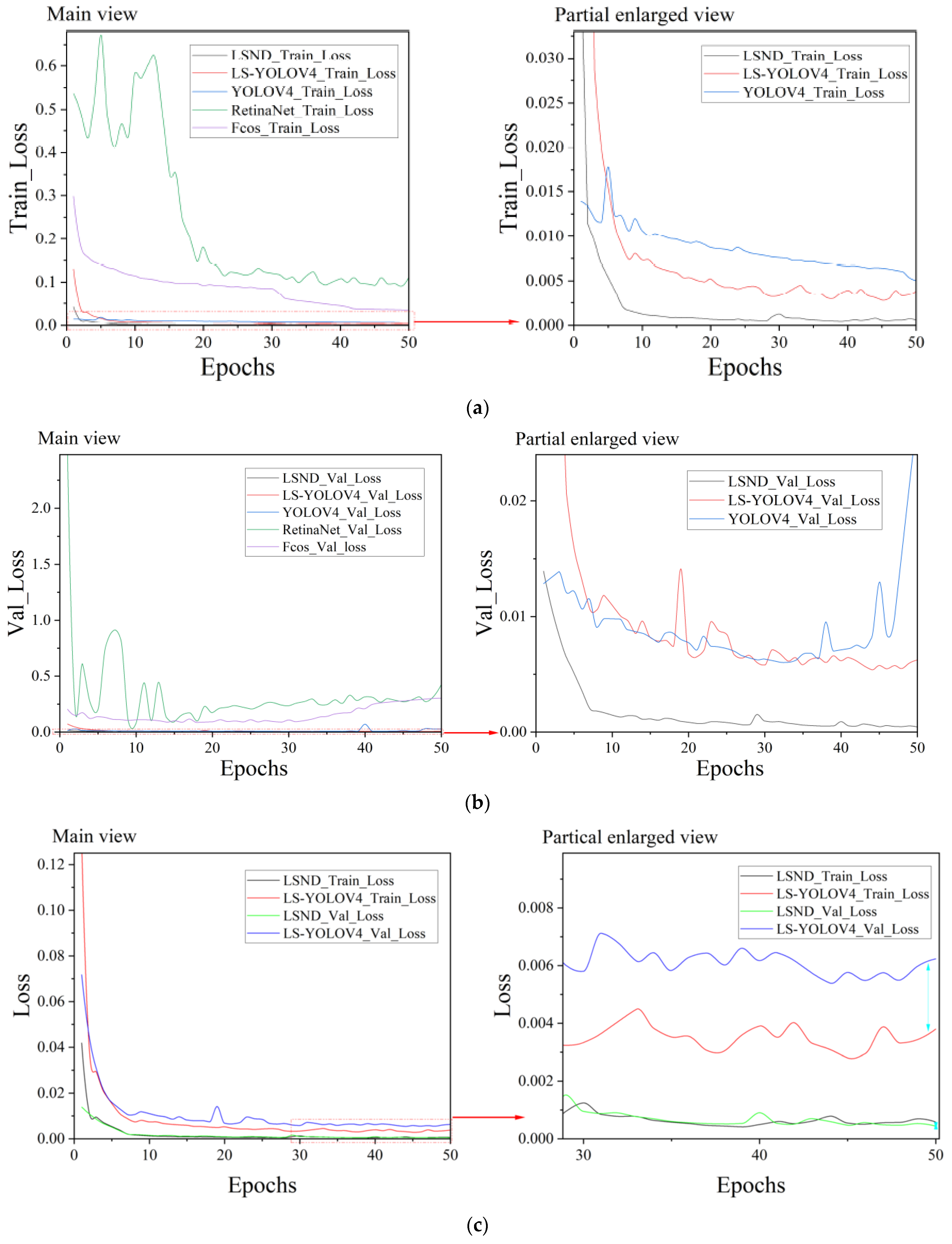
4.3. Loss Curve Analysis
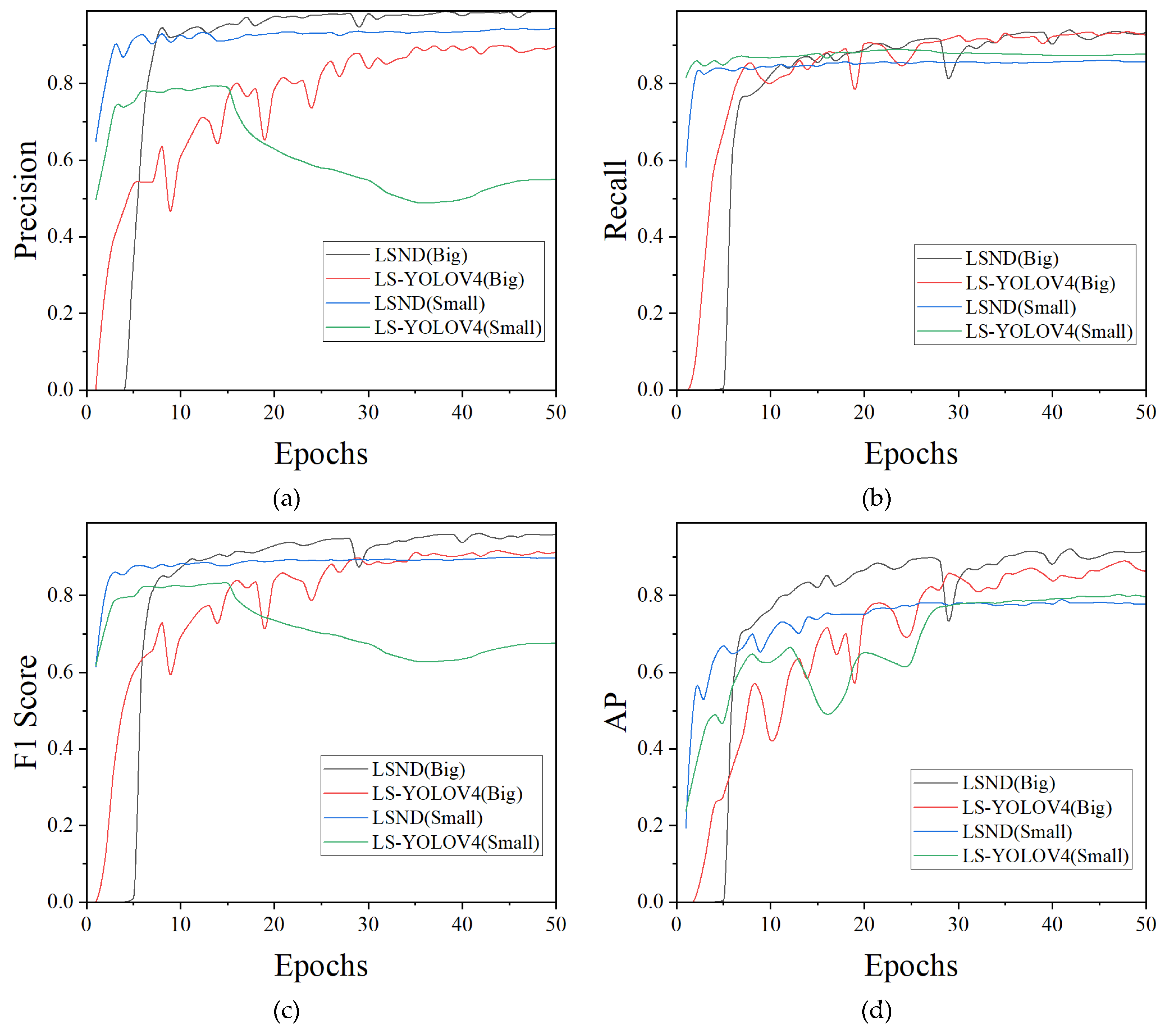
4.4. Model Evaluation
4.4.1. Model Evaluation Indicators
4.4.2. Determination of the Prediction Confidence Threshold
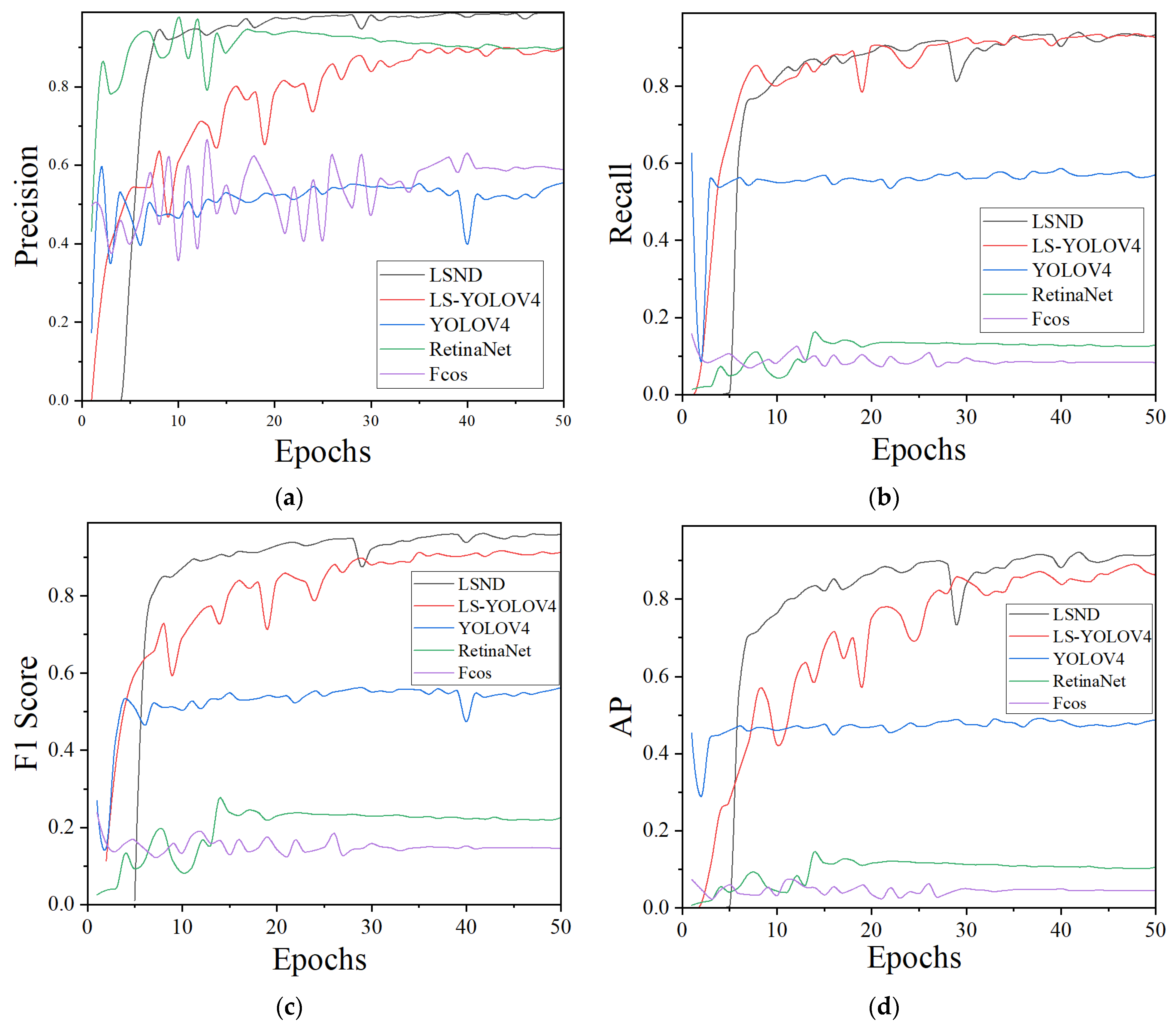
4.4.3. Analysis of the Evaluation Indicators
4.4.4. Robustness Analysis
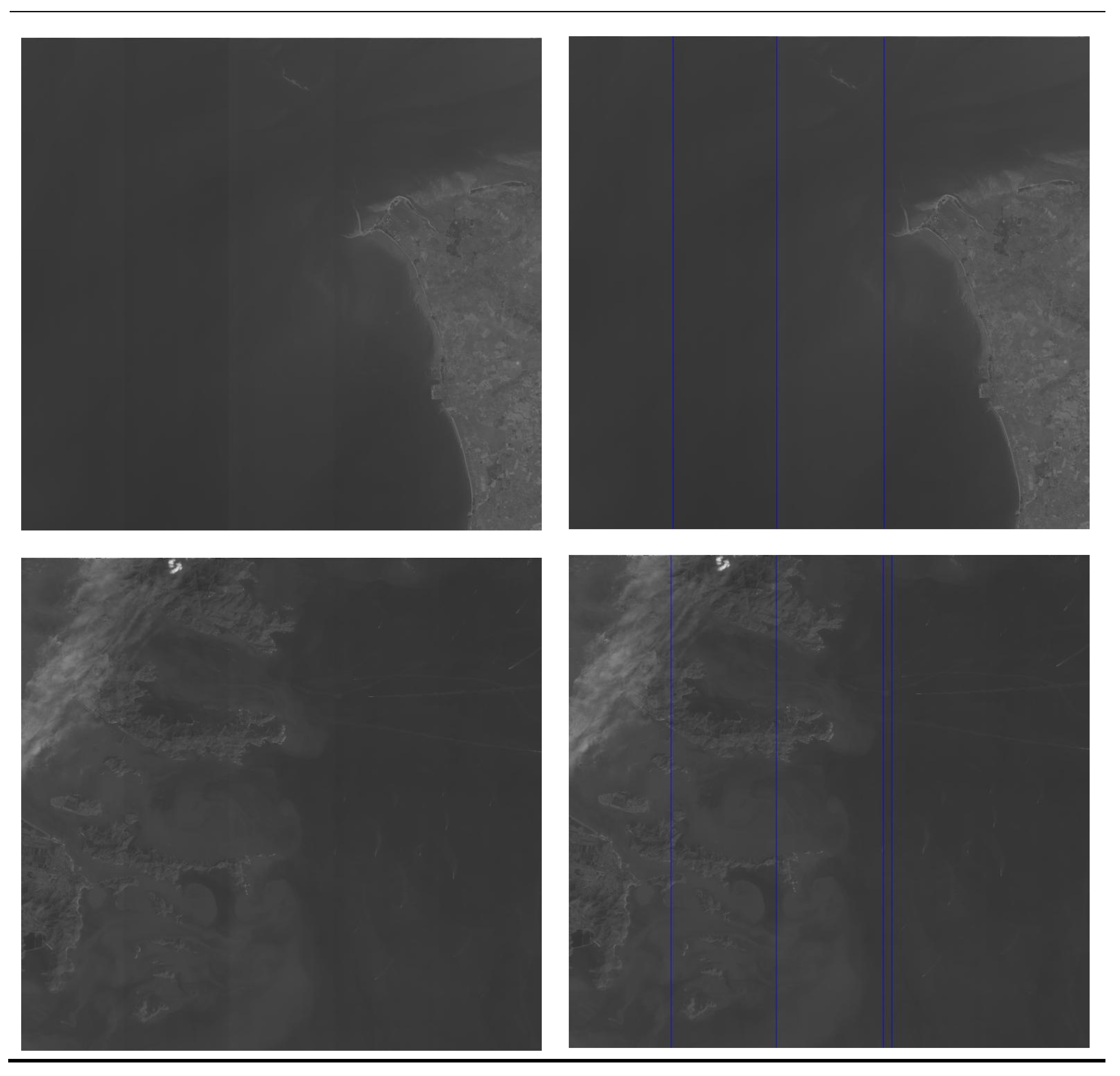
4.5. Image Detection Results
4.6. Real Image Detection Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Algorithms | Backbone | Input Size/Pixel | Test Dataset | mAP/% | Speed f/s | Innovation Points | |
|---|---|---|---|---|---|---|---|
| R-CNN [33] | TWO STAGE MODELS | VGG16 | 1000 × 600 | VOC 2007 | 58.5 | 0.5 | Uses a large number of CNNs to apply bottom-up candidate regions to locate and segment objects. |
| SPP-Net [34] | ZF-5 | 1000 × 600 | VOC 2007 | 59.2 | 2 | Uses the spatial pyramid pooling structure. | |
| Fast R-CNN [35] | VGG16 | 1000 × 600 | VOC 2007 | 70 | 3 | Based on the R-CNN, an improved ROI pooling layer is used. The feature maps of differently sized candidate frames are resampled into fixed-size features. | |
| Faster R-CNN [36] | VGG16 | 1000 × 600 | VOC 2007 | 73.2 | 7 | Based on Fast R-CNN, it proposes the use of a region proposal network (RPN) to generate candidate regions and integrate the steps of generating the candidate regions, feature extraction, object classification, and position regression into a model. | |
| R-FCN [37] | ResNet-101 | 1000 × 600 | VOC 2007 | 80.5 | 9 | Solves the contradiction between “translation-invariance in image classification” and “translation-variance in object detection”, and uses “Position-sensitive score maps” to improve detection speed while improving accuracy | |
| Mask-RCNN [38] | ResNeXt-101 | 1300 × 800 | MS COCO | 39.8 | 11 | Based on Faster R-CNN, it proposes the replacement of the ROI pooling layer with ROI Align, and uses bilinear interpolation to fill the pixels at non-integer positions. No position error occurs when the downstream feature map is mapped to the upstream. | |
| Cascade RCNN [39] | ResNeXt-101-FPN | 1300 × 800 | MS COCO | 42.8 | 8 | It is composed of a series of cascades of detectors with increasing IoU thresholds. With increasing thresholds, high-quality detectors can be trained without reducing the number of samples. | |
| SSD [40] | ONE STAGE MODELS | VGG16 | 300 × 300 | VOC 2007 | 7.1 | 46 | Based on the feature map output by different convolutional layers, it detects objects of different sizes. |
| YOLOv2 [41] | DarkNet-19 | 544 × 544 | VOC 2007 | 8.6 | 40 | (1) Increases the number of candidate boxes compared with the YOLO and uses a powerful constraint positioning method. (2) Proposes multi-scale feature fusion. (3) Use the K-means clustering method for clustering to obtain the anchor boxes. | |
| RetinaNet [42] | ResNet-101-FPN | 800 × 800 | MSCOCO | 39.1 | 5 | Uses the focal loss function to solve unbalanced sample numbers in different categories. | |
| YOLOv3 [43] | DarkNet-53 | 608 × 608 | MS COCO | 33 | 20 | (1) Based on YOLOv2, it changes the backbone. (2) The feature pyramid network (FPN) is used to fuse small feature maps through up-sampling and large-scale integration. (3) Uses the cross-entropy function to support multi-label prediction. | |
| YOLOv4 [44] | CSPDarkNet-53 | 512 × 512 | MS COCO | 3.5 | 23 | Based on YOLOv3, it uses training tricks (such as CmBN, PAN, and SAM) of the latest object detection algorithms based on deep learning to modify and make single GPU training more efficient in terms of both the speed and accuracy. | |
| EfficientDet [45] | EfficientNet | 1536 × 1536 | MS COCO | 51 | 13 | (1) Weighted bidirectional feature fusion network (BiFPN): Weighting improves the efficiency based on the traditional FPN. (2) Hybrid expansion technology: a consistent expansion method is used to improve the efficiency of the input resolution, depth, and width of the backbone, FPN, and box/class. | |
| YOLO [46] | ANCHOR FREE MODELS | VGG16 | 448 × 448 | VOC 2007 | 66.4 | 45 | The first generation of YOLO can be considered a one-stage or anchor-free model. It removes the branch used to extract candidate boxes and directly implements feature extraction, non-selective box classification, and regression in a branched neural network. The network structure is simple compared with the area-based method, and the detection speed is greatly improved. |
| CornerNet [47] | Hourglass-104 | 511 × 511 | MS COCO | 42.1 | 4.1 | (1) Detects the object by detecting a pair of corner points of the bounding box. (2) Proposes corner pooling to better locate the corners of the bounding box. | |
| FCOS [48] | ResNet-101-FPN | - | MS COCO | 44.7 | - | (1) Uses the idea of semantic segmentation to solve the problem of object detection. (2) Changes the classification network to a fully CNN, which explicitly involves converting a fully connected layer to a convolutional layer and up-sampling through de-convolution. (3) Avoids considerable calculations between the IoUs of the GT and anchor boxes during the training process, reducing the memory consumption of the training process. | |
| CenterNet [49] | Hourglass-104 | 511 × 511 | MS COCO | 47.0 | 7.8 | Abandons anchors, and there is no judgment of the positive or negative anchors. The object has only one center point, which is predicted using a heatmap, and does not need to be screened by NMS, and the center point and size of the object are directly detected. | |
References
- Algazi, V.R.; Ford, G.E. Radiometric equalization of non-periodic striping in satellite data. Comput. Graph. Image Process 1981, 16, 287–295. [Google Scholar] [CrossRef]
- Ahern, F.J.; Brown, R.J.; Cihlar, J.; Gauthier, R.; Murphy, J.; Neville, R.A.; Teillet, P.M. Review article: Radiometric correction of visible and infrared remote sensing data at the Canada centre for remote sensing. Int. J. Remote Sens. 1987, 8, 1349–1376. [Google Scholar] [CrossRef]
- Bernstein, R.; Lotspiech, J.B. LANDSAT-4 Radiometric and Geometric Correction and Image Enhancement Results. 1984; Volume 1984, pp. 108–115. Available online: https://ntrs.nasa.gov/citations/19840022301 (accessed on 3 September 2021).
- Chen, J.S.; Shao, Y.; Zhu, B.Q. Destriping CMODIS Based on FIR Method. J. Remote. Sens. 2004, 8, 233–237. [Google Scholar]
- Xiu, J.H.; Zhai, L.P.; Liu, H. Method of removing striping noise in CCD image. Dianzi Qijian/J. Electron Devices 2005, 28, 719–721. [Google Scholar]
- Wang, R.; Zeng, C.; Jiang, W.; Li, P. Terra MODIS band 5th stripe noise detection and correction using MAP-based algorithm. Hongwai yu Jiguang Gongcheng/Infrared Laser Eng. 2013, 42, 273–277. Available online: https://ieeexplore.ieee.org/abstract/document/5964181/ (accessed on 3 September 2021).
- Qu, Y.; Zhang, X.; Wang, Q.; Li, C. Extremely sparse stripe noise removal from nonremote-sensing images by straight line detection and neighborhood grayscale weighted replacement. IEEE Access 2018, 6, 76924–76934. [Google Scholar] [CrossRef]
- Sun, Y.-J.; Huang, T.-Z.; Ma, T.-H.; Chen, Y. Remote Sensing Image Stripe Detecting and Destriping Using the Joint Sparsity Constraint with Iterative Support Detection. Remote Sens. 2019, 11, 608. [Google Scholar] [CrossRef] [Green Version]
- Wang, Q.; Ma, J.; Yu, S.; Tan, L. Noise detection and image denoising based on fractional calculus. Chaos Solitons Fractals 2020, 131, 109463. [Google Scholar] [CrossRef]
- Hao, Z. Deep learning review and discussion of its future development. MATEC Web Conf. 2019, 277, 02035. [Google Scholar] [CrossRef]
- LeCun, Y. Learning invariant feature hierarchies. In European Conference on Computer Vision; Lect. Notes Comput. Sci. (including Subser. Lect. Notes Artif. Intell. Lect. Notes Bioinformatics); Springer: Berlin/Heidelberg, Germany, 2012; Volume 7583 LNCS, pp. 496–505. [Google Scholar] [CrossRef]
- Mohamed, A.-R.; Dahl, G.; Hinton, G. Deep Belief Networks for Phone Recognition. Scholarpedia 2009, 4, 1–9. [Google Scholar] [CrossRef]
- Teng, P. Technical Features of GF-2 Satellite. Aerospace China 2015, 3–9. Available online: http://qikan.cqvip.com/Qikan/Article/Detail?id=665902279 (accessed on 1 December 2021).
- Wei, Z. A Summary of Research and Application of Deep Learning. Int. Core J. Eng. 2019, 5, 167–169. Available online: https://www.airitilibrary.com/Publication/alDetailedMesh?docid=P20190813001-201908-201908130007-201908130007-167-169 (accessed on 3 September 2021).
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2323. [Google Scholar] [CrossRef] [Green Version]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2012. Available online: https://proceedings.neurips.cc/paper/4824-imagenet-classification-with-deep-convolutional-neural-networks.pdf (accessed on 3 September 2021). [CrossRef]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, 7–9 May 2015; Available online: https://arxiv.org/abs/1409.1556 (accessed on 3 September 2021).
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar] [CrossRef] [Green Version]
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the Inception Architecture for Computer Vision. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 2818–2826. [Google Scholar] [CrossRef] [Green Version]
- Szegedy, C.; Ioffe, S.; Vanhoucke, V.; Alemi, A.A. Inception-v4, inception-ResNet and the impact of residual connections on learning. In Proceedings of the 31st AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017; pp. 4278–4284. Available online: https://www.aaai.org/ocs/index.php/AAAI/AAAI17/paper/viewPaper/14806 (accessed on 3 September 2021).
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef] [Green Version]
- Xie, S.; Girshick, R.; Dollár, P.; Tu, Z.; He, K. Aggregated residual transformations for deep neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 5987–5995. [Google Scholar] [CrossRef] [Green Version]
- Huang, G.; Liu, Z.; van der Maaten, L.; Weinberger, K.Q. Densely connected convolutional networks. In Proceedings of the 30th IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2016; pp. 2261–2269. [Google Scholar] [CrossRef] [Green Version]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7132–7141. Available online: http://openaccess.thecvf.com/content_cvpr_2018/html/Hu_Squeeze-and-Excitation_Networks_CVPR_2018_paper (accessed on 3 September 2021).
- Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. MobileNets: Efficient Convolutional Neural Networks for Mobile Vision Applications. arXiv 2017, arXiv:1704.04861. Available online: http://arxiv.org/abs/1704.04861 (accessed on 3 September 2021).
- Zhang, X.; Zhou, X.; Lin, M.; Sun, J. ShuffleNet: An Extremely Efficient Convolutional Neural Network for Mobile Devices. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 6848–6856. [Google Scholar] [CrossRef] [Green Version]
- Srinivas, A.; Lin, T.-Y.; Parmar, N.; Shlens, J.; Abbeel, P.; Vaswani, A. Bottleneck Transformers for Visual Recognition. 2021, pp. 16519–16529. Available online: http://arxiv.org/abs/2101.11605 (accessed on 3 September 2021).
- Zhong, L.; Hu, L.; Zhou, H. Deep learning based multi-temporal crop classification. Remote Sens. Environ. 2019, 221, 430–443. [Google Scholar] [CrossRef]
- Liu, T.; Yang, L.; Lunga, D. Change detection using deep learning approach with object-based image analysis. Remote Sens. Environ. 2021, 256, 112308. [Google Scholar] [CrossRef]
- Wu, F.; Wang, C.; Zhang, H.; Li, J.; Li, L.; Chen, W.; Zhang, B. Built-up area mapping in China from GF-3 SAR imagery based on the framework of deep learning. Remote Sens. Environ. 2021, 262, 112515. [Google Scholar] [CrossRef]
- Zhiqiang, W.; Jun, L. A review of object detection based on convolutional neural network. In Proceedings of the 2017 36th Chinese Control Conference (CCC), Dalian, China, 26–28 July 2017; pp. 11104–11109. [Google Scholar] [CrossRef]
- Wang, X.; Zhi, M. Summary of Object Detection Based on Convolutional Neural Network. In Proceedings of the Eleventh International Conference on Graphics and Image Processing (ICGIP 2019), Hangzhou, China, 12–14 October 2019; Available online: https://www.spiedigitallibrary.org/conference-proceedings-of-spie/11373/113730L/Summary-of-object-detection-based-on-convolutional-neural-network/10.1117/12.2557219.short (accessed on 3 September 2021).
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Rich feature hierarchies for accurate object detection and semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 580–587. [Google Scholar] [CrossRef] [Green Version]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Spatial Pyramid Pooling in Deep Convolutional Networks for Visual Recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 1904–1916. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Girshick, R. Proceedings of the IEEE International Conference on Computer Vision (ICCV). 2015, pp. 1440–1448. Available online: http://openaccess.thecvf.com/content_iccv_2015/html/Girshick_Fast_R-CNN_ICCV_2015_paper.html (accessed on 3 September 2021).
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 1137–1149. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dai, J.; Li, Y.; He, K.; Sun, J. R-fcn: Object Detection Via Region-Based Fully Convolutional Networks. Adv. Neural Inf. Process. Syst. 2016, 29. Available online: http://papers.nips.cc/paper/6464-r-fcn-object-detection-via-region-based-fully-convolutional-networks (accessed on 3 September 2021).
- He, K.; Gkioxari, G.; Dollar, P.; Girshick, R. Proceedings of the IEEE International Conference on Computer Vision (ICCV). 2017, pp. 2961–2969. Available online: http://openaccess.thecvf.com/content_iccv_2017/html/He_Mask_R-CNN_ICCV_2017_paper.html (accessed on 3 September 2021).
- Cai, Z.; Vasconcelos, N. Cascade R-CNN: Delving into High Quality Object Detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 6154–6162. [Google Scholar] [CrossRef] [Green Version]
- Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C.; Reed, S.; Fu, C.Y.; Berg, A.C. SSD: Single shot multibox detector. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; Lect. Notes Comput. Sci. (including Subser. Lect. Notes Artif. Intell. Lect. Notes Bioinformatics). Volume 9905 LNCS, pp. 21–37. [Google Scholar] [CrossRef] [Green Version]
- Redmon, J.; Farhadi, A. YOLO9000: Better, faster, stronger. In Proceedings of the 30th IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 6517–6525. [Google Scholar] [CrossRef] [Green Version]
- Lin, T.; Goyal, P.; Girshick, R.; He, K.; Dollar, P. Proceedings of the IEEE International Conference on Computer Vision (ICCV). 2017, pp. 2980–2988. Available online: http://openaccess.thecvf.com/content_iccv_2017/html/Lin_Focal_Loss_for_ICCV_2017_paper.html (accessed on 3 September 2021).
- Redmon, J.; Farhadi, A. YOLOv3: An Incremental Improvement. arXiv 2018, arXiv:1804.02767. Available online: http://arxiv.org/abs/1804.02767 (accessed on 3 September 2021).
- Bochkovskiy, A.; Wang, C.-Y.; Liao, H.-Y.M. YOLOv4: Optimal Speed and Accuracy of Object Detection. arXiv 2020, arXiv:2004.10934. Available online: http://arxiv.org/abs/2004.10934 (accessed on 3 September 2021).
- Tan, M.; Pang, R.; Le, Q.V. EfficientDet: Scalable and efficient object detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 10778–10787. [Google Scholar] [CrossRef]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You only look once: Unified, real-time object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 779–788. [Google Scholar] [CrossRef] [Green Version]
- Law, H.; Deng, J. CornerNet: Detecting Objects as Paired Keypoints. Int. J. Comput. Vis. 2018, 128, 642–656. [Google Scholar] [CrossRef] [Green Version]
- Tian, Z.; Shen, C.; Chen, H.; He, T. FCOS: Fully convolutional one-stage object detection. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 27–28 October 2019; pp. 9626–9635. [Google Scholar] [CrossRef] [Green Version]
- Zhou, X.; Wang, D.; Krähenbühl, P. Objects as Points. Available online: http://arxiv.org/abs/1904.07850 (accessed on 3 September 2021).
- Cui, J.; Shi, P.; Bai, W.; Liu, X. Destriping model of GF-2 image based on moment matching. Remote Sens. Land Resour. 2017, 29, 34–38. [Google Scholar]
- Lin, T.-Y.; Dollár, P.; Girshick, R.; He, K.; Hariharan, B.; Belongie, S. Feature Pyramid Networks for Object Detection. December 2016. Available online: https://arxiv.org/abs/1612.03144v2 (accessed on 5 September 2021).
- Wang, C.-Y.; Bochkovskiy, A.; Liao, H.-Y.M. Scaled-YOLOv4: Scaling Cross Stage Partial Network. arXiv 2020, arXiv:2011.08036. Available online: http://arxiv.org/abs/2011.08036 (accessed on 3 September 2021).
- Zheng, Z.; Wang, P.; Liu, W.; Li, J.; Ye, R.; Ren, D. Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression. arXiv 2019, arXiv:1911.08287. [Google Scholar] [CrossRef]
- Loshchilov, I.; Hutter, F. SGDR: Stochastic gradient descent with warm restarts. In Proceedings of the 5th International Conference on Learning Representations, Toulon, France, 24–26 April 2017. [Google Scholar]
- Kingma, D.P.; Ba, J.L. Adam: A method for stochastic optimization. In Proceedings of the 3rd International Conference on Learning Representations, San Diego, CA, USA, 7–9 May 2015; Available online: https://arxiv.org/abs/1412.6980v9 (accessed on 3 September 2021).
- Zhang, Z.; He, T.; Zhang, H.; Zhang, Z.; Xie, J.; Li, M. Bag of Freebies for Training Object Detection Neural Networks. arXiv 2019, arXiv:1902.04103. [Google Scholar]
- Carion, N.; Massa, F.; Synnaeve, G.; Usunier, N.; Kirillov, A.; Zagoruyko, S. End-to-End Object Detection with Transformers. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; Lect. Notes Comput. Sci. (including Subser. Lect. Notes Artif. Intell. Lect. Notes Bioinformatics). Volume 12346 LNCS, pp. 213–229. [Google Scholar] [CrossRef]












| References | Detection Method |
|---|---|
| Destriping CMODIS based on the FIR method [5] | The wavelet transform is used to detect the singularity of the signal, and the periodic distribution of the stripe noise in the wavelet coefficients is used to detect the position of the stripe noise. |
| Terra MODIS band 5th stripe noise detection and correction using the MAP-based algorithm [6] | The gradient of each pixel in each direction is calculated. Then, the noise pixels in the stripe noise image are extracted based on the threshold, to finally realize the detection of stripe noise. |
| Extremely sparse stripe noise removal from non-remote-sensing images using straight-line detection and neighborhood grayscale-weighted replacement [7] | Preselected stripe noise lines are detected using a local progressive probabilistic Hough transform. Subsequently, the real stripe noise lines are screened from the detected lines according to the features of the grayscale discontinuities. |
| Remote sensing image stripe detection and destriping using the joint sparsity constraint with iterative support detection [8] | The ℓw,2,1-norm is used to characterize the joint sparsity of the stripes, and iterative support detection (ISD) is applied to calculate the weight vector in the ℓw,2,1-norm, which shows the stripe position in the observed image. |
| Noise detection and image denoising based on fractional calculus [9] | The noise detection method determines the noise position by the fractional differential gradient; it achieves detection of the noise, snowflake and stripe anomalies by utilizing the neighborhood information feature of the image and the contour and direction distribution of various noise anomalies in the spatial domain. |
| Category | Center Point X | Center Point Y | Length H |
|---|---|---|---|
| 0 | 477 | 320 | 640 |
| 0 | 615 | 320 | 640 |
| 0 | 625 | 320 | 640 |
| Category | Center Point X | Center Point Y | Width H | Length H |
|---|---|---|---|---|
| 0 | 477 | 320 | 2 | 640 |
| 0 | 615 | 320 | 2 | 640 |
| 0 | 625 | 320 | 2 | 640 |
| Algorithm | Backbone | Size | GT | Precision Rate (%) | Recall Rate (%) | F1-Score Rate (%) | AP Rate (%) |
|---|---|---|---|---|---|---|---|
| LSND | CSPDarkNet53 | 640 | 2420 | 98.74 | 93.85 | 96.09 | 92.07 |
| LS-YOLOv4 | CSPDarkNet53 | 640 | 2420 | 89.98 | 93.56 | 91.60 | 88.84 |
| YOLOv4 | CSPDarkNet53 | 640 | 2420 | 59.43 | 62.65 | 56.25 | 49.08 |
| RetinaNet | ResNet50-FPN | 640 | 2420 | 97.66 | 16.26 | 27.70 | 14.56 |
| FCOS | ResNet50-FPN | 640 | 2420 | 66.48 | 15.79 | 23.96 | 7.36 |
| Algorithm | Backbone | Size | GT | Precision Rate (%) | Recall Rate (%) | F1-Score Rate (%) | AP Rate (%) |
|---|---|---|---|---|---|---|---|
| LSND | CSPDarkNet53 | 640 | 2420 | 98.74 | 93.85 | 96.09 | 92.07 |
| LS-YOLOv4 | CSPDarkNet53 | 640 | 2420 | 89.99 | 93.56 | 91.60 | 88.84 |
| LSND | CSPDarkNet53 | 64 | 18390 | 94.28 | 86.03 | 89.93 | 78.86 |
| LS-YOLOv4 | CSPDarkNet53 | 64 | 18390 | 79.22 | 88.88 | 83.19 | 80.21 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, B.; Zhou, Y.; Xie, D.; Zheng, L.; Wu, Y.; Yue, J.; Jiang, S. Stripe Noise Detection of High-Resolution Remote Sensing Images Using Deep Learning Method. Remote Sens. 2022, 14, 873. https://doi.org/10.3390/rs14040873
Li B, Zhou Y, Xie D, Zheng L, Wu Y, Yue J, Jiang S. Stripe Noise Detection of High-Resolution Remote Sensing Images Using Deep Learning Method. Remote Sensing. 2022; 14(4):873. https://doi.org/10.3390/rs14040873
Chicago/Turabian StyleLi, Binbo, Ying Zhou, Donghai Xie, Lijuan Zheng, Yu Wu, Jiabao Yue, and Shaowei Jiang. 2022. "Stripe Noise Detection of High-Resolution Remote Sensing Images Using Deep Learning Method" Remote Sensing 14, no. 4: 873. https://doi.org/10.3390/rs14040873
APA StyleLi, B., Zhou, Y., Xie, D., Zheng, L., Wu, Y., Yue, J., & Jiang, S. (2022). Stripe Noise Detection of High-Resolution Remote Sensing Images Using Deep Learning Method. Remote Sensing, 14(4), 873. https://doi.org/10.3390/rs14040873







