Lunar Crater Detection on Digital Elevation Model: A Complete Workflow Using Deep Learning and Its Application
Abstract
1. Introduction
- In data preparation, a global DEM image is divided into a less number of sub-region images than the previous work [20] through a carefully designed grid cropped strategy. The new strategy can not only improve the detection rate of lunar craters by exploiting their size compensation, but also effectively reduce the cost of computation in both inference and post-processing steps as the number of each duplicate crater is reduced in an order of magnitude.
- In the detection process, the cropped DEM images are input into a CNN model for joint detection of multiple lunar craters, which predicts their classification probabilities and location coordinates in an end-to-end manner.
- During the post processing step, we merge all the detected craters while transforming their pixel coordinates to the geographical coordinates, and remove the duplicate craters by using a non-maximum suppression (NMS) algorithm before and after the merger.
- In performance evaluation, we adopt the Average Precision (AP), a standard detection metric for the object detection task. Comparing to the single precision and recall metrics usually used in previous works [20,21], the AP metric can fully verify the detection performance of a CDA by considering a full range of precision and recall rates.
2. Methods
2.1. Data Preparation
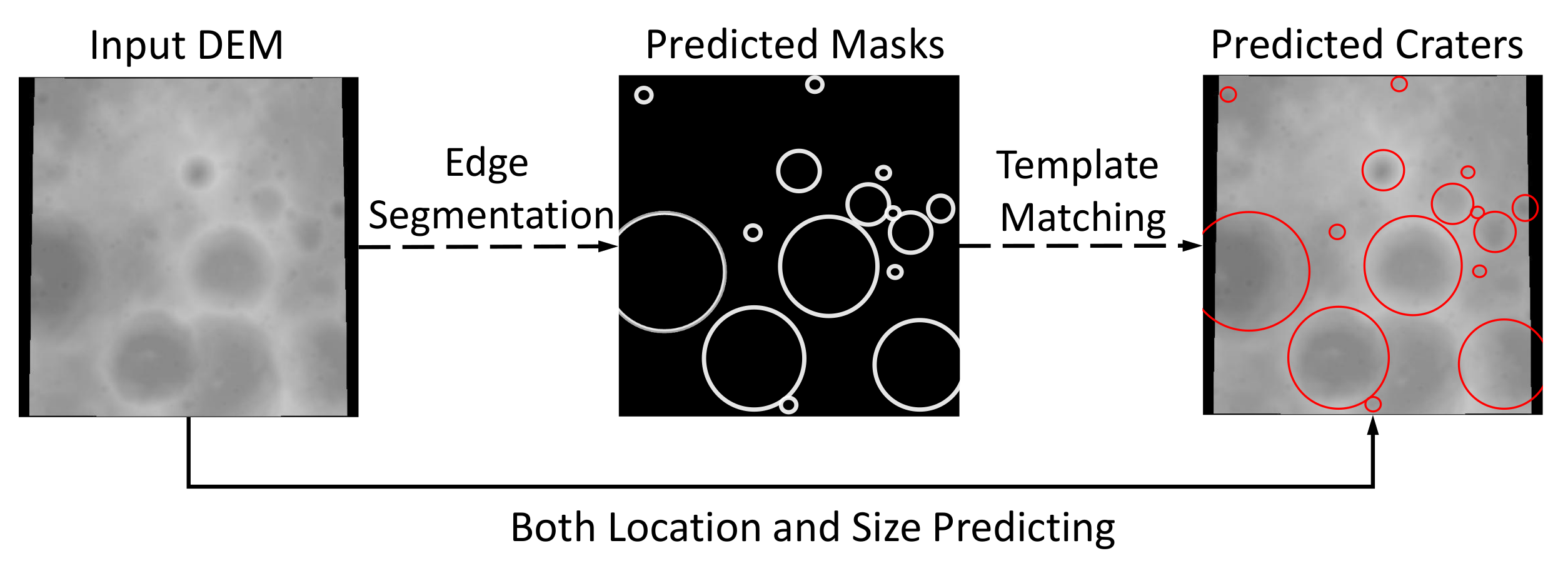
2.2. Crater Detection Process via Convolutional Neural Network
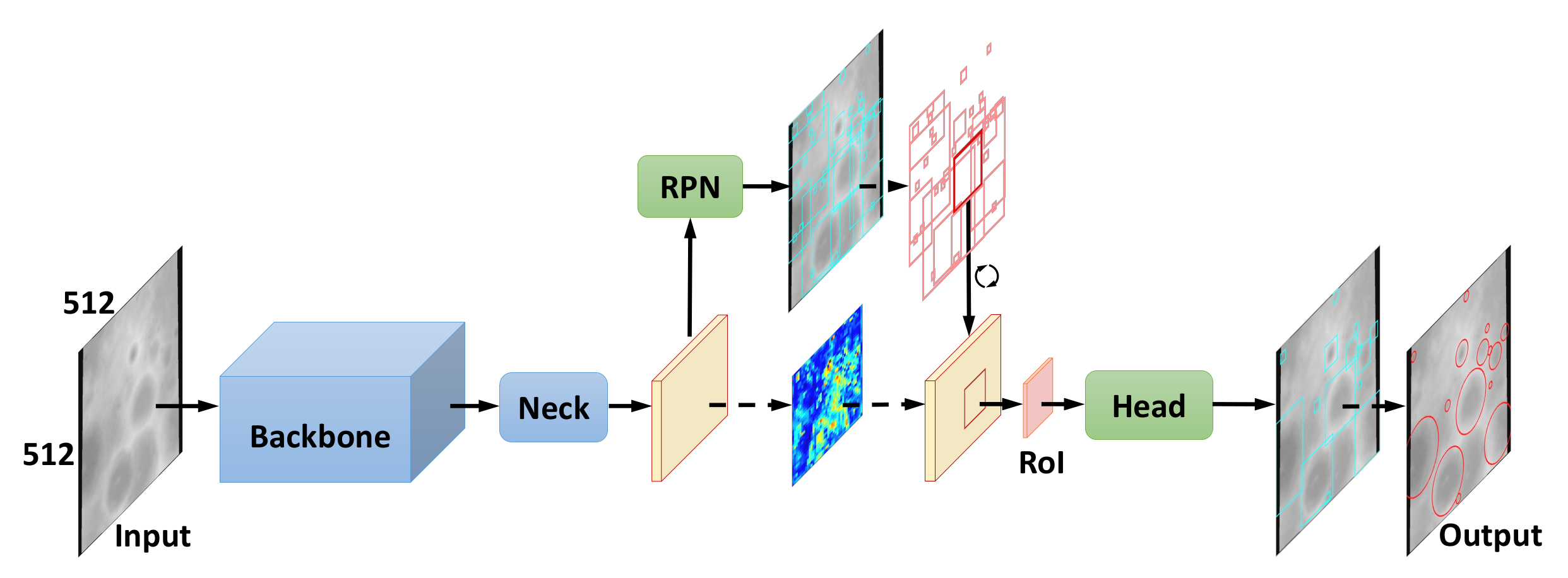
2.2.1. Region-Based Detection Network (RDN)
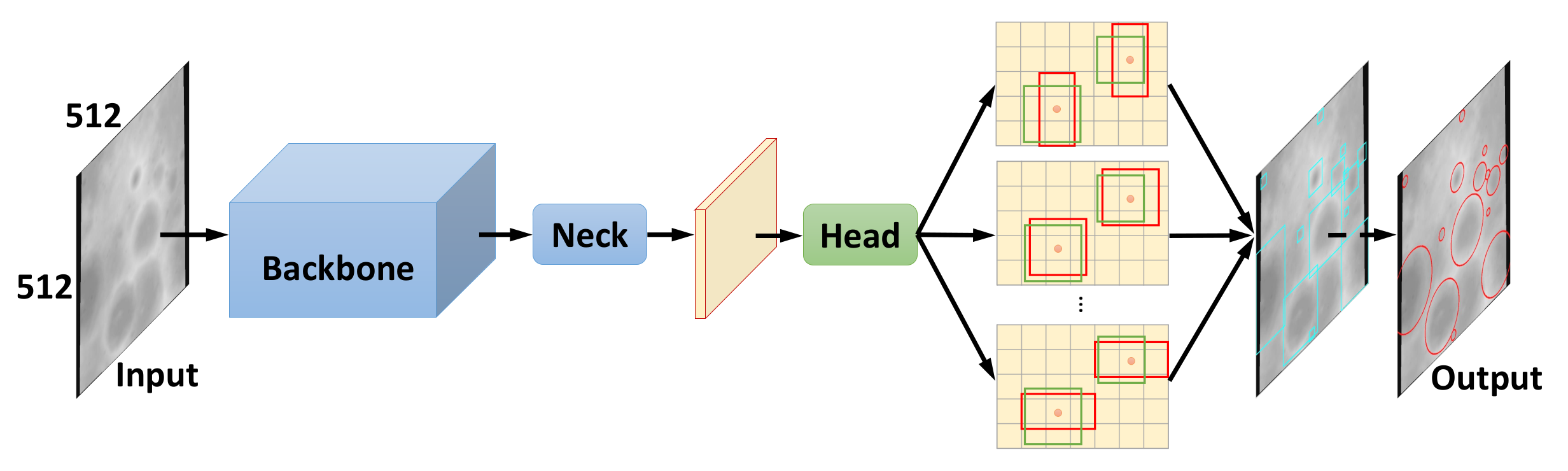
2.2.2. Anchor-Based Detection Network (ADN)
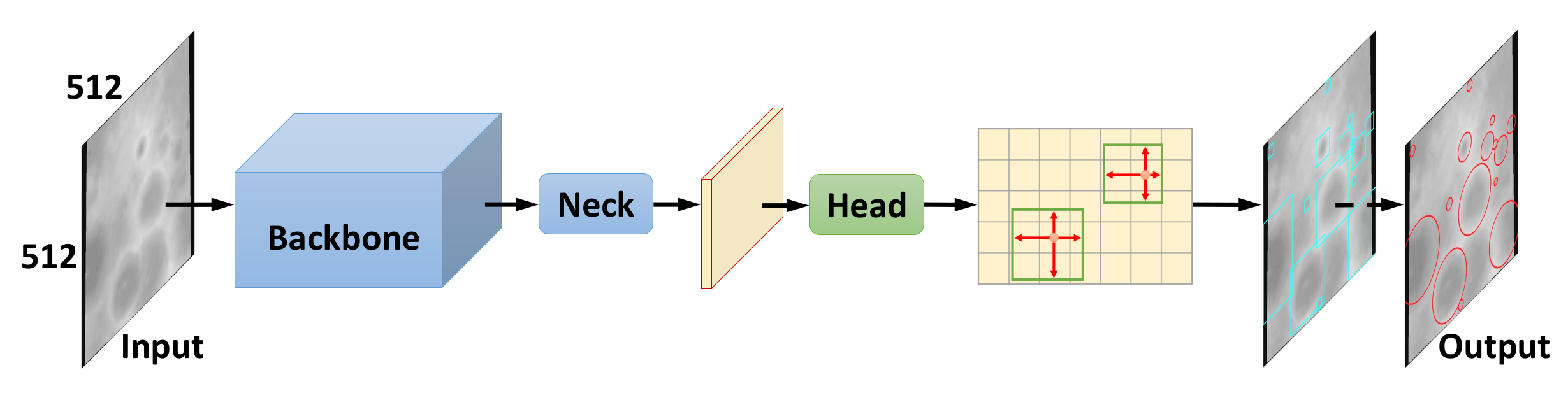
2.2.3. Point-Based Detection Network (PDN)
2.3. Post Processing
2.4. Model Evaluation
- Calculate a cumulative set of precision and recall values. We first sort all detected craters in reverse order with respect to their classification probabilities, and use Formula (4) with a pre-defined IoU threshold to calculate the cumulative numbers of true positives (TP) and false positives (FP) according to their maximum IoU overlaps with the associated GT targets. Note that we only regard the detected crater with the highest classification probability as TP when a GT target matches multiple predicted craters. And then, we can get the corresponding precision and recall values by using the following formulas:
- Draw the P-R curve with interpolation of all points. We first get the P-R scatter plot according to a given set of precision and recall values, and then interpolate the precision of each point by using the maximum precision whose recall value is greater or equal than the one of the current point. The interpolation formula is as follows:where denotes the interpolated precision at recall .
- Calculate the AP value. We can use the following formula to get the area under curve (AUC) of the P-R curve, which is the AP value for crater detection.
3. Results
3.1. Hyper-Parameter Setting
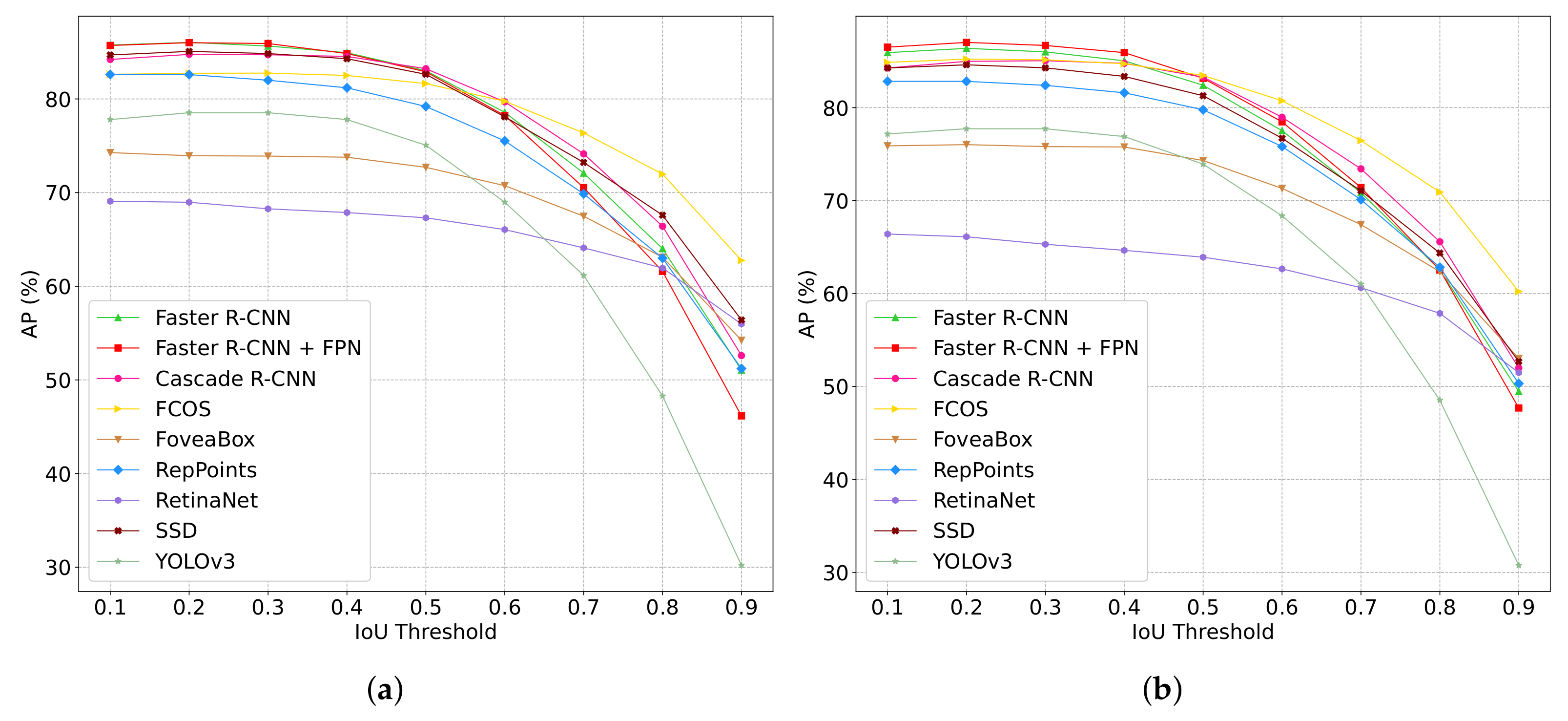
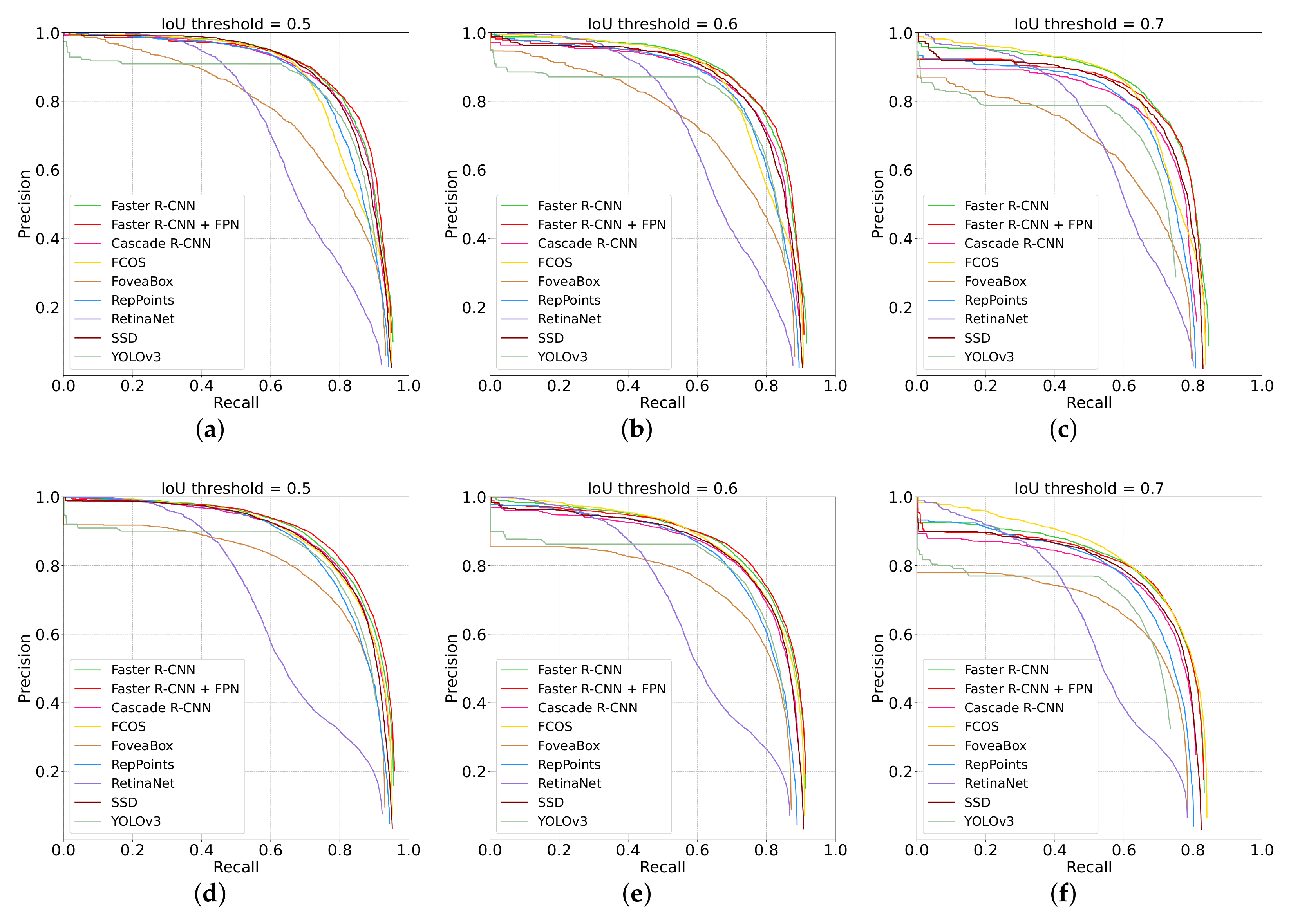
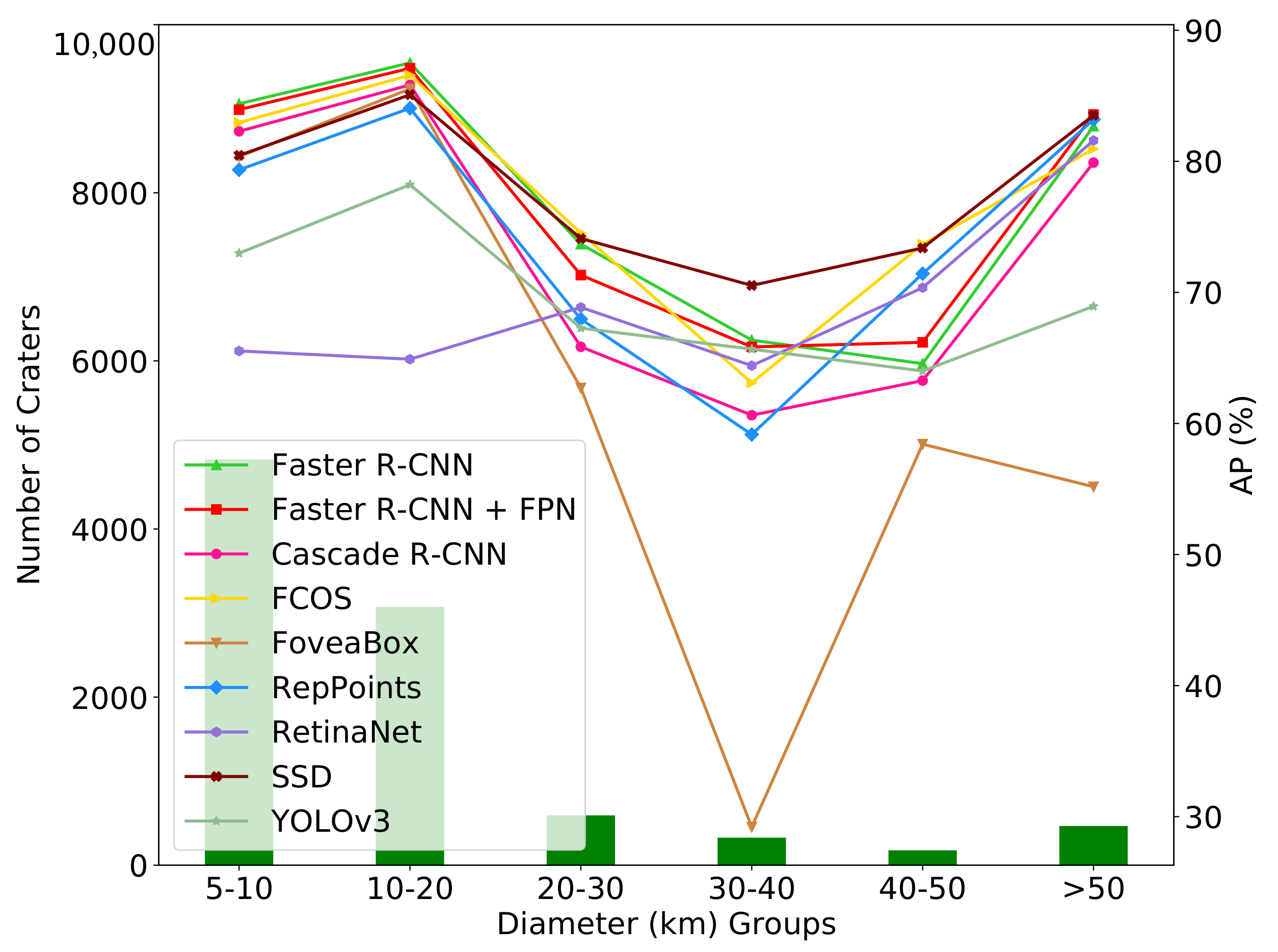
3.2. Experimental Results
4. Discussion
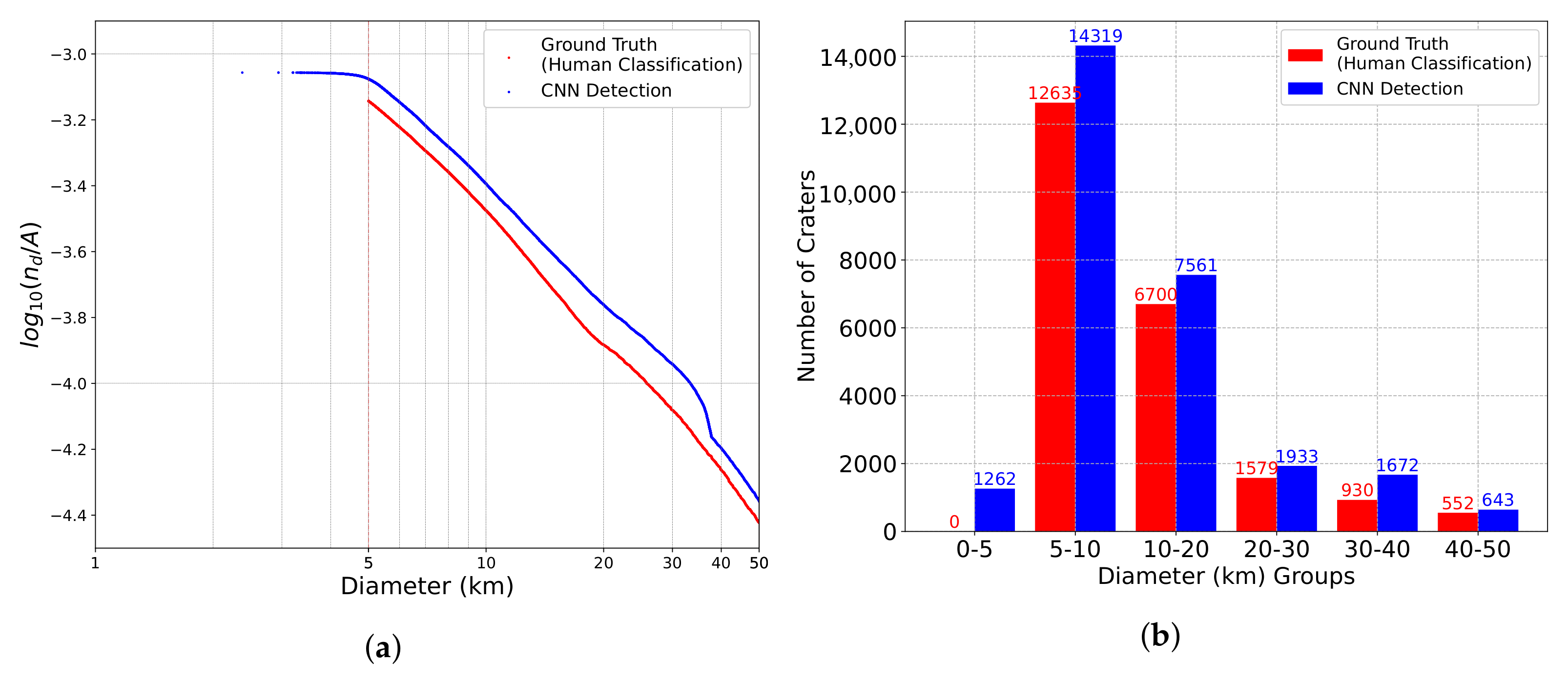
4.1. Lunar Crater Detection
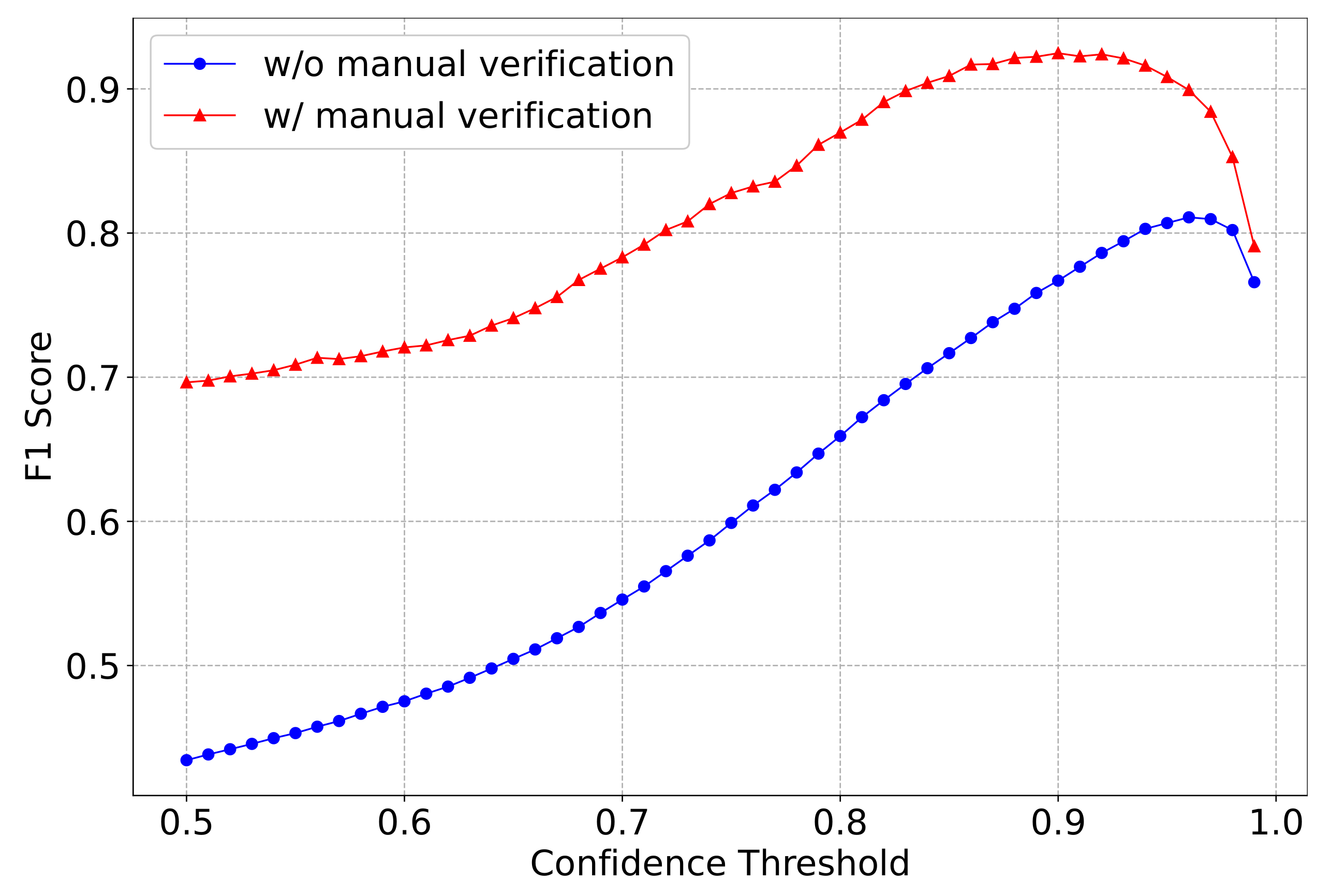
4.2. Lunar Crater Verification
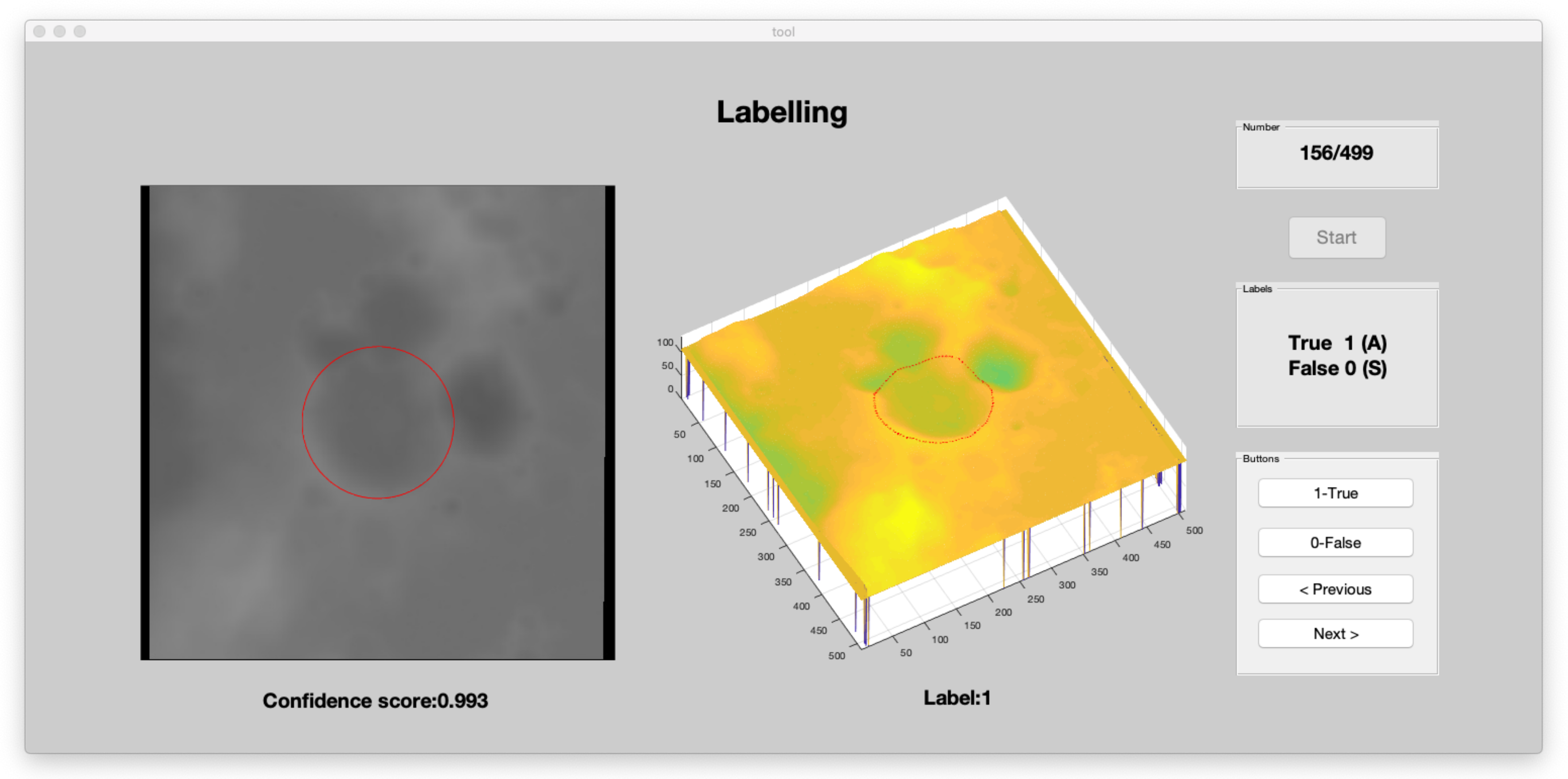
4.3. Visualization Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wiesli, R.A.; Beard, B.L.; Taylor, L.A.; Johnson, C.M. Space weathering processes on airless bodies: Fe isotope fractionation in the lunar regolith. Earth Planet. Sci. Lett. 2003, 216, 457–465. [Google Scholar] [CrossRef]
- Head, J.W.; Fassett, C.I.; Kadish, S.J.; Smith, D.E.; Zuber, M.T.; Neumann, G.A.; Mazarico, E. Global distribution of large lunar craters: Implications for resurfacing and impactor populations. Science 2010, 329, 1504–1507. [Google Scholar] [CrossRef] [PubMed]
- Neukum, G.; Ivanov, B.A.; Hartmann, W.K. Cratering records in the inner solar system in relation to the lunar reference system. In Chronology and Evolution of Mars; Springer: Berlin/Heidelberg, Germany, 2001; pp. 55–86. [Google Scholar]
- Salih, A.L.; Schulte, P.; Grumpe, A.; Wöhler, C.; Hiesinger, H. Automatic crater detection and age estimation for mare regions on the lunar surface. In Proceedings of the 25th European Signal Processing Conference (EUSIPCO), Kos Island, Greece, 28 August–2 September 2017; pp. 518–522. [Google Scholar]
- Povilaitis, R.; Robinson, M.; Van der Bogert, C.; Hiesinger, H.; Meyer, H.; Ostrach, L. Crater density differences: Exploring regional resurfacing, secondary crater populations, and crater saturation equilibrium on the moon. Planet. Space Sci. 2018, 162, 41–51. [Google Scholar] [CrossRef]
- Leroy, B.; Medioni, G.; Johnson, E.; Matthies, L. Crater detection for autonomous landing on asteroids. Image Vis. Comput. 2001, 19, 787–792. [Google Scholar] [CrossRef]
- Kim, J.R.; Muller, J.P.; van Gasselt, S.; Morley, J.G.; Neukum, G. Automated crater detection, a new tool for Mars cartography and chronology. Photogramm. Eng. Remote Sens. 2005, 71, 1205–1217. [Google Scholar] [CrossRef]
- Sawabe, Y.; Matsunaga, T.; Rokugawa, S. Automated detection and classification of lunar craters using multiple approaches. Adv. Space Res. 2006, 37, 21–27. [Google Scholar] [CrossRef]
- Ding, M.; Cao, Y.; Wu, Q. Novel approach of crater detection by crater candidate region selection and matrix-pattern-oriented least squares support vector machine. Chin. J. Aeronaut. 2013, 26, 385–393. [Google Scholar] [CrossRef]
- Cohen, J.P.; Ding, W. Crater detection via genetic search methods to reduce image features. Adv. Space Res. 2014, 53, 1768–1782. [Google Scholar] [CrossRef][Green Version]
- Salamuniccar, G.; Loncaric, S. Method for crater detection from martian digital topography data using gradient value/orientation, morphometry, vote analysis, slip tuning, and calibration. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2317–2329. [Google Scholar] [CrossRef]
- Xie, Y.; Tang, G.; Yan, S.; Lin, H. Crater detection using the morphological characteristics of Chang’E-1 digital elevation models. IEEE Geosci. Remote Sens. Lett. 2013, 10, 885–889. [Google Scholar]
- Liu, D.; Chen, M.; Qian, K.; Lei, M.; Zhou, Y. Boundary detection of dispersal impact craters based on morphological characteristics using lunar digital elevation model. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 5632–5646. [Google Scholar] [CrossRef]
- Chen, M.; Liu, D.; Qian, K.; Li, J.; Lei, M.; Zhou, Y. Lunar crater detection based on terrain analysis and mathematical morphology methods using digital elevation models. IEEE Trans. Geosci. Remote Sens. 2018, 56, 3681–3692. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, B.; Xue, H.; Li, X.; Ma, J. An Improved Global Catalog of Lunar Impact Craters (≥1 km) with 3D Morphometric Information and Updates on Global Crater Analysis. J. Geophys. Res. Planets 2021, 126, e2020JE006728. [Google Scholar] [CrossRef]
- Di, K.; Li, W.; Yue, Z.; Sun, Y.; Liu, Y. A machine learning approach to crater detection from topographic data. Adv. Space Res. 2014, 54, 2419–2429. [Google Scholar] [CrossRef]
- Boukercha, A.; Al-Tameemi, A.; Grumpe, A.; Wöhler, C. Automatic Crater Recognition Using Machine Learning with Different Features and Their Combination. In Proceedings of the 45th Lunar and Planetary Science Conference (LPSC), The Woodlands, TX, USA, 17–21 March 2014; p. 2842. [Google Scholar]
- Palafox, L.; Alvarez, A.; Hamilton, C. Automated detection of impact craters and volcanic rootless cones in mars satellite imagery using convolutional neural networks and support vector machines. In Proceedings of the 46th Lunar and Planetary Science Conference (LPSC), The Woodlands, TX, USA, 16–20 March 2015; pp. 1–2. [Google Scholar]
- Emami, E.; Bebis, G.; Nefian, A.; Fong, T. Automatic crater detection using convex grouping and convolutional neural networks. In Proceedings of the 11th International Symposium on Visual Computing (ISVC), Las Vegas, NV, USA, 14–16 December 2015; pp. 213–224. [Google Scholar]
- Silburt, A.; Ali-Dib, M.; Zhu, C.; Jackson, A.; Valencia, D.; Kissin, Y.; Tamayo, D.; Menou, K. Lunar crater identification via deep learning. Icarus 2019, 317, 27–38. [Google Scholar] [CrossRef]
- Ali-Dib, M.; Menou, K.; Jackson, A.P.; Zhu, C.; Hammond, N. Automated crater shape retrieval using weakly-supervised deep learning. Icarus 2020, 345, 113749. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Lake Tahoe, NV, USA, 3–8 December 2012; pp. 1097–1105. [Google Scholar]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster r-cnn: Towards real-time object detection with region proposal networks. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Montreal, QC, Canada, 7–12 December 2015; pp. 91–99. [Google Scholar]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Dalal, N.; Triggs, B. Histograms of oriented gradients for human detection. In Proceedings of the 2005 International Conference on Computer Vision Pattern Recognition (CVPR), San Diego, CA, USA, 20–26 June 2005; pp. 886–893. [Google Scholar]
- Cohen, J.P.; Lo, H.Z.; Lu, T.; Ding, W. Crater detection via convolutional neural networks. In Proceedings of the 47th Lunar and Planetary Science Conference (LPSC), The Woodlands, TX, USA, 21–25 March 2016; p. 1143. [Google Scholar]
- Wang, H.; Jiang, J.; Zhang, G. CraterIDNet: An End-to-End Fully Convolutional Neural Network for Crater Detection and Identification in Remotely Sensed Planetary Images. Remote Sens. 2018, 10, 1067. [Google Scholar] [CrossRef]
- Hashimoto, S.; Mori, K. Lunar crater detection based on grid partition using deep learning. In Proceedings of the 2019 IEEE 13th International Symposium on Applied Computational Intelligence and Informatics (SACI), Timisoara, Romania, 29–31 May 2019; pp. 75–80. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the 18th International Conference on Medical Image Computing and Computer-assisted Intervention (MICCAI), Munich, Germany, 5–9 October 2015; pp. 234–241. [Google Scholar]
- He, K.; Gkioxari, G.; Dollár, P.; Girshick, R. Mask r-cnn. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2961–2969. [Google Scholar]
- Jia, Y.; Wan, G.; Liu, L.; Wang, J.; Wu, Y.; Xue, N.; Wang, Y.; Yang, R. Split-Attention Networks with Self-Calibrated Convolution for Moon Impact Crater Detection from Multi-Source Data. Remote Sens. 2021, 13, 3193. [Google Scholar] [CrossRef]
- Wang, S.; Fan, Z.; Li, Z.; Zhang, H.; Wei, C. An Effective Lunar Crater Recognition Algorithm Based on Convolutional Neural Network. Remote Sens. 2020, 12, 2694. [Google Scholar] [CrossRef]
- Jia, Y.; Liu, L.; Zhang, C. Moon Impact Crater Detection Using Nested Attention Mechanism Based UNet++. IEEE Access 2021, 9, 44107–44116. [Google Scholar] [CrossRef]
- Wu, Y.; Wan, G.; Liu, L.; Wei, Z.; Wang, S. Intelligent Crater Detection on Planetary Surface Using Convolutional Neural Network. In Proceedings of the IEEE 5th Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), Chongqing, China, 12–14 March 2021; pp. 1229–1234. [Google Scholar]
- Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C.; Reed, S.; Fu, C.Y.; Berg, A.C. Ssd: Single shot multibox detector. In Proceedings of the 14th European Conference on Computer Vision (ECCV), Amsterdam, The Netherlands, 8–16 October 2016; pp. 21–37. [Google Scholar]
- Lin, T.Y.; Dollár, P.; Girshick, R.; He, K.; Hariharan, B.; Belongie, S. Feature pyramid networks for object detection. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 2117–2125. [Google Scholar]
- Tian, Z.; Shen, C.; Chen, H.; He, T. Fcos: Fully convolutional one-stage object detection. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea, 27–28 October 2019; pp. 9627–9636. [Google Scholar]
- Cai, Z.; Vasconcelos, N. Cascade r-cnn: Delving into high quality object detection. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 6154–6162. [Google Scholar]
- Redmon, J.; Farhadi, A. Yolov3: An incremental improvement. arXiv 2018, arXiv:1804.02767. [Google Scholar]
- Lin, T.Y.; Goyal, P.; Girshick, R.; He, K.; Dollár, P. Focal loss for dense object detection. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2980–2988. [Google Scholar]
- Kong, T.; Sun, F.; Liu, H.; Jiang, Y.; Li, L.; Shi, J. Foveabox: Beyound anchor-based object detection. IEEE Trans. Image Process. 2020, 29, 7389–7398. [Google Scholar] [CrossRef]
- Yang, Z.; Liu, S.; Hu, H.; Wang, L.; Lin, S. Reppoints: Point set representation for object detection. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea, 27–28 October 2019; pp. 9657–9666. [Google Scholar]
- Barker, M.; Mazarico, E.; Neumann, G.; Zuber, M.; Haruyama, J.; Smith, D. A new lunar digital elevation model from the Lunar Orbiter Laser Altimeter and SELENE Terrain Camera. Icarus 2016, 273, 346–355. [Google Scholar] [CrossRef]
- Scholten, F.; Oberst, J.; Matz, K.D.; Roatsch, T.; Wählisch, M.; Speyerer, E.; Robinson, M. GLD100: The near-global lunar 100 m raster DTM from LROC WAC stereo image data. J. Geophys. Res. Planets 2012, 117, E00H17. [Google Scholar] [CrossRef]
- Girshick, R. Fast r-cnn. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 1440–1448. [Google Scholar]
- Met Office. Cartopy: A Cartographic Python Library with a Matplotlib Interface; Met Office: Exeter, UK, 2010. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Fei-Fei, L. Imagenet: A large-scale hierarchical image database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar]
- Zeiler, M.D.; Fergus, R. Visualizing and understanding convolutional networks. In Proceedings of the 13th European Conference on Computer Vision (ECCV), Zurich, Switzerland, 6–12 September 2014; pp. 818–833. [Google Scholar]
- Lin, X.; Liang, Y.; Wan, J.; Lin, C.; Li, S.Z. Region-Based Context Enhanced Network for Robust Multiple Face Alignment. IEEE Trans. Multimedia 2019, 21, 3053–3067. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Eslami, M.E.S.A.; Van Gool, L.; Williams, C.K.; Winn, J.; Zisserman, A. The pascal visual object classes challenge: A retrospective. Int. J. Comput. Vis. 2015, 111, 98–137. [Google Scholar]
- Lin, T.Y.; Maire, M.; Belongie, S.; Hays, J.; Perona, P.; Ramanan, D.; Dollár, P.; Zitnick, C.L. Microsoft coco: Common objects in context. In Proceedings of the 13th European Conference on Computer Vision (ECCV), Zurich, Switzerland, 6–12 September 2014; pp. 740–755. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. In Proceedings of the 3rd International Conference on Learning Representations (ICLR), San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Liu, W.; Liao, S.; Ren, W.; Hu, W.; Yu, Y. High-level semantic feature detection: A new perspective for pedestrian detection. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 5187–5196. [Google Scholar]
- Yu, J.; Jiang, Y.; Wang, Z.; Cao, Z.; Huang, T. Unitbox: An advanced object detection network. In Proceedings of the 24th ACM International Conference on Multimedia (MM), New York, NY, USA, 15–19 October 2016; pp. 516–520. [Google Scholar]
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Rich feature hierarchies for accurate object detection and semantic segmentation. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Columbus, OH, USA, 23–28 June 2014; pp. 580–587. [Google Scholar]
- Ivanov, B. Size-frequency distribution of small lunar craters: Widening with degradation and crater lifetime. Sol. Syst. Res. 2018, 52, 1–25. [Google Scholar] [CrossRef]
- Bottke, W.F.; Norman, M.D. The late heavy bombardment. Annu. Rev. Earth Planet. Sci. 2017, 45, 619–647. [Google Scholar] [CrossRef]
- Bottke, W. Dynamical Evolution and Bombardment of the Early Solar System: A Few Highlights of the Last 50 Years. In Proceedings of the 50th Lunar and Planetary Science Conference (LPSC), The Woodlands, TX, USA, 18–22 March 2019; p. 1545. [Google Scholar]
- Crater Analysis Techniques Working Group. Standard techniques for presentation and analysis of crater size-frequency data. Icarus 1979, 37, 467–474. [Google Scholar] [CrossRef]


| Method | AP↑ (IoU thr = 0.5) | AP↑ (IoU thr = 0.6) | AP↑ (IoU thr = 0.7) | Parameters | GFLOPs | |||
|---|---|---|---|---|---|---|---|---|
| Validation | Test | Validation | Test | Validation | Test | |||
| Faster R-CNN | 86.04% | 86.38% | 81.80% | 80.70% | 72.74% | 68.79% | 33.57 M | 760.86 |
| Faster R-CNN + FPN | 86.01% | 87.02% | 80.92% | 80.70% | 70.58% | 67.94% | 41.53 M | 63.65 |
| Cascade R-CNN | 84.76% | 84.98% | 78.36% | 77.31% | 66.23% | 64.37% | 69.17 M | 91.29 |
| SSD | 85.08% | 84.61% | 79.02% | 78.28% | 69.42% | 66.20% | 36.04 M | 98.81 |
| RetinaNet | 68.97% | 66.11% | 65.72% | 61.76% | 58.37% | 53.43% | 37.74 M | 61.22 |
| YOLOv3 | 78.53% | 77.73% | 71.15% | 70.46% | 57.26% | 54.34% | 61.95 M | 50.06 |
| FoveaBox | 73.94% | 76.02% | 67.24% | 66.73% | 55.60% | 54.86% | 36.19 M | 52.77 |
| FCOS | 82.74% | 85.22% | 78.52% | 80.22% | 70.77% | 71.18% | 32.02 M | 51.32 |
| RepPoints | 82.60% | 82.83% | 77.06% | 75.76% | 65.79% | 64.37% | 36.62 M | 48.66 |
| Method | AP↑ (IoU Threshold = 0.5) | ||||||
|---|---|---|---|---|---|---|---|
| 5–10 km | 10–20 km | 20–30 km | 30–40 km | 40–50 km | ≥50 km | Total | |
| Faster R-CNN | 84.39% | 87.51% | 73.68% | 66.36% | 64.56% | 82.68% | 86.38% |
| Faster R-CNN + FPN | 83.94% | 87.10% | 71.32% | 65.84% | 66.19% | 83.57% | 87.02% |
| Cascade R-CNN | 82.29% | 85.83% | 65.85% | 60.63% | 63.27% | 79.90% | 84.98% |
| SSD | 80.45% | 85.08% | 74.11% | 70.53% | 73.39% | 83.51% | 84.61% |
| RetinaNet | 65.53% | 64.90% | 68.86% | 64.41% | 70.36% | 81.59% | 66.11% |
| YOLOv3 | 72.99% | 78.22% | 67.27% | 65.67% | 64.00% | 68.94% | 77.73% |
| FoveaBox | 80.36% | 85.53% | 62.71% | 29.21% | 58.42% | 55.17% | 76.02% |
| FCOS | 82.96% | 86.57% | 74.53% | 63.10% | 73.67% | 80.95% | 85.22% |
| RepPoints | 79.35% | 84.05% | 67.96% | 59.16% | 71.43% | 83.19% | 82.83% |
| Accuracy Metric | DeepMoon | Our Method | ||
|---|---|---|---|---|
| Validation | Test | Validation | Test | |
| Recall↑ | 92% | 92% | 81.20% | 79.39% |
| Precision↑ | 53% | 56% | 80.99% | 82.97% |
| Precision(diameter ≥ 5 km)↑ | - | - | 90.67% | 91.61% |
| F1 score↑ | 0.67 | 0.69 | 0.81 | 0.81 |
| F1 score(diameter ≥ 5 km)↑ | - | - | 0.86 | 0.85 |
| Fractional longitude error↓ | 13% | 11% | 6.19% | 7.33% |
| Fractional latitude error↓ | 10% | 9% | 9.39% | 9.25% |
| Fractional radius error↓ | 6% | 7% | 6.05% | 6.76% |
| Number of Lunar Craters | |||
|---|---|---|---|
| Diameter Range | Head et al. [2] | Povilaitis et al. [5] | Ours |
| 1–5 km | - | - | 991 |
| 5–20 km | - | 19,335 | 24,186 |
| ≥20 km | 4301 | - | 6429 |
| Total | 4301 | 19,335 | 31,606 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, X.; Zhu, Z.; Yu, X.; Ji, X.; Luo, T.; Xi, X.; Zhu, M.; Liang, Y. Lunar Crater Detection on Digital Elevation Model: A Complete Workflow Using Deep Learning and Its Application. Remote Sens. 2022, 14, 621. https://doi.org/10.3390/rs14030621
Lin X, Zhu Z, Yu X, Ji X, Luo T, Xi X, Zhu M, Liang Y. Lunar Crater Detection on Digital Elevation Model: A Complete Workflow Using Deep Learning and Its Application. Remote Sensing. 2022; 14(3):621. https://doi.org/10.3390/rs14030621
Chicago/Turabian StyleLin, Xuxin, Zhenwei Zhu, Xiaoyuan Yu, Xiaoyu Ji, Tao Luo, Xiangyu Xi, Menghua Zhu, and Yanyan Liang. 2022. "Lunar Crater Detection on Digital Elevation Model: A Complete Workflow Using Deep Learning and Its Application" Remote Sensing 14, no. 3: 621. https://doi.org/10.3390/rs14030621
APA StyleLin, X., Zhu, Z., Yu, X., Ji, X., Luo, T., Xi, X., Zhu, M., & Liang, Y. (2022). Lunar Crater Detection on Digital Elevation Model: A Complete Workflow Using Deep Learning and Its Application. Remote Sensing, 14(3), 621. https://doi.org/10.3390/rs14030621







