Deep Hash Remote-Sensing Image Retrieval Assisted by Semantic Cues
Abstract
1. Introduction
- (1)
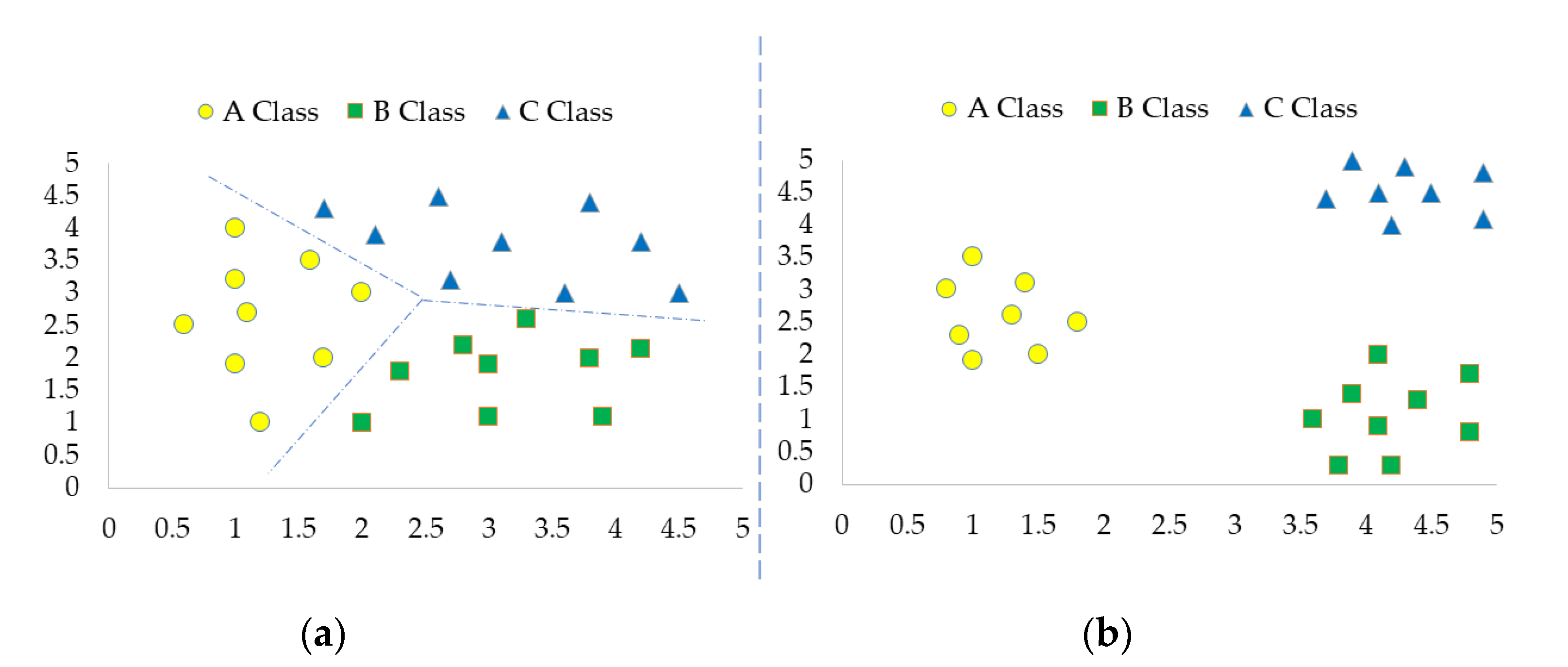
- We propose a new deep hash network structure for retrieving and classifying remote-sensing images in a unified framework. This network structure uses semantic information from the classification task to assist in the training of the network, which compensates for the underutilization of label information by previous metric-learning methods and thus improves feature distinctiveness.
- (2)
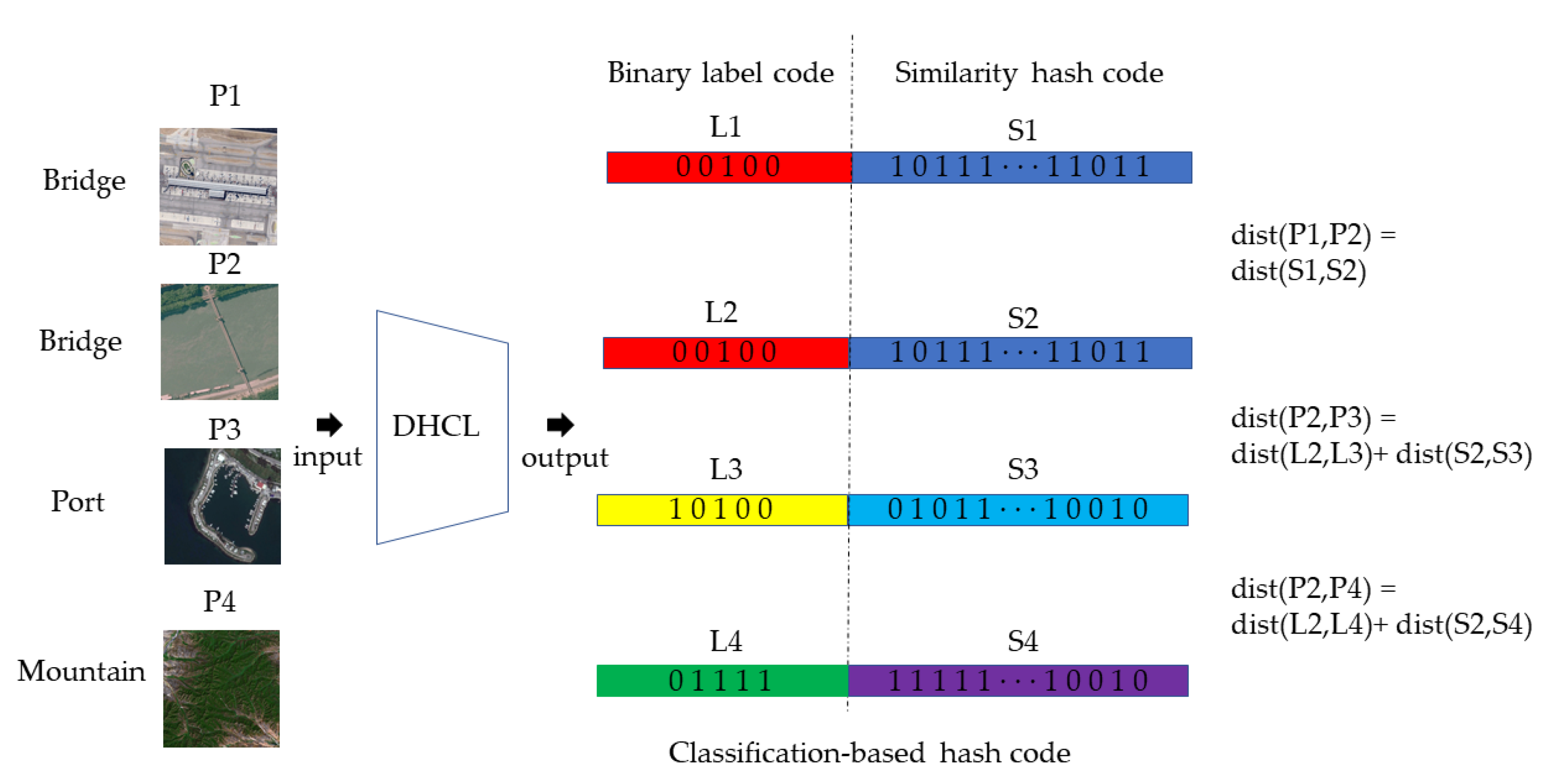
- We propose a new hash code structure, which we call a classification-based hash code. This structure can explicitly combine the classification labels with similarity hash codes as a complement in the retrieval process to obtain better ranking relationships.
- (3)
- Extensive experiments and comparisons with other methods confirm the effectiveness of our proposed method.
2. Related Works
2.1. Hashing Method
2.1.1. Traditional Hashing Method
2.1.2. Deep Hash Method
2.2. Deep Metric Learning
2.2.1. Pair-Based Deep Metric Learning
2.2.2. Proxy-Based Deep Metric Learning
3. Method
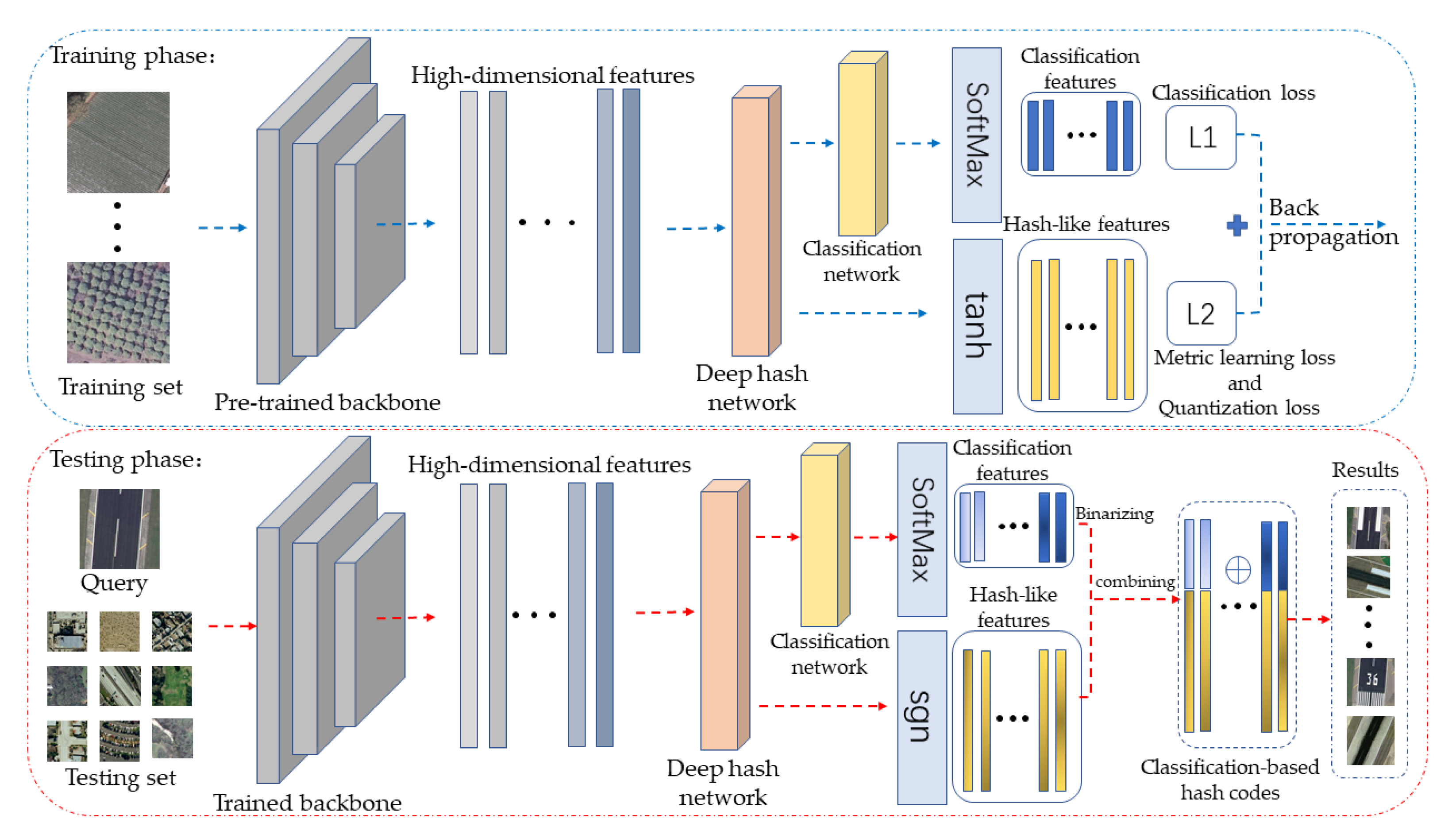
3.1. Global Architecture
3.2. Loss Function
| Algorithm 1: Optimization algorithm of our proposed DHCL method. |
| Input: |
| A batch of remote-sensing images. |
| Output: |
| The network parameter W of the DHCL method. |
| Initialization: |
| Random initialize parameter W. |
| Repeat: |
| 1: Compute hash-like feature and classification label feature by forward propagation; |
| 2: Compute similarity hash code by ; 3: Utilize , to calculate loss according to Equation (5); |
| 4: Use AdamW optimizer to recalculate W. |
| Until: |
| A stopping criterion is satisfied |
| Return: W. |
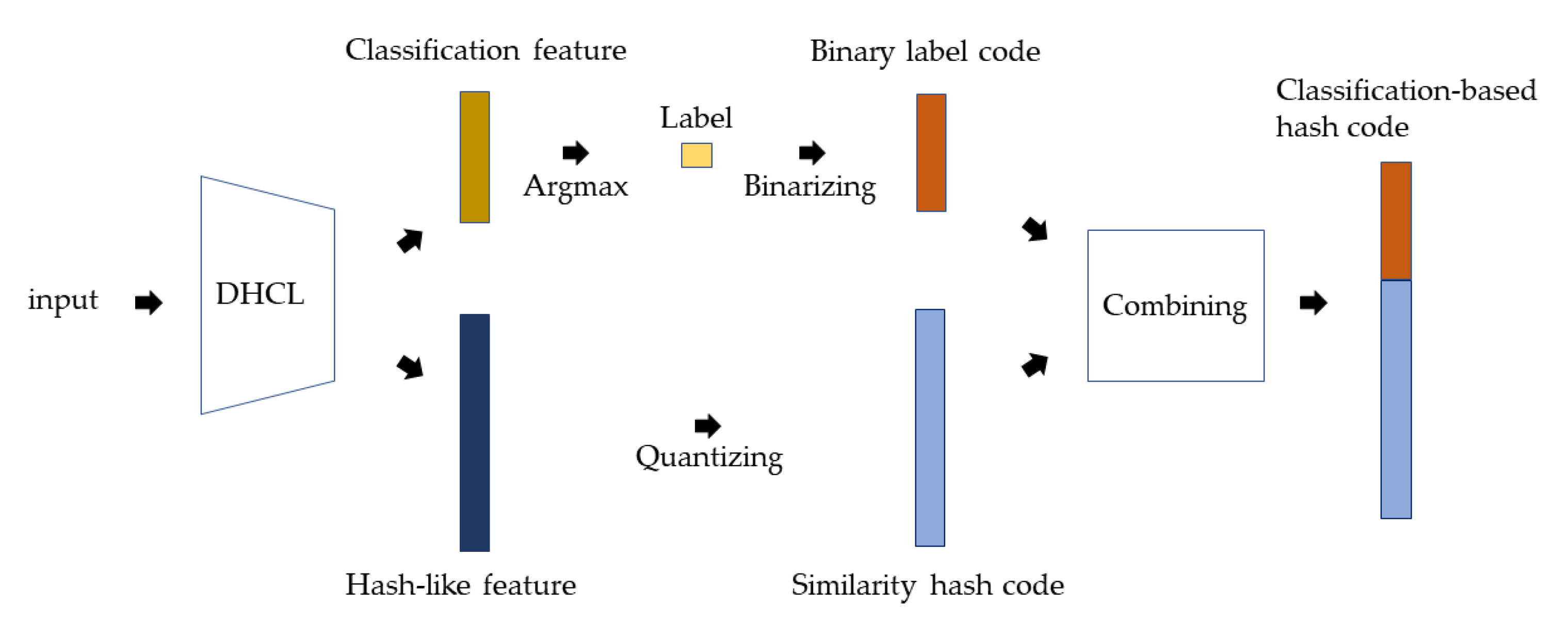
3.3. Hash Code Generation
4. Experiments
4.1. Dataset and Criteria
4.2. Implementation Details
4.3. Experimental Results
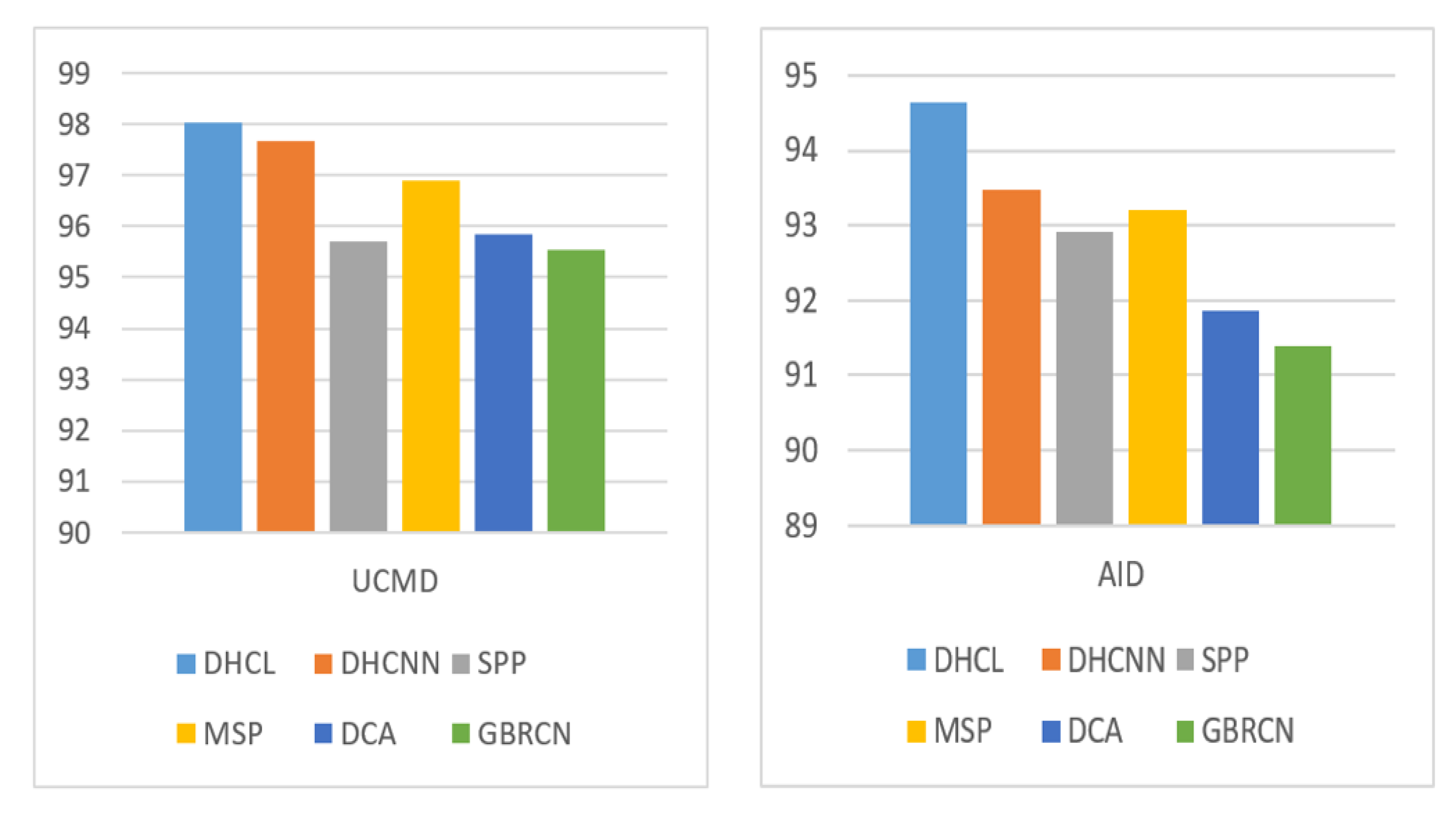
4.3.1. Results on UCMD
4.3.2. Results on AID
4.3.3. Results on RSD46-WHU
4.4. Ablation Study
4.5. Results on Classification
4.6. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ma, Y.; Wu, H.; Wang, L.; Huang, B.; Ranjan, R.; Zomaya, A.; Jie, W. Remote sensing big data computing: Challenges and opportunities. Future Gener. Comput. Syst. 2015, 51, 47–60. [Google Scholar] [CrossRef]
- Zheng, J.; Song, X.; Yang, G.; Du, X.; Mei, X.; Yang, X. Remote Sensing Monitoring of Rice and Wheat Canopy Nitrogen: A Review. Remote Sens. 2022, 14, 5712. [Google Scholar] [CrossRef]
- Sklyar, E.; Rees, G. Assessing Changes in Boreal Vegetation of Kola Peninsula via Large-Scale Land Cover Classification between 1985 and 2021. Remote Sens. 2022, 14, 5616. [Google Scholar] [CrossRef]
- Jeon, J.; Tomita, T. Investigating the Effects of Super Typhoon HAGIBIS in the Northwest Pacific Ocean Using Multiple Observational Data. Remote Sens. 2022, 14, 5667. [Google Scholar] [CrossRef]
- Daschiel, H.; Datcu, M. Information mining in remote sensing image archives: System evaluation. IEEE Trans. Geosci. Remote Sens. 2005, 43, 188–199. [Google Scholar] [CrossRef]
- Tong, X.-Y.; Xia, G.-S.; Hu, F.; Zhong, Y.; Datcu, M.; Zhang, L. Exploiting Deep Features for Remote Sensing Image Retrieval: A Systematic Investigation. IEEE Trans. Big Data 2020, 6, 507–521. [Google Scholar] [CrossRef]
- Xing, E.; Jordan, M.; Russell, S.J.; Ng, A. Distance metric learning with application to clustering with side-information. Adv. Condens. Matter Phys. 2002, 15. [Google Scholar]
- Lowe, D.G. Similarity metric learning for a variable-kernel classifier. Neural Comput. 1995, 7, 72–85. [Google Scholar] [CrossRef]
- Xuan, S.; Zhang, S. Intra-inter camera similarity for unsupervised person re-identification. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 21–24 June 2021; pp. 11926–11935. [Google Scholar]
- Chen, H.; Wang, Y.; Lagadec, B.; Dantcheva, A.; Bremond, F. Joint generative and contrastive learning for unsupervised person re-identification. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 21–24 June 2021; pp. 2004–2013. [Google Scholar]
- Sun, Y.; Cheng, C.; Zhang, Y.; Zhang, C.; Zheng, L.; Wang, Z.; Wei, Y. Circle loss: A unified perspective of pair similarity optimization. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 6398–6407. [Google Scholar]
- Song, W.; Li, S.; Benediktsson, J.A. Deep hashing learning for visual and semantic retrieval of remote sensing images. IEEE Trans. Geosci. Remote Sens. 2020, 59, 9661–9672. [Google Scholar] [CrossRef]
- Li, P.; Han, L.; Tao, X.; Zhang, X.; Grecos, C.; Plaza, A.; Ren, P. Hashing nets for hashing: A quantized deep learning to hash framework for remote sensing image retrieval. IEEE Trans. Geosci. Remote Sens. 2020, 58, 7331–7345. [Google Scholar] [CrossRef]
- Wang, Y.; Gan, W.; Yang, J.; Wu, W.; Yan, J. Dynamic curriculum learning for imbalanced data classification. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 5017–5026. [Google Scholar]
- Luo, H.; Gu, Y.; Liao, X.; Lai, S.; Jiang, W. Bag of tricks and a strong baseline for deep person re-identification. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Long Beach, CA, USA, 16–17 June 2019. [Google Scholar]
- Yang, Y.; Newsam, S. Bag-of-visual-words and spatial extensions for land-use classification. In Proceedings of the 18th SIGSPATIAL International Conference on Advances in Geographic Information Systems, San Jose, CA, USA, 2–5 November 2010; pp. 270–279. [Google Scholar]
- Xia, G.-S.; Hu, J.; Hu, F.; Shi, B.; Bai, X.; Zhong, Y.; Zhang, L.; Lu, X. AID: A benchmark data set for performance evaluation of aerial scene classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3965–3981. [Google Scholar] [CrossRef]
- Long, Y.; Gong, Y.; Xiao, Z.; Liu, Q. Accurate Object Localization in Remote Sensing Images Based on Convolutional Neural Networks. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2486–2498. [Google Scholar] [CrossRef]
- Xiao, Z.; Long, Y.; Li, D.; Wei, C.; Tang, G.; Liu, J. High-Resolution Remote Sensing Image Retrieval Based on CNNs from a Dimensional Perspective. Remote Sens. 2017, 9, 725. [Google Scholar] [CrossRef]
- Lowe, D. Distinctive image features from scale-invariant key points. Int. J. Comput. Vis. 2003, 20, 91–110. [Google Scholar] [CrossRef]
- Oliva, A.; Torralba, A. Modeling the Shape of the Scene: A Holistic Representation of the Spatial Envelope. Int. J. Comput. Vis. 2001, 42, 145–175. [Google Scholar] [CrossRef]
- Wei, L.; Wang, J.; Ji, R.; Jiang, Y.G.; Chang, S.F. Supervised Hashing with Kernels. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012. [Google Scholar]
- Gong, Y.; Lazebnik, S.; Gordo, A.; Perronnin, F. Iterative Quantization: A Procrustean Approach to Learning Binary Codes for Large-Scale Image Retrieval. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 2916–2929. [Google Scholar] [CrossRef]
- Xia, R.; Pan, Y.; Lai, H.; Liu, C.; Yan, S. Supervised hashing for image retrieval via image representation learning. In Proceedings of the Twenty-eighth AAAI conference on artificial intelligence, Québec City, QC, Canada, 27–31 July 2014. [Google Scholar]
- Demir, B.; Bruzzone, L. Hashing-Based Scalable Remote Sensing Image Search and Retrieval in Large Archives. IEEE Trans. Geosci. Remote Sens. 2016, 54, 892–904. [Google Scholar] [CrossRef]
- Li, W.-J.; Wang, S.; Kang, W.-C. Feature Learning based Deep Supervised Hashing with Pairwise Labels. arXiv 2015. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Y.; Huang, X.; Zhu, H.; Ma, J. Large-Scale Remote Sensing Image Retrieval by Deep Hashing Neural Networks. IEEE Trans. Geosci. Remote Sens. 2018, 56, 950–965. [Google Scholar] [CrossRef]
- Roy, S.; Sangineto, E.; Demir, B.; Sebe, N. Deep Metric and Hash-Code Learning for Content-Based Retrieval of Remote Sensing Images. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018. [Google Scholar]
- Hadsell, R.; Chopra, S.; Lecun, Y. Dimensionality Reduction by Learning an Invariant Mapping. In Proceedings of the 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’06), New York, NY, USA, 17–22 June 2006. [Google Scholar]
- Hoffer, E.; Ailon, N. Deep Metric Learning Using Triplet Network; Springer: Cham, Switzerland, 2015. [Google Scholar] [CrossRef]
- Sohn, K. Improved deep metric learning with multi-class N-pair loss objective. In Proceedings of the Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016. [Google Scholar]
- Song, H.O.; Yu, X.; Jegelka, S.; Savarese, S. Deep Metric Learning via Lifted Structured Feature Embedding. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Wang, X.; Han, X.; Huang, W.; Dong, D.; Scott, M.R. Multi-Similarity Loss With General Pair Weighting for Deep Metric Learning. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Kim, S.; Kim, D.; Cho, M.; Kwak, S. Proxy Anchor Loss for Deep Metric Learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020. [Google Scholar] [CrossRef]
- Movshovitz-Attias, Y.; Toshev, A.; Leung, T.K.; Ioffe, S.; Singh, S. No Fuss Distance Metric Learning Using Proxies. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 360–368. [Google Scholar]
- Qian, Q.; Shang, L.; Sun, B.; Hu, J.; Li, H.; Jin, R. SoftTriple Loss: Deep Metric Learning Without Triplet Sampling. arXiv 2019. [Google Scholar] [CrossRef]
- Teh, E.W.; Devries, T.; Taylor, G.W. ProxyNCA++: Revisiting and Revitalizing Proxy Neighborhood Component Analysis. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020. [Google Scholar] [CrossRef]
- Liu, W.; Wen, Y.; Yu, Z.; Yang, M. Large-Margin Softmax Loss for Convolutional Neural Networks. arXiv 2016. [Google Scholar] [CrossRef]
- Shan, X.; Liu, P.; Wang, Y.; Zhou, Q.; Wang, Z. Deep Hashing Using Proxy Loss on Remote Sensing Image Retrieval. Remote Sens. 2021, 13, 2924. [Google Scholar] [CrossRef]
- Zhou, W.; Shao, Z.; Diao, C.; Cheng, Q. High-resolution remote-sensing imagery retrieval using sparse features by auto-encoder. Remote Sens. Lett. 2015, 6, 775–783. [Google Scholar] [CrossRef]
- Ioffe, S.; Szegedy, C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. In Proceedings of the International Conference on Machine Learning, Lille, France, 6–11 July 2015. [Google Scholar] [CrossRef]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, F.F. ImageNet: A Large-Scale Hierarchical Image Database. In Proceedings of the 2009 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR 2009), Miami, FL, USA, 20–25 June 2009. [Google Scholar]
- Zhu, X.; Zhang, L.; Huang, Z. A Sparse Embedding and Least Variance Encoding Approach to Hashing. IEEE Trans. Image Process. 2014, 23, 3737–3750. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.; Cai, D.; Li, C. Density Sensitive Hashing. IEEE Trans. Cybern. 2013, 44, 1362–1371. [Google Scholar] [CrossRef]
- Weiss, Y.; Torralba, A.; Fergus, R. Spectral hashing. Adv. Neural Inf. Process. Syst. 2009, 282, 1753–1760. [Google Scholar]
- Liu, Q.; Hang, R.; Song, H.; Li, Z. Learning Multiscale Deep Features for High-Resolution Satellite Image Scene Classification. IEEE Trans. Geosci. Remote Sens. 2017, 56, 117–126. [Google Scholar] [CrossRef]
- Zheng, X.; Yuan, Y.; Lu, X. A Deep Scene Representation for Aerial Scene Classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4799–4809. [Google Scholar] [CrossRef]
- Chaib, S.; Liu, H.; Gu, Y.; Yao, H. Deep Feature Fusion for VHR Remote Sensing Scene Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4775–4784. [Google Scholar] [CrossRef]
- Zhang, F.; Du, B.; Zhang, L. Scene Classification via a Gradient Boosting Random Convolutional Network Framework. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1793–1802. [Google Scholar] [CrossRef]



| Method | Hash Code Length | |||
|---|---|---|---|---|
| 16 Bits | 32 Bits | 48 Bits | 64 Bits | |
| DHCL | 98.97 | 99.34 | 99.54 | 99.60 |
| DHPL [39] | 98.53 | 98.83 | 99.01 | 99.21 |
| DHCNN [12] | 96.52 | 96.98 | 97.46 | 98.02 |
| DHNN-L2 [27] | 67.73 | 78.23 | 82.43 | 85.59 |
| DPSH [26] | 53.64 | 59.33 | 62.17 | 65.21 |
| KSH [22] | 75.50 | 83.62 | 86.55 | 87.22 |
| ITQ [23] | 42.65 | 45.63 | 47.21 | 47.64 |
| SELVE [43] | 36.12 | 40.36 | 40.38 | 38.58 |
| DSH [44] | 28.82 | 33.07 | 33.15 | 34.59 |
| SH [45] | 29.52 | 30.08 | 30.37 | 29.31 |
| Method | Hash Code Length | |||
|---|---|---|---|---|
| 16 Bits | 32 Bits | 48 Bits | 64 Bits | |
| DHCL | 94.75 | 98.08 | 98.93 | 99.02 |
| DHPL [39] | 93.53 | 97.36 | 98.28 | 98.54 |
| DHCNN [12] | 89.05 | 92.97 | 94.21 | 94.27 |
| DHNN-L2 [27] | 57.87 | 70.36 | 73.98 | 77.20 |
| DPSH [26] | 28.92 | 35.30 | 37.84 | 40.78 |
| KSH [22] | 48.26 | 58.15 | 61.59 | 63.26 |
| ITQ [23] | 23.35 | 27.31 | 28.79 | 29.99 |
| SELVE [43] | 34.58 | 37.87 | 39.09 | 36.81 |
| DSH [44] | 16.05 | 18.08 | 19.36 | 19.72 |
| SH [45] | 12.69 | 16.99 | 16.16 | 16.21 |
| Method | Hash Code or Feature Length | |||||||
|---|---|---|---|---|---|---|---|---|
| 16 Bits | 32 Bits | 48 Bits | 64 Bits | |||||
| mAP | Time (ms) | mAP | Time (ms) | mAP | Time (ms) | mAP | Time (ms) | |
| DHCL (Hamming) | 90.87 | 848.9 | 94.61 | 859.0 | 95.03 | 865.8 | 95.38 | 869.2 |
| DHCL (Euclidean) | 92.26 | 1179.2 | 95.05 | 1202.6 | 95.25 | 1212.8 | 95.60 | 1226.4 |
| DHPL [39] (Hamming) | 89.94 | 848.9 | 92.58 | 859.2 | 93.67 | 865.8 | 94.05 | 869.2 |
| DHPL [39] (Euclidean) | 91.34 | 1179.4 | 93.38 | 1202.6 | 93.72 | 1212.7 | 94.27 | 1226.5 |
| VDCC [19] (Euclidean) | 54.25 | 1179.2 | 60.30 | 1202.5 | 62.78 | 1212.7 | 66.59 | 1226.4 |
| Method | Training | Testing | ||
|---|---|---|---|---|
| Training Loss | Hash Code | |||
| Classification Loss | Metric-Learning Loss | Binary Label Code | Similarity Hash Code | |
| Method 1 (DHCL) | √ | √ | √ | √ |
| Method 2 | √ | √ | √ | |
| Method 3 | √ | √ | √ | |
| Method | Hash Code Length | |||
|---|---|---|---|---|
| 16 Bits | 32 Bits | 48 Bits | 64 Bits | |
| Method 1(DHCL) | 98.97 | 99.34 | 99.54 | 99.60 |
| Method 2 | 98.42 | 98.54 | 99.46 | 99.53 |
| Method 3 | 85.30 | 86.40 | 86.93 | 87.02 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, P.; Liu, Z.; Shan, X.; Zhou, Q. Deep Hash Remote-Sensing Image Retrieval Assisted by Semantic Cues. Remote Sens. 2022, 14, 6358. https://doi.org/10.3390/rs14246358
Liu P, Liu Z, Shan X, Zhou Q. Deep Hash Remote-Sensing Image Retrieval Assisted by Semantic Cues. Remote Sensing. 2022; 14(24):6358. https://doi.org/10.3390/rs14246358
Chicago/Turabian StyleLiu, Pingping, Zetong Liu, Xue Shan, and Qiuzhan Zhou. 2022. "Deep Hash Remote-Sensing Image Retrieval Assisted by Semantic Cues" Remote Sensing 14, no. 24: 6358. https://doi.org/10.3390/rs14246358
APA StyleLiu, P., Liu, Z., Shan, X., & Zhou, Q. (2022). Deep Hash Remote-Sensing Image Retrieval Assisted by Semantic Cues. Remote Sensing, 14(24), 6358. https://doi.org/10.3390/rs14246358







