Abstract
We used the Constellation Observing System for Meteorology, Ionosphere, and Climate-2 (COSMIC-2) dry temperature profile data from December 2019 to November 2021 to study the vertical wavenumber spectra of the potential energy of stratospheric gravity waves (GWs Ep) in the Asian monsoon region (15–45°N, 70–150°E). The GW Ep decreases with increasing vertical wavenumber, and the spectral slope varies with wavenumber. The spectral slope becomes smaller over a wavenumber range of 0.1–0.45 km−1, and larger from 0.45–1 km−1, with increasing wavenumber. The energy density distribution at middle and low latitudes shows seasonal variations. Over a wavenumber range of 0.05–0.5 km−1, the energy density in winter is higher at middle latitudes than at low latitudes, and the opposite is observed in summer over a wavenumber range from 0.1 to 1 km−1. Both the spectral amplitude and characteristic wavelength exhibit band-like patterns, and the large-value bands and their centers vary significantly with the season. In winter, the middle latitude spectral amplitude is larger than that at low latitudes, and the significant large-value band-like distribution is at ~40°N. In summer, the distribution is opposite, with large-value band regions over the Bay of Bengal and Indo-China Peninsula. The large-value region of the middle latitude spectral amplitude corresponds to a longer characteristic wavelength, while the large-value region of the low latitude spectral amplitude corresponds to a shorter characteristic wavelength. There is also significant seasonal variation in the distribution of spectral slopes. Over a wavenumber range of 0.1 to 0.5 km−1, the slope is smaller at middle latitudes and larger at low latitudes in winter; the opposite is observed in summer. There is a significant annual cycle of spectral amplitude at middle and low latitudes, and a 4.8 month cycle at middle latitudes.
1. Introduction
Gravity waves (GWs) are one of the main forms of motion in the stratosphere. The propagation and dissipation of these waves couples the energy and momentum between different atmospheric layers, which affects and even determines the dynamic and thermal structure of the global atmosphere. Wave–wave and wave–flow interactions directly affect the energy spectrum structure of the atmosphere. Therefore, the characteristics of atmospheric GWs are an important research field for stratospheric atmospheric dynamics [1,2,3]. Zhang et al. [4] showed that a reasonable parameterization of GWs in atmospheric circulation models can improve the simulation results. The GW parameterization scheme requires a clear understanding of the spectra of GWs. VanZandt [5] proposed a universal spectral feature whereby the wave energy decreases with increasing vertical wavenumber, and this feature does not vary significantly with different seasons, meteorological conditions, or geographical locations. As such, it can provide a simplified framework for a global GW parameterization scheme.
Numerous theories have been proposed to explain the universality of the wavenumber spectra of GWs, and the saturation spectrum theory [6,7] has been accepted by most studies. According to this theory, the spectral density is proportional to , and the spectral slope is −3 in the logarithmic coordinate system, where N is the buoyancy frequency and m is the vertical wavenumber. Due to ongoing improvements in observational techniques, the slope obtained in recent studies differs from the canonical value of −3, especially in the stratosphere [8,9,10,11,12]. Therefore, it is necessary to conduct continuous vertical wavenumber spectral studies over a large region using the latest observational data.
Satellite data cover a large region and are unaffected by weather and other factors, making them suitable for studying GWs and their vertical wavenumber spectra [13,14,15]. However, the vertical resolution of satellite observations from GPS/Meteorology [16], the High Resolution Dynamics Limb Sounder (HIRDLS), the Sounding of the Atmosphere using Broadband Emission Radiometry (SABER) and COSMIC [17] in the stratosphere is >1 km, and the density of these data is relatively low at middle and low latitudes. Therefore, based on these data, we have limited knowledge of the distribution of the vertical wavenumber spectra in a given region. The vertical resolution of COSMIC-2 data is 20 m, and the data density is higher than that of previous satellite data [18]; consequently, COSMIC-2 data are suitable for studying seasonal variations in the vertical wavenumber spectra in the Asian monsoon region. Qu et al. [18] studied the distribution and seasonal variations of GW potential energy (Ep) at different heights in the stratosphere in the Asian monsoon region based on COSMIC-2 data, and found that the middle and low latitude GW Ep distribution exhibited seasonal variations. However, Qu et al. [18] did not undertake spectral analysis.
The main objective of this study was to investigate the vertical wavenumber spectra of GWs and its seasonal variations in the stratosphere using COSMIC-2 data, based on the study of Qu et al. [18]. The remainder of this paper is organized as follows. The data and methods are described in Section 2. Section 3 presents the seasonal variations and distribution of the vertical wavenumber spectra. Section 4 is the discussion. Finally, a summary of this study is provided in Section 5.
2. Materials and Methods
The data used in this study are the COSMIC-2 level 2 dry temperature profiles produced by the COSMIC Data Analysis and Archive Center (CDAAC; Schreiner et al., 2020), and the period of investigation is 24 months, from December 2019 to November 2021. The data were downloaded from https://cdaac-www.cosmic.ucar.edu/ (accessed on 1 August 2022). The Asian monsoon is selected as the study area, with the specific domain being 70–150°E and 15–45°N. Qu et al. [18] reported the monthly average sampling density of COSMIC-2 data to be 25 times at 15–30°N and 15 times at 30–45°N, with a 2.5° × 2.5° grid resolution during this period. The vertical range of the COSMIC-2 dry temperature profile data is 0–60 km. The altitude range considered in the present study is 20–40 km. The main considerations for selecting this altitude range are as follows: (1) the data below 40 km are unaffected by the ionosphere [19]; (2) the region in the tropopause with a rapid vertical change in N2 is excluded at altitudes of >20 km [15]; and (3) for the spectral analysis, the height interval of 20–40 km provides sufficient data and a wide range of vertical wavelengths. In addition, Ho et al. [20] estimated the temperature retrieval accuracy to be 0.2 K between 8 and 35 km for COSMIC-2 data. Scheiner et al. [21] found that the bending angle and reflectivity of COSMIC-2 data have small errors as compared with radiosonde data, short-term operational forecasts, and MERRA-2 data from altitudes of 2 to 40 km. Therefore, in this altitude range, the observational errors of the COSMIC-2 data are small.
For the COSMIC-2 temperature profiles, the individual temperature profiles () consist mainly of background () and perturbation () components (i.e., ) [16]. Due to the irregular vertical resolution of the raw observational data, each raw dry temperature profile was interpolated to a regular 100 m resolution [18]. All temperature profiles were then processed horizontally and vertically. The daily COSMIC-2 temperature profile was separated into 15° × 10° longitude–latitude bins [22]. Firstly, according to Qu et al.’s [18] approach, the 0–6 zonal wavenumber information [22,23] as “large-scale” temperature was extracted using the least-squares method. Then, the remaining background temperature was obtained using a second-order polynomial fit for in the vertical direction [24]. Finally, the background temperature and temperature perturbation were obtained. The Ep per unit mass of GWs [16,25] can be expressed as:
where is the temperature perturbation, is the background temperature, is gravitational acceleration, is the Brunt–Väisälä frequency, and is the heat capacity at constant pressure. Accordingly, the vertical wavenumber spectrum of Ep can be calculated from [26,27]:
where is the discrete Fourier transform of the relative temperature perturbations , is the vertical resolution of the temperature profile, is the sum of points in an individual vertical profile, is the unweighted height of the Brunt–Väisälä frequency N, j is the jth position of an individual vertical profile, and k is the kth number of wavenumber . The definition of above is shown in Equation (3), where is the kth vertical wavenumber. Based on Allen and Vincent [13] and Zhang et al. [9], each vertical wavenumber spectrum was normalized, and then the normalized vertical wavenumber spectra were averaged to obtain the monthly and seasonally averaged vertical wavenumber spectra.
3. Results
3.1. Distribution and Seasonal Variations of the Vertical Wavenumber Spectra
To fully reveal the variations in the vertical wavenumber spectra of the Ep density, vertical filtering was not performed when calculating . However, due to limitations in the available height range of COSMIC-2 data, the maximum effective wavelength that can be described by a discrete Fourier transform is 20 km, and features of <1 km in size cannot be reliably distinguished from noise in the Global Positioning System radio occultation (GPS–RO) temperature profiles [28]. Therefore, we mainly consider the energy distribution in the region where the vertical wavenumber is >0.05 and <1 km−1 (i.e., the vertical wavelength is <20 km and >1 km). Figure 1a shows the mean vertical wavenumber spectrum of the GW Ep in the study region, which has a magnitude of 104 J/kg (1/m)−1 in the energy density that is consistent with the results obtained by Yan et al. [26] using COSMIC data. The energy density decreases with increasing wavenumber (Figure 1a). The decrease in the energy density varies with wavenumber, and, thus, the spectral slope (S) is not constant. For wavenumbers of 0.05–0.1 km−1, the energy density decays slowly with increasing wavenumber, and for wavenumbers from 0.1 to 1 km−1, the energy density decays rapidly with increasing wavenumber. To quantify the variations of the energy density with wavenumber, the S at each wavenumber was calculated by the central differential method. The equation is
S has a maximum value (−0.40) at a wavenumber = 0.1 km−1 (wavelength = 10 km), and a minimum value (−4.69) at a wavenumber = 0.45 km−1 (wavelength = 2.2 km) (Figure 1b). This shows that when the vertical wavenumber is between 0.1 and 0.45 km−1, the degree of energy reduction increases as the wavenumber increases, and when the wavenumber is >0.45 km−1, the degree of energy reduction decreases as the wavenumber increases.
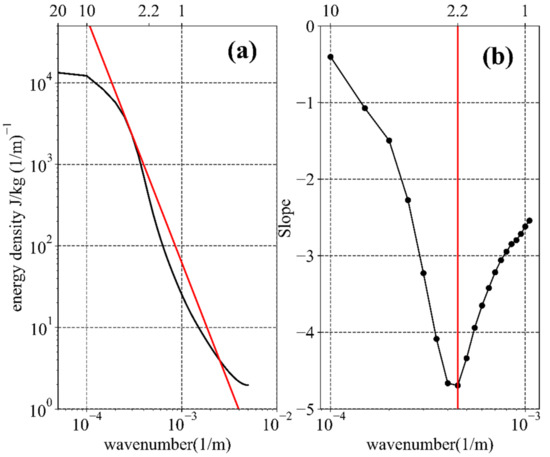
Figure 1.
(a) Annual mean vertical wavenumber spectra of the GW Ep (black line) and the spectrum with a slope of −3 (red line). (b) Variation in the slope with wavenumber, with the red solid line marking the minimum slope value at a vertical wavenumber of 0.45 km−1 (wavelength = 2.2 km). The upper coordinate represents the vertical wavelength (unit: m).
We note that the slope of each point of Figure 1b deviates from −3, especially at wavenumber 0.45 km−1. This phenomenon was also found in Yan et al. [26], but Yan et al. [26] did not elaborate on it. From Figure 2 in Yan et al. [26] we can clearly see that the vertical wavenumber spectrum becomes steep at wavenumber 0.5 km−1, where the slope is much smaller than −3. The cause of this phenomenon may be the occurrence of energy cascading, i.e., the cascading of energy from the large wavenumber region to the small wavenumber region. This causes the slope to be steeper in the large wavenumber region than that in the small wavenumber region.
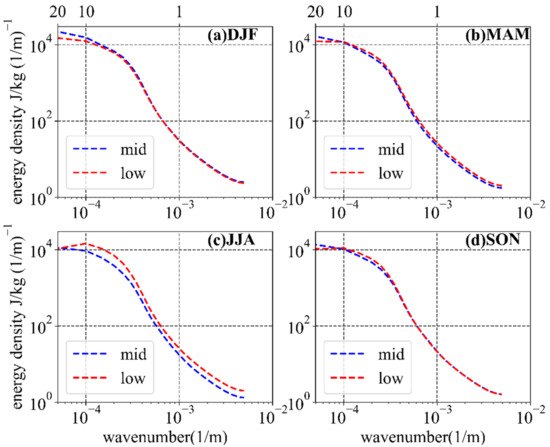
Figure 2.
Vertical wavenumber spectra of the GW Ep. (a–d) Mean winter, spring, summer, and autumn spectra, respectively. The blue line represents the average for the middle latitude region, and the red line represents the average for the low latitude region.
To examine the regional and seasonal differences in the vertical wavenumber spectra, Figure 2a–d shows the seasonal average spectra of the GW Ep density in winter, spring, summer, and autumn at middle latitudes (MLs; 30–45°N, 70–150°E) and low latitudes (LLs; 15–30°N, 70–150°E) [18]. We defined the maximum energy density as the spectral amplitude , and the corresponding vertical wavenumber as the characteristic wavenumber [9]. The energy density shows a significant decrease with increasing wavenumber and is 0.05 km−1 in all four seasons at MLs (Figure 2a–d), namely, the energy density is largest when the vertical wavelength is 20 km. Additionally, there are obvious seasonal variations in . The values at MLs in winter, spring, summer, and autumn are 2.20 × 104, 1.65 × 104, 1.13 × 104, and 1.36 × 104 J/kg (1/km)−1, respectively. This indicates that the ML area of the Asian monsoon region has a larger GW intensity in winter and a smaller intensity in summer, which is consistent with the results of Qu et al. [18] obtained with COSMIC-2 data.
The seasonal variations in the vertical wavenumber spectra at LLs are different from those at MLs. is 0.05 km−1 in winter and 0.1 km−1 in the other three seasons at LLs, and the corresponding vertical wavelengths are 20 and 10 km, respectively. In winter, is the same as at LLs and MLs, whereas in the other three seasons it is larger at LLs (i.e., the vertical wavelength is smaller). Similar to the MLs, values at LLs also exhibit obvious seasonal changes, with values in winter, spring, summer, and autumn of 1.50 × 104, 1.22 × 104, 1.46 × 104, and 1.11 × 104 J/kg (1/m)−1, respectively. In winter, spring, and autumn, values in the ML region are greater than those in the LL region, whereas in summer the opposite is the case.
A comparison of the vertical wavenumber spectral distributions shows that and are different in the ML and LL regions, as is the spectral density at various wavenumbers. Figure 3 shows the distribution of the difference in energy density between the ML and LL regions as a function of wavenumber. In winter, the energy density at MLs is larger than that at LLs for wavenumbers of 0.05–0.5 km−1, and the energy density at MLs is broadly the same as that at LLs for wavenumbers of 0.5 to 1 km−1 (Figure 3). In spring and autumn, the energy density at MLs is larger than that at LLs for wavenumbers of 0.05 km−1, and the energy density at LLs is larger than that at MLs for wavenumbers of 0.1–0.5 km−1. In summer, the energy density at LLs is larger than that at MLs, apart from at a wavenumber of 0.05 km−1.
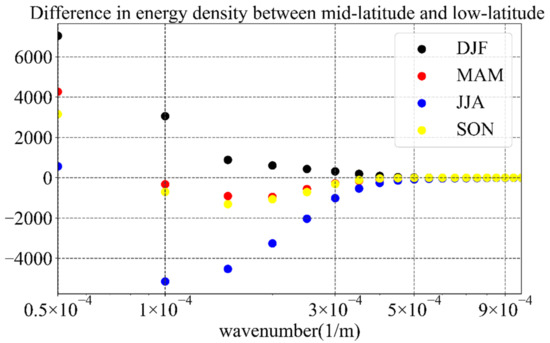
Figure 3.
Variations in the differences of the energy density between the middle and low latitude regions as a function of vertical wavenumber in each season.
3.2. Latitude–Longitude Distribution and Seasonal Variations of the Vertical Wavenumber Spectra
Figure 4 shows the latitude–longitude distribution of the seasonally averaged and values. We define the sum of the mean value and standard deviation of in the four seasons as the reference value, and the region with values larger than the reference value is defined as the large-value region of [18]. In Figure 4, the reference value is 2.59 × 104 J/kg (1/m)−1. It is evident from Figure 4 that exhibits significant seasonal variations. The regional averages of are 2.60 × 104, 2.13 × 104, 1.89 × 104, and 1.84 × 104 J/kg (1/m)−1, and the standard deviations of are 4.9 × 103, 3.3 × 103, 3.7 × 103, and 1.5 × 103 J/kg (1/m)−1 in winter, spring, summer, and autumn, respectively. In the Asian monsoon region, is largest in winter and smaller in summer and autumn. The standard deviation is larger in winter and summer, and smaller in autumn and spring. In general, in the Asian monsoon region, GWs are strongest in winter and weaker in summer and autumn, and the distribution of GWs in winter and summer is quite different, whereas the distribution in spring and autumn is more uniform. The distribution and seasonal variations of and are analyzed in detail below.
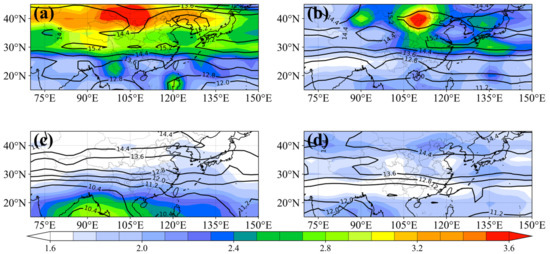
Figure 4.
Distribution of the seasonally averaged spectral amplitude (color shading; units of 104 J/kg (1/m)−1) and the vertical characteristic wavelength (solid black line; units of km). (a) DJF, (b) MAM, (c) JJA, and (d) SON.
In winter, a large value region appears at MLs, and the maximum value occurs over northern China and the Sea of Japan near 40°N. In summer, a large value region occurs at LLs, with the center of the region occurring over the Bay of Bengal and the Indo-China Peninsula south of 30°N, yielding a central value of 2.59 × 104 J/kg (1/m)−1. The distribution of in winter and summer is different in the regions north and south of 30°N.
To examine the relationship between the distribution and characteristic wavenumber , the vertical wavelength corresponding to (i.e., the characteristic wavelength ) is also shown in Figure 4. values during all four seasons have a band-like distribution along the zonal direction, and increase from south to north. In winter, spring, and autumn, the values at MLs range from 12.8 to 15.2 km, while in summer, values at LLs range from 10.4 to 14.4 km. At the maximum band in winter, there are two maximum centers with wavelengths of >14.4 km and >15.2 km, located over northwestern China and the Korean Peninsula. In spring and autumn, there are also high centers in the region where is greater than 3.6 × 104 J/kg (1/m)−1 at MLs and where is >15.2 km. In the large value region in summer, is 10.4 km near the Bay of Bengal and Indo-China Peninsula. Based on the above analysis, it can be seen that the corresponding vertical wavelengths can reach 15.2 km when the mid-latitude is larger, such as in winter and spring. Except for summer, the minimum vertical wavelength at low latitudes is 12 km in the rest of the season, and when the low-latitude GWs are active in summer, the vertical wavelength can reach 10.4 km.
The spectral slope S varies with wavenumber (Figure 1b). To examine the seasonal variations of S, S was calculated by linear fitting over the wavenumber range of 0.1–0.5 km−1 (wavelength = 2–10 km). According to Yan et al. [26] and Lu et al. [27], we set the upper bound to 0.5 km−1. Since is 0.1 km−1 in summer, we set the lower bound to 0.1 km−1 to ensure uniformity across the seasons. Figure 5 shows the distribution of the seasonally averaged S values. S varies from –2.2 to –3.0, which is less steep than the saturation spectrum slope of −3 [6]. S exhibits significant seasonal variations (Figure 5). In winter, the slopes are smaller at MLs and larger at LLs. There are high S value regions over the southern Tibetan Plateau and southern China. This shows that in the northern Asian monsoon region, the energy density shows a greater decrease with increasing wavenumber than in the southern Asian monsoon region. The distribution of S is similar in spring and winter, with smaller S values in the northern Asian monsoon region and larger S values in the southern Asian monsoon region. The distribution of S values in summer is the opposite to that in winter. In the study area in summer, S shows an increasing trend from southeast to northwest, which means that with increasing wavenumber, the energy density decreases more rapidly at LLs, whereas in the western MLs, the energy density decreases more slowly with increasing wavenumber. The distribution of S in autumn is different than that in the other three seasons. Larger S values characterize the mainland of China and the Sea of Japan north of 30°N, which reflect the slow decrease in energy density in this area with increasing wavenumber. In addition, the large value area in the northern part of the Sea of Japan in winter is caused by the sparse data during the interpolation process, so it will not be discussed in this paper.
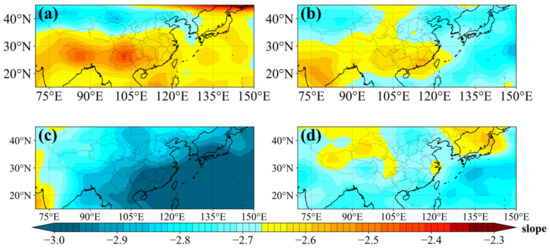
Figure 5.
Distribution of average S values in (a) DJF, (b) MAM, (c) JJA, and (d) SON.
3.3. Latitude–Temporal Distribution of the Spectral Amplitude
The above analysis shows that has an obvious band-like distribution with latitude. To examine the variations in with time and latitude, Figure 6a shows the latitude–temporal distribution of the monthly averaged from December 2019 to November 2021. The range of in Figure 6a is 1–4.5 × 104 J/kg (1/m)−1. The temporal evolution at each latitude shows significant seasonal variations in , and these variations are different at MLs and LLs. At MLs, the large value region appears in winter, and is smaller in summer and autumn. The maximum value at LLs occurs in spring and summer, and smaller values occur in winter and autumn. The maximum value at MLs is larger than that at LLs, and appears near 40°N, whereas the maximum value at LLs occurs south of 20°N.
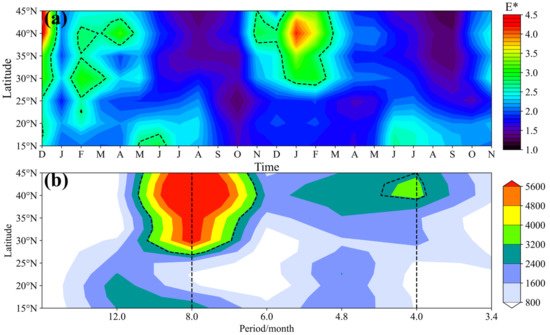
Figure 6.
(a) Latitude–time variations of the spectral amplitude (units of 104 J/kg (1/m)−1). The area surrounded by the black dotted line in Figure 6a is the region with large values (>2.67 × 104 J/kg (1/m)−1). (b) Latitude–period variation of the spectral amplitude . The black dotted line represents the significant frequency spectrum intensity, which was calculated as the mean value of the frequency spectrum plus the standard deviation (3.1 × 103 J/kg (1/m)−1). The red dotted lines shown from left to right in Figure 6b represent cycles of 12 and 4.8 months.
To show the seasonal variations of more clearly, Figure 6b presents the period spectrum of . Figure 6b shows an obvious annual variation in the 27.5–45.0°N region, and the period spectrum intensity is 5.6 × 103 J/kg (1/m)−1. The most significant latitude of the annual cycle is 40°N. A 4.8 months cycle on the order of 3.2 × 103 J/kg (1/m)−1 occurs at 40–45°N. Yan et al. [26] used COSMIC-2 data to study global cycles, and found obvious annual changes near 20°N and 30–90°N, and a clear semi-annual cycle at 30–40°N.
4. Discussion
This study has documented the distribution of the vertical wavenumber spectra of stratospheric GW Ep, the spectral parameter including, such as the spectral amplitude , characteristic wavenumber and spectral slope S, and its seasonal variations. is covered by 1.6–3.6 × 104 J/kg (1/m)−1 in Figure 4, and this result is similar to the results of Yan et al. [26], whose results is 0.8–2.7 × 104 J/kg (1/m)−1 in the Asian Monsoon region. It can be seen that the spectral amplitude we obtained is larger than those of Yan et al. [26]. The reason for this difference may be due to the following two aspects: one is the different data used in the study, and the other is the different height range of the study. The height range was 19.6–35 km in Yan et al. [26], while the height range was 20–40 km in this paper. For comparison purposes, we also calculated the vertical wavenumber spectra in the altitude range of 20–35 km (Figure omitted), and the results are comparable to the results of Yan et al. [26] in the Asian monsoon region, with only slight differences in the magnitude of the values. As the atmospheric density decreases with height, it causes the gravity wave amplitude to increase with height [29], which may be the reason for this result phenomenon. This mechanism is also responsible for the difference between our results and those of Zhang et al. [9], who obtained smaller than the value of this paper and Yan et al. [26]. Zhang et al. [9] studied the range of 18–25 km, near the top of the troposphere. The value of in Zhang et al. [9] is about three times smaller than that of this paper, which is probably due to the Doppler shift caused by the tropospheric jet, resulting in the absorption of GWs energy by the background atmosphere.
In addition, was more active at mid-latitudes in winter and more active at low latitudes in summer. It is worth noting that the large winter value area in Figure 4 is located near 105°E and 40°N, which is similar to the findings in Qu et al. [18]. In Qu et al. [18], GWs are generated by the combination of topography and subtropical rapids at 20 km on the western side of the Tibetan Plateau in winter. The GWs propagate northward to near 40°N due to the “reflection factor” of the latitudinal wind shear [30] during the upward propagation. Faber et al. [23] studied GW Ep activity using COSMIC data in 2006 and found that the GW intensity was significantly greater in winter than in summer at middle and high latitudes in the Northern Hemisphere. Khan and Jin [31] found that the main source of the northern winter stratospheric GWs is the subtropical jet stream. Ratnam et al. [32] suggested that convection is the main wave source of GWs in equatorial and low latitude regions. These results also support the characteristics of distribution and their causes. Therefore, the strengthening of the mid-latitude subtropics jet and the effect of topography are responsible for the large in winter, and the increase in precipitation at low latitudes is responsible for the large in summer.
The characteristic wavenumber corresponding to is 0.05 km−1 in winter and 0.1 km−1 in summer, which is much smaller than the value of Zhang et al. [9], that is, the vertical wavelength is larger than those in Zhang et al. [9]. The reason for the difference is due to the different height range of the study, since the maximum wavelength identified by the Fourier transform is the height range studied. Additionally, a limited altitude range in observational data may result in a lack of sensitivity to motions with larger vertical scales [1]. Lu et al. [27] found a characteristic wavelength of 11.3 km at 35–60 km and 25 km at 80–105 km at station McMurdo (77.8°S, 166.7°E). Additionally, multiple data sets suggest characteristic vertical wavenumbers, corresponding to vertical wavelengths of 2–5 km in the lower stratosphere increasing to 10–30 km near the mesopause [1]. In order to confirm this cause, we calculate the 18-25 km vertical wavenumber spectrum using the COSMIC-2 data in 2021, which is the same height range as Zhang et al. [9]. The characteristic wavenumber is found to be 0.28 km−1 (characteristic wavelength is 3.57 km), and these value are similar to the results of Zhang et al. [9] with the value of being 0.5 km−1. Therefore, when the studied vertical range is large, the obtained characteristic wavelength is also long. In other words, the occurs at larger wavelengths.
From Figure 4 we can see that the vertical wavelength shows an increasing trend from low latitude to high latitude. This fact was also found in previous studies. Wang and Alexander [22] analyzed COSMIC data using the S-transform method and found that the dominant GW vertical wavelength increases from the equator to the poles. Faber et al. [23] also obtained a similar result using COSMIC data. However, Wang and Alexander [22] and Faber et al. [23] both studied the lower stratosphere and had a small height range, so their characteristic wavelengths were smaller than ours.
It can be seen from Figure 5 that the S range is covered by −2.3 to −3, which is less steep compared to the theoretical spectrum −3, which is close to the result of Yan et al. [26]. Due to the increased horizontal resolution of COSMIC-2, we obtained a more detailed S distribution than Yan et al. [26]. Especially in winter we found the less steep S region over the southern Tibetan Plateau and the Sichuan Basin in southern China. However, in the study of Yan et al. [26], the S is essentially the same for the entire southern region of the Asian monsoon region due to the rough resolution. This shows that high-resolution data are intentional to reveal the detailed distribution structure of gravity wave parameters within the Asian monsoon region.
The Asian monsoon region has complex underlying surface characteristics, there must be complex weather system activity and its significant seasonal variation in this region, which will be controlled and affected by different weather systems in the middle and lower latitudes. The change of atmospheric thermal and dynamic structures exhibits significant seasonality and complexity. GWs are excited by different weather systems in different area and different season. So, GWs excited by different wave sources have different dynamic mechanisms and wave parameter characteristics. Therefore, tracking the wave source and the relationship between the wave source and the wave parameters is also a problem worthy of an in-depth study using long-term observational data.
5. Conclusions
COSMIC-2 dry temperature profile data for 2019–2021 were used to study the vertical wavenumber spectra of the stratospheric GW Ep in the Asian monsoon region. The spectra distribution and seasonal variations were analyzed, which revealed the basic characteristics and seasonal variations of the spectral amplitude , characteristic wavenumber , and spectral slope S. Our main conclusions are as follows.
- (1)
- In the Asian monsoon region, the Ep spectral density of the stratospheric GWs at heights of 20–40 km decreases with increasing vertical wavenumber, and the spectral slope S varies with wavenumber. From 0.1 to 0.45 km−1, S becomes smaller as the wavenumber increases, and from 0.45 to 1 km−1, S becomes larger with increasing wavenumber.
- (2)
- In different seasons, there are also differences in the spectral distributions at MLs and LLs. In winter, is larger at MLs than at LLs for wavenumbers of 0.05–0.5 km−1. In summer, is larger at LLs than at MLs for wavenumbers of 0.1 to 1 km−1.
- (3)
- Both and exhibit a band-like distribution, and the high-value bands and their centers show obvious seasonal variations. In winter, at MLs is larger than that at LLs, and the high value band is at ~40°N. In contrast, in summer, at LLs is greater than that at MLs, and there are high value regions over the Bay of Bengal and Indo-China Peninsula. The intensification of the subtropical jet at MLs in winter and an increase in convection at LLs in summer may explain these observations. The high values at MLs correspond to a longer characteristic wavelength with values of >15.2 km. The high values of at LLs correspond to a shorter vertical wavelength with value of 10.4 km.
- (4)
- The distribution of S also exhibits significant seasonal variations. In winter, S at MLs is smaller and at LLs is larger, whereas in summer this pattern is reversed.
Author Contributions
Conceptualization, T.Q. and L.Z.; methodology, T.Q. and L.Z.; software, T.Q.; validation, L.Z., T.Q. and Y.W.; formal analysis, T.Q. and L.Z.; investigation, T.Q.; resources, Y.W.; data curation, J.G.; writing—original draft preparation, T.Q.; writing—review and editing, L.Z., Y.W. and X.W.; visualization, T.Q.; supervision, L.Z.; project administration, L.Z.; funding acquisition, L.Z. and Y.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China grant 41975066, the National Natural Science Foundation for Young Scientists of China grant 42005053, the Science and Technology Innovation Program of Hunan Province grant 2021RC3072, and the Research Project of National University of Defense Technology grant ZK21-46.
Data Availability Statement
The COSMIC-2 level 2 dry temperature data is available at COSMIC Data Analysis and Archive Center (https://cdaac-www.cosmic.ucar.edu/, accessed on 1 August 2022).
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Fritts, D.C.; Alexander, M.J. Gravity wave dynamics and effects in the middle atmosphere. Rev. Geophys. 2003, 41, 1003. [Google Scholar] [CrossRef]
- Schmidt, T.; Alexander, P.; Torre, A. Stratospheric gravity wave momentum flux from radio occultations. J. Geophys. Res. 2016, 121, 4443–4467. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, L.; Zhang, Y.; Guan, J. Effects of Tropospheric Vertical Wind Shear on Gravity Waves Generated by Tropical Cyclones. Geophys. Res. Lett. 2019, 46, 4523–4530. [Google Scholar] [CrossRef]
- Zhang, S.D.; Yi, F.; Huang, C.M.; Zhou, Q.J. Latitudinal and seasonal variations of lower atmospheric inertial gravity wave energy revealed by US radiosonde data. Ann. Geophys. 2010, 28, 1065–1074. [Google Scholar] [CrossRef]
- VanZandt, T.E. A universal spectrum of buoyancy waves in the atmosphere. Geophys. Res. Lett. 1982, 9, 575–578. [Google Scholar] [CrossRef]
- Dewan, E.M.; Good, R.E. Saturation and the Universal Spectrum for Vertical Profiles of Horizontal Scalar Winds in the Atmosphere. J. Geophys. Res. 1986, 91, 2742–2748. [Google Scholar] [CrossRef]
- Smith, S.A.; Fritts, D.C.; Vanzandt, T.E. Evidence for a Saturated Spectrum of Atmospheric Gravity Waves. J. Atmos. Sci. 1987, 44, 1404–1410. [Google Scholar] [CrossRef]
- Dewan, E.M.; Grossbard, N.J. Power spectral artifacts in published balloon data and implications regarding saturated gravity wave theories. J. Geophys. Res. 2000, 105, 4667–4683. [Google Scholar] [CrossRef]
- Zhang, S.; Huang, C.; Yi, F. Radiosonde observations of vertical wave number spectra for gravity waves in the lower atmosphere over Central China. Ann. Geophys. 2006, 24, 3257–3265. [Google Scholar] [CrossRef]
- Zhang, S.; Yi, F.; Huang, C.; Chen, Z. Intensive radiosonde observations of gravity waves in the lower atmosphere over Yichang (111°18″ E, 30°42″ N), China. Ann. Geophys. 2008, 26, 2005–2018. [Google Scholar] [CrossRef]
- Zhang, S.; Huang, C.; Huang, K.; Zhang, Y.; Gong, Y.; Gan, Q. Vertical wavenumber spectra of three-dimensional winds revealed by radiosonde observations at midlatitude. Ann. Geophys. 2017, 35, 107–116. [Google Scholar] [CrossRef]
- Wu, Y.; Yuan, W.; Xu, J. Gravity wave activity in the troposphere and lower stratosphere: An observational study of seasonal and interannual variations(Article). J. Geophys. Res. 2013, 118, 11352–11359. [Google Scholar] [CrossRef]
- Allen, S.J.; Vincent, R.A. Gravity wave activity in the lower atmosphere-seasonal and latitudinal variations. J. Geophys. Res. 1995, 100, 1327–1350. [Google Scholar] [CrossRef]
- Steiner, A.K.; Kirchengast, G. Gravity wave spectra from GPS/MET occultation observations. J. Atmos. Ocean. Technol. 2000, 17, 495–503. [Google Scholar] [CrossRef]
- Noersomadi; Tsuda, T. Global distribution of vertical wavenumber spectra in the lower stratosphere observed using high-vertical-resolution temperature profiles from COSMIC GPS radio occultation. Ann. Geophys. 2016, 34, 203–213. [Google Scholar] [CrossRef]
- Tsuda, T.; Nishida, M.; Rocken, C.; Ware, R.H. A global morphology of gravity wave activity in the stratosphere revealed by the GPS occultation data (GPS/MET). J. Geophys. Res. 2000, 105, 7257–7273. [Google Scholar] [CrossRef]
- Wright1, C.J.; Rivas1, M.B.; Gille, J.C. Intercomparisons of HIRDLS, COSMIC and SABER for the detection of stratospheric gravity waves. Atmos. Meas. Tech. 2011, 4, 1581–1591. [Google Scholar] [CrossRef]
- Qu, T.; Zhang, L.; Wang, Y.; Wang, X.; Guan, J. Seasonal Variation of Stratospheric Gravity Waves in the Asian Monsoon Region Derived from COSMIC-2 Data. Remote Sens. 2022, 14, 4096. [Google Scholar] [CrossRef]
- Hindley, N.P.; Wright, C.J.; Smith, N.D.; Mitchell, N.J. The southern stratospheric gravity-wave hot spot: Individual waves and their momentum fluxes measured by COSMIC GPS-RO. Atmos. Chem. Phys. Discuss. 2015, 15, 3173–3217. [Google Scholar] [CrossRef]
- Ho, S.P.; Zhou, X.; Shao, X.; Zhang, B.; Adhikari, L.; Kireev, S.; He, Y.; Yoe, J.G.; Xia-Serafino, W.; Lynch, E. Initial Assessment of the COSMIC-2/FORMOSAT-7 Neutral Atmosphere Data Quality in NESDIS/STAR Using In Situ and Satellite Data. Remote Sens. 2020, 12, 4099. [Google Scholar] [CrossRef]
- Schreiner, W.S.; Weiss, J.P.; Anthes, R.A.; Braun, J.; Chu, V.; Fong, J.; Hunt, D.; Kuo, Y.H.; Meehan, T.; Serafino, W.; et al. COSMIC-2 Radio Occultation Constellation: First Results. Geophys. Res. Lett. 2020, 47, e2019GL086841. [Google Scholar] [CrossRef]
- Wang, L.; Alexander, M.J. Global estimates of gravity wave parameters from GPS radio occultation temperature data. J. Geophys. Res. Atmos. 2010, 115. [Google Scholar] [CrossRef]
- Faber, A.; Llamedo, P.; Schmidt, T.; Torre, A.D.; Wickert, J. On the determination of gravity wave momentum flux from GPS radio occultation data. Atmos. Meas. Tech. 2013, 11, 3169–3180. [Google Scholar] [CrossRef]
- Wang, L.; Geller, M.A. Morphology of gravity-wave energy as observed from 4 years (1998–2001) of high vertical resolution U.S. radiosonde data. J. Geophys. Res. 2003, 108, 4489. [Google Scholar] [CrossRef]
- Strelnikova, I.; Almowafy, M.; Baumgarten, G.; Baumgarten, K.; Ern, M.; Gerding, M.; Lubken, F.J. Seasonal Cycle of Gravity Wave Potential Energy Densities from Lidar and Satellite Observations at 54° and 69° N. J. Atmos. Sci. 2021, 78, 1359–1386. [Google Scholar] [CrossRef]
- Yan, Y.Y.; Zhang, S.D.; Huang, C.M.; Huang, K.M.; Gong, Y.; Gan, Q. The vertical wave number spectra of potential energy density in the stratosphere deduced from the COSMIC satellite observation. Q. J. R. Meteorol. Soc. 2019, 145, 318–336. [Google Scholar] [CrossRef]
- Lu, X.; Chu, X.; Fong, W.; Chen, C.; Yu, Z.; Roberts, B.R.; McDonald, A.J. Vertical evolution of potential energy density and vertical wave number spectrum of Antarctic gravity waves from 35 to 105km at McMurdo (77.8° S, 166.7° E). J. Geophys. Res. 2015, 120, 2719–2737. [Google Scholar] [CrossRef]
- Marquardt, C.; Healy, S.B. Measurement Noise and Stratospheric Gravity Wave Characteristics Obtained from GPS Occultation Data. J. Meteorol. Soc. Jpn. Ser. II 2005, 83, 417–428. [Google Scholar] [CrossRef]
- Liu, X.; Xu, J.; Jia, Y.; Kogure, M. Persistent Layers of Enhanced Gravity Wave Dissipation in the Upper Mesosphere Revealed From SABER Observations. Geophys. Res. Lett. 2022, 49, e2021GL097038. [Google Scholar] [CrossRef]
- Dunkerton, T.J. Inertia–Gravity Waves in the Stratosphere. J. Atmos. Sci. 1984, 41, 3396–3404. [Google Scholar] [CrossRef]
- Khan, A.; Jin, S. Gravity wave activities in Tibet observed by COSMIC GPS radio occultation. Geod. Geodyn. 2018, 9, 504–511. [Google Scholar] [CrossRef]
- Ratnam, M.; Tetzlaff, G.; Jacobi, C. Global and seasonal variations of stratospheric gravity wave activity deduced from the CHAMP/GPS satellite. J. Atmos. Sci. 2004, 61, 1610–1620. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).