Optimization Method of Airborne LiDAR Individual Tree Segmentation Based on Gaussian Mixture Model
Abstract
1. Introduction
2. Materials and Methods
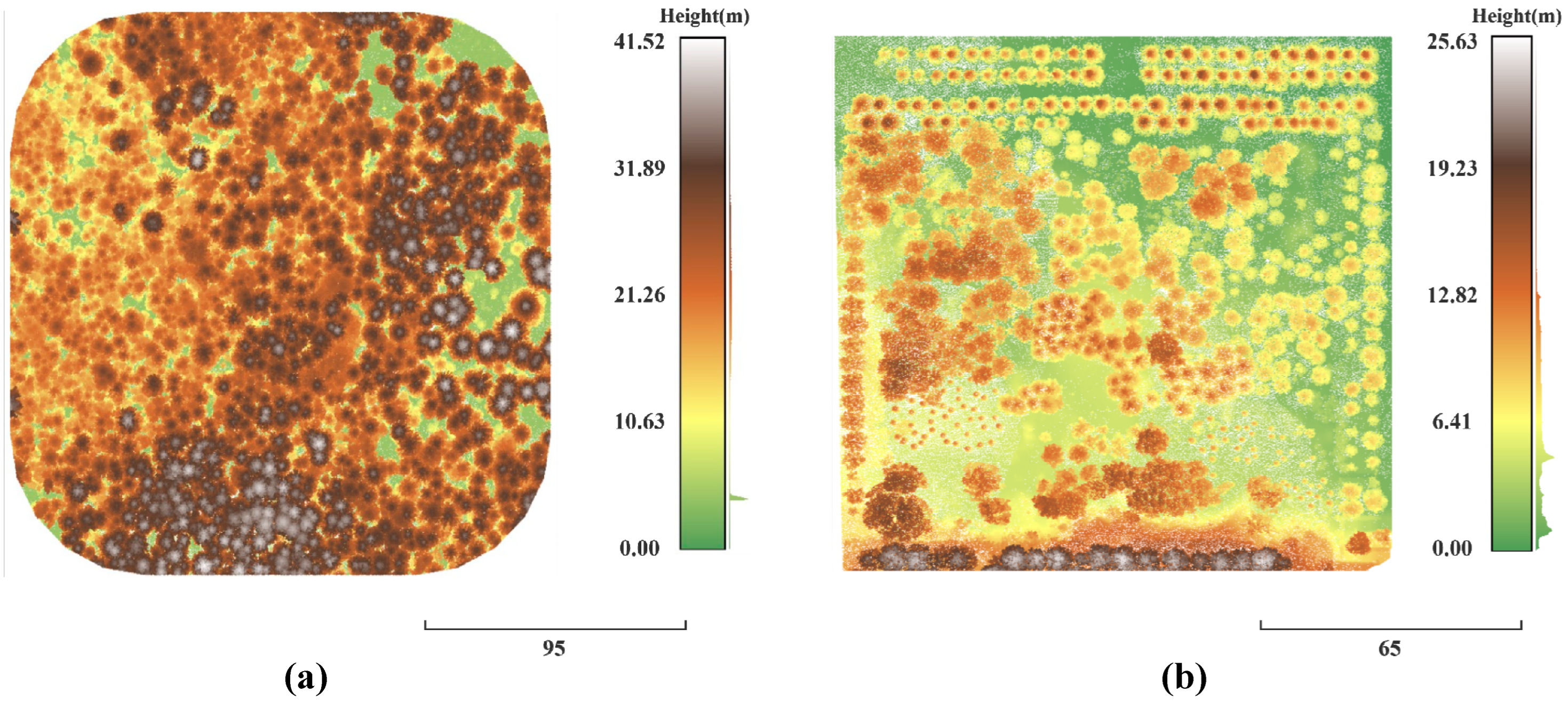
2.1. Study Area
2.2. Dataset
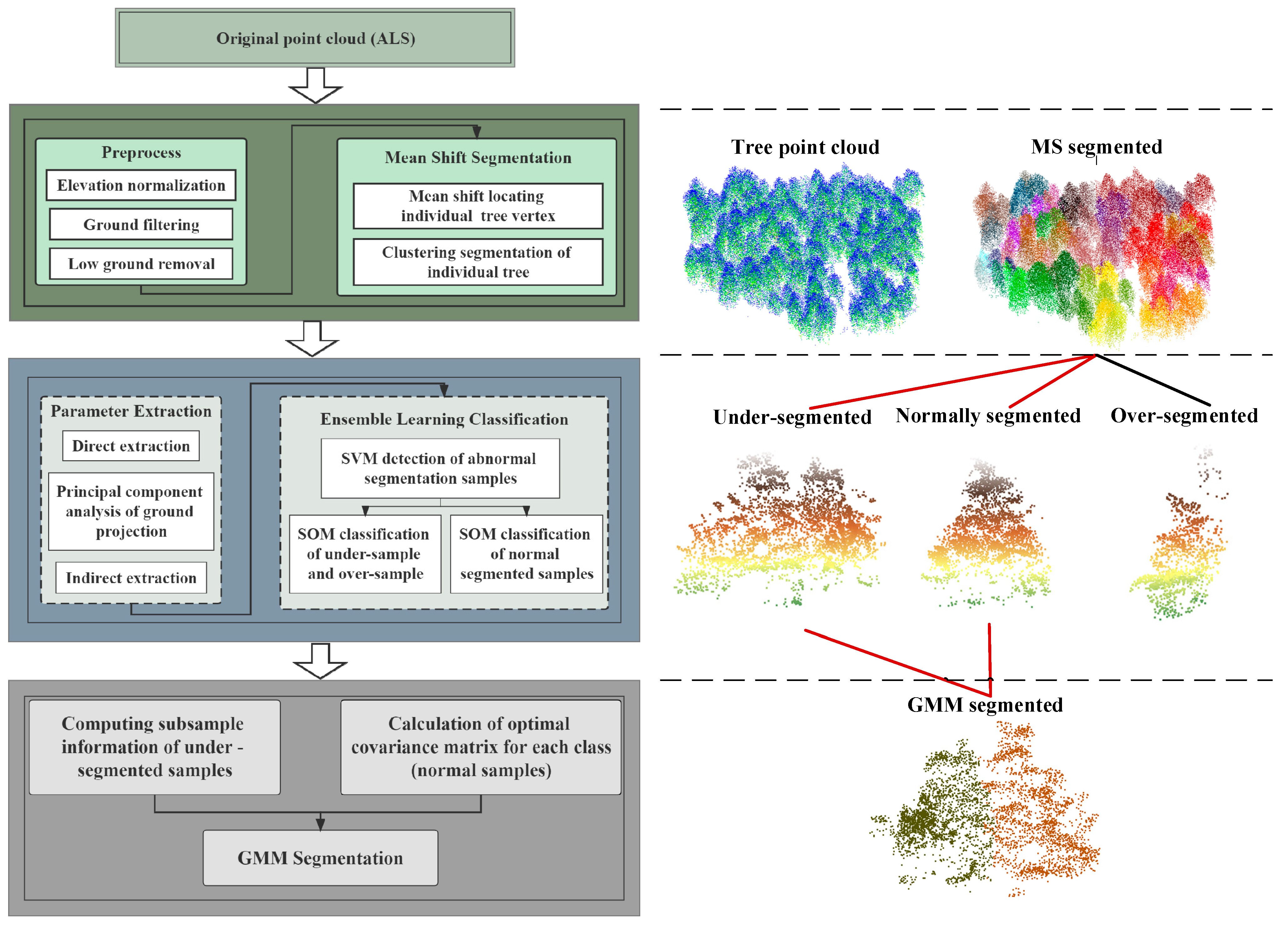
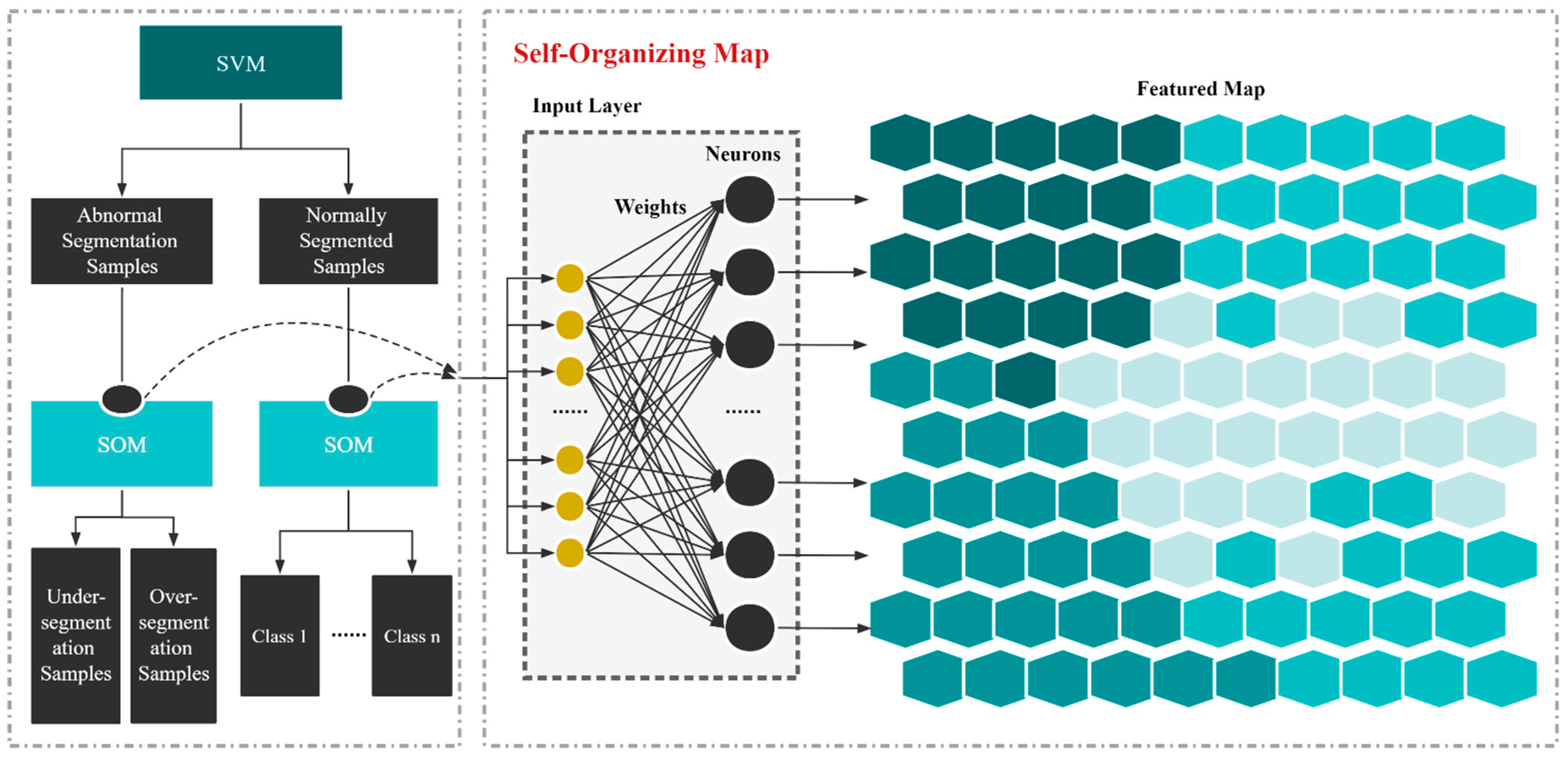
2.3. Overview of the Proposed Methodology
2.4. Pre-Processing
2.5. ITS Based on MS
2.6. Optimal Covariance Matrix Calculation
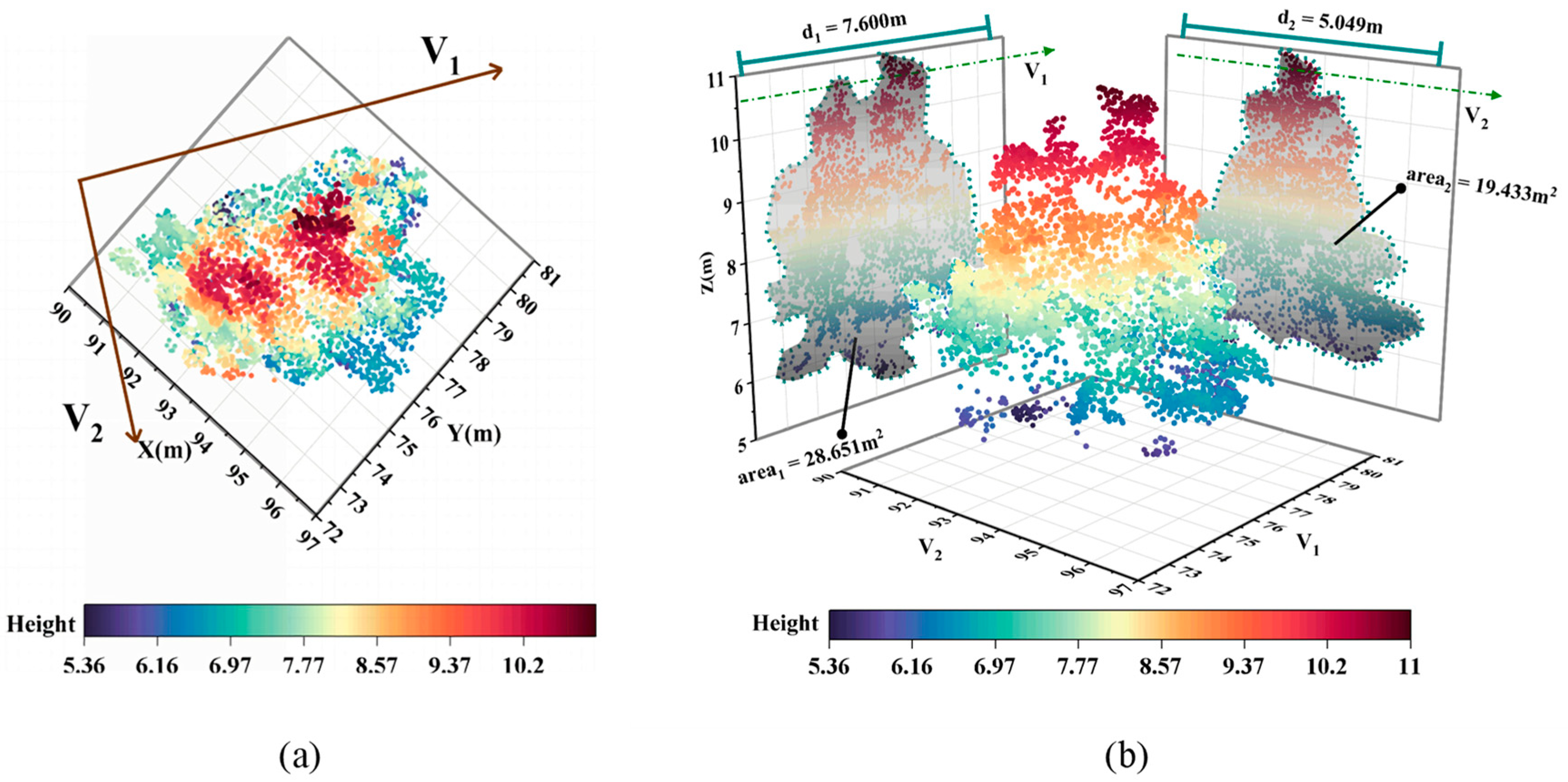
2.6.1. Parameter Extraction and Sample Classification
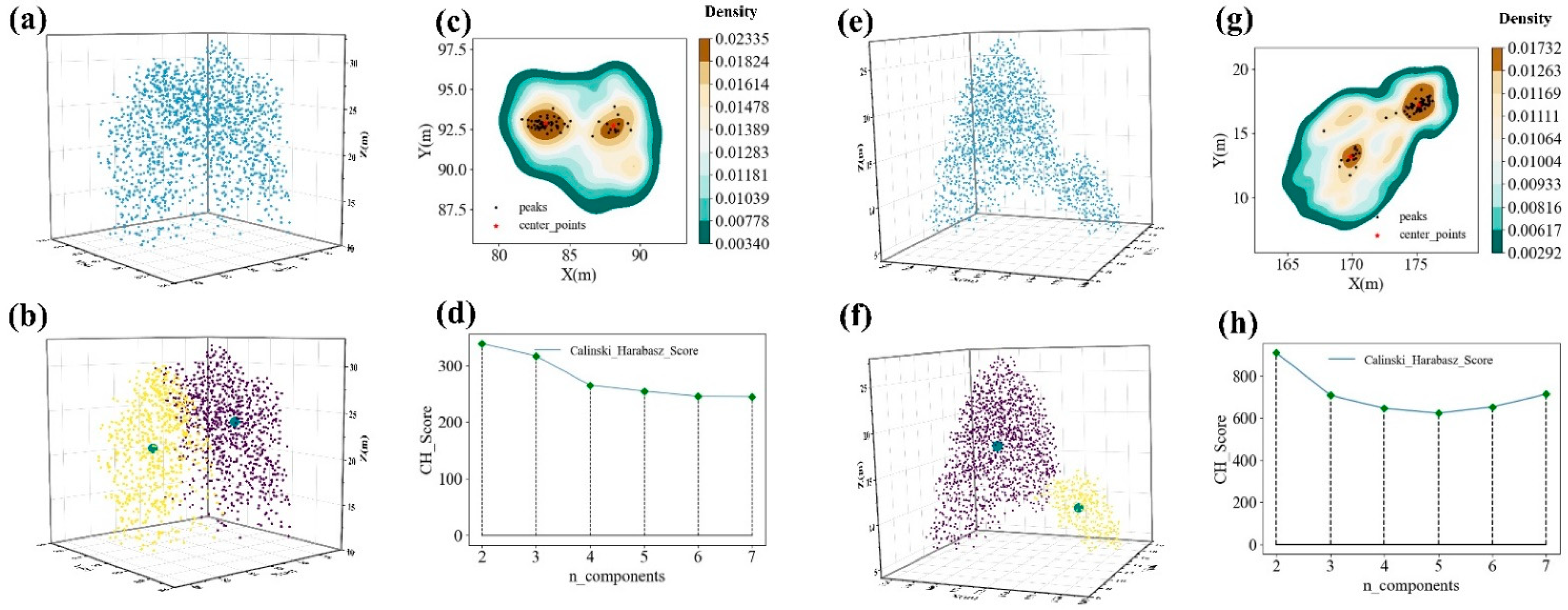
2.6.2. Calculation of Optimal Covariance Matrix
2.7. GMM-Optimized Segmentation
2.8. Validation Procedure
3. Result
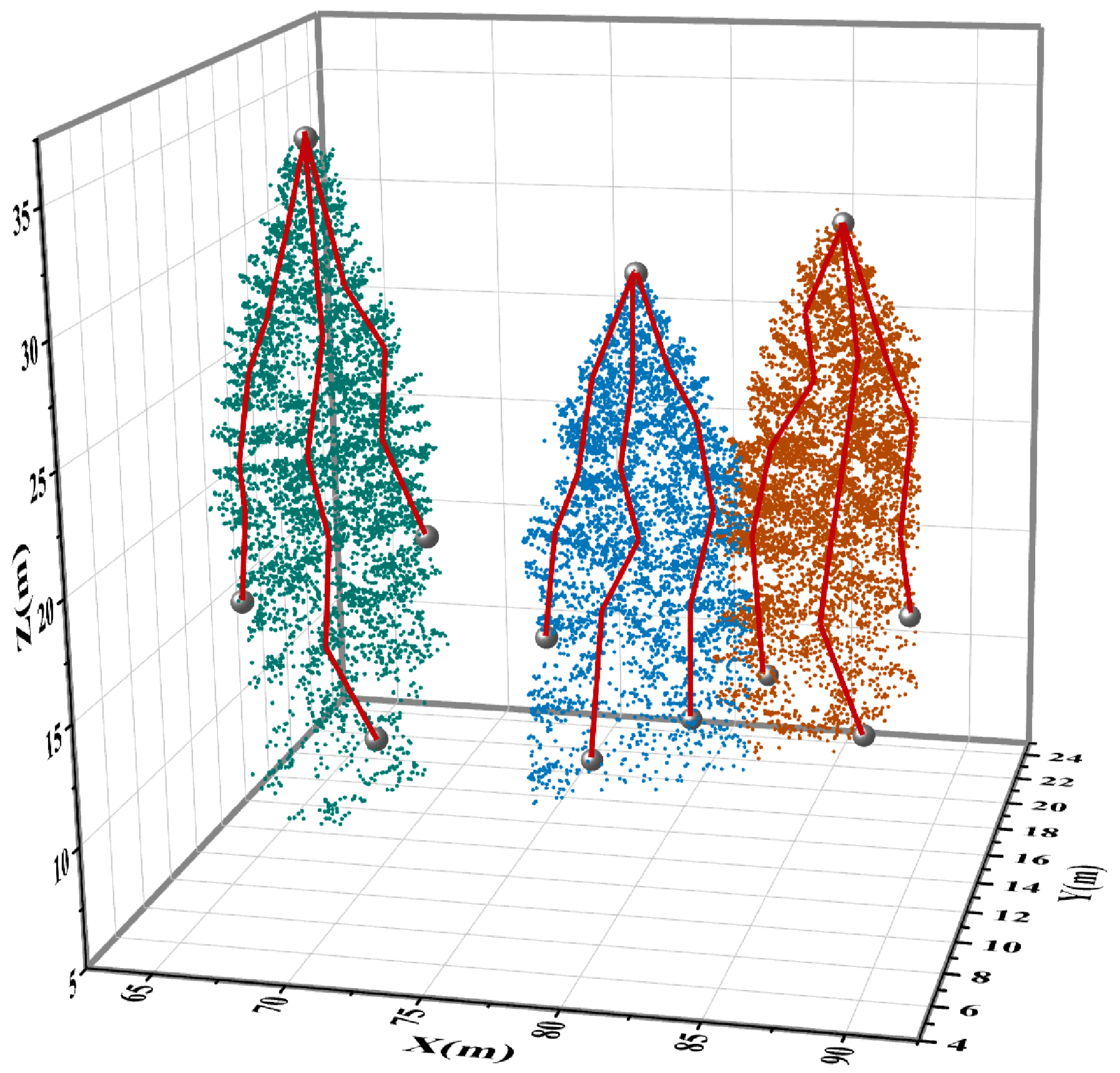
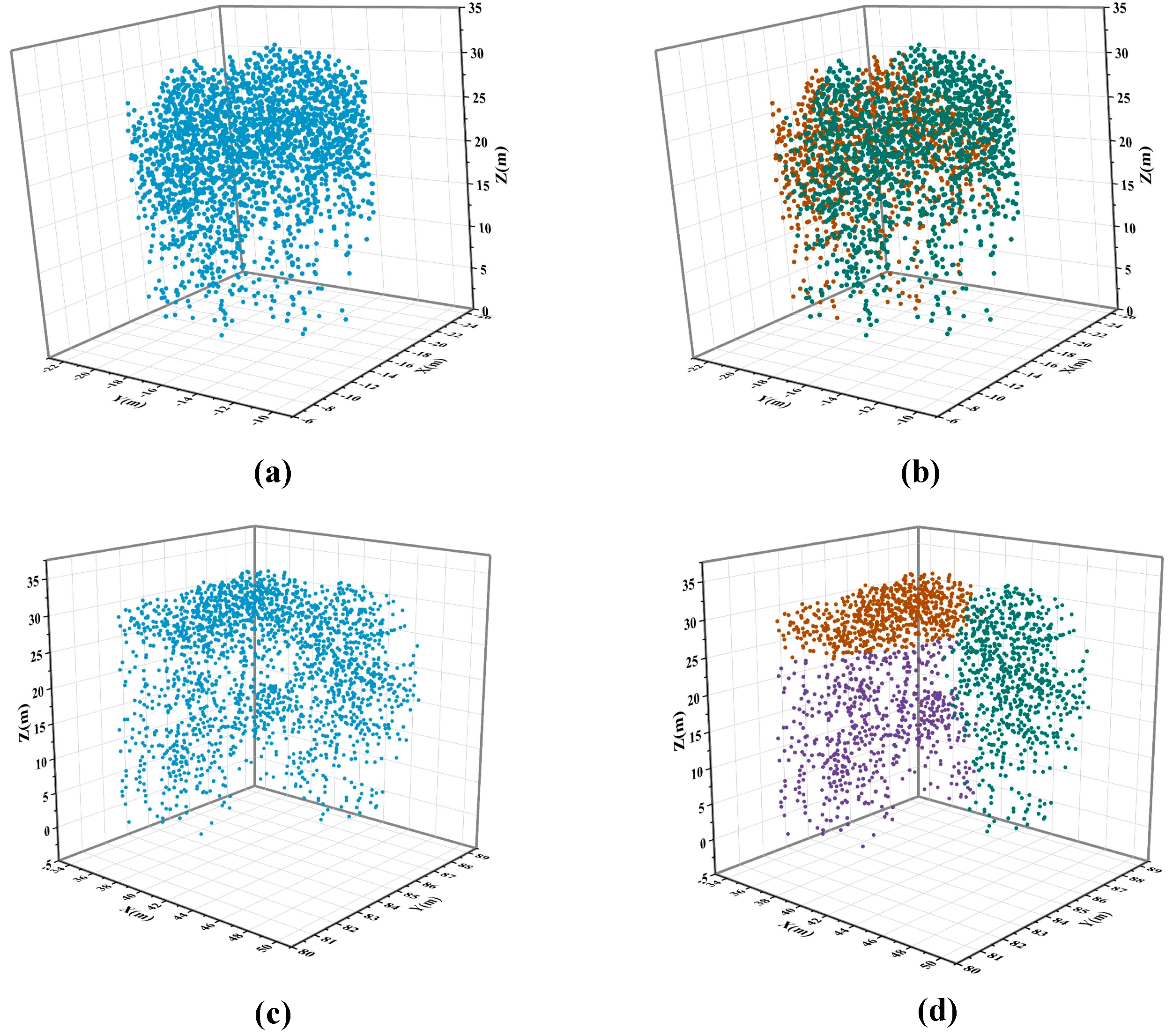
3.1. ITS Results Based on MS
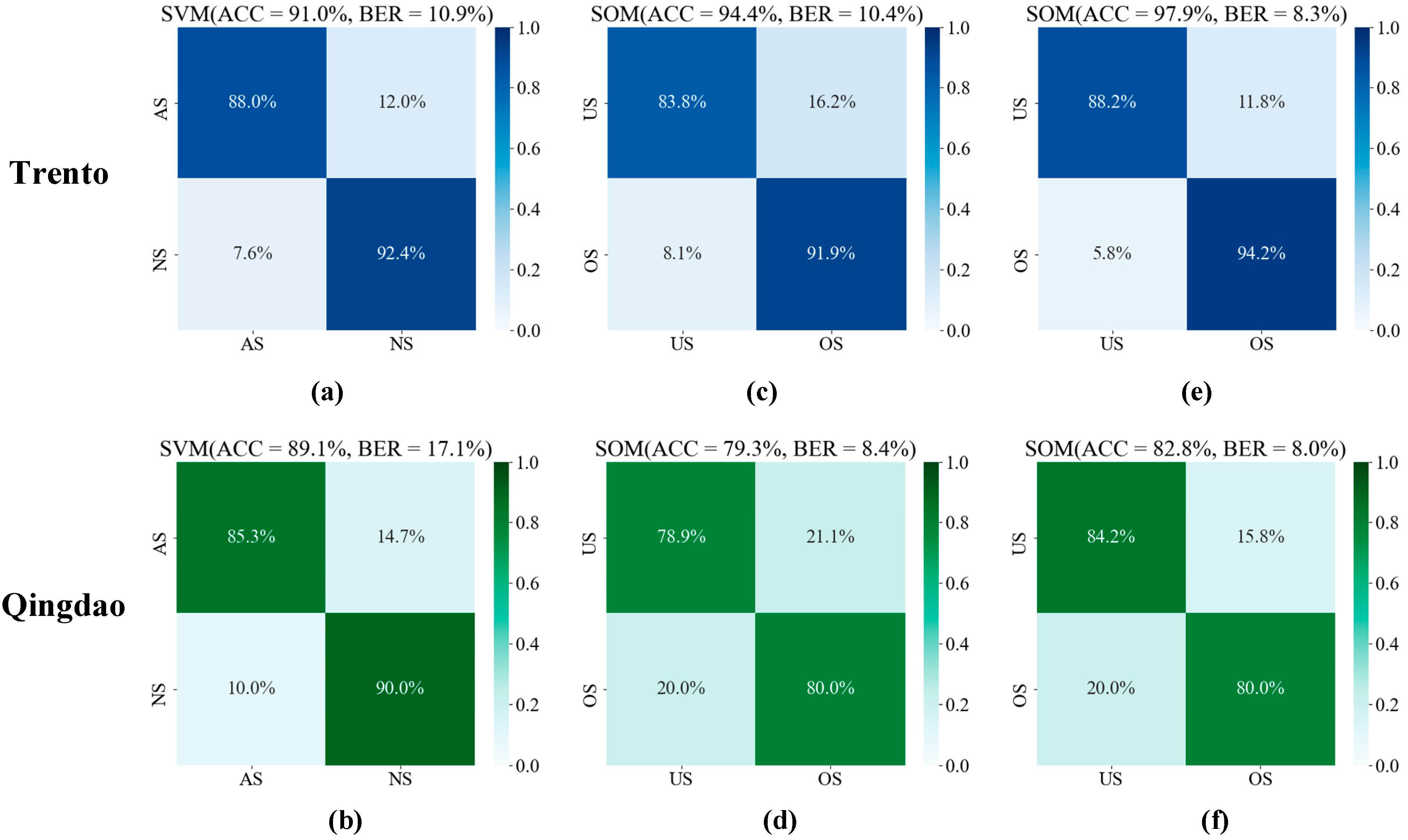
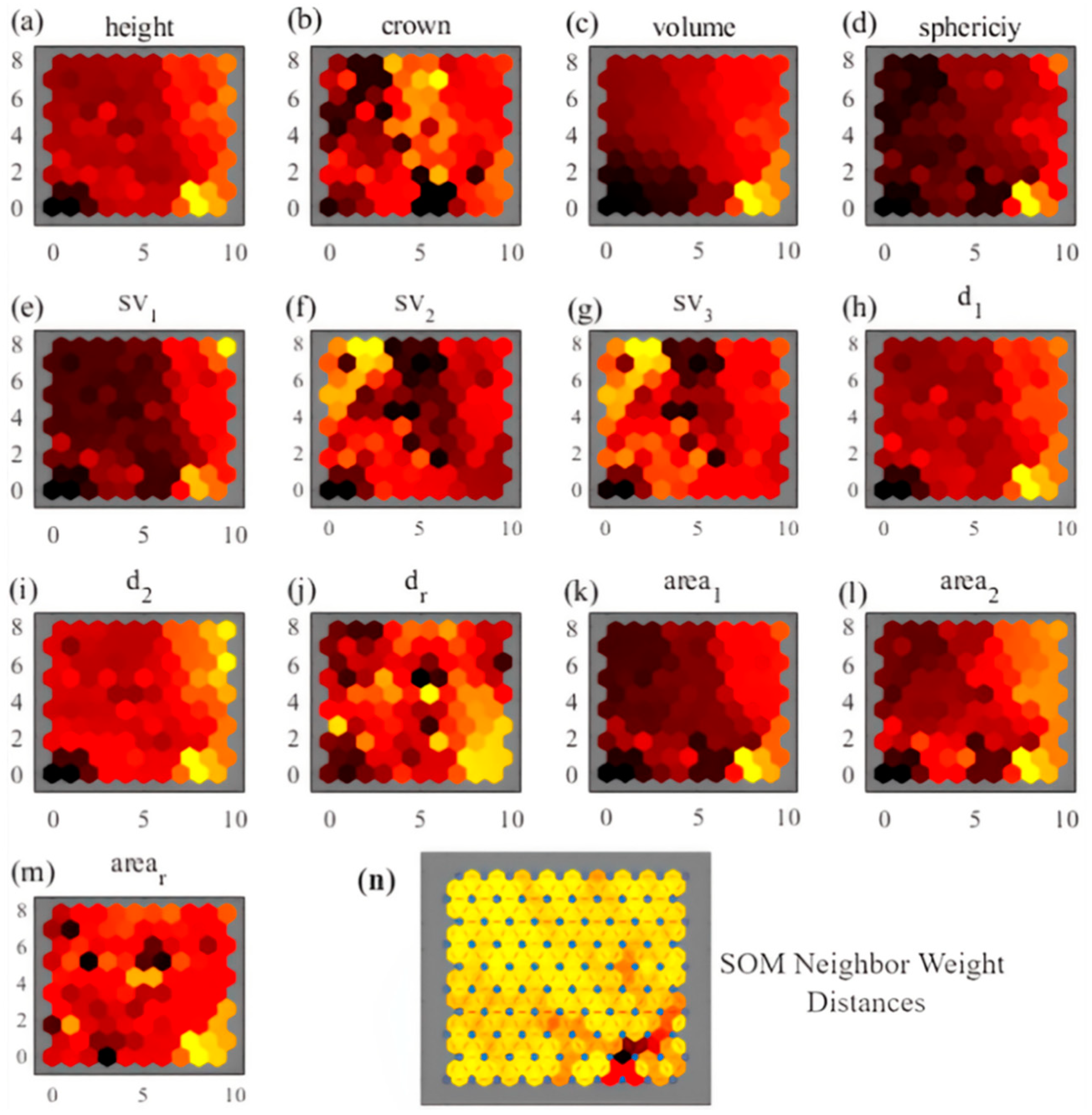
3.2. SVM and SOM Classification Results
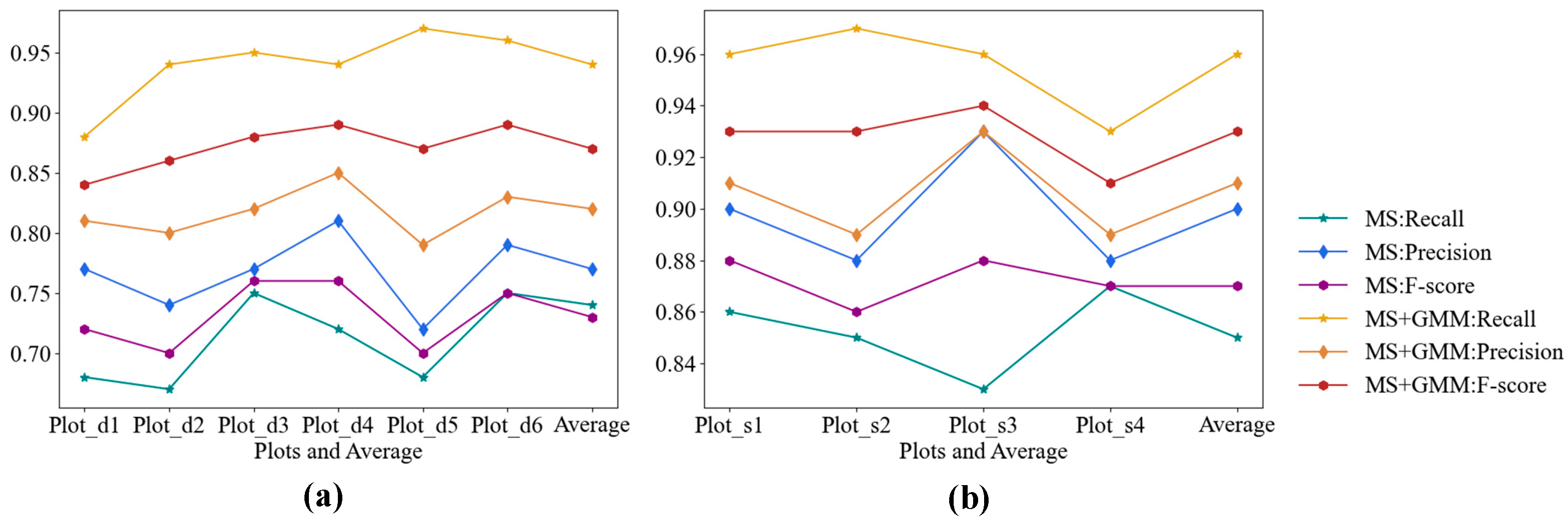
3.3. GMM-Optimized Segmentation Results
4. Discussion
4.1. Under-Segmentation Sample Extraction
- dr differs too less able to represent features than d1 and d2. Calculating dr would interfere with the construction of a clear feature space based on canopy length features;
- arear is almost as able as, or even better able than, area1 and area2 to represent features. Calculating arear helps to construct a clear feature space based on canopy area features;
- The feature space distribution of crown, sv1, sv2, and sv3 is too chaotic to be used as effective features for classification.
4.2. GMM-Optimized Segmentation
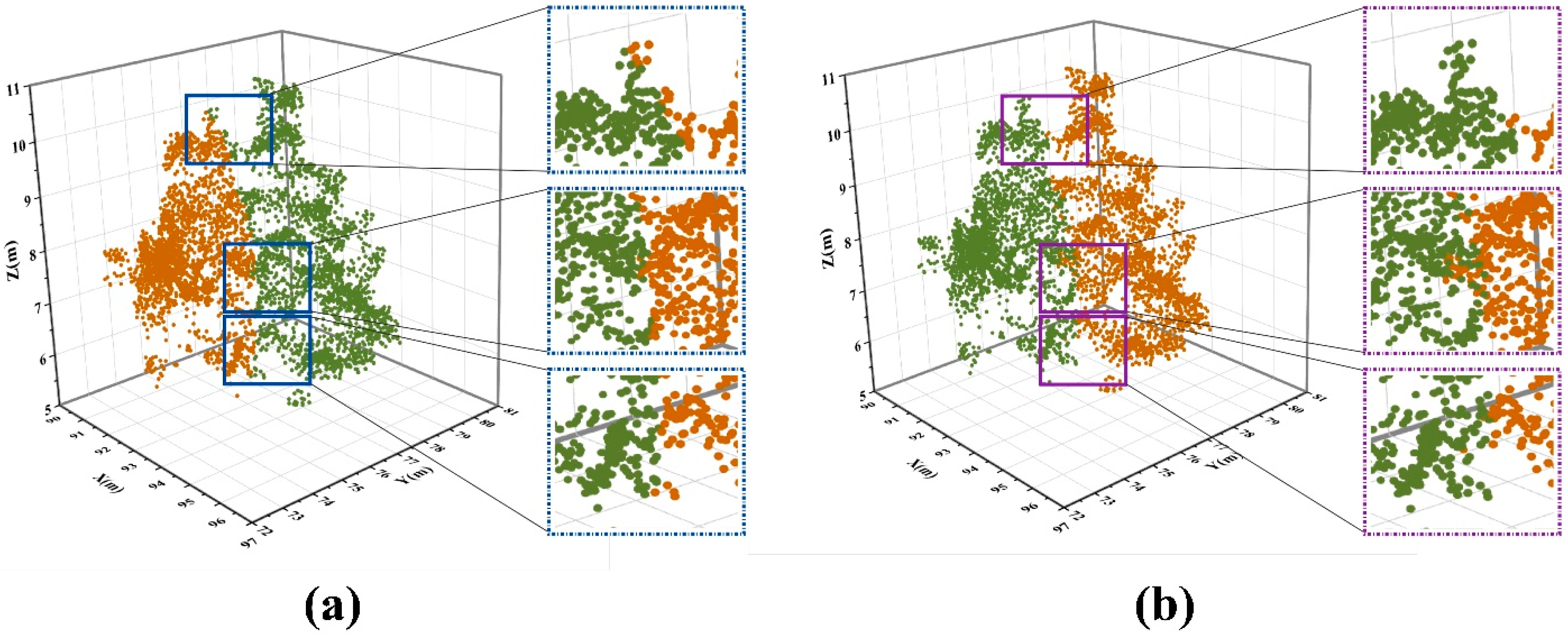
4.3. Analysis of Failure Cases
- i.
- It cannot extract under-segmented samples due to misclassification by SVM or SOM and cannot optimize them by GMM;
- ii.
- It determines the number of subsamples or calculates the center point position incorrectly as the density peak points are too centralized or decentralized, eventually leading to failure of optimized segmentation (Figure 14a,b);
- iii.
- It can calculate the number of subsamples and the approximate centers, but cannot optimize the under-segmented samples correctly (Figure 14c,d).
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yu, X.; Kukko, A.; Kaartinen, H.; Wang, Y.; Liang, X.; Matikainen, L.; Hyyppä, J. Comparing features of single and multi-photon lidar in boreal forests. ISPRS J. Photogramm. Remote Sens 2020, 168, 268–276. [Google Scholar] [CrossRef]
- Tang, Z.; Xia, X.; Huang, Y.; Lu, Y.; Guo, Z. Estimation of National Forest Aboveground Biomass from Multi-Source Remotely Sensed Dataset with Machine Learning Algorithms in China. Remote Sens. 2020, 14, 5487. [Google Scholar] [CrossRef]
- Shao, J.; Zhang, W.; Mellado, N.; Wang, N.; Jin, S.; Cai, S.; Yan, G. SLAM-aided forest plot mapping combining terrestrial and mobile laser scanning. ISPRS J. Photogramm. Remote Sens. 2020, 163, 214–230. [Google Scholar] [CrossRef]
- Nguyen, V.T.; Fournier, R.A.; Côté, J.F.; Pimont, F. Estimation of vertical plant area density from single return terrestrial laser scanning point clouds acquired in forest environments. Remote Sens. Environ. 2022, 279, 113115. [Google Scholar] [CrossRef]
- Liu, X.; Ma, Q.; Wu, X.; Hu, T.; Liu, Z.; Liu, L.; Su, Y. A novel entropy-based method to quantify forest canopy structural complexity from multiplatform lidar point clouds. Remote Sens. Environ. 2022, 282, 113280. [Google Scholar] [CrossRef]
- Baltsavias, E.P. Airborne laser scanning: Basic relations and formulas. ISPRS J. Photogramm. Remote Sens. 1999, 54, 199–214. [Google Scholar] [CrossRef]
- Kim, C.; Habib, A.; Pyeon, M.; Kwon, G.R.; Jung, J.; Heo, J. Segmentation of Planar Surfaces from Laser Scanning Data Using the Magnitude of Normal Position Vector for Adaptive Neighborhoods. Sensors 2016, 16, 140. [Google Scholar] [CrossRef]
- Wang, R.; Hu, Y.; Wu, H.; Wang, J. Automatic extraction of building boundaries using aerial LiDAR data. J. Appl. Remote Sens. 2016, 10, 016022. [Google Scholar] [CrossRef]
- Lefsky, M.A.; Cohen, W.B.; Parker, G.G.; Harding, D.J. Lidar Remote Sensing for Ecosystem Studies. BioScience 2002, 52, 19–30. [Google Scholar] [CrossRef]
- Wulder, M.A.; White, J.C.; Nelson, R.F.; Næsset, E.; Ørka, H.O.; Coops, N.C.; Hilke, T.; Bater, C.W.; Gobakken, T. Lidar Sampling for Large-Area Forest Characterization: A Review. Remote Sens. Environ. 2012, 121, 196–209. [Google Scholar] [CrossRef]
- Cao, W.; Wu, J.; Shi, Y.; Chen, D. Restoration of Individual Tree Missing Point Cloud Based on Local Features of Point Cloud. Remote Sens. 2022, 14, 1346. [Google Scholar] [CrossRef]
- Zhao, Y.; Ma, Y.; Quackenbush, L.J.; Zhen, Z. Estimation of Individual Tree Biomass in Natural Secondary Forests Based on ALS Data and WorldView-3 Imagery. Remote Sens. 2022, 14, 271. [Google Scholar] [CrossRef]
- Unger, D.; Hung, I.; Brooks, R.E.; Williams, H.M. Estimating number of trees, tree height and crown width using Lidar data. GIScience Remote Sens. 2014, 51, 227–238. [Google Scholar] [CrossRef]
- Ene, L.T.; Gobakken, T.; Andersen, H.E.; Næsset, E.; Cook, B.D.; Morton, D.C.; Babcock, C.; Nelson, R. Large-scale estimation of aboveground biomass in miombo woodlands using airborne laser scanning and national forest inventory data. Remote Sens. Environ. 2017, 186, 626–636. [Google Scholar] [CrossRef]
- Schlund, M.; Erasmi, S.; Scipal, K. Comparison of Aboveground Biomass Estimation from InSAR and LiDAR Canopy Height Models in Tropical Forests. IEEE Geosci. Remote Sens. Lett. 2020, 17, 367–371. [Google Scholar] [CrossRef]
- Aaron, J.; Baoxin, H.; Jili, L.; Linhai, J. Improving the efficiency and accuracy of individual tree crown delineation from high-density LiDAR data. Int. J. Appl. Earth Obs. Geoinf. 2014, 26, 145–155. [Google Scholar]
- Duncanson, L.I.; Cook, B.D.; Hurtt, G.C.; Dubayah, R.O. An efficient, multi-layered crown delineation algorithm for mapping individual tree structure across multiple ecosystems. Remote Sens. Environ. 2014, 154, 378–386. [Google Scholar] [CrossRef]
- Mongus, D.; Žalik, B. An efficient approach to 3D single tree-crown delineation in LiDAR data. ISPRS J. Photogramm. Remote Sens. 2015, 108, 219–233. [Google Scholar] [CrossRef]
- Liu, L.; Lim, S.; Shen, X.; Yebra, M. A hybrid method for segmenting individual trees from airborne lidar data. Comput. Electron. Agric. 2019, 163, 104871. [Google Scholar] [CrossRef]
- Liu, H.; Dong, P.; Wu, C.; Wang, P.; Fang, M. Individual tree identification using a new cluster-based approach with discrete-return airborne LiDAR data. Remote Sens. Environ. 2021, 258, 112382. [Google Scholar] [CrossRef]
- Douss, R.; Farah, I.R. Extraction of individual trees based on Canopy Height Model to monitor the state of the forest. Trees For. People 2022, 8, 100257. [Google Scholar] [CrossRef]
- Khosravipour, A.; Skidmore, A.K.; Isenburg, M. Generating spike-free digital surface models using LiDAR raw point clouds: A new approach for forestry applications. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 104–114. [Google Scholar] [CrossRef]
- Yun, T.; Jiang, K.; Li, G.; Eichhorn, M.P.; Fan, J.; Liu, F.; Chen, B.; An, F.; Cao, L. Individual tree crown segmentation from airborne LiDAR data using a novel Gaussian filter and energy function minimization-based approach. Remote Sens. Environ. 2021, 256, 112307. [Google Scholar] [CrossRef]
- Alon, A.S.; Enrique, D.F.; Drandreb, E.O.J. Tree Detection using Genus-Specific RetinaNet from Orthophoto for Segmentation Access of Airborne LiDAR Data. In Proceedings of the 2019 IEEE 6th International Conference on Engineering Technologies and Applied Sciences (ICETAS), Kuala Lumpur, Malaysia, 20–21 December 2019; pp. 1–6. [Google Scholar]
- Aubry-Kientz, M.; Dutrieux, R.; Ferraz, A.; Saatchi, S.; Hamraz, H.; Williams, J.; Coomes, D.; Piboule, A.; Vincent, G. A Comparative Assessment of the Performance of Individual Tree Crowns Delineation Algorithms from ALS Data in Tropical Forests. Remote Sens. 2019, 11, 1086. [Google Scholar] [CrossRef]
- Chen, Q.; Gao, T.; Zhu, J.; Wu, F.; Li, X.; Lu, D.; Yu, F. Individual Tree Segmentation and Tree Height Estimation Using Leaf-Off and Leaf-On UAV-LiDAR Data in Dense Deciduous Forests. Remote Sens. 2022, 31, 2787. [Google Scholar] [CrossRef]
- Amiri, N.; Polewski, P.; Heurich, M.; Krzystek, P. Adaptive stopping criterion for top-down segmentation of ALS point clouds in temperate coniferous forests. ISPRS J. Photogramm. Remote Sens. 2018, 141, 265–274. [Google Scholar] [CrossRef]
- Jaskierniak, D.; Lucieer, A.; Kuczera, G.; Turner, D.; Lane, P.N.J.; Benyon, R.G.; Haydon, S. Individual tree detection and crown delineation from Unmanned Aircraft System (UAS) LiDAR in structurally complex mixed species eucalypt forests. ISPRS J. Photogramm. Remote Sens. 2021, 171, 171–187. [Google Scholar] [CrossRef]
- Harikumar, A.; Bovolo, F.; Bruzzone, L. A Local Projection-Based Approach to Individual Tree Detection and 3-D Crown Delineation in Multistoried Coniferous Forests Using High-Density Airborne LiDAR Data. IEEE Trans. Geosci. Remote Sens. 2019, 57, 1168–1182. [Google Scholar] [CrossRef]
- Xu, S.; Ye, N.; Xu, S.; Zhu, F. A supervoxel approach to the segmentation of individual trees from LiDAR point clouds. Remote Sens. Lett. 2018, 9, 515–523. [Google Scholar] [CrossRef]
- Amr, A.; Rrn, A.; Rk, B. Individual tree detection from airborne laser scanning data based on supervoxels and local convexity. Remote Sens. Appl. Soc. Environ. 2019, 15, 100242. [Google Scholar]
- Yan, W.; Guan, H.; Cao, L.; Yu, Y.; Li, C.; Lu, J. A self-adaptive mean shift tree-segmentation method Using UAV LiDAR data. Remote Sens. 2020, 12, 515. [Google Scholar] [CrossRef]
- Estornell, J.; Hadas, E.; Martí, J.; López-Cortés, I. Tree extraction and estimation of walnut structure parameters using airborne LiDAR data. Int. J. Appl. Earth Obs. Geoinf. 2021, 96, 102273. [Google Scholar] [CrossRef]
- Sun, C.; Huang, C.; Zhang, H.; Chen, B.; An, F.; Wang, L.; Yun, T. Individual Tree Crown Segmentation and Crown Width Extraction From a Heightmap Derived From Aerial Laser Scanning Data Using a Deep Learning Framework. Front. Plant Sci. 2022, 13, 914974. [Google Scholar] [CrossRef] [PubMed]
- Dai, W.; Yang, B.; Dong, Z.; Shakerb, A. A new method for 3D individual tree extraction using multispectral airborne LiDAR point clouds. ISPRS J. Photogramm. Remote Sens. 2018, 144, 400–411. [Google Scholar] [CrossRef]
- Eysn, L.; Hollaus, M.; Lindberg, E.; Berger, F.; Monnet, J.M.; Dalponte, M.; Kobal, M.; Pellegrini, M.; Lingua, E.; Mongus, D.; et al. A Benchmark of Lidar-Based Single Tree Detection Methods Using Heterogeneous Forest Data from the Alpine Space. Forests 2015, 6, 1721–1747. [Google Scholar] [CrossRef]
- Li, Y.; Wang, J.; Li, B.; Sun, W.; Li, Y. An adaptive filtering algorithm of multilevel resolution point cloud. Surv. Rev. 2020, 53, 300–311. [Google Scholar] [CrossRef]
- Comaniciu, D.; Meer, P. Mean shift: A robust approach toward feature space analysis. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 603–619. [Google Scholar] [CrossRef]
- Fukunaga, K.; Hostetler, L.D. The estimation of the gradient of a density function, with applications in pattern recognition. IEEE Trans. Inf. Theory 1975, 21, 32–40. [Google Scholar] [CrossRef]
- Cheng, Y. Mean shift, mode seeking, and clustering. IEEE Trans. Pattern Anal. Mach. Intell. 1995, 17, 790–799. [Google Scholar] [CrossRef]
- Ferraz, A.; Bretar, F.; Jacquemoud, S.; Gonçalves, G.R.; Pereira, L.G.; Tomé, M.; Soares, P. 3-D mapping of a multi-layered Mediterranean forest using ALS data. Remote Sens. Environ. 2012, 121, 210–223. [Google Scholar] [CrossRef]
- Ferraz, A.S.; Saatchi, S.S.; Mallet, C.; Meyer, V. Lidar detection of individual tree size in tropical forests. Remote Sens. Environ. 2016, 183, 318–333. [Google Scholar] [CrossRef]
- Liang, X.; Litkey, P.; Hyyppa, J.; Kaartinen, H.; Vastaranta, M.; Holopainen, M. Automatic Stem Mapping Using Single-Scan Terrestrial Laser Scanning. IEEE Trans. Geosci. Remote Sens. 2012, 50, 661–670. [Google Scholar] [CrossRef]
- Sun, H.; Wang, S.; Jiang, Q. FCM-Based Model Selection Algorithms for Determining the Number of Clusters. Pattern Recognit. 2004, 37, 2027–2037. [Google Scholar] [CrossRef]
- Sun, W.; Wang, J.; Yang, Y.; Jin, F. Rock Mass Discontinuity Extraction Method Based on Multiresolution Supervoxel Segmentation of Point Cloud. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 8436–8446. [Google Scholar] [CrossRef]
- Li, W.; Guo, Q.; Jakubowski, M.K.; Kelly, M. A New Method for Segmenting Individual Trees from the Lidar Point Cloud. Photogramm. Eng. Remote Sens. 2012, 78, 75–84. [Google Scholar] [CrossRef]
- Yin, D.; Wang, L. How to assess the accuracy of the individual tree-based forest inventory derived from remotely sensed data: A review. Int. J. Remote Sens. 2016, 37, 4521–4553. [Google Scholar] [CrossRef]
- Xiao, L.; Wang, K.; Teng, Y.; Zhang, J. Component plane presentation integrated self-organizing map for microarray data analysis. FEBS Lett. 2003, 538, 117–124. [Google Scholar] [CrossRef] [PubMed]
- Richardson, J.J.; Moskal, L.M. Strengths and limitations of assessing forest density and spatial configuration with aerial LiDAR. Remote Sens. Environ. 2011, 115, 2640–2651. [Google Scholar] [CrossRef]
- Paric, C.; Valduga, D.; Bruzzone, L. A Hierarchical Approach to Three-Dimensional Segmentation of LiDAR Data at Single-Tree Level in a Multilayered Forest. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4190–4203. [Google Scholar]


| Dataset | Proportion of Species (%) | Plot | Numbers of Tree | Height (m) | Crown Width (m) | Crown Area (m2) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Max | Min | Average | Max | Min | Average | Max | Min | Average | ||||
| Trento (Complex) | Coniferous forest: 80% Broadleaf forest: 20% | Plot_d1 | 40 | 37.1 | 18.9 | 29.9 | 12.6 | 1.3 | 7.2 | 123.8 | 11.3 | 48.1 |
| Plot_d2 | 63 | 32.9 | 17.7 | 25.6 | 11.2 | 2.1 | 6.6 | 98.9 | 10.8 | 38.1 | ||
| Plot_d3 | 64 | 34.7 | 19.3 | 28.5 | 11.9 | 2.4 | 6.6 | 110.5 | 10.3 | 37.4 | ||
| Plot_d4 | 108 | 37.2 | 14.7 | 24.9 | 13.2 | 2.1 | 6.1 | 137.8 | 8.8 | 36.7 | ||
| Plot_d5 | 62 | 34.1 | 20.5 | 24.8 | 13.3 | 2.9 | 7.1 | 137.9 | 7.4 | 31.5 | ||
| Plot_d6 | 114 | 38.2 | 21.5 | 32.1 | 11.2 | 2.4 | 6.2 | 97.7 | 10.3 | 35.1 | ||
| Total | 451 | |||||||||||
| Qingdao (Simple) | Coniferous forest: 45% Broadleaf forest: 55% | Plot_s1 | 76 | 10.8 | 7.0 | 8.2 | 6.3 | 3.0 | 4.6 | 102.1 | 4.1 | 18.4 |
| Plot_s2 | 61 | 11.2 | 6.7 | 8.8 | 7.5 | 2.4 | 5.1 | 56.2 | 3.9 | 13.0 | ||
| Plot_s3 | 89 | 14.1 | 8.5 | 11.5 | 7.4 | 2.3 | 6.2 | 68.6 | 4.6 | 17.6 | ||
| Plot_s4 | 75 | 15.9 | 6.7 | 12.8 | 7.7 | 3.7 | 5.4 | 84.9 | 4.2 | 13.6 | ||
| Total | 301 | |||||||||||
| ID | Parameter Name | Description |
|---|---|---|
| 1 | height | The height of the canopy |
| 2 | crown | The average of the north–south and east–west widths of the trees |
| 3 | volume | Volume of the canopy |
| 4 | sphericity | Sphericity of the canopy point cloud |
| 5 | sv1 | Canopy point cloud matrix singular value 1 |
| 6 | sv2 | Canopy point cloud matrix singular value 2 |
| 7 | sv3 | Canopy point cloud matrix singular value 3 |
| 8 | d1 | Maximum length of canopy horizontal projection |
| 9 | d2 | Minimum length of canopy horizontal projection |
| 10 | dr | The ratio of d1 to d2 |
| 11 | area1 | The first principal component projects polygon area perpendicularly |
| 12 | area2 | The second principal component projects polygon area perpendicularly |
| 13 | arear | The ratio of area1 to area2 |
| Dataset | Plot | Number of Detected | True Positive (TP) | False Negative (FN) | False Positive (FP) | Recall | Precision | F-Score | ||
|---|---|---|---|---|---|---|---|---|---|---|
| Trento | Plot_d1 | 35 | 27 | 13 | 8 | 0.68 | 0.77 | 0.72 | Average Recall | 0.74 |
| Plot_d2 | 57 | 42 | 21 | 15 | 0.67 | 0.74 | 0.70 | |||
| Plot_d3 | 62 | 48 | 16 | 14 | 0.75 | 0.77 | 0.76 | Average Precision | 0.77 | |
| Plot_d4 | 96 | 78 | 30 | 18 | 0.72 | 0.81 | 0.76 | |||
| Plot_d5 | 58 | 42 | 20 | 16 | 0.68 | 0.72 | 0.70 | Average F-score | 0.73 | |
| Plot_d6 | 108 | 85 | 29 | 23 | 0.75 | 0.79 | 0.75 | |||
| Total | 418 | 324 | 127 | 94 | ||||||
| Qingdao | Plot_s1 | 73 | 66 | 10 | 7 | 0.86 | 0.90 | 0.88 | Average Recall | 0.85 |
| Plot_s2 | 59 | 52 | 9 | 7 | 0.85 | 0.88 | 0.86 | |||
| Plot_s3 | 80 | 74 | 15 | 6 | 0.83 | 0.93 | 0.88 | Average Precision | 0.90 | |
| Plot_s4 | 74 | 65 | 10 | 9 | 0.87 | 0.88 | 0.87 | |||
| Total | 286 | 257 | 44 | 29 | Average F-score | 0.87 |
| Dataset | Plot | True Positive (TP) | False Negative (FN) | False Positive (FP) | Recall | Precision | F-Score | ||
|---|---|---|---|---|---|---|---|---|---|
| Trento | Plot_d1 | 35 | 5 | 8 | 0.88 | 0.81 | 0.84 | Average Recall | 0.94 |
| Plot_d2 | 59 | 4 | 15 | 0.94 | 0.80 | 0.86 | |||
| Plot_d3 | 61 | 3 | 14 | 0.95 | 0.82 | 0.88 | Average Precision | 0.82 | |
| Plot_d4 | 102 | 6 | 18 | 0.94 | 0.85 | 0.89 | |||
| Plot_d5 | 60 | 2 | 16 | 0.97 | 0.79 | 0.87 | Average F-score | 0.87 | |
| Plot_d6 | 109 | 5 | 23 | 0.96 | 0.83 | 0.89 | |||
| Total | 426 | 25 | 94 | ||||||
| Qingdao | Plot_s1 | 73 | 3 | 7 | 0.96 | 0.91 | 0.93 | Average Recall | 0.96 |
| Plot_s2 | 59 | 2 | 7 | 0.97 | 0.89 | 0.93 | |||
| Plot_s3 | 85 | 4 | 6 | 0.96 | 0.93 | 0.94 | Average Precision | 0.91 | |
| Plot_s4 | 70 | 5 | 9 | 0.93 | 0.89 | 0.91 | |||
| Total | 287 | 14 | 29 | Average F-score | 0.93 |
| Case | (i) | (ii) | (iii) | Total | (i) | (ii) | (iii) | Total | ||
|---|---|---|---|---|---|---|---|---|---|---|
| Trento | Numbers of tree | 12 | 8 | 5 | 25 | Qingdao | 3 | 4 | 7 | 14 |
| Percentage | 48% | 32% | 20% | 100% | 21% | 29% | 50% | 100% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Wang, J.; Li, Z.; Zhao, Y.; Wang, R.; Habib, A. Optimization Method of Airborne LiDAR Individual Tree Segmentation Based on Gaussian Mixture Model. Remote Sens. 2022, 14, 6167. https://doi.org/10.3390/rs14236167
Zhang Z, Wang J, Li Z, Zhao Y, Wang R, Habib A. Optimization Method of Airborne LiDAR Individual Tree Segmentation Based on Gaussian Mixture Model. Remote Sensing. 2022; 14(23):6167. https://doi.org/10.3390/rs14236167
Chicago/Turabian StyleZhang, Zhenyu, Jian Wang, Zhiyuan Li, Youlong Zhao, Ruisheng Wang, and Ayman Habib. 2022. "Optimization Method of Airborne LiDAR Individual Tree Segmentation Based on Gaussian Mixture Model" Remote Sensing 14, no. 23: 6167. https://doi.org/10.3390/rs14236167
APA StyleZhang, Z., Wang, J., Li, Z., Zhao, Y., Wang, R., & Habib, A. (2022). Optimization Method of Airborne LiDAR Individual Tree Segmentation Based on Gaussian Mixture Model. Remote Sensing, 14(23), 6167. https://doi.org/10.3390/rs14236167








