ArithFusion: An Arithmetic Deep Model for Temporal Remote Sensing Image Fusion
Abstract
1. Introduction
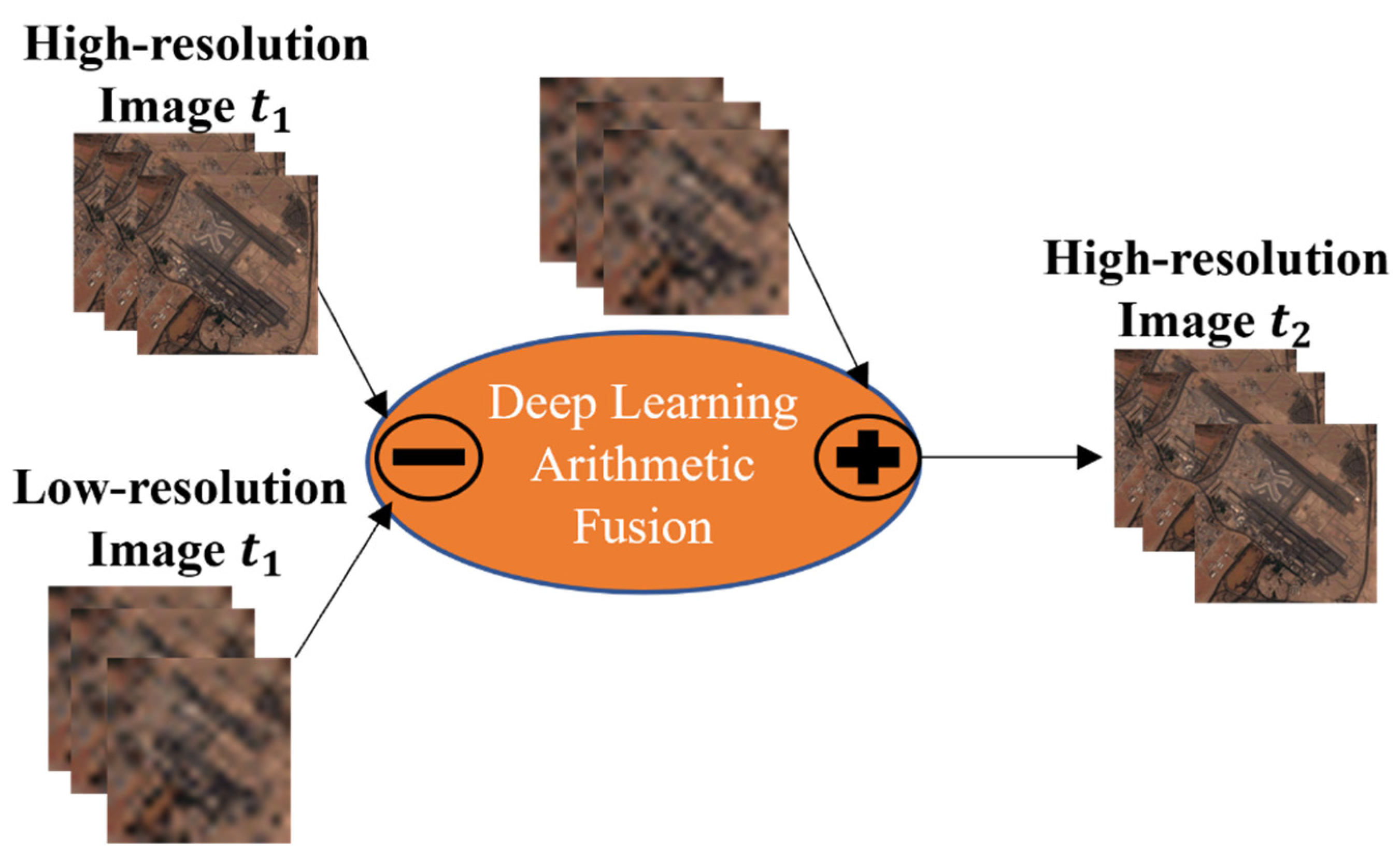
- We propose a deep learning model that performs arithmetic operations in feature space to fuse multimodal temporal remote sensing images. The arithmetic operation can effectively carry temporal changes and obtain high-resolution fused images, making it suitable for change detection applications.
- We successfully applied the proposed model to fuse historical satellite image pairs, including Sentinel-2 satellite images (10 m spatial resolution), NAIP aerial images (1 m spatial resolution), Landsat-8 images (30 m spatial resolution), and Sentinel-2 images, to reconstruct high-resolution images. To the best of our knowledge, this is the first attempt to bridge the 10× resolution gap in remote sensing images.
- We contribute a benchmark dataset that contains 45 pairs of low-resolution and high-resolution images collected by the LandSat-8 and Sentinel-2 satellites.
2. Related Work
3. Methodology
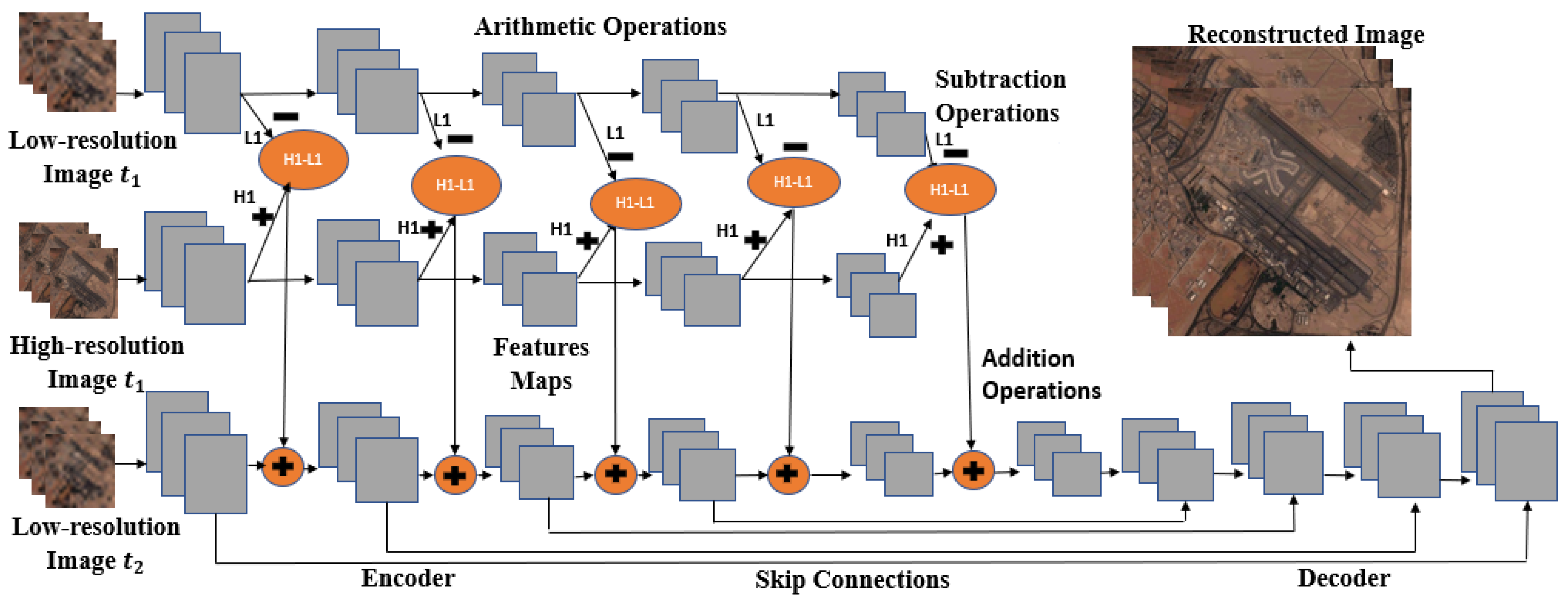
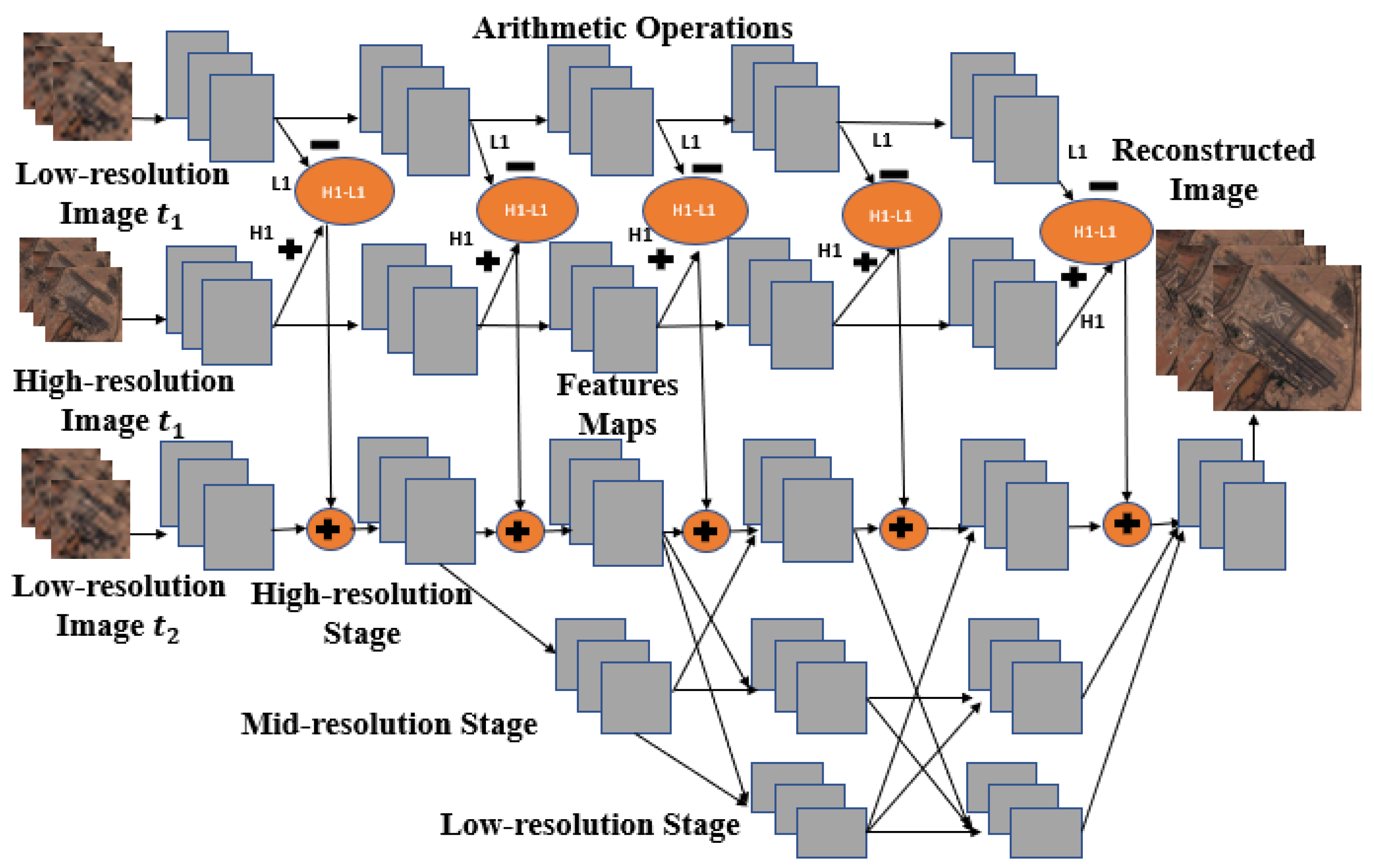
3.1. Proposed Model
3.1.1. U-Net Architecture
3.1.2. HRNet Architecture
3.2. Loss Functions
3.3. Performance Metrics
4. Experimental Setup
4.1. Datasets
4.2. Preprocessing
4.3. Experiments
4.3.1. Experiment 1
4.3.2. Experiment 2
4.3.3. Experiment 3
4.3.4. Experiment 4
4.3.5. Experiment 5: Statistical Tests
4.4. Competing Methods and Abbreviations
5. Results and Discussion
5.1. Hyperparameter Determination
5.2. Results and Analysis
5.2.1. Results of Experiment 1 and Analysis
5.2.2. Results of Experiment 2 and Analysis
5.2.3. Results of Experiment 3 and Analysis
5.2.4. Results of Experiment 4 and Analysis
5.2.5. Results of Statistical Tests
5.2.6. Visual Inspection
5.2.7. Images with Temporal Changes
5.2.8. Images with High-Frequency Details
5.2.9. Upper Limit of the Downsampling Factor
6. Discussion
7. Conclusions and Future Research
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shen, M.; Tang, Y.; Chen, J.; Zhu, X.; Zheng, Y. Influences of temperature and precipitation before the growing season on spring phenology in grasslands of the central and eastern Qinghai-Tibetan Plateau. Agric. For. Meteorol. 2011, 151, 1711–1722. [Google Scholar] [CrossRef]
- Amoros-Lopez, J.; G’omez-Chova, L.; Alonso, L.; Guanter, L.; Zurita-Milla, R.; Moreno, J.; Camps-Valls, G. Multitemporal fusion of landsat/tm and envisat/meris for crop monitoring. Int. J. Appl. Earth Obs. Geoinf. 2013, 23, 132–141. [Google Scholar] [CrossRef]
- Liao, C.; Wang, J.; Dong, T.; Shang, J.; Liu, J.; Song, Y. Using spatio-temporal fusion of landsat-8 and modis data to derive phenology, biomass and yield estimates for corn and soybean. Sci. Total Environ. 2019, 650, 1707–1721. [Google Scholar] [CrossRef] [PubMed]
- Johnson, M.D.; Hsieh, W.W.; Cannon, A.J.; Davidson, A.; Bedard, F. Crop yield forecasting on the Canadian prairies by remotely sensed vegetation indices and machine learning methods. Agric. For. Meteorol. 2016, 218, 74–84. [Google Scholar] [CrossRef]
- Yang, X.; Lo, C. Using a time series of satellite imagery to detect land use and land cover changes in the Atlanta, Georgia metropolitan area. Int. J. Remote Sens. 2002, 23, 1775–1798. [Google Scholar] [CrossRef]
- Li, X.; Zhou, Y.; Asrar, G.R.; Mao, J.; Li, X.; Li, W. Response of vegetation phenology to urbanization in the conterminous united states. Glob. Chang. Biol. 2017, 23, 2818–2830. [Google Scholar] [CrossRef]
- Hilker, T.; Wulder, M.A.; Coops, N.C.; Seitz, N.; White, J.C.; Gao, F.; Masek, J.G.; Stenhouse, G. Generation of dense time series synthetic Landsat data through data blending with modis using a spatial and temporal adaptive reflectance fusion model. Remote Sens. Environ. 2009, 113, 1988–1999. [Google Scholar] [CrossRef]
- Ranson, K.; Kovacs, K.; Sun, G.; Kharuk, V. Disturbance recognition in the boreal forest using radar and landsat-7. Can. J. Remote Sens. 2003, 29, 271–285. [Google Scholar] [CrossRef]
- Buying Satellite Imagery: Pricing Information for High Resolution Satellite Imagery. Available online: http://landinfo.com/satellite-imagery-pricing/ (accessed on 5 February 2021).
- Fu, P.; Weng, Q. Consistent land surface temperature data generation from irregularly spaced Landsat imagery. Remote Sens. Environ. 2016, 184, 175–187. [Google Scholar] [CrossRef]
- Zhu, X.; Cai, F.; Tian, J.; Williams, T. Spatiotemporal fusion of multisource remote sensing data: Literature survey, taxonomy, principles, applications, and future directions. Remote Sens. 2018, 10, 527. [Google Scholar] [CrossRef]
- Shao, Z.; Cai, J.; Fu, P.; Hu, L.; Liu, T. Deep learning-based fusion of landsat-8 and sentinel-2 images for a harmonized surface reflectance product. Remote Sens. Environ. 2019, 235, 111425. [Google Scholar] [CrossRef]
- Gao, F.; Masek, J.; Schwaller, M.; Hall, F. On the blending of the Landsat and modis surface reflectance: Predicting daily Landsat surface reflectance. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2207–2218. [Google Scholar]
- Zhu, X.; Chen, J.; Gao, F.; Chen, X.; Masek, J. An enhanced spatial and temporal adaptive reflectance fusion model for complex heterogeneous regions. Remote Sens. Environ. 2010, 114, 2610–2623. [Google Scholar] [CrossRef]
- Shen, H.; Wu, P.; Liu, Y.; Ai, T.; Wang, Y.; Liu, X. A spatial and temporal reflectance fusion model considering sensor observation differences. Int. J. Remote Sens. 2013, 34, 4367–4383. [Google Scholar] [CrossRef]
- Zurita-Milla, R.; Clevers, J.G.; Schaepman, M.E. Unmixing-based Landsat tm and meris fr data fusion. IEEE Geosci. Remote Sens. Lett. 2008, 5, 453–457. [Google Scholar] [CrossRef]
- Zurita-Milla, R.; Kaiser, G.; Clevers, J.; Schneider, W.; Schaepman, M.E. Downscaling time series of meris full resolution data to monitor vegetation seasonal dynamics. Remote Sens. Environ. 2009, 113, 1874–1885. [Google Scholar] [CrossRef]
- Huang, B.; Song, H. Spatiotemporal reflectance fusion via sparse representation. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3707–3716. [Google Scholar] [CrossRef]
- Song, H.; Huang, B. Spatiotemporal satellite image fusion through one-pair image learning. IEEE Trans. Geosci. Remote Sens. 2012, 51, 1883–1896. [Google Scholar] [CrossRef]
- Wang, Q.; Shi, W.; Atkinson, P.M.; Zhao, Y. Downscaling modis images with area-to-point regression kriging. Remote Sens. Environ. 2015, 166, 191–204. [Google Scholar] [CrossRef]
- Wang, Q.; Blackburn, G.A.; Onojeghuo, A.O.; Dash, J.; Zhou, L.; Zhang, Y.; Atkinson, P.M. Fusion of Landsat 8 oli and sentinel2 msi data. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3885–3899. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Devlin, J.; Chang, M.-W.; Lee, K.; Toutanova, K. Bert: Pre-training of deep bidirectional transformers for language understanding. arXiv 2018, arXiv:1810.04805. [Google Scholar]
- Yang, L.; Zhang, M.; Li, C.; Bendersky, M.; Najork, M. Beyond 512 tokens: Siamese multi-depth transformer-based hierarchical encoder for long-form document matching. In Proceedings of the 29th ACM International Conference on Information & Knowledge Management, Online, 19–23 October 2020; pp. 1725–1734. [Google Scholar]
- Hannun, A.; Case, C.; Casper, J.; Catanzaro, B.; Diamos, G.; Elsen, E.; Prenger, R.; Satheesh, S.; Sengupta, S.; Coates, A.; et al. Deep speech: Scaling up end-to-end speech recognition. arXiv 2014, arXiv:1412.5567. [Google Scholar]
- Graves, A.; Mohamed, A.-r.; Hinton, G. Speech recognition with deep recurrent neural networks. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 6645–6649. [Google Scholar]
- Petersson, H.; Gustafsson, D.; Bergstrom, D. Hyperspectral image analysis using deep learning—A review. In Proceedings of the 2016 Sixth International Conference on Image Processing Theory, Tools and Applications (IPTA), Oulu, Finland, 12–15 December 2016; pp. 1–6. [Google Scholar]
- Zhu, X.X.; Tuid, D.; Mou, L.; Xia, G.-S.; Zhang, L.; Xu, F.; Fraundorfer, F. Deep learning in remote sensing: A comprehensive review and list of resources. IEEE Geosci. Remote Sens. Mag. 2017, 5, 8–36. [Google Scholar] [CrossRef]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Image super-resolution using deep convolutional networks. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 38, 295–307. [Google Scholar] [CrossRef] [PubMed]
- Song, H.; Liu, Q.; Wang, G.; Hang, R.; Huang, B. Spatiotemporal satellite image fusion using deep convolutional neural networks. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 821–829. [Google Scholar] [CrossRef]
- Li, Y.; Li, J.; He, L.; Chen, J.; Plaza, A. A new sensor bias-driven spatio-temporal fusion model based on convolutional neural networks. Sci. China Inf. Sci. 2020, 63, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Chen, B.; Li, J.; Jin, Y. Deep learning for feature-level data fusion: Higher resolution reconstruction of historical Landsat archive. Remote Sens. 2021, 13, 167. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; Springer: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar]
- Wang, J.; Sun, K.; Cheng, T.; Jiang, B.; Deng, C.; Zhao, Y.; Xiao, B. Deep high-resolution representation learning for visual recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 43, 3349–3364. [Google Scholar] [CrossRef]
- Sun, L.; Fan, Z.; Ding, X.; Huang, Y.; Paisley, J. Region-of-interest undersampled mri reconstruction: A deep convolutional neural network approach. Magn. Reson. Imaging 2019, 63, 185–192. [Google Scholar] [CrossRef]
- Han, Y.; Du, H.; Lam, F.; Mei, W.; Fang, L. Image reconstruction using analysis model prior. Comput. Math. Methods Med. 2016, 2016, 7571934. [Google Scholar] [CrossRef] [PubMed]
- Vivone, G.; Alparone, L.; Chanussot, J.; Dalla Mura, M.; Garzelli, A.; Licciardi, G.A.; Restaino, R.; Wald, L. A critical comparison among pansharpening algorithms. IEEE Trans. Geosci. Remote Sens. 2014, 53, 2565–2586. [Google Scholar] [CrossRef]
- Vickers, A.J. Parametric versus non-parametric statistics in the analysis of randomized trials with non-normally distributed data. BMC Med. Res. Methodol. 2005, 5, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Xu, M.; Fralick, D.; Zheng, J.Z.; Wang, B.; Tu, X.M.; Feng, C. The differences and similarities between two-sample t-test and paired t-test. Shanghai Arch. Psychiatry 2017, 29, 184. [Google Scholar]
- Zhang, H.; Song, Y.; Han, C.; Zhang, L. Remote sensing image spatiotemporal fusion using a generative adversarial network. IEEE Trans. Geosci. Remote Sens. 2020, 59, 4273–4286. [Google Scholar] [CrossRef]
- Keras. Available online: https://keras.io/ (accessed on 7 February 2020).
- Chitwan, S.; Ho, J.; Chan, W.; Salimans, T.; Fleet, D.J.; Norouzi, M. Image super-resolution via iterative refinement. arXiv 2021, arXiv:2104.07636. [Google Scholar]
- Ayhan, B.; Kwan, C. Tree, Shrub, and Grass Classification Using Only RGB Images. Remote Sens 2020, 12, 1333. [Google Scholar] [CrossRef]
- Ayhan, B.; Kwan, C.; Larkin, J.; Kwan, L.; Skarlatos, D.; Vlachos, M. Deep learning model for accurate vegetation classification using RGB image only. In Proceedings of the SPIE 11398, Geospatial Informatics X, Online, 27 April–8 May 2020. [Google Scholar]









| Systems | Modality | Bands | Resolution | Revisit Frequency | Charge |
|---|---|---|---|---|---|
| Landsat-8 | Satellite | 8 | 30 m | 16 days | Free |
| Sentinel-2 | Satellite | 12 | 10 m | 10 days | Free |
| NAIP | Aerial | 4 | 1 m | 3 years | Variable |
| WV-2 | Satellite | 8 | 0.46 m | Less than 4 days | Expensive |
| Experiments | Type | Dimension | No. of Images |
|---|---|---|---|
| WV-2 (Experiment 1) | Training | 1024 × 1024 × 3 | 1 |
| WV-2 (Experiment 1) | Testing | 200 × 300 × 3–700 × 800 × 3 | 20 |
| Landsat-8 & Sentinel-2 (Experiment 2) | Training | 406 × 766 × 3 | 1 |
| Landsat-8 & Sentinel-2 (Experiment 2) | Testing | 200 × 200 × 3–300 × 300 × 3 | 20 |
| Sentinel-2 and NAIP (Experiment 3) | Training | 1500 × 1500 × 3 | 1 |
| Sentinel-2 and NAIP (Experiment 3) | Testing | 100 × 200 × 3–500 × 800 × 3 | 20 |
| Landsat-8 & Sentinel-2 (Experiment 4) | Testing | 100 × 200 × 3–400 × 600 × 3 | 45 |
| Methods | Scale-10× | ||||
| PSNR | SSIM | SAM | RMSE | ERGAS | |
| ARPRK | 17.85 (5.75) | 0.48 (0.12) | 2.51 (0.40) | 34.27 (11.49) | 26.18 (3.45) |
| ESRCNN | 39.43 (3.49) | 0.95 (0.01) | 2.70 (0.77) | 2.91 (1.01) | 12.56 (2.88) |
| GAN | 36.87 (2.41) | 0.92 (0.01) | 4.01 (1.39) | 3.76 (0.77) | 14.26 (2.14) |
| STFGAN | 36.51 (1.69) | 0.93 (0.01) | 4.17 (1.28) | 3.96 (1.18) | 14.97 (3.72) |
| UMSE | 40.30 (2.91) | 0.96 (0.01) | 2.47 (0.55) | 2.58 (0.77) | 10.52 (2.22) |
| UMSEh | 40.05 (2.65) | 0.96 (0.01) | 2.71 (0.98) | 2.64 (0.74) | 10.66 (2.25) |
| HMSE | 38.80 (2.47) | 0.94 (0.01) | 2.94 (0.68) | 3.03 (0.78) | 14.77 (2.49) |
| HMSEh | 39.50 (2.77) | 0.95 (0.01) | 2.74 (0.64) | 2.82 (0.80) | 12.89 (2.30) |
| Methods | Scale-6× | ||||
| PSNR | SSIM | SAM | RMSE | ERGAS | |
| ARPRK | 19.32 (2.93) | 0.54 (0.13) | 2.31 (1.01) | 29.26 (11.43) | 24.69 (4.02) |
| ESRCNN | 40.93 (2.67) | 0.95 (0.01) | 4.97 (1.07) | 2.38 (0.64) | 10.29 (1.83) |
| GAN | 39.34 (1.85) | 0.93 (0.01) | 5.83 (1.27) | 2.80 (0.56) | 12.43 (1.90) |
| STFGAN | 40.54 (2.53) | 0.95 (0.01) | 4.17 (0.92) | 2.50 (0.88) | 10.43 (2.94) |
| UMSE | 40.65 (2.05) | 0.95 (0.01) | 5.16 (1.15) | 2.42 (0.53) | 10.24 (1.61) |
| UMSEh | 40.72 (2.62) | 0.95 (0.01) | 4.87 (1.08) | 2.43 (0.64) | 11.44 (1.76) |
| HMSE | 40.97 (2.17) | 0.95 (0.01) | 4.87 (1.15) | 2.35 (0.55) | 9.92 (1.72) |
| HMSEh | 41.14 (2.47) | 0.95 (0.01) | 4.99 (1.10) | 2.33 (0.59) | 9.98 (1.70) |
| Methods | Scale-4× | ||||
| PSNR | SSIM | SAM | RMSE | ERGAS | |
| ARPRK | 20.43 (2.92) | 0.58 (0.14) | 5.37 (1.06) | 26.32 (11.14) | 23.24 (4.61) |
| ESRCNN | 41.63 (2.56) | 0.95 (0.01) | 4.76 (0.99) | 2.19 (0.59) | 9.51 (2.19) |
| GAN | 39.73 (1.08) | 0.94 (0.01) | 5.67 (1.28) | 2.64 (0.34) | 11.43 (2.01 |
| STFGAN | 39.63 (5.35) | 0.94 (0.06) | 4.45 (1.41) | 3.32 (3.08) | 13.29 (10.01) |
| UMSE | 41.87 (2.32) | 0.95 (0.01) | 5.02 (1.21) | 2.12 (0.55) | 10.31 (2.36) |
| UMSEh | 42.16 (2.54) | 0.96 (0.01) | 4.76 (1.14) | 2.06 (0.57) | 9.02 (2.04) |
| HMSE | 41.82 (2.38) | 0.96 (0.01) | 4.91 (1.16) | 2.13 (0.55) | 9.70 (2.09) |
| HMSEh | 40.32 (1.66) | 0.95 (0.01) | 4.91 (1.07) | 2.49 (0.45) | 13.04 (2.84) |
| Methods | Scale-2× | ||||
| PSNR | SSIM | SAM | RMSE | ERGAS | |
| ARPRK | 22.98 (3.42) | 0.68 (0.17) | 2.48 (0.90) | 19.71 (9.99) | 20.95 (6.19) |
| ESRCNN | 42.19 (2.53) | 0.97 (0.01) | 3.32 (0.71) | 2.06 (0.58) | 9.31 (2.22) |
| GAN | 39.90 (3.82) | 0.96 (0.01) | 4.33 (0.58) | 2.62 (1.11) | 13.33 (3.58) |
| STFGAN | 38.81 (4.34) | 0.96 (0.02) | 4.53 (1.55) | 3.24 (4.94) | 14.62 (4.81) |
| UMSE | 42.19 (2.53) | 0.97 (0.01) | 3.32 (0.71) | 2.02 (0.58) | 9.31 (2.22) |
| UMSEh | 42.16 (2.19) | 0.97 (0.01) | 3.29 (0.58) | 2.05 (0.53) | 8.71 (2.38) |
| HMSE | 41.41 (1.76) | 0.97 (0.01) | 3.77 (1.05) | 2.21 (0.46) | 10.95 (3.42) |
| HMSEh | 42.40 (2.54) | 0.98 (0.01) | 3.72 (1.00) | 2.01 (0.58) | 9.20 (2.39) |
| Methods | Experiment 2 | ||||
| PSNR | SSIM | SAM | RMSE | ERGAS | |
| ARPRK | 23.40 (1.86) | 0.70 (0.07) | 6.81 (1.23) | 18.87 (4.00) | 19.57 (1.65) |
| ESRCNN | 27.34 (1.99) | 0.80 (0.04) | 5.91 (1.05) | 10.15 (2.61) | 15.83 (2.27) |
| GAN | 28.05 (1.74) | 0.82 (0.03) | 5.89 (1.03) | 9.36 (2.02) | 14.10 (0.89) |
| STFGAN | 28.28 (1.69) | 0.81 (0.04) | 5.90 (0.59) | 9.09 (1.88) | 14.02(0.88) |
| UMSE | 29.11 (1.95) | 0.83 (0.04) | 5.50 (0.79) | 9.12 (1.98) | 13.57 (1.02) |
| UMSEh | 29.55 (1.84) | 0.85 (0.03) | 5.95 (0.95) | 7.80 (1.74) | 12.84 (0.89) |
| HMSE | 28.64 (1.87) | 0.82 (0.04) | 5.39 (0.85) | 8.87 (2.06) | 13.95 (1.20) |
| HMSEh | 28.57 (1.91) | 0.82 (0.04) | 5.57 (0.64) | 9.41 (2.10) | 13.76 (1.25) |
| Methods | Experiment 3 | ||||
| PSNR | SSIM | SAM | RMSE | ERGAS | |
| ARPRK | 10.07 (3.90) | 0.22 (0.12) | 15.33 (6.63) | 84.81 (36.33) | 20.19 (7.85) |
| ESRCNN | 9.16 (1.68) | 0.14 (0.04) | 7.30 (2.54) | 96.25 (19.80) | 27.97 (9.20) |
| GAN | 10.72 (4.03) | 0.30 (0.11) | 5.55 (0.80) | 83.93 (37.27) | 17.79 (8.07) |
| STFGAN | 10.45 (2.70) | 0.30 (0.09) | 6.83 (1.13) | 80.05 (24.91) | 12.35 (3.86) |
| UMSE | 10.98 (2.52) | 0.22 (0.09) | 6.72 (2.17) | 79.68 (27.92) | 14.51 (5.53) |
| UMSEh | 12.37 (3.80) | 0.33 (0.11) | 5.95 (1.23) | 70.63 (35.97) | 10.62 (7.79) |
| HMSE | 11.72 (3.42) | 0.30 (0.10) | 5.54 (0.92) | 75.72 (33.64) | 13.90 (7.07) |
| HMSEh | 11.45 (2.99) | 0.23 (0.10) | 4.67 (0.65) | 78.62 (31.08) | 20.76 (6.21) |
| Methods | PSNR | SSIM | SAM | RMSE | ERGAS |
|---|---|---|---|---|---|
| ARPRK | 9.88 (1.37) | 0.14 (0.03) | 5.35 (1.63) | 82.71 (12.96) | 30.69 (1.47) |
| ESRCNN | 13.73 (0.75) | 0.31 (0.02) | 2.26 (0.50) | 52.62 (4.41) | 27.68 (0.51) |
| GAN | 13.74 (0.73) | 0.32 (0.02) | 2.45 (0.57) | 52.56 (4.28) | 27.66 (0.50) |
| STFGAN | 14.08 (0.93) | 0.31 (0.04) | 2.87 (1.25) | 50.66 (5.19) | 27.73 (0.69) |
| UMSE | 14.13 (0.63) | 0.33 (0.02) | 2.68 (0.41) | 50.24 (3.54) | 27.44 (0.54) |
| UMSEh | 14.50 (0.71) | 0.34 (0.02) | 2.55 (0.46) | 48.16 (3.82) | 27.44 (0.53) |
| HMSE | 14.17 (0.64) | 0.33 (0.03) | 2.23 (0.55) | 49.99 (3.57) | 27.42 (0.57) |
| HMSEh | 14.23 (0.63) | 0.33 (0.02) | 2.76 (0.48) | 49.63 (3.55) | 27.38 (0.55) |
| Metrics | Experiment 1 | Experiment 2 | ||||||
| Two Sampled T-Test | Wilcoxon Rank Sum Test | Two Sampled T-Test | Wilcoxon Rank Sum Test | |||||
| p-Value | h | p-Value | h | p-Value | h | p-Value | h | |
| PSNR | 4.0 × | 1 | 1.50 × | 1 | 7.1 × | 1 | 7.1 × | 1 |
| SSIM | 1.0 × | 1 | 1.79 × | 1 | 1.7 × | 1 | 1.7 × | 1 |
| SAM | 2.2 × | 1 | 1.03 × | 1 | 9.1 × | 0 | 9.1 × | 0 |
| RMSE | 4.0 × | 1 | 1.50 × | 1 | 7.8 × | 1 | 7.8 × | 1 |
| ERGAS | 6.0 × | 1 | 6.86 × | 1 | 1.0 × | 1 | 1.0 × | 1 |
| Experiment 3 | Experiment 4 | |||||||
| Metrics | Two Sampled T-Test | Wilcoxon Rank Sum Test | Two Sampled T-Test | Wilcoxon Rank Sum Test | ||||
| p-Value | h | p-Value | h | p-Value | h | p-Value | h | |
| PSNR | 2.60 × | 0 | 1.13 × | 0 | 3.42 × | 1 | 1.18 × | 1 |
| SSIM | 4.10 × | 0 | 3.89 × | 0 | 2.48 × | 1 | 6.69 × | 1 |
| SAM | 4.80 × | 0 | 6.29 × | 0 | 3.82 × | 0 | 2.24 × | 1 |
| RMSE | 3.40 × | 0 | 1.13 × | 0 | 1.58 × | 1 | 1.18 × | 1 |
| ERGAS | 1.06 × | 0 | 6.50 × | 1 | 1.56 × | 1 | 1.82 × | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hoque, M.R.U.; Wu, J.; Kwan, C.; Koperski, K.; Li, J. ArithFusion: An Arithmetic Deep Model for Temporal Remote Sensing Image Fusion. Remote Sens. 2022, 14, 6160. https://doi.org/10.3390/rs14236160
Hoque MRU, Wu J, Kwan C, Koperski K, Li J. ArithFusion: An Arithmetic Deep Model for Temporal Remote Sensing Image Fusion. Remote Sensing. 2022; 14(23):6160. https://doi.org/10.3390/rs14236160
Chicago/Turabian StyleHoque, Md Reshad Ul, Jian Wu, Chiman Kwan, Krzysztof Koperski, and Jiang Li. 2022. "ArithFusion: An Arithmetic Deep Model for Temporal Remote Sensing Image Fusion" Remote Sensing 14, no. 23: 6160. https://doi.org/10.3390/rs14236160
APA StyleHoque, M. R. U., Wu, J., Kwan, C., Koperski, K., & Li, J. (2022). ArithFusion: An Arithmetic Deep Model for Temporal Remote Sensing Image Fusion. Remote Sensing, 14(23), 6160. https://doi.org/10.3390/rs14236160






