Image Inpainting with Bilateral Convolution
Abstract
1. Introduction

- We designed a novel BC operator to adaptively preserve and propagate informative features from known regions to damaged regions with feature distance and surrounding elements. This expands the convolution receptive fields and dynamically adjusts the results of regular convolution.
- We proposed a MWA module to model multi-range dependencies from different size patches of features, which can effectively associate features at different ranges to synthesize more appropriate contents for damaged regions.
- The presented bilateral convolution network is based on the proposed BC and MWA with a one-stage image inpainting model, which can reconstruct various irregular corrupted images and improve qualitative and quantitative inpainting performance.
2. Related Work
2.1. Missing Information Reconstruction of Remote Sensing Image
2.2. Learning-Based Image Inpainting
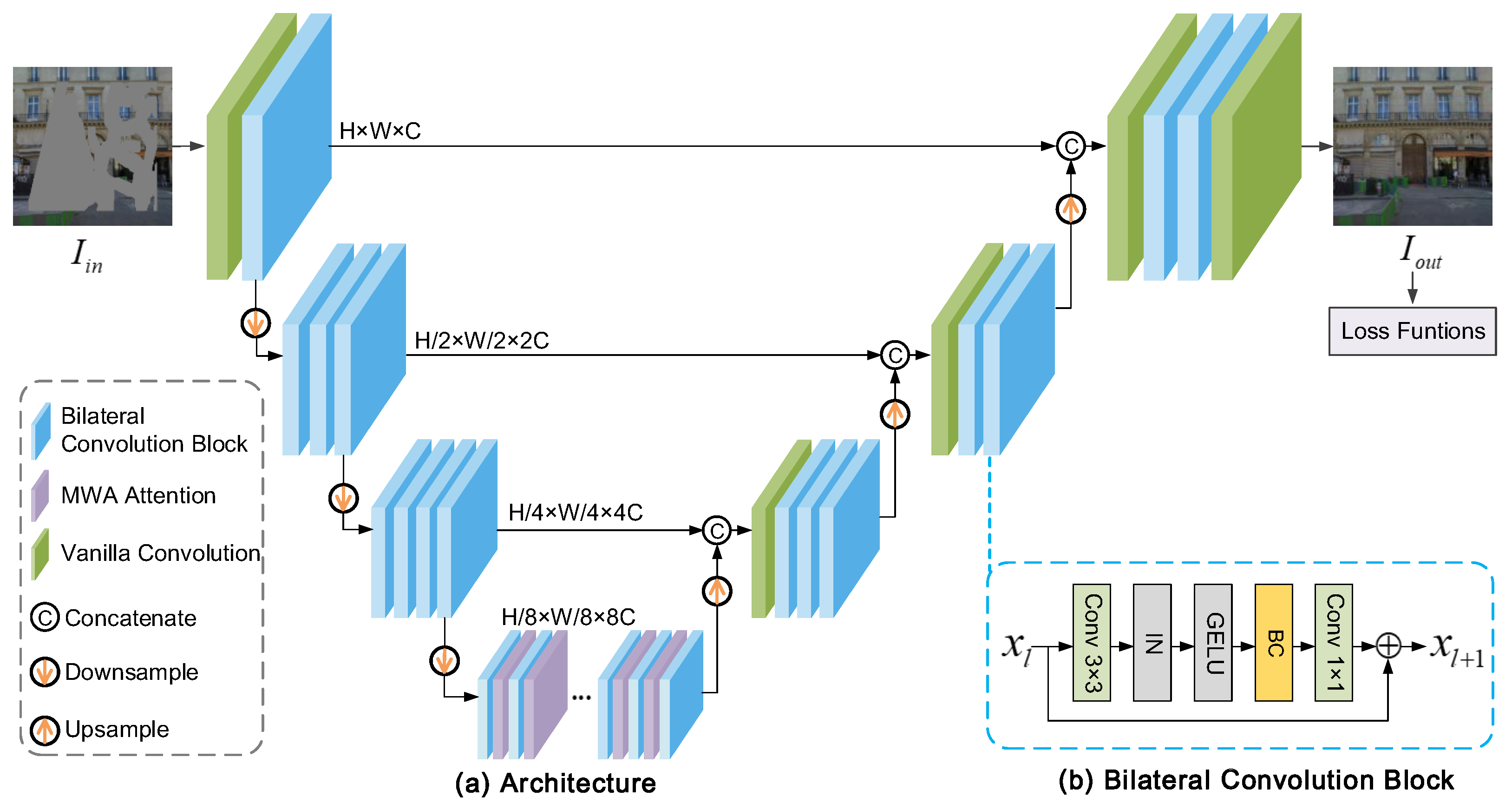
3. Our Approach
3.1. Bilateral Convolution (BC)
3.1.1. Preliminaries
3.1.2. Bilateral Convolution (BC)
3.2. Multi-Range Window Attention (MWA)
3.3. Loss Functions
4. Experiments
4.1. Datasets
- The AID dataset was released by Wuhan University, containing data extracted from different Google Earth sensors [66]. It contains 10,000 RS images with 30 scene categories. We used 500 images for testing, with approximately 17 images in each category.
- The NWPU-RESISC45 dataset was released by Northwestern Polytechnical University containing data extracted from Google Earth [67]. It includes 31,500 images with 45 scene categories. We selected 500 images for testing, with approximately 11 images in each category.
- PatternNet is a remote sensing image dataset with 256 × 256 resolution. It mainly obtains 38 scenes with 30,400 images from Google Earth imagery or the Google Map API [11]. We used 400 images for testing, including 10 or 11 images of each scene.
- The Paris StreetView dataset contains images of Paris from Google StreetView. It mainly contains the structural information of windows, doors, and buildings, and has 14,900 training images and 100 test images [12].
- The Places2 dataset was released by MIT. It contains over 1.8 million training images from over 365 scenes [13]. We randomly selected 4000 images from the original validation set for testing.
4.2. Experimental Setting
4.3. Comparison Models
- PC [8]: An encoder–decoder inpainting model that adopts a rule-based updating mask, renormalized only on valid pixels in the U-Net architecture;
- GC [9]: A two-stage inpainting model representing an improvement on the PC model, having learned a dynamic gating mask. This model can achieve better inpainting results;
- DSN [10]: A two-parallel U-Net inpainting model used to validate migratable convolution and regional composite normalization in order to select valid information dynamically;
- RFR [52]: A recurrent encoder–decoder inpainting model adopting the partial convolution of U-Net architecture, which recurrently gathers the hole boundary features and recovers structures to strengthen the results;
- PUT [54]: A pluralistic inpainting model adopting the patch-based VQVAE without downsampling, using a transformer without quantization to reduce information loss;
- SpA-GAN [40]: The SpA-GAN model uses the spatial attention generative adversarial network to recover the corrupted or cloud obscuration regions and generate realistic images of remotely sensed scenes.
5. Results
5.1. Quantitative Comparison
5.2. Qualitative Comparison
5.3. Experiments of Cloud Removal on Real Images
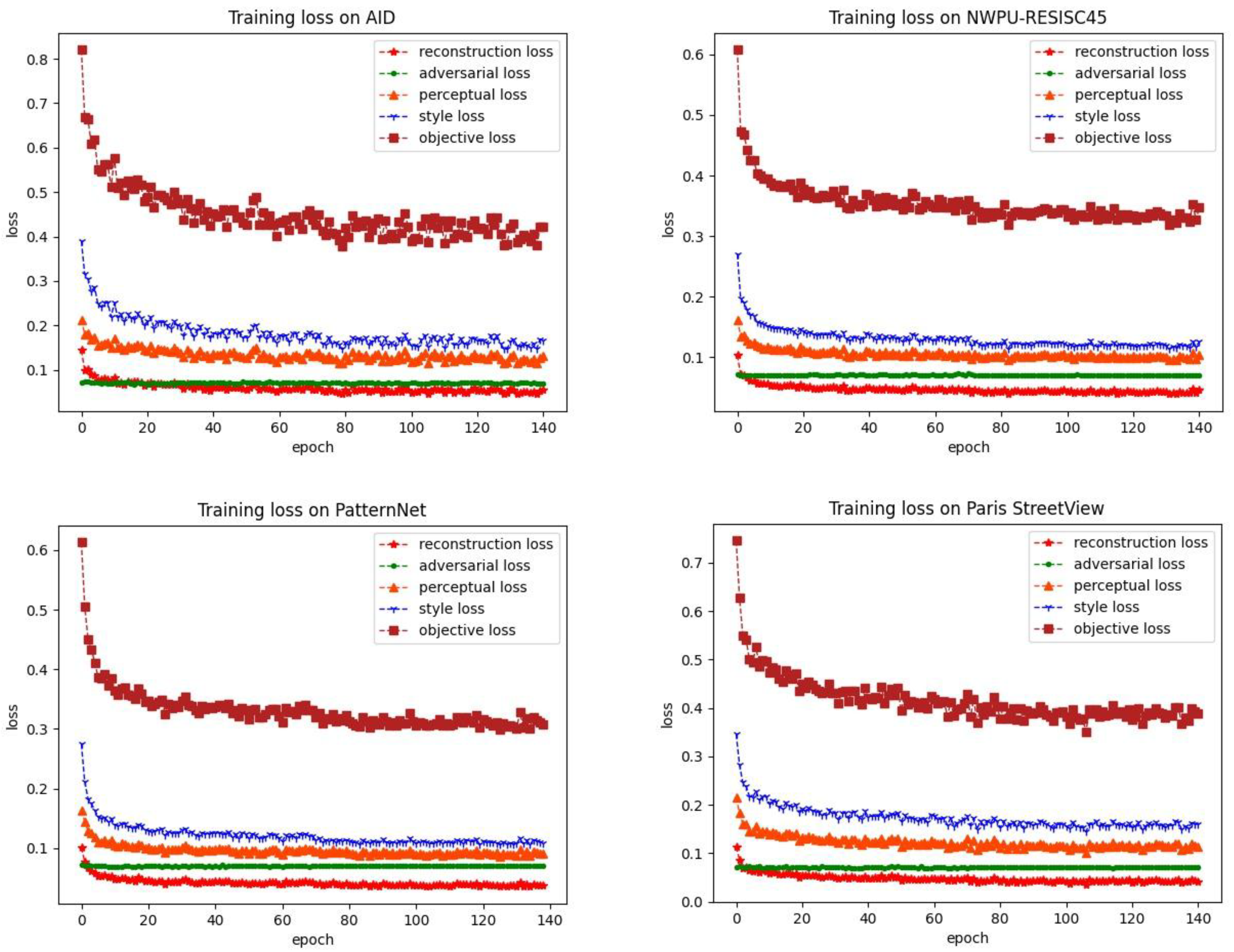
5.4. Loss Analysis
5.5. Ablation Studies
- Two experiments are conducted to analyze the effectiveness of the BC block. The first experiment is denoted as “CONV”, which replaces each layer with standard convolution operators in our designed U-Net style network. The second experiment is denoted as “BC”, which uses the proposed BC block of each layer in our network.
- Two experiments are conducted to validate the effectiveness of the MWA. The “w/ CA” experiment consists of replacing the MWA in our network with the contextual attention (CA) [17]. The “w/o g” experiment consists of replacing the header of the global attention with a window attention of size 8 in MWA.
5.5.1. Effectiveness of the BC Block
5.5.2. Effectiveness of the MWA
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| RS | Remote Sensing |
| BC | Bilateral Convolution |
| MWA | Multi-range Window Attention |
| CNNs | Convolutional Neural Networks |
| PC | Partial Convolution |
| GC | Gated Convolution |
| DSN | Dynamic Selection Network |
| RFR | Recurrent Feature Reasoning Network |
| CE | Context Encoders |
| PGN | Progressive Generative Networks |
| IN | Instance Normalization |
| GAN | Generative Adversarial Network |
| PSNR | Peak Signal-to-Noise Ratio |
| SSIM | Structural Similarity Index Measure |
| FID | Fréchet Inception Distance |
Appendix A. Network Architecture
Appendix A.1. Bilateral Convolution Network
| Stage Name | Input Feature Size | Operators |
|---|---|---|
| Input | 256 × 256 × 3 | - |
| Stem | 256 × 256 × 48 | Conv-7-s1 |
| Encoder1 | 256 × 256 × 48 | BCB * 1 |
| Down1 | 256 × 256 × 48 | Conv-3-s2 |
| Encoder2 | 128 × 128 × 96 | BCB * 3 |
| Down2 | 128 × 128 × 96 | Conv-3-s2 |
| Encoder3 | 64 × 64 × 192 | BCB * 4 |
| Down3 | 64 × 64 × 192 | Conv-3-s2 |
| Encoder4 | 32 × 32 × 384 | [BCB, MWA] * 7, BCB × 1 |
| Up3 | 32 × 32 × 384 | Upsample 2 times, Conv-3-s1 |
| Fuse3 | 64 × 64 × 192 | Concat(Up3, Encoder3), Conv-1-s1 |
| Decoder3 | 64 × 64 × 192 | BCB * 3 |
| Up2 | 64 × 64 × 192 | Upsample 2 times, Conv-3-s1 |
| Fuse2 | 128 × 128 × 96 | Concat(Up2, Encoder 2), Conv-1-s1 |
| Decoder2 | 128 × 128 × 96 | BCB * 2 |
| Up1 | 128 × 128 × 96 | Upsample 2 times, Conv-3-s1 |
| Fuse1 | 256 × 256 × 48 | Concat(Up1, Encoder 1), Conv-1-s1 |
| Decoder1 | 256 × 256 × 48 | BCB * 1 |
| Refine | 256 × 256 × 48 | Conv-7-s1 |
| Output | 256 × 256 × 3 | Tanh |
Appendix A.2. Discriminator
| Module Name | Filter Size | Output Channels | Stride | Output Feature Size |
|---|---|---|---|---|
| SN-Conv2d | 4 × 4 | 64 | 2 | 128 × 128 |
| SN-Conv2d | 4 × 4 | 128 | 2 | 64 × 64 |
| SN-Conv2d | 4 × 4 | 256 | 2 | 32 × 32 |
| SN-Conv2d | 4 × 4 | 512 | 1 | 32 × 32 |
| SN-Conv2d | 4 × 4 | 1 | 1 | 32 × 32 |
References
- Shen, H.; Li, X.; Cheng, Q.; Zeng, C.; Yang, G.; Li, H.; Zhang, L. Missing information reconstruction of remote sensing data: A technical review. IEEE Geosci. Remote Sens. Mag. 2015, 3, 61–85. [Google Scholar] [CrossRef]
- Shao, M.; Wang, C.; Wu, T.; Meng, D.; Luo, J. Context-based multiscale unified network for missing data reconstruction in remote sensing images. IEEE Geosci. Remote Sens. Lett. 2020, 19, 1–5. [Google Scholar] [CrossRef]
- Ng, M.K.P.; Yuan, Q.; Yan, L.; Sun, J. An adaptive weighted tensor completion method for the recovery of remote sensing images with missing data. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3367–3381. [Google Scholar] [CrossRef]
- Zhao, H.; Duan, S.; Liu, J.; Sun, L.; Reymondin, L. Evaluation of five deep learning models for crop type mapping using sentinel-2 time series images with missing information. Remote Sens. 2021, 13, 2790. [Google Scholar] [CrossRef]
- Bertalmio, M.; Sapiro, G.; Caselles, V.; Ballester, C. Image inpainting. In Proceedings of the 27th Annual Conference on Computer Graphics and Interactive Techniques, New Orleans, LA, USA, 23–28 July 2000; pp. 417–424. [Google Scholar]
- Gao, Y.; Sun, X.; Liu, C. A General Self-Supervised Framework for Remote Sensing Image Classification. Remote Sens. 2022, 14, 4824. [Google Scholar] [CrossRef]
- Pathak, D.; Krahenbuhl, P.; Donahue, J.; Darrell, T.; Efros, A.A. Context Encoders: Feature Learning by Inpainting. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Liu, G.; Reda, F.A.; Shih, K.J.; Wang, T.C.; Tao, A.; Catanzaro, B. Image Inpainting for Irregular Holes Using Partial Convolutions. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 85–100. [Google Scholar]
- Yu, J.; Lin, Z.; Yang, J.; Shen, X.; Lu, X.; Huang, T.S. Free-form image inpainting with gated convolution. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 4471–4480. [Google Scholar]
- Wang, N.; Zhang, Y.; Zhang, L. Dynamic selection network for image inpainting. IEEE Trans. Image Process. 2021, 30, 1784–1798. [Google Scholar] [CrossRef] [PubMed]
- Zhou, W.; Newsam, S.; Li, C.; Shao, Z. PatternNet: A benchmark dataset for performance evaluation of remote sensing image retrieval. ISPRS J. Photogramm. Remote Sens. 2018, 145, 197–209. [Google Scholar] [CrossRef]
- Doersch, C.; Singh, S.; Gupta, A.; Sivic, J.; Efros, A. What makes paris look like paris? ACM Trans. Graph. 2012, 31, hal-01053876. [Google Scholar] [CrossRef]
- Zhou, B.; Lapedriza, A.; Khosla, A.; Oliva, A.; Torralba, A. Places: A 10 Million Image Database for Scene Recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 1452–1464. [Google Scholar] [CrossRef]
- Liu, H.; Jiang, B.; Song, Y.; Huang, W.; Yang, C. Rethinking image inpainting via a mutual encoder-decoder with feature equalizations. In Computer Vision–ECCV 2020, Proceedings of the European Conference on Computer Vision (ECCV), Glasgow, UK, 2–28 August 2020; Springer: Cham, Switzerland, 2020; pp. 725–741. [Google Scholar]
- Ballester, C.; Bertalmio, M.; Caselles, V.; Sapiro, G.; Verdera, J. Filling-in by joint interpolation of vector fields and gray levels. IEEE Trans. Image Process. 2001, 10, 1200–1211. [Google Scholar] [CrossRef] [PubMed]
- Tomasi, C.; Manduchi, R. Bilateral filtering for gray and color images. In Proceedings of the Sixth International Conference on Computer Vision, Bombay, India, 7 January 1998; pp. 839–846. [Google Scholar]
- Yu, J.; Lin, Z.; Yang, J.; Shen, X.; Lu, X.; Huang, T.S. Generative Image Inpainting with Contextual Attention. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Zeng, Y.; Fu, J.; Chao, H.; Guo, B. Learning Pyramid-Context Encoder Network for High-Quality Image Inpainting. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Liu, H.; Jiang, B.; Xiao, Y.; Yang, C. Coherent Semantic Attention for Image Inpainting. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019. [Google Scholar]
- Yang, R.; Ma, H.; Wu, J.; Tang, Y.; Xiao, X.; Zheng, M.; Li, X. ScalableViT: Rethinking the Context-oriented Generalization of Vision Transformer. arXiv 2022, arXiv:2203.10790. [Google Scholar]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin transformer: Hierarchical vision transformer using shifted windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 10–17 October 2021; pp. 10012–10022. [Google Scholar]
- Vaswani, A.; Ramachandran, P.; Srinivas, A.; Parmar, N.; Hechtman, B.; Shlens, J. Scaling local self-attention for parameter efficient visual backbones. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 12894–12904. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015, Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; Springer: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar]
- Li, X.; Shen, H.; Zhang, L.; Zhang, H.; Yuan, Q. Dead pixel completion of aqua MODIS band 6 using a robust M-estimator multiregression. IEEE Geosci. Remote Sens. Lett. 2013, 11, 768–772. [Google Scholar]
- Wang, Q.; Wang, L.; Li, Z.; Tong, X.; Atkinson, P.M. Spatial–spectral radial basis function-based interpolation for Landsat ETM+ SLC-off image gap filling. IEEE Trans. Geosci. Remote Sens. 2020, 59, 7901–7917. [Google Scholar] [CrossRef]
- Zeng, C.; Shen, H.; Zhang, L. Recovering missing pixels for Landsat ETM+ SLC-off imagery using multi-temporal regression analysis and a regularization method. Remote Sens. Environ. 2013, 131, 182–194. [Google Scholar] [CrossRef]
- Li, X.; Shen, H.; Zhang, L.; Zhang, H.; Yuan, Q.; Yang, G. Recovering quantitative remote sensing products contaminated by thick clouds and shadows using multitemporal dictionary learning. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7086–7098. [Google Scholar]
- Siu, W.C.; Hung, K.W. Review of image interpolation and super-resolution. In Proceedings of the Asia Pacific Signal and Information Processing Association Annual Summit and Conference, Hollywood, CA, USA, 3–6 December 2012; pp. 1–10. [Google Scholar]
- Criminisi, A.; Perez, P.; Toyama, K. Region Filling and Object Removal by Exemplar-Based Image Inpainting. IEEE Trans. Image Process. 2004, 13, 1200–1212. [Google Scholar] [CrossRef]
- Barnes, C.; Shechtman, E.; Finkelstein, A.; Goldman, D.B. PatchMatch: A randomized correspondence algorithm for structural image editing. ACM Trans. Graph. 2009, 28, 24–35. [Google Scholar] [CrossRef]
- Chan, T.F.; Shen, J. Nontexture inpainting by curvature-driven diffusions. J. Vis. Commun. Image Represent. 2001, 12, 436–449. [Google Scholar] [CrossRef]
- Shen, H.; Zhang, L. A MAP-based algorithm for destriping and inpainting of remotely sensed images. IEEE Trans. Geosci. Remote Sens. 2008, 47, 1492–1502. [Google Scholar] [CrossRef]
- Bugeau, A.; Bertalmío, M.; Caselles, V.; Sapiro, G. A comprehensive framework for image inpainting. IEEE Trans. Image Process. 2010, 19, 2634–2645. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Q.; Shen, H.; Zhang, L.; Li, P. Inpainting for remotely sensed images with a multichannel nonlocal total variation model. IEEE Trans. Geosci. Remote Sens. 2013, 52, 175–187. [Google Scholar] [CrossRef]
- Gao, J.; Yuan, Q.; Li, J.; Su, X. Unsupervised missing information reconstruction for single remote sensing image with Deep Code Regression. Int. J. Appl. Earth Obs. Geoinf. 2021, 105, 102599. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, X.; Ao, Z.; Xiao, K.; Yan, C.; Xin, Q. Gap-Filling and Missing Information Recovery for Time Series of MODIS Data Using Deep Learning-Based Methods. Remote Sens. 2022, 14, 4692. [Google Scholar] [CrossRef]
- Zhang, Q.; Yuan, Q.; Zeng, C.; Li, X.; Wei, Y. Missing data reconstruction in remote sensing image with a unified spatial–temporal–spectral deep convolutional neural network. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4274–4288. [Google Scholar] [CrossRef]
- Lin, D.; Xu, G.; Wang, Y.; Sun, X.; Fu, K. Dense-Add Net: An novel convolutional neural network for remote sensing image inpainting. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 4985–4988. [Google Scholar]
- Singh, P.; Komodakis, N. Cloud-gan: Cloud removal for sentinel-2 imagery using a cyclic consistent generative adversarial networks. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 1772–1775. [Google Scholar]
- Pan, H. Cloud removal for remote sensing imagery via spatial attention generative adversarial network. arXiv 2020, arXiv:2009.13015. [Google Scholar]
- Shao, M.; Wang, C.; Zuo, W.; Meng, D. Efficient Pyramidal GAN for Versatile Missing Data Reconstruction in Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Czerkawski, M.; Upadhyay, P.; Davison, C.; Werkmeister, A.; Cardona, J.; Atkinson, R.; Michie, C.; Andonovic, I.; Macdonald, M.; Tachtatzis, C. Deep internal learning for inpainting of cloud-affected regions in satellite imagery. Remote Sens. 2022, 14, 1342. [Google Scholar] [CrossRef]
- Zheng, W.J.; Zhao, X.L.; Zheng, Y.B.; Pang, Z.F. Nonlocal Patch-Based Fully Connected Tensor Network Decomposition for Multispectral Image Inpainting. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1–5. [Google Scholar] [CrossRef]
- He, S.; Li, Q.; Liu, Y.; Wang, W. Semantic Segmentation of Remote Sensing Images With Self-Supervised Semantic-Aware Inpainting. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Du, Y.; He, J.; Huang, Q.; Sheng, Q.; Tian, G. A Coarse-to-Fine Deep Generative Model With Spatial Semantic Attention for High-Resolution Remote Sensing Image Inpainting. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–13. [Google Scholar] [CrossRef]
- Nazeri, K.; Ng, E.; Joseph, T.; Qureshi, F.; Ebrahimi, M. Edgeconnect: Structure guided image inpainting using edge prediction. In Proceedings of the Proceedings of the IEEE/CVF International Conference on Computer Vision Workshops, Seoul, Republic of Korea, 27–28 October 2019. [Google Scholar]
- Ren, Y.; Yu, X.; Zhang, R.; Li, T.H.; Li, G. StructureFlow: Image Inpainting via Structure-aware Appearance Flow. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019. [Google Scholar]
- Peng, J.; Liu, D.; Xu, S.; Li, H. Generating Diverse Structure for Image Inpainting With Hierarchical VQ-VAE. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021. [Google Scholar]
- Song, Y.; Chao, Y.; Shen, Y.; Peng, W.; Kuo, C. Spg-net: Segmentation prediction and guidance network for image inpainting. arXiv 2018, arXiv:1805.03356. [Google Scholar]
- Xiong, W.; Yu, J.; Lin, Z.; Yang, J.; Lu, X.; Barnes, C.; Luo, J. Foreground-Aware Image Inpainting. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Guo, X.; Yang, H.; Huang, D. Image Inpainting via Conditional Texture and Structure Dual Generation. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 10–17 October 2021; pp. 14134–14143. [Google Scholar]
- Li, J.; Wang, N.; Zhang, L.; Du, B.; Tao, D. Recurrent Feature Reasoning for Image Inpainting. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020. [Google Scholar]
- Liu, H.; Wan, Z.; Huang, W.; Song, Y.; Han, X.; Liao, J. PD-GAN: Probabilistic Diverse GAN for Image Inpainting. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 9371–9381. [Google Scholar]
- Liu, Q.; Tan, Z.; Chen, D.; Chu, Q.; Dai, X.; Chen, Y.; Liu, M.; Yuan, L.; Yu, N. Reduce Information Loss in Transformers for Pluralistic Image Inpainting. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; pp. 11347–11357. [Google Scholar]
- Yu, T.; Guo, Z.; Jin, X.; Wu, S.; Chen, Z.; Li, W.; Zhang, Z.; Liu, S. Region normalization for image inpainting. In Proceedings of the the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 12733–12740. [Google Scholar]
- Wang, Y.; Chen, Y.C.; Tao, X.; Jia, J. Vcnet: A robust approach to blind image inpainting. In Computer Vision—ECCV 2020, Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; Springer: Cham, Switzerland, 2020; pp. 752–768. [Google Scholar]
- Wang, Y.; Chen, Y.C.; Zhang, X.; Sun, J.; Jia, J. Attentive normalization for conditional image generation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 5094–5103. [Google Scholar]
- Wang, N.; Ma, S.; Li, J.; Zhang, Y.; Zhang, L. Multistage attention network for image inpainting. Pattern Recognit. 2020, 106, 107448. [Google Scholar] [CrossRef]
- Xie, C.; Liu, S.; Li, C.; Cheng, M.M.; Ding, E. Image Inpainting with Learnable Bidirectional Attention Maps. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019. [Google Scholar]
- Wang, W.; Yao, L.; Chen, L.; Cai, D.; He, X.; Liu, W. Crossformer: A versatile vision transformer based on cross-scale attention. arXiv 2021, arXiv:2108.00154. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 5998–6008. [Google Scholar]
- Isola, P.; Zhu, J.Y.; Zhou, T.; Efros, A.A. Image-to-Image Translation with Conditional Adversarial Networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Johnson, J.; Alahi, A.; Fei-Fei, L. Perceptual Losses for Real-Time Style Transfer and Super-Resolution. In Computer Vision—ECCV 2016, Proceedings of the European Conference on Computer Vision (ECCV), Amsterdam, The Netherlands, 11–14 October 2016; Springer: Cham, Switzerland, 2016; pp. 694–711. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Sajjadi, M.S.; Scholkopf, B.; Hirsch, M. Enhancenet: Single image super-resolution through automated texture synthesis. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 4491–4500. [Google Scholar]
- Xia, G.S.; Hu, J.; Hu, F.; Shi, B.; Bai, X.; Zhong, Y.; Zhang, L.; Lu, X. AID: A benchmark data set for performance evaluation of aerial scene classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3965–3981. [Google Scholar] [CrossRef]
- Cheng, G.; Han, J.; Lu, X. Remote sensing image scene classification: Benchmark and state of the art. Proc. IEEE 2017, 105, 1865–1883. [Google Scholar] [CrossRef]
- Karras, T.; Aila, T.; Laine, S.; Lehtinen, J. Progressive Growing of GANs for Improved Quality, Stability, and Variation. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Liu, Z.; Luo, P.; Wang, X.; Tang, X. Deep learning face attributes in the wild. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 3730–3738. [Google Scholar]
- Lin, D.; Xu, G.; Wang, X.; Wang, Y.; Sun, X.; Fu, K. A remote sensing image dataset for cloud removal. arXiv 2019, arXiv:1901.00600. [Google Scholar]
- Zhu, J.Y.; Park, T.; Isola, P.; Efros, A.A. Unpaired image-to-image translation using cycle-consistent adversarial networks. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2223–2232. [Google Scholar]
- Miyato, T.; Kataoka, T.; Koyama, M.; Yoshida, Y. Spectral Normalization for Generative Adversarial Networks. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]






| Dataset | AID | NWPU-RESISC45 | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Metrics | Mask Ratio | PC | GC | RFR | DSN | PUT | SpA-GAN | Ours | PC | GC | RFR | DSN | PUT | SpA-GAN | Ours |
| FID ↓ | 10–20% | 55.56 | 39.05 | 31.04 | 20.77 | 20.29 | 52.29 | 16.86 | 46.39 | 31.73 | 25.53 | 17.13 | 14.97 | 41.34 | 13.09 |
| 20–30% | 83.30 | 65.28 | 45.95 | 35.75 | 34.04 | 79.62 | 28.04 | 70.60 | 54.56 | 33.35 | 29.02 | 24.86 | 64.03 | 22.32 | |
| 30–40% | 106.24 | 87.61 | 58.14 | 48.56 | 45.65 | 106.75 | 38.03 | 90.10 | 75.61 | 41.39 | 40.42 | 33.79 | 83.93 | 30.76 | |
| 40–50% | 122.87 | 114.62 | 72.28 | 61.35 | 56.85 | 130.71 | 48.14 | 107.52 | 100.11 | 51.23 | 51.70 | 43.19 | 108.64 | 40.29 | |
| AVG | 91.99 | 76.64 | 51.85 | 41.61 | 39.21 | 92.34 | 32.77 | 78.65 | 65.50 | 37.88 | 34.57 | 29.20 | 74.49 | 26.62 | |
| SSIM ↑ | 10–20% | 0.809 | 0.904 | 0.887 | 0.917 | 0.915 | 0.835 | 0.920 | 0.819 | 0.916 | 0.905 | 0.931 | 0.931 | 0.862 | 0.935 |
| 20–30% | 0.672 | 0.826 | 0.822 | 0.845 | 0.841 | 0.717 | 0.851 | 0.695 | 0.847 | 0.858 | 0.868 | 0.865 | 0.769 | 0.877 | |
| 30–40% | 0.550 | 0.742 | 0.742 | 0.763 | 0.754 | 0.593 | 0.772 | 0.579 | 0.766 | 0.788 | 0.791 | 0.786 | 0.659 | 0.806 | |
| 40–50% | 0.436 | 0.644 | 0.646 | 0.670 | 0.657 | 0.461 | 0.681 | 0.457 | 0.668 | 0.699 | 0.699 | 0.691 | 0.528 | 0.717 | |
| AVG | 0.617 | 0.779 | 0.774 | 0.799 | 0.792 | 0.652 | 0.806 | 0.638 | 0.799 | 0.813 | 0.822 | 0.818 | 0.705 | 0.834 | |
| PSNR ↑ | 10–20% | 23.67 | 28.31 | 27.39 | 28.96 | 28.65 | 24.90 | 29.05 | 24.32 | 29.36 | 28.56 | 30.14 | 30.02 | 26.26 | 30.43 |
| 20–30% | 20.61 | 25.65 | 25.18 | 26.05 | 25.77 | 22.13 | 26.27 | 21.44 | 26.68 | 26.62 | 27.18 | 26.97 | 23.77 | 27.52 | |
| 30–40% | 18.65 | 23.91 | 23.59 | 24.16 | 23.79 | 19.90 | 24.35 | 19.39 | 24.83 | 24.90 | 25.08 | 24.81 | 21.48 | 25.47 | |
| 40–50% | 17.23 | 22.48 | 22.21 | 22.68 | 22.21 | 17.88 | 22.81 | 17.75 | 23.31 | 23.39 | 23.43 | 23.06 | 19.31 | 23.75 | |
| AVG | 20.04 | 25.09 | 24.59 | 25.46 | 25.11 | 21.20 | 25.62 | 20.73 | 26.05 | 25.87 | 26.46 | 26.22 | 22.71 | 26.79 | |
| Dataset | PatternNet | Paris StreetView | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Metrics | Mask Ratio | PC | GC | RFR | DSN | PUT | SpA-GAN | Ours | PC | GC | RFR | DSN | PUT | SpA-GAN | Ours |
| FID ↓ | 10–20% | 53.63 | 27.48 | 33.79 | 17.33 | 14.15 | 39.78 | 12.72 | 63.78 | 20.69 | 20.33 | 16.28 | 15.14 | 37.70 | 13.29 |
| 20–30% | 82.55 | 49.46 | 48.77 | 28.85 | 23.28 | 64.95 | 21.60 | 102.11 | 39.48 | 28.93 | 29.39 | 27.57 | 63.49 | 23.32 | |
| 30–40% | 105.78 | 72.84 | 62.81 | 42.58 | 32.76 | 94.60 | 29.98 | 131.91 | 58.66 | 39.84 | 42.02 | 38.85 | 85.08 | 34.14 | |
| 40–50% | 128.51 | 97.72 | 76.61 | 54.16 | 41.31 | 124.08 | 39.74 | 158.82 | 82.51 | 49.96 | 53.66 | 49.56 | 114.18 | 46.83 | |
| AVG | 92.62 | 61.88 | 55.50 | 35.73 | 27.88 | 80.85 | 26.01 | 114.16 | 50.34 | 34.77 | 35.34 | 32.78 | 75.11 | 29.40 | |
| SSIM ↑ | 10–20% | 0.822 | 0.930 | 0.898 | 0.933 | 0.937 | 0.877 | 0.939 | 0.843 | 0.952 | 0.943 | 0.952 | 0.956 | 0.907 | 0.960 |
| 20–30% | 0.696 | 0.872 | 0.841 | 0.875 | 0.881 | 0.783 | 0.887 | 0.730 | 0.915 | 0.908 | 0.914 | 0.913 | 0.837 | 0.926 | |
| 30–40% | 0.580 | 0.797 | 0.766 | 0.803 | 0.813 | 0.672 | 0.822 | 0.622 | 0.865 | 0.861 | 0.859 | 0.857 | 0.742 | 0.877 | |
| 40–50% | 0.456 | 0.700 | 0.673 | 0.718 | 0.734 | 0.541 | 0.742 | 0.498 | 0.792 | 0.799 | 0.791 | 0.791 | 0.608 | 0.812 | |
| AVG | 0.639 | 0.825 | 0.795 | 0.832 | 0.841 | 0.718 | 0.848 | 0.673 | 0.881 | 0.878 | 0.879 | 0.879 | 0.774 | 0.894 | |
| PSNR ↑ | 10–20% | 24.00 | 29.66 | 27.84 | 29.76 | 29.98 | 26.39 | 30.32 | 24.06 | 31.52 | 30.18 | 31.06 | 31.71 | 27.59 | 32.13 |
| 20–30% | 21.12 | 27.05 | 25.79 | 26.91 | 27.05 | 23.68 | 27.53 | 21.02 | 28.50 | 27.76 | 28.05 | 28.25 | 24.82 | 29.18 | |
| 30–40% | 19.13 | 24.90 | 24.02 | 24.66 | 24.86 | 21.33 | 25.28 | 19.02 | 26.03 | 25.99 | 25.92 | 26.06 | 22.37 | 26.87 | |
| 40–50% | 17.47 | 23.17 | 22.55 | 23.05 | 23.20 | 19.16 | 23.59 | 17.14 | 24.80 | 24.25 | 24.05 | 24.15 | 19.71 | 24.87 | |
| AVG | 20.43 | 26.20 | 25.05 | 26.10 | 26.27 | 22.64 | 26.68 | 20.31 | 27.71 | 27.05 | 27.27 | 27.54 | 23.62 | 28.26 | |
| Dataset | CelebA-HQ | Places2 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Metrics | Mask Ratio | PC | GC | RFR | DSN | PUT | Ours | PC | GC | RFR | DSN | PUT | Ours |
| FID ↓ | 10–20% | 9.20 | 2.54 | 5.17 | 1.91 | 1.87 | 1.42 | 11.27 | 5.57 | 5.23 | 3.63 | 4.19 | 2.90 |
| 20–30% | 18.53 | 4.49 | 4.06 | 3.18 | 3.21 | 2.43 | 22.02 | 10.67 | 6.58 | 6.28 | 7.65 | 4.92 | |
| 30–40% | 34.63 | 6.84 | 4.89 | 4.70 | 4.57 | 3.58 | 35.73 | 17.60 | 8.64 | 9.59 | 12.00 | 6.96 | |
| 40–50% | 56.45 | 9.83 | 6.11 | 6.20 | 5.80 | 4.70 | 53.01 | 27.80 | 12.00 | 13.71 | 16.93 | 9.43 | |
| AVG | 29.70 | 5.93 | 5.06 | 4.00 | 3.86 | 3.03 | 30.51 | 15.41 | 8.11 | 8.30 | 10.19 | 6.05 | |
| SSIM ↑ | 10–20% | 0.925 | 0.979 | 0.969 | 0.981 | 0.978 | 0.983 | 0.880 | 0.951 | 0.937 | 0.954 | 0.945 | 0.956 |
| 20–30% | 0.860 | 0.959 | 0.958 | 0.963 | 0.958 | 0.966 | 0.791 | 0.906 | 0.903 | 0.910 | 0.889 | 0.914 | |
| 30–40% | 0.785 | 0.931 | 0.939 | 0.939 | 0.929 | 0.944 | 0.700 | 0.852 | 0.858 | 0.856 | 0.822 | 0.863 | |
| 40–50% | 0.699 | 0.896 | 0.913 | 0.910 | 0.895 | 0.916 | 0.600 | 0.784 | 0.797 | 0.791 | 0.742 | 0.798 | |
| AVG | 0.817 | 0.941 | 0.945 | 0.948 | 0.940 | 0.952 | 0.743 | 0.873 | 0.874 | 0.878 | 0.850 | 0.883 | |
| PSNR ↑ | 10–20% | 25.50 | 32.26 | 30.93 | 32.72 | 32.10 | 33.13 | 23.16 | 28.57 | 27.34 | 28.51 | 27.42 | 28.72 |
| 20–30% | 22.21 | 29.10 | 28.94 | 29.53 | 28.81 | 29.93 | 20.23 | 25.46 | 24.99 | 25.32 | 24.06 | 25.53 | |
| 30–40% | 19.78 | 26.71 | 27.11 | 27.15 | 26.34 | 27.48 | 18.24 | 23.33 | 23.15 | 23.12 | 21.74 | 23.32 | |
| 40–50% | 17.87 | 24.78 | 25.47 | 25.34 | 24.43 | 25.55 | 16.62 | 21.53 | 21.47 | 21.33 | 19.84 | 21.45 | |
| AVG | 21.34 | 28.21 | 28.11 | 28.69 | 27.92 | 29.02 | 19.56 | 24.72 | 24.24 | 24.57 | 23.27 | 24.76 | |
| Models | FID ↓ | SSIM ↑ | PSNR ↑ |
|---|---|---|---|
| SpA-GAN | 45.44 | 0.731 | 29.74 |
| Ours | 39.68 | 0.789 | 30.97 |
| Dataset | AID | Paris StreetView | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Metrics | FID ↓ | SSIM ↑ | PSNR ↑ | FID ↓ | SSIM ↑ | PSNR ↑ | ||||||
| Mask Ratio | CONV | BC | CONV | BC | CONV | BC | CONV | BC | CONV | BC | CONV | BC |
| 10–20% | 22.59 | 18.81 | 0.905 | 0.914 | 28.12 | 28.69 | 16.76 | 13.44 | 0.951 | 0.958 | 31.05 | 31.95 |
| 20–30% | 37.47 | 31.98 | 0.830 | 0.842 | 25.48 | 25.94 | 31.28 | 24.09 | 0.911 | 0.923 | 28.09 | 28.98 |
| 30–40% | 51.09 | 43.36 | 0.744 | 0.759 | 23.69 | 24.05 | 45.38 | 34.96 | 0.847 | 0.872 | 25.69 | 26.72 |
| 40–50% | 64.89 | 55.82 | 0.644 | 0.662 | 22.16 | 22.50 | 61.88 | 46.07 | 0.763 | 0.807 | 23.48 | 24.71 |
| AVG | 44.01 | 37.49 | 0.781 | 0.794 | 24.86 | 25.30 | 38.83 | 29.64 | 0.868 | 0.890 | 27.08 | 28.09 |
| Dataset | AID | Paris StreetView | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Metrics | FID ↓ | SSIM ↑ | PSNR ↑ | FID ↓ | SSIM ↑ | PSNR ↑ | ||||||||||||
| Mask Ratio | w/ CA | w/o g | Ours | w/ CA | w/o g | Ours | w/ CA | w/o g | Ours | w/ CA | w/o g | Ours | w/ CA | w/o g | Ours | w/ CA | w/o g | Ours |
| 10–20% | 20.62 | 17.09 | 16.86 | 0.912 | 0.917 | 0.920 | 28.51 | 28.84 | 29.05 | 14.45 | 13.55 | 13.29 | 0.957 | 0.959 | 0.960 | 31.74 | 32.06 | 32.13 |
| 20–30% | 35.12 | 28.24 | 28.04 | 0.837 | 0.847 | 0.851 | 25.77 | 26.09 | 26.27 | 26.57 | 24.60 | 23.32 | 0.921 | 0.925 | 0.926 | 28.81 | 29.13 | 29.18 |
| 30–40% | 47.61 | 38.73 | 38.03 | 0.753 | 0.767 | 0.772 | 23.91 | 24.19 | 24.35 | 37.58 | 34.80 | 34.14 | 0.866 | 0.875 | 0.877 | 26.46 | 26.78 | 26.87 |
| 40–50% | 60.91 | 48.84 | 48.14 | 0.655 | 0.673 | 0.681 | 22.37 | 22.64 | 22.81 | 50.04 | 48.18 | 46.83 | 0.796 | 0.807 | 0.812 | 24.38 | 24.75 | 24.87 |
| AVG | 41.07 | 33.23 | 32.77 | 0.789 | 0.801 | 0.806 | 25.14 | 25.44 | 25.62 | 32.16 | 30.29 | 29.39 | 0.885 | 0.892 | 0.894 | 27.85 | 28.18 | 28.26 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, W.; Deng, Y.; Hui, S.; Wang, J. Image Inpainting with Bilateral Convolution. Remote Sens. 2022, 14, 6140. https://doi.org/10.3390/rs14236140
Huang W, Deng Y, Hui S, Wang J. Image Inpainting with Bilateral Convolution. Remote Sensing. 2022; 14(23):6140. https://doi.org/10.3390/rs14236140
Chicago/Turabian StyleHuang, Wenli, Ye Deng, Siqi Hui, and Jinjun Wang. 2022. "Image Inpainting with Bilateral Convolution" Remote Sensing 14, no. 23: 6140. https://doi.org/10.3390/rs14236140
APA StyleHuang, W., Deng, Y., Hui, S., & Wang, J. (2022). Image Inpainting with Bilateral Convolution. Remote Sensing, 14(23), 6140. https://doi.org/10.3390/rs14236140






