Comparative Analysis and Comprehensive Trade-Off of Four Spatiotemporal Fusion Models for NDVI Generation

Abstract

It is still difficult to obtain high-resolution and fast-updated NDVI data, and spatiotemporal fusion is an effective means to solve this problem. The purpose of this study is to carry out the comparative analysis and comprehensive trade-off of spatiotemporal fusion models for NDVI generation and to provide references for scholars in this field. In this study, four spatiotemporal fusion models (STARFM, ESTARFM, FSDAF, and GF-SG) were selected to carry out NDVI image fusion in grassland, forest, and farmland test areas, and three indicators of root mean square error (RMSE), average difference (AD), and edge feature richness difference (EFRD) were used. A detailed evaluation and analysis of the fusion results and comprehensive trade-off were carried out. The results show that: (1) all four models can predict fine-resolution NDVI images well, but the phenomenon of over-smoothing generally exists, which is more serious in high-heterogeneity areas; (2) GF-SG performed well in the evaluation of the three indicators, with the highest comprehensive trade-off score (CTS) of 0.9658. Followed by ESTARFM (0.9050), FSDAF (0.8901), and STARFM (0.8789); (3) considering the comparative analysis and comprehensive trade-off results of the three test areas and the three indicators, among the four models, GF-SG has the best accuracy in generating NDVI images. GF-SG is capable of constructing NDVI time series data with high spatial and temporal resolution.

1. Introduction

Vegetation is an important part of the terrestrial ecosystem and plays an important role in regulating the climate, conserving water sources, and maintaining soil and water [1,2]. The study of global and regional vegetation changes is the main means of monitoring climate and environmental changes [3]. The normalized difference vegetation index (NDVI) is the best indicator of plant growth state and vegetation spatial distribution density, which is linearly correlated with vegetation distribution density. Compared with other vegetation indicators, it has the outstanding advantages of simple calculation and small uncertainty. As an effective indicator for monitoring vegetation density, coverage, and growth characteristics by satellite remote sensing, NDVI is widely used in detecting forest disturbance, monitoring grassland degradation, and assessing disasters, crop yield, and the ecological environment [4,5,6,7,8].

In scientific research and economic and social analysis, the dynamic change information of vegetation growth, density, and coverage cannot be ignored. For example, the early or late greening of spring vegetation under the influence of COVID-19, the progress of autumn grain harvesting in a region, the health monitoring and yield assessment of wheat pollination and filling stage, etc. High-precision and fast-updated NDVI data can provide support for dynamic monitoring of these surface vegetation features, especially under the scenario of rapid changes in vegetation features within a short period of time [9].

However, due to the conflict and trade-off between the resolution and the revisit period of the remote sensing sensor, it is difficult for a single remote sensing image to have both high-quality attributes, which makes it difficult to obtain high-spatiotemporal resolution NDVI sequence data [10,11]. For example, the spatial resolution of the Landsat series of remote sensing images is 30 m, but its 16-day revisit period makes it difficult to monitor the dynamic changes in vegetation characteristics. More importantly, due to the cloud conditions, atmospheric environment, and other factors, the period of obtaining continuous, high-quality images in the same area will be longer [12]. On the other hand, MODIS data enable daily global observations, but its low spatial resolution (250–1000 m) limits its application in many fields [13]. Although with the development of remote sensing technology, some satellites with high spatial and temporal resolution (such as Sentinel series, 5 days, 10 m) have appeared. However, factors such as weather still seriously affect the continuity of remote sensing imaging, so acquiring NDVI data is uncertain [14,15]. In this context, the comprehensive use of multi-source satellite remote sensing data, the fusion of high spatial-resolution and high temporal-resolution information, and the formation of high temporal and spatial resolution images have become feasible and low-cost solutions to this problem [16,17].

In the past two decades, spatiotemporal fusion has developed rapidly, and more than 100 models have been proposed successively, which facilitates the research of scholars in different fields [18]. However, due to the different mechanisms and algorithms of various methods, the fusion accuracy varies greatly in different areas, vegetation coverage characteristics, and application fields [19]. Although some classical algorithms are widely used (STARFM [20], ESTARFM [21], etc.), there is currently no universal spatiotemporal fusion method recognized by most scholars [22]. The comparative and comprehensive trade-off research of spatiotemporal NDVI fusion methods will help to clarify the accuracy characteristics of different fusion methods and their application effects in NDVI generation. This will have important guiding significance to produce high-resolution, fast-updating and long time series NDVI data. Furthermore, it will help to carry out scientific research in related fields and contribute to economic and social development, agricultural monitoring, agronomic production, and other fields.

Many scholars have conducted comparative studies on spatiotemporal fusion methods. Gevaert et al. used time profiles to evaluate the ability of the STARFM and STRUM methods to reconstruct the NDVI time series [23]. The results show that the temporal profile of STARFM NDVI is very similar to the reference data in the presence of more high-resolution images. In the case of few high-resolution input images, STRUM produces reconstructed NDVI trajectories that are more accurate and thus more suitable for areas with heavy cloud influence. Chen et al. [24] used correlation coefficient (CC), average absolute difference (AAD), RMSE, peak signal-to-noise ratio (PSNR), and Kling–Gupta efficiency (KGE) to evaluate the prediction accuracy of four spatiotemporal fusion algorithms (STARFM, ESTARFM, ISTARFM, and SPSTFM [25]). The results show that ESTARFM and ISTARFM are more stable, and the application effect of ESTARFM in high-heterogeneity areas is significantly better than the other three. Ping et al. [26] used CC, RMSE, AAD, and the structural similarity index measure (SSIM) to analyze the accuracy and effectiveness of four spatiotemporal fusion algorithms (STARFM, Fit_FC [27], FSDAF [28], and STDFA [29]). The results show that the four methods can well achieve the fusion of the GF-1 image (16 m) and MODIS image (500 m), and the simulation results of the former two methods are better than the latter two. These studies provide references for scholars to choose spatiotemporal fusion methods. However, in terms of comparison methods, the existing research cases also have some shortcomings, such as the correlation between evaluation indicators makes the results redundant; the evaluation indicators do not include both spectral features and spatial features, and the results are incomplete; fusion tests do not include a variety of natural geographic areas, making the evaluation incomplete; comparative studies are based on multiple single indicators and lack comprehensive trade-off methods. Recently, Zhu et al. showed that choosing three indicators, RMSE, AD, and Edge, is sufficient to quantify the spectral and spatial information of fusion images and to greatly reduce information redundancy and computational complexity [30]. However, the comprehensive visualization of the three indicators using the all-around performance assessment (APA) graph is not intuitive enough.

In conclusion, the reconstruction of NDVI time series data with high temporal resolution and high spatial resolution is of great significance. However, there are some problems in the comparative study of spatiotemporal fusion methods (redundant assessment, incomplete assessment, not including multiple natural geo-graphic areas, lack of comprehensive trade-off methods, and visualization not being intuitive). Our hypothesis was to construct a framework of comparative analysis and comprehensive trade-off of various models to overcome the above shortcomings. Therefore, this study intends to choose four spatiotemporal fusion models (STARFM [20], ESTARFM [21], FSDAF [28], and GF-SG [31]), carry out NDVI fusion tests in three typical natural geographic areas (grassland, forest, and farmland), and conduct a detailed comparative analysis and comprehensive trade-off. The research aims to achieve the following three purposes:

(1)

Comprehensively evaluate the fusion results of each model in terms of spectral characteristics and spatial characteristics;

(2)

Analyze the application characteristics and accuracy of each model in different natural geographic areas;

(3)

Visually display the comprehensive trade-off results of two aspects and three indicators and provide suggestions for relevant scholars to choose the spatiotemporal fusion models for NDVI generation.

2. Test Areas and Data

In this paper, three test areas (Figure 1) were selected for the comparative analysis of the spatiotemporal fusion models, representing three typical natural geographic areas: grassland, forest, and farmland. The grassland test area (Figure 1B) is in the western part of Hulunbeier, in the Inner Mongolia Autonomous Region, China (48.81°N–49.06°N, 118.58°E–118.82°E), which is a typical temperate continental grassland. The spectral and spatial characteristics of the vegetation are relatively simple and homogeneous. The forest test area (Figure 1C) is in the west-central part of Yan’an, Shaanxi Province, China (36.11°N–36.36°N, 108.84°E–109.08°E), which belongs to the hilly and gully area of the Loess Plateau in Northern Shaanxi. It is a typical forest distribution area with a semi-humid inland monsoon climate and abundant forest resources. The vegetation has complex spectral and spatial characteristics and is less homogeneous. The farmland test area (Figure 1D) is in the northeastern part of Dezhou, Shandong Province, China (37.39°N–37.63°N, 116.93°E–117.17°E). It is an alluvial plain with a humid climate, good water and heat conditions, and abundant arable land resources, making it a typical agricultural area. Thefarmland is interspersed with villages and roads in the region, with very complex spectral and spatial characteristics and obvious heterogeneity.

Within each test area, we selected three high-quality, fine-resolution images and coarse-resolution images of the corresponding dates to form NDVI data, forming three pairs of fine-resolution/coarse-resolution NDVI combinations. The data were downloaded and pre-processed based on the Google Earth Engine (GEE) platform. The fine-resolution NDVI data were produced using Landsat 9 OLI data (LANDSAT/LC09/C02/T1_L2) with a resolution of 30 m; the naming format is LC09_124026_20220520, with 127 and 35 being the path and row numbers of the Landsat image, respectively. 20220520 is the date of imaging. The coarse resolution NDVI data were produced using MODIS 8-day synthetic data (MODIS/006/MOD09Q1) at a 250 m resolution; the naming format is MOD09Q1/2022_05_17, where 2022_05_17 is the first day of the 8 days, indicating that the NDVI image was produced on 17 May–25 May 2022. The specific NDVI data for the three test areas are shown in Figure 2.

For the fusion experiments in different test areas and different models, we used MODIS NDVI data of the intermediate date as the coarse-resolution image input for the prediction date, and Landsat NDVI data of the corresponding date as the reference image to verify the fusion results. In addition, as STARFM and FSDAF only require a pair of base period images, we selected the data closest to the prediction date, i.e.,: in the grassland test area, LC09_124026_20220520 (Figure 2A) and MOD09Q1/2022_05_17 (Figure 2D) were used; in the forest test area, LC09_127035_20220728 (Figure 2I) and MOD09Q1/2022_07_28 (Figure 2L) were used; in the farmland test area, LC09_122034_20220607 (Figure 2O) and MOD09Q1/2022_06_02 (Figure 2R) were used.

3. Methods

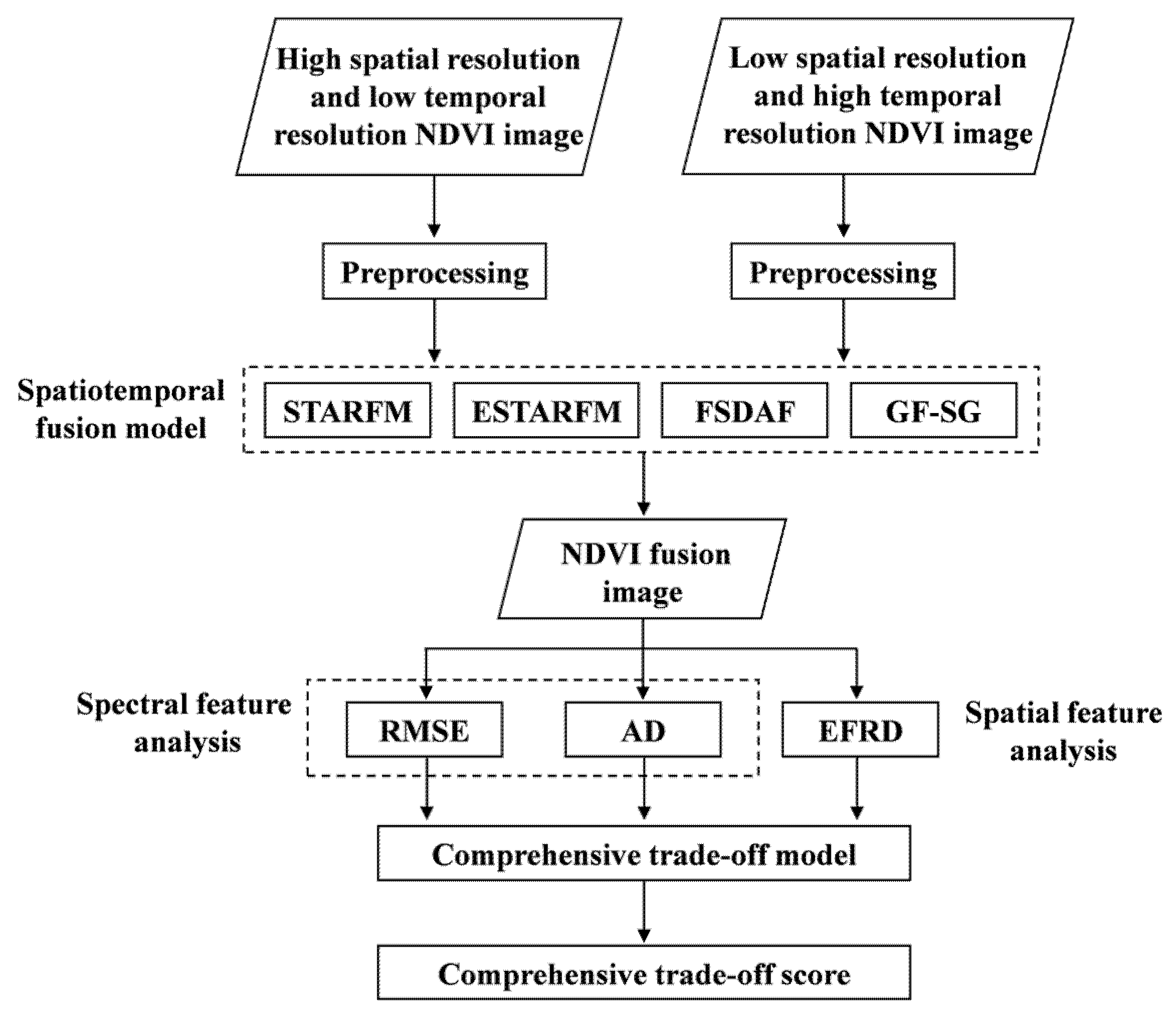
3.1. Overall Research Framework

The flowchart of this research is shown in Figure 3. Firstly, we preprocessed NDVI images with high spatial resolution and low temporal resolution, and NDVI images with low spatial resolution and high temporal resolution, so that they could meet the input requirements of the spatiotemporal fusion models. After that, STARFM, ESTARFM, FSDAF, and GF-SG models were respectively used to carry out NDVI fusion. We used different models to obtain fusion NDVI images for comparative analysis and comprehensive trade-off. The comparative analysis is mainly carried out in two aspects: spectral features and spatial features. The spectral features include root mean square error (RMSE) and average difference (AD). The spatial feature is edge feature richness difference (EFRD). After that, we input the results of the three indicators into the comprehensive trade-off model to obtain a unified index: comprehensive trade-off score. Based on the above indicators and scores, we can evaluate the features and accuracy of different spatiotemporal fusion models and give the evaluation conclusions of different models in NDVI fusion.

3.2. Spatiotemporal Fusion Models

3.2.1. STARFM

STARFM [20] requires at least one pair of fine-resolution and coarse-resolution NDVI data, as well as coarse-resolution NDVI data for the predicted period as input. It combines the spectral information from the fine- and coarse-resolution data and uses a weighting function to calculate the fine-resolution NDVI image element values for the predicted period. The specific steps are as follows:

(1)

Select candidates with similar image elements. In the fine-resolution image, each image element in turn is used as the central image element, and candidate similar image elements are selected for them using the neighborhood window and thresholding methods. The threshold is determined by the standard deviation of the fine-resolution image and the estimated number of land use/cover types.

(2)

Filtering samples. A constraint function is introduced to remove low-quality observations from the candidate similar elements.

(3)

Determine weights. A combination function is used to calculate the degree of influence of the similar image element on the central image element, i.e., the weight, considering three aspects: spectral difference, temporal difference, and distance difference.

(4)

Calculating central image element values. Using a weighting function, the fine-resolution image element values for the predicted period are calculated based on the spectral information of similar image elements combining fine-resolution and coarse-resolution data.

The key equation is as follows:

$$L\left(x_{\frac{w}{2}},y_{\frac{w}{2}},t_p\right)={\displaystyle \sum }_{i=1}^w{\displaystyle \sum }_{j=1}^w{\displaystyle \sum }_{k=1}^n{W}_{ijk}\times \left(L\left(x_{\frac{w}{2}},y_{\frac{w}{2}},t_k\right)-M\left(x_i,y_j,t_k\right)+M\left(x_i,y_i,t_p\right)\right)$$

(1)

where $w$ is the size of the neighborhood window; $\left(x_{\frac{w}{2}},y_{\frac{w}{2}}\right)$ is the central image element; $W_{ijk}$ is the similar image element weight; $n$ indicates the number of fine-resolution images involved in the fusion. $L\left(x_{\frac{w}{2}},y_{\frac{w}{2}},t_k\right)$, $M\left(x_i,y_j,t_k\right)$ are the fine-resolution image element values and coarse-resolution image element values for the known period, respectively; and $M\left(x_i,y_i,t_p\right)$ is the coarse-resolution image element value for the predicted period.

3.2.2. ESTARFM

ESTARFM [21] requires at least two pairs of fine-resolution and coarse-resolution NDVI data, and coarse-resolution NDVI data for the predicted period as the input. As an enhanced version of STARFM, ESTARFM adds conversion factors to the calculation of similar image element weights to reduce the effect of mixed image elements. The specific steps are as follows:

(1)

Selection of similar image elements. ESTARFM uses the same threshold determination method as STARFM. However, since there are two pairs of fine-resolution and coarse-resolution NDVI data, ESTARFM first selects the candidate neighboring similar elements from the two pairs of images separately and then takes the intersection afterward.

(2)

Determination of weights. Considering the spectral difference and distance difference between the central image element and the similar image element, a combination function is used to calculate the weight of the similar image element.

(3)

Calculate the conversion factor. Based on the linear relationship between the spectral values of the image element and the end element in the coarse-resolution image, the end element is used as the fine-resolution image element in the coarse-resolution image element, and the slope is obtained by linear regression, which is called the conversion factor. The conversion factor characterizes the conversion relationship between coarse-resolution image elements (mixed image elements) and fine-resolution image elements.

(4)

Calculate the central image element value. Based on the similar image weights and conversion coefficients, the central image value is calculated for each input image pair separately to form the transition image. Then, based on the overall spectral similarity between their coarse-resolution image and the coarse-resolution image of the predicted date, the weights are determined, and the final central image element value is calculated.

The key equation is as follows:

$$L_k\left(x_{\frac{w}{2}},y_{\frac{w}{2}},t_p\right)=L\left(x_{\frac{w}{2}},y_{\frac{w}{2}},t_k\right)+{\displaystyle \sum }_{i=1}^N{W}_i{V}_i\left(M\left(x_i,y_i,t_p\right)-M\left(x_i,y_i,t_k\right)\right)$$

(2)

$$L\left(x_{\frac{w}{2}},y_{\frac{w}{2}},t_p\right)=T_m{L}_m\left(x_{\frac{w}{2}},y_{\frac{w}{2}},t_p\right)+T_n{L}_n\left(x_{\frac{w}{2}},y_{\frac{w}{2}},t_p\right)$$

(3)

where $w$ is the size of the neighborhood window; $\left(x_{w/2},y_{w/2}\right)$ is the central image element; $L_k\left(x_{\frac{w}{2}},y_{\frac{w}{2}},t_p\right)$ is the transition image formed based on the kth image pair; $L\left(x_{\frac{w}{2}},y_{\frac{w}{2}},t_k\right)$ is the input kth fine resolution image; $N$ is the number of similar image elements; $W_i$, $V_i$ are the weights and conversion factors of the ith similar image element respectively; and $T_m$, $T_n$ are the weights of the transition images $L_m\left(x_{\frac{w}{2}},y_{\frac{w}{2}},t_p\right)$ and $L_n\left(x_{\frac{w}{2}},y_{\frac{w}{2}},t_p\right)$.

3.2.3. FSDAF

FSDAF [28] requires at least one pair of fine-resolution and coarse-resolution NDVI data, as well as coarse-resolution NDVI data for the predicted period as the input. FSDAF takes into account the changes in feature types and the “block effect” at different periods and superimposes the calculated changes on the input fine-resolution image, which is effective in predicting areas with changes in feature types [32]. The steps are as follows:

(1)

Calculate richness. Based on the unsupervised classification method, the input fine-resolution images are classified, and the richness of the category is counted in each coarse-resolution image element.

(2)

Fitting the category change values. For each category, the coarse-resolution image elements with the highest richness are selected and their differences between the known and predicted periods are calculated; afterward, the change values of each fine-resolution image element are fitted by least squares.

(3)

Feature change correction. The coarse-resolution images of the predicted period are interpolated by three splines, the errors between homogeneous and heterogeneous areas are analyzed, and the two errors are combined by homogeneity coefficients to correct the change values.

(4)

Elimination of the “block effect”. Select adjacent similar image elements and calculate the weight value, then calculate the change value of the central image element based on the weight function. The change values are then superimposed on the fine-resolution image elements to obtain the result.

The key formula is as follows:

$$L\left(x_{\frac{w}{2}},y_{\frac{w}{2}},t_p\right)=L\left(x_{\frac{w}{2}},y_{\frac{w}{2}},t_k\right)+{\displaystyle \sum }_{i=1}^N{W}_i\times ∆F\left(x_i,y_i\right)$$

(4)

where $L\left(x_{\frac{w}{2}},y_{\frac{w}{2}},t_p\right)$ and $L\left(x_{\frac{w}{2}},y_{\frac{w}{2}},t_k\right)$ are the central image element values of the predicted period and the known period, respectively; $N$ is the number of similar image elements in the neighborhood; and $W_i$, $∆F\left(x_i,y_i\right)$ are the weight and change value of the ith similar image element.

3.2.4. GF-SG

Unlike the above three methods, GF-SG [31] requires as many coarse- and fine-resolution images as possible as input data and no longer requires them to be of optimal quality, i.e., it allows the input images to contain clouds, cloud shadows, and seams [33]. At the same time, GF-SG is based on the Google Earth Engine (GEE) cloud platform for loading and processing remote sensing imagery, which has the unique advantage of running fast and allowing for large-scale applications. The specific steps are as follows:

(1)

Pre-processing images. Select all the coarse resolution and fine resolution remote sensing images within a period (generally six months to one year), remove the parts of the images with clouds and cloud shadows, and calculate the NDVI.

(2)

Matching shapes. The coarse-resolution NDVI image is downscaled to fine resolution using double triple convolution, capturing the pattern of change and temporal shape of the coarse-resolution NDVI values on each fine image element. For each fine-resolution center image, the fine-resolution NDVI time shape is matched to the coarse-resolution image within a neighborhood window, and neighboring images with correlation coefficients greater than a threshold are identified as similar.

(3)

Fill time series. For each fine-resolution central image, the time shapes of the similar images are combined by weighting them as their reference time series, and the possible difference in magnitude between the fine-resolution and coarse-resolution image values is corrected by shape fitting. The corrected reference time series is used to fill in the missing values in the original fine-resolution NDVI image and to produce fine-resolution data between the two scenes of fine-resolution images.

(4)

Noise removal. The original fine-resolution NDVI values are given maximum weight, the image element values with a smaller standard deviation of adjacent pixels in the neighborhood are given larger weights, and the fine-resolution NDVI time series are smoothed using a weighted SG filter to remove the effects of residual cloud contamination as well as random noise and other factors.

The key equation is as follows:

$$M\_reference\left(x,y\right)={\displaystyle \sum }_{i=1}^N{W}_{\left(x_i,y_i\right)}\times M\_similar\left(x_i,y_i\right)$$

(5)

where $M\_reference\left(x,y\right)$ is the reference time shape sequence at the image element $\left(x,y\right)$; $N$ is the number of similar image elements; and $W_{\left(x_i,y_i\right)}$ and $M\_similar\left(x_i,y_i\right)$ are the weights and time shape sequence at similar image elements $\left(x_i,y_i\right)$, respectively.

In this study, we set the time range of the input data from 1 March 2022 to 30 August 2020 and excluded Landsat NDVI images from the prediction period and used them as parameter data to validate the prediction results.

3.3. Comparative Analysis Methods

3.3.1. Root Mean Square Error

Root mean square error (RMSE) is a measure of the difference between two sets of values and is often used in model prediction data or in the comparison of observed data with reference data [34]. In error analysis of spatiotemporal fusion images, RMSE is calculated using all image element values and provides an intuitive measure of the magnitude of error in the fusion results. Compared to metrics of the same type (e.g., AAD), RMSE assigns a higher weight to larger errors due to the use of a square-then-average strategy; therefore, it is better assessed when large errors are particularly undesirable [30]. The RMSE is calculated as follows:

$$RMSE=\sqrt{\frac{{{\displaystyle \sum }}_{i=1}^N{\left(F_i-R_i\right)}^2}{N}}$$

(6)

where $N$ is the total number of image elements; $F_i$ and $R_i$ are the predicted and reference values of the ith image element position; and $RMSE$ takes values of 0–1, with 0 showing perfect fusion and larger values showing greater spectral error in the fusion result.

3.3.2. Average Difference

RMSE measures the magnitude of the spectral error in the fusion results but does not show the direction of the error (under-prediction or over-prediction). We therefore chose average difference (AD), which subtracts the predicted values from the reference values on the image elements and averages them to show the overall deviation at the image level [30]. The AD is calculated as follows:

$$AD=\frac{{{\displaystyle \sum }}_{i=1}^N\left(F_i-R_i\right)}{N}$$

(7)

where $N$ is the total number of image elements; $F_i$ and $R_i$ are the predicted and reference values for the ith image element position respectively; and AD takes values in the range −1–1, with negative numbers showing under-prediction of the spectral value of the fusion result, positive numbers showing over-prediction, 0 showing no overall deviation, and the absolute value of AD showing the overall degree of deviation.

3.3.3. Edge Feature Richness Difference

RMSE and AD measure the difference in spectral features between the fusion image and the reference image but do not show how well the fusion method reconstructs the spatial features of the feature. Based on the study by Zhu et al. [30], edge features, texture features, and other parameters (contrast, homogeneity, angular second-order moments, etc.) derived based on the grey-scale co-occurrence matrix can all reflect the spatial characteristics of the image and are correlated. Therefore, the researcher can choose one of them for image quality assessment. In this study, we chose the Roberts edge feature (RE) [35], which runs quickly and shows spatial features clearly. The formula is as follows:

$$R{E}_{i,j}=\sqrt{{\left(D_{i,j}-D_{i+1, j+1}\right)}^2+{\left(D_{i,j+1}-D_{i+1, j}\right)}^2}$$

(8)

where $R{E}_{i,j}$ is the Roberts edge value on the image element $\left(i,j\right)$; $D_{i,j}$, $D_{i+1, j+1}$, $D_{i,j+1}$, and $D_{i+1, j}$ are the image values on the image element $\left(i,j\right)$, $\left(i+1,j+1\right)$, $\left(i,j+1\right)$, and $\left(i+1,j\right)$ respectively.

Equation (8) converts the NDVI image into an edge eigenvalue image, after which non-edge elements and those with insignificant edge features need to be filtered. In the implementation, the edge-valued images were unified to a range of values from 0–255, and thresholds were set for different test areas to extract the edges by binarization. The edge feature richness (ERF) of the different fusion results was calculated and the edge feature richness difference (EFRD) from the reference image was calculated to show the smoothness or over-sharpening characteristics. The equations are as follows:

$$ERF=\frac{N_E}{N}$$

(9)

$$EFRD=\frac{ER{F}_F-ER{F}_R}{E{R}_R}$$

(10)

where $ERF$ is the edge feature richness of the image; $N_E$ is the number of edge pixels in the image; $N$ is the total number of pixels in the image; $E{R}_F$ and $E{R}_R$ are the edge feature richness of the predicted image and the reference image, respectively, obtained by counting the number of edge pixels; and $ERFD$ is the edge feature richness difference between the predicted image and the reference image, and the value ranges in −1–1. A negative number indicates smoothing of the fusion result and under-prediction of edge features, a positive number indicates over-sharpening, 0 indicates no overall deviation, and the absolute value of $ERFD$ indicates the overall degree of difference.

3.3.4. Comprehensive Trade-Off Method

The above three evaluation metrics allow comparison of fusion results in individual aspects (spectral error, direction of deviation, and spatial feature reconstruction), but it is difficult to assess the combined quality of multiple aspects. Therefore, a multi-situational, multi-indicator integrated trade-off method is designed: for each scenario (test area), each assessment is dimensionless, and their geometric mean is then obtained as a trade-off score (TS); the TS for each test area is then weighted and averaged to obtain a comprehensive trade-off score (CTS). The TS shows how well the fusion results in a given test area reproduce the reference data, while the CTS weighs the overall quality of the fusion results in multiple test areas.

In this study, the process is as follows: within each test area, each assessment indicator of the fusion result is compared with the reference data to obtain a single score; after that, the three scores of each fusion result are multiplied and squared three times to obtain the TS; finally, the CTS is obtained by the weighted average of the TS of each test area. The formula is as follows:

$$T{S}_{i,j}=\sqrt[3]{{\displaystyle \prod }_{k=1}^3\left(1-\frac{\left|S_{\left(i,j,k\right)}-S_{\left(1,j,k\right)}\right|}{\left|S_{\left(\max \right)}-S_{\left(1,j,k\right)}\right|}\right)}$$

(11)

$$CT{S}_i={\displaystyle \sum }_{j=1}^3{w}_{\left(i,j\right)}\times T{S}_{\left(i,j\right)}$$

(12)

where $i, j, k$ represent the fusion method, test area, and evaluation metrics (RMSE, AD, and EFRD), respectively; $S_{\left(i,j,k\right)}$ is the $k$ indicator of the result of the ith fusion method in the jth test area; $S_{\left(1,j,k\right)}$ is the $k$ indicator of the reference data in the jth test area, which takes the value of 0 in this study; $S_{\left(\max \right)}$ is the maximum value that can be achieved by the assessment indicator, which takes the value of 1 in this study; and $w_{\left(i,j\right)}$ is the weight of the weighting score of different test areas, which can be set according to the importance of the test area or the area share of the test area in the study area, and the weight of each test area is set to be the same in this study, i.e., $w_{\left(i,j\right)}$ takes the value of 1/3.

4. Results and Analysis

4.1. NDVI Fusion Results

In this study, fine-resolution NDVI images for the predicted period were obtained based on four spatiotemporal fusion methods and compared with the reference Landsat NDVI images, and the results are shown in Figure 4. In general, the fusion results of all four methods can better reflect the vegetation conditions in the three test areas.

In the grassland test area, STARFM (Figure 4B), ESTARFM (Figure 4C), and GF-SG (Figure 4E) were good, while the fusion results of FSDAF (Figure 4D) showed significant over-smoothing, especially in the southwest of the test area. In the forest test area, the fusion results of all four methods were good, and the visual effect was like that of the reference image (Figure 4F). In the farmland test area, the fusion results of the four methods varied greatly; among them, the fusion result of GF-SG (Figure 4O) was most similar to the reference image (Figure 4K); the fusion result of ESTARFM (Figure 4M) had less contrast; the fusion result of FSDAF (Figure 4N) had more contrast. The fusion result of STARFM (Figure 4L) showed significant blurring, with the low NDVI values of the built-up land affecting the prediction of the NDVI values of the surrounding farmland.

4.2. Root Mean Square Error Analysis

The RMSE of each fusion result was calculated based on the reference image and the results are shown in

Table 1. RMSE of the fusion results of different methods.

Test Area	STARFM	ESTARFM	FSDAF	GF-SG
Grassland	0.1118	0.0248	0.0668	0.0477
Forest	0.1359	0.0282	0.0413	0.0108
Farmland	0.1057	0.0738	0.1217	0.0166

.

In the grassland test area, the RMSEs of the four methods in descending order were: STARFM (0.1118) > FSDAF (0.0668) > GF-SG (0.0477) > ESTARFM (0.0248). The RMSE of ESTARFM was the smallest, showing its reliability in modeling the NDVI values of the grassland. The RMSE of STARFM was the largest and was significantly higher than the other three methods.

In the forest test area, the RMSEs of the four methods in descending order were: STARFM (0.1359) > FSDAF (0.0413) > ESTARFM (0.0282) > GF-SG (0.0108); the RMSE of GF-SG was the smallest, and the RMSEs of ESTARFM and FSDAF were also at a low level. The RMSE for STARFM was the largest at over 0.13.

In the farmland test area, the RMSEs of the four methods in descending order were: FSDAF (0.1217) > STARFM (0.1057) > ESTARFM (0.0738) > GF-SG (0.0166); GF-SG had the lowest RMSE and was significantly lower than the other three methods.

Overall, GF-SG had excellent fusion results in all three test areas and always had low RMSE; ESTARFM was second only to GF-SG and performed consistently in all three areas; followed by FSDAF, which produced medium to high RMSE in all three test areas; and STARFM was the worst, with the RMSE being the worst, with it being the highest RMSE in all three test areas.

4.3. Average Difference Analysis

The fusion results were compared with the reference image and the AD was calculated, and the results are shown in

Table 2. AD of fusion results of different models with reference images.

Test Area	STARFM	ESTARFM	FSDAF	GF-SG
Grassland	0.0632	−0.0203	0.062	−0.0038
Forest	−0.012	−0.0193	−0.0279	−0.0003
Farmland	0.0606	−0.0266	0.1002	−0.031

.

In the grassland test area, the Ads of STARFM and FSDAF were greater than 0 and both values exceeded 0.06, showing their overall over-prediction. The Ads of ESTARFM and GF-SG were −0.0203 and −0.0038, showing their overall under-prediction.

In the forest test area, the AD values of all four methods were less than 0, showing under-prediction. However, to a lesser extent, the absolute values did not exceed 0.03, and the deviation of GF-SG was the smallest, with an absolute AD value of 0.0003 only.

In the farmland test area, the over-prediction and under-prediction of the four methods were the same as in the grassland test area. However, the over-prediction of FSDAF was much greater, with the AD value even exceeding 0.1.

In general, the four methods showed the least deviation from the predicted values in the forest test area and the greatest deviation in the farmland test area. Among the four methods, ESTARFM and GF-SG showed under-prediction of NDVI values in all three test areas. GF-SG showed the least overall deviation in the three test areas, followed by ESTARFM. STARFM and FSDAF showed greater over-prediction in the grassland and farmland test areas, with AD values exceeding 0.06. The AD values exceeded 0.06 and even 0.1.

4.4. Edge Feature Richness Difference Analysis

Edge features can reflect the spatial characteristics of the image. We chose the Roberts edge feature (RE) for image quality assessment. Based on the obtained fine-resolution NDVI images and reference images in the prediction period, the Roberts edge features were calculated and compared. The edge features of the fusion image are shown in Figure 5, and the EFRD between the edge feature richness of the reference image is shown in

Table 3. EFRD of fusion images and reference images.

Test Area	STARFM	ESTARFM	FSDAF	GF-SG
Grassland	−16.22	−10.17	−21.53	7.72
Forest	−12.78	−18.81	18.8	−2.4
Farmland	−28.54	−32.72	−14.71	−9.29

.

Based on the analysis in Figure 5, overall, the terrain of the grassland test area is flat, and the vegetation composition is relatively simple. The edge features reflected by NDVI images are also less, with them being mainly grassland boundaries, paths, and changes in vegetation types and coverage caused by surface fluctuations. The edge features of the forest test area are rich, but the shape features are easy to identify and have a strong correlation with the topography. The farmland, roads, construction land, and trees in the farmland test area are mixed, and the edge features are the most complex.

Combined with the analysis of Figure 5 and Table 3, in the grassland test area, the order of the EFRD between the fusion result and the reference image is GF-SG (7.72%) > ESTARFM (−10.17%) > STARFM (−16.22%) > FSDAF (−21.53%); only GF-SG showed over-sharpening of edge features, the other three models showed under-prediction of edge features, and the NDVI images were smoother. Among them, ESTAFFM has the smallest degree, and the absolute value of the EFRD from the reference image is 10.17%; STARFM is worse, more than 16%; FSDAF is the worst, more than 21%, and it can be seen in Figure 5 that its edge features are less.

In the forest test area, the prediction results of GF-SG were the most like the edge features of the reference image, with a difference of only −2.40%; followed by STARFM, with a difference of −12.78%. The predicted images of ESTARFM and FSDAF differ greatly from the reference images, with them both exceeding 18%. Among them, ESTARFM is over-smoothed, with fewer edge features than predicted images; FSDAF is over-sharpened, with more edge features.

In the farmland test area, the four models all show the characteristics of fewer edge features. Among them, the degree of over-smoothing of GF-SG is the smallest, and the difference between the prediction result and the edge feature of the reference image is −9.29%; the degree of over-smoothing of FSDAF is greater, with the difference being −14.71%; the over-smoothing phenomenon of STARFM and ESTARFM is more prominent, with STARFM exceeding −28% and ESTARFM being close to 33%.

In general, the fusion models generally show the characteristics of over-smoothness in the fine-resolution NDVI prediction of the three test areas, and it is difficult to completely reconstruct the edge features of the image, especially in the farmland test area. Among the four models, GF-SG performed the best, with over-sharpening or over-smoothing within 10%. The performance of STARFM, ESTARFM, and FSDAF is average, and the range of over-smoothing or sharpening is large.

4.5. Comprehensive Trade-Off Analysis

By analyzing the trade-off scores (

Table 4. The trade-off score and comprehensive trade-off score of the fusion results.

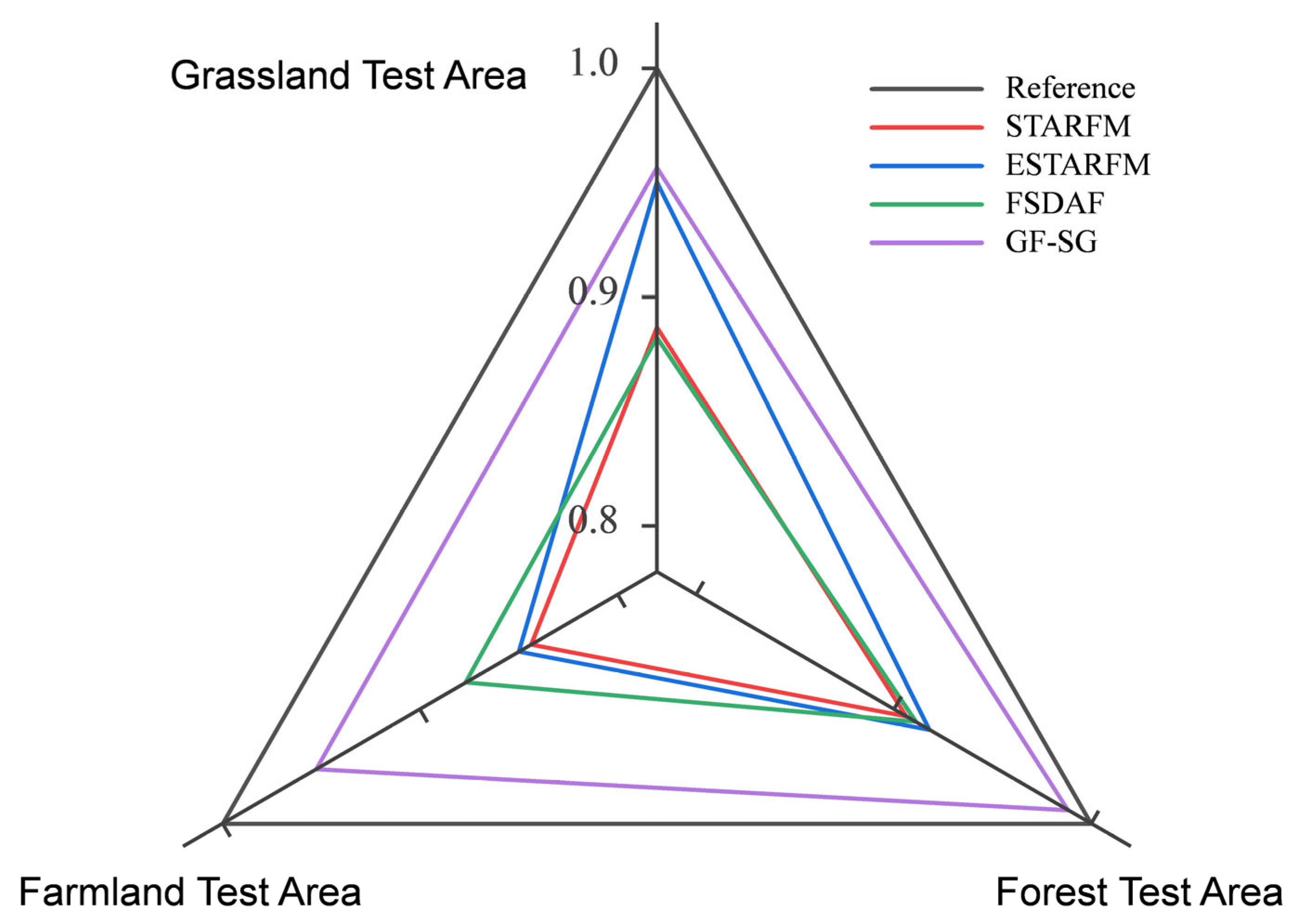
	Trade-Off Score			Comprehensive Trade-Off Score
	Grassland	Forest	Farmland
STARFM	0.8867	0.9064	0.8436	0.8789
ESTARFM	0.9503	0.9181	0.8465	0.9050
FSDAF	0.8823	0.9113	0.8768	0.8901
GF-SG	0.9566	0.9883	0.9526	0.9658

and Figure 6) of the fusion results of the four methods, it can be found that: GF-SG has the highest trade-off score (TS) in the three test areas, and in all of them, it exceed 95%; the TS of the four methods in the grassland test area is GF-SG > ESTARFM > STARFM > FSDAF; in the forest test area, it is: GF-SG > ESTARFM > FSDAF > STARFM; in the farmland test area, it is: GF-SG > FSDAF > ESTARFM > STARFM.

The comprehensive trade-off score (CTS) of the four methods is ranked as GF-SG > ESTARFM > FSDAF > STARFM.

The high RMSE of STARFM in the grassland test area and the over-smoothing in the farmland test area affected the TSs in both test areas and ultimately resulted in the lowest CTS. The high RMSE and high AD of FSDAF in the farmland test area and the over-smoothing problem in the grassland test area affected the TSs in the two test areas and lowered the result of the CTS. ESTARFM is in the middle-to-upper level in the evaluation of RMSE and AD, but the over-smoothing problem in all three test areas, especially the farmland test area, limits the further improvement of the CTS. GF-SG showed excellent performance in the evaluation of the three indicators, no large error occurred, and the TS in the three test areas was the highest, so the CTS was also the highest among the four methods.

5. Discussion

As an important index to monitor vegetation growth characteristics, NDVI has been widely used in forest disturbance detection, grassland degradation monitoring, crop yield assessment, and other fields. High-resolution, high-precision, and fast-updating NDVI data are of great significance for dynamic monitoring of vegetation characteristics in scientific research and economic and social analysis, especially under the situation of rapid change in vegetation characteristics. However, due to the conflict between the resolution and the revisit period of the remote sensing sensor, it is difficult for a single remote sensing image to have two quality attributes at the same time. This makes it difficult to obtain NDVI sequence data with high spatial and temporal resolution. In this context, spatiotemporal data fusion develops rapidly, and many methods have been proposed. However, their characteristics and performance are different. At present, there is no space fusion method recognized by most scholars, let alone the widely recognized NDVI spatiotemporal fusion method. Based on such problems, this study conducted a comprehensive study from two aspects, three indexes, and multiple test areas trying to clarify the accuracy characteristics and application effects of different fusion methods in NDVI generation. This will have important guiding significance to produce high-resolution, fast-updating and long time series NDVI data. Furthermore, it will help to carry out scientific research in related fields and contribute to economic and social development, agricultural monitoring, agronomic production, and other fields.

Through the comparative analysis and comprehensive weighing of the NDVI fusion results of the four methods (STARFM, ESTARFM, FSDAF, and GF-SG) in three typical natural geographic areas (grassland, forest, and farmland), their accuracy in the spatiotemporal fusion of NDVI data can be assessed. The fusion results of GF-SG in the grassland, forest, and farmland test areas are all good, and it shows advantages in quantitative analysis in many aspects, and finally obtains the highest CTS. The performance of ESTARFM in terms of prediction accuracy and overall deviation is relatively stable, with it being at an upper-middle level; however, there is a problem of over-smoothing in the three test areas, which limits the further improvement of the CTS. The high RMSE and AD of FSDAF in the farmland test area and the over-smoothing problem in the grassland test area lowered the results of the CTS. STARFM is in the middle and lower level in all three indicator evaluations and finally obtains the lowest CTS. It is worth noting that the results of quantitative analysis may be different if other indicators, other scoring methods, and more test areas are selected. However, the comparative analysis in this study has included the spectral characteristics and spatial characteristics, there is no strong correlation between the indicators, and the test areas have included the main land use/cover types. Therefore, the conclusion reached in this study is reliable: GF-SG has the best fusion accuracy among the four methods and is suitable for the construction of NDVI time series data with high spatial and temporal resolution. On the other hand, the four methods we have chosen are just a few of the many methods of spatiotemporal fusion. However, the framework of comparative analysis and comprehensive trade-off constructed in the paper will have reference value for research in the field.

In different spatiotemporal fusion methods, there are some important input parameters, such as the size of the neighborhood window, the maximum value, the minimum value, the number of similar pixels, the number of land classifications, etc. [36]. Before carrying out the comparative analysis of different models, we first conducted parameter experiments. We found that under the premise of ensuring that the model normally produces NDVI fusion images, adjusting the input parameters has little effect on the results; it is 1–2 orders of magnitude smaller than the differences between the fusion results of different methods, so it can be ignored. The main influencing factors of fusion accuracy are model principle and input data. Among them, the influence of model principle is the key content to be explored in this paper. To highlight this point, we tried to make the input data identical across the models. Although they have different requirements for the number of input image pairs, we maintain the consistency of the common part. Therefore, the accuracy analysis results of this study mainly indicate the performance of the spatiotemporal fusion models.

Except for the fusion image pairs, the four spatiotemporal fusion models do not require additional vegetation data. In the process of fusion experiments, we also found that the four methods also have large differences in data input, which may affect the model operation and large-scale application. STARFM and FSDAF need to input a pair of fine-resolution and coarse-resolution images acquired in a known period, and a coarse-resolution image of the prediction period, which needs to be downloaded and preprocessed (clipping, geometric correction, and resampling) in advance. At the same time, they have high-quality requirements for input data, cannot contain clouds and gaps, and remove cloud shadows as much as possible [37]. Therefore, in large-area applications, there may be problems with input image acquisition. For ESTARFM, it is necessary to input two pairs of images of a known period, which further increases the data requirements for its large-scale application, especially in areas with perennial cloudy conditions, which will be difficult to achieve [38]. GF-SG is based on the principle of pixel time series matching and no longer requires the input image to be seamless and cloud-free. Although, it requires multiple images over a long time (usually six months to one year) as input data. However, under the background of the open-source acquisition of remote sensing images and rapid invocation and processing of remote sensing cloud computing platforms, the construction of high spatial and temporal resolution-images can be easily achieved. Therefore, it has the advantages of both data and speed and has the possibility of a wide range of applications [31,39].

6. Conclusions

In this paper, three test areas of grassland, forest, and farmland were selected, and four spatiotemporal fusion models (STARFM, ESTARFM, FSDAF, GF-SG) were used to carry out the fusion experiment of NDVI images. In addition, from the two dimensions of spectral characteristics and spatial characteristics, using RMSE, AD, and EFRD three indicators to carry out a comparative study of the fusion results, and conduct comprehensive trade-off and analysis. This study summarizes the application accuracy of four methods in NDVI image spatiotemporal fusion and discusses their feasibility in constructing large-scale, high spatiotemporal-resolution NDVI time series data. This study can provide a reference for method selection and result evaluation for related scholars to conduct NDVI data spatiotemporal fusion and NDVI time series data construction.

This study shows that all four methods can produce fine-resolution NDVI images in the forecast period well. However, there is a common phenomenon that EFRD < 0, and the fusion result is difficult to completely reconstruct the edge features of the image, showing the characteristics of over-smoothing. The order of comprehensive trade-off scores of the four models is GF-SG > ESTARFM > FSDAF > STARFM. GF-SG has advantages in the evaluation of the three test areas and three indicators, and the comprehensive trade-off score (CTS) is the highest. ESTARFM is relatively good in terms of prediction accuracy and overall bias, but the over-smoothing problem limits the further improvement of the CTS. Due to the high RMSE and AD in the farmland test area and the over-smoothing problem in the grassland test area, FSDAF lowered the CTS. STARFM is in the middle and lower levels in the evaluation of the three indicators, and the CTS is the lowest. Considering the comparative analysis and comprehensive trade-off results of three test areas and three indicators, among the four models, GF-SG fusion has the best accuracy in generating NDVI images. GF-SG is suitable for the construction of NDVI time series data with high spatial and temporal resolution.