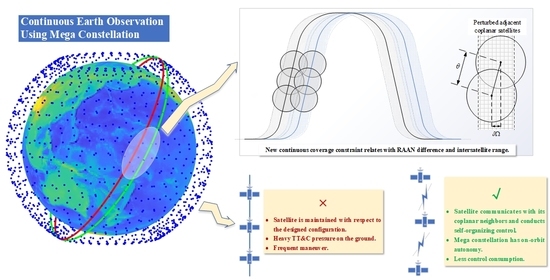
Self-Organizing Control of Mega Constellations for Continuous Earth Observation
Abstract
1. Introduction
2. Materials and Methods
2.1. Continuous Coverage Constraint of Mega Constellation
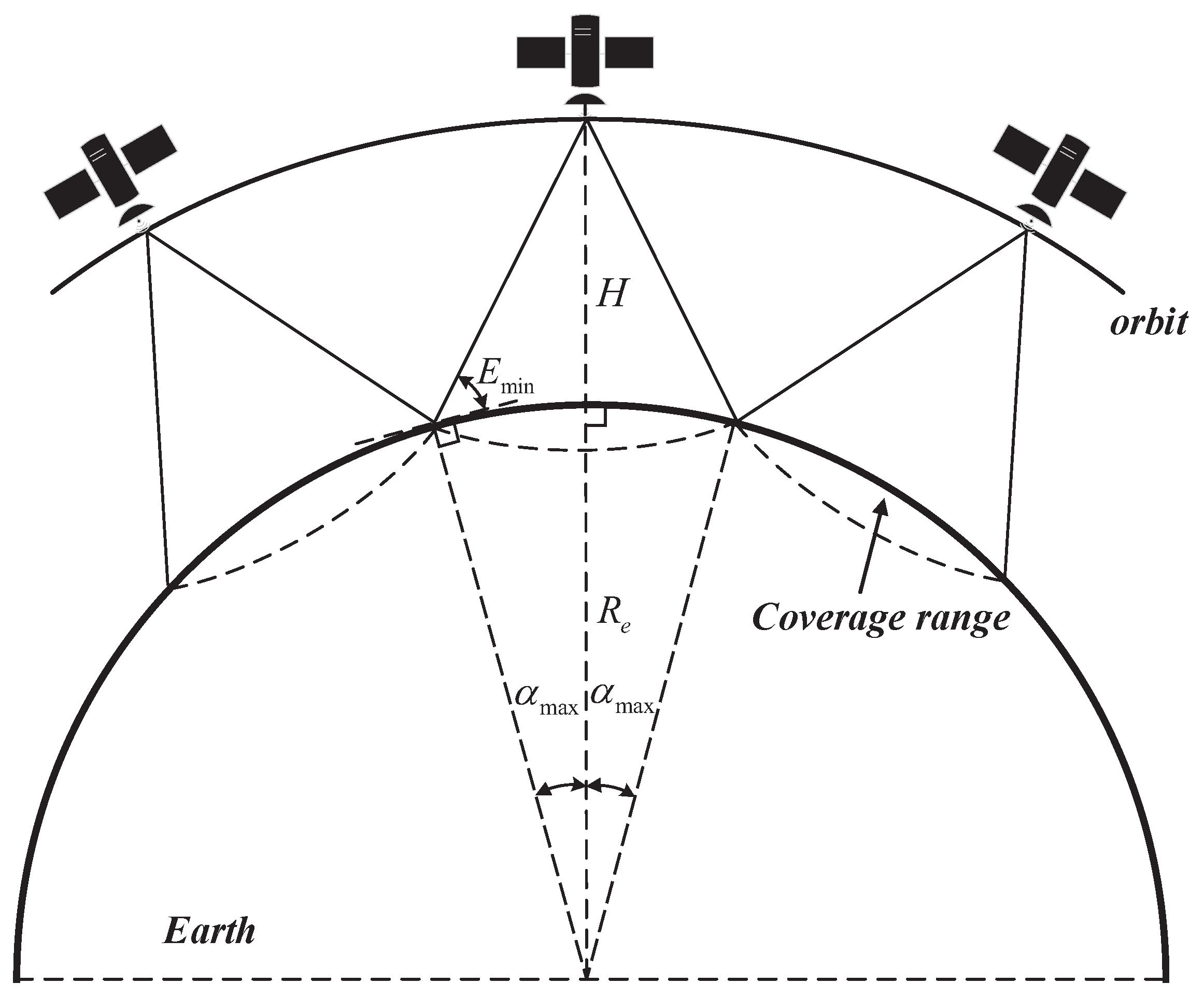
2.1.1. Definition of Continuous Coverage
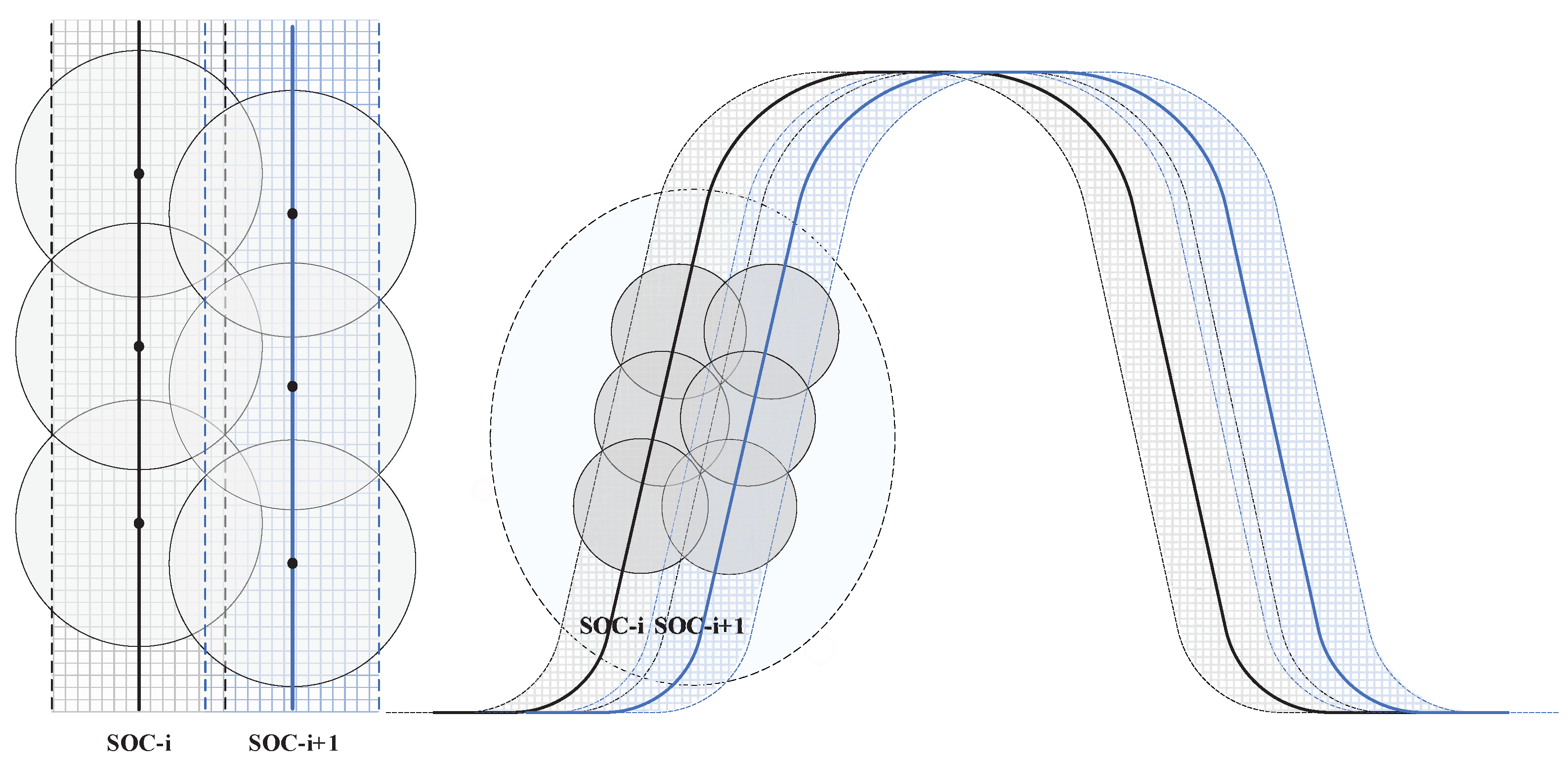
2.1.2. Configuration Requirements for Mega Constellations
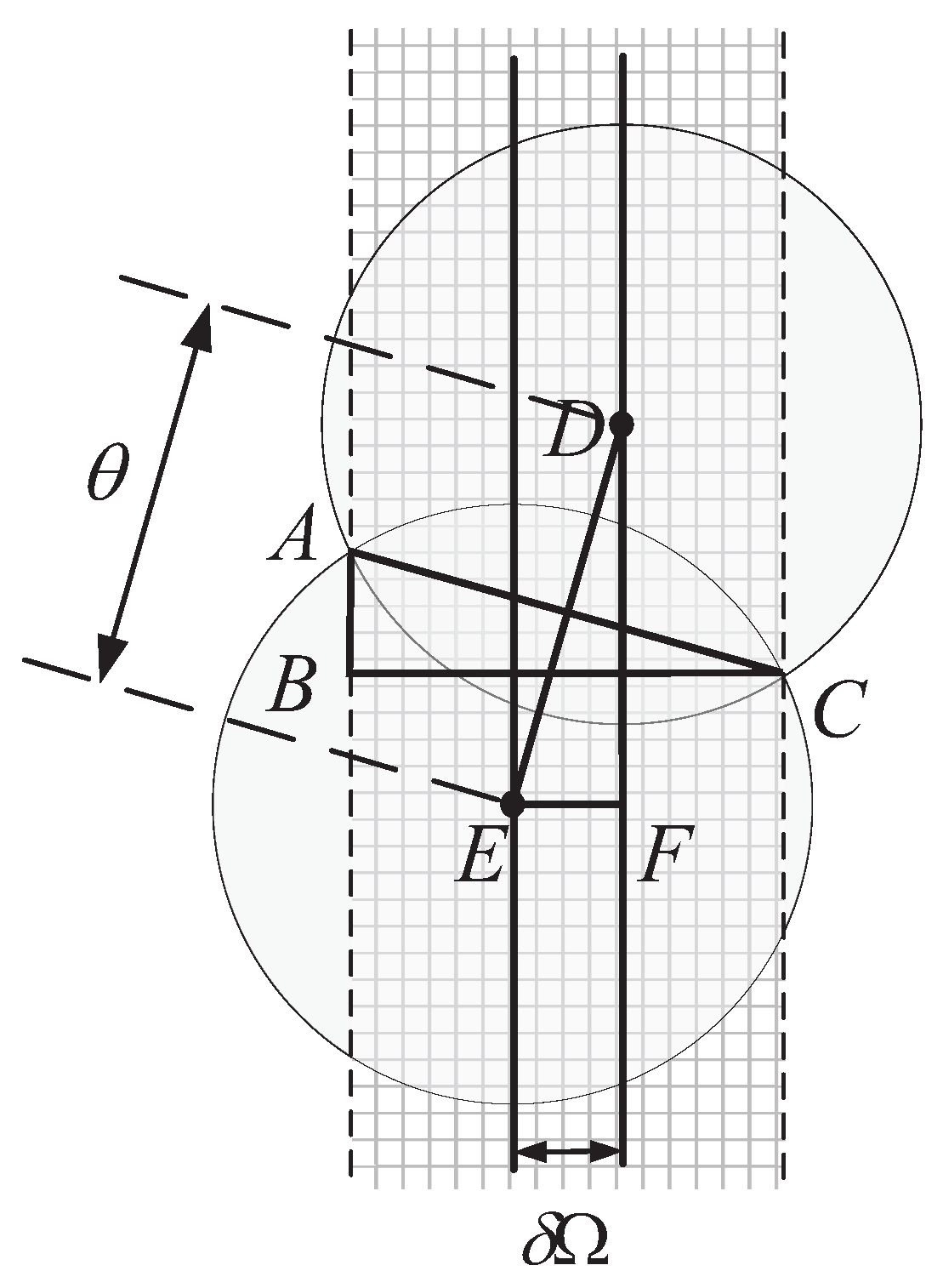
2.1.3. Intersatellite Motion Constraints
2.2. Self-Organizing Control Using Artificial Potential Functions
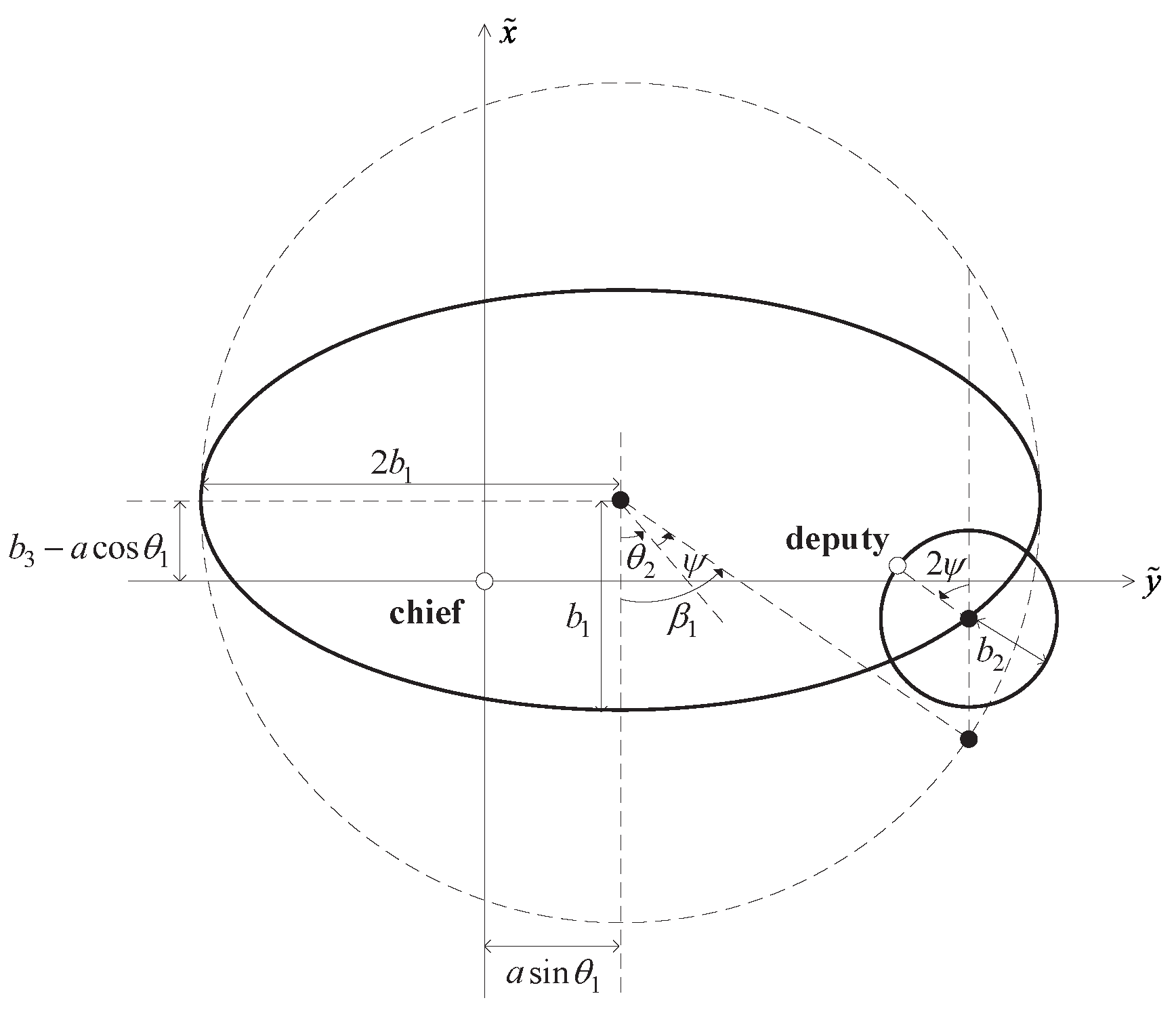
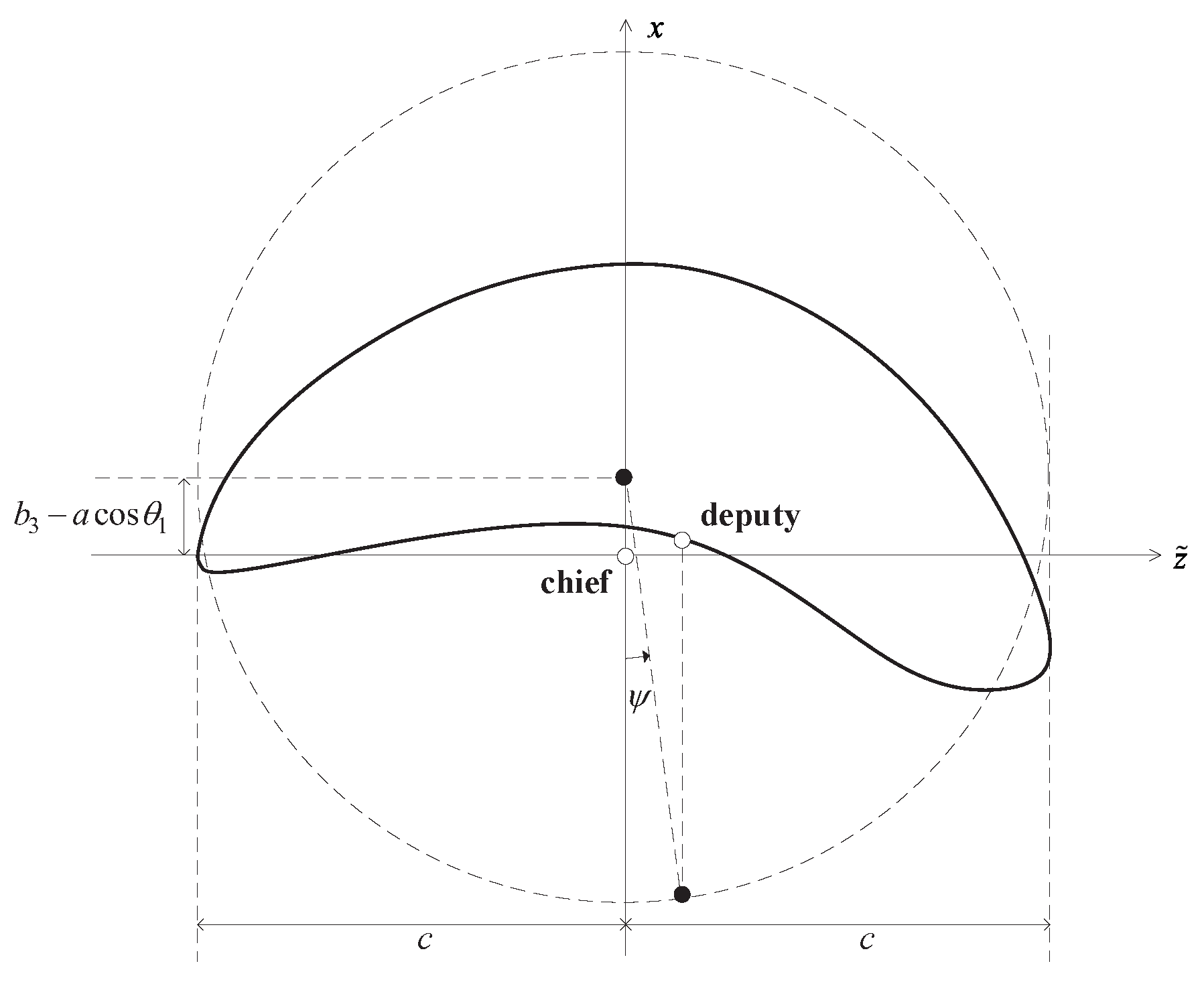
2.2.1. Scale-Independent Relative Orbital Elements and Bound Formulations
2.2.2. Design of Artificial Potential Functions for Single Satellite Control
- (1)
- RAAN Control
- (2)
- Relative Motion-bound Control
- (3)
- Semi-Major Axis Control
2.2.3. Self-Organizing Control Rules for Coplanar Satellites
2.3. Stability Proof of Satellite Control
2.3.1. Stability Proof of RAAN Control and Semi-Major Axis Control
2.3.2. Stability Proof of Relative Motion-Bound Control
2.3.3. Selection Criteria of Quadratic Potential Function Variables
- (1)
- Using and as Control Variables
- (2)
- Using Orbital Elements as Control Variables
- (3)
- Using Relative Orbital Elements as Control Variables
3. Results and Discussion
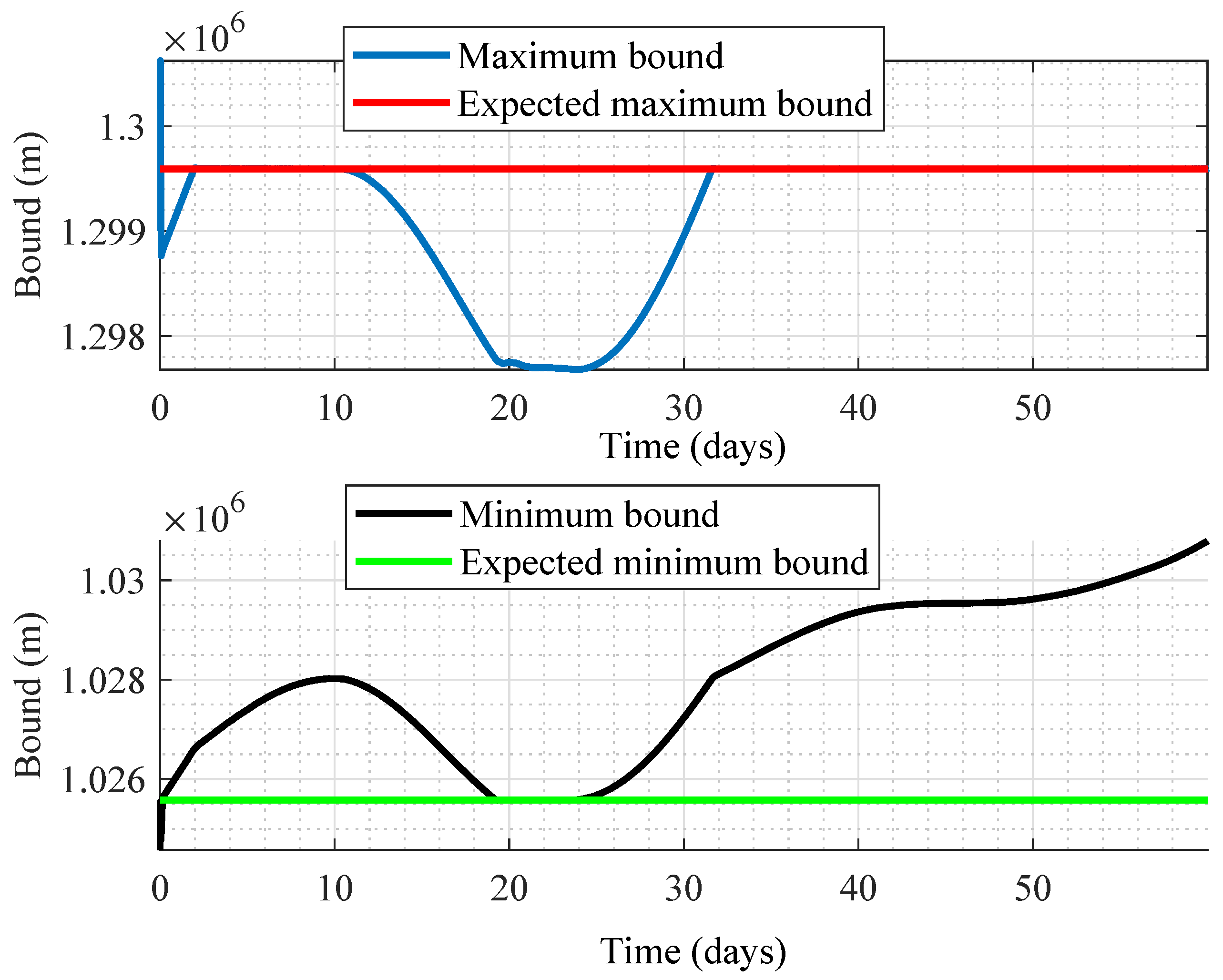
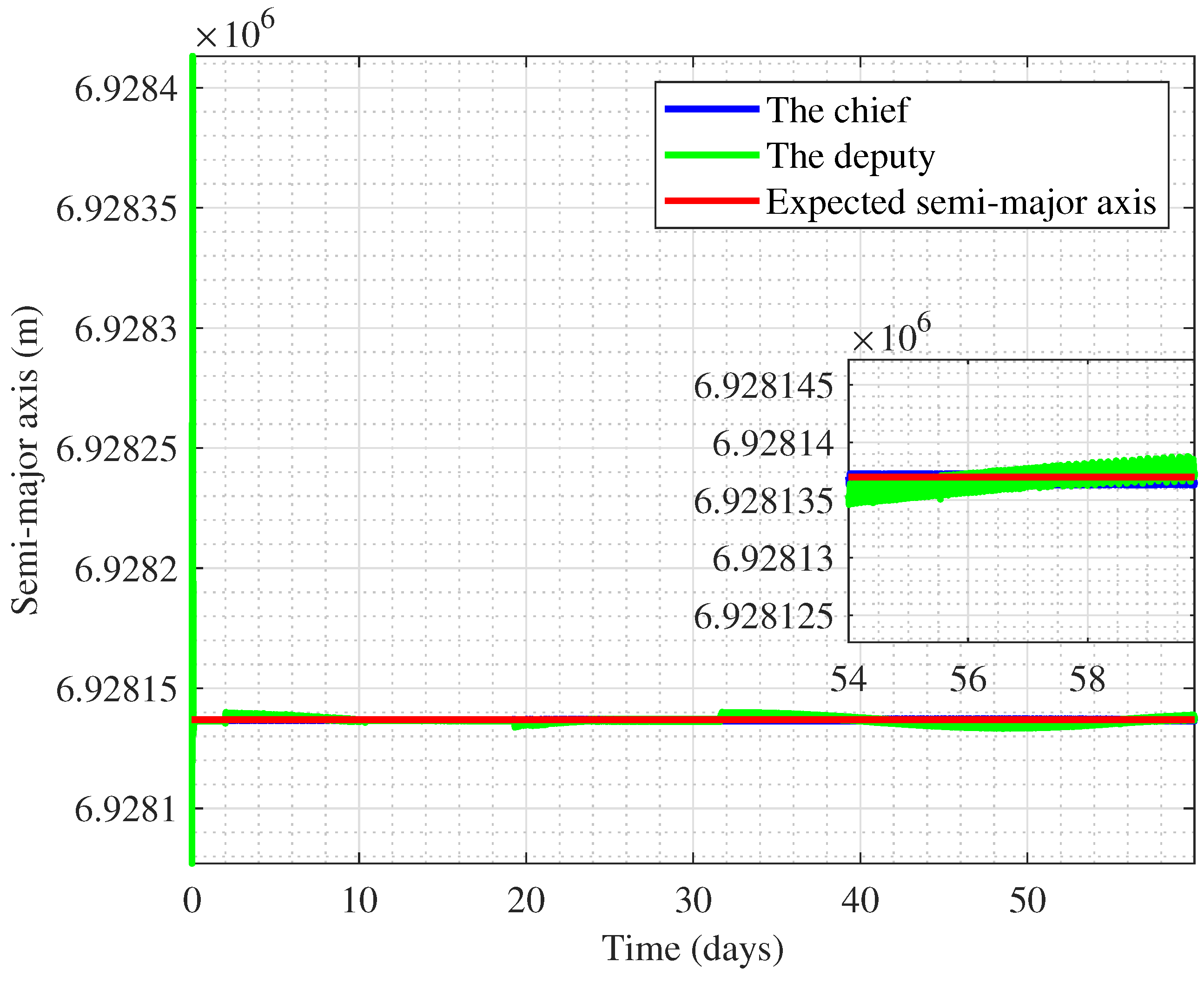
3.1. Self-Organizing Control of Two Satellites
3.2. Self-Organizing Control of Coplanar Satellites
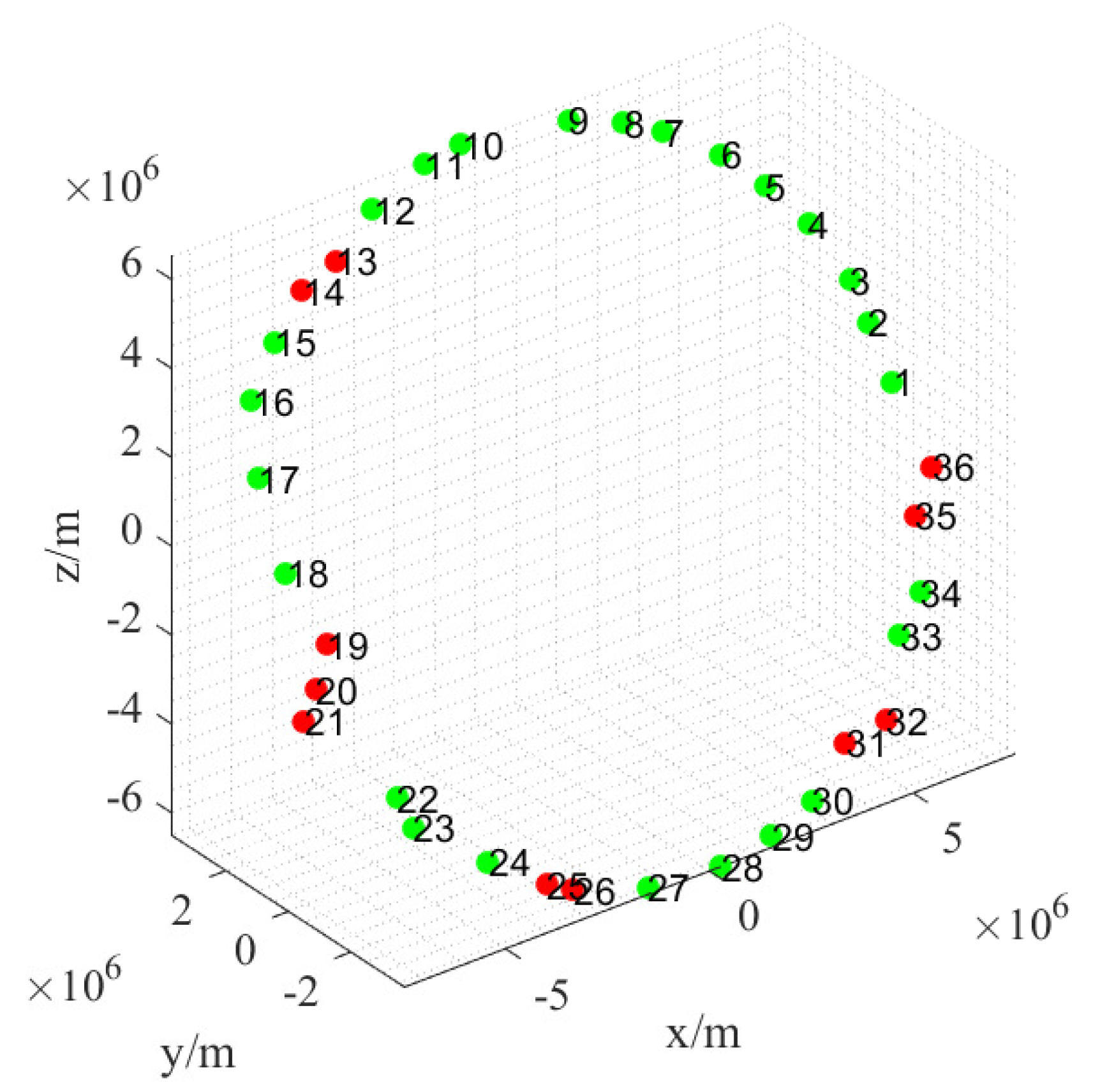
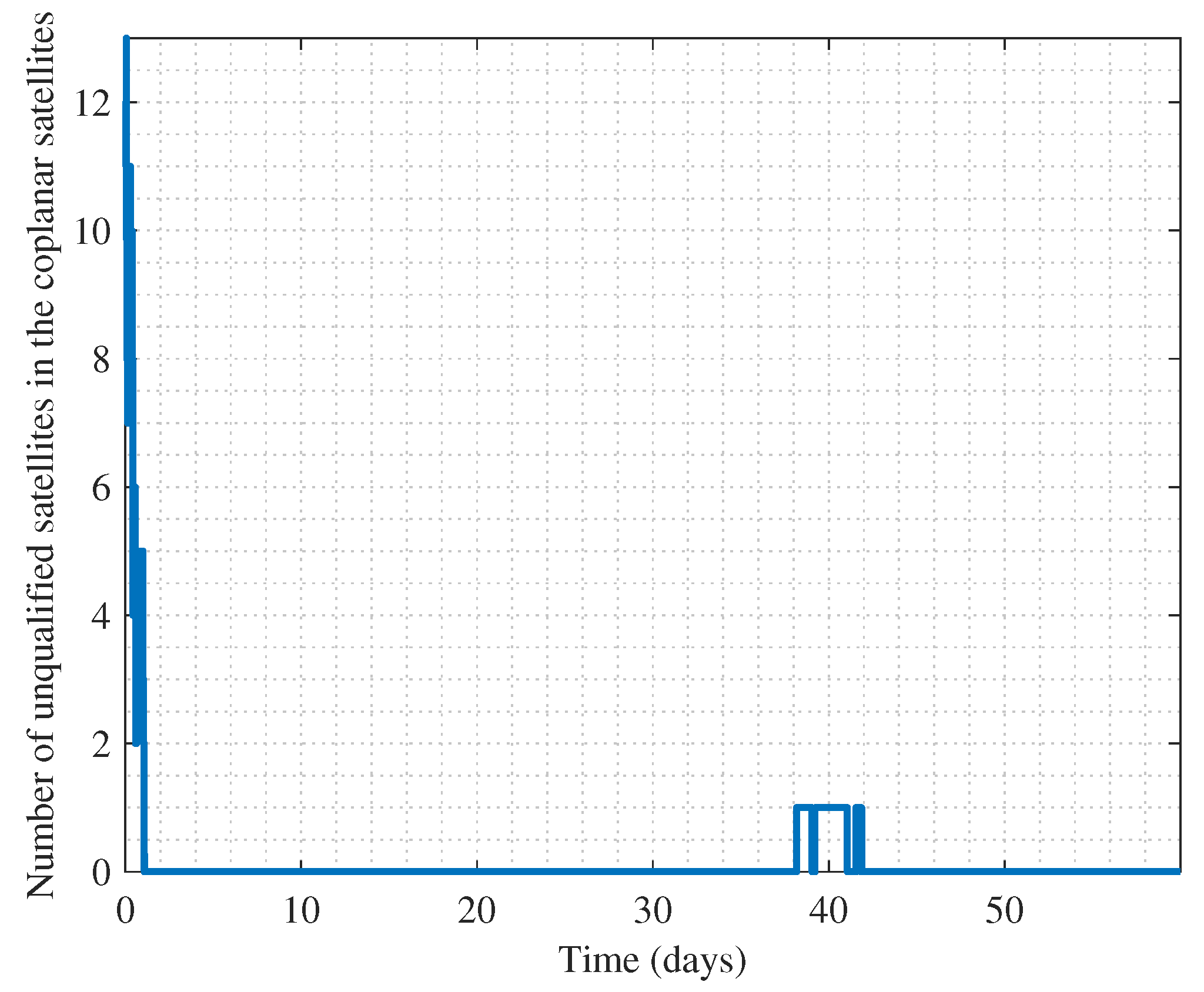
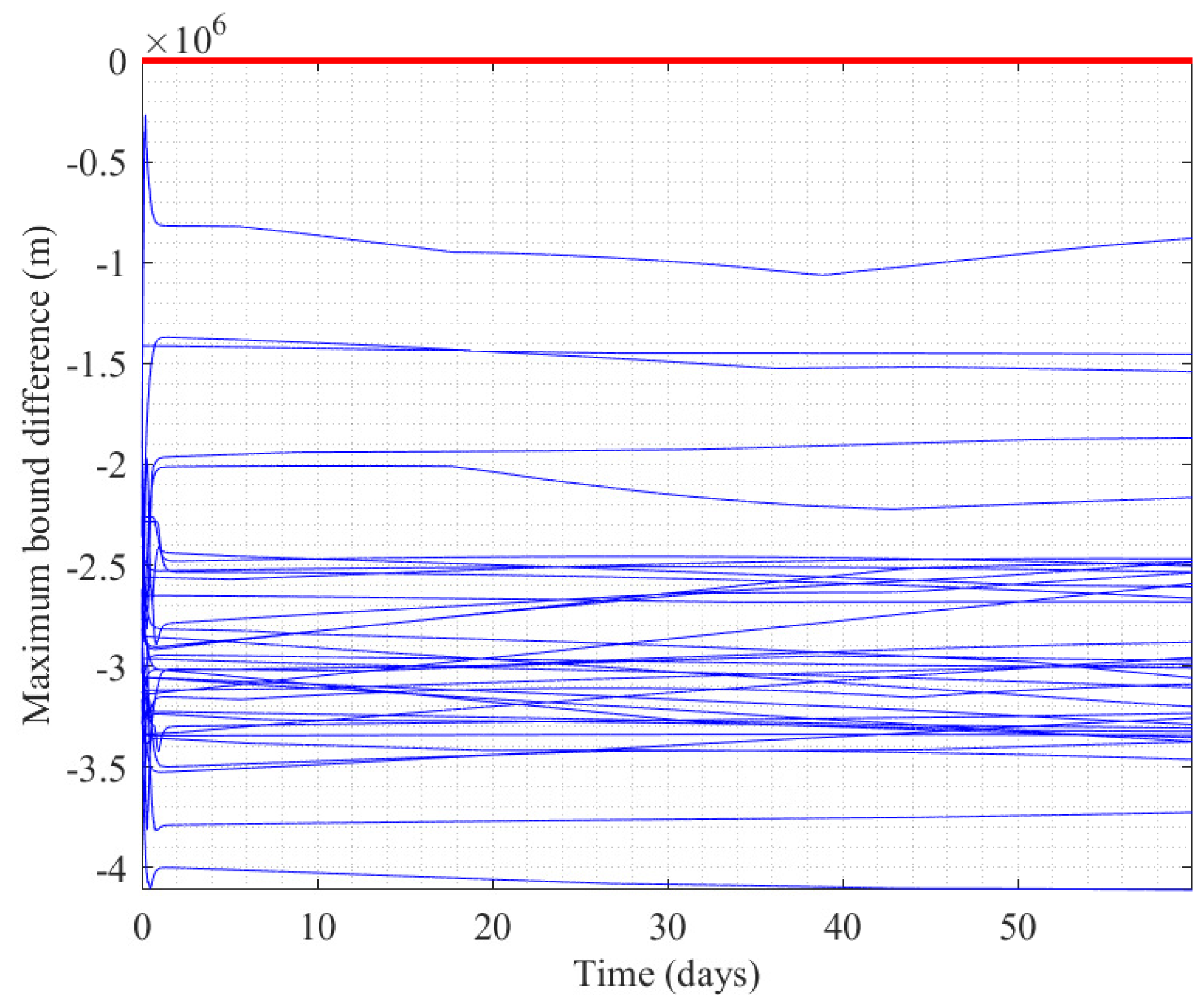
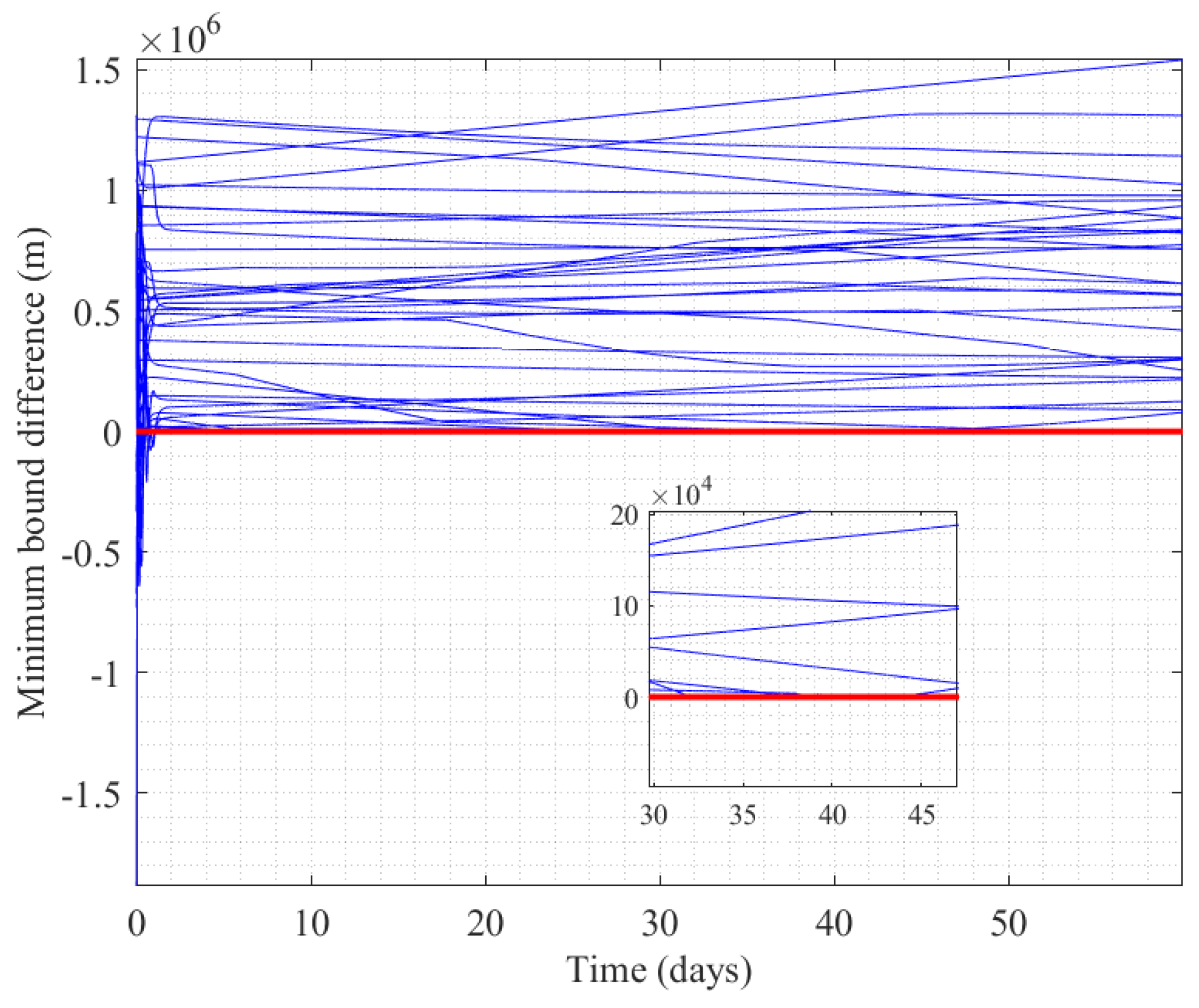
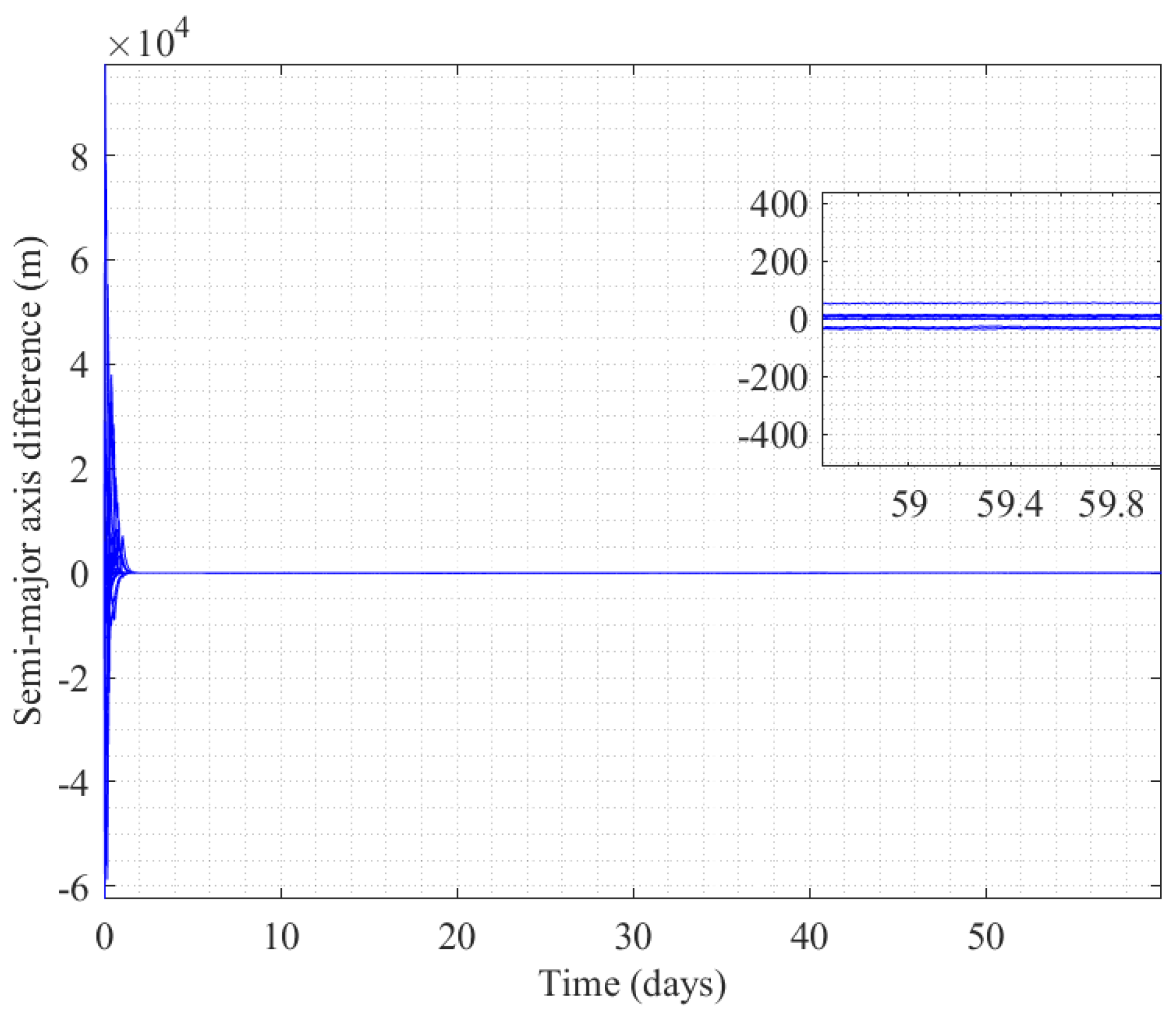
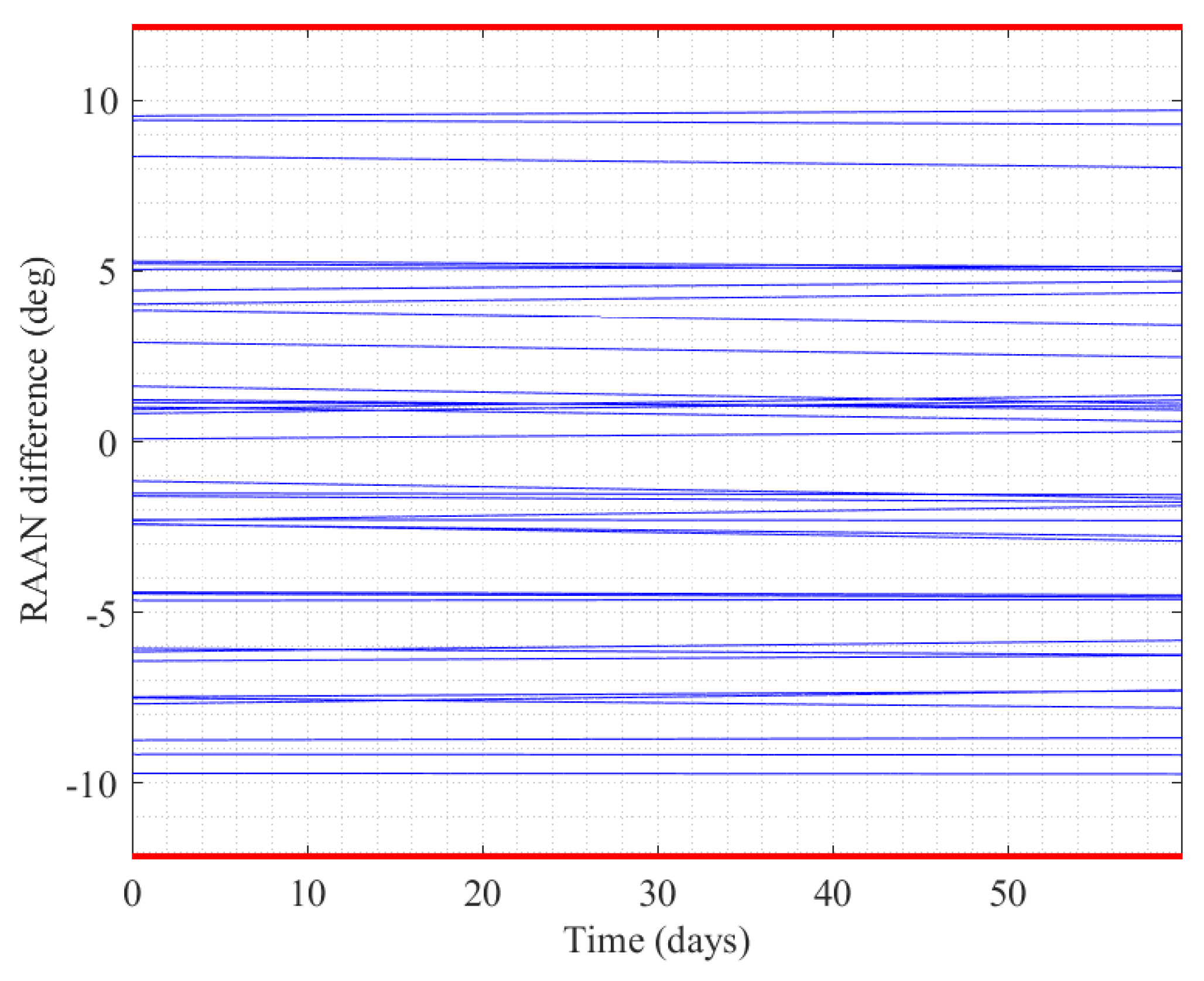
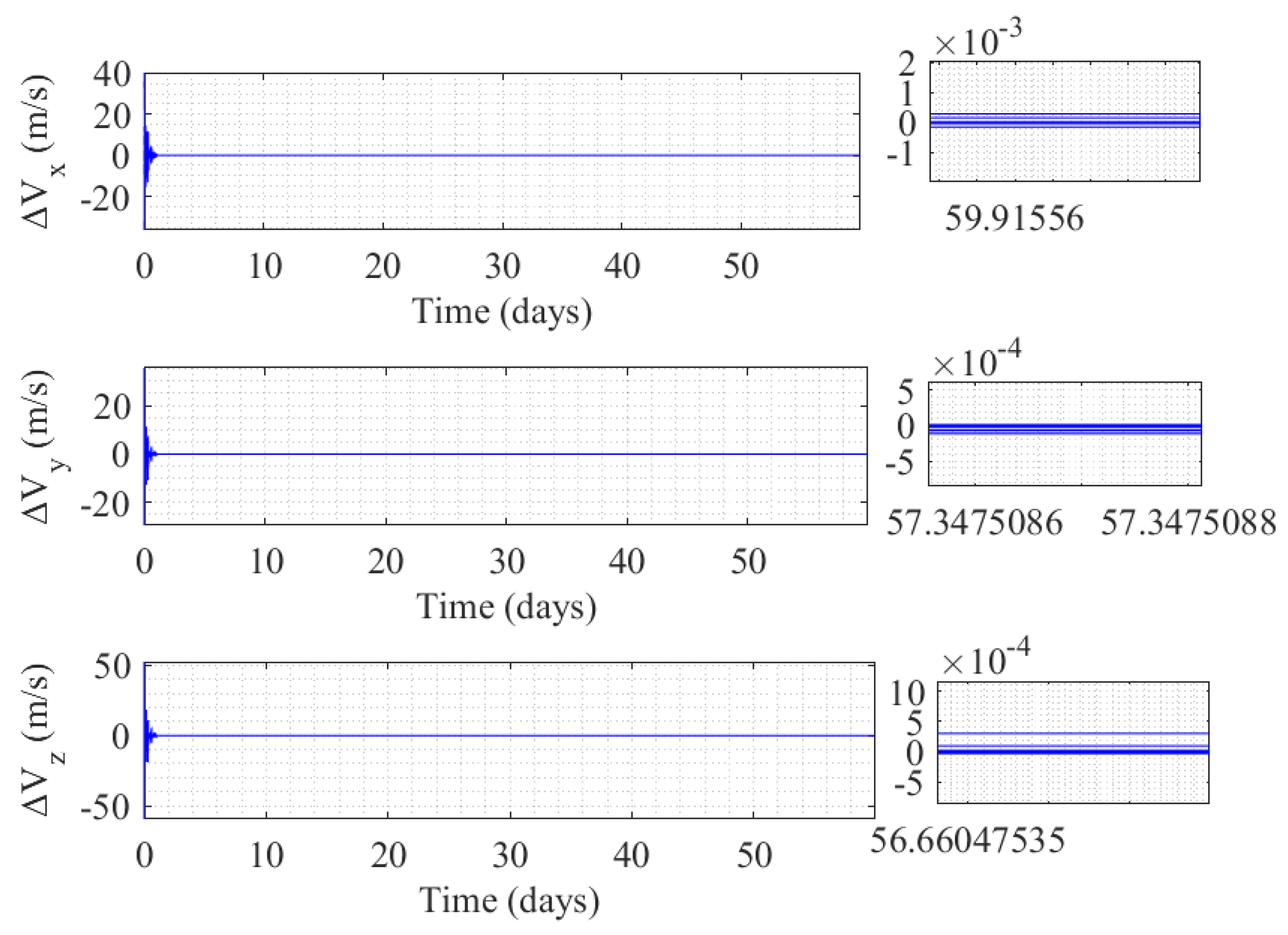
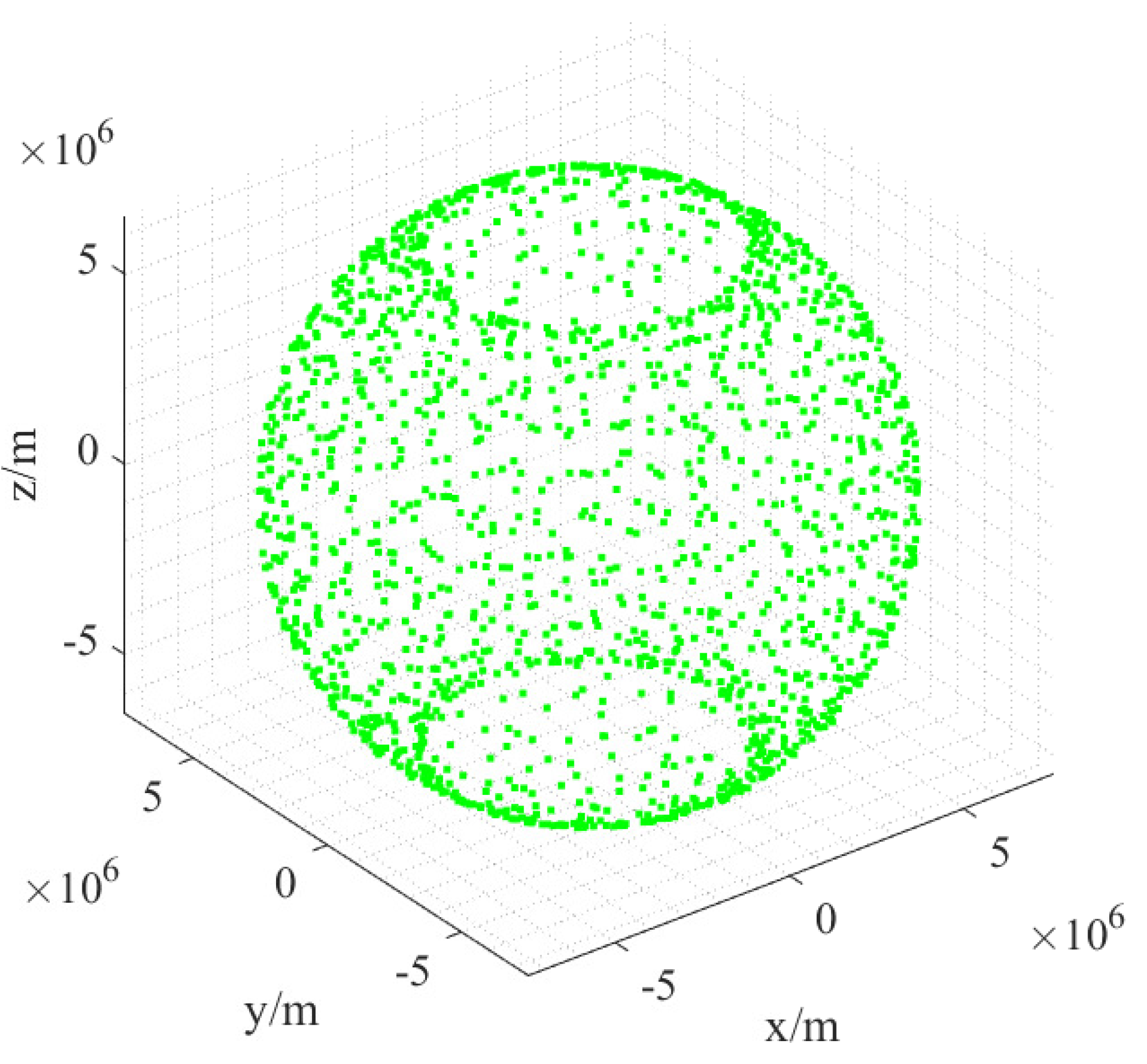
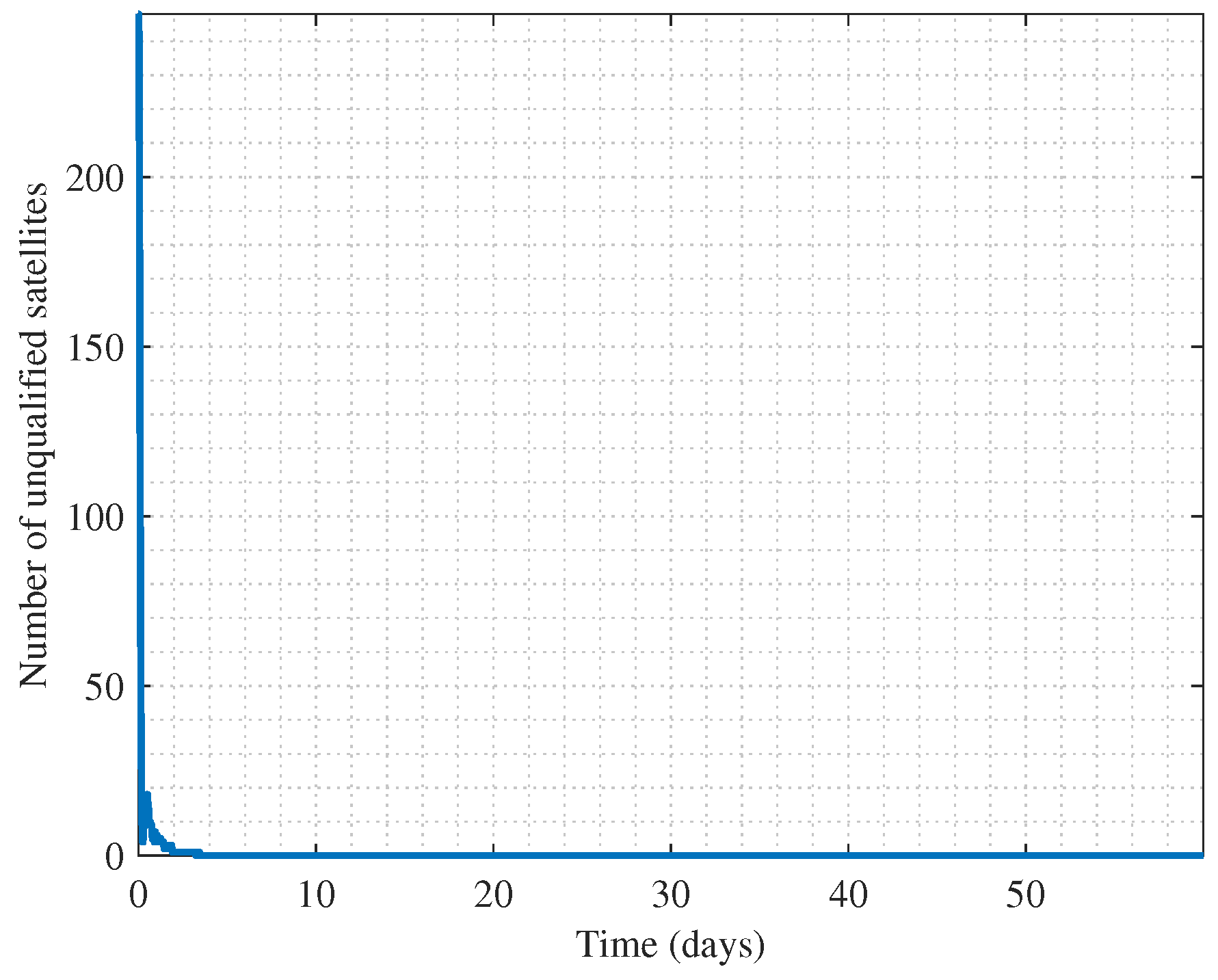
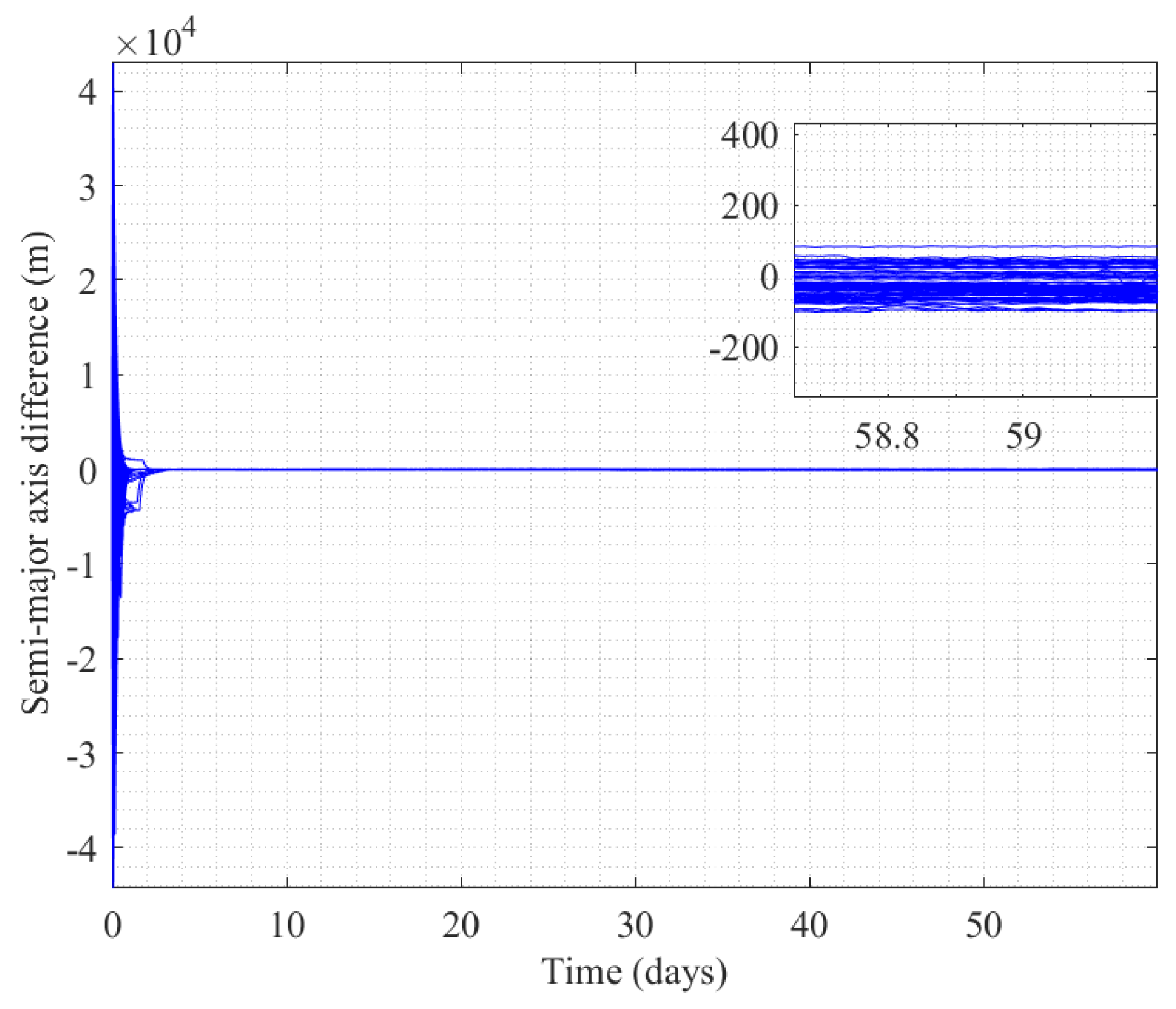
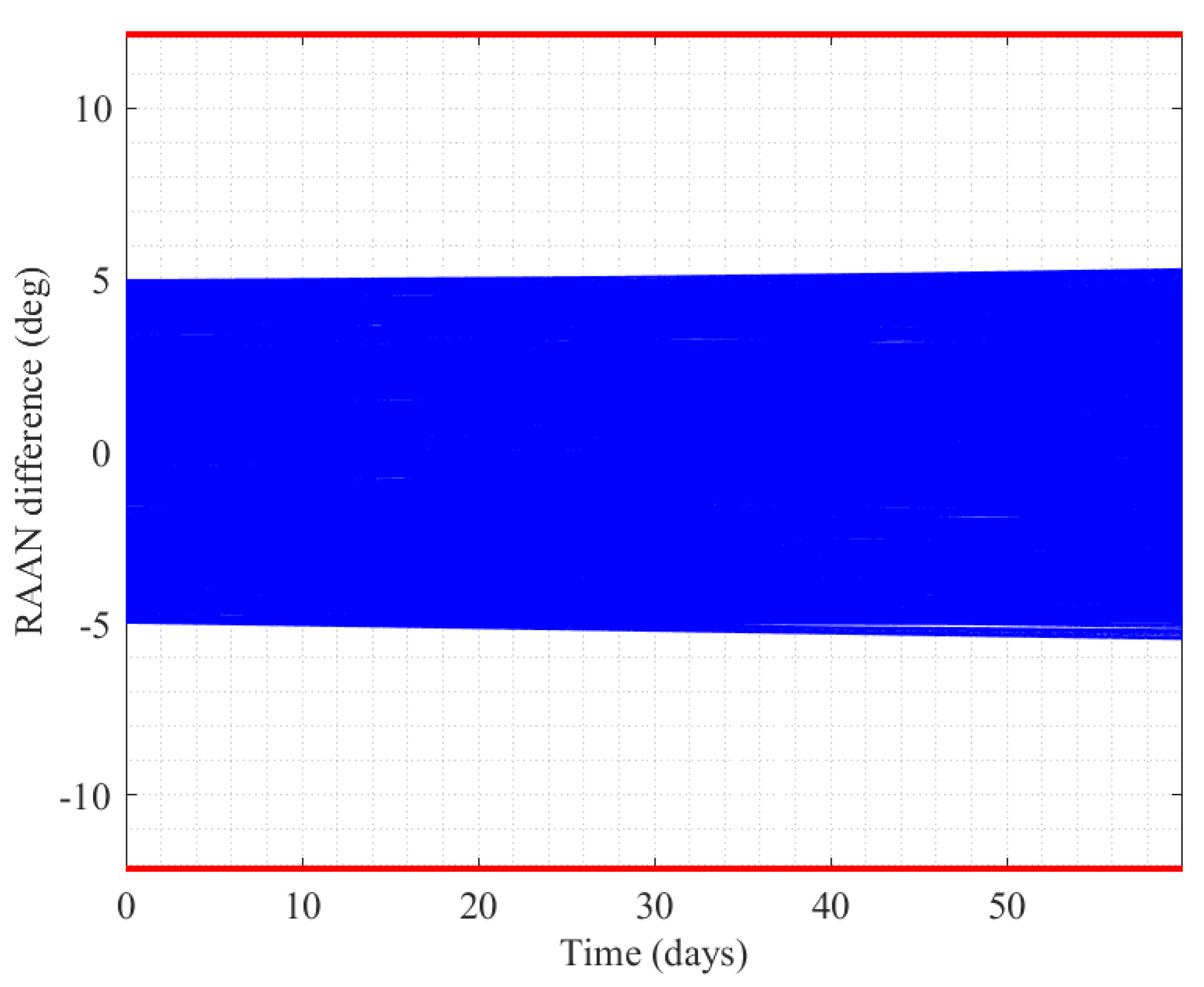
3.3. Self-Organizing Control of Mega Constellation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Del Portillo, I.; Cameron, B.G.; Crawley, E.F. A technical comparison of three low earth orbit satellite constellation systems to provide global broadband. Acta Astronaut. 2019, 159, 123–135. [Google Scholar] [CrossRef]
- Williams, A.; Hainaut, O.; Otarola, A.; Tan, G.H.; Rotola, G. Analysing the impact of satellite constellations and ESO’s role in supporting the astronomy community. arXiv 2021, arXiv:2108.04005. [Google Scholar]
- Boggio, M.; Colangelo, L.; Virdis, M.; Pagone, M.; Novara, C. Earth Gravity In-Orbit Sensing: MPC Formation Control Based on a Novel Constellation Model. Remote Sens. 2022, 14, 2815. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, Y.; Wen, G.; Bai, S.; Cai, Y.; Huang, P.; Han, D.; He, Y. Atmospheric Density Model Optimization and Spacecraft Orbit Prediction Improvements Based on Q-Sat Orbit Data. arXiv 2021, arXiv:2112.03113. [Google Scholar]
- Mastro, P.; Masiello, G.; Serio, C.; Pepe, A. Change Detection Techniques with Synthetic Aperture Radar Images: Experiments with Random Forests and Sentinel-1 Observations. Remote Sens. 2022, 14, 3323. [Google Scholar] [CrossRef]
- Lang, T. Low Earth orbit satellite constellations for continuous coverage of the mid-latitudes. In Proceedings of the Astrodynamics Conference, San Diego, CA, USA, 29 July–31 July 1996; p. 3638. [Google Scholar]
- Santos, M.; Shapiro, B. Relating satellite coverage to orbital geometry. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference and Exhibit, Honolulu, HI, USA, 18–21 August 2008; p. 6609. [Google Scholar]
- Hackett, T.M.; Bilén, S.G.; Bell, D.J.; Lo, M.W. Geometric approach for analytical approximations of satellite coverage statistics. J. Spacecr. Rocket. 2019, 56, 1286–1299. [Google Scholar] [CrossRef]
- Dai, G.; Chen, X.; Wang, M.; Fernández, E.; Nguyen, T.N.; Reinelt, G. Analysis of satellite constellations for the continuous coverage of ground regions. J. Spacecr. Rocket. 2017, 54, 1294–1303. [Google Scholar] [CrossRef]
- Gong, Y.; Zhang, S.; Peng, X. Quick coverage analysis of mega Walker Constellation based on 2D map. Acta Astronaut. 2021, 188, 99–109. [Google Scholar] [CrossRef]
- Huang, S.; Colombo, C.; Bernelli-Zazzera, F. Multi-criteria design of continuous global coverage Walker and Street-of-Coverage constellations through property assessment. Acta Astronaut. 2021, 188, 151–170. [Google Scholar] [CrossRef]
- Arnas, D.; Casanova, D.; Tresaco, E. Relative and absolute station-keeping for two-dimensional–lattice flower constellations. J. Guid. Control. Dyn. 2016, 39, 2602–2604. [Google Scholar] [CrossRef]
- Chen, Y.; Zhao, L.; Liu, H.; Li, L.; Liu, J. Analysis of configuration and maintenance strategy of LEO walker constellation. J. Astronaut. 2019, 40, 1296–1303. [Google Scholar]
- Li, J.; Hu, M.; Wang, X.; Li, F.; Xu, J. Analysis of configuration offsetting maintenance method for LEO Walker constellation. Chin. Space Sci. Technol. 2021, 41, 38. [Google Scholar]
- Izzo, D.; Pettazzi, L. Autonomous and distributed motion planning for satellite swarm. J. Guid. Control. Dyn.s 2007, 30, 449–459. [Google Scholar] [CrossRef]
- Nag, S.; Summerer, L. Behaviour based, autonomous and distributed scatter manoeuvres for satellite swarms. Acta Astronaut. 2013, 82, 95–109. [Google Scholar] [CrossRef]
- Hu, Q.; Dong, H.; Zhang, Y.; Ma, G. Tracking control of spacecraft formation flying with collision avoidance. Aerosp. Sci. Technol. 2015, 42, 353–364. [Google Scholar] [CrossRef]
- McInnes, C.R. Autonomous proximity manoeuvring using artificial potential functions. ESA J. 1993, 17, 159–169. [Google Scholar]
- Cao, L.; Qiao, D.; Xu, J. Suboptimal artificial potential function sliding mode control for spacecraft rendezvous with obstacle avoidance. Acta Astronaut. 2018, 143, 133–146. [Google Scholar] [CrossRef]
- Spencer, D.A. Automated trajectory control using artificial potential functions to target relative orbits. J. Guid. Control. Dyn. 2016, 39, 2142–2148. [Google Scholar] [CrossRef]
- Wang, Z.; Xu, Y.; Jiang, C.; Zhang, Y. Self-organizing control for satellite clusters using artificial potential function in terms of relative orbital elements. Aerosp. Sci. Technol. 2019, 84, 799–811. [Google Scholar] [CrossRef]
- Xu, Y.; Wang, Z.; Zhang, Y. Bounded flight and collision avoidance control for satellite clusters using intersatellite flight bounds. Aerosp. Sci. Technol. 2019, 94, 105425. [Google Scholar] [CrossRef]
- Xu, Y.; Wang, Z.; Zhang, Y. Modeling and control of scale-independent relative orbital elements for near-circular orbits. Acta Astronaut. 2022, 198, 642–658. [Google Scholar]
- Jiang, C.; Wang, Z.; Zhang, Y. Decomposition analysis of spacecraft relative motion with different inter-satellite ranges. Acta Astronaut. 2019, 163, 56–68. [Google Scholar]
- An, M.; Wang, Z.; Zhang, Y. Self-organizing control strategy for asteroid intelligent detection swarm based on attraction and repulsion. Acta Astronaut. 2017, 130, 84–96. [Google Scholar] [CrossRef]
- Sun, Y.; Shen, H. The control of mega-constellation at low earth orbit based on TLE. Acta Astronaut. 2020, 42, 156. [Google Scholar]










| Constellation | Altitude | Inclination | Planes | Satellites per Plane | Whether Continuous Coverage Constraint Is Satisfied |
|---|---|---|---|---|---|
| Starlink Genaration 1 | 550 km | 53 | 72 | 22 | Yes |
| 540 km | 53.2 | 72 | 22 | Yes | |
| 570 km | 70 | 36 | 20 | Yes | |
| 560 km | 97.6 | 6 | 58 | No | |
| 560 km | 97.6 | 4 | 43 | No | |
| OneWeb | 1120 km | 87.9 | 18 | 40 | Yes |
| 1150 km | 53 | 32 | 50 | Yes | |
| 1110 km | 53.8 | 32 | 50 | Yes | |
| GW-A59 | 590 km | 85 | 16 | 30 | No |
| 600 km | 50 | 40 | 50 | Yes | |
| 508 km | 55 | 60 | 60 | Yes | |
| GW-2 | 1145 km | 30 | 48 | 36 | Yes |
| 1145 km | 40 | 48 | 36 | Yes | |
| 1145 km | 50 | 48 | 36 | Yes | |
| 1145 km | 60 | 48 | 36 | Yes |
| Parameters | Values |
|---|---|
| Simulation Time | 60 days |
| Step Length | 600 s |
| Initial Conditions | |
| Perturbations | , atmospheric drag, lunar gravity, solar gravity |
| Control Coefficients | |
| Ballistic Coefficient | |
| Expected Range |
| Parameters | Values |
|---|---|
| Simulation Time | 60 days |
| Step Length | 600 s |
| Designed Configuration | |
| Initial Orbit Errors | |
| Perturbations | , atmospheric drag, lunar gravity, solar gravity |
| Control Coefficients | |
| Ballistic Coefficient | |
| Minimum Elevation Angle |
| Parameters | Values |
|---|---|
| Simulation Time | 60 days |
| Step Length | 600 s |
| Designed Configuration | |
| Initial Orbit Errors | |
| Perturbations | , atmospheric drag, lunar gravity, solar gravity |
| Control Coefficients | |
| Ballistic Coefficient | |
| Minimum Elevation Angle |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Y.; Zhang, Y.; Wang, Z.; He, Y.; Fan, L. Self-Organizing Control of Mega Constellations for Continuous Earth Observation. Remote Sens. 2022, 14, 5896. https://doi.org/10.3390/rs14225896
Xu Y, Zhang Y, Wang Z, He Y, Fan L. Self-Organizing Control of Mega Constellations for Continuous Earth Observation. Remote Sensing. 2022; 14(22):5896. https://doi.org/10.3390/rs14225896
Chicago/Turabian StyleXu, Yun, Yulin Zhang, Zhaokui Wang, Yunhan He, and Li Fan. 2022. "Self-Organizing Control of Mega Constellations for Continuous Earth Observation" Remote Sensing 14, no. 22: 5896. https://doi.org/10.3390/rs14225896
APA StyleXu, Y., Zhang, Y., Wang, Z., He, Y., & Fan, L. (2022). Self-Organizing Control of Mega Constellations for Continuous Earth Observation. Remote Sensing, 14(22), 5896. https://doi.org/10.3390/rs14225896