WDBSTF: A Weighted Dual-Branch Spatiotemporal Fusion Network Based on Complementarity between Super-Resolution and Change Prediction
Abstract
1. Introduction
- (1)
- We built an edge-enhanced remote sensing SR network with a reference image to enhance the performance of the SR branch. At the same time, we simplified the radiometric correction network design in STFDCNN using the union form.
- (2)
- We decomposed the complex problem into a two-layer network in the CP branch to reduce the complexity. At the same time, attention mechanisms were introduced to enhance the performance of the model.
- (3)
- We designed a weighted network instead of the traditional empirical formulas to fuse the two branches. The weighted network fully mines the complementarity between the two branches through training to offset their respective shortcomings.
- (4)
- We also carried out contrastive experiments and ablation experiments to validate the effectiveness of the WDBSTF on three datasets.
2. Materials and Methods
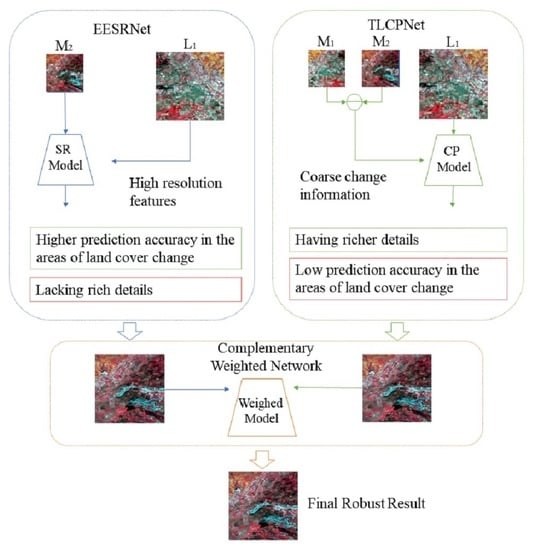
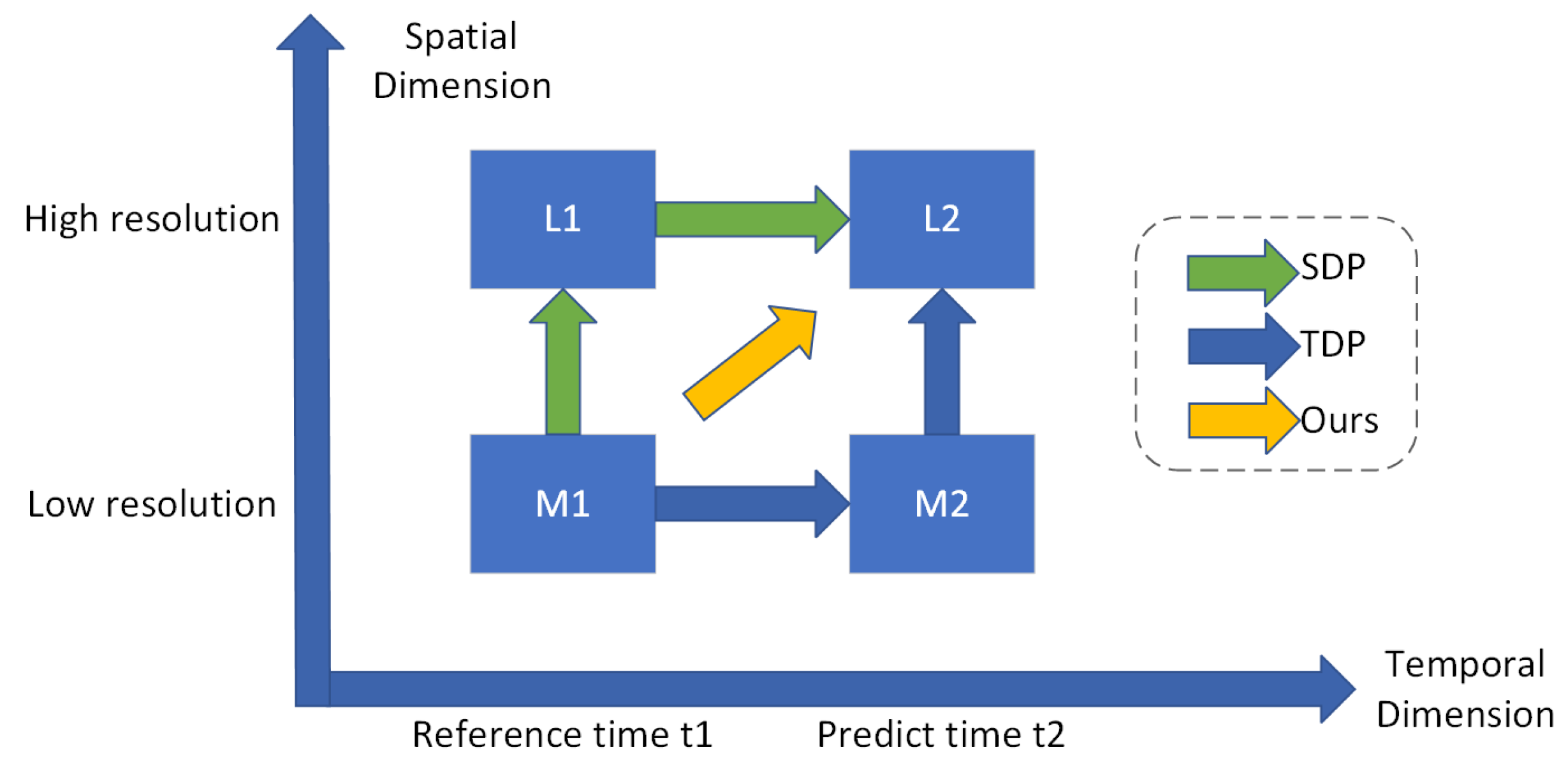
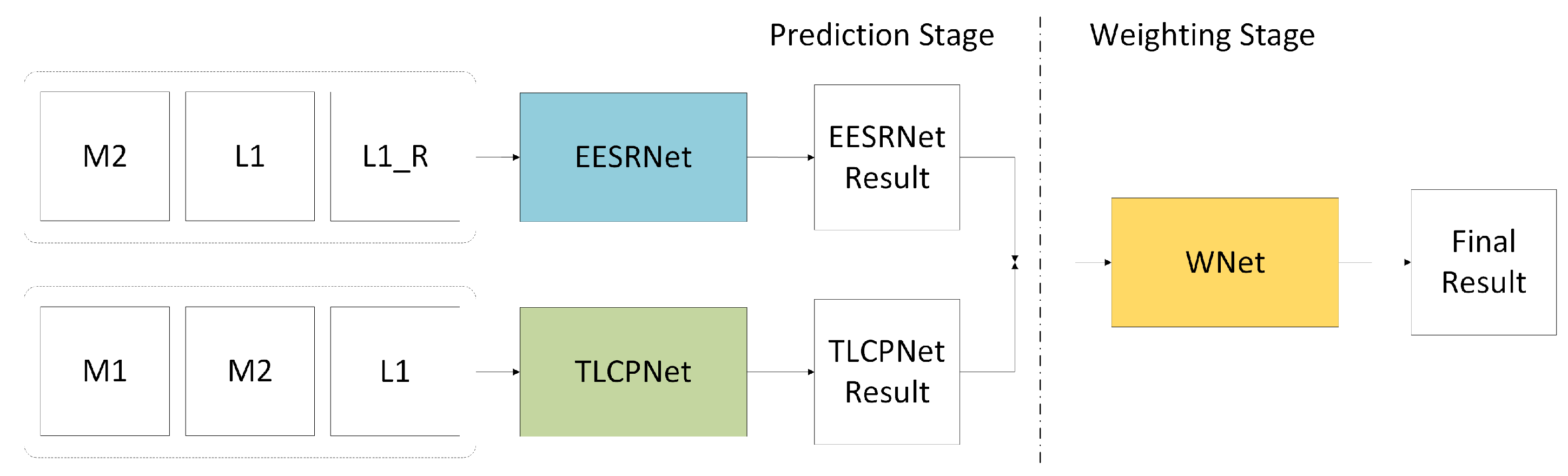
2.1. Method Overview
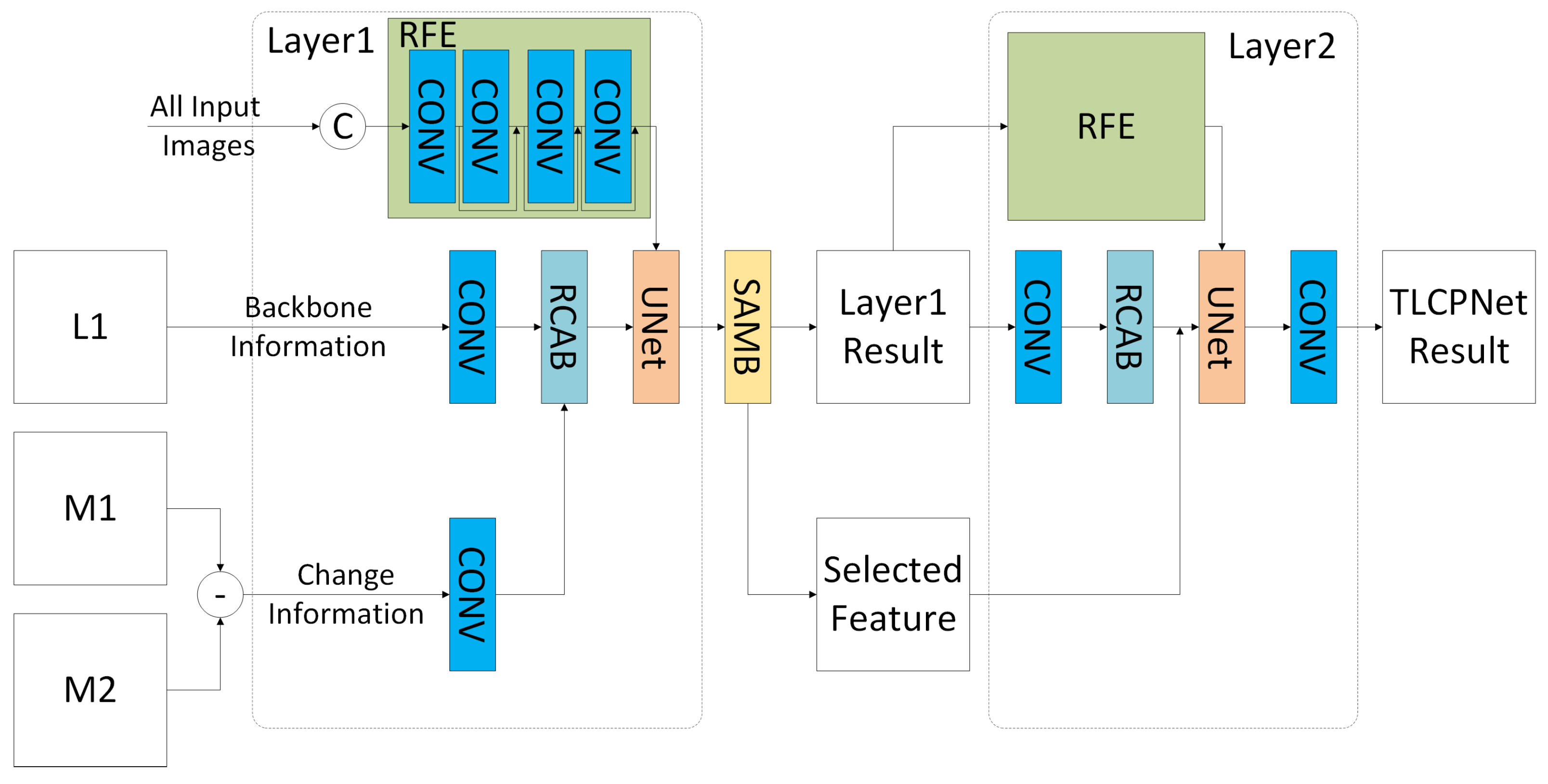
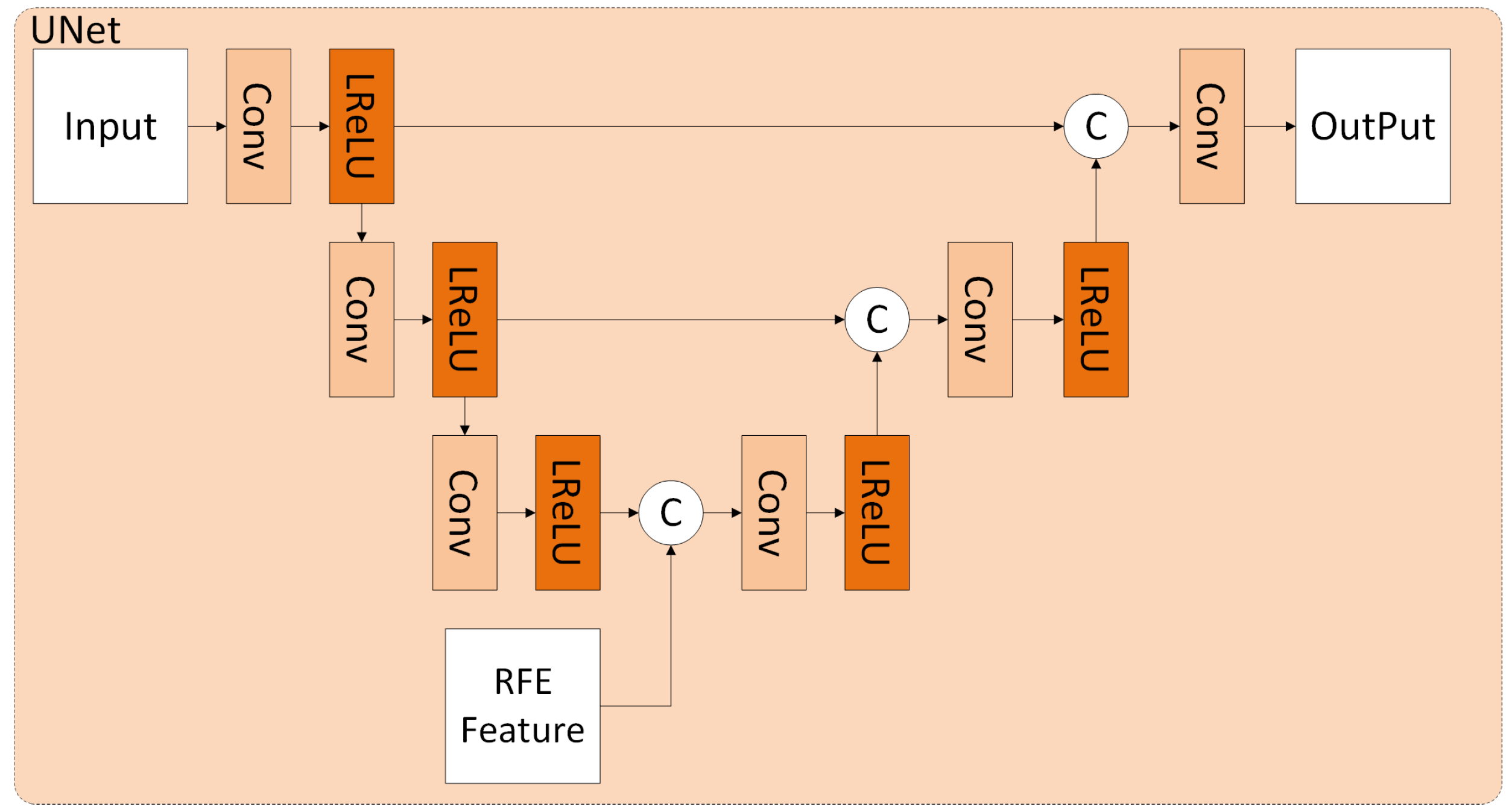
2.2. Edge-Enhanced Remote Sensing Super-Resolution Network with Reference Image

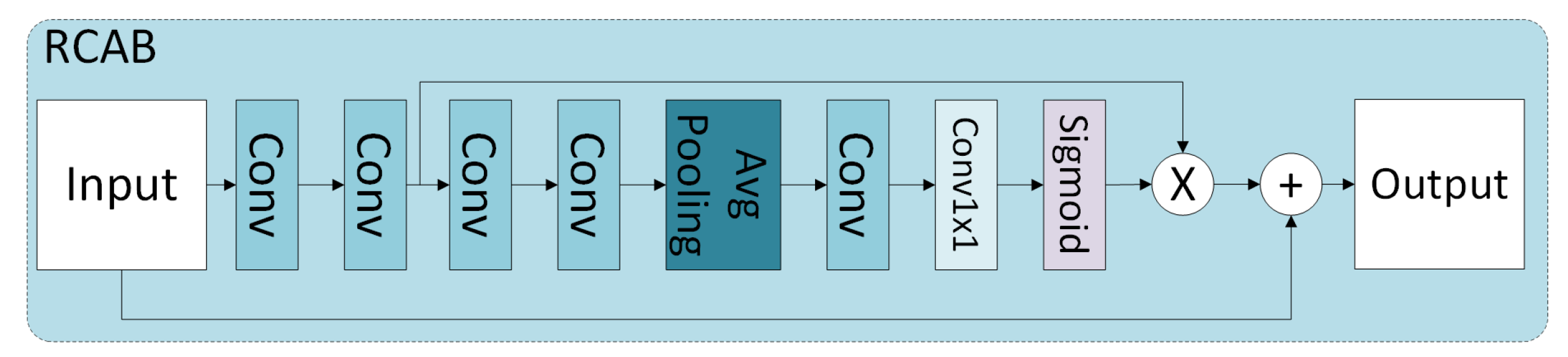
2.3. Two-Layer Change Prediction Network Based on Attention Mechanisms
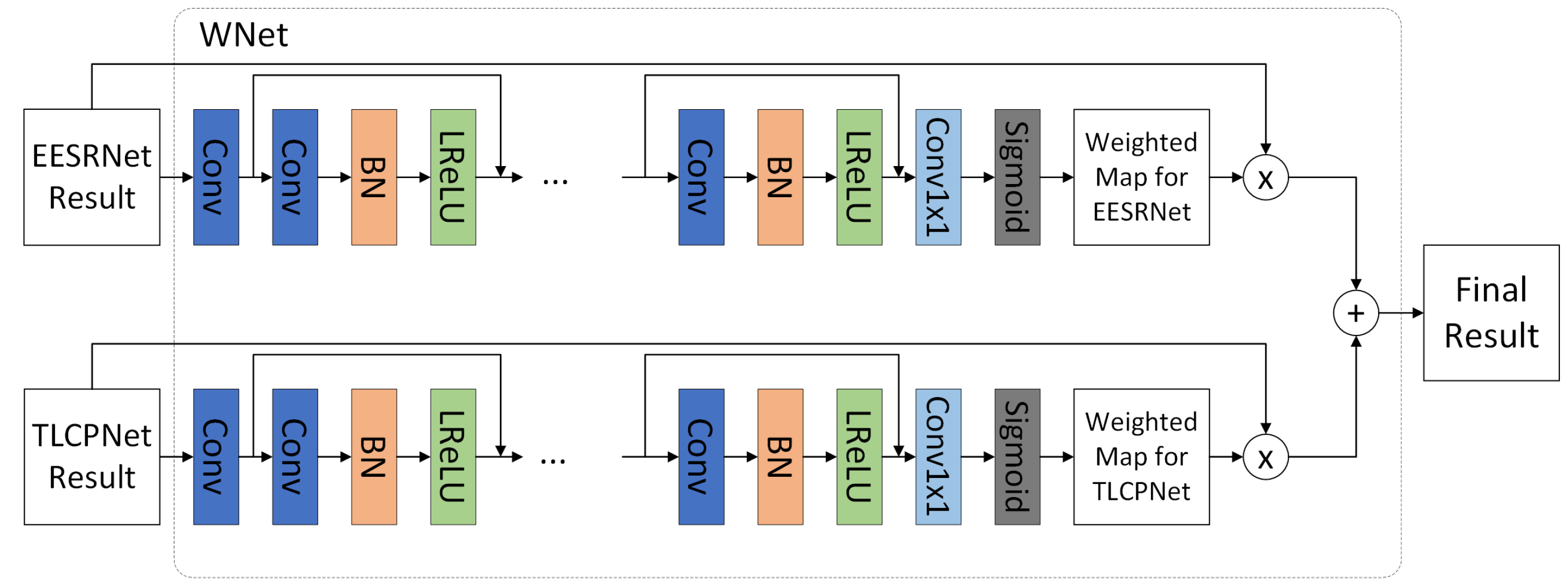
2.4. Weighted Network
2.5. Loss Function
3. Experiment
3.1. Experiment Datasets



3.2. Experiment Design and Evaluation
3.3. Experiment Results
3.3.1. Experiment A: Exploring the Performance of Algorithm in Type Change
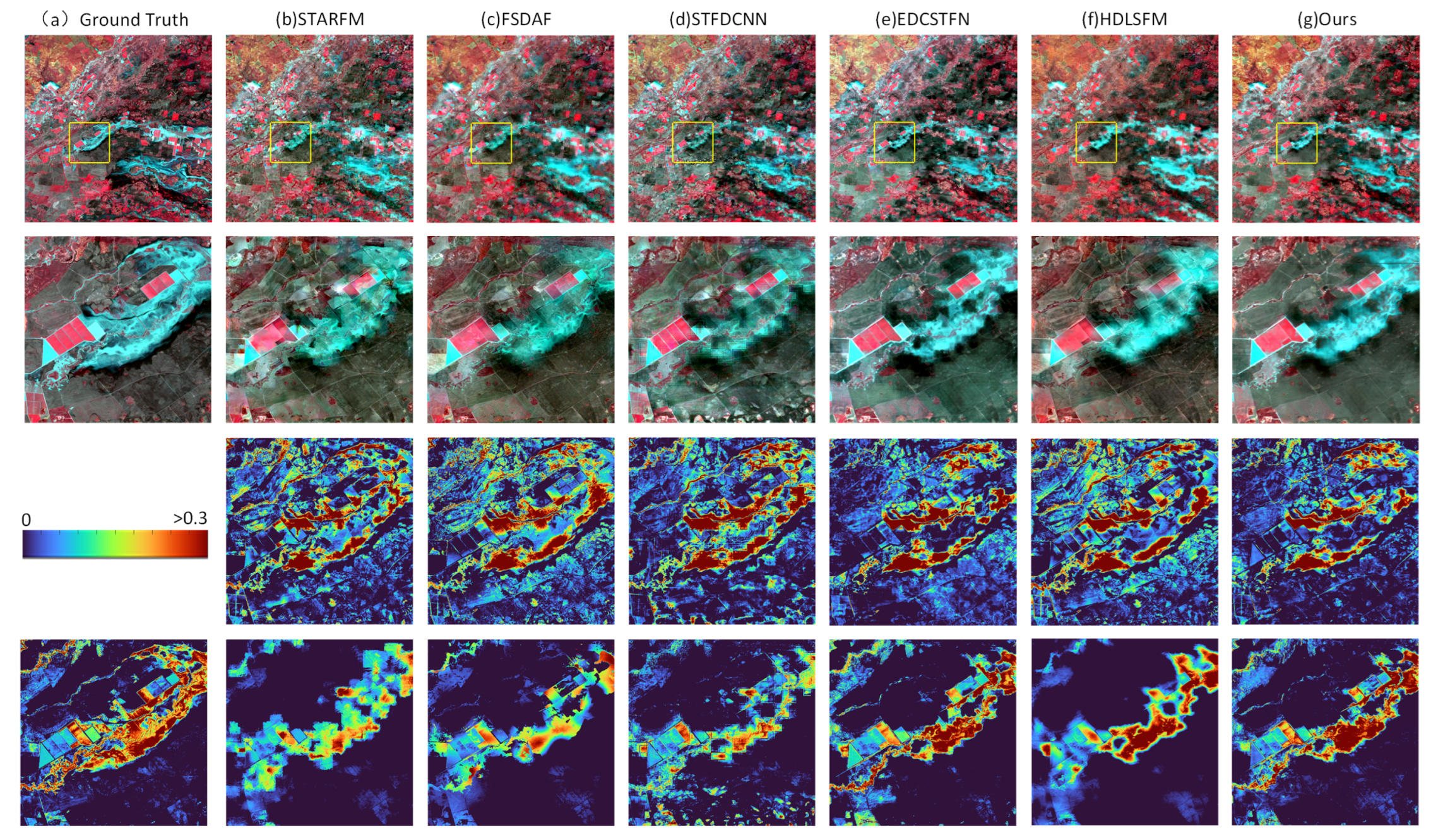
3.3.2. Experiment B: Exploring the Performances of Algorithms in Phenological Changes

3.3.3. Experiment C: Exploring the Performance of the Algorithm in a Heterogeneous Landscape
4. Discussion
4.1. Exploring the Influence of Edge Enhancement on Prediction Results
4.2. Exploring the Influence of Attention Mechanism on Prediction Results
4.3. Comparison with Other STF Algorithms
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shi, C.; Wang, X.; Zhang, M.; Liang, X.; Niu, L.; Han, H.; Zhu, X. A comprehensive and automated fusion method: The enhanced flexible spatiotemporal data fusion model for monitoring dynamic changes of land surface. Appl. Sci. 2019, 9, 3693. [Google Scholar] [CrossRef]
- Shen, Y.; Shen, G.; Zhai, H.; Yang, C.; Qi, K. A Gaussian Kernel-Based Spatiotemporal Fusion Model for Agricultural Remote Sensing Monitoring. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 3533–3545. [Google Scholar] [CrossRef]
- Li, P.; Ke, Y.; Wang, D.; Ji, H.; Chen, S.; Chen, M.; Lyu, M.; Zhou, D. Human impact on suspended particulate matter in the Yellow River Estuary, China: Evidence from remote sensing data fusion using an improved spatiotemporal fusion method. Sci. Total Environ. 2021, 750, 141612. [Google Scholar] [CrossRef] [PubMed]
- Zhu, X.; Cai, F.; Tian, J.; Williams, T.K.A. Spatiotemporal fusion of multisource remote sensing data: Literature survey, taxonomy, principles, applications, and future directions. Remote Sens. 2018, 10, 527. [Google Scholar] [CrossRef]
- Gao, F.; Masek, J.; Schwaller, M.; Hall, F. On the blending of the Landsat and MODIS surface reflectance: Predicting daily Landsat surface reflectance. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2207–2218. [Google Scholar]
- Hilker, T.; Wulder, M.A.; Coops, N.C.; Linke, J.; McDermid, G.; Masek, J.G.; Gao, F.; White, J.C. A new data fusion model for high spatial-and temporal-resolution mapping of forest disturbance based on Landsat and MODIS. Remote Sens. Environ. 2009, 113, 1613–1627. [Google Scholar] [CrossRef]
- Zhu, X.; Chen, J.; Gao, F.; Chen, X.; Masek, J.G. An enhanced spatial and temporal adaptive reflectance fusion model for complex heterogeneous regions. Remote Sens. Environ. 2010, 114, 2610–2623. [Google Scholar] [CrossRef]
- Zhu, X.; Helmer, E.H.; Gao, F.; Liu, D.; Chen, J.; Lefsky, M.A. A flexible spatiotemporal method for fusing satellite images with different resolutions. Remote Sens. Environ. 2016, 172, 165–177. [Google Scholar] [CrossRef]
- Huang, B.; Song, H. Spatiotemporal reflectance fusion via sparse representation. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3707–3716. [Google Scholar] [CrossRef]
- Song, H.; Huang, B. Spatiotemporal satellite image fusion through one-pair image learning. IEEE Trans. Geosci. Remote Sens. 2012, 51, 1883–1896. [Google Scholar] [CrossRef]
- Wu, B.; Huang, B.; Zhang, L. An error-bound-regularized sparse coding for spatiotemporal reflectance fusion. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6791–6803. [Google Scholar] [CrossRef]
- Wei, J.; Wang, L.; Liu, P.; Song, W. Spatiotemporal fusion of remote sensing images with structural sparsity and semi-coupled dictionary learning. Remote Sens. 2016, 9, 21. [Google Scholar] [CrossRef]
- Song, H.; Liu, Q.; Wang, G.; Hang, R.; Huang, B. Spatiotemporal satellite image fusion using deep convolutional neural networks. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 821–829. [Google Scholar] [CrossRef]
- Tan, Z.; Di, L.; Zhang, M.; Guo, L.; Gao, M. An enhanced deep convolutional model for spatiotemporal image fusion. Remote Sens. 2019, 11, 2898. [Google Scholar] [CrossRef]
- Jia, D.; Cheng, C.; Song, C.; Shen, S.; Ning, L.; Zhang, T. A hybrid deep learning-based spatiotemporal fusion method for combining satellite images with different resolutions. Remote Sens. 2021, 13, 645. [Google Scholar] [CrossRef]
- Tan, Z.; Gao, M.; Li, X.; Jiang, L. A flexible reference-insensitive spatiotemporal fusion model for remote sensing images using conditional generative adversarial network. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–13. [Google Scholar] [CrossRef]
- Song, Y.; Zhang, H.; Huang, H.; Zhang, L. Remote Sensing Image Spatiotemporal Fusion via a Generative Adversarial Network with One Prior Image Pair. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–17. [Google Scholar] [CrossRef]
- Lei, D.; Ran, G.; Zhang, L.; Li, W. A Spatiotemporal Fusion Method Based on Multiscale Feature Extraction and Spatial Channel Attention Mechanism. Remote Sens. 2022, 14, 461. [Google Scholar] [CrossRef]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Learning a deep convolutional network for image super-resolution. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; Springer: Berlin/Heidelberg, Germany, 2014; pp. 184–199. [Google Scholar]
- Ledig, C.; Theis, L.; Huszár, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.; Tejani, A.; Totz, J.; Wang, Z.; et al. Photo-realistic single image super-resolution using a generative adversarial network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4681–4690. [Google Scholar]
- Zhang, H.; Song, Y.; Han, C.; Zhang, L. Remote sensing image spatiotemporal fusion using a generative adversarial network. IEEE Trans. Geosci. Remote Sens. 2020, 59, 4273–4286. [Google Scholar] [CrossRef]
- Tan, Z.; Yue, P.; Di, L.; Tang, J. Deriving high spatiotemporal remote sensing images using deep convolutional network. Remote Sens. 2018, 10, 1066. [Google Scholar] [CrossRef]
- Li, W.; Zhang, X.; Peng, Y.; Dong, M. DMNet: A network architecture using dilated convolution and multiscale mechanisms for spatiotemporal fusion of remote sensing images. IEEE Sens. J. 2020, 20, 12190–12202. [Google Scholar] [CrossRef]
- Wang, Q.; Atkinson, P.M. Spatio-temporal fusion for daily Sentinel-2 images. Remote Sens. Environ. 2018, 204, 31–42. [Google Scholar] [CrossRef]
- Zhao, B.; Wu, X.; Feng, J.; Peng, Q.; Yan, S. Diversified visual attention networks for fine-grained object classification. IEEE Trans. Multimed. 2017, 19, 1245–1256. [Google Scholar] [CrossRef]
- Yang, X.; Mei, H.; Zhang, J.; Xu, K.; Yin, B.; Zhang, Q.; Wei, X. DRFN: Deep recurrent fusion network for single-image super-resolution with large factors. IEEE Trans. Multimed. 2018, 21, 328–337. [Google Scholar] [CrossRef]
- Zamir, S.W.; Arora, A.; Khan, S.; Hayat, M.; Khan, F.S.; Yang, M.H.; Shao, L. Multi-stage progressive image restoration. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 14821–14831. [Google Scholar]
- Wang, F.; Jiang, M.; Qian, C.; Yang, S.; Li, C.; Zhang, H.; Wang, X.; Tang, X. Residual attention network for image classification. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 3156–3164. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- Zhao, H.; Gallo, O.; Frosio, I.; Kautz, J. Loss functions for neural networks for image processing. arXiv 2015, arXiv:1511.08861. [Google Scholar]
- Li, J.; Li, Y.; He, L.; Chen, J.; Plaza, A. Spatio-temporal fusion for remote sensing data: An overview and new benchmark. Sci. China Inf. Sci. 2020, 63, 140301. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Khan, M.M.; Alparone, L.; Chanussot, J. Pansharpening quality assessment using the modulation transfer functions of instruments. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3880–3891. [Google Scholar] [CrossRef]
- Yuhas, R.H.; Goetz, A.F.; Boardman, J.W. Discrimination among semi-arid landscape endmembers using the spectral angle mapper (SAM) algorithm. In Proceedings of the JPL, Summaries of the Third Annual JPL Airborne Geoscience Workshop, Pasadena, CA, USA, 1–5 June 1992. Volume 1: AVIRIS Workshop. [Google Scholar]
- Deshpande, A.M.; Patnaik, S. A novel modified cepstral based technique for blind estimation of motion blur. Optik 2014, 125, 606–615. [Google Scholar] [CrossRef]
- Canny, J. A computational approach to edge detection. IEEE Trans. Pattern Anal. Mach. Intell. 1986, 679–698. [Google Scholar] [CrossRef]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16×16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin transformer: Hierarchical vision transformer using shifted windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 10012–10022. [Google Scholar]

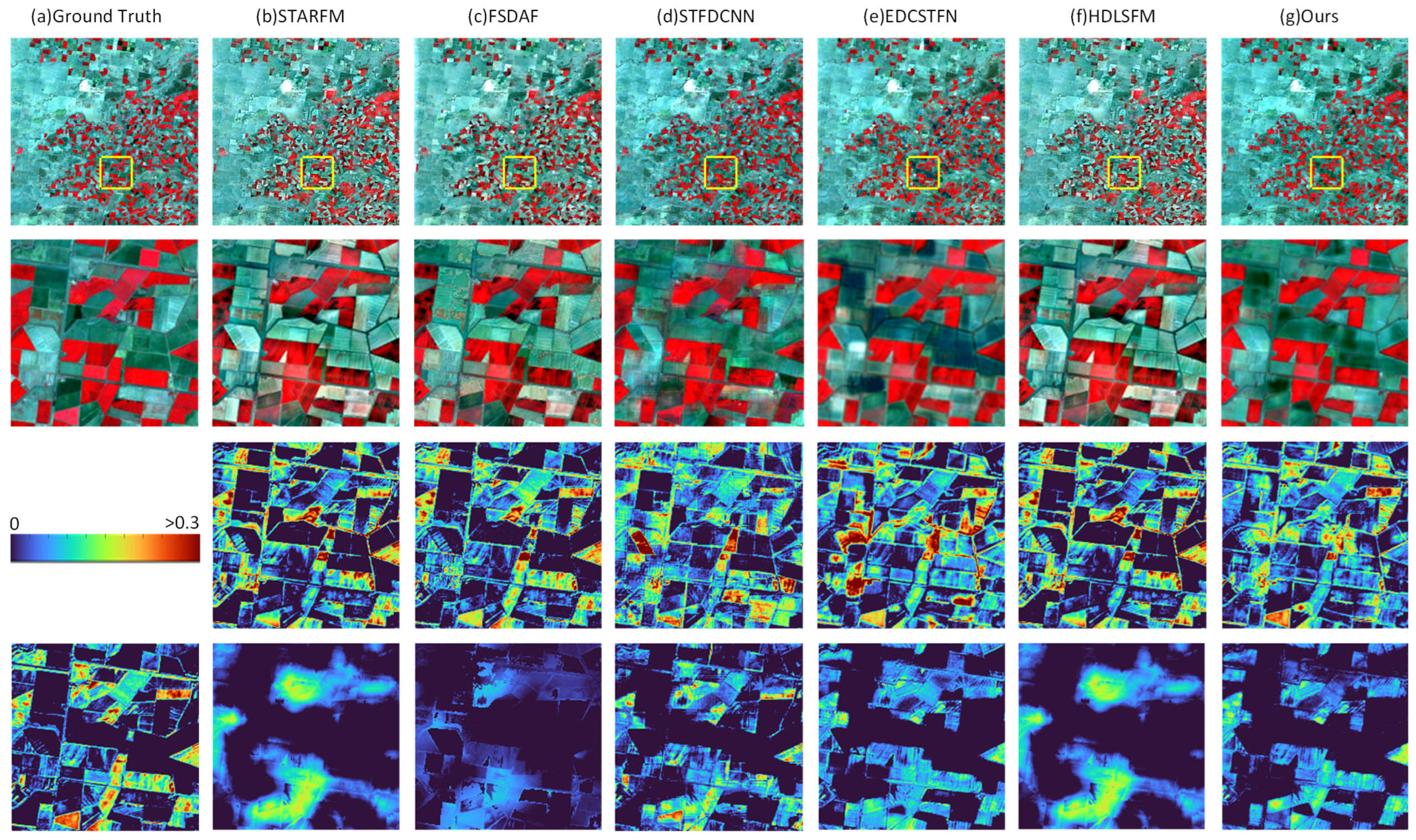


| Band | STARFM | FSDAF | STFDCNN | EDCSTFN | HDLSFM | Ours | |
|---|---|---|---|---|---|---|---|
| RMSE | band1 | 0.0671 | 0.0608 | 0.0577 | 0.0575 | 0.0709 | 0.0495 |
| band2 | 0.0915 | 0.0829 | 0.0803 | 0.0801 | 0.1063 | 0.0701 | |
| band3 | 0.1121 | 0.1018 | 0.0989 | 0.1013 | 0.1306 | 0.0869 | |
| band4 | 0.1638 | 0.1615 | 0.1346 | 0.1509 | 0.1634 | 0.1423 | |
| band5 | 0.2727 | 0.2738 | 0.2180 | 0.2308 | 0.2633 | 0.2206 | |
| band7 | 0.2380 | 0.2396 | 0.1703 | 0.1727 | 0.1983 | 0.1636 | |
| avg | 0.1576 | 0.1534 | 0.1266 | 0.1322 | 0.1555 | 0.1222 | |
| SSIM | band1 | 0.6980 | 0.7218 | 0.7399 | 0.7661 | 0.7028 | 0.7934 |
| band2 | 0.6808 | 0.7115 | 0.7283 | 0.7485 | 0.6712 | 0.7831 | |
| band3 | 0.6861 | 0.7116 | 0.7422 | 0.7459 | 0.6780 | 0.7888 | |
| band4 | 0.7933 | 0.8007 | 0.8510 | 0.8219 | 0.7922 | 0.8267 | |
| band5 | 0.7465 | 0.7388 | 0.8161 | 0.8264 | 0.7740 | 0.8246 | |
| band7 | 0.6756 | 0.6600 | 0.7995 | 0.8176 | 0.7680 | 0.8319 | |
| avg | 0.7134 | 0.7241 | 0.7795 | 0.7877 | 0.7310 | 0.8081 | |
| CC | band1 | 0.7002 | 0.7250 | 0.7416 | 0.7830 | 0.7130 | 0.8059 |
| band2 | 0.6813 | 0.7174 | 0.7345 | 0.7703 | 0.6839 | 0.7993 | |
| band3 | 0.6863 | 0.7186 | 0.7446 | 0.7644 | 0.6921 | 0.8014 | |
| band4 | 0.8059 | 0.8276 | 0.8614 | 0.8329 | 0.7996 | 0.8484 | |
| band5 | 0.7704 | 0.7764 | 0.8247 | 0.8322 | 0.7847 | 0.8368 | |
| band7 | 0.7390 | 0.7438 | 0.8053 | 0.8255 | 0.7819 | 0.8432 | |
| avg | 0.7305 | 0.7515 | 0.7853 | 0.8014 | 0.7425 | 0.8225 | |
| PSNR | band1 | 50.8121 | 51.4574 | 51.7529 | 51.6421 | 50.3942 | 52.7013 |
| band2 | 48.6171 | 49.3067 | 49.5108 | 49.4070 | 47.5024 | 50.3989 | |
| band3 | 47.0945 | 47.8015 | 48.0375 | 47.8118 | 45.9352 | 48.9266 | |
| band4 | 44.1177 | 44.2285 | 45.6888 | 44.7855 | 44.1405 | 45.2478 | |
| band5 | 39.8971 | 39.8665 | 41.7810 | 41.3061 | 40.1913 | 41.6843 | |
| band7 | 41.0475 | 40.9871 | 43.8792 | 43.7893 | 42.5744 | 44.2330 | |
| avg | 45.2643 | 45.6079 | 46.7750 | 46.4570 | 45.1230 | 47.1987 | |
| ERGAS | 4.0797 | 4.0170 | 3.4131 | 3.2708 | 3.8665 | 3.1786 | |
| SAM | 13.8487 | 12.9682 | 8.9418 | 9.1865 | 12.1420 | 8.8463 | |
| Band | STARFM | FSDAF | STFDCNN | EDCSTFN | HDLSFM | Ours | |
|---|---|---|---|---|---|---|---|
| RMSE | band1 | 0.1223 | 0.1219 | 0.0200 | 0.0137 | 0.0237 | 0.0081 |
| band2 | 0.1061 | 0.1058 | 0.0168 | 0.0139 | 0.0195 | 0.0099 | |
| band3 | 0.1429 | 0.1415 | 0.0244 | 0.0168 | 0.0263 | 0.0140 | |
| band4 | 0.1337 | 0.1307 | 0.0348 | 0.0326 | 0.0365 | 0.0244 | |
| avg | 0.1263 | 0.1250 | 0.0240 | 0.0193 | 0.0265 | 0.0141 | |
| SSIM | band1 | 0.5747 | 0.5705 | 0.8878 | 0.9266 | 0.8097 | 0.9644 |
| band2 | 0.6867 | 0.6848 | 0.9519 | 0.9550 | 0.9241 | 0.9712 | |
| band3 | 0.6446 | 0.6454 | 0.9435 | 0.9660 | 0.9131 | 0.9698 | |
| band4 | 0.7845 | 0.7897 | 0.9469 | 0.9530 | 0.9019 | 0.9590 | |
| avg | 0.6726 | 0.6726 | 0.9325 | 0.9501 | 0.8872 | 0.9661 | |
| CC | band1 | 0.4368 | 0.6668 | 0.5658 | 0.6148 | 0.5228 | 0.7177 |
| band2 | 0.6289 | 0.6953 | 0.6571 | 0.7176 | 0.5659 | 0.7598 | |
| band3 | 0.6023 | 0.6512 | 0.5955 | 0.7252 | 0.4847 | 0.7401 | |
| band4 | 0.5864 | 0.6162 | 0.5278 | 0.6844 | 0.4448 | 0.6975 | |
| avg | 0.5636 | 0.6574 | 0.5865 | 0.6855 | 0.5045 | 0.7288 | |
| PSNR | band1 | 18.2502 | 18.2795 | 33.9727 | 37.2373 | 32.4955 | 41.8343 |
| band2 | 19.4867 | 19.5102 | 35.4971 | 37.1236 | 34.2032 | 40.0772 | |
| band3 | 16.9014 | 16.9856 | 32.2522 | 35.5138 | 31.5848 | 37.0757 | |
| band4 | 17.4744 | 17.6777 | 29.1667 | 29.7241 | 28.7553 | 32.2565 | |
| avg | 18.0282 | 18.1132 | 32.7222 | 34.8997 | 31.7597 | 37.8109 | |
| ERGAS | 5.3351 | 5.3112 | 3.8448 | 3.5259 | 3.9795 | 3.1030 | |
| SAM | 20.4020 | 20.3929 | 7.6826 | 3.9386 | 11.1393 | 2.7584 | |
| Band | STARFM | FSDAF | STFDCNN | EDCSTFN | HDLSFM | Ours | |
|---|---|---|---|---|---|---|---|
| RMSE | band1 | 0.1024 | 0.0889 | 0.0757 | 0.0799 | 0.0951 | 0.0692 |
| band2 | 0.1632 | 0.1326 | 0.1038 | 0.1109 | 0.1412 | 0.0974 | |
| band3 | 0.2717 | 0.2079 | 0.1600 | 0.2075 | 0.2276 | 0.1405 | |
| band4 | 0.4716 | 0.3971 | 0.2754 | 0.3417 | 0.4176 | 0.2862 | |
| band5 | 0.3340 | 0.2807 | 0.2659 | 0.2739 | 0.3055 | 0.2625 | |
| band7 | 0.2662 | 0.2336 | 0.2312 | 0.2364 | 0.2443 | 0.2327 | |
| avg | 0.2682 | 0.2235 | 0.1853 | 0.2084 | 0.2385 | 0.1814 | |
| SSIM | band1 | 0.8740 | 0.9005 | 0.9264 | 0.8997 | 0.8898 | 0.9278 |
| band2 | 0.8367 | 0.8823 | 0.9190 | 0.8878 | 0.8662 | 0.9169 | |
| band3 | 0.8337 | 0.8906 | 0.9261 | 0.9080 | 0.8699 | 0.9365 | |
| band4 | 0.5863 | 0.6618 | 0.8574 | 0.8023 | 0.6250 | 0.8567 | |
| band5 | 0.9062 | 0.9311 | 0.9371 | 0.9241 | 0.9205 | 0.9357 | |
| band7 | 0.9269 | 0.9416 | 0.9431 | 0.9344 | 0.9375 | 0.9384 | |
| avg | 0.8273 | 0.8680 | 0.9182 | 0.8927 | 0.8515 | 0.9187 | |
| CC | band1 | 0.8816 | 0.9045 | 0.9278 | 0.9108 | 0.8929 | 0.9352 |
| band2 | 0.8517 | 0.8889 | 0.9194 | 0.9056 | 0.8720 | 0.9266 | |
| band3 | 0.8557 | 0.8993 | 0.9264 | 0.9163 | 0.8803 | 0.9402 | |
| band4 | 0.5865 | 0.6716 | 0.8591 | 0.8032 | 0.6351 | 0.8572 | |
| band5 | 0.9075 | 0.9312 | 0.9372 | 0.9332 | 0.9211 | 0.9443 | |
| band7 | 0.9272 | 0.9416 | 0.9432 | 0.9409 | 0.9377 | 0.9464 | |
| avg | 0.8350 | 0.8729 | 0.9189 | 0.9017 | 0.8565 | 0.9250 | |
| PSNR | band1 | 52.0626 | 52.8371 | 53.8265 | 53.2995 | 52.1282 | 53.7872 |
| band2 | 48.9261 | 50.2918 | 52.0281 | 51.7482 | 49.8488 | 52.4045 | |
| band3 | 45.1920 | 47.2700 | 49.0842 | 47.1689 | 46.5798 | 49.8942 | |
| band4 | 40.6068 | 42.0486 | 45.0620 | 43.2943 | 41.6327 | 44.7219 | |
| band5 | 43.4576 | 44.8760 | 45.3143 | 45.0985 | 44.1878 | 45.4340 | |
| band7 | 45.2783 | 46.2860 | 46.3466 | 46.0842 | 45.9509 | 46.2221 | |
| avg | 45.9206 | 47.2682 | 48.6103 | 47.7823 | 46.7214 | 48.7440 | |
| ERGAS | 2.9060 | 2.6700 | 2.3985 | 2.5402 | 2.8036 | 2.3886 | |
| SAM | 5.8321 | 4.8365 | 3.9851 | 4.7364 | 5.4252 | 3.7658 | |
| With Edge Enhancement | Without Edge Enhancement | |||||
|---|---|---|---|---|---|---|
| LGC | AHB | CIA | LGC | AHB | CIA | |
| RMSE | 0.1222 | 0.0141 | 0.1814 | 0.1275 | 0.0169 | 0.1986 |
| SSIM | 0.8081 | 0.9661 | 0.9187 | 0.7972 | 0.9580 | 0.8995 |
| CC | 0.8225 | 0.7288 | 0.9250 | 0.8133 | 0.6751 | 0.9055 |
| PSNR | 47.1987 | 37.8109 | 48.7440 | 46.8941 | 36.6753 | 48.1105 |
| ERGAS | 3.1786 | 3.1030 | 2.3886 | 3.2134 | 3.2536 | 2.4739 |
| SAM | 8.8463 | 2.7584 | 3.7658 | 9.1642 | 3.1826 | 4.3976 |
| With Attention Mechanism | Without RCAB | Without SAMB | |||||||
|---|---|---|---|---|---|---|---|---|---|
| LGC | AHB | CIA | LGC | AHB | CIA | LGC | AHB | CIA | |
| RMSE | 0.1222 | 0.0141 | 0.1814 | 0.1238 | 0.0170 | 0.1989 | 0.1245 | 0.0197 | 0.2080 |
| SSIM | 0.8081 | 0.9661 | 0.9187 | 0.8047 | 0.9532 | 0.8907 | 0.8018 | 0.9360 | 0.8997 |
| CC | 0.8225 | 0.7288 | 0.9250 | 0.8179 | 0.6951 | 0.9019 | 0.8150 | 0.6884 | 0.9066 |
| PSNR | 47.1987 | 37.8109 | 48.7440 | 47.1112 | 36.1273 | 48.0364 | 47.0286 | 34.5176 | 47.7171 |
| ERGAS | 3.1786 | 3.1030 | 2.3886 | 3.2001 | 3.3196 | 2.4484 | 3.2071 | 3.5358 | 2.4360 |
| SAM | 8.8463 | 2.7584 | 3.7658 | 8.8418 | 2.9602 | 4.3116 | 8.9166 | 2.8246 | 4.2420 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, S.; Guo, Q.; Cao, Y. WDBSTF: A Weighted Dual-Branch Spatiotemporal Fusion Network Based on Complementarity between Super-Resolution and Change Prediction. Remote Sens. 2022, 14, 5883. https://doi.org/10.3390/rs14225883
Fang S, Guo Q, Cao Y. WDBSTF: A Weighted Dual-Branch Spatiotemporal Fusion Network Based on Complementarity between Super-Resolution and Change Prediction. Remote Sensing. 2022; 14(22):5883. https://doi.org/10.3390/rs14225883
Chicago/Turabian StyleFang, Shuai, Qing Guo, and Yang Cao. 2022. "WDBSTF: A Weighted Dual-Branch Spatiotemporal Fusion Network Based on Complementarity between Super-Resolution and Change Prediction" Remote Sensing 14, no. 22: 5883. https://doi.org/10.3390/rs14225883
APA StyleFang, S., Guo, Q., & Cao, Y. (2022). WDBSTF: A Weighted Dual-Branch Spatiotemporal Fusion Network Based on Complementarity between Super-Resolution and Change Prediction. Remote Sensing, 14(22), 5883. https://doi.org/10.3390/rs14225883