Abstract
Nowadays, Space Information Networks represented by the satellite internet are developing rapidly. For example, the Starlink of SpaceX plans to provide network access services worldwide and has drawn much attention. To operate and maintain Space Information Networks, e.g., performing collision avoidance maneuvers and forensic investigation, statistic information on networks such as the average of orbital inclination needs to be shared with analysts. However, for some particular reasons, such as safety or confidentiality, accurate information on networks cannot be shared with analysts. To solve this contradiction, we design a differentially private mechanism for the Space Information Network so that the entities of a network can keep accurate information privacy while sharing statistic information. In particular, we extend differentially private mechanisms based on personalized sampling to distributed communication systems such as Space Information Networks. In comparison with other mechanisms, the proposed mechanism has better data utility. Moreover, the proposed mechanism has a hierarchical privacy guarantee. In particular, there are differences between the privacy guarantees made between system entities and between the system and the user.
1. Introduction
Revolutionary distributed communication infrastructures called Space Information Networks (SINs) are made up of satellites, stratospheric airships, unmanned aerial vehicles (UAV), and other platforms. SINs are distinct from multi-layered satellite networks. They are heterogeneous integrated information networks, including terrestrial Internet, Deep Space Network (DSN), Near-Earth Network (NEN), and satellite networks as the backbone. As a result, they have a variety of unique characteristics, such as heterogeneous network integration, dynamically changing network topology, extraordinarily long and variable propagation latency, asymmetrical forward and reverse link capacities, high bit error rate, intermittent link connectivity, lack of fixed communication resources, good network scalability, etc. Applications of SINs include satellite location, navigation, timing, and Internet access, in addition to satellite communication and remote sensing. SINs intend to achieve the networking and integration of space satellite systems, efficiently arrange the system’s nodes via satellite-terrestrial and interstellar linkages, and increase the system’s adaptability, mobility, and intelligence. Due to Space Information Networks’ advantages such as long-distance message delivery, they have been applied to many scenarios, including emergency communications, marine operations, aircraft communications, specific military missions, and so on [1]. Space Information Networks have developed rapidly in recent years. For example, dozens of satellite internet emerge such as SpaceX’s Starlink [2], the British government’s OneWeb [3], and Amazon’s Kuiper [4]. So far, the Starlink has more than 1700 active satellites, and it plants to increase its bandwidth from 150 Mbps to 300 Mbps at the end of 2021.
Privacy issues emerge in the process of maintaining Space Information Networks. In particular, some information on Space Information Networks needs to be shared for the sake of operation and maintenance, but accurate information should not be shared for the sake of safety. For example, the location of satellites needs to be public so that the user knows which satellite and how many satellites are available. However, the accurate location of satellites needs to be private in case the adversary attacks satellites for particular reasons such as political issues. Similarly, other statistical information such as the average of power consumption, the number of active satellites, and so on also needs to be available for analysts so that they can analyze the operation of the satellites, but for safety reasons, these analysts do not have to know the information on an individual satellite.
Differential privacy a technology that allows data analysis while keeping individuals’ information private. In particular, differential privacy allows analysts to analyze statistic information such as average, frequency, and standard deviation, while it keeps the individuals’ information private. In this paper, we design a differentially private mechanism for distributed communication systems such that entities of systems can communicate with each other while their privacy is protected. Although we take the Space Information Networks as an example, the proposed differentially private mechanism also can be applied into other distributed communication systems such as edge computing, ad-hoc networks, and so on.
1.1. Related Works
In distributed communication systems, for example Space Information Networks, the deluge of data generated by the terminal poses a serious threat to its privacy. The distributed communications systems have advantages that every entity can control its own data. Distributed communication systems also need to consider privacy protection in their foundations so that they can provide user-centric support for privacy [5].
Many technologies have been applied to distributed communication systems to solve privacy issues. For example, the secure multi-party computation was used to protect the privacy of transform protocols [6,7]. Blockchain technology was introduced into satellite communication networks to solve privacy issues [8]. Homomorphic encryption was used by the nodes in distributed communication systems to perform integer operations (additions only or additions and multiplications) in a privacy-preserving manner to calculate the average of their integer initial values [3]. Deep learning of layer-partitioned training with step-wise activation functions was used to safeguard sensitive information [9].
Compared with cryptography tools such as secure multi-party computation, differential privacy is a promising technology, which can solve privacy problems of distributed communication systems with the lower power consumption. Differential privacy was proposed by Dwork et al. from a sequence of papers [10,11,12]. Then, differential privacy was extended to local differential privacy [13] so that it can be used in a distributed architecture. However, local differential privacy suffered from low data utility [14]. To improve the utility, many new concepts were proposed such as elastic sensitivity [15], record sensitivity [16]. Furthermore, many other technologies were combined to differential privacy to improve its data utility. Anonymous communication such as Mix Networks [17] was combined to differential privacy to improve data utility [18,19]. Sampling technology was introduced into differential privacy by Nissim et al. [20]. Wen et al. introduced personalized sampling into differential privacy to further improve the data utility of differential privacy [21,22].
Compared to the previous work, we extend differentially private mechanisms based on personalized sampling to distributed communication systems such as Space Information Network. On the one hand, through comparing with other mechanisms, the proposed mechanism has better data utility. On the other hand, the proposed mechanism has a hierarchical privacy guarantee.
1.2. Organization
The first section gives a quick summary of how geographic information networks are currently progressing as well as the significance of privacy protection problems in these networks. Additionally, Section 1 provides a quick summary of the related work that has been completed thus far. Section 2 of the background information is where the Space Information Networks and differential privacy are briefly discussed. In Section 3, the proposed mechanism is elaborated. The suggested differential privacy protection system is presented in Section 3. In Section 4, the experiment’s fourth component is given. In Section 5, conclusions are offered.
2. Background Knowledge
2.1. Space Information Networks
The coined SINs paradigm is an integrated high-speed self-organizing hyper network consisting of terrestrial ground-based information networks, e.g., Internet, mobile communication networks, sensor networks, etc., and space-and deep space-based entities within outer space, e.g., satellites, robotic spacecraft, crewed vehicles, rovers, landers, sensors, etc., to provide maximum network capacity [23,24]. The Space Information Network consists of the space-based backbone network, space-based access network, and ground-based node network. Its structure is shown in Figure 1a. The space-based backbone network consists of GEO (Geosynchronous Earth Orbit) satellites and their laser links. The space-based backbone network is responsible for remote transmission, control, and data exchange. The space-based access network consists of air floating platforms and LEO (Low Earth Orbit) satellites. The space-based access network provides access for many communication systems’ entities including specialized sub-networks, entities in near space, air-based entities, ground-based entities, sea-based entities and so on. The ground-based node network comprises ground stations (gateways), internet, and mobile telecommunication networks.
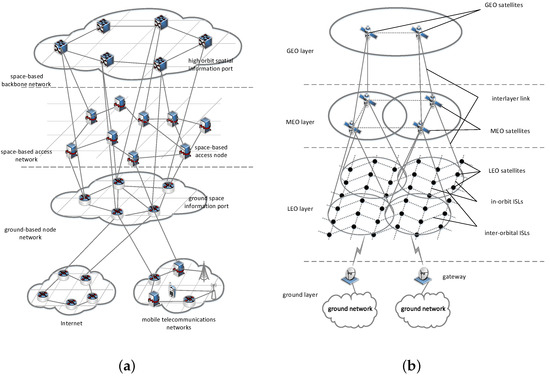
Figure 1.
Networking structure of Space Information Networks. (a) is architecture of space information network. (b) is topological structure of space information network.
The complete Space Information Network is made up of GEO satellites, MEO (Medium Earth Orbit), and LEO satellites, as shown in Figure 1b. GEO satellites make up the majority of the space-based backbone network because they are required for broadcasting events. LEO and MEO satellites serve as the space-based access networks since they are required for real-time services. SpaceX’s project Starlink provides high-speed Internet service via LEO communication satellites. In this paper, experiments are considered on 1665 satellites of Starlink in a two-line element set, which CelesTrak collects.
2.2. Differential Privacy
Differential privacy is a method of protecting data sharing. It may be accomplished by withholding personally identifiable information about particular people and just giving statistical data that can be used to define the database as a whole. Differential privacy is the theory that if the impact of inserting a single random replacement in the database is tiny enough, the query result cannot be utilized to infer a lot about a specific person and so offers privacy. The following is a formal definition of differential privacy.
The two output distributions derived for a randomized algorithm A acting on two neighboring data sets, D and , are identical. The randomized algorithm indicates that given a specific input, the algorithm’s output is not a fixed value but follows a particular probability distribution.
Differential privacy is also the state-of-the-art technology of privacy preservation. There are various differentially private mechanisms for various application scenarios. It is not only in SINs but also in other scenarios in healthcare, finance, insurance, and public safety, where differential privacy technologies are needed to protect clients’ private information. For instance, a significant proportion of CTs collected by patients are awaiting analysis and diagnosis by physicians because of the recent COVID-19 pandemic. Based on CT pictures, an AI system may assess whether a patient has COVID-19 (positive or negative). The hospital gives computer vision technology-equipped third-party professional organization access to the tagged data, which includes the patient’s name, gender, and even address. It would compromise the patient’s privacy and maybe breach various data protection laws and regulations while significantly increasing the diagnosis’s accuracy and effectiveness. Differentiated privacy aims to safeguard patient privacy while developing deep-learning models for hospitals. Google employs localized differential privacy to gather data on the Chrome browser used by more than 14 million people daily. Apple safeguards user privacy on iOS and macOS via localized differential privacy approaches. The sampling and aggregation method, the Laplace mechanism for distributed systems, and other differentially private techniques that may be used in a distributed setting are the main topics of this work.
Laplace mechanism [25]. The outcome of the Laplace mechanism M is Equation (2) for a given database D, a query q, and privacy budget .
Here, is the privacy budget, which controls the privacy guarantee of differentially private mechanisms. Specifically, the privacy guarantee is stronger when the value of privacy budget is smaller. represents a number (which is named noise in the context of differential privacy) from the Laplace distribution with location parameter 0 and scale parameter . Global sensitivity, also known as , measures the largest difference brought on by the presence or absence of a single data record.
Global sensitivity [21]. The global sensitivity indicated by for a given database D and query q may be determined using Equation (3).
Here, is the dataset that is different from D on only one data record.
Sample and aggregation mechanism. The sample and aggregation mechanism based on random sampling method was proposed by Nissim et al. [22]. This mechanism is shown in Figure 2. The target queries are calculated across each of the n subsets of the dataset. An aggregation function computes the outcome in a way that satisfies differential privacy.
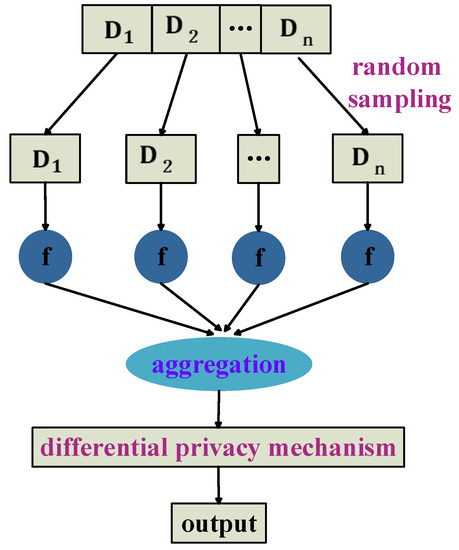
Figure 2.
Sample and aggregation mechanism.
3. Proposed Mechanism
Differentiating privacy strategies are applied to address the privacy leakage issue brought on by a minor change in the data source. It should consider that the nodes in SINs are exposed to an open space environment and produce a significant quantity of remote sensing data. Owners of satellites, observers, and attackers may mine and analyze the remote sensing data to get important information. However, remote sensing data may include sensitive user information, and for end users, the danger of acute information exposure or leakage emerges if the info above affects privacy or security. Therefore, preventing the leakage of remote sensing data while allowing for data sharing after differential privacy processing may promote remote sensing data mining. Therefore, this section elaborates the proposed mechanism. First, the simplified system structure of Space Information Network is introduced. Then, the proposed mechanisms is elaborated. Finally, analyses of privacy guarantee are given.
3.1. System Structure
The system structure diagram of Space Information Network is shown in Figure 3. The Space Information Network has three entities including the user, the master satellite, and satellites.
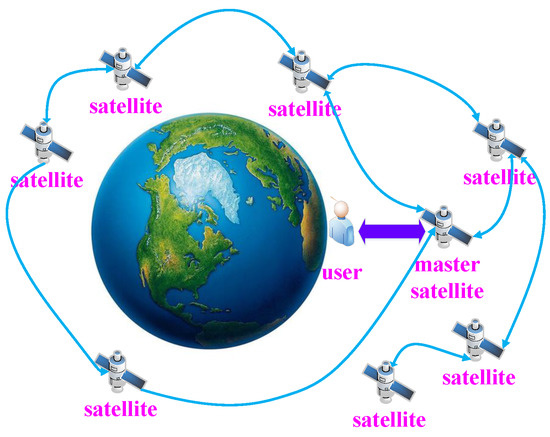
Figure 3.
System structure diagram of this work.
The user is the person who uses the Space Information Network. The user can be operation and maintenance personnel who send management commands such as counting query to figure out how many satellites are active. The user can also be someone who uses the Space Information Network to communicate.
Master satellite is the satellite that is directly connected to the user. In the Space Information Network, satellites keep moving and many of them are out of the user’s reach. Thus, the user’s messages or commands need a satellite to forward such that these messages or commands can be sent to satellites out of reach. In the context of this paper, the satellite which is responsible for interacting with the user is named the master satellite.
Satellites are components of the Space Information Network. Satellites execute specific functions such as calculating queries sent by the user.
3.2. Proposed Differentially Private Mechanism
In order to safeguard the privacy of the Space Information Networks, this study integrates customized sampling technology into local differentially private processes and makes use of distributed noise. Based on personalized sampling and distributed noise, this paper proposes a new differentially private mechanism with high data utility. Figure 4 shows how the proposed mechanism handles queries from the user.
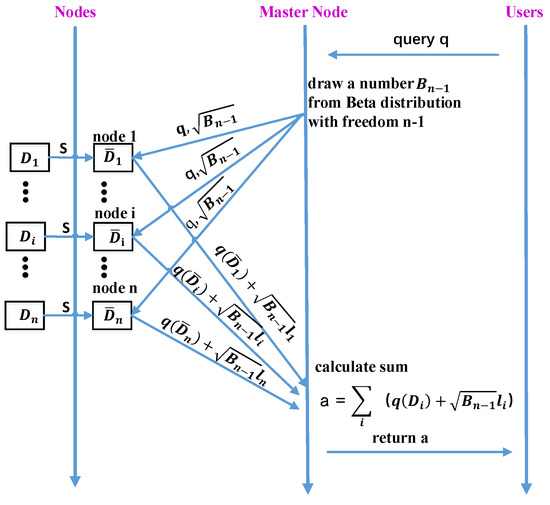
Figure 4.
The process of proposed mechanism handles queries from the user.
In particular, the user sends a query q to the master satellite. Then, the master satellite draws a number obeying the Beta distribution. The master satellite sends the query q together with the square root of drawn number to other satellites.
The number is used to generate a number obeying a particular Laplace distribution in a distributed way. Specifically, generating a number obeying a particular Laplace distribution can be simulated by generating other numbers obeying the same Laplace distribution, as defined by the following formula [26]
Notably, the target Laplace distribution’s mean needs to be zero. The number follows the Beta distribution and has a probability density function . is the same for every satellite so it is generated and distributed by the master satellite in the proposed mechanism.
When receiving a query q together with a number from the master satellite, the ith satellite calculates each record’s sampling probability in his dataset . The complete process of the proposed differentiated private mechanism M can be represented by the following Algorithm 1 pseudo-code.
| Algorithm 1 Proposed differentially private mechanism M |
|
It is necessary to provide the sample probability for each data record in order to increase the data usefulness of the suggested technique. To offset the largest change brought on by the existence or absence of a single data record, noise is injected in differentially private techniques. The suggested technique provides a comparatively lesser sample probability to data records, which causes a relatively higher difference on queries’ results if these data records are available, in order to decrease the necessary noise. In order to measure the impact of the presence or absence of any particular record on the outcomes of the queries, we first propose a notion called local record sensitivity.
Definition 1 (Local record sensitivity).
Assume that x represents a single record in the database . The local record sensitivity of the record x for dataset of the ith satellite and query q is Equation (5).
The specific formula of calculating sampling probability of record is
Here, is named balance parameter, which is used to maximize the utility of the proposed mechanism, and it may be determined using Equation (7) if the original dataset is and the dataset generated by sampling is [21,22].
Here, represents the set of data records with . is the error boundary.
The ith satellite samples the dataset into through the sampling process S with calculated sampling probabilities and calculates . The ith satellite then generates a number with probability density function and obeys the Laplace distribution, where . Finally, the ith satellite calculates and then sends to the master satellite.
After receiving from all n satellites, the master satellite calculates and returns the calculated sum to the user as the answer to the query submitted by the user.
Notably, the query q is the linear query. For the linear query, the following Equation (8)
holds provided that . This equation makes it possible to calculate the correct answer to query by the master satellite through returned values , , ⋯, , ⋯, .
For the non-linear query, the proposed differentially private mechanism also works if existing an aggregation function f such that
The characteristic of the non-linear query determines which aggregation function should be used. The average function, mod function, median function, and other aggregation functions are often employed.
3.3. Privacy Analyses
This subsection analyzes the proposed mechanism in terms of the privacy guarantee. In particular, Theorem 1 analyzes the privacy guarantee aspect to the user, and Theorem 2 analyzes the privacy guarantee between each satellite and the master satellite.
Theorem 1.
The proposed mechanism M is a ϵ differentially private mechanism.
Proof.
For the output a of the proposed mechanism M, we have
Let and . Due to the linear property of query q, we have
The record x is in a dataset, as indicated by the index . For instance, the record x in is indicated by the notation . The record x is not in a dataset, as shown by the index . Record x, for instance, is not in , which is shown by . In the case when the dataset acquired by the sampling procedure S is , let represent the output a.
When x is in , we have
Therefore,
Let . l complies with probability density function and the Laplace distribution. Therefore,
Similarly, when x is not in , we have
Therefore, we have
For the symmetry, we have
Let . Without loss of generality, we assume . For the proposed mechanism M, we have
For , the . We have
For , the we have
Therefore, we have
Because of the symmetry, we have
Consequently, the suggested mechanism M is a distinct private mechanism that complies with . □
Theorem 2.
The output of each satellite satisfies differential privacy.
Proof.
For output of ith satellite, we have
The record x is indicated by the index of datasets as being in those datasets, while the record x is indicated by the index as not being in those datasets.
In the event that the dataset acquired from by sampling procedure S is , let represent the output . We have Equation (24) when record x is present in dataset .
Due to complies with probability density function and the Laplace distribution, where . Therefore,
Similarly, When a record x is not in dataset , we have
Therefore, we have
Let represent local differentially private mechanism used by the ith satellite. We have
For , the we have
For , the we have
Therefore, we have
For the symmetry, we have
Therefore, the mechanism is a differentially private mechanism. That is, the output of each satellite satisfies differential privacy. □
According to Theorem 1 and Theorem 2, the proposed mechanism is hierarchical in terms of privacy guarantee. Specifically, the privacy guarantee between each satellite and the master satellite is . Moreover, the privacy guarantee between the whole system and the user is .
4. Experiments
The sampling and aggregation mechanism, the Laplace mechanism, and the suggested mechanism are three differentially private mechanisms that are compared in this section. The robustness of these processes is another major topic in this area. This section specifically looks at the effects of the number of subgroups and the amount of records in each subset.
4.1. Datasets and Experimental Setup
The dataset used in experiments is on 1665 satellites of Starlink in two-line element set, which is collected by CelesTrak. CelesTrak provides SOCRATES-Satellite Orbital Conjunction Reports Assessing Threatening Encounters in Space as a service to the satellite operator community. On 24 March 2005, Air Force Space Command gave CelesTrak the go-ahead to offer TLEs in support of SOCRATES. A list of an object’s orbital components is encoded using the TLE (Two-Line Element set) data format. TLE data can be used to estimate the state(position and velocity) of satellites. Therefore, by foreseeing the orbital pathways of space debris in the future, TLE data are utilized to perform risk analysis, close approach analysis, collision avoidance measures, and forensic investigation. The TLE consists of three rows of data, and each row has 69 characters. The first row has a satellite’s name; the second and third rows provide information on the satellite, including its orbital inclination, ascending node’s right ascension, perigee’s argument, orbital eccentricity, semi-major axis, true anomaly, etc.
The used queries in experiments are the average function and standard deviation function. They were picked because many real-world application situations make use of them. The standard deviation function is non-linear, whereas the average function is linear. The values of privacy budget are from 0.1 to 0.5, which are suitable values in most application scenarios in terms of privacy preservation. The root means square error (RMSE) is used in the experiments in this part as a standard for comparing errors. RMSE is the squared sum of the squared root of the mean difference between the value of the function without privacy protection and the value of the position that received privacy protection. A smaller RMSE indicates better data utility as opposed to a bigger RMSE.
4.2. Results and Discussion
The first experiment focuses on the influence of the number of records in each subset. The chosen values of the number of records in each subset are 50, 100, and 150. The experiment was repeated 500 times, and the average outcome was determined. The experiment results are shown in Figure 5.
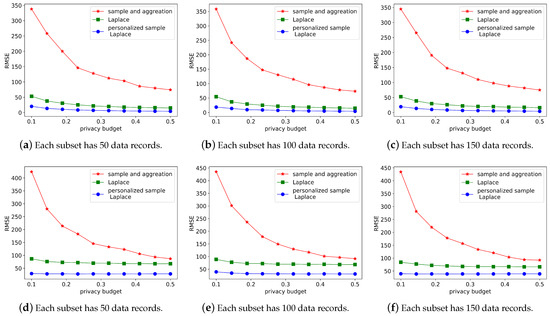
Figure 5.
The influences of the number of records in each subset.
The results of Figure 5 show that the proposed method has greater data usefulness than the other two techniques. No matter how many data records are in each subset, when the privacy budget is 0.1, the RMSE of the mechanism proposed in this paper is half of the Laplace mechanism and much lower than that of the sampling and aggregation mechanisms. As would be predicted, the inaccuracy diminishes as the privacy budget increases. The comparison between Figure 5a–c shows that the resilience of the three techniques, and that the amount of records in each subgroup practically has no affects on the inaccuracy.
The effects of the subset size are the main topic of the second experiment. Figure 6 displays the test’s findings. The suggested mechanism outperforms the other two mechanisms in terms of data usefulness, according to the findings of the experiment. The number of subgroups affects the Laplace mechanism because of the comparisons between Figure 6a–c and Figure 6d–f. The error decreases as the number of subsets increases. The sample and aggregation mechanism is not robust enough for the standard deviation function. In particular, the error fluctuates as the number of subsets increases.
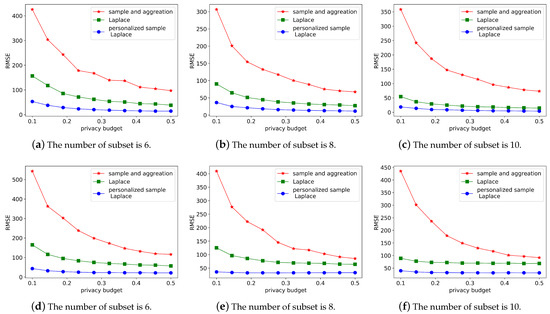
Figure 6.
The influences of the number of subsets.
The related RMSE deterioration rates for various subsets and their data records for linear and nonlinear query functions are shown in Table 1 and Table 2, respectively. Since the proposed mechanism and the other two mechanisms in the comparison have a similar pattern of change, it virtually has the same data used as the other two mechanisms. It demonstrates the resilience of the method this research proposes. The technique suggested in this research is deployable for actual SINs because of the robustness illustrated by the experimental findings.

Table 1.
RMSE degradation rates corresponding to linear and nonlinear query functions for different data records.

Table 2.
RMSE degradation rates corresponding to linear and nonlinear query functions for different subset number.
5. Conclusions
In this paper, we design a differential privacy mechanism for distributed communication systems and demonstrate the proposed mechanism with the example of space information networks. Comparing the proposed mechanism to Laplace, sampling, and aggregation mechanisms reveals that it is more beneficial for data. Additionally, the technique allows network nodes to exchange statistical data while preserving correct information privacy. 1665 Starlink satellites are used in this paper’s investigations on a bilinear element set gathered by CelesTrak. By comparing the suggested mechanism to existing mechanisms, it is discovered that it has superior data usefulness, excellent robustness and stability. Just as differential privacy can be applied to many fields, it can also be used to other distributed communication systems, not only space information networks, for solving privacy data problems.
Author Contributions
Conceptualization, M.Z. and W.H.; methodology, M.Z. and W.H.; software, W.H.; validation, M.Z.; formal analysis, W.H.; investigation, L.L. and Z.T.; resources, S.Z.; data curation, M.Z.; writing—original draft preparation, W.H. and M.Z.; writing—review and editing, M.Z. and W.H.; visualization, Z.T.; supervision, S.Z.; project administration, S.Z.; funding acquisition, S.Z. and L.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by 1. The General Program of Sichuan Provincial Department of Science and Technology (Grant No. 2022YFG0207). 2. National Natural Science Foundation of China (Grant No. 62272089). 3. The Open Project of Intelligent Terminal Key Laboratory of Sichuan Province, P.R.China (Grant No. SCITLAB-20006). 4. Intelligent Terminal Key Laboratory of Sichuan Province (Grant No. SCITLAB-20001). 5. The Cooperative Program of Sichuan University and Yibin (2020CDYB-30).
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- “New Infrastructure” White Paper on the Development of China’s Satellite Internet Industry. China Center for Information Industry Development & SINA 5G. 2020. Available online: https://n2.sinaimg.cn/tech/cbc3161f/20200528/SatelliteInternetWhitePaper.pdf (accessed on 8 June 2022).
- Chamikara, M.A.P.; Bertok, P.; Khalil, I.; Liu, D.; Camtepe, S. Privacy preserving distributed machine learning with federated learning. Comput. Commun. 2021, 171, 112–125. [Google Scholar] [CrossRef]
- Hadjicostis, C.N. Privacy-Preserving Distributed Averaging via Homomorphically Encrypted Ratio Consensus. IEEE Trans. Autom. Control. 2020, 65, 3887–3894. [Google Scholar] [CrossRef]
- Boyle, A. Amazon to offer broadband access from orbit with 3236-satellite ‘Project Kuiper’constellation. Geek Wire, 4 April 2019. Available online: https://mobility21.cmu.edu/amazon-to-offer-broadband-access-from-orbit-with-3236-satellite-project-kuiper-constellation/ (accessed on 8 June 2022).
- Cavoukian, A. Privacy by design: The 7 foundational principles. Inf. Priv. Comm. Ont. Can. 2009, 5, 12. [Google Scholar]
- Shen, Y.; Pearson, S. Privacy Enhancing Technologies: A Review. Hewlet Packard Development Company Disponible. Available online: https://bitly/3cfpAKz.2011 (accessed on 8 June 2022).
- Hemenway, B.; Lu, S.; Ostrovsky, R.; Welser Iv, W. High-precision secure computation of satellite collision probabilities. In Security and Cryptography for Networks, Proceedings of the International Conference on Security and Cryptography for Networks, Amalfi, Italy, 31 August–2 September 2016; Springer: Cham, Switzerland, 2016; pp. 169–187. [Google Scholar]
- Li, C.; Sun, X.; Zhang, Z. Effective Methods and Performance Analysis of a Satellite Network Security Mechanism Based on Blockchain Technology. IEEE Access 2021, 9, 113558–113565. [Google Scholar] [CrossRef]
- Yu, C.H.; Chou, C.N.; Chang, E. Distributed Layer-Partitioned Training for Privacy-Preserved Deep Learning. In Proceedings of the 2019 IEEE Conference on Multimedia Information Processing and Retrieval (MIPR), San Jose, CA, USA, 28–30 March 2019; pp. 343–346. [Google Scholar]
- Dinur, I.; Nissim, K. Revealing information while preserving privacy. In Proceedings of the Twenty-Second ACM SIGMOD-SIGACT-SIGART Symposium on Principles of Database Systems, San Diego, CA, USA, 9–11 June 2003; pp. 202–210. [Google Scholar]
- Dwork, C.; Nissim, K. Privacy-preserving datamining on vertically partitioned databases. In Advances in Cryptology—CRYPTO 2004, Proceedings of the Annual International Cryptology Conference, Santa Barbara, CA, USA, 15–19 August 2004; Springer: Berlin/Heidelberg, Germany, 2004; pp. 528–544. [Google Scholar]
- Blum, A.; Dwork, C.; McSherry, F.; Nissim, K. Practical privacy: The SuLQ framework. In Proceedings of the Twenty-Fourth ACM SIGMOD-SIGACTSIGART Symposium on Principles of Database Systems, Baltimore, MD, USA, 13–15 June 2005; pp. 128–138. [Google Scholar]
- Kasiviswanathan, S.P.; Lee, H.K.; Nissim, K.; Raskhodnikova, S.; Smith, A. What can we learn privately? Siam J. Comput. 2011, 40, 793–826. [Google Scholar] [CrossRef]
- McSherry, F.; Talwar, K. Mechanism design via differential privacy. In Proceedings of the 48th Annual IEEE Symposium on Foundations of Computer Science (FOCS’07), Providence, RI, USA, 21–23 October 2007; pp. 94–103. [Google Scholar]
- Johnson, N.; Near, J.P.; Song, D. Towards practical differential privacy for SQL queries. Proc. VLDB Endow. 2018, 11, 526–539. [Google Scholar] [CrossRef]
- Huang, W.; Zhou, S.; Liao, Y.; Chen, H. An Efficient Differential Privacy Logistic Classification Mecha-nism. IEEE Internet Things J. 2019, 6, 10620–10626. [Google Scholar] [CrossRef]
- Chaum, D.L. Untraceable electronic mail, return addresses, and digital pseudonyms. Commun. ACM 1981, 24, 84–90. [Google Scholar] [CrossRef]
- Erlingsson, U.; Feldman, V.; Mironov, I.; Raghunathan, A.; Talwar, K.; Thakurta, A. Amplification by shuffling: From local to central differential privacy via anonymity. In Proceedings of the Thirtieth Annual ACM-SIAM Symposium on Discrete Algorithms, San Diego, CA, USA, 6–9 January 2019; SIAM: Philadelphia, PA, USA, 2019; pp. 2468–2479. [Google Scholar]
- Cheu, A.; Smith, A.; Ullman, J.; Zeber, D.; Zhilyaev, M. Distributed differential privacy via shuffling. In Advances in Cryptology—EUROCRYPT 2019, Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, Darmstadt, Germany, 19–23 May 2019; Springer: Cham, Switzerland, 2019; pp. 375–403. [Google Scholar]
- Nissim, K.; Raskhodnikova, S.; Smith, A. Smooth sensitivity and sampling in private data analysis. In Proceedings of the Thirty-Ninth Annual ACM Symposium on Theory of Computing, San Diego, CA, USA, 11–13 June 2007; pp. 75–84. [Google Scholar]
- Huang, W.; Zhou, S.; Zhu, T.; Liao, Y.; Wu, C.; Qiu, S. Improving Laplace Mechanism of Differential Privacy by Personalized Sampling. In Proceedings of the 2020 IEEE 19th International Conference on Trust, Security and Privacy in Computing and Communications (TrustCom), Guangzhou, China, 29 December–1 January 2020; pp. 623–630. [Google Scholar]
- Huang, W.; Zhou, S.; Zhu, T.; Liao, Y. Privately Publishing Internet of Things Data: Bring Personalized Sampling into Differentially Private Mechanisms. IEEE Internet Things J. 2021, 9, 80–91. [Google Scholar] [CrossRef]
- Zhang, L.; Zhou, X. Hop-by-Hop Dynamic Congestion Control with Contact Interruption Probability for Intermittently Connected Deep Space Information Networks. Wireless Pers. Commun. 2013, 71, 399–424. [Google Scholar] [CrossRef]
- Zhuo, M.; Liu, L.; Zhou, S.; Tian, Z. Survey on security issues of routing and anomaly detection for space information networks. Sci. Rep. 2021, 11, 22261. [Google Scholar] [CrossRef] [PubMed]
- Huang, W.; Zhou, S.; Liao, Y. Unexpected Information Leakage of Differential Privacy Due to the Linear Property of Queries. IEEE Trans. Inf. Forensics Secur. 2021, 16, 3123–3137. [Google Scholar] [CrossRef]
- Goryczka, S.; Xiong, L.; Sunderam, V. Secure multiparty aggregation with differential privacy: A comparative study. In Proceedings of the Joint EDBT/ICDT 2013 Workshops, Genoa, Italy, 18–22 March 2013; pp. 155–163. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).