3.1. Research Concept and Methodology
Physical methods yield accurate results but require many parameters. Moreover, the equation solving process is complicated and cannot be easily realized using conventional methods. Statistical methods are simple to implement and widely used in practice. However, these methods exhibit a low generality (portability). Most physical methods cannot describe and represent all situations and need to be supplemented by statistical methods. In general, if a system of equations is solvable, then a fully connected DL-NN can approximate the curve of any complex equation solution. Furthermore, DL can simultaneously solve statistical methods if the input parameters (dimensions) and output parameters of the statistical methods are consistent with those of the physical methods. Therefore, we used DL to couple physical and statistical methods to exploit the advantages of the different methods and overcome the shortcomings of traditional methods.
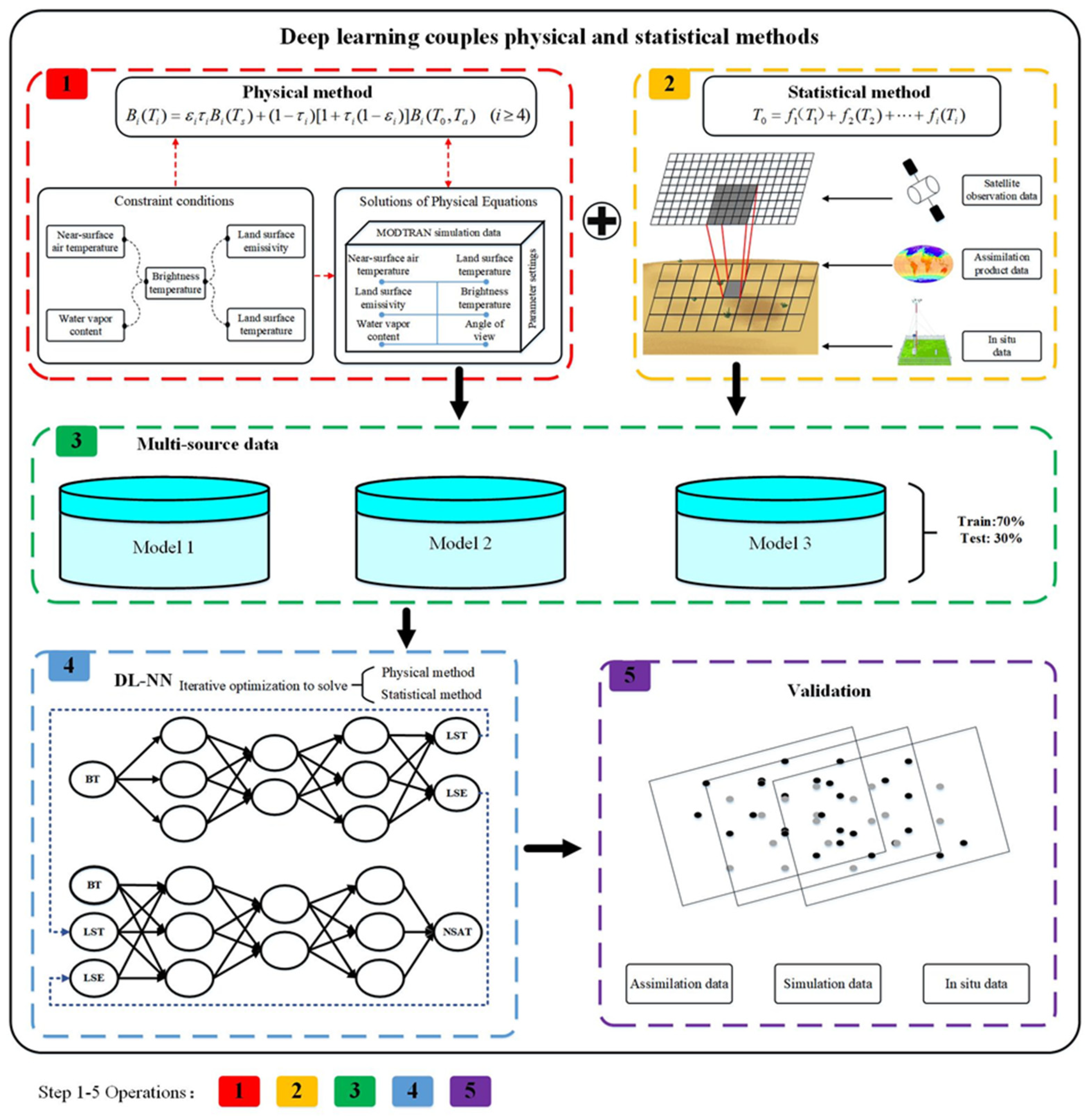
The framework of the PS-DL method is shown in
Figure 2. Step 1 (dashed red rectangle) involves the physical method based on the radiative transfer energy balance equation. A physical forward model system is constructed, and the classical MODTRAN model is implemented to simulate the radiative transfer processes to obtain the solution of the physical equation system. Step 2 (dashed yellow rectangle) involves the statistical method, in which high-precision data from the assimilation model, in situ meteorological observations, and satellite BT data are used to generate a high-precision statistical database. In Step 3, the solutions of the physical method are combined with the solutions of high-precision statistical methods to build training and testing databases for DL. In order to improve the retrieval accuracy of near-surface air temperature, we first retrieve LST and LSE, and then use LST and LSE as prior knowledge to further retrieve NSAT, and these improve the information of the NSAT signal and enhance the retrieval accuracy. In Step 4, DL is used to optimize and solve the physical and statistical methods to achieve the required accuracy through repeated training and testing. Step 5 involves the validation and application of the preceding operations.
3.2. Physical Method
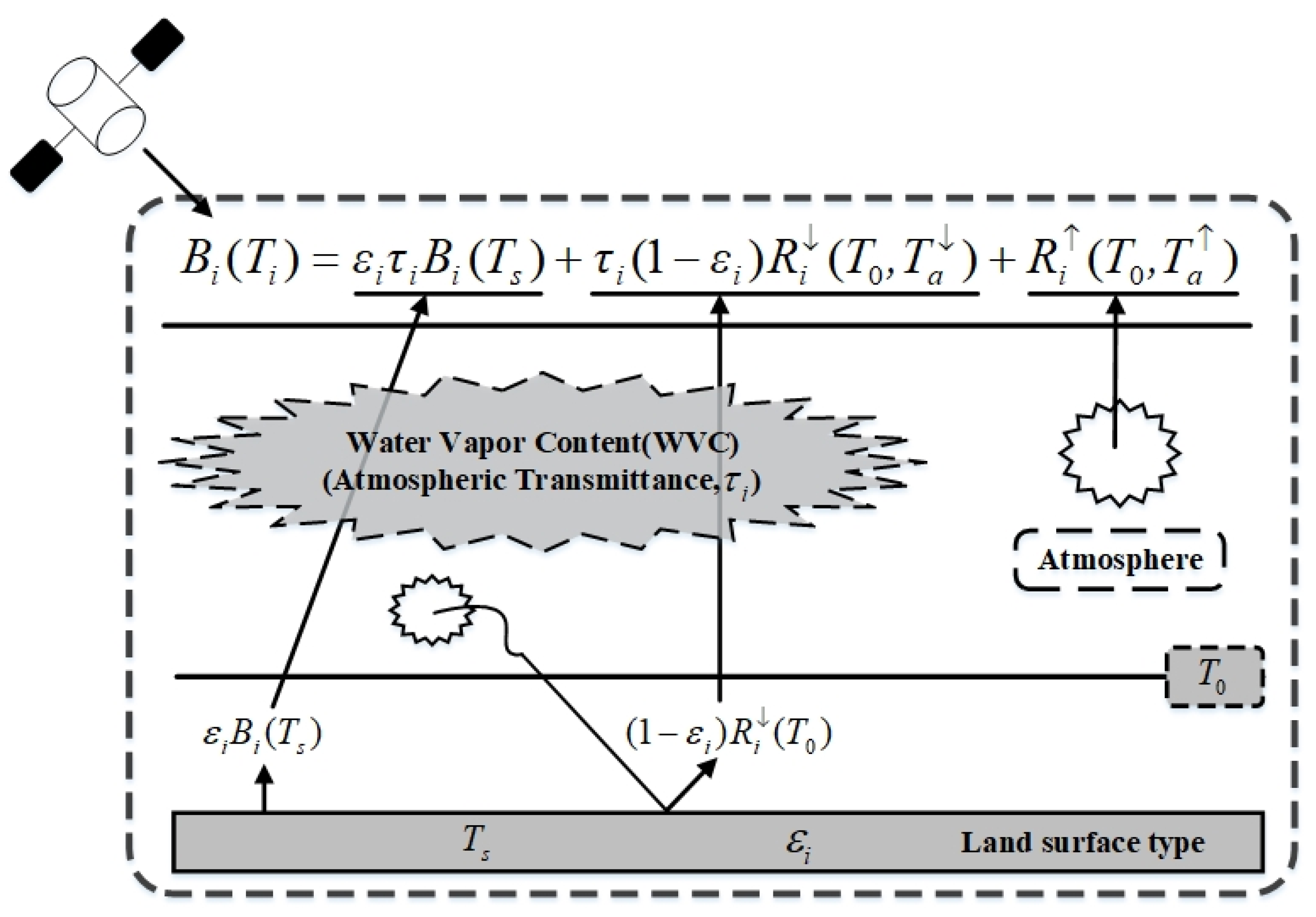
The physical method for NSAT is established based on the thermal radiance of the ground and its transfer from the ground and near-surface air to the remote sensor. The radiation transfer process is shown in
Figure 3. The theoretical basis for the remote sensing of NSAT is that the near-surface air exchanges energy with the ground surface and atmospheric profile owing to the temperature difference and transmits the radiation through the atmosphere to the sensor. The type of surface influences the surface radiation, resulting in different intensities of energy exchange with the near-surface air. Therefore, the inversion equation must consider the effect of the surface type (LSE). In other words, the LST influences the NSAT, which in turn affects the atmospheric profile temperature. Surface and near-surface energy is absorbed by the atmosphere, especially, by the water vapor, as it travels through the atmosphere to the sensor [
40]. The spectral distribution of radiation emitted from the ground and near the surface depends on the wavelength. The simplified radiation energy balance equation is presented as Equation (1).
where
is the thermal radiance received by the sensor in band
i;
is the satellite BT;
is the LSE for band
i;
is the atmospheric transmittance of band
i;
is the radiance emitted by the surface;
is the LST;
and
represent the downwelling and upwelling atmospheric radiation of band
i, respectively;
is the NSAT; and
, and
denote the downwelling and upwelling effective mean temperature of the atmosphere, respectively.
The atmospheric upwelling radiation
can be expressed as in Equation (2) [
41,
42]:
where
is the atmospheric temperature at elevation
h,
H is the sensor height, and
is the atmospheric upwelling transmittance between elevations
h and
H. Equation (3) can be obtained by solving Equation (2) using the mean value theorem [
41,
42].
The atmospheric downwelling radiation
can be considered an integral of the atmospheric radiation from a hemispherical direction and can be expressed as in Equation (4) [
41,
42].
where
is the direction angle of the atmospheric downwelling radiation,
represents the elevation of the top of the Earth’s atmosphere (km), and
represents the atmospheric downwelling transmittance from elevation z to the surface. According to Franc and Cracknell (1994) [
41], in clear sky conditions, the upwelling and downwelling transmittances can be considered equal for each thin layer of the atmosphere, i.e.,
. Equation (5) can be obtained using the mean value theorem of integrals:
Therefore, the atmospheric downwelling radiation can be defined as in Equation (6).
The substitution of Equations (3) and (6) into Equation (1) yields Equation (7)
Here,
and
represent the average atmospheric temperatures. Qin et al. (2001) analyzed these two variables and noted no substantial difference in the solution when the two variables were combined to generate one variable.
The key contribution of atmospheric radiation pertains to the bottom layer of the atmosphere [
43]. According to the derivation analysis, a nearly linear relationship (Equation (9)) exists between the NSAT and average temperature of the atmosphere in the given conditions [
42]. According to the reciprocity theory, a similar relationship exists between the NSAT and satellite BT (Equation (10)) [
44].
where
and
are coefficients,
and
are constants, and
is the satellite BT for band
i. The coefficients in Equations (9) and (10) vary across regions and seasons. Therefore, one variable (
) can be substituted for the other (
Ta) to decrease the unknowns in Equation (8). This analysis shows that although a certain constraint relationship exists between the different temperature variables in the energy balance equation, this relationship cannot be strictly determined, which introduces uncertainties in the calculation process of traditional methods.
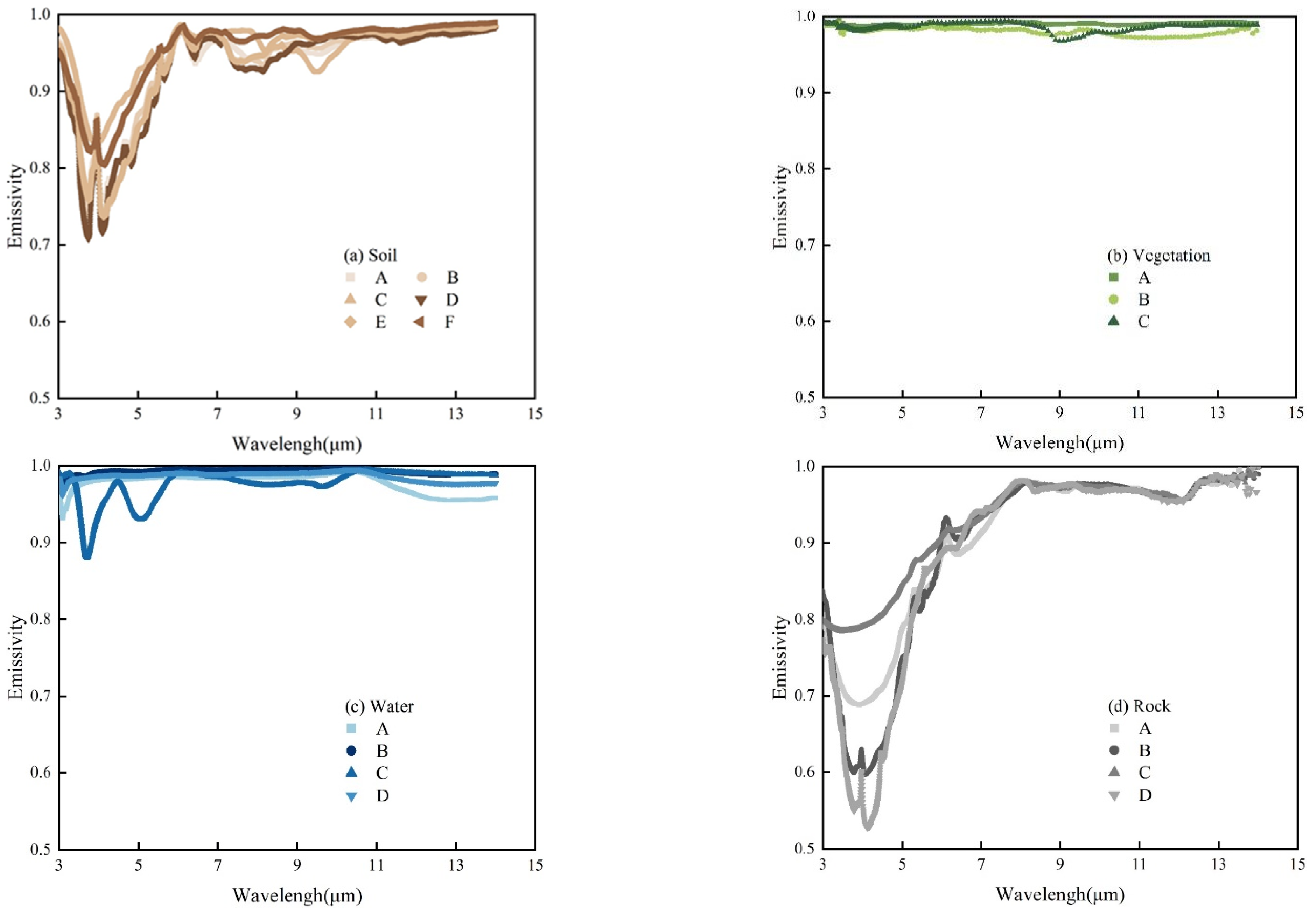
The LSE represents the magnitude of radiant energy absorbed and emitted by the ground surface, which is related to the surface type, surface roughness, and water content. The measured values vary with the wavelength and viewing angle. In general, the spectral curve is unique for each surface type, and thus, if the surface type of a pixel is known, the LSE for each band can be obtained. Therefore, it is reasonable to assume that the LSE for all bands can be reduced to an unknown parameter with respect to the surface type, as shown in Equation (11).
The atmospheric transmittance (
) in the energy balance equation (Equation (8)) is affected by the atmospheric water vapor and other gases. In general, the WVC undergoes significant fluctuations, whereas the content of other gases (O) remains relatively stable. Therefore, only the atmospheric WVC needs to be determined to obtain the transmittance at different wavelengths. As shown in Equation (12), the transmittance of different wavelength bands can be summarized as a function of the atmospheric WVC.
Equation (10) contains four unknowns (LST, NSAT, atmospheric WVC, and surface type). If the physical method is used to invert the NSAT, at least four thermal infrared bands are needed to construct four radiative transfer equations. According to the simulation analysis, the thermal radiation energy emitted by the surface accounts for 75% of the energy received by the sensor when the atmospheric transmittance is higher than 0.65. Consequently, the NSAT inversion algorithm that directly uses the thermal infrared band is not adequately accurate, and thermal infrared remote sensing is more suitable for retrieving the surface temperature. To enhance the accuracy and versatility of the NSAT inversion algorithm, we first invert the LST and LSE and then use the LST and LSE as prior knowledge to further invert the NSAT. Equation (8) indicates that if the atmospheric WVC is known, the NSAT can be retrieved using the three thermal infrared bands. Additionally, if the surface temperature and atmospheric WVC are known, the NSAT can be retrieved using the two thermal infrared bands. The MODTRAN model can obtain as many solutions of equations as possible by setting the variation ranges of parameters such as the surface temperature, air temperature, and atmospheric state under clear sky conditions. The solutions of physical and statistical methods constitute the training and test data for DL, and DL optimization can then be performed to solve the inversion equations.
3.4. DL
In recent years, DL has been widely used in many fields and received considerable attention from the remote sensing community. However, DL techniques are typically regarded as a black box, and the physical mechanism remains to be clarified [
23,
45,
46,
47]. As discussed in
Section 3.1, DL can be used to couple physical and statistical algorithms. Moreover,
Section 3.2 and
Section 3.3 describe the sufficient conditions for physical and statistical methods to optimize calculations with DL techniques, which can render the use of DL physically meaningful. Many researchers have presented the principles and technical details associated with the use of DL in the inversion of geophysical parameters and the surface temperature [
48,
49]. As shown in
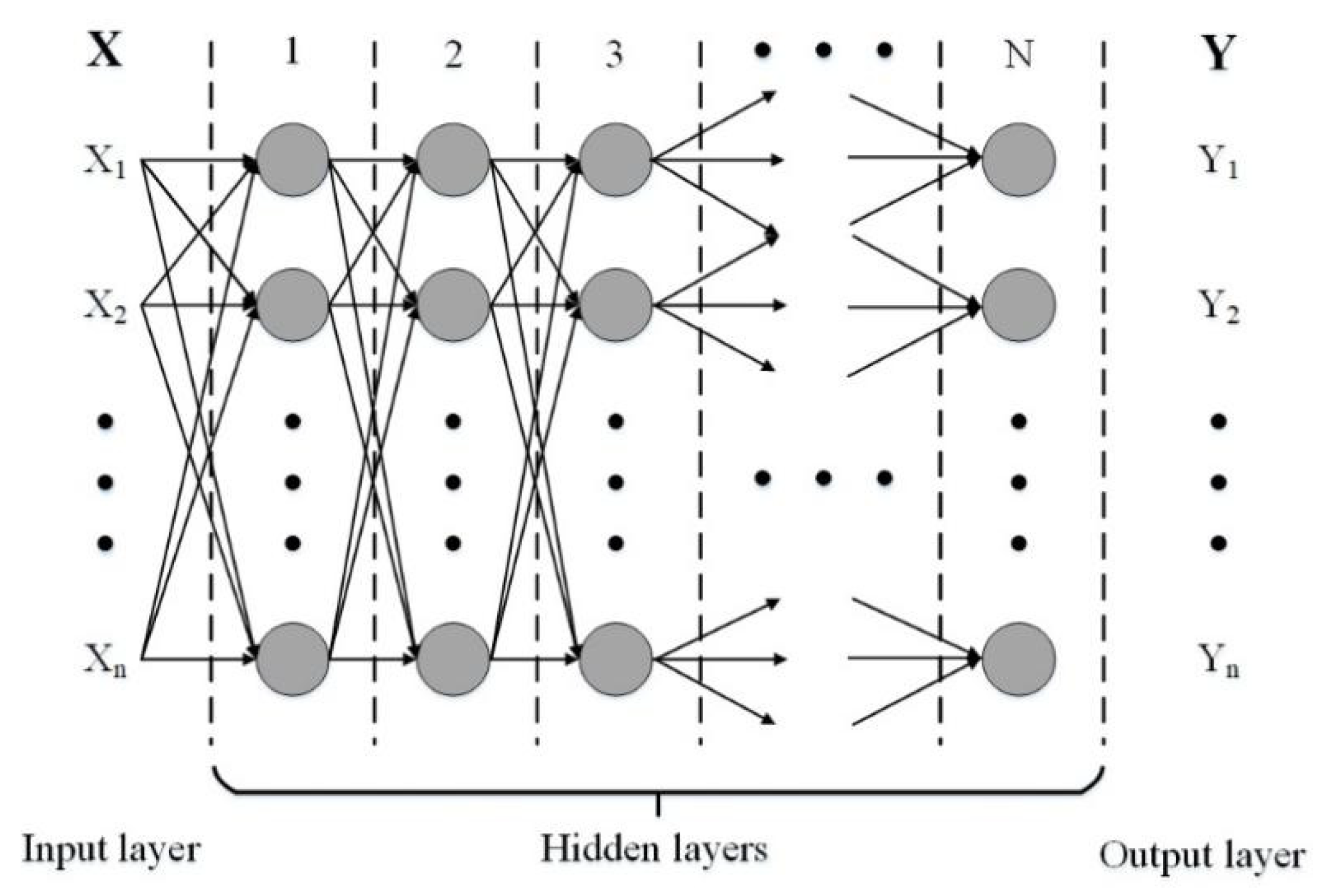
Figure 4, a fully connected DL-NN consists of an input layer, an output layer, and multiple hidden layers, and the number of neurons in each layer depends on the setting of the initial parameters. The weight and bias of a single neuron are
, which is activated by the nonlinear function sigmoid function. The result of the activation is the input of the next neuron or output of the entire network. The input of the neuron can be the actual input
X of the entire network or the output of the previous neuron.
In the training process, the Kalman filter algorithm is used to enhance the convergence speed of the learning phase and separation ability for highly nonlinear problems. The initial neural network weights are set to be small random numbers (−1, 1). The Kalman filtering process is a recursive mean square estimation process, and the NN weight for each update is calculated based on the previous estimation results and new input data. Consequently, the weights connected to each output node can be updated independently. To rapidly obtain the required root-mean-square error (RMSE), the DL requires only a few iterations, and the results obtained by the NN are highly stable [
12,
44].
3.5. Model Construction
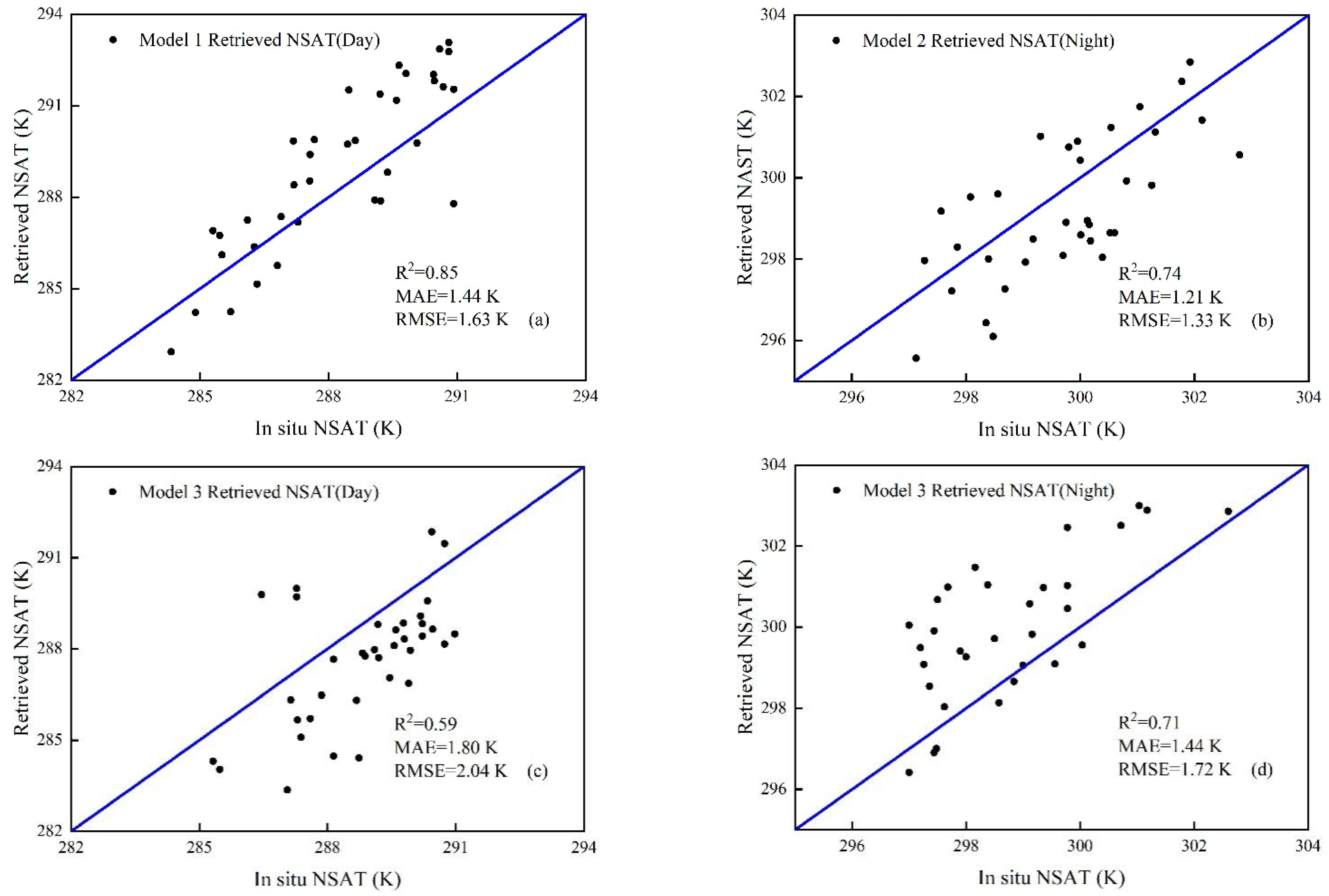
MODIS consists of multiple mid-infrared and thermal infrared bands. MODIS bands 20, 22, and 23 range from 3.5 to 7.2 µm, and bands 29, 30, 31, 32, and 33 range from 8 to 13.5 µm. The mid-infrared band (3.5–4.2 μm) is affected by solar radiation, and its use is therefore mainly suitable for night retrieval, whereas the thermal infrared bands (8–13.5 μm) are suitable for both day and night retrieval. According to the position of the central wavelength and characteristics of the MODIS bands, we constructed three combinatorial modes (
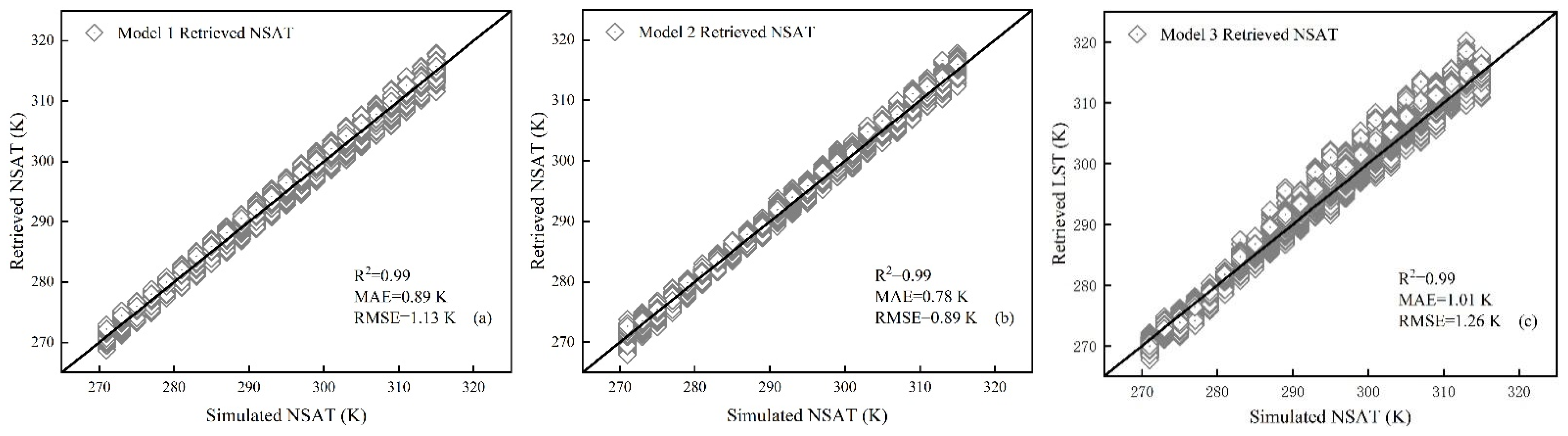
Table 2): (1) combinations suitable for day retrievals: LST, LSE, and BT in thermal infrared bands 29, 31, and 32 and WVC (2/5/17/18/19); (2) combinations suitable for night retrievals: LST, LSE, and BT in thermal infrared bands 29, 31, and 32 and infrared bands 20, 22, and 23; and (3) combinations suitable for day and night retrievals: LST, LSE, and BT in thermal infrared bands 29, 31, 32, and 33. Through the trial and error, we set the number of hidden nodes and hidden layers from small to large, and obtained the relatively optimal results. Some of the results are shown in
Table 3,
Table 4 and
Table 5. The first row of the table represents the number of hidden nodes, and the second row represents the accuracy, and the first column represents the number of hidden layers.