Novel Airborne EM Image Appraisal Tool for Imperfect Forward Modeling
Abstract
1. Introduction
2. Method
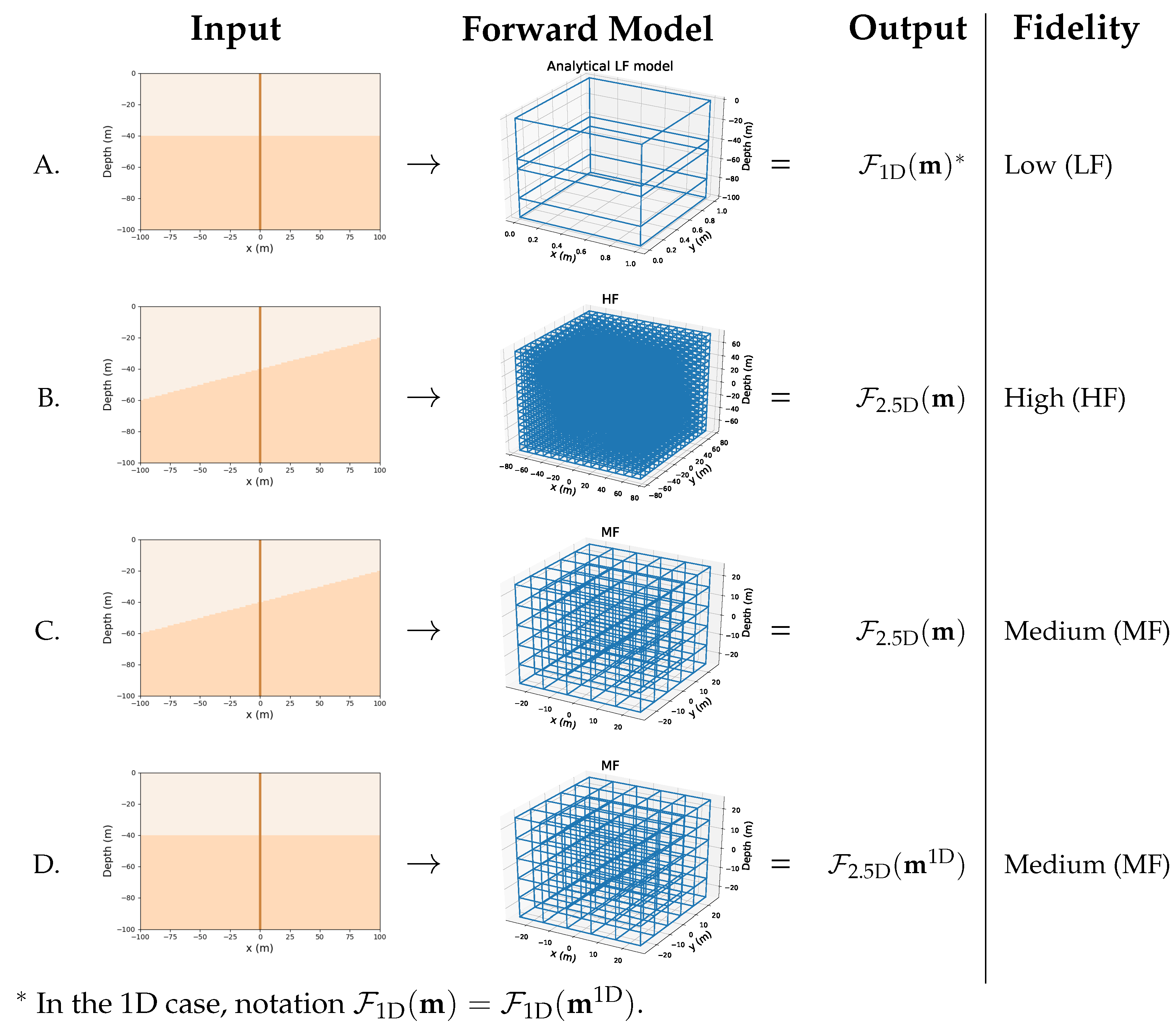
2.1. Three Types of Forward Modeling
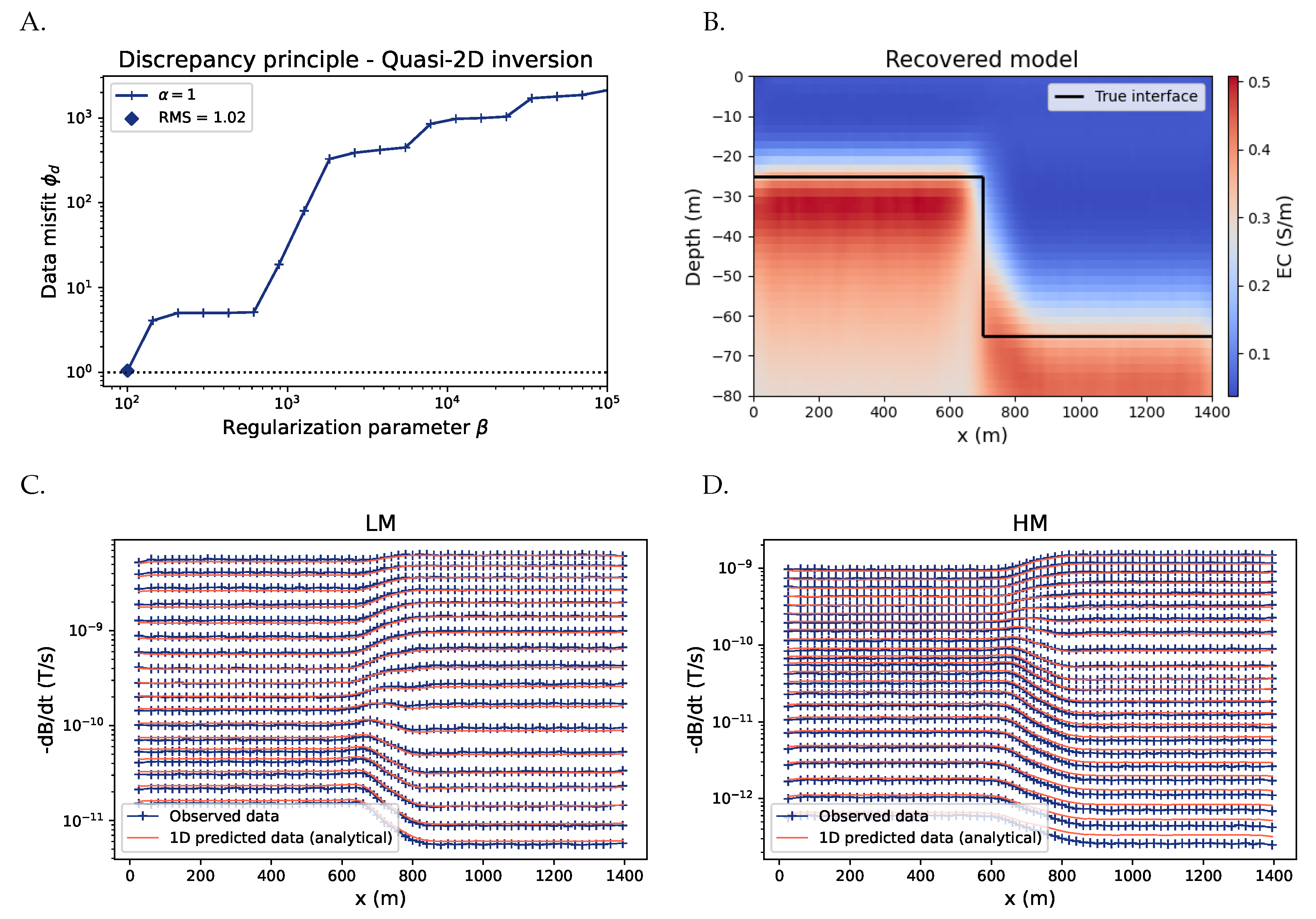
2.2. Quasi-2D Inversion
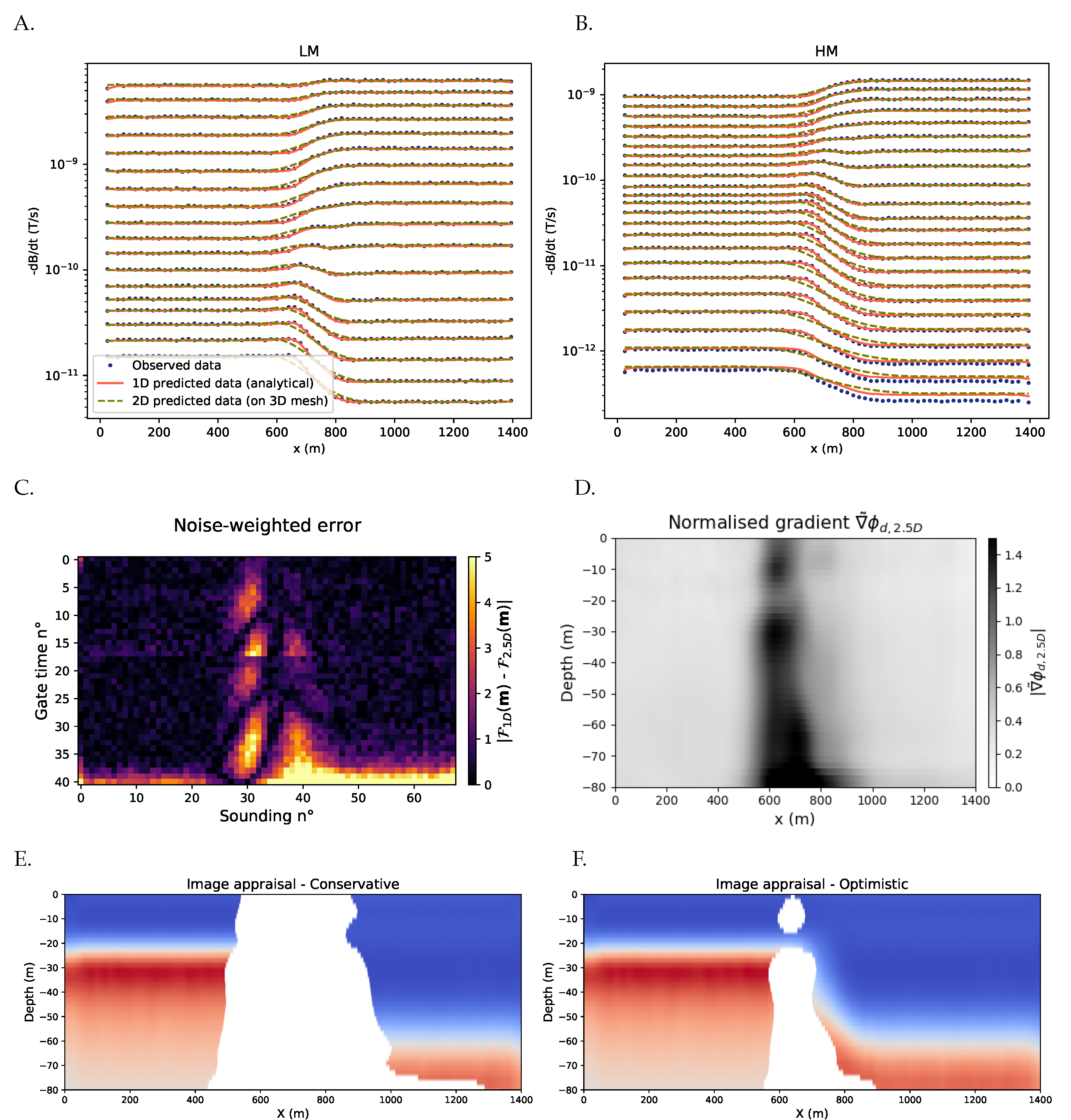
2.3. Normalized Gradient
2.4. Accounting for Imperfect Modeling
3. Results
3.1. Synthetic Model
3.1.1. Perfect Modeling Approach
3.1.2. Imperfect Modeling—Approach with Forced Modeling Error
3.2. Field Data Case
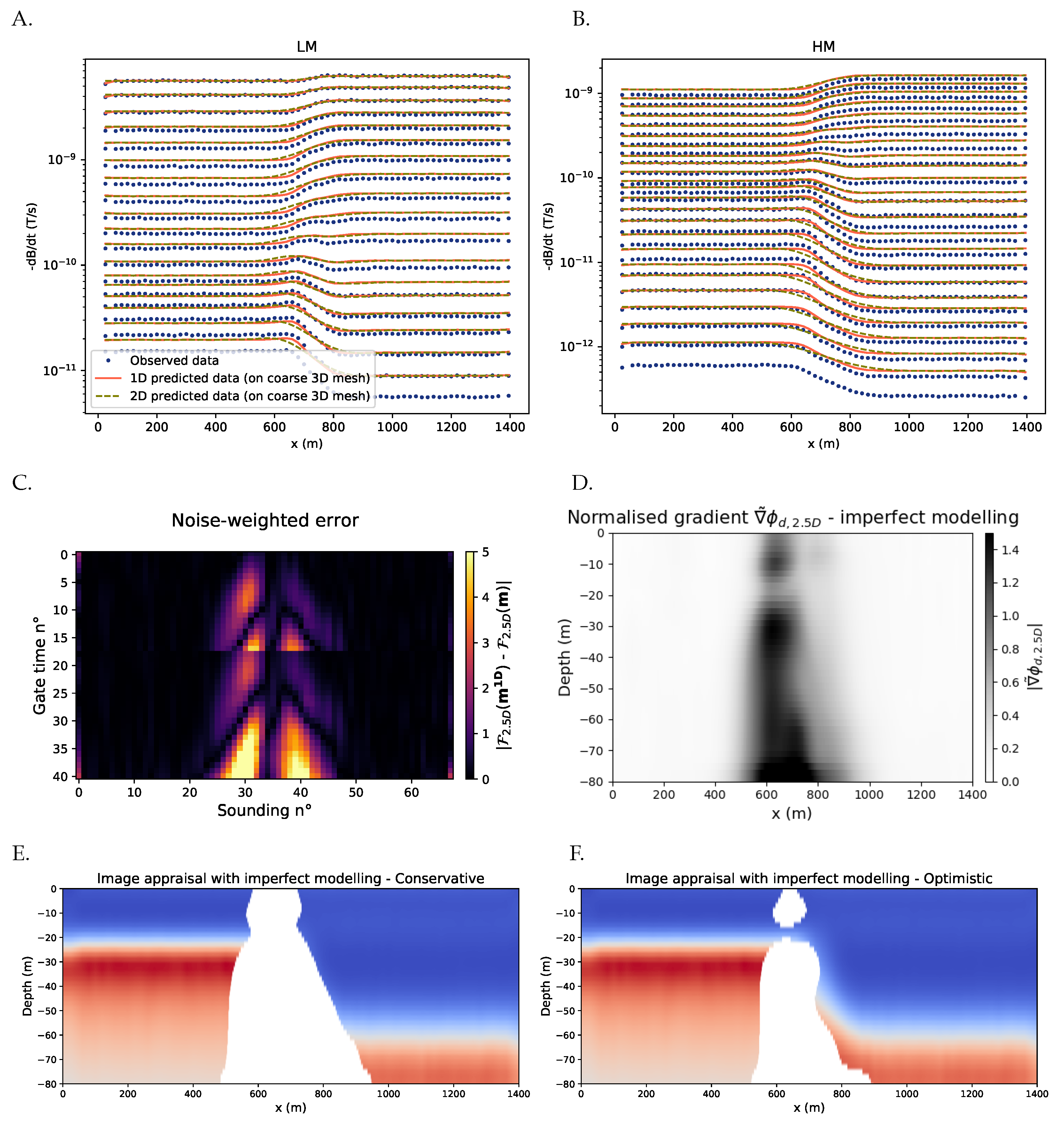
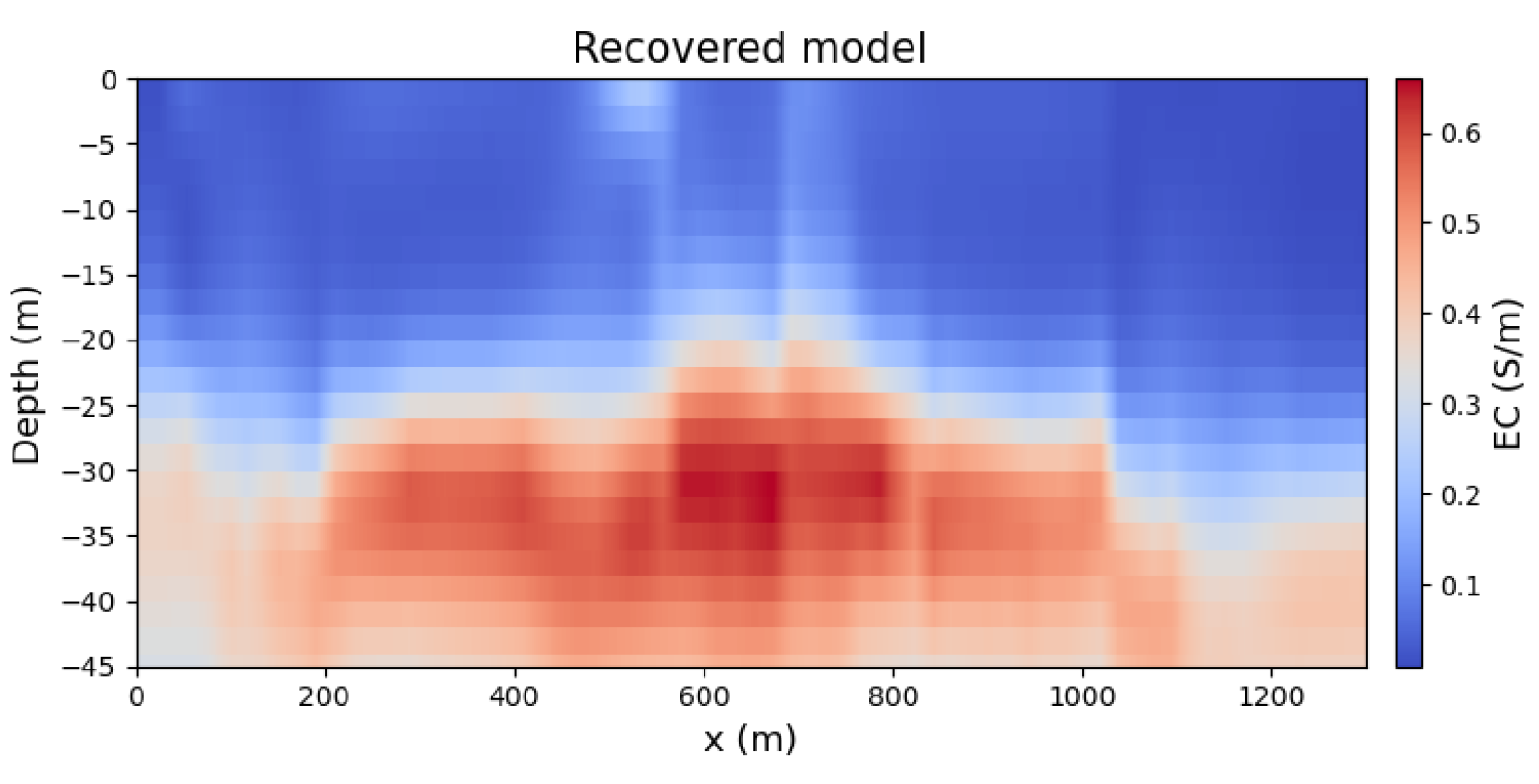


4. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Practical Guide for Constructing a Medium/High-Fidelity Mesh
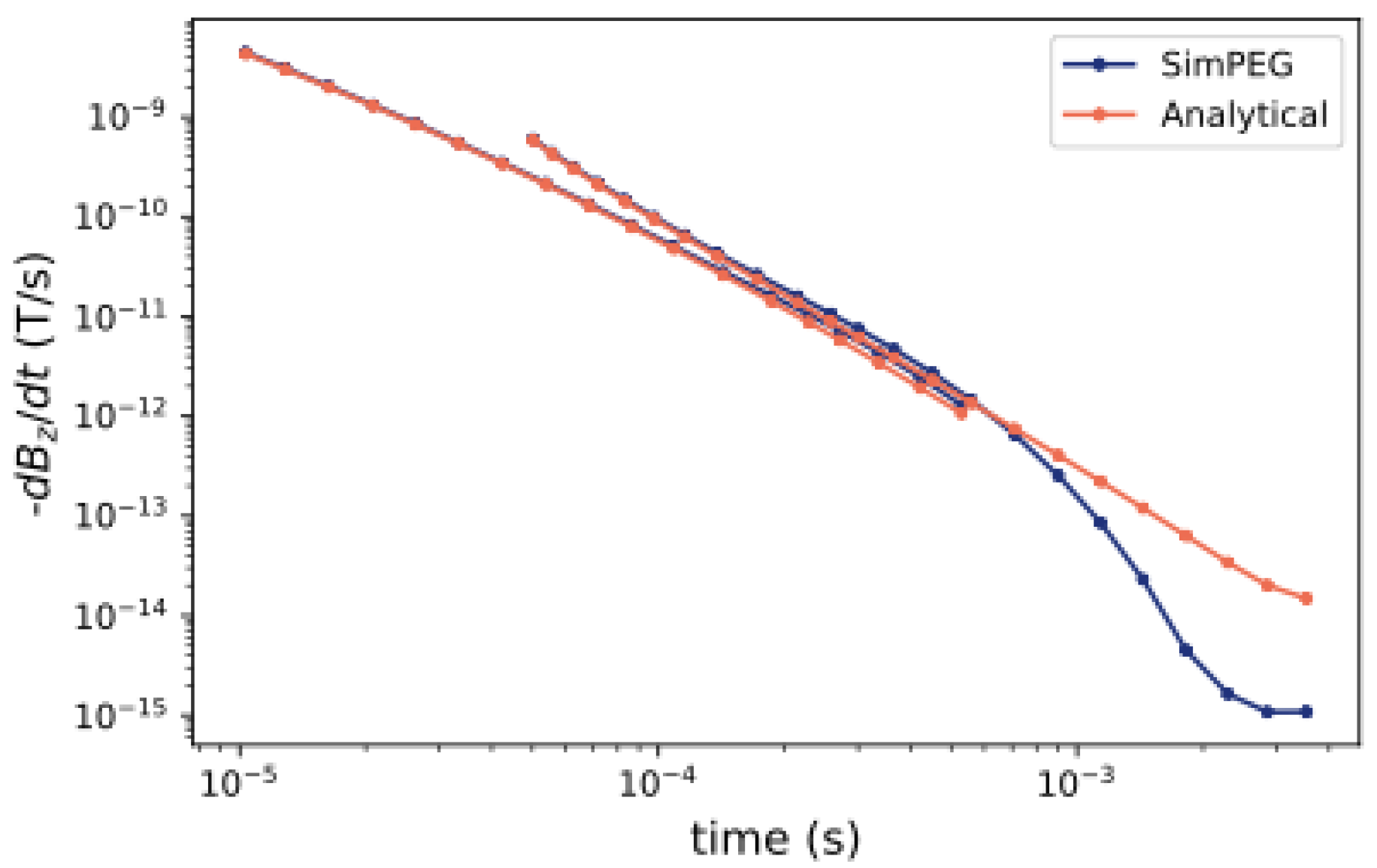

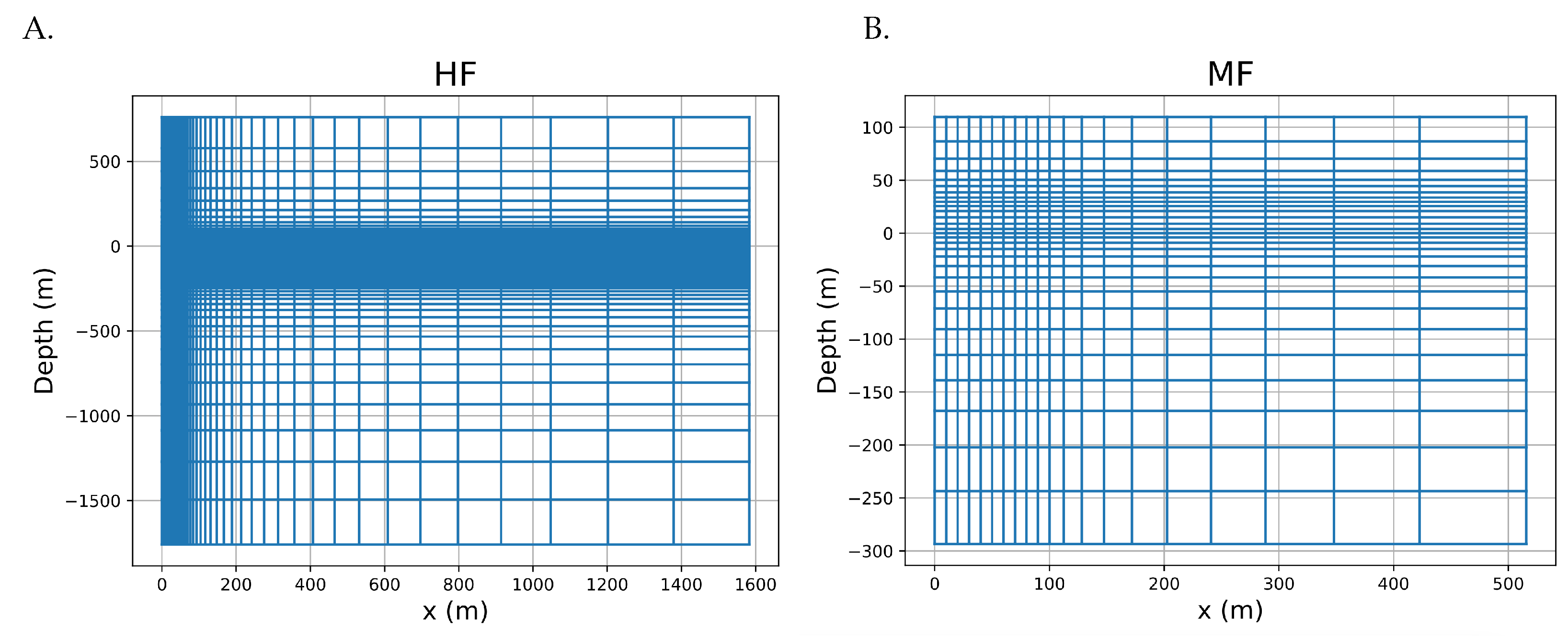
References
- Macnae, J.; Milkereit, B. Developments in broadband airborne electromagnetics in the past decade. Proc. Explor. 2007, 7, 387–398. [Google Scholar]
- Mikucki, J.A.; Auken, E.; Tulaczyk, S.; Virginia, R.; Schamper, C.; Sørensen, K.; Doran, P.; Dugan, H.; Foley, N. Deep groundwater and potential subsurface habitats beneath an Antarctic dry valley. Nat. Commun. 2015, 6, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Podgorski, J.E.; Auken, E.; Schamper, C.; Vest Christiansen, A.; Kalscheuer, T.; Green, A.G. Processing and inversion of commercial helicopter time-domain electromagnetic data for environmental assessments and geologic and hydrologic mapping. Geophysics 2013, 78, E149–E159. [Google Scholar] [CrossRef]
- Goebel, M.; Knight, R.; Halkjær, M. Mapping saltwater intrusion with an airborne electromagnetic method in the offshore coastal environment, Monterey Bay, California. J. Hydrol. Reg. Stud. 2019, 23, 100602. [Google Scholar] [CrossRef]
- Siemon, B.; van Baaren, E.; Dabekaussen, W.; Delsman, J.; Dubelaar, W.; Karaoulis, M.; Steuer, A. Automatic identification of fresh–saline groundwater interfaces from airborne electromagnetic data in Zeeland, the Netherlands. Surf. Geophys. 2019, 17, 3–25. [Google Scholar]
- Deleersnyder, W.; Maveau, B.; Hermans, T.; Dudal, D. Flexible quasi-2D inversion of time-domain AEM data, using a wavelet-based complexity measure. arXiv 2022, arXiv:2205.06458. [Google Scholar]
- Pfaffhuber, A.A.; Lysdahl, A.O.; Sørmo, E.; Skurdal, G.H.; Thomassen, T.; Anschütz, H.; Scheibz, J. Delineating hazardous material without touching—AEM mapping of Norwegian alum shale. First Break 2017, 35, 89807. [Google Scholar] [CrossRef]
- Auken, E.; Boesen, T.; Christiansen, A.V. A review of airborne electromagnetic methods with focus on geotechnical and hydrological applications from 2007 to 2017. Adv. Geophys. 2017, 58, 47–93. [Google Scholar] [CrossRef]
- Engebretsen, K.W.; Zhang, B.; Fiandaca, G.; Madsen, L.M.; Auken, E.; Christiansen, A.V. Accelerated 2.5-D inversion of airborne transient electromagnetic data using reduced 3-D meshing. Geophys. J. Int. 2022, 230, 643–653. [Google Scholar] [CrossRef]
- Heagy, L.J.; Cockett, R.; Kang, S.; Rosenkjaer, G.K.; Oldenburg, D.W. A framework for simulation and inversion in electromagnetics. Comput. Geosci. 2017, 107, 1–19. [Google Scholar] [CrossRef]
- Cai, H.; Hu, X.; Xiong, B.; Auken, E.; Han, M.; Li, J. Finite element time domain modeling of controlled-source electromagnetic data with a hybrid boundary condition. J. Appl. Geophys. 2017, 145, 133–143. [Google Scholar] [CrossRef]
- Yin, C.; Qi, Y.; Liu, Y. 3D time-domain airborne EM modeling for an arbitrarily anisotropic earth. J. Appl. Geophys. 2016, 131, 163–178. [Google Scholar] [CrossRef]
- Ansari, S.; Farquharson, C.; MacLachlan, S. A gauged finite-element potential formulation for accurate inductive and galvanic modelling of 3-D electromagnetic problems. Geophys. J. Int. 2017, 210, 105–129. [Google Scholar] [CrossRef]
- Börner, R.U.; Ernst, O.G.; Güttel, S. Three-dimensional transient electromagnetic modelling using rational Krylov methods. Geophys. J. Int. 2015, 202, 2025–2043. [Google Scholar] [CrossRef]
- Cox, L.H.; Wilson, G.A.; Zhdanov, M.S. 3D inversion of airborne electromagnetic data using a moving footprint. Explor. Geophys. 2010, 41, 250–259. [Google Scholar] [CrossRef]
- Oldenburg, D.W.; Li, Y. Estimating depth of investigation in dc resistivity and IP surveys. Geophysics 1999, 64, 403–416. [Google Scholar] [CrossRef]
- Binley, A.; Kemna, A. DC resistivity and induced polarization methods. In Hydrogeophysics; Springer: Berlin/Heidelberg, Germany, 2005; pp. 129–156. [Google Scholar]
- Caterina, D.; Beaujean, J.; Robert, T.; Nguyen, F. A comparison study of different image appraisal tools for electrical resistivity tomography. Surf. Geophys. 2013, 11, 639–658. [Google Scholar] [CrossRef]
- Paepen, M.; Deleersnyder, W.; De Latte, S.; Walraevens, K.; Hermans, T. Effect of Groundwater Extraction and Artificial Recharge on the Geophysical Footprints of Fresh Submarine Groundwater Discharge in the Western Belgian Coastal Area. Water 2022, 14, 1040. [Google Scholar] [CrossRef]
- Alumbaugh, D.L.; Newman, G.A. Image appraisal for 2-D and 3-D electromagnetic inversion. Geophysics 2000, 65, 1455–1467. [Google Scholar] [CrossRef]
- Christiansen, A.V.; Christensen, N.B. A quantitative appraisal of airborne and ground-based transient electromagnetic (TEM) measurements in Denmark. Geophysics 2003, 68, 523–534. [Google Scholar] [CrossRef]
- Werthmüller, D. An open-source full 3D electromagnetic modeler for 1D VTI media in Python: Empymod. Geophysics 2017, 82, WB9–WB19. [Google Scholar] [CrossRef]
- Hunziker, J.; Thorbecke, J.; Slob, E. The electromagnetic response in a layered vertical transverse isotropic medium: A new look at an old problem. Geophysics 2015, 80, F1–F18. [Google Scholar] [CrossRef]
- Constable, S.C.; Parker, R.L.; Constable, C.G. Occam’s inversion: A practical algorithm for generating smooth models from electromagnetic sounding data. Geophysics 1987, 52, 289–300. [Google Scholar] [CrossRef]
- Tikhonov, A.N. On the stability of inverse problems. Proc. Dokl. Akad. Nauk SSSR 1943, 39, 195–198. [Google Scholar]
- Zhang, B.; Engebretsen, K.W.; Fiandaca, G.; Cai, H.; Auken, E. 3D inversion of time-domain electromagnetic data using finite elements and a triple mesh formulation. Geophysics 2021, 86, E257–E267. [Google Scholar] [CrossRef]
- Delsman, J.; van Baaren, E.; Vermaas, T.; Karaoulis, M.; Bootsma, H.; de Louw, P.; Pauw, P.; Oude Essink, G.; Dabekaussen, W.; Van Camp, M.; et al. TOPSOIL Airborne EM Kartering Van Zoet en Zout Grondwater in Vlaanderen; Technical Report; VMM: Aalst, Belgium, 2019. [Google Scholar]
- Sørense, K.; Auken, E. SkyTEM? A new high-resolution helicopter transient electromagnetic system. Explor. Geophys. 2004, 35, 194–202. [Google Scholar] [CrossRef]
- Hansen, P.C. Discrete Inverse Problems: Insight and Algorithms; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2010; Volume 7. [Google Scholar]
- Flanders Environment Agency; Vandevelde, D.; Lermytte, J. Airborne EM data (Belgium) from flight line 306025. Zenodo. 2022. Available online: https://doi.org/10.5281/zenodo.7015419 (accessed on 1 May 2022).
- Deleersnyder, W. WouterDls/AEM_Appraisal: First Release (0.0.0). Zenodo. 2022. Available online: https://doi.org/10.5281/zenodo.7015876 (accessed on 1 May 2022).
- Cockett, R.; Kang, S.; Heagy, L.J.; Pidlisecky, A.; Oldenburg, D.W. SimPEG: An open source framework for simulation and gradient based parameter estimation in geophysical applications. Comput. Geosci. 2015, 85, 142–154. [Google Scholar] [CrossRef]
- Ward, S.H.; Hohmann, G.W. Electromagnetic Theory for Geophysical Applications Version 4; Society of Exploration Geophysicists: Houston, TX, USA, 1988. [Google Scholar]
- Deleersnyder, W.; Hermans, T.; Dudal, D. An efficient Gaussian process regression surrogate model for Airborne TDEM multidimensional modelling. 2022, manuscript in preparation.
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deleersnyder, W.; Dudal, D.; Hermans, T. Novel Airborne EM Image Appraisal Tool for Imperfect Forward Modeling. Remote Sens. 2022, 14, 5757. https://doi.org/10.3390/rs14225757
Deleersnyder W, Dudal D, Hermans T. Novel Airborne EM Image Appraisal Tool for Imperfect Forward Modeling. Remote Sensing. 2022; 14(22):5757. https://doi.org/10.3390/rs14225757
Chicago/Turabian StyleDeleersnyder, Wouter, David Dudal, and Thomas Hermans. 2022. "Novel Airborne EM Image Appraisal Tool for Imperfect Forward Modeling" Remote Sensing 14, no. 22: 5757. https://doi.org/10.3390/rs14225757
APA StyleDeleersnyder, W., Dudal, D., & Hermans, T. (2022). Novel Airborne EM Image Appraisal Tool for Imperfect Forward Modeling. Remote Sensing, 14(22), 5757. https://doi.org/10.3390/rs14225757







