1. Introduction
In the field of intelligent robots, localization and mapping are the basic modules for realizing autonomous capabilities. The localization module solves the problem of pose estimation and is indispensable in the robot’s obstacle avoidance and control. The mapping module mainly completes the environment modeling during the movement process, which is the prerequisite for decision making and path planning. With the development of the robotics field, intelligent robots are being increasingly used in off-road environments. However, it is usually difficult to carry out accurate positioning in the off-road environment because the intelligent robot is affected by factors such as unstructured roads and irregular environmental characteristics in the off-road environment. In terms of mapping, it is generally unnecessary to detect urban traffic elements such as lane lines and traffic lights in the off-road environment, but more attention is paid to the identification of the accessible area on the target task path (which can complete the global and local path planning). However, the road boundaries in the off-road environment are uneven, and sensors have blind sensing areas, which increases the difficulty of mapping. In practical applications, it is usually difficult to complete the environmental modeling of the off-road environment in advance, and the off-road environment is often an unknown environment. Simultaneous location and mapping (SLAM) can solve the problem of location and mapping simultaneously in unknown environments. The mainstream method is to use constraints to construct a nonlinear least squares problem and then solve it. Therefore, the constraint construction method and its weight calculation in the optimization function are key issues to consider.
LiDAR can perceive the obstacle information of the environment and output it in the form of point cloud data. Due to its high precision and strong anti-interference ability, it is widely used in the field of SLAM. In order to complete the autonomous navigation of the robot, a navigable grid map is essential. The grid map is scaled according to the scale of the real world, in which it is possible to mark whether the area is a passable attribute, which is one of the common output forms of SLAM.
According to the review by Cadena et al. [
1], 1986 to 2004 was called the classical era of SLAM. During this period, some classical filtering-based SLAM methods were proposed, such as the method based on extended Kalman filters and Rao-Blackwellized particle filters. These methods and the maximum likelihood estimation method are no longer the mainstream methods due to the problems of excessive computation and memory consumption based on the filtering method in a large-scale environment. From 2004 to 2015 was called the era of algorithm analysis. It mainly analyzed the observability, convergence and consistency of SLAM. During this period, the concept of front-end and back-end was also proposed. The back-end is mainly used for optimization to minimize errors in the front-end, which mainly involves graph optimization, probability estimation, and numerical analysis.
The front-end registration methods of SLAM mainly include ICP [
2] (Iterative Closest Point), NDT [
3] (Normal Distributions Transform), optimization-based methods [
4] and related matching methods CSM [
5] (Correlative Scan Match). Among them, ICP contains a variety of variants, such as VICP [
6], which can estimate the motion speed at the same time, and PL-ICP [
7], which constructs a point-line metric ICP that is more in line with the real physical environment. Ji Zhang et al. [
8] proposed a real-time LiDAR odometry and mapping method, LOAM, and it has been in a state-of-the-art position since it was proposed. Its advantage is that it extracts line and surface feature points and uses the optimization method based on point line and point surface for registration, which is essentially a variant of ICP. However, this method of extracting feature points significantly improves computing efficiency and stability. It can achieve very good registration effects in real time.
At present, the mainstream SLAM back-end method is based on graph optimization. Ref. [
9] is the pioneering work of SLAM based on graph optimization and was first implemented by [
10]. For graph-optimized SLAM using LiDAR as the main sensor, Tixiao Shan et al. proposed a smoothing and map-building, tightly coupled LiDAR-inertial odometry (LIO-SAM) [
11], which implemented a graph-optimized framework based on iSAM2 [
12] and added constraints such as inter-frame point cloud registration, IMU pre-integration, GPS and loop closure. Although the open source implementation adopts a direct truncation method for the fusion IMU pre-integration part, it has a good reference in the engineering sense. Haoyang Ye et al. proposed a tightly coupled LiDAR-inertial odometry and mapping (LIO-Mapping) [
13] framework, which is used to maintain the scale of variables in graph optimization based on the sliding window method; the point-line of the feature point cloud between frames, point-surface registration constraints and constraints such as IMU pre-integration are jointly optimized. The sliding window algorithm removes some optimization variables so as to maintain the keyframes within a certain size; however, directly removing optimization variables affects the accuracy, so marginalization constraints are usually added [
14]. Unlike LIO-SAM, LIO-Mapping adopts a marginalized method, which is more reasonable and complete on a theoretical basis. However, in practical application effects, LIO-Mapping takes each feature point as a constraint, and LIO-SAM has degenerated the constraints of multiple feature points into pose increment constraints. In addition, the amount of calculations in LIO-Mapping is much larger than that of LIO-SAM. However, in unknown and possibly loop-free environments, sliding-window-based optimization methods are more applicable. Kaijin Ji et al. proposed a SLAM algorithm based on a grid which combines probability and features by expectation maximization (EM) [
15].
Intelligent robots need not only high-precision positioning, but also high-precision navigation maps when completing traffic mapping. The construction method of the classic two-dimensional probability grid map is mature, and the traditional two-dimensional LiDAR SLAM scheme uses the probability grid map as the output target, such as Gmapping [
16], Cartographer [
17] and so on. As early as 1989, Moeavec proposed a probability method for occupancy grid maps [
18]. By assigning each grid an occupancy probability value, and using the LiDAR inversion observation model to dynamically update the occupancy probability, the two-dimensional probability grid can be obtained. The map distinguishes traversable areas and removes the effects of dynamic obstacles in multiple observations. The most advanced three-dimensional LiDAR SLAM algorithm LOAM [
8] and a series of variant mapping algorithms (such as Lego LOAM [
19]) are all discrete point cloud maps obtained by directly splicing point clouds, which can be used to create Octomap [
20]. It is also easy to navigate when compressing maps, but due to the impact of dynamic obstacles, it will leave ghosts on the map. To remove dynamic obstacles, Xieyuanli Chen et al. proposed SuMa++ [
21], which takes bins as map elements and then introduces the difference of semantic information as observation information to dynamically update the stability of the bins and directly eliminate unstable bins. However, maintaining bins requires a lot of resources.
For the demand of off-road environment map construction, we should give full play to the advantages of incremental SLAM map construction and design a variety of map forms, for example: using satellite maps to complete the global path planning of vehicles, using point cloud maps for location registration and using grid maps for local path planning. The construction of grid maps will be integrated based on filtering algorithms and have richer local perceptual information than single-frame data to narrow the perceptual blind area. The obstacle occupation information in the observation area can be updated many times to provide feedback information for vehicle positioning. As a common navigation map, a probability grid map is preferred. In an unstructured off-road environment, different observations may determine different traffic results for a region, such as the observation of steep slopes at different angles, the observation of dynamic obstacles, etc. Therefore, it is necessary to dynamically update the traffic probability by integrating multi-frame observation results. However, 3D probability grids are rarely used due to the problem of excessive computation, and other forms of 3D maps also require a lot of resources.
The current mainstream 3D LiDAR SLAM solution is to insert the scan-to-map constraint of the point cloud into the graph optimization framework, and this constraint can only constrain the current pose and cannot take advantage of the graph optimization. In order to take advantage of LiDAR constraints, this paper will generate the widely used LiDAR and occupancy grid map, propose a dual-constraint construction method using LiDAR and use the grid map as the medium to calculate the weight of the constraint. The main contributions of this paper are as follows:
For the SLAM algorithm based on sliding window optimization, two constraint construction methods for LiDAR are proposed—in-window constraints and out-of-window constraints—to make up for the disadvantage of having fewer feature points during the inter-frame registration in off-road open scenes. According to the size of the sliding window, the pose accuracy and algorithm solution time can be compromised;
Using the grid map as a medium, the occupancy information of the grid map is abstracted into the binary semantics of occupancy, weighting the out-of-window constraints of the LiDAR and further proposing a strategy based on a two-dimensional grid map to eliminate dynamic obstacles in the point cloud map.
The remainder of this paper is organized as follows.
Section 2 describes the proposed method specifically. Then,
Section 3 shows and analyzes the experiment results,
Section 4 carries out relevant discussions and presents prospects for future work, and
Section 5 summarizes the article.
2. Methods
The system framework is shown in
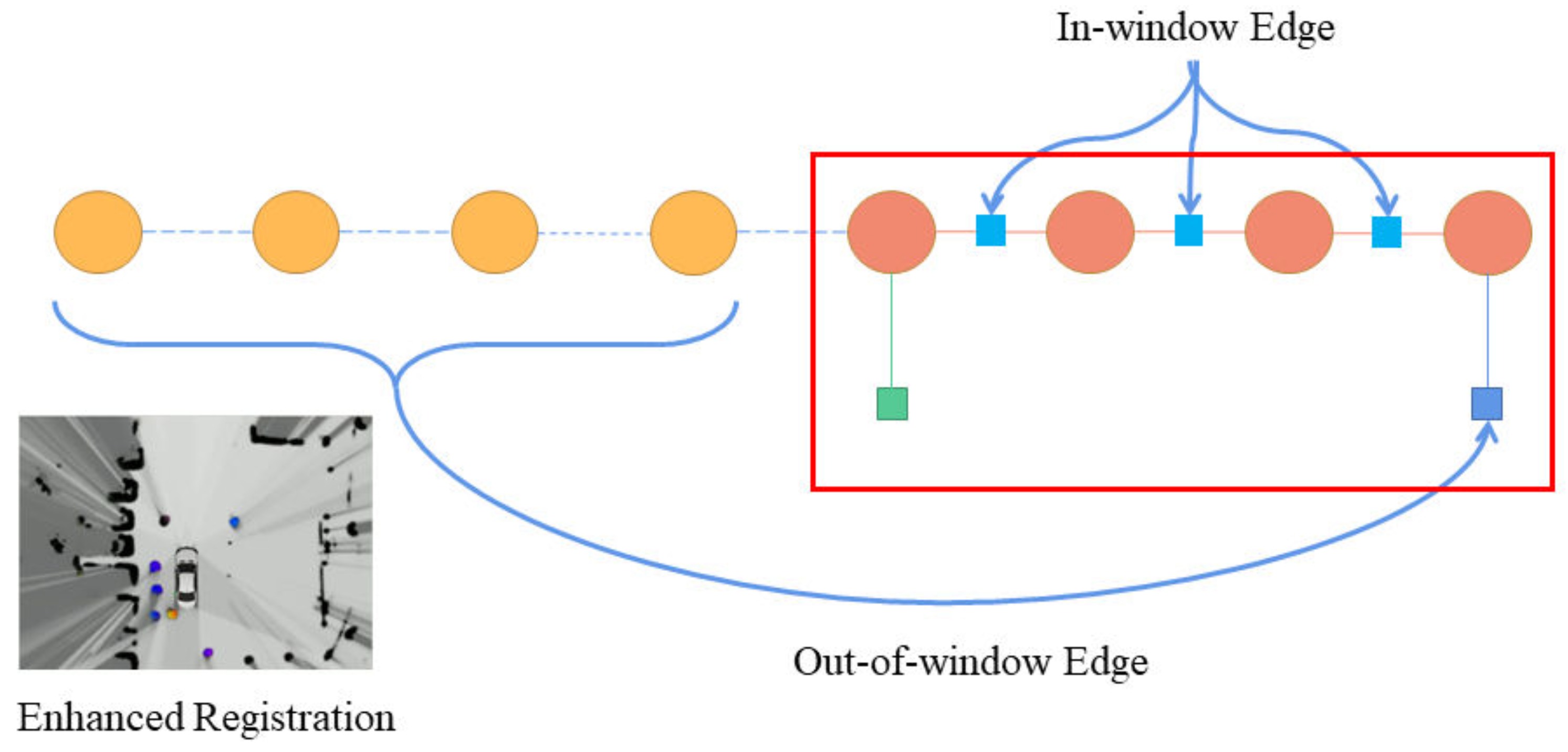
Figure 1. We use the graph optimization method based on a sliding window to build a SLAM system and abstract the constraints of LiDAR into two constraints, namely, the constraint edge inside the window and the constraint edge outside the window. The residual edge in the window is a binary edge, similar to ICP, by taking the distance value of the matching point as the error, and adjusting the two-frame pose associated with it. The residual outside the window is an unary edge, and the key frame outside the window is extracted to form a local map to match the point cloud of the current frame. Since the optimization variables outside the window will not be adjusted, only the pose of the current frame is adjusted. In order to provide better constraint information for the residual outside the window, we use a two-dimensional grid map. The grid map is used to dynamically adjust the weights of the constraint edges outside the window to enhance the point cloud registration.
2.1. Graph Optimization Based on a Sliding Window
In the graph optimization fusion framework, the “vertices” in the graph are used as optimization variables, which are usually the pose of the vehicle in the localization (the graph is also called a Pose Graph). The “edges” in the graph are used as constraints (that is, observation) and are divided into the unary edge, binary edge and multi-element edge according to the number of optimization variables bound by constraints. For example, the GPS absolute localization constraint is the unary edge, and IMU, wheel odometer, inter-frame registration, loopback and other constraints are binary edges. For example, the observation equation of the binary edge is:
, where
is the 6-DOF pose, and
. Considered from the perspective of least squares, the observed residuals can be written as:
. If we add other observations, we can obtain the overall cost function:
where
,
n represents the number of optimized poses.
The optimization equation is solved by the Gauss–Newton method, that is, each residual term is first-order expanded and then squared and summed. For example, the first-order Taylor expansion of the residual of the
k observation is performed:
So, the nonlinear function can be approximated as:
Differentiate
and set the result to 0:
Therefore, the equations built each time look like this:
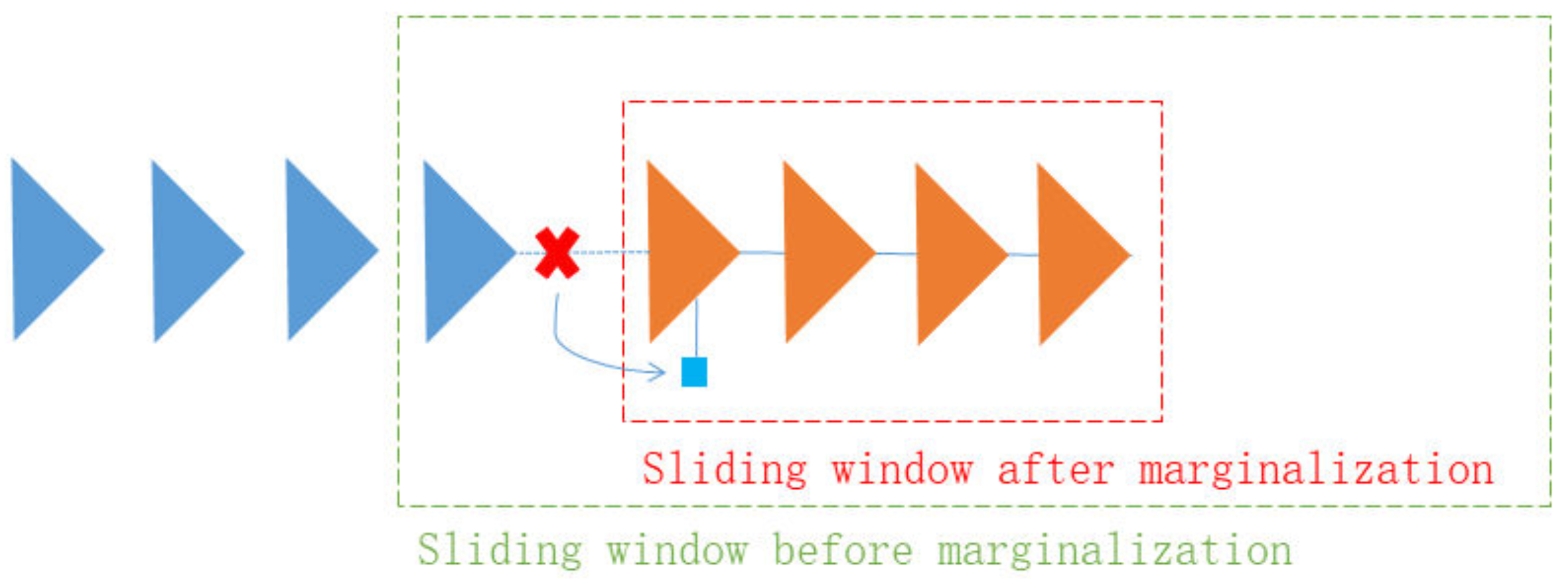
However, as time goes on, there will be more and more poses. In order to avoid excessive calculation in the optimization process, the sliding window method is used to control the scale of the optimization variables. When an optimization variable needs to be discarded, it should be considered that the information after the linearization of the variable in the last iteration of the variable remains in the
H matrix and
b vector, and this information should be transferred to the remaining variables. Therefore, it is necessary to compare the
H matrix and
b vector. The vector is marginalized, and the optimization variables that need to be discarded in Equation (6) are disassembled:
where
is the reserved optimization variable, and
is the optimization variable that needs to be marginalized, so the reserved variables are constrained by the following:
This constraint is used as a prior constraint and directly added to the next iteration, but the prior constraint has lost the residual information. After the remaining variables are adjusted, it is necessary to dynamically adjust the right-hand side of Equation (8). The half side is updated, assuming that
changes
; then, it is equivalent to
changing
. Then, the right half is updated as:
So far, the graph optimization solution framework based on a sliding window has been completed. The sliding window’s marginalization is shown in
Figure 2. The process of marginalization is mainly described intuitively, that is, the constraint information of the variables to be discarded is transferred to the prior constraints of the variables in the window.
2.2. In-Window Constrains
For the in-window constraint of LiDAR, it is similar to the scan-to-scan registration of LiDAR, that is, the point–line and point–surface distances between frames are constructed as errors, where a “point” is the feature point of the current frame, and “line” and “surface” are the feature points of the previous frame. Thus, for each feature point, the registration error between frames can be obtained as:
where
is the normal vector of the line and surface features,
is the laser point of the
k frame,
is the laser point that matches the
of the
frame and
is the conversion of the laser point from the
k frame to the
frame transformation.
Since the optimization variable is the pose vector under the
w system, it is necessary to transform
in Equation (10):
Since Equation (11) is bound to two poses, and both poses need to be optimized, the constraint edge is a binary edge, which can be called the “in-window residual” of LiDAR. This constraint is added to the graph optimization solution framework, and the residuals and normals of the line and surface features, as well as the Jacobian matrix of the residuals to the optimization variables, need to be calculated.
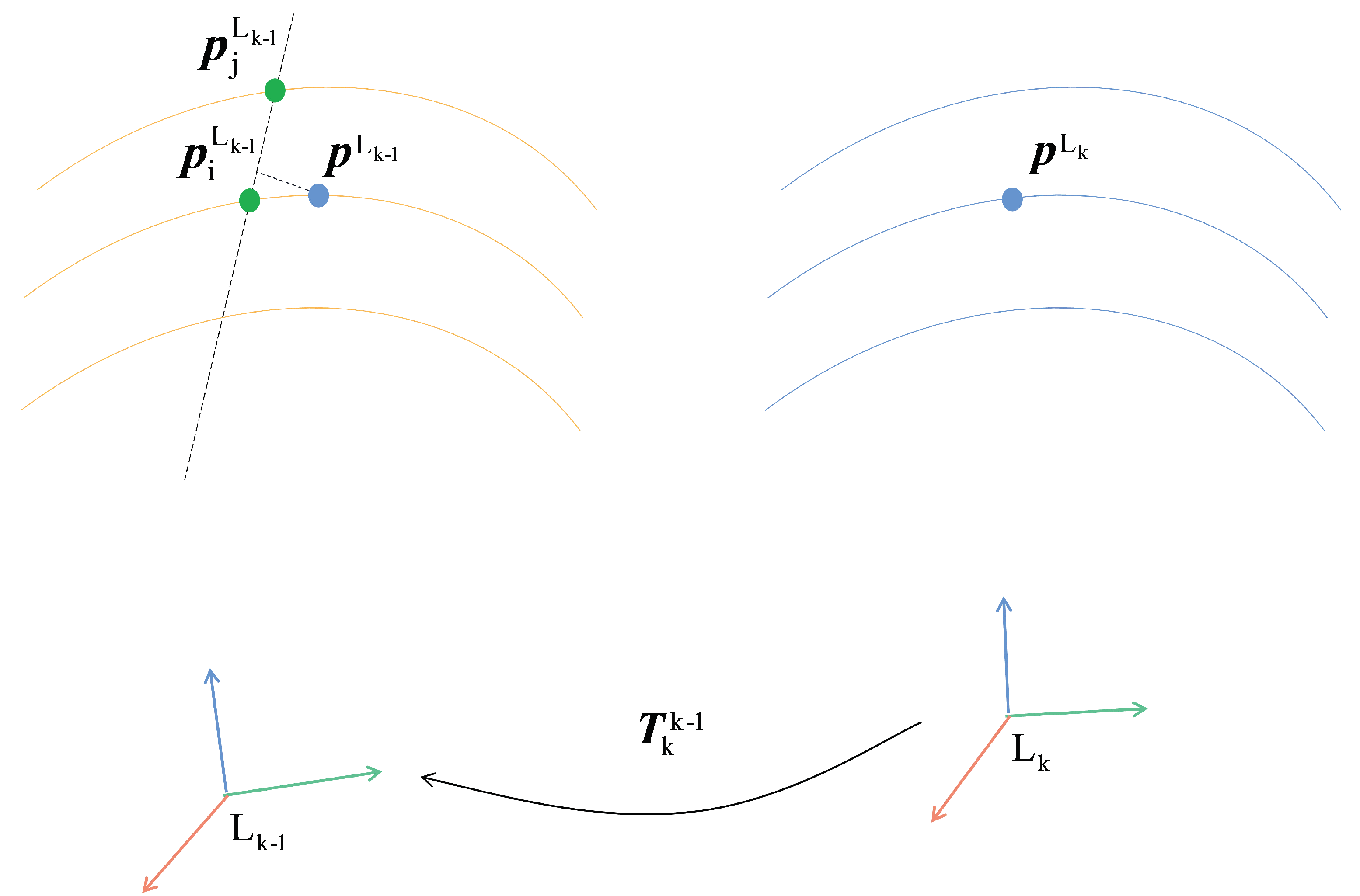
For line features, as shown in
Figure 3, first transform the line feature point
of the
k frame to
in the
frame according to the current pose estimation, and search for the nearest Euclidean distance to
in the
frame. The line feature point
is searched again for the nearest line feature point
in the adjacent LiDAR beams of the
frame and
, thus avoiding the collinearity of the three points
,
and
and taking the distance between
and the straight line
as the residual. The residual error is minimized by adjusting the poses of the
frame and the
k frame.
The residual and normal vector can be calculated by obtaining the three points
,
and
. The residual and normal vector can be calculated by calculating the area of the parallelogram with the line segment
and the line segment
as the side lengths and the length of the line segment
:
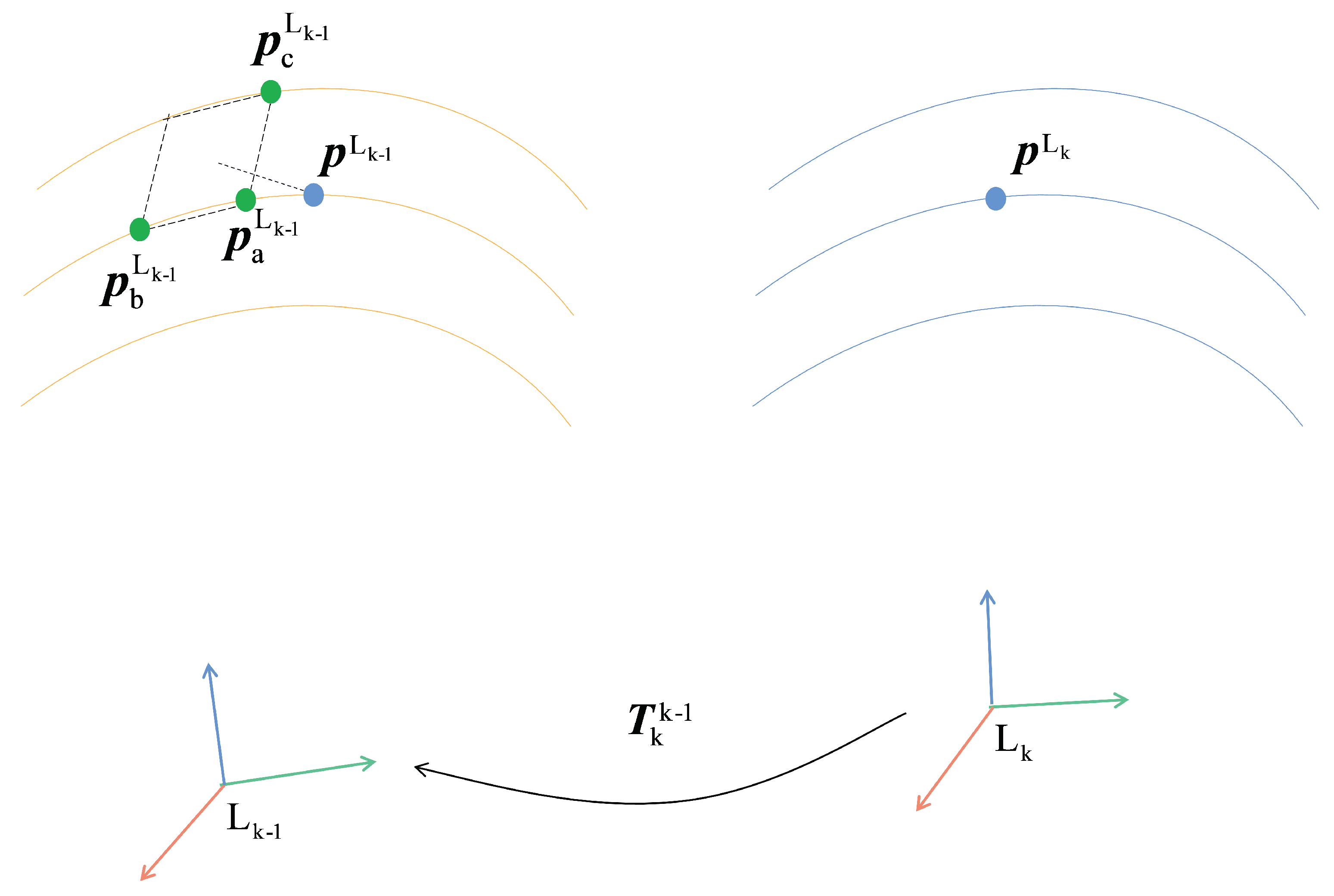
For the surface feature, as shown in
Figure 4, first transform the surface feature point
of the
k frame to
in the
frame according to the current pose estimation and search for the nearest Euclidean distance to
in the
frame. The surface feature point
of the
k − 1 frame is searched again for the nearest surface feature point
in the same LiDAR beam as
and the nearest surface feature point
in the adjacent LiDAR beam with
, thus avoiding
,
,
and
. The four points are coplanar; the distance between
and the plane
is used as the residual; and the residual is minimized by adjusting the poses of the
frame and the
k frame.
The residual and normal vector can be calculated by obtaining the four points
,
,
and
. The residual can be calculated by the area of the parallelogram with the line segments
and
as the side lengths and its normal vector:
2.3. Constrained Edge outside the Window
For the pose outside the sliding window, we can select the part that has a common viewing area with the current vehicle localization. Since the variables outside the window are no longer involved in the optimization, we can directly convert their point cloud data to the global coordinate system as a local map. Then, a registration constraint between the current frame and the local map is constructed, which is similar to the scan-to-scan registration of LiDAR and can make up for the defect of fewer feature points during inter-frame registration.
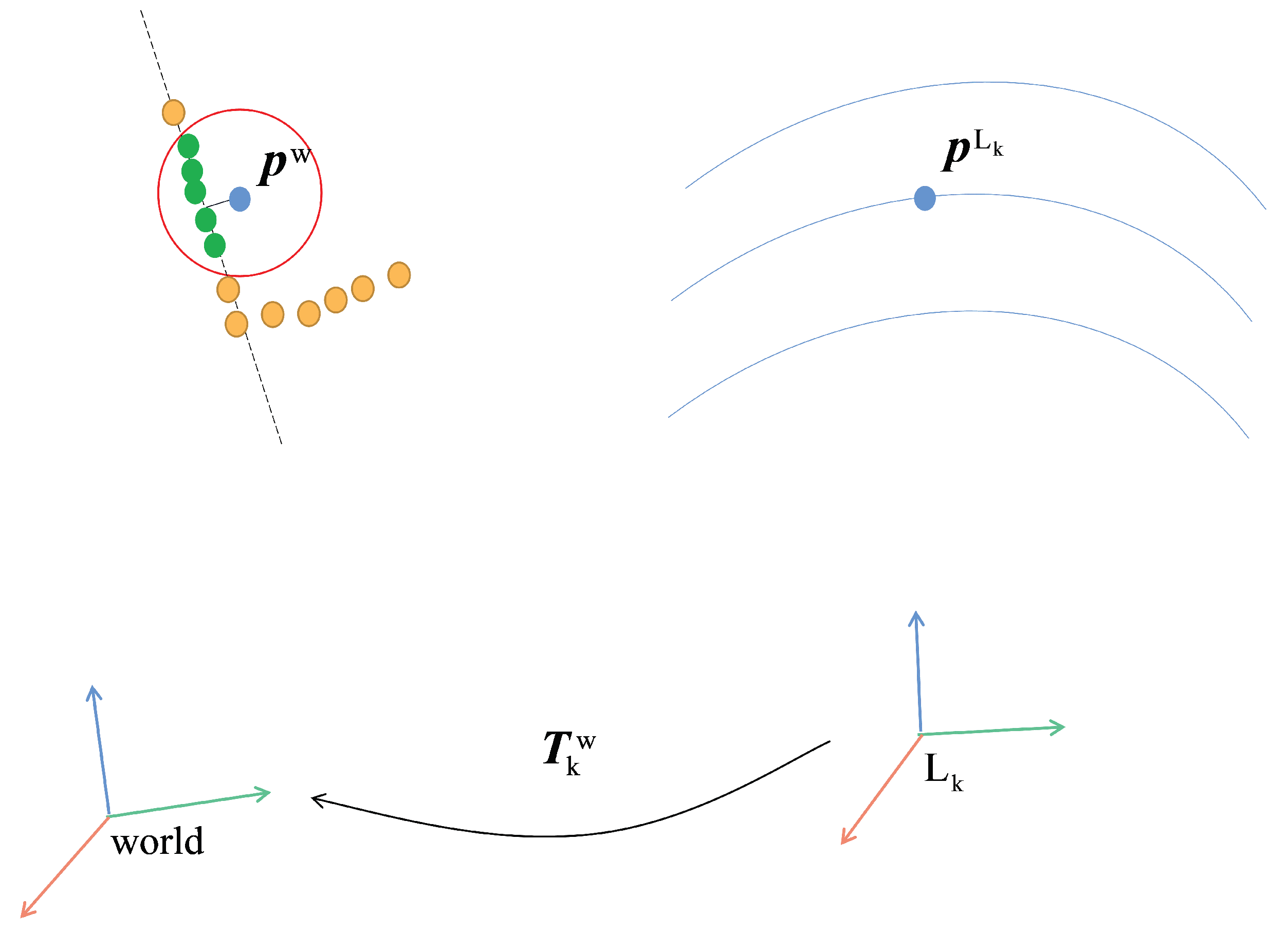
For line features, as shown in
Figure 5, first transform the line feature point
of the
k frame to
in the world system according to the current pose estimation, and search for the 5 line feature points in the local map that are closest to the Euclidean distance of
(that is, the green point in the
Figure 5). Next, solve the mean and covariance matrix of these five points using Equations (16) and (17) and decompose the covariance matrix of Equation (17) by SVD, finally obtaining the minimum eigenvalue. The corresponding feature vector is the normal vector of the line feature. Through the mean value
and normal vector of these 5 points, 2 virtual matching points,
and
, can be generated, corresponding to
and
in
Figure 5. Then, directly use Equations (12) and (13) to solve residuals and normals for outgoing features:
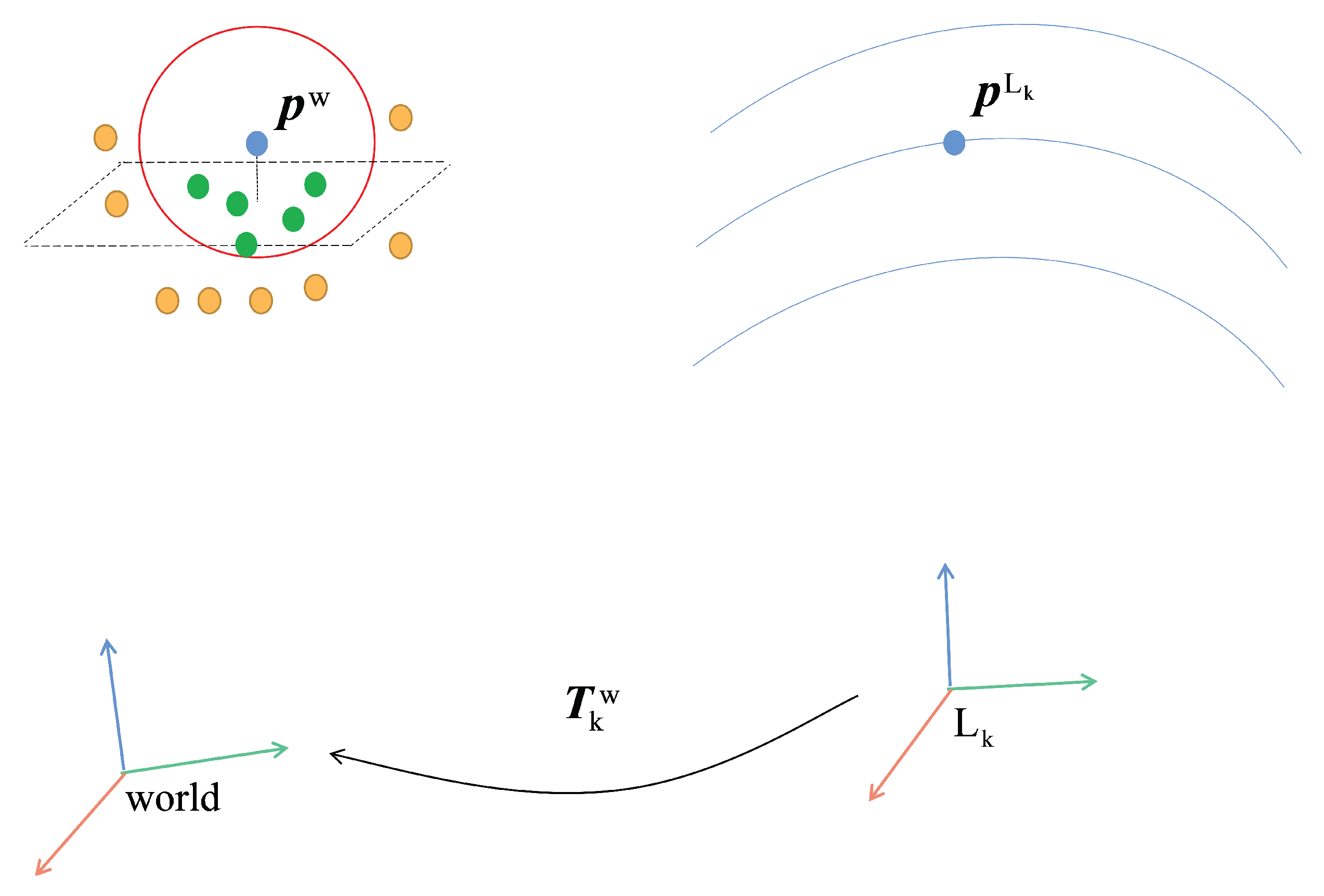
For surface features, as shown in
Figure 6, first transform the surface feature point
of the
k frame to
in the world system according to the current pose estimation, and search for the five surface feature points in the local map that are closest to the Euclidean distance of
(the green dots in the
Figure 6) and the plane equation from them:
The parameters
a,
b and
c in the plane equation in Equation (18) are formulated by linear least squares and solved by constructing Equation (19):
After the plane equation is solved, the point-to-plane distance can be calculated by substituting
into the following equation, which is directly used as the residual:
Among them, the plane normal vector that makes the absolute value of the residual along the increasing direction is:
2.4. Occupancy Grid Map Construction Method
The impassable area is often a place with a steep slope. This article will mark the obstacle by calculating the slope of the laser point. If the slope is too large, it will be marked as an obstacle point, which can effectively segment the obstacle. The equation for calculating the slope of the laser point is:
Among them, (
,
,
) is the laser point for calculating the slope, and (
,
,
) is the laser point in the adjacent row and the same column of the laser point on the range image. In this paper, the laser point whose slope exceeds the threshold is marked as an obstacle, indicating that the area is impassable. The schematic diagram is shown in
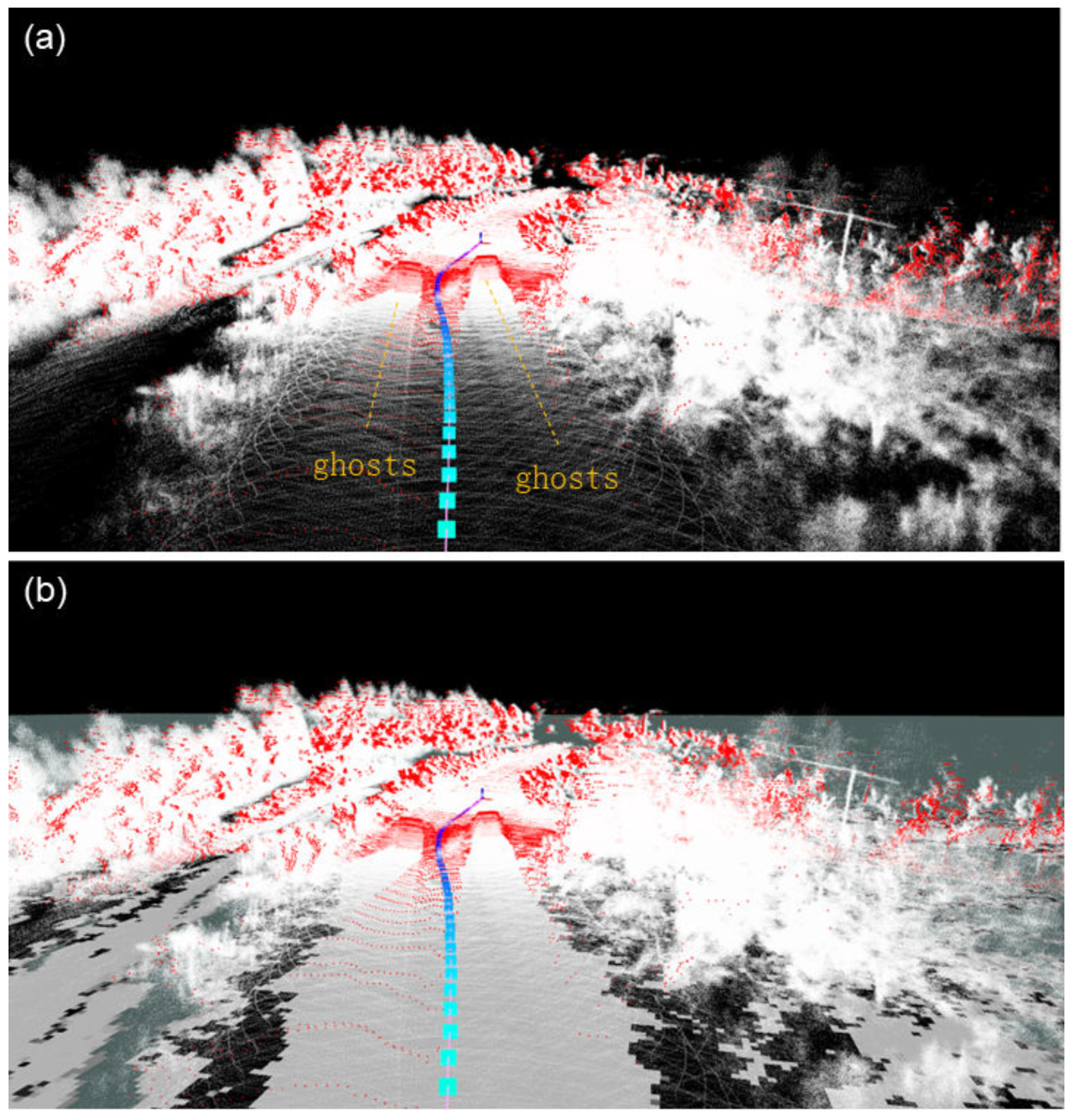
Figure 7, where the part marked in red will be regarded as an obstacle point cloud. It can be seen in the figure that the single point cloud observation of the frame will have blind spots due to the angle problem, and it is necessary to integrate the information of multiple frames to construct an accurate navigation map.
Project the point cloud marked with slope obstacles to the two-dimensional elevation grid map and the occupancy grid map. Binary data are occupied by obstacles. When the point cloud is projected to the grid, if the laser point has been marked as an obstacle according to the slope, it is directly marked in the corresponding occupied grid, and the maximum height and minimum height projected to the corresponding elevation grid are recorded at the same time. When a grid is projected by the laser point, it can be called observable, and the height difference of all observable grids is calculated one by one. If the height difference is greater than the threshold, it will be marked in the occupied grid, as shown in
Figure 8. A schematic diagram of the projection of a single point cloud frame to the occupancy grid map, that is, the grid with a large slope or a large height difference in the grid is marked as the occupied grid and represented by a red border.
This paper expresses the global occupancy grid map by introducing occupancy probability. Different from 2D LiDAR SLAM, this paper has already marked the grid with obstacles, so there is no need to use the hitting point or passing point of the laser beam to carry out update. In order to avoid the huge amount of calculation in the 3D scene, we use binary Bayesian filtering to update the occupancy probabilities. We assume that occupancy values between grids are independent and establish a posterior probability for each occupied grid
:
where
and
represent the pose and occupancy observations, respectively, from the first to the
k frame (binary observations, that is, whether it is an obstacle or not); that is, infer the occupied grid from the pose and occupancy observations of all historical frames. For Equation (23), using the Bayesian formula, we can obtain:
Since the observations are independent of each other and are only related to the pose and state at the current moment, and the grid state is simultaneously related to the pose and state at a certain moment, the above equation can be rewritten as:
Furthermore, using the Bayesian formula on the above equation, we obtain:
Then, the probability ratio is:
Take the logarithm of both sides:
Define Log Odds Ratio to better describe:
Then, Equation (28) can be rewritten as:
where
is the inferred grid occupancy probability logarithm from frames 1 to
k,
is the inferred grid occupancy probability logarithm from frames 1 to
, and
is the grid occupancy probability observed in the
k frame The number of comparisons,
, is the number of the prior grid occupancy probability ratios.
When the grid is observed in a certain frame, the occupancy probability logarithm of the grid observed in this frame is added, and then converted to the occupancy probability by the following:
2.5. Enhanced Registration
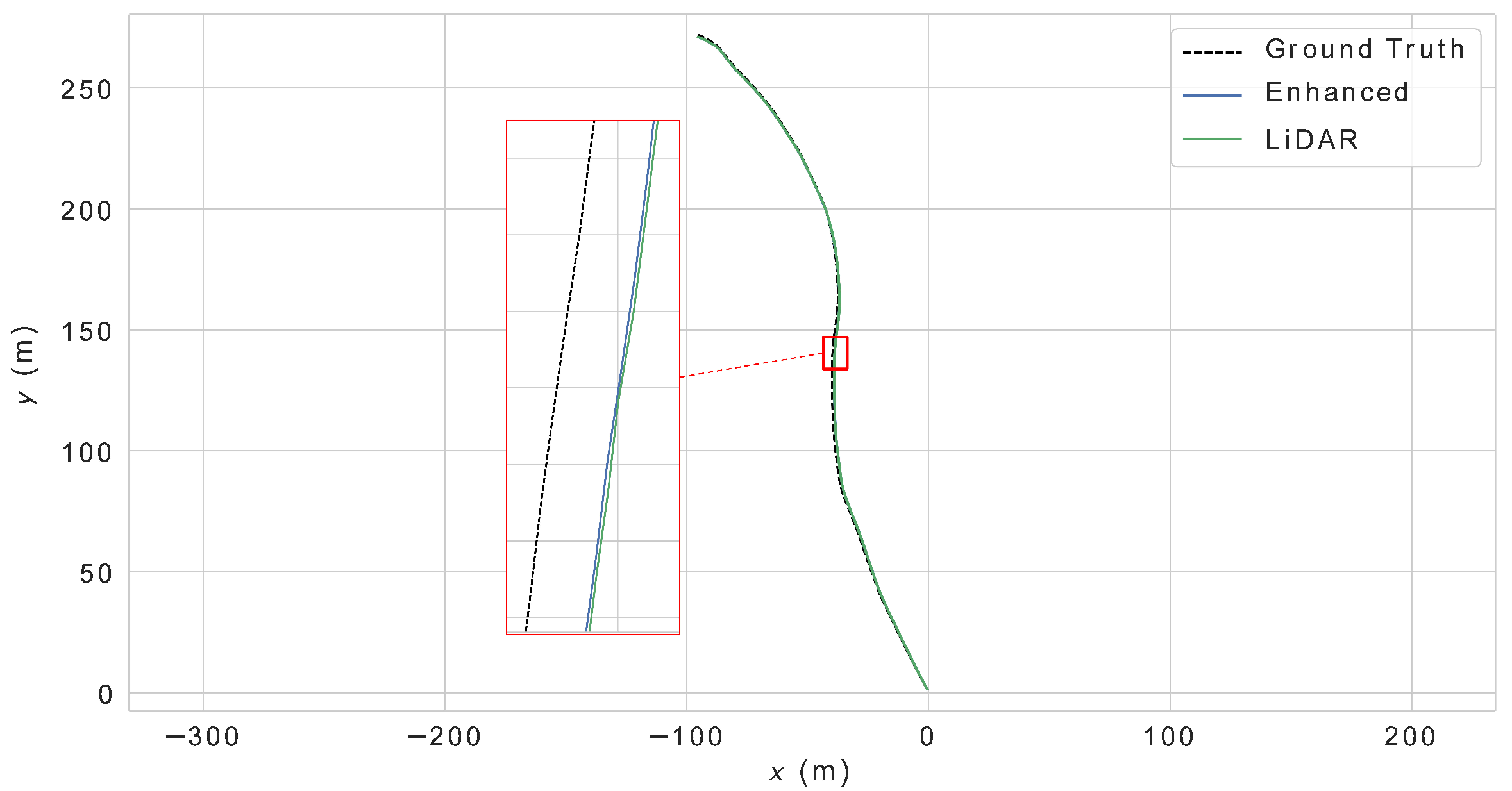
SLAM is simultaneous localization and mapping, in which Localization and Mapping are two independent modules, but they are simultaneously estimated. When all sensors are gathered for pose estimation, feeding back the constructed historical map to the localization module can not only further improve the localization accuracy, but also improve the consistency of the map because the current localization and environment observations are also inserted into the map for updates.
The feedback from the map to the localization module is the essence of SLAM. The common feedback method is to construct a local map to construct a scan-to-map constraint, that is, the constraint edge outside the window mentioned above. Although the variables outside the window cannot be optimized again, we constructed a grid map can also provide additional feedback information. The following mainly discusses the feedback method of the two-dimensional grid map.
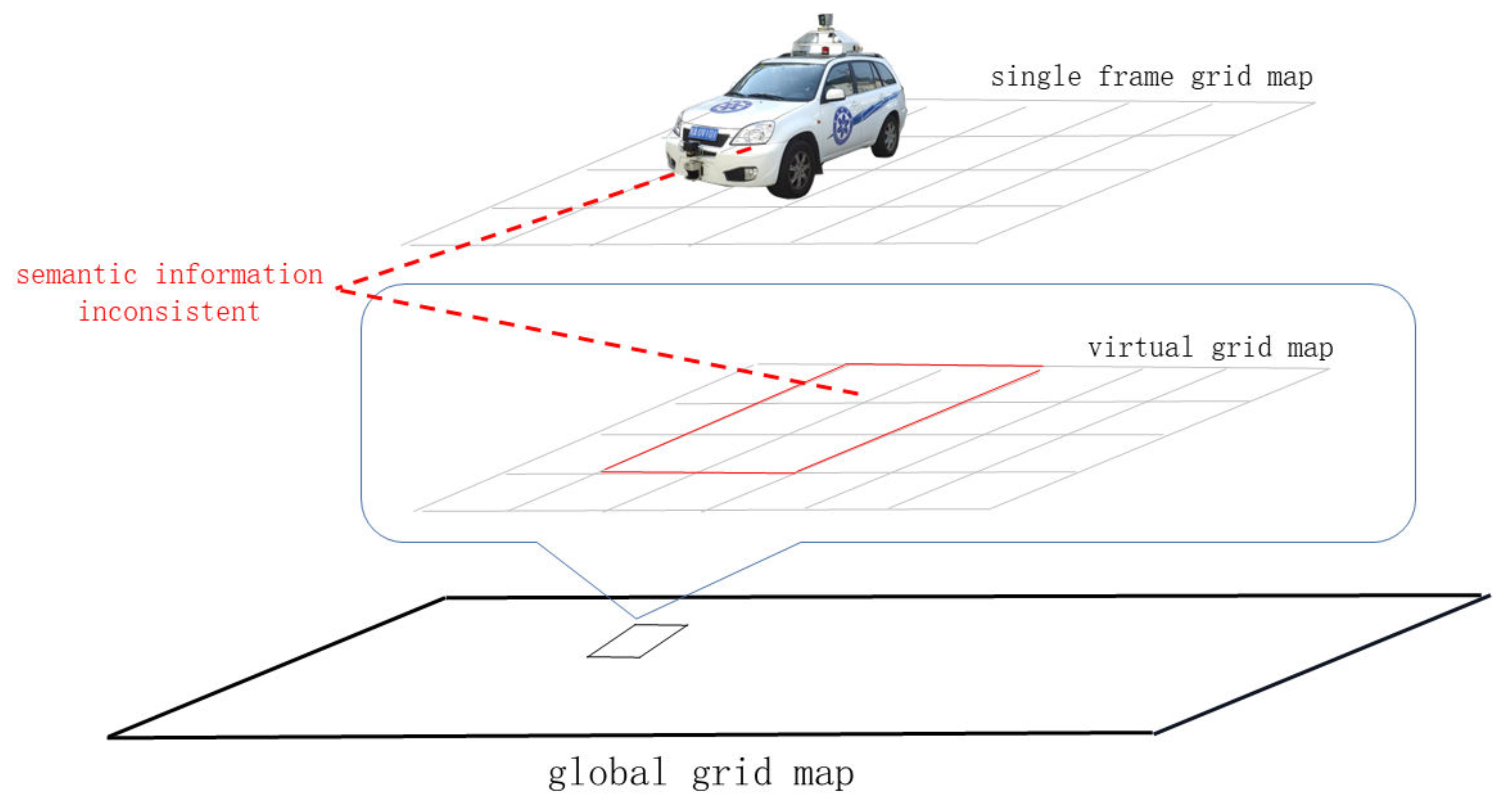
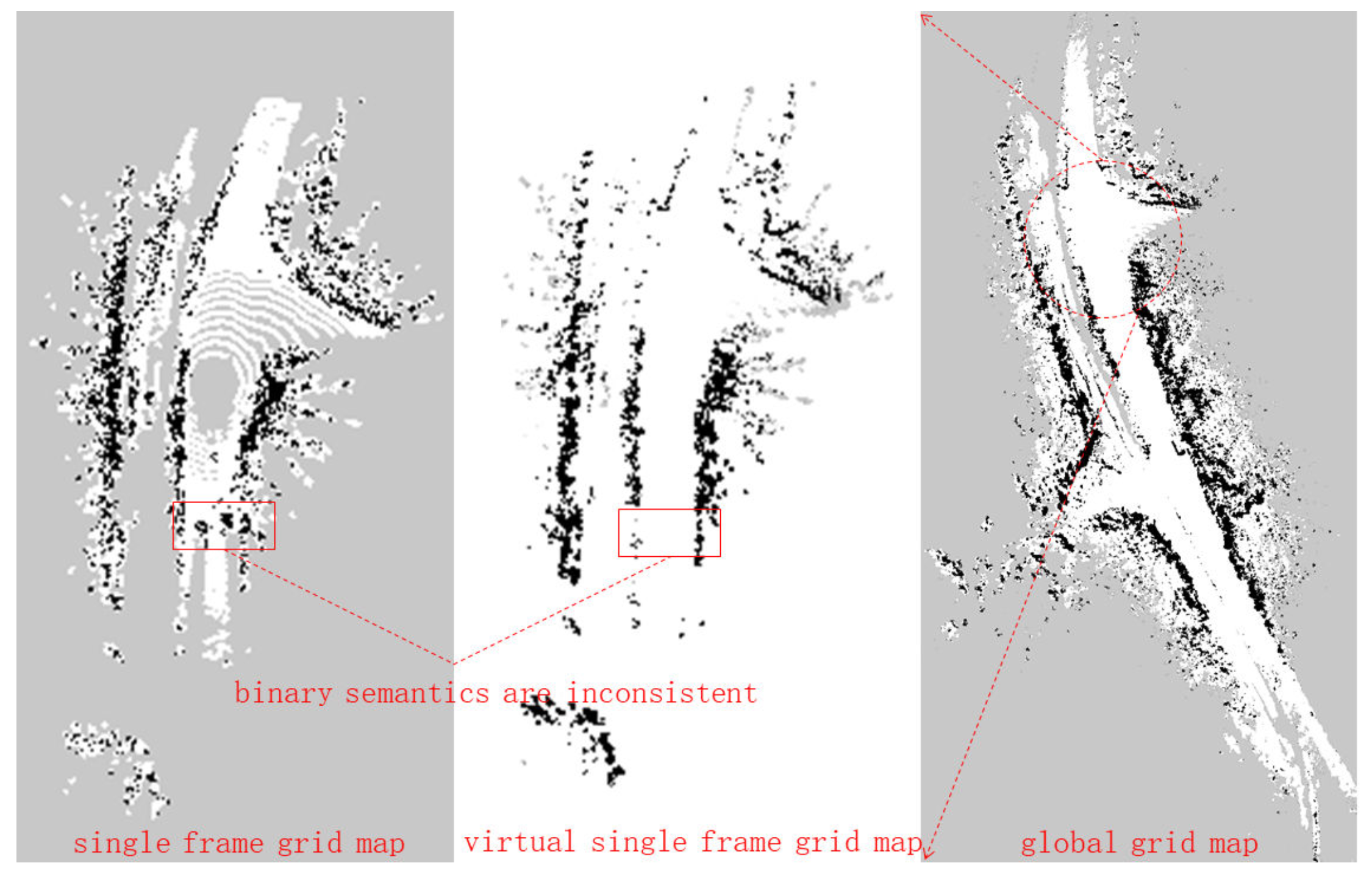
The probability grid map actually gives semantic information to a certain extent, that is, the binary semantics of whether the area is an obstacle, so this information can be used to improve the accuracy of point cloud registration (enhanced registration). In the part of the constraint edge outside the window, this paper constructs the registration constraint of scan-to-map on the LiDAR constraint, in which the map part is constructed using the keyframes outside the sliding window. Since these frames are no longer involved in the optimization, the local maps constructed from keyframes are also not adjusted. Then, during scan-to-map registration, it is very reasonable to weight each feature point by drawing on the occupancy grid map of the current frame and the obstacle occupancy information of the global occupancy grid map. The weight of each constraint can be set as:
where
is the Huber robust kernel function, whose definition is shown in Equation (33), and
is the semantic weight of the matching point between the current frame and the global map with binary semantic labels, whose definition is shown in Equation (34):
Among them,
and
are the semantic labels of the current frame and the next pair of matching points in the global coordinate system. For matching points with consistent semantics, the weight of
is given. In the program implementation,
can be set according to the occupancy probability value.
Figure 9 is the illustration of the enhanced registration. By generating a virtual single-frame occupied grid map from the global map, a binary semantic comparison is made with the occupied grid map of this frame. Because dynamic obstacles have less impact on the global grid map, the area where the dynamic obstacle is located is likely to be semantically inconsistent. According to Equation (34), the semantic weight of the laser point registration in this area will generate a very small value to reduce the registration process effects of small dynamic obstacles.