Analyzing Spatial Variations of Cloud Attenuation by a Network of All-Sky Imagers
Abstract
1. Introduction
2. Materials
2.1. Reference Measurements of Solar Irradiance
2.2. Atmospheric Conditions and Datasets
3. Methods
3.1. Reference Analysis Approaches
3.2. Development of the ASI Network’s Cloud Modeling Procedure
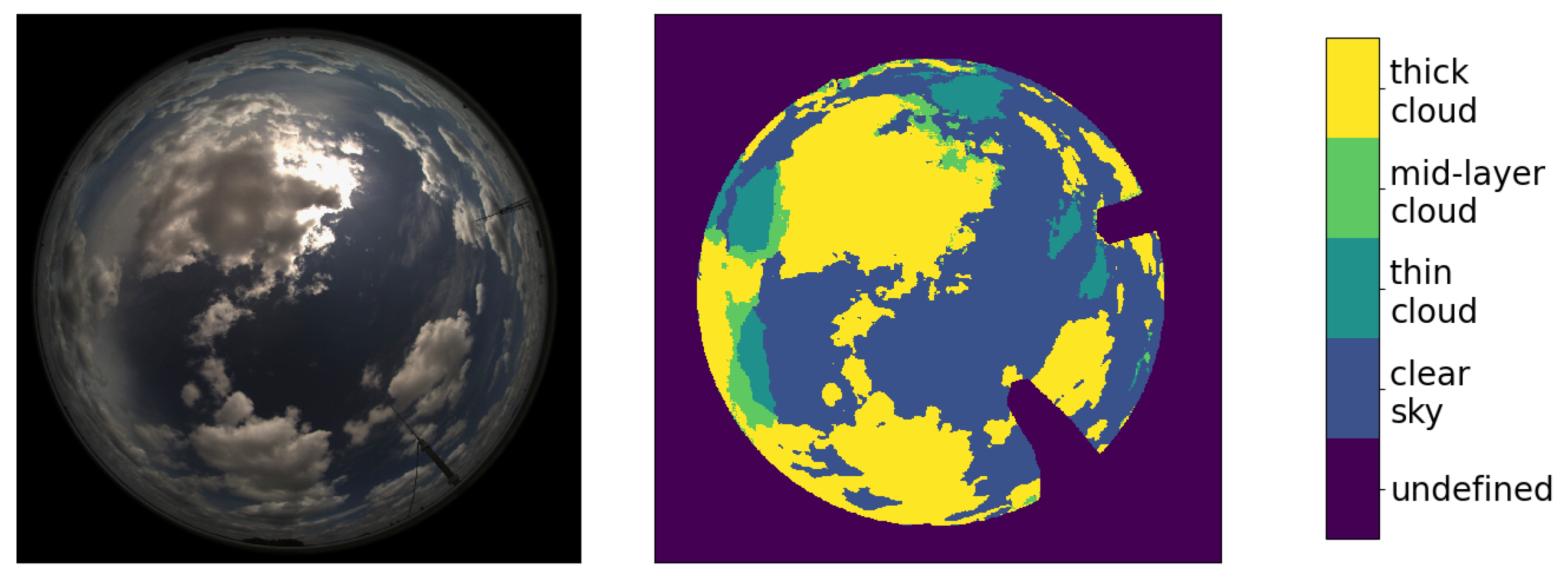
3.2.1. Cloud Classification and Cloud Mapping
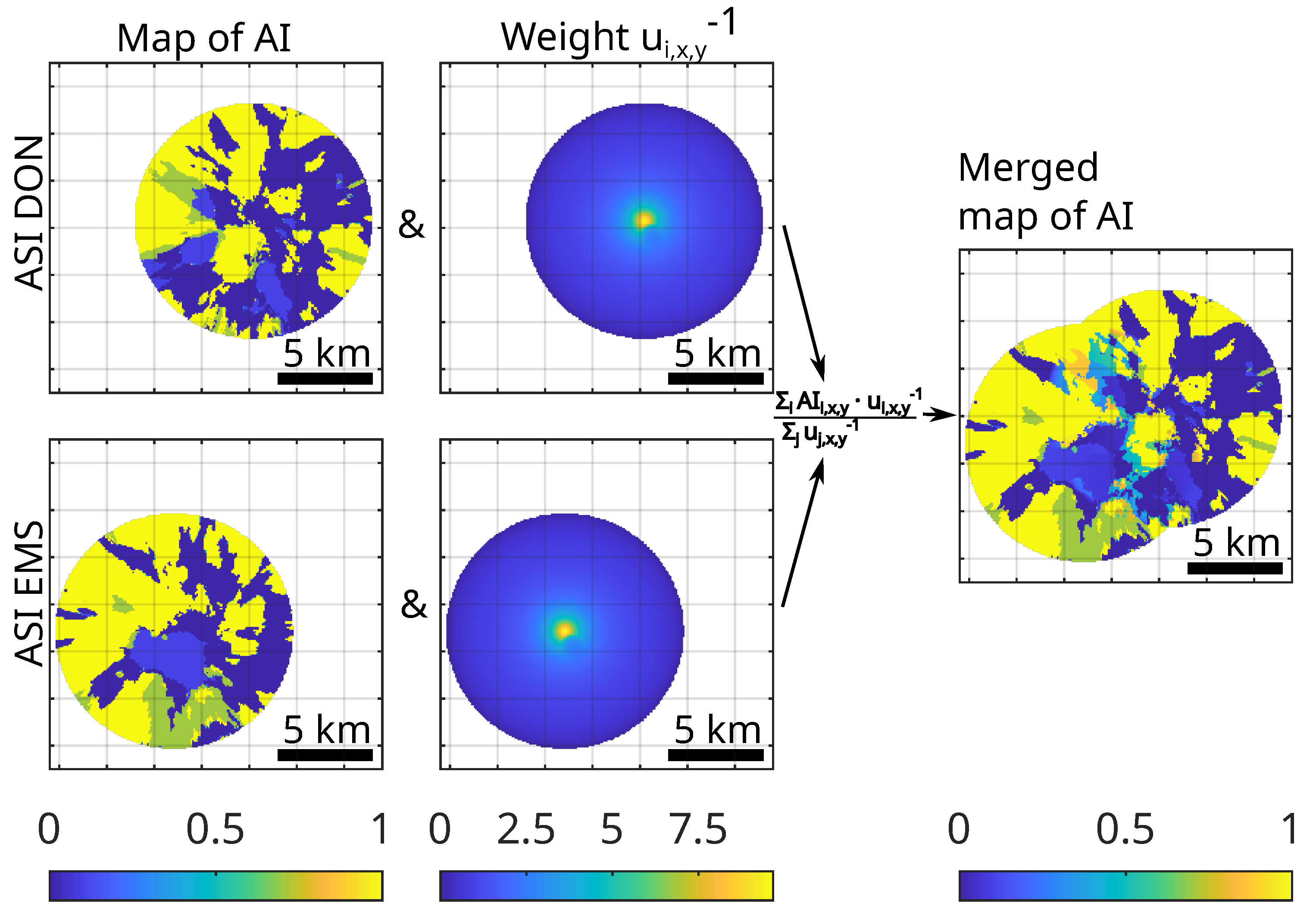
3.2.2. Merging Maps of Attenuation Index
3.2.3. Clear Sky DNI
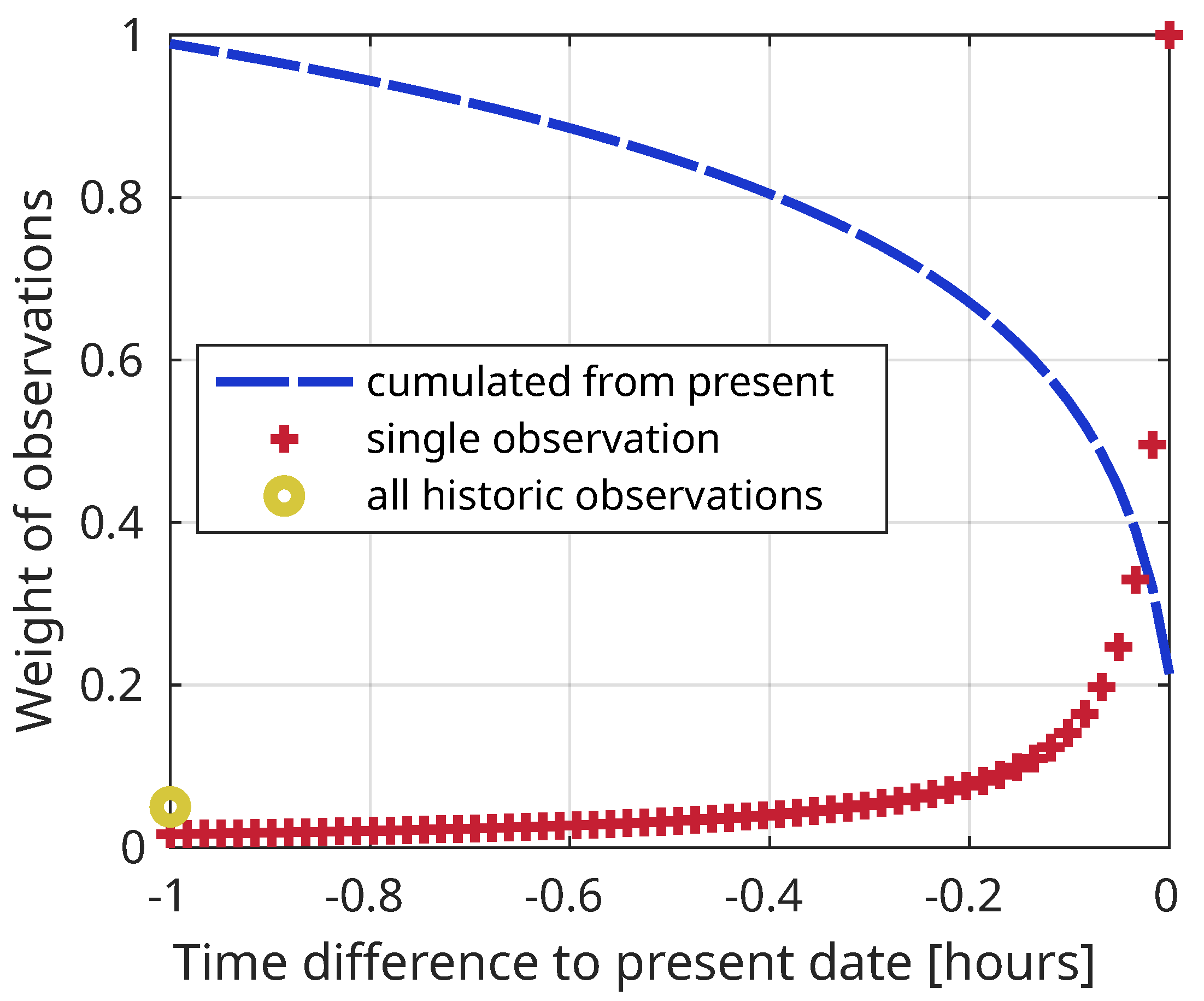
3.2.4. Assigning Cloud Attenuation
4. Results and Discussion
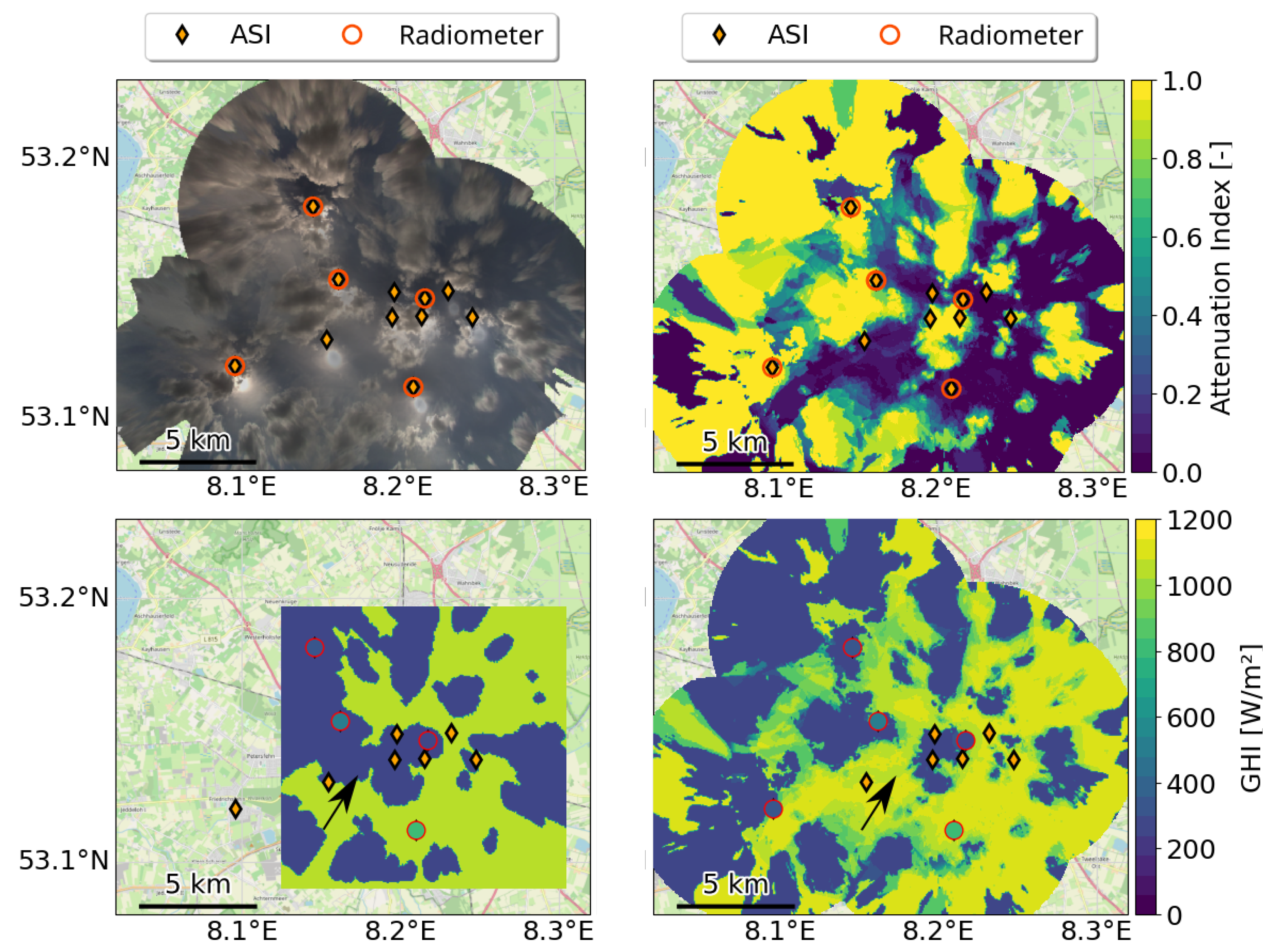
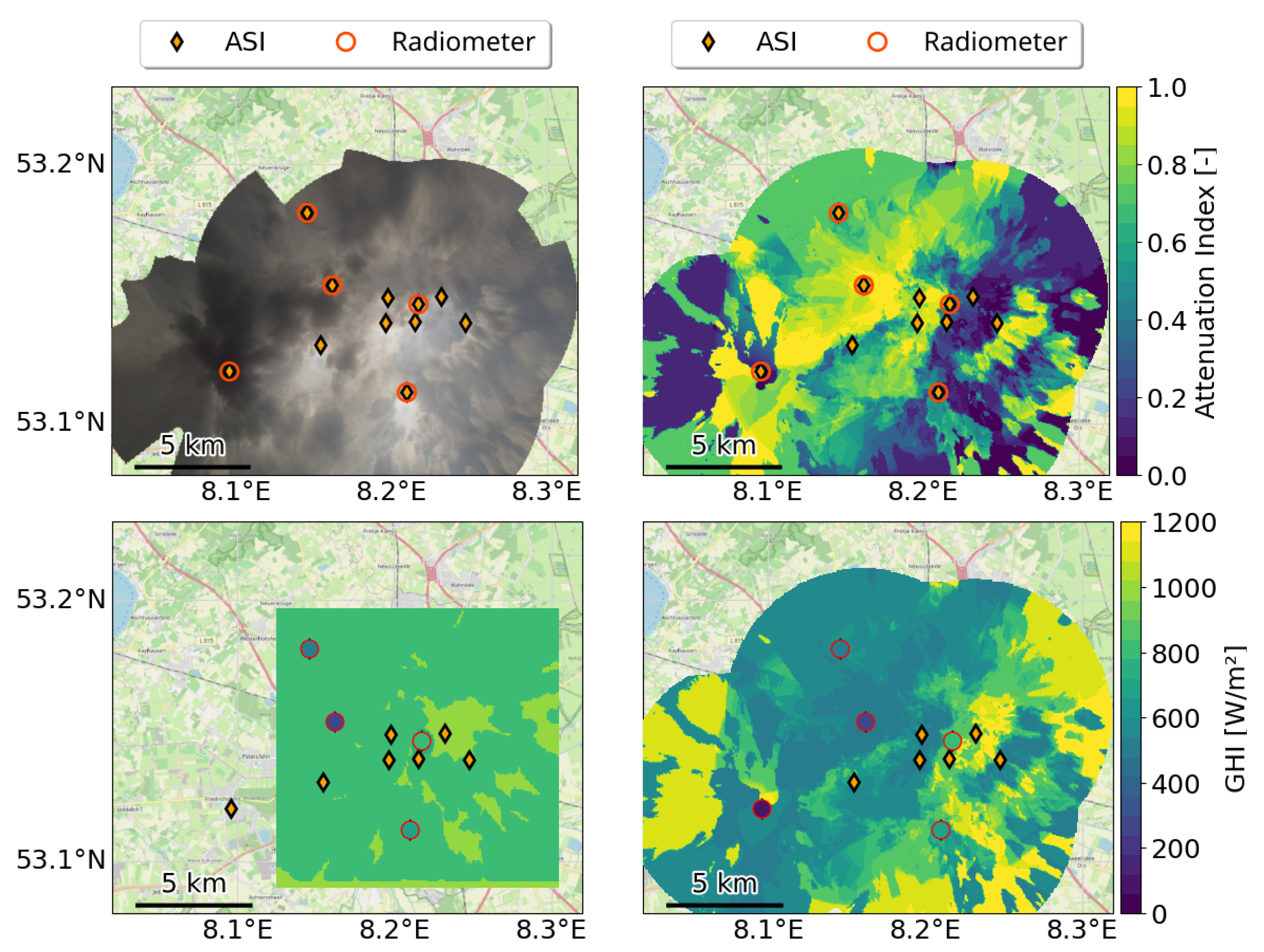
4.1. Maps of Attenuation Index and GHI in Different Cloud Conditions
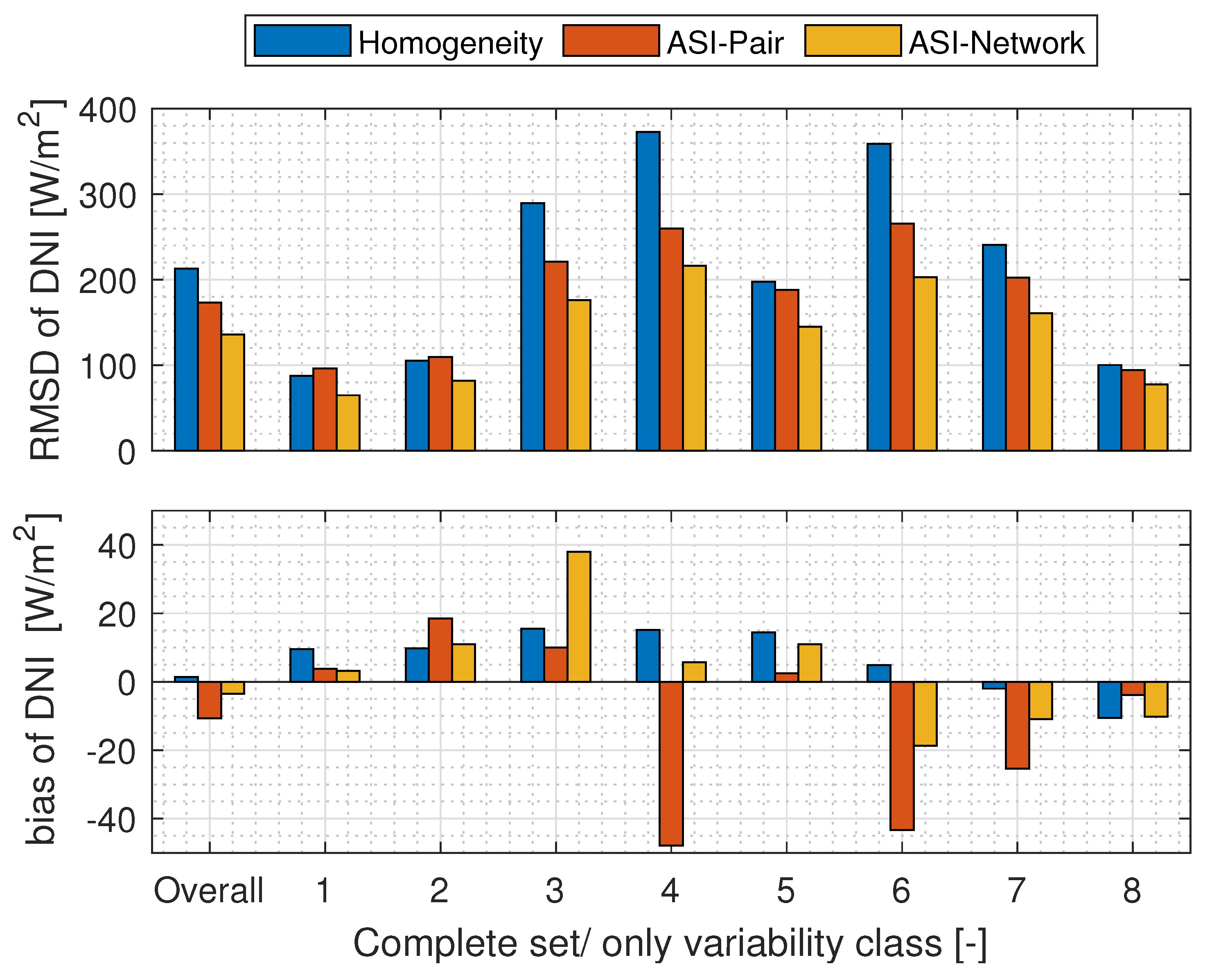
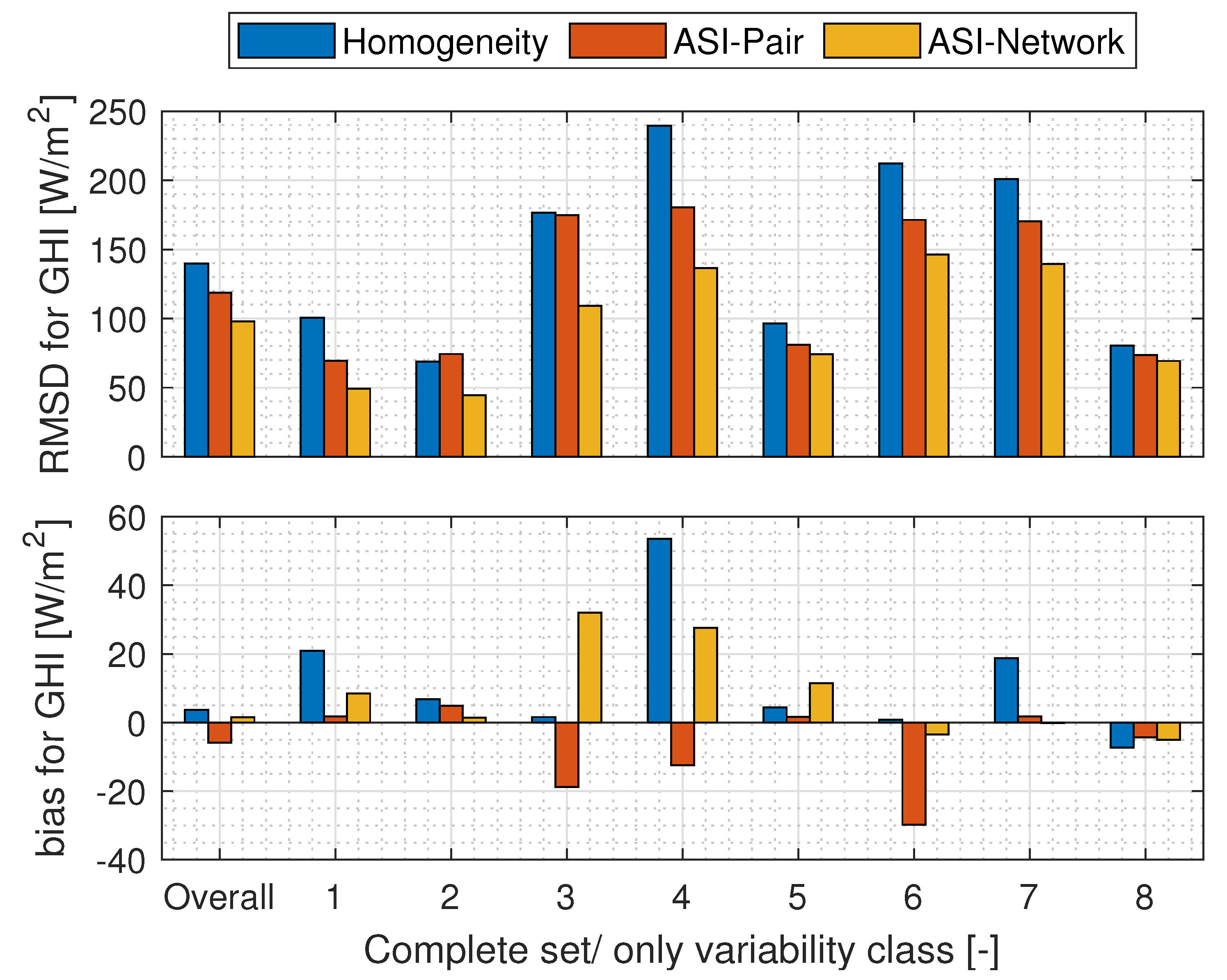
4.2. Performance Overall and by Temporal Variability Class
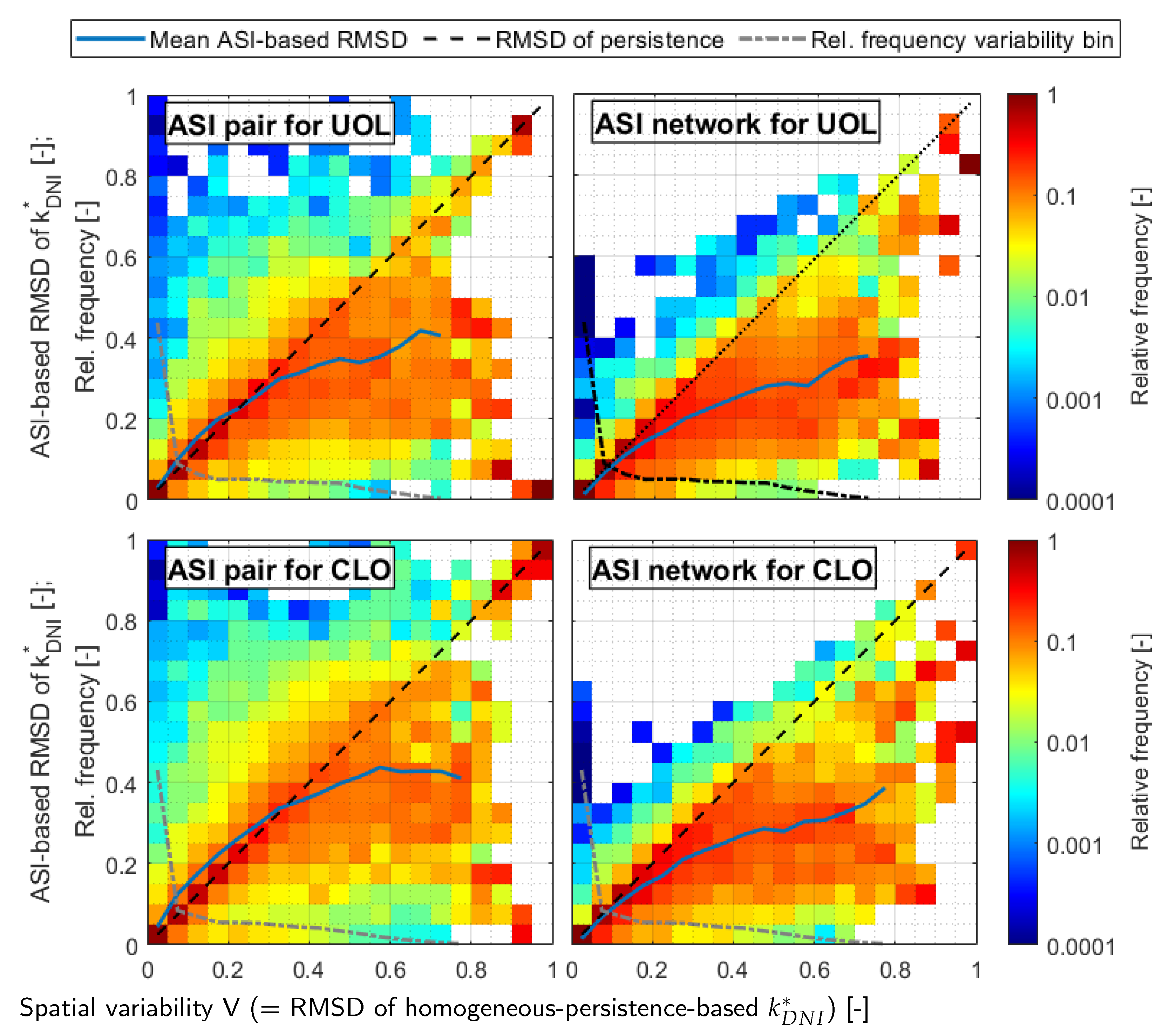
4.3. Influence of Spatial Variability on the Estimations’ Errors
4.4. Correlation of Predicted and Measured DNI
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Estimating the Uncertainty in Maps of the Attenuation Index
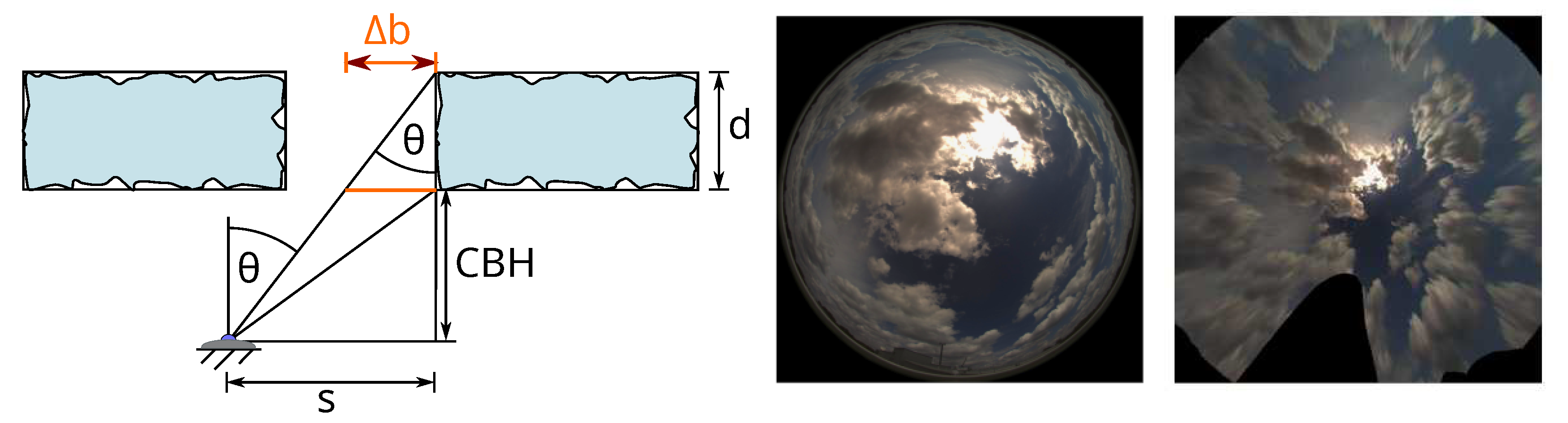

Appendix B. Derivation of the Uncertainty Related to Perspective Errors
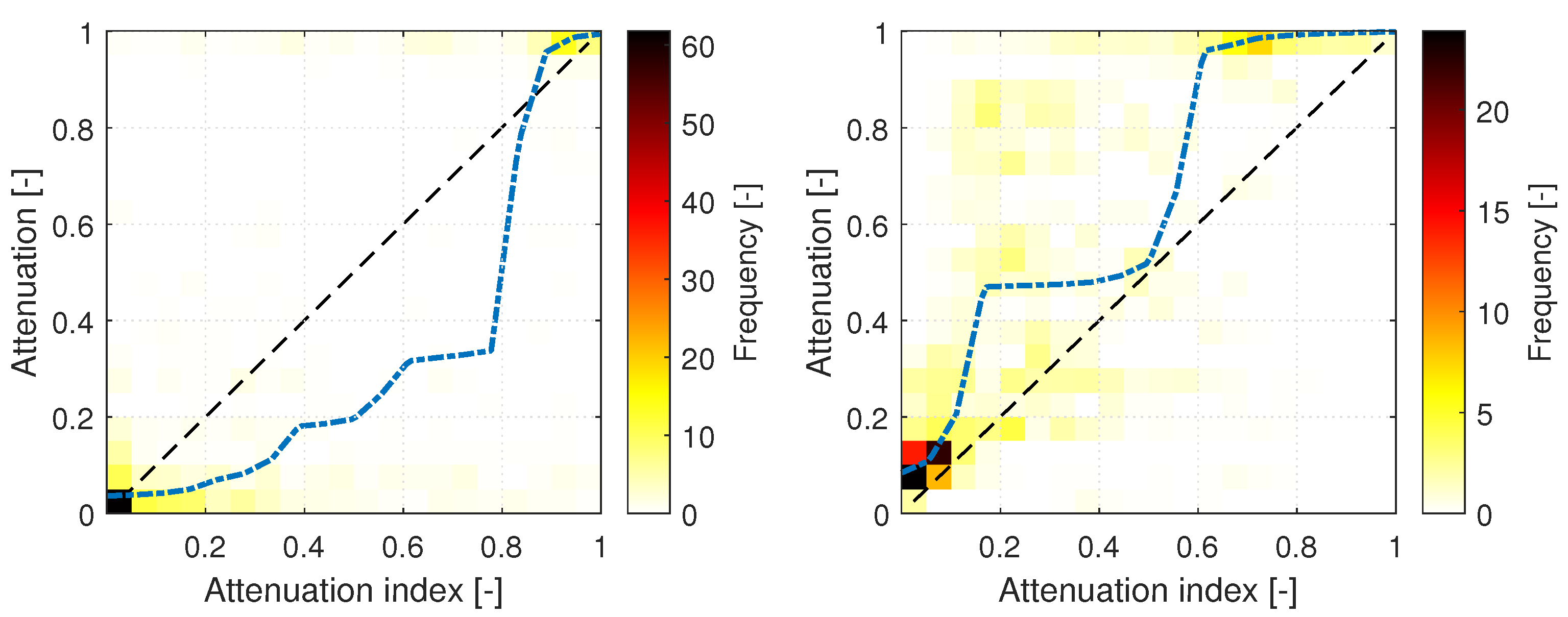
Appendix C. A Piecewise Linear Fit Function for the Relationship of and
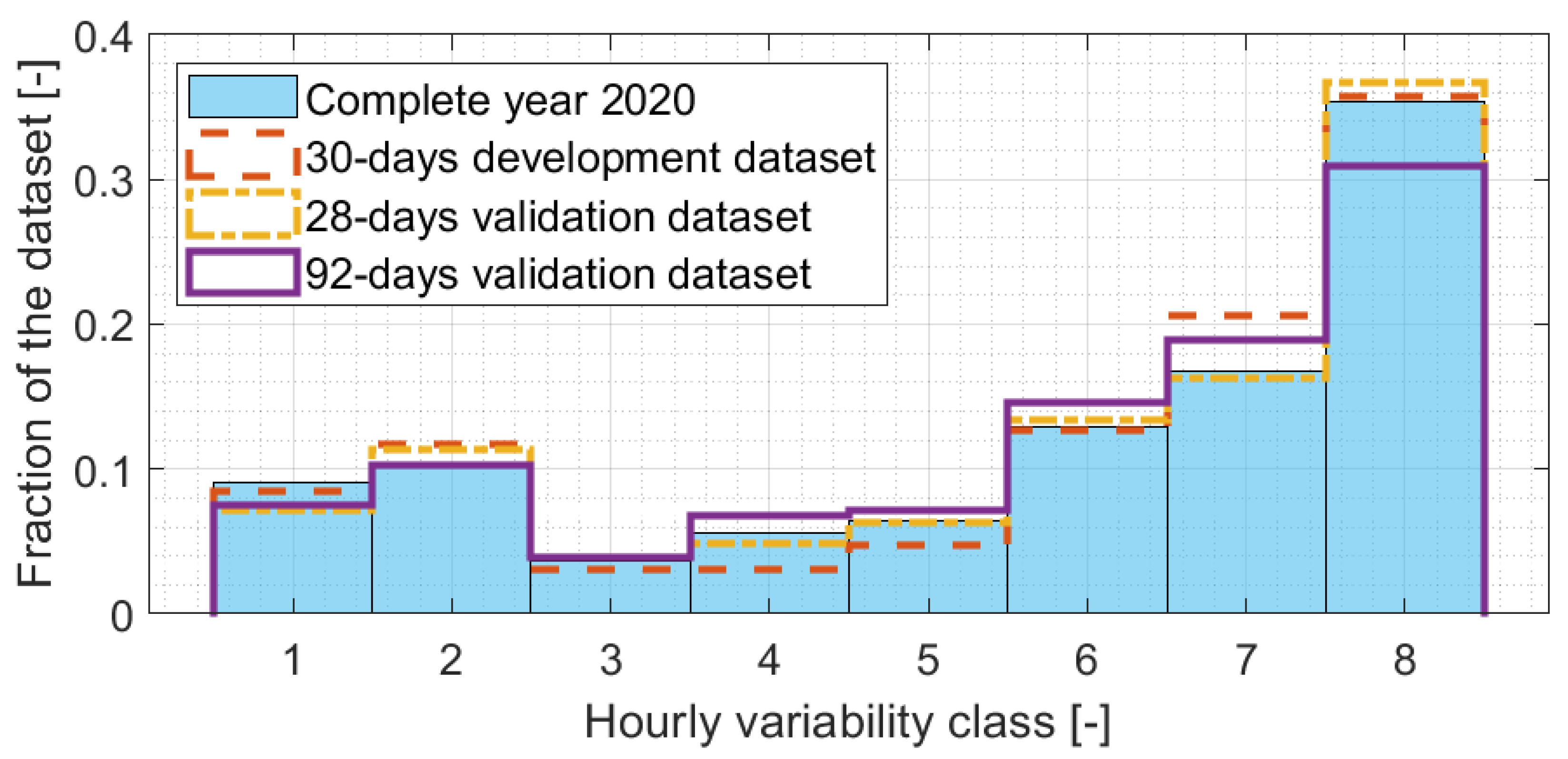
Appendix D. Definition of Representative Datasets
References
- Mahdavi, N.; Braslavsky, J.H.; Seron, M.M.; West, S.R. Model predictive control of distributed air-conditioning loads to compensate fluctuations in solar power. IEEE Trans. Smart Grid 2017, 8, 3055–3065. [Google Scholar] [CrossRef]
- Ghosh, S.; Rahman, S.; Pipattanasomporn, M. Distribution voltage regulation through active power curtailment with PV inverters and solar generation forecasts. IEEE Trans. Sustain. Energy 2016, 8, 13–22. [Google Scholar] [CrossRef]
- Saleh, M.; Meek, L.; Masoum, M.A.S.; Abshar, M. Battery-Less Short-Term Smoothing of Photovoltaic Generation Using Sky Camera. IEEE Trans. Ind. Inform. 2018, 14, 403–414. [Google Scholar] [CrossRef]
- Kaur, A.; Nonnenmacher, L.; Pedro, H.T.; Coimbra, C.F. Benefits of solar forecasting for energy imbalance markets. Renew. Energy 2016, 86, 819–830. [Google Scholar] [CrossRef]
- Ryu, A.; Ishii, H.; Hayashi, Y. Battery smoothing control for photovoltaic system using short-term forecast with total sky images. Electr. Power Syst. Res. 2020, 190, 106645. [Google Scholar] [CrossRef]
- Kurzrock, F.; Hochebner, A.; Millerioux, Q.; Schmutz, N.; Reinhardt, M.; Acevedo, W.; Potthast, R. Hour-scale cloud cover forecasting using WRF and an infrared all-sky imager. In Proceedings of the EMS Annual Meeting 2022, Bonn, Germany, 5–9 September 2022. [Google Scholar]
- Hammer, A.; Nouri, B. Advanced weather forecasting for Renewable Energy System applications: Multi-source observations to improve solar forecasting within the Smart4Res project. In Proceedings of the ISGAN—International Smart Grid Action Network, Smart4RES Webinar Series No. 3.2 Data Observation & Assimilation, Online, 29 April 2021. [Google Scholar]
- Huxley, O.T. Measuring the Uncertainty Associated with Estimating National Photovoltaic Electricity Generation: A Great Britain Case Study. Ph.D. Thesis, University of Sheffield, Sheffield, UK, 19 July 2021. [Google Scholar]
- Sengupta, M.; Habte, A.; Wilbert, S.; Gueymard, C.; Remund, J. Best Practices Handbook for the Collection and Use of Solar Resource Data for Solar Energy Applications; Technical Report; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2021.
- Bright, J.M.; Killinger, S.; Lingfors, D.; Engerer, N.A. Improved satellite-derived PV power nowcasting using real-time power data from reference PV systems. Sol. Energy 2018, 168, 118–139. [Google Scholar] [CrossRef]
- Benz, T.; Dickert, J.; Erbert, M.; Erdmann, N.; Johae, C.; Katzenbach, B.; Glaunsinger, W.; Müller, H.; Schegner, P.; Schwarz, J. Der Zellulare Ansatz—Grundlage einer Erfolgreichen, Regionen Übergreifenden Energiewende; Technical Report; VDE e.V.—Verband der Elektrotechnik Elektronik Informationstechnik: Frankfurt am Main, Germany, 2015. [Google Scholar]
- Kleineidam, G.; Krasser, M.; Reischböck, M. The cellular approach: Smart energy region Wunsiedel. Testbed for smart grid, smart metering and smart home solutions. Electr. Eng. 2016, 98, 335–340. [Google Scholar] [CrossRef]
- Volk, K.; Rupp, L.; Konermann, M. Grid-Control—Optimiertes Engpassmanagement durch Dynamischen-Quotenbasierten Netzampelansatz; Technical Report; Netze BW GmbH: Stuttgart, Germany, 2018. [Google Scholar]
- Nordmann, T. PV Eigenverbrauch und Eigenverbrauchsgemeinschaften Energiepolitik nach Schweizer Art–Ein Werkstattbericht. In Proceedings of the 34. PV-Symposium Bad Staffelstein, Bad Staffelstein, Germany, 19–21 March 2019; pp. 135–145. [Google Scholar]
- Sun, C.; Sun, F.; Moura, S.J. Nonlinear predictive energy management of residential buildings with photovoltaics & batteries. J. Power Sources 2016, 325. [Google Scholar] [CrossRef]
- Wille-Haussmann, B.; Brunner, M.; Gerhardt, N.; ETG, M.K.; Mayrhofer, P.; LEW, A.P.; Rummeni, J. Wärme-und Kälteversorgung in Städten und Regionen mit Hohen Anteilen an Erneuerbaren Energien in der Stromversorgung. In Proceedings of the VDE Kongress, Frankfurt am Main, Germany, 20–21 October 2014. Authors: Thank you this is fine. [Google Scholar]
- Fischer, D.; Madani, H. On heat pumps in smart grids: A review. Renew. Sustain. Energy Rev. 2017, 70, 342–357. [Google Scholar] [CrossRef]
- Lazos, D.; Sproul, A.B.; Kay, M. Optimisation of energy management in commercial buildings with weather forecasting inputs: A review. Renew. Sustain. Energy Rev. 2014, 39, 587–603. [Google Scholar] [CrossRef]
- Uebermasser, S.; Groiss, C.; Einfalt, A.; Thie, N.; Vasconcelos, M.; Helguero, J.; Laaksonen, H.; Hovila, P. Requirements for coordinated ancillary services covering different voltage levels. CIRED—Open Access Proc. J. 2017, 2017, 1421–1424. [Google Scholar] [CrossRef]
- Nouri, B.; Wilbert, S.; Blum, N.; Kuhn, P.; Schmidt, T.; Yasser, Z.; Schmidt, T.; Zarzalejo, L.F.; Lopes, F.M.; Silva, H.G.; et al. Evaluation of an All Sky Imager Based Nowcasting System for Distinct Conditions and Five sites. AIP Conf. Proc. 2020, 2303, 180006. [Google Scholar] [CrossRef]
- Schmidt, T.; Kalisch, J.; Lorenz, E.; Heinemann, D. Evaluating the spatio-temporal performance of sky-imager-based solar irradiance analysis and forecasts. Atmos. Chem. Phys. 2016, 16, 3399–3412. [Google Scholar] [CrossRef]
- Nouri, B.; Kuhn, P.; Wilbert, S.; Prahl, C.; Pitz-Paal, R.; Blanc, P.; Schmidt, T.; Yasser, Z.; Santigosa, L.R.; Heineman, D. Nowcasting of DNI maps for the solar field based on voxel carving and individual 3D cloud objects from all sky images. AIP Conf. Proc. 2018, 2033, 190011. [Google Scholar] [CrossRef]
- Peng, Z.; Yu, D.; Huang, D.; Heiser, J.; Yoo, S.; Kalb, P. 3D cloud detection and tracking system for solar forecast using multiple sky imagers. Sol. Energy 2015, 118, 496–519. [Google Scholar] [CrossRef]
- Nouri, B.; Noureldin, K.; Schlichting, T.; Wilbert, S.; Hirsch, T.; Schroedter-Homscheidt, M.; Kuhn, P.; Kazantzidis, A.; Zarzalejo, L.F.; Blanc, P.; et al. Optimization of parabolic trough power plant operations in variable irradiance conditions using all sky imagers. Sol. Energy 2020, 198, 434–453. [Google Scholar] [CrossRef]
- Howie, R.M.; Paxman, J.; Bland, P.A.; Towner, M.C.; Cupak, M.; Sansom, E.K.; Devillepoix, H.A. How to build a continental scale fireball camera network. Exp. Astron. 2017, 43, 237–266. [Google Scholar] [CrossRef]
- Spurny, P. Photographic monitoring of fireballs in Central Europe. In Proceedings of the Optical Science, Engineering and Instrumentation ’97, Small Spacecraft, Space Environments, and Instrumentation Technologies, San Diego CA, USA, 27 July–1 August 1997; pp. 144–155. [Google Scholar] [CrossRef]
- Bhatt, A.; Kendall, E.; Zalles, D.; Baumgardner, J.; Marshall, R.; Kaltenbacher, E. All Sky Imager Network for Science and Education. In Proceedings of the AGU Fall Meeting Abstracts, San Francisco, CA, USA, 3–7 December 2012; pp. ED33C–0775. [Google Scholar]
- Aides, A.; Levis, A.; Holodovsky, V.; Schechner, Y.Y.; Althausen, D.; Vainiger, A. Distributed Sky Imaging Radiometry and Tomography. In Proceedings of the 2020 IEEE International Conference on Computational Photography (ICCP), Saint Louis, MO USA, 24–26 April 2020; pp. 1–12. [Google Scholar] [CrossRef]
- SERIS. Sky Cameras. Available online: https://www.solar-repository.sg/sky-cameras (accessed on 8 July 2020).
- Chu, Y.; Li, M.; Pedro, H.T.C.; Coimbra, C.F.M. A network of sky imagers for spatial solar irradiance assessment. Renew. Energy 2022, 187, 1009–1019. [Google Scholar] [CrossRef]
- Straver, F. Pleidooi: Wolkencameras Kunnen Piek en Dip in Stroomvoorziening Voorkomen. Available online: https://www.trouw.nl/duurzaamheid-natuur/pleidooi-wolkencamera-s-kunnen-piek-en-dip-in-stroomvoorziening-voorkomen~b5486ffa/ (accessed on 29 November 2021).
- Schmidt, T.; Heinemann, D.; Vogt, T.; Blum, N.; Nouri, B.; Wilbert, S.; Kuhn, P. Energiemeteorologisches Wolkenkameranetzwerk für die Hochaufgelöste Kurzfristprognose der Solaren Einstrahlung. In Proceedings of the DACH-Tagung, Garmisch-Partenkirchen, Germany, 18–22 March 2019. [Google Scholar]
- Mejia, F.A.; Kurtz, B.; Levis, A.; de la Parra, Í.; Kleissl, J. Cloud tomography applied to sky images: A virtual testbed. Sol. Energy 2018, 176, 287–300. [Google Scholar] [CrossRef]
- Elsinga, B.; van Sark, W.G.J.H.M. Short-term peer-to-peer solar forecasting in a network of photovoltaic systems. Appl. Energy 2017, 206, 1464–1483. [Google Scholar] [CrossRef]
- Lorenzo, A.T.; Holmgren, W.F.; Cronin, A.D. Irradiance forecasts based on an irradiance monitoring network, cloud motion, and spatial averaging. Sol. Energy 2015, 122, 1158–1169. [Google Scholar] [CrossRef]
- Chen, X.; Du, Y.; Lim, E.; Wen, H.; Jiang, L. Sensor network based PV power nowcasting with spatio-temporal preselection for grid-friendly control. Appl. Energy 2019, 255, 113760. [Google Scholar] [CrossRef]
- Blum, N.B.; Wilbert, S.; Nouri, B.; Lezaca, J.; Huckebrink, D.; Kazantzidis, A.; Heinemann, D.; Zarzalejo, L.F.; Jiménez, M.J.; Pitz-Paal, R. Measurement of diffuse and plane of array irradiance by a combination of a pyranometer and an all-sky imager. Sol. Energy 2022, 232, 232–247. [Google Scholar] [CrossRef]
- Chauvin, R.; Nou, J.; Thil, S.; Grieu, S. Modelling the clear-sky intensity distribution using a sky imager. Sol. Energy 2015, 119, 1–17. [Google Scholar] [CrossRef]
- Kurtz, B.; Kleissl, J. Measuring diffuse, direct, and global irradiance using a sky imager. Sol. Energy 2017, 141, 311–322. [Google Scholar] [CrossRef]
- Nouri, B.; Blum, N.; Wilbert, S.; Zarzalejo, L.F. A hybrid solar irradiance nowcasting approach: Combining all sky imager systems and persistence irradiance models for increased accuracy. Solar RRL 2021, 6, 2100442. [Google Scholar] [CrossRef]
- Fabel, Y.; Nouri, B.; Wilbert, S.; Blum, N.; Triebel, R.; Hasenbalg, M.; Kuhn, P.; Zarzalejo, L.F.; Pitz-Paal, R. Applying self-supervised learning for semantic cloud segmentation of all-sky images. Atmos. Meas. Tech. 2022, 15, 797–809. [Google Scholar] [CrossRef]
- Meyer, R.; Torres Butron, J.; Marquardt, G.; Schwandt, M.; Geuder, N.; Hoyer-Klick, C.; Lorenz, E.; Hammer, A.; Beyer, H.G. Combining solar irradiance measurements and various satellite-derived products to a site-specific best estimate. In Proceedings of the 14th Biennial SolarPACES Symposium, Las Vegas, NV, USA, 4–7 March 2008. [Google Scholar]
- Ramirez, L.; Hanrieder, N.; Zarzalejo, L.; Landelius, T.; Müller, S.; Homscheidt, M.S.; Wilbert, S.; Dubranna, J.; Remund, J.; Vindel, J.M. Optimized DNI forecast using combinations of nowcasting methods from the DNICast project. In Proceedings of the SolarPACES Conference, Santiago, Chile, 26–29 September 2017. [Google Scholar]
- Nguyen, D.; Kleissl, J. Stereographic methods for cloud base height determination using two sky imagers. Sol. Energy 2014, 107, 495–509. [Google Scholar] [CrossRef]
- Nouri, B.; Kuhn, P.; Wilbert, S.; Hanrieder, N.; Prahl, C.; Zarzalejo, L.; Kazantzidis, A.; Blanc, P.; Pitz-Paal, R. Cloud height and tracking accuracy of three all sky imager systems for individual clouds. Sol. Energy 2019, 177, 213–228. [Google Scholar] [CrossRef]
- Nouri, B.; Wilbert, S.; Kuhn, P.; Hanrieder, N.; Schroedter-Homscheidt, M.; Kazantzidis, A.; Zarzalejo, L.; Blanc, P.; Kumar, S.; Goswami, N. Real-Time Uncertainty Specification of All Sky Imager Derived Irradiance Nowcasts. Remote Sens. 2019, 11, 1059. [Google Scholar] [CrossRef]
- Nouri, B.; Wilbert, S.; Segura, L.; Kuhn, P.; Hanrieder, N.; Kazantzidis, A.; Schmidt, T.; Zarzalejo, L.; Blanc, P.; Pitz-Paal, R. Determination of cloud transmittance for all sky imager based solar nowcasting. Sol. Energy 2019, 181, 251–263. [Google Scholar] [CrossRef]
- Mobotix. Technical Specifications MOBOTIX Q25 Hemispheric; Data Sheet; Mobotix AG: Langmeil, Germany, 2017. [Google Scholar]
- Alonso-Montesinos, J.; Batlles, F. The use of a sky camera for solar radiation estimation based on digital image processing. Energy 2015, 90, 377–386. [Google Scholar] [CrossRef]
- West, S.R.; Rowe, D.; Sayeef, S.; Berry, A. Short-term irradiance forecasting using skycams: Motivation and development. Sol. Energy 2014, 110, 188–207. [Google Scholar] [CrossRef]
- Kazantzidis, A.; Tzoumanikas, P.; Nikitidou, E.; Salamalikis, V.; Wilbert, S.; Prahl, C. Application of simple all-sky imagers for the estimation of aerosol optical depth. AIP Conf. Proc. 2017, 1850, 140012. [Google Scholar] [CrossRef]
- Wacker, S.; Gröbner, J.; Zysset, C.; Diener, L.; Tzoumanikas, P.; Kazantzidis, A.; Vuilleumier, L.; Stöckli, R.; Nyeki, S.; Kämpfer, N. Cloud observations in Switzerland using hemispherical sky cameras. J. Geophys. Res. Atmos. 2015, 120, 695–707. [Google Scholar] [CrossRef]
- Blum, N.B.; Nouri, B.; Wilbert, S.; Schmidt, T.; Lünsdorf, O.; Stührenberg, J.; Heinemann, D.; Kazantzidis, A.; Pitz-Paal, R. Cloud height measurement by a network of all-sky imagers. Atmos. Meas. Tech. 2021, 14, 5199–5224. [Google Scholar] [CrossRef]
- Scaramuzza, D.; Martinelli, A.; Siegwart, R. A Toolbox for Easily Calibrating Omnidirectional Cameras. In Proceedings of the RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–15 October 2006; pp. 5695–5701. [Google Scholar] [CrossRef]
- Google; GeoContent; Technologies, M.; GeoBasis-DE/BKG. Google Maps. Available online: https://www.google.de/maps/@53.1571263,8.2126775,16367m/data=!3m1!1e3 (accessed on 29 November 2021).
- CSPS, C.S.P.S.G. Rotating Shadowband Irradiometer CSPS Twin-RSI Measurement Sensor for DNI, GHI and DHI; Technical Report; Concentrating Solar Power Services GmbH: Cologne, Germany, 2021. [Google Scholar]
- Forstinger, A.; Wilbert, S.; Driesse, A.; Kraas, B. Uncertainty Calculation Method for Photodiode Pyranometers. Sol. RRL 2022, 6, 2100468. [Google Scholar] [CrossRef]
- Geuder, N.; Wolfertstetter, F.; Wilbert, S.; Schüler, D.; Affolter, R.; Kraas, B.; Lüpfert, E.; Espinar, B. Screening and Flagging of Solar Irradiation and Ancillary Meteorological Data. Energy Procedia 2015, 69, 1989–1998. [Google Scholar] [CrossRef]
- Geuder, N.; Pulvermüller, B.; Vorbrugg, O. Corrections for rotating shadowband pyranometers for solar resource assessment. In Proceedings of the Solar Energy + Applications, Optical Modeling and Measurements for Solar Energy Systems II, San Diego, CA, USA, 11 September 2008. [Google Scholar] [CrossRef]
- Schroedter-Homscheidt, M.; Kosmale, M.; Jung, S.; Kleissl, J. Classifying ground-measured 1 minute temporal variability within hourly intervals for direct normal irradiances. Meteorol. Z. 2018, 27, 161–179. [Google Scholar] [CrossRef]
- Wilbert, S.; Nouri, B.; Prahl, C.; Garcia, G.; Ramirez, L.; Zarzalejo, L.; Valenzuela, R.; Ferrera, F.; Kozonek, N.; Liria, J. Application of Whole Sky Imagers for Data Selection for Radiometer Calibration. In Proceedings of the EUPVSEC, Munich, Germany, 21–24 June 2016; pp. 1493–1498. [Google Scholar] [CrossRef]
- Hasenbalg, M.; Kuhn, P.; Wilbert, S.; Nouri, B.; Kazantzidis, A. Benchmarking of six cloud segmentation algorithms for ground-based all-sky imagers. Sol. Energy 2020, 201, 596–614. [Google Scholar] [CrossRef]
- Kuhn, P.; Nouri, B.; Wilbert, S.; Hanrieder, N.; Prahl, C.; Ramirez, L.; Zarzalejo, L.; Schmidt, T.; Yasser, Z.; Heinemann, D.; et al. Determination of the optimal camera distance for cloud height measurements with two all-sky imagers. Sol. Energy 2019, 179, 74–88. [Google Scholar] [CrossRef]
- Ineichen, P.; Perez, R. A new airmass independent formulation for the Linke turbidity coefficient. Sol. Energy 2002, 73, 151–157. [Google Scholar] [CrossRef]
- Su, F.; Jiang, W.; Zhang, J.; Wang, H.; Zhang, M. A local features-based approach to all-sky image prediction. IBM J. Res. Dev. 2015, 59, 6: 1–6: 10. [Google Scholar] [CrossRef]
- Hanrieder, N.; Sengupta, M.; Xie, Y.; Wilbert, S.; Pitz-Paal, R. Modeling beam attenuation in solar tower plants using common DNI measurements. Sol. Energy 2016, 129, 244–255. [Google Scholar] [CrossRef]
- Schroedter-Homscheidt, M.; Arola, A.; Killius, N.; Lefèvre, M.; Saboret, L.; Wandji, W.; Wald, L.; Wey, E. The Copernicus atmosphere monitoring service (CAMS) radiation service in a nutshell. In Proceedings of the SOLARPACES 2016: International Conference on Concentrating Solar Power and Chemical Energy Systems, Abu Dhabi, United Arab Emirates, 11–14 October 2016; AIP Conference Proceedings 1850. pp. 11–14. [Google Scholar]
- Lefèvre, M.; Oumbe, A.; Blanc, P.; Espinar, B.; Gschwind, B.; Qu, Z.; Wald, L.; Schroedter-Homscheidt, M.; Hoyer-Klick, C.; Arola, A.; et al. McClear: A new model estimating downwelling solar radiation at ground level in clear-sky conditions. Atmos. Meas. Tech. 2013, 6, 2403–2418. [Google Scholar] [CrossRef]
- Marquez, R.; Coimbra, C.F.M. Proposed Metric for Evaluation of Solar Forecasting Models. J. Sol. Energy Eng. 2013, 135. [Google Scholar] [CrossRef]
- Wang, J.; Rossow, W.B.; Zhang, Y. Cloud Vertical Structure and Its Variations from a 20-Yr Global Rawinsonde Dataset. J. Clim. 2000, 13, 3041–3056. [Google Scholar] [CrossRef]
- Dong, X.; Minnis, P.; Xi, B. A Climatology of Midlatitude Continental Clouds from the ARM SGP Central Facility: Part I: Low-Level Cloud Macrophysical, Microphysical, and Radiative Properties. J. Clim. 2005, 18, 1391–1410. [Google Scholar] [CrossRef]
- Rodts, S.M.A.; Duynkerke, P.G.; Jonker, H.J.J. Size Distributions and Dynamical Properties of Shallow Cumulus Clouds from Aircraft Observations and Satellite Data. J. Atmos. Sci. 2003, 60, 1895–1912. [Google Scholar] [CrossRef]
- Sengupta, S.K.; Welch, R.M.; Navar, M.S.; Berendes, T.A.; Chen, D.W. Cumulus Cloud Field Morphology and Spatial Patterns Derived from High Spatial Resolution Landsat Imagery. J. Appl. Meteorol. Climatol. 1990, 29, 1245–1267. [Google Scholar] [CrossRef]
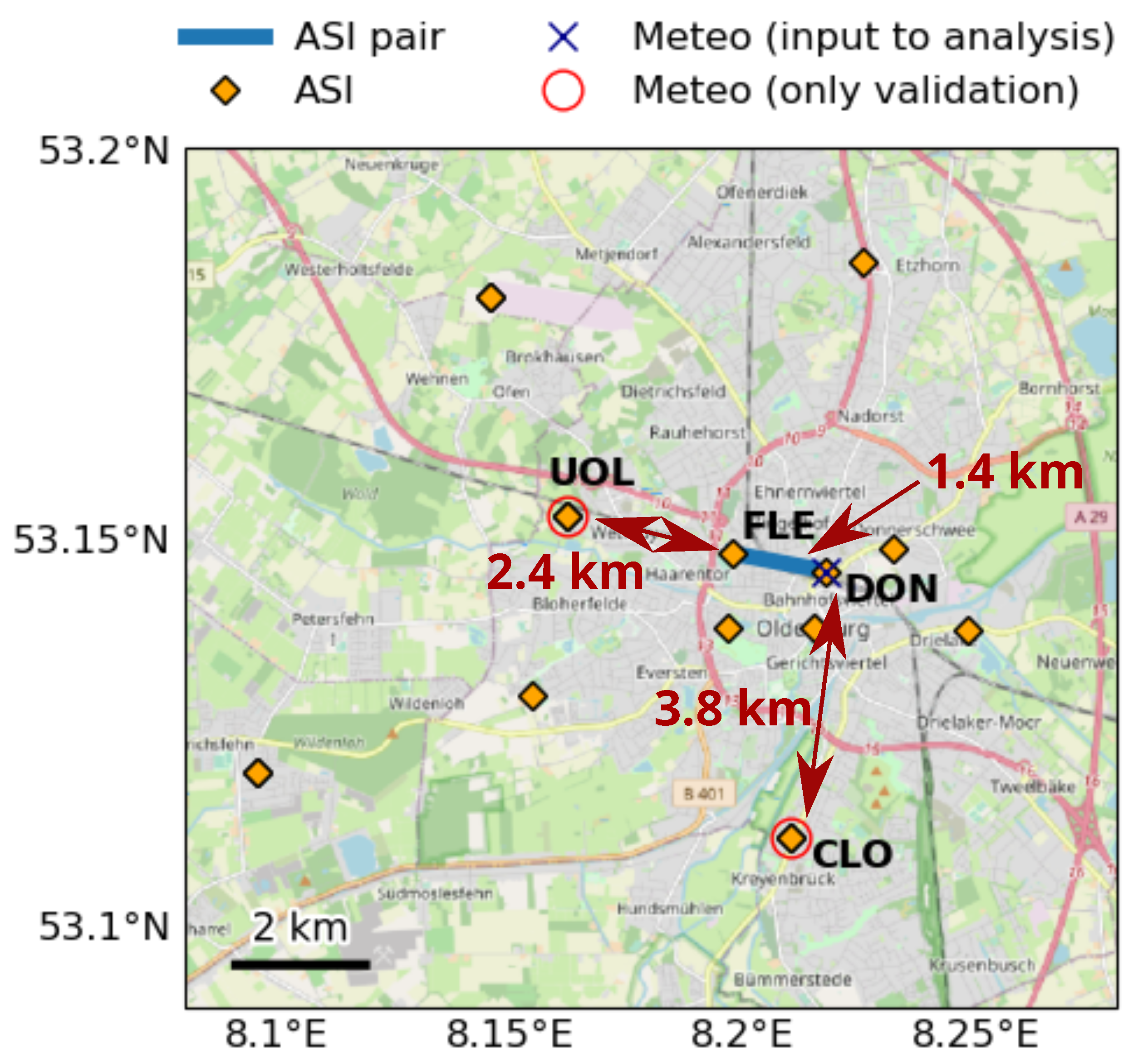


| Station | Geolocation | Distance from [km] | |||
|---|---|---|---|---|---|
| ID | Lat. [N] | Lon. [E] | UOL | DON | CLO |
| AMM | 53.1816 | 8.1456 | |||
| BFE | 53.1492 | 8.23204 | |||
| CLO | 53.11200 | 8.21004 | 0 | ||
| DON | 53.14638 | 8.21734 | 0 | ||
| ETZ | 53.186205 | 8.225326 | |||
| EMS | 53.13021 | 8.15472 | |||
| FLE | 53.14861 | 8.19747 | |||
| HOL | 53.13873 | 8.24786 | |||
| JET | 53.1204 | 8.09583 | |||
| MAR | 53.13918 | 8.21504 | |||
| TIR | 53.13892 | 8.19640 | |||
| UOL | 53.15342 | 8.16191 | 0 | ||
| Variability Class | Sky Conditions | DNI Clear Sky Index | Variability |
|---|---|---|---|
| 1 | mostly clear sky | very high | low |
| 2 | almost clear sky | high | low |
| 3 | almost clear sky | high/intermediate | intermediate |
| 4 | partly cloudy | intermediate | high |
| 5 | partly cloudy | intermediate | intermediate |
| 6 | partly cloudy | intermediate/low | high |
| 7 | almost overcast | low | intermediate |
| 8 | mostly overcast | very low | low |
| Cloud Class | Attenuation Index AI |
|---|---|
| undefined | n.d. |
| low layer/thick cloud | 1 |
| mid-layer cloud | 0.7 |
| high layer/thin cloud | 0.2 |
| clear sky | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Blum, N.B.; Wilbert, S.; Nouri, B.; Stührenberg, J.; Lezaca Galeano, J.E.; Schmidt, T.; Heinemann, D.; Vogt, T.; Kazantzidis, A.; Pitz-Paal, R. Analyzing Spatial Variations of Cloud Attenuation by a Network of All-Sky Imagers. Remote Sens. 2022, 14, 5685. https://doi.org/10.3390/rs14225685
Blum NB, Wilbert S, Nouri B, Stührenberg J, Lezaca Galeano JE, Schmidt T, Heinemann D, Vogt T, Kazantzidis A, Pitz-Paal R. Analyzing Spatial Variations of Cloud Attenuation by a Network of All-Sky Imagers. Remote Sensing. 2022; 14(22):5685. https://doi.org/10.3390/rs14225685
Chicago/Turabian StyleBlum, Niklas Benedikt, Stefan Wilbert, Bijan Nouri, Jonas Stührenberg, Jorge Enrique Lezaca Galeano, Thomas Schmidt, Detlev Heinemann, Thomas Vogt, Andreas Kazantzidis, and Robert Pitz-Paal. 2022. "Analyzing Spatial Variations of Cloud Attenuation by a Network of All-Sky Imagers" Remote Sensing 14, no. 22: 5685. https://doi.org/10.3390/rs14225685
APA StyleBlum, N. B., Wilbert, S., Nouri, B., Stührenberg, J., Lezaca Galeano, J. E., Schmidt, T., Heinemann, D., Vogt, T., Kazantzidis, A., & Pitz-Paal, R. (2022). Analyzing Spatial Variations of Cloud Attenuation by a Network of All-Sky Imagers. Remote Sensing, 14(22), 5685. https://doi.org/10.3390/rs14225685









