Abstract
Facilitated by the Internet of Things (IoT) and diverse IoT devices, remote sensing data are evolving into the multimedia era with an expanding data scale. Massive remote sensing data are collected by IoT devices to monitor environments and human activities. Because IoT devices are involved in the data collection, there are probably private data contained in the collected remote sensing data, such as the device owner information and the precise location. Therefore, when data analysts, researchers, and other stakeholders require remote sensing data from numerous IoT devices for different analyses and investigations, how to distribute massive remote sensing data efficiently and regulate different people to view different parts of the distributed remote sensing data is a challenge to be addressed. Many general solutions rely on granular access control for content distribution but do not consider the low computational efficiency caused by the huge file size of the remote sensing data or certain IoT devices only have a constrained computational performance. Therefore, we propose a new granular content distribution scheme, which is more lightweight and practical for the distribution of multimedia remote sensing data with the consideration of the large data size to avoid complicated operations to the data. Furthermore, a dual data integrity check (hash summary and watermark) designed in our scheme can detect tampering or forgery from encrypted remote sensing data before decrypting it and validate it again after decryption. The security analyses and experimental results manifest that our new scheme can maintain high computational efficiency and block tampering and forgery during the granular content distribution for IoT remote sensing data.
1. Introduction
The Internet of Things (IoT) describes physical objects embedded with sensors that connect with other objects and devices over the Internet and other communication networks to construct holistic systems for seamless interactions between people and objects [1,2]. It is reported that the global IoT market is anticipated to reach around USD 1842 billion by 2028 [3]. The increasing tendency of the IoT indicates that the IoT is playing a much more significant role in the evolution of the smart world. An IoT system consists of numerous sensors and smart devices to collect, exchange, and process data that can not only provide high-quality services but also boost a smarter life and work for people [4,5]. The advances of the IoT have resulted in proliferated IoT applications ranging from healthcare and analyses of human activities and smart cities to remote sensing, environmental monitoring, and agriculture [6,7].
Recently, employing IoT devices and networks shows an incremental trend in collecting remote sensing data for different purposes, such as the analysis of population mobility, indoor/outdoor air quality monitoring, and the surveillance of crops in agriculture [8,9]. Due to the involvement of different IoT devices for remote sensing, the collected data are various in types (e.g., images, videos, and text data) so that remote sensing data are shifting to be more multimedia. To be specific, IoT remote sensing data can contain not only conventional images but also text data and videos, such as carbon dioxide values and video records of plant growth [6,10,11]. Compared with text data, the other two kinds of media (i.e., image and video) are more massive in terms of their data size. Such a large data size raised by the multimedia trend challenges related organisations and institutions to systemically harness the collected remote sensing data in research and analysis, especially for data distribution. For different research purposes, remote sensing data collected by IoT devices can be distributed to different people, such as data analysts and scientists, governmental staff, epidemiological investigators, etc. However, there are two challenges in content distribution that should be considered for IoT remote sensing data.
The first challenge is how to control the contents distributed to various roles without exposing the private information, which is a practical and urgent issue to be addressed for distributing IoT remote sensing data. For example, data analysts and epidemiological investigators should only obtain the targeted data they need to analyse, such as human activity tracks and traffic flows, whilst precise location information and car information should not be public [12]. When traffic accidents occur and traffic risks are detected by IoT-based remote sensing, governmental staff may require concrete location information for emergency assistance [13]. On the other hand, all the contents of the distributed remote sensing data should be protected during the transmission to avoid privacy leakage if there are malicious users (attackers) eavesdropping on the transmission or the transmission has to pass an untrusted third party (e.g., public clouds) [14].
The second challenge is that the large data size caused by multimedia remote sensing data may result in slow encryption and signing in content distribution. For example, some IoT devices can collect videos with a large data size in remote sensing. When we consider privacy preservation to enable different roles to view different videos in content distribution, some operations of encrypting and signing are needed. However, some current content distribution approaches [15,16] are difficult for processing such data with a large data size because their public key operations require the collected data to participate in, leading to quite slow encryption and signing operations.
Therefore, a lightweight granular content distribution scheme should be considered for distributing IoT remote sensing data to protect sensitive information and fit the large data size and resource-constrained IoT devices simultaneously.
In this paper, we consider the large data size raised by the multimedia characteristics of IoT remote sensing data and propose a customised content distribution scheme with granularity control based on the elliptic-curve signcryption, the GCD-RSD (granular content distribution for remote sensing data), which achieves privacy protection (for sensitive information) and a higher computational efficiency to be more suitable for large-scale remote sensing data distributions. The GCD-RSD can be used to efficiently distribute IoT remote sensing data with different data sizes from small to large. Meanwhile, the granularity designed in the proposed GCD-RSD can enable different roles to access different parts of the data. Compared with the current studies [15,16,17,18,19], the novel contributions of the proposed scheme GCD-RSD lie in:
- Considering the large data size introduced by the multimedia feature of IoT remote sensing data, we avoid signing the distributed data directly or involving them in the public key operations for granularity control, i.e., the only operation to the distributed data is the fast symmetric encryption;
- Dual data integrity: Unlike [16,19], who only check the data integrity after decryption, the GCD-RSD verifies the data integrity of the received encrypted remote sensing data before decrypting it and then utilises the watermark to check the data integrity after the encrypted data are decrypted;
- Lightweight cryptography: The applied cryptographic basis is the elliptic curve instead of a costly bilinear pairing to encourage the GCD-RSD to be more lightweight.
The remainder of this paper is organised as follows. Section 2 introduces the related work, including some discussions about the security of IoT remote sensing and some studies on privacy-preserving content distribution in the IoT. The preliminaries and our system model to better understand the proposed scheme GCD-RSD are presented in Section 3. Then, in Section 4, the definition of each phase in the GCD-RSD is demonstrated before we formally illustrate the design of the GCD-RSD and show the correctness and the security analysis for the GCD-RSD. Section 5 analyses the performance of the GCD-RSD by comparing it with other mainstream schemes in terms of the time efficiency and encrypted data size in the experiments, which is followed by the final Section 6 which concludes our work.
2. Related Work
In the field of IoT remote sensing, Triantafyllou et al. [20] proposed a seven-layer architecture for IoT remote sensing monitoring in agriculture. In the middleware and management layers of the architecture, one requirement is that the collected remote sensing data can be securely distributed to different stakeholders for further processing and utilisation, such as data mining. Furthermore, this architecture suggested encrypting remote sensing data in data transmission to avoid data leakage. However, it is only a high-level design without any concrete encryption or access control schemes for data management. To protect IoT remote sensing data in transmission, Adi et al. [21] proposed an on-chip (hardware) encryption scheme using a secret random number against manipulation attacks. This method can secure transmitted remote sensing data but cannot restrict accessible content by roles to achieve granularity control. Gao et al. [22] proposed to encrypt remote sensing images in distribution for cloud-based object recognition. This algorithm can encrypt the matrices of images based on the eigenvalue decomposition, but it has the same drawback with the scheme [21] to be unable to support granularity control. In addition, when encrypting quite large remote sensing images, this algorithm may be slow in computation due to complex matrix operations. Overall, the current studies on data security and privacy in IoT remote sensing are limited. Most of the current studies only focus on data encryption in data collection, but the research about data security and privacy for data/content distribution is still in its infancy in IoT remote sensing.
In IoT and other smart-related fields, there are different technical routes, which have been discussed for content distribution in the current studies. In order to share massive smart health data, Li et al. [17] proposed to sign the data to be distributed with the organisation signature. This method can avoid tampering as the receiver can validate the data integrity of the distributed data to find out forged data, but there is no encryption applied in their constructed scheme. Therefore, the plain data can be browsed by both the legitimate receivers and the malicious attackers in the distribution. Furthermore, the signature scheme in [17] does not consider the granularity control to restrict different data receivers to access different parts of the data. Similarly, Yang et al. [15] demonstrated a data management system with data signing to ensure the data integrity in the data distribution, but the authors do not consider the granularity control or define any access policies in the authorisation. To address the granularity control issue in distribution and avoid plain data, Li et al. [18] divided users into social and professional domains and then presented an advanced encryption scheme which can provide different parts of encrypted sensing data for different users. The core method the authors employed is attribute-based encryption (ABE) to encrypt data with the key generated by the user’s attributes. Meanwhile, the scalability of the scheme [18] is noticeable as the ABE can allow the system authority to update (add and delete) the users and the attributes of each user. Based upon the work of [18], Liu et al. [16] integrated signcryption (signature and encryption) [23] with ABE to implement an improved data-sharing system with fine-grained access control in the cloud computing environment. After that, Rao [19] pointed out that the bilinear pairing used in the scheme [16] is much more time-consuming than the modular exponentiation and elliptic multiplication in the computation. Therefore, Rao [19] refined the scheme in [16] by reducing the use of bilinear pairing operations to construct a more efficient scheme. Compared with the scheme [18] supporting confidentiality only, two recent schemes [16,19] can also ensure the integrity (i.e., authenticity and unforgeability) to avoid malicious data manipulations during data transmission. Karati et al. [24] proposed a lightweight certificateless data-sharing scheme based on a bilinear pairing for the industrial IoT (IIoT), but it only fits to encrypt small data. Later, Truong et al. [25] and Chen et al. [26] proposed to utilise blockchain to share IoT data, but the network latency is high (few seconds) because all the nodes require a time-consuming proof of work (PoW) to achieve consensus sharing. Apart from the high time consumption, the decentralised blockchain may not fit to the scenario of content distribution in IoT remote sensing. The decentralised information sharing is more suitable to share data in large-scale groups, where each participant possesses some data equally, e.g., the data scale is similar. However, the content distribution of IoT remote sensing data is more centralised because large-scale remote sensing data that probably need to be distributed are only possessed by a few national/international institutions and giant companies [27].
Recently, Chen et al. [28] employed signcryption and a bilinear pairing to protect IoT data collection. However, this scheme has a similar issue to [15,16], i.e., it heavily relies on a bilinear pairing to lead to a slow encryption. Furthermore, this scheme still requires the data (to be encrypted) to participate in the public key operations, which may also result in a slow encryption process when the data size is quite large, e.g., large videos and images collected in IoT remote sensing. On the other hand, Fadlullah and Kato [29] applied federated learning in IoT remote sensing for edge nodes to build models for the forest fire detection. This solution can protect the privacy of the acquired remote sensing data during the aggregation of the trained models but does not consider that parts of the raw sensing data may contain sensitive or private information that should not be accessed by edge nodes in the federated learning.
Based on the above analysis, we notice that efficient and granular content distribution has not been considered for distributing IoT remote sensing data. Furthermore, all these studies neglect two important characteristics brought by IoT remote sensing data.
- Large data size caused by multimedia: IoT remote sensing data are going to multimedia which means such data can contain text data (e.g., values), images, videos, and so on. Therefore, the size of the current IoT remote sensing data can be quite large and probably incur slow signing operations [15,17] and signcryption operations [16,19,28], especially for the data whose size is over gigabytes.
- Watermark: Some remote sensing data are watermarked by its owners [30], but this feature has not been considered as a potential approach to realise an integrity check in the data distribution.
Hence, when facing large multimedia remote sensing data collected by the IoT, the current methods from the literature may not be suitable to be utilised for the content distribution of such data if the time efficiency and privacy preservation are considered. To achieve granular content distribution for IoT remote sensing data efficiently, we propose the GCD-RSD, considering not only the watermark feature as an integrity check method but also the large data size caused by multimedia IoT remote sensing data. To process large-size data efficiently, the GCD-RSD does not encrypt the data using public key operations like other granular content distribution schemes [15,16,28]. Instead, the GCD-RSD encrypts the data with a fast symmetric encryption AES (Advanced Encryption Standard) [31]. Meanwhile, the GCD-RSD is constructed based on signcryption to protect the data integrity but does not involve time-consuming public key operations, such as a bilinear pairing, to be lightweight.
In order to summarise the literature review, we compare some state-of-the-art schemes with our proposed GCD-RSD. Because there is no similar content distribution scheme for IoT remote sensing data, we select some schemes related to granular content distribution in the IoT field for the comparison. The security and computational efficiency features of the compared schemes [15,16,17,19,28] and GCD-RSD are summarised in Table 1.

Table 1.
The comparison of security and performance features for [15,16,17,19,28] and GCD-RSD.
Most of the compared schemes can realise the confidentiality and integrity, but only three schemes [16,19] and the GCD-RSD consider the granularity control in content distribution. As for the computational overhead for encrypting and decrypting the distributed data, the scheme [17] and the proposed GCD-RSD schemes are lightweight to fit IoT devices in remote sensing as they do not require complex cryptographic operations, such as a bilinear pairing to the distributed data, but the scheme [17] is not secure, as we discussed above. As a result, our proposed scheme GCD-RSD is the only one that can meet all the features in the comparison.
3. Preliminaries and Model
3.1. Notations
In this part, the notations used to describe the cryptographic assumption and our proposed scheme are summarised in Table 2.

Table 2.
Notations.
3.2. Elliptic Curve Computational Diffie–Hellman (ECCDH) Assumption
The ECCDH assumption [31] is a public key computational problem with the following cryptographic description. Let be a secure elliptic curve in cryptography. For any point and , any probabilistic polynomial-time algorithm computes with its advantage
The ECCDH assumption can hold if for any probabilistic polynomial-time algorithm , its advantage is negligible.
There are two reasons for us to select the ECCDH assumption as the foundation to construct our GCD-RSD scheme. The first one is that the ECCDH can achieve a higher security level with a shorter key size, which has been recommended by the National Institute of Standards and Technology (NIST), US [32]. The other reason is the higher computational efficiency and lower energy consumption of elliptic curve scalar multiplication in ECCDH than other cryptographic operations, such as bilinear pairing and modular exponentiation, which has been widely evaluated, especially for IoT devices [33,34,35].
3.3. System Model
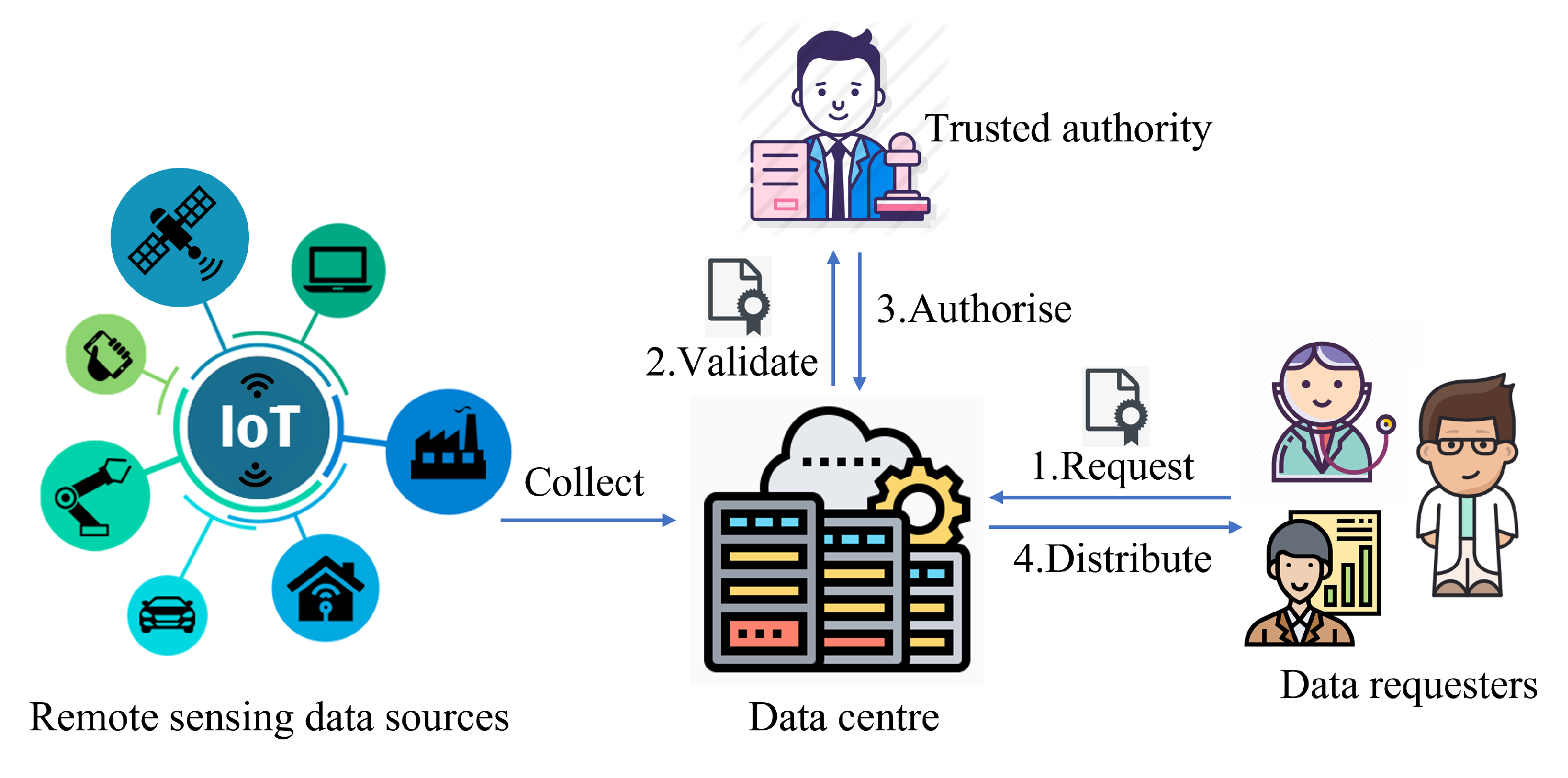
Our system model is depicted in Figure 1 with four entities: remote sensing data sources, data centre, data requesters, and a trusted authority (TA). The data centre acts as the management role to store and update the remote sensing data collected by different remote sensing data sources, including IoT devices, sensors, satellites, etc. Databases can be used to maintain plain remote sensing data by the data centre. When a data requester requires the specific data from the data centre, the data centre can delegate the trusted authority to validate the identity and access attributes of the data requester. If the trusted authority confirms the data requester is authorised to access the requested data, the data centre encrypts the requested data and distributes them to the data requester. After receiving the encrypted data, the data requester can use the key negotiated with the data centre to decrypt the encrypted data and check its integrity. Note that data requesters may use some mobile devices or IoT devices to receive the requested data in practice [36].
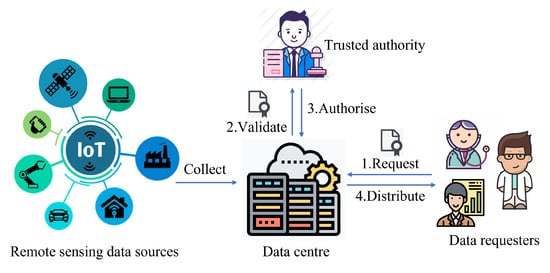
Figure 1.
The system model of GCD-RSD.
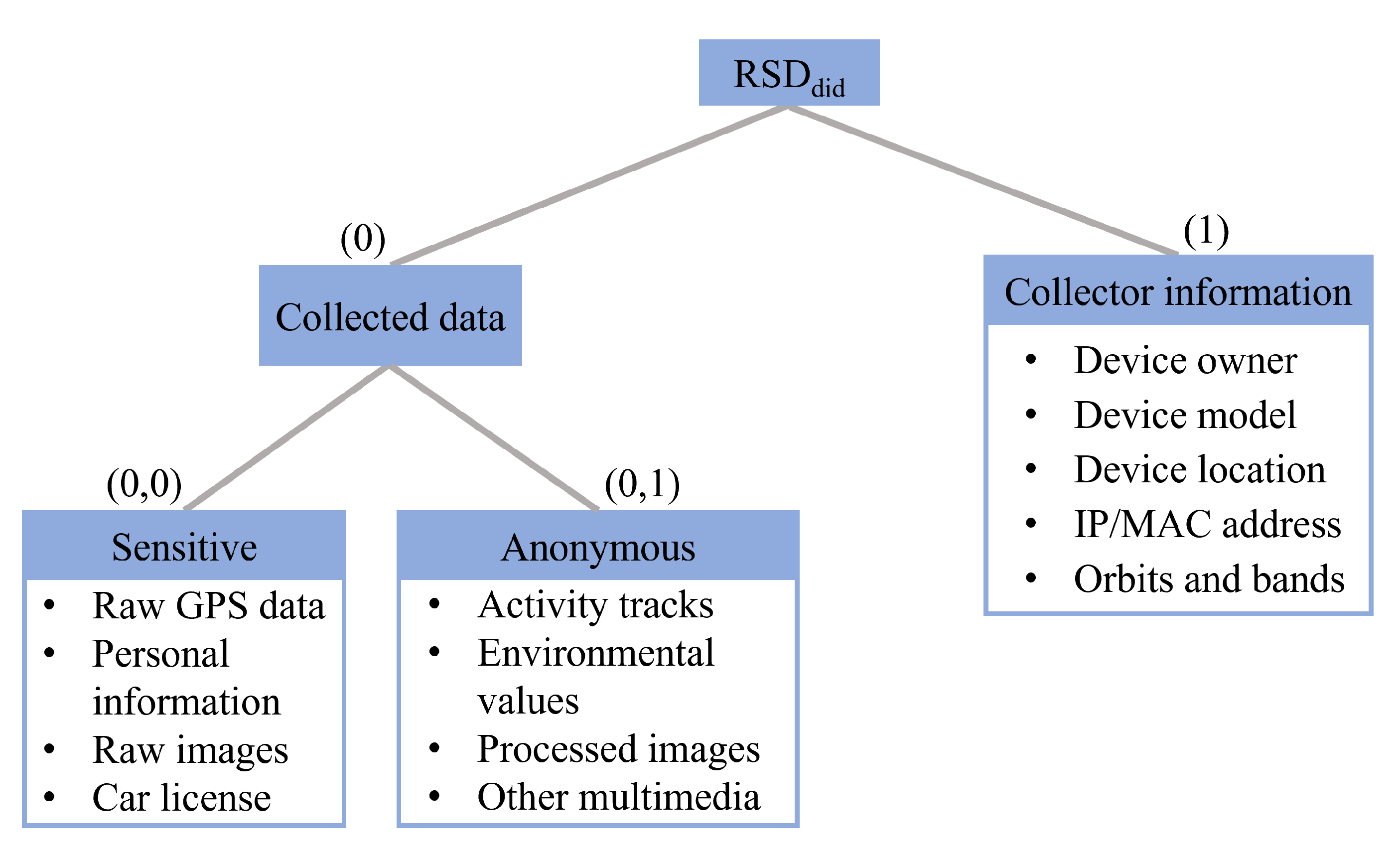
3.4. Attribute Tree
The attribute tree is used to control the access granularity (i.e., granular authorisation) in the content distribution. For each remote sensing data archive , it has an attribute tree defined by the data centre. Different may have different attribute trees. Here, an exemplar attribute tree corresponding to the remote sensing data archive is shown in Figure 2 (tree depth ). Because can involve different collected data and collector information, its exemplar attribute tree is constructed by four attribute tags in two layers. In the first layer of Figure 2, involves two attribute tags, “Collected data” and “Collector information”. Then, in the second layer, the collected data are divided into two parts (tags): “Sensitive” and “Anonymous”. As shown in Figure 2, each node in has an attribute tag, such as for “Collected data” and for “Anonymous”. Note that in the category of sensitive, personal information represents individuals’ faces and other characteristics (e.g., tattoos and clothes). Meanwhile, the sensitive information should be removed from all the data in the anonymous category.
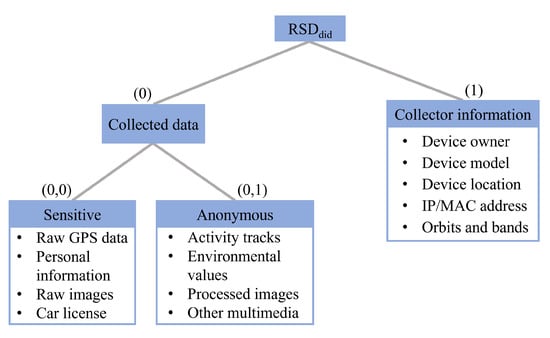
Figure 2.
An exemplar attribute tree .
Before the content distribution, the attribute tree for each remote sensing data archive should be defined by the data centre clearly. After that, the attributes different data requesters can own should be issued by the data centre and the trusted authority jointly. Based upon attribute trees and issued attributes, the attributes possessed by the data requester can be used to achieve granular content distribution. For example, a governmental data requester may own several attributes, such as , which means that this user can access the collected data of several data archives regulated by . On the other hand, a data analyst can possess the attribute to be allowed to access the anonymous parts of only.
4. Proposed Scheme
We formally propose our GCD-RSD scheme by describing how the authorisation and granularity control work in the Authorise phase and elaborating the detailed algorithms in the Signcrypt and Unsigncrypt phases. Then, the correctness of GCD-RSD is illustrated, followed by the security analysis, including confidentiality, integrity, resistance to sniffing, tampering and tracing, and formal verification. Note that the detailed theoretical security models and proofs of confidentiality and integrity for GCD-RSD are presented in Appendix A and Appendix B.
4.1. Scheme Definitions
There are five phases in our proposed scheme GCD-RSD, including Setup, Request, Authorise, Signcrypt, and Unsigncrypt, for the granular content distribution. The data centre and the data requester are denoted by and , respectively. The detailed definition of each phase is manifested as follows.
•Setup (λ): This algorithm takes the security parameter and generates the public parameters for the following remote sensing data distribution.
•KeyInitialise (): The data centre and the data requester initialise their public keys () and private keys () for the data distribution.
•Request (, ): The data requester uses this algorithm to send an access request Q for the data identity to the data centre. Note that Q also contains the identity information and access attributes of the data requester.
•Authorise (): The data centre sends Q to the trusted authority to verify the access legitimacy of the data requester to the requested data.
•Signcrypt (, , , ): The data centre retrieves the requested data M by and then signs and encrypts M with its private key and the data requester’s public key , then returns the ciphertext C to the data requester.
•Unsigncrypt (, C, , ): After receiving the encrypted data C, the data requester decrypts the encrypted data C with their private key and the data centre’s public key to retrieve the requested data M.
4.2. GCD-RSD Scheme
•Setup ():
This algorithm outputs public parameters with the security parameter through the following steps.
1. Pick a cryptographic secure elliptic curve group with a base point G on the curve, where the order of is .
2. Select two cryptographic secure hash functions: and .
3. Select a fast and secure symmetric encryption algorithm, for example, Advanced Encryption Standard (AES) [31]. Note that is defined as the AES encryption with the secret key k and represents the AES decryption with the secret key k.
4. The watermarked remote sensing data set is denoted by , where is the data identification number.
5. The data centre defines the attribute tree for each data set as illustrated in Section 3.4 for the granular authorisation in the content distribution.
6. Output the public parameters .
•KeyInitialise (): This subroutine is executed by both the data centre and the data requester with their corresponding private keys and to generate the key pairs for the remote sensing data distribution:
Note that and have the certificates and issued by the trusted authority (TA): , where , , and represent ’s identity, the access attribute(s) possessed by , and ’s private key, respectively; , where and denote ’s identity and ’s private key, respectively. can be a set to contain multiple attributes, such as , , , and so on. The structure of each attribute can be different depending on different structures of the corresponding attribute trees, as discussed in Section 3.4. In addition, the public keys A and B can be shared; however, the private keys and the certificates should be kept by and secretly.
•Request (): The request scenario we use to describe our scheme is a data analyst requires the specific remote sensing data from the data centre .
constructs the request , then sends Q to securely.
•Authorise (, Q): There are two steps in this phase after Q is received by .
1. sends Q to TA for validation, then TA validates and .
2. If TA confirms has valid and correct attribute(s) to access by referring to , authorises the request Q and then executes the following phases; otherwise, denies ’s request Q.
•Signcrypt (, Q, , a, B): The data centre follows the shown steps to sign and encrypt the requested data.
1. Prepare the requested data M by extracting the data allowed to be accessed by in , which is defined by .
2. Choose a random number .
3. Compute: ,
,
,
.
4. Send the ciphertext to .
•Unsigncrypt (, C, A, b): After receiving C from , can execute the following steps to retrieve the requested data M.
1. Compute:
,
.
2. If the condition holds, continues the next steps; otherwise, it means the first integrity check fails and this algorithm outputs ⊥ (error).
3. Decrypt to retrieve M by computing .
4. If the watermark of M is intact, this algorithm outputs M to ; otherwise, it indicates the second integrity check is not passed then this algorithm outputs ⊥ (error).
•Correctness: When observing the phases Signcrypt and Unsigncrypt, we can notice that the important condition is to ensure can obtain the correct M via calculating . In the Unsigncrypt phase,
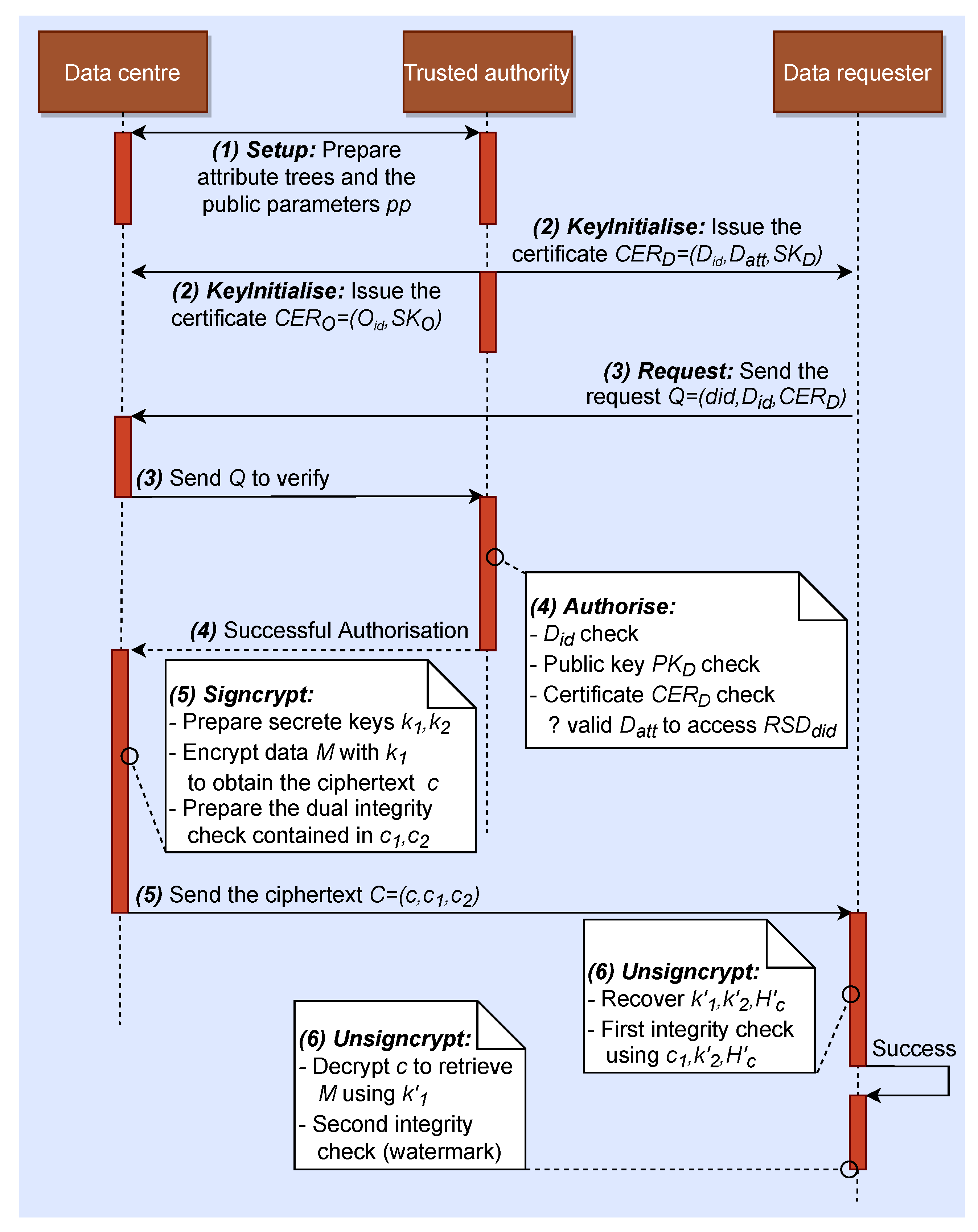
Therefore, after receiving the correct , can retrieve the requested M correctly by executing the algorithm Unsigncrypt. To summarise how GCD-RSD works, the workflow of GCD-RSD is presented in Figure 3.
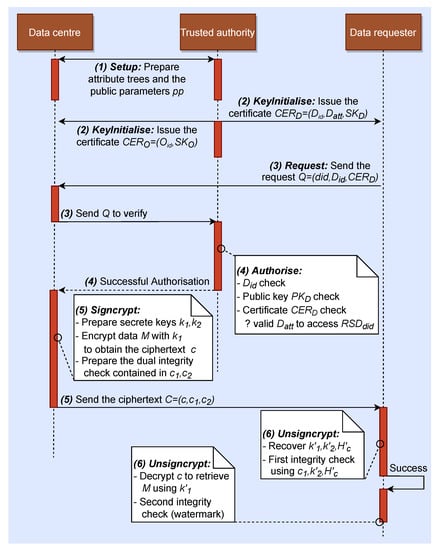
Figure 3.
The workflow of GCD-RSD.
4.3. Security Analysis
In this section, we briefly illustrate how GCD-RSD can satisfy confidentiality and integrity in the remote sensing data distribution as the backbone of GCD-RSD signcryption primitive has been proved to be secure in terms of confidentiality and integrity in [23]. The formally theoretical proofs (with security models), including indistinguishability under chosen ciphertext attack (IND-CCA) and existential unforgeability under chosen message attack (EUF-CMA), to manifest the confidentiality and integrity of GCD-RSD are illustrated in Appendix A and Appendix B, respectively. Apart from confidentiality and integrity, we analyse the resistance of sniffing, tampering, and tracing attacks and provide the result of formal verification for GCD-RSD in the content distribution.
4.3.1. Confidentiality
If an attacker can obtain the ciphertext from the communication between and , M cannot be recovered as the attacker does not know ’s secret key to calculate correct or based upon the correctness analysis. Even though the attacker always knows the public keys of and , calculating with to recover is still a difficult problem due to the ECCDH assumption. Hence, the confidentiality of GCD-RSD can be ensured to avoid data leakage during the data distribution.
4.3.2. Data Integrity
Because the attacker cannot acquire based on the confidentiality analysis, it is infeasible to manipulate c and generate the matched . Therefore, the tampered or forged can be found out at step 2 (the first integrity check) in the Unsigncrypt phase. On the other hand, if the attacker can tamper c then generate matched occasionally, the watermark check (the second integrity check) at step 4 in the phase Unsigncrypt can prevent from obtaining corrupted M. This is because the tampering to c is irregular (i.e., not following the original remote sensing data format) that can result in the corrupted watermark or even the damaged M directly. Hence, GCD-RSD can achieve dual data integrity checks.
4.3.3. Sniffing Resistance
When facing sniffing attacks in content distribution, the proposed GCD-RSD scheme can avoid plain data leakage in two aspects. Firstly, the ciphertext c is encrypted and is a hash value so then cannot be compromised. Meanwhile, even though the attacker can obtain and by sniffing, it cannot compute the secret key a of the data centre because the random number r is not involved in the transmitted ciphertext C. Secondly, r is generated as a random number in each content distribution so the probability of sniffing the same secret keys in different content distributions can be negligible. Therefore, our scheme GCD-RSD can resist sniffing attacks to prevent attackers to obtain effective information in sniffing.
4.3.4. Tampering Resistance
The tampering in the communication for the content distribution may threaten the integrity of the distributed content. However, GCD-RSD can resist tampering attacks because any tampering can be detected by the data requester based on the above analysis of data integrity. If the attacker replaces c or with random data, the steps 2 and 4 cannot be passed in Unsigncrypt because the hash value hidden in and the replaced c cannot match. On the other hand, the attacker cannot generate valid c and to replace the original c and with the generated ones because are unknown based on the analyses of confidentiality and sniffing.
4.3.5. Tracing Resistance
Another potential attack is tracing, i.e., attackers may trace the identities of data requesters using sniffing data. GCD-RSD can resist the tracking attack because the ciphertext C does not contain any identity information. The public information that can be used to identify the data requester is the public key of the data requester. However, this information is not contained in the ciphertext directly. Furthermore, the public key B is hashed by in Signcrypt of GCD-RSD. It indicates the probability of recovering B from the hash value can be negligible. Therefore, our scheme GCD-RSD can have tracing resistance to protect data requesters’ identity information in content distributions.
4.3.6. Formal Verification
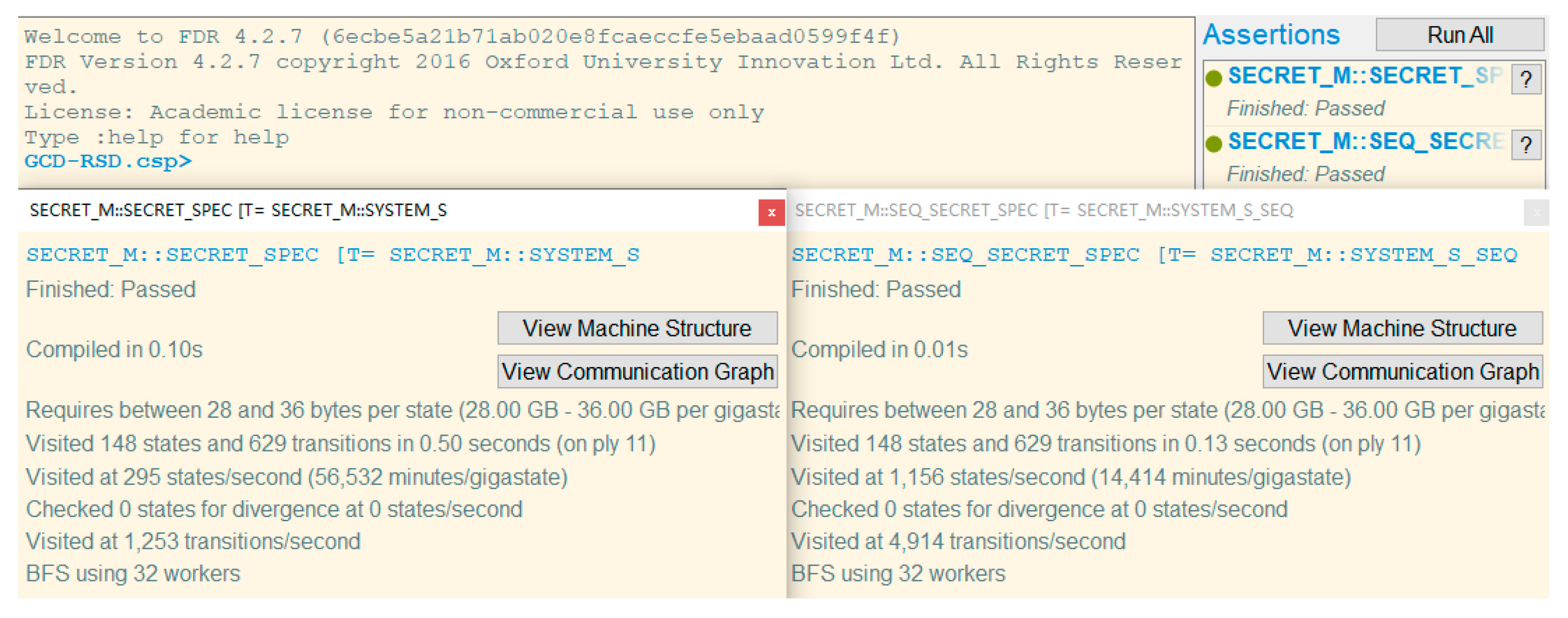
This section yields the formal verification result of the proposed scheme GCD-RSD by adopting the widely-used automated security protocol simulator, termed “Casper/FDR”, including the compiler Casper [37] of the communicating sequential process (CSP) language [38] and a CSP model checker Failures Divergences Refinement (FDR) [39]. CSP is a formal language to describe the interaction and states to model communications and security protocols.
The security properties of GCD-RSD are modelled by the CSP language and compiled by Casper. Then, the output from Casper is analysed with FDR. In the model, the data requester and the data centre are represented by two roles, Alice and Bob, respectively. The used version of Casper is 2.1, and the used version of FDR is FDR4. The results are demonstrated in Figure 4, where the overview result of two verification items (i.e., message secret and sequence secret) is passed, shown in the top right corner. The detailed results are displayed in two sub-windows. The left sub-window presents the verification result of the message secret. Our scheme GCD-RSD can pass this verification so it means GCD-RSD can ensure the confidentiality of the transmitted data. Meanwhile, the right sub-window shows the verification result of the sequence secret. The passed result manifests that GCD-RSD can protect the ciphertext to be intact in the communication so the integrity of the transmitted data can be ensured. Through this analysis, it is shown that the proposed scheme GCD-RSD is secure enough to ensure the confidentiality and integrity of the distributed content in the communication.
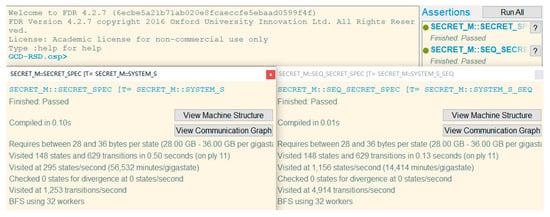
Figure 4.
The formal verification results of GCD-RSD using Casper/FDR.
5. Experiments and Results
In this section, we use four actual IoT remote sensing data samples to conduct our experiments. Because there is no similar content distribution scheme or best practice for distributing IoT remote sensing data, we select several schemes [15,16,17,19,28] related to granular content distribution in IoT-related fields for the comparisons with our scheme GCD-RSD in terms of the computational time consumption and the size of the generated ciphertext in actuality.
5.1. Data Preparation
In order to involve more multimedia data of IoT remote sensing in the samples, we prepare four different multimedia remote sensing data obtained from satellites and IoT sensors as the samples for our experiments, described in Table 3 with their size information. Note that we compress each sample into a single file (zip format) to load them into the memory more quickly in our experiments.

Table 3.
Sample description of the used IoT remote sensing data in our experiments.
contains PM2.5 sensor values extracted from the national air quality observation data set in the national urban air quality real-time publishing platform (National Urban Air Quality Real-time Publishing Platform: https://air.cnemc.cn:18007/, accessed on 27 February 2022) of the China Environmental Monitoring Sites. involves low-resolution images of processed aerosol optical thickness data with a 1 km pixel resolution collected by satellites’ sensors from the NASA MCD19A2 data set (https://lpdaac.usgs.gov/products/mcd19a2v006/, accessed on 3 June 2018). is a video made by the land surface temperature and emissivity (LST&E) from January 2021 to February 2022 based on the NASA MOD11C2 data set (https://ladsweb.modaps.eosdis.nasa.gov/missions-and-measurements/products/MOD11C2, accessed on 26 February 2022). is a large-scale terrain image observed by synthetic aperture radars (SAR) [40] from the European Space Agency (https://sentinels.copernicus.eu/web/sentinel/user-guides/sentinel-1-sar/acquisition-modes/interferometric-wide-swath, accessed on 5 May 2018).
5.2. Experiments
Because the computational time cost and the actual ciphertext size are decided by the detailed algorithm, we implement the signing and verifying algorithms in [15,17], the signcryption and unsigncryption algorithms in [16,19], and our GCD-RSD scheme based on the cryptographic SDK MIRACL [41]. A Raspberry Pi 2 with a Wi-Fi module acts as an IoT device of the data requester and a conventional computer with an Intel i5 processor running at 3.30 GHz works as the data centre and the trusted authority to conduct our experiments. Note that because the compared schemes [15,16] may involve complicated algorithms to encrypt and decrypt data that are quite time-consuming for the IoT device, the data verification and decryption that should be performed by the IoT device in practice are delegated to the conventional computer in our experiments for the comparison. To reduce the programs’ running time, we invoke the corresponding APIs from OpenSSL [42] when the AES encryption/decryption and hash summary are required. For each algorithm, we run it 100 times for each sample to obtain the mean of the computational time consumption and the ciphertext size. Note that for the scheme [16], we only run it 2 times when it processes the sample as the computational time cost of [16] is extremely high (about several days). All the security parameters in the implemented experiments are under the equivalent cryptographic security level (128-bit security) [32].
5.3. Results and Analysis
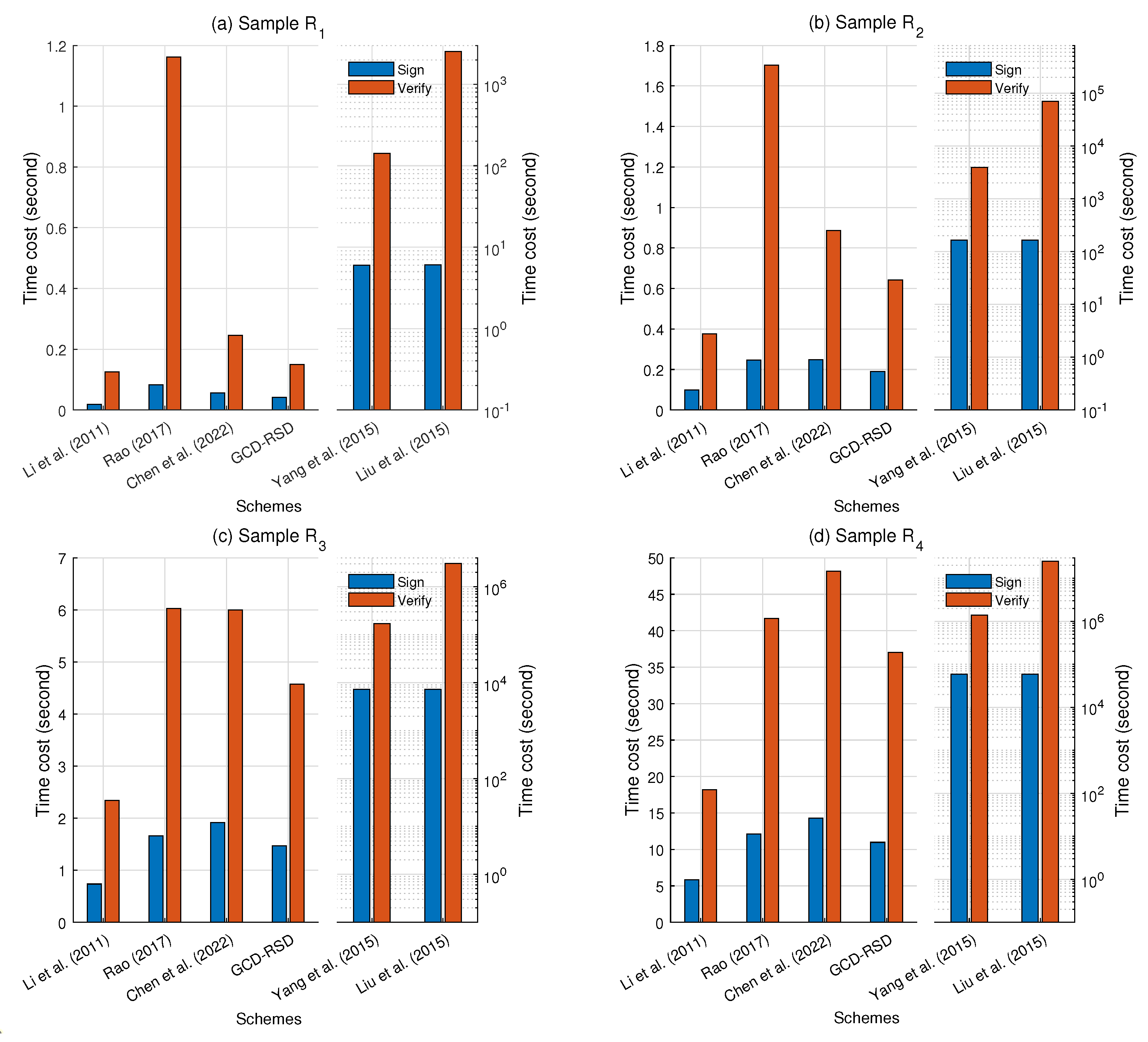
The results of our time cost experiments are shown in Figure 5 and Figure 6. It is clear that [15,16] are quite costly in the computation in Figure 5 because their schemes are sensitive to the data size, i.e., these two schemes involve the distributed data in public key operations for encryption and signing in the content distribution. Meanwhile, the scheme [17] is the most efficient scheme, but it only signs the samples to ensure the data integrity without any encryption. On the contrary, compared with the scheme [17], the schemes [19,28] and GCD-RSD can ensure the confidentiality and data integrity in the data distribution and achieve a comparable efficiency simultaneously. However, Chen et al.’s scheme [28] does not have the design of granularity control to achieve the granular content distribution as shown in Table 1. In processing the small-scale data ( and ), the time cost of our scheme GCD-RSD for signing and verifying is less than that of the schemes [19,28] with an average advantage of 31.2% and 54.1%, respectively. When the size of the distributed data increases significantly ( and ), the superiority of the GCD-RSD becomes more and more slight (less than 20%) as the major time cost comes from the encryption, decryption, and hash operations. However, if the attacker tampers or forges the ciphertext C, the GCD-RSD can find out the malicious manipulations in advance because of the designed data integrity check before the decryption. For example, the GCD-RSD requires only 5.85 s to detect the abnormal ciphertext C, while the scheme [19] needs 11.97 s for the sample .
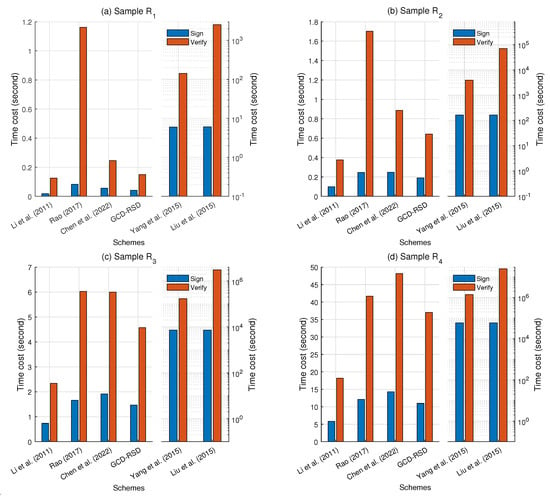
Figure 5.
The comparison of the time cost for 6 schemes [15,16,17,19,28] and GCD-RSD to process , , , and in terms of Sign (or Signcrypt) and Verify (or Unsigncrypt).
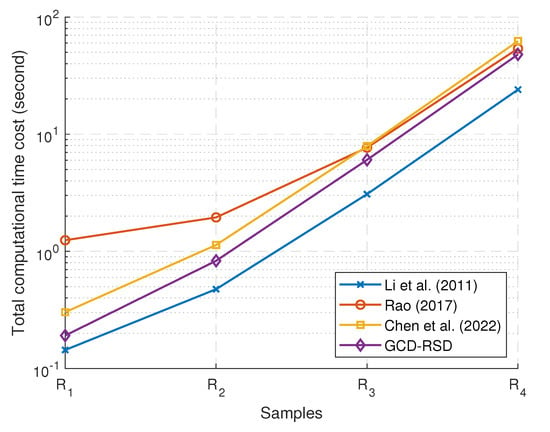
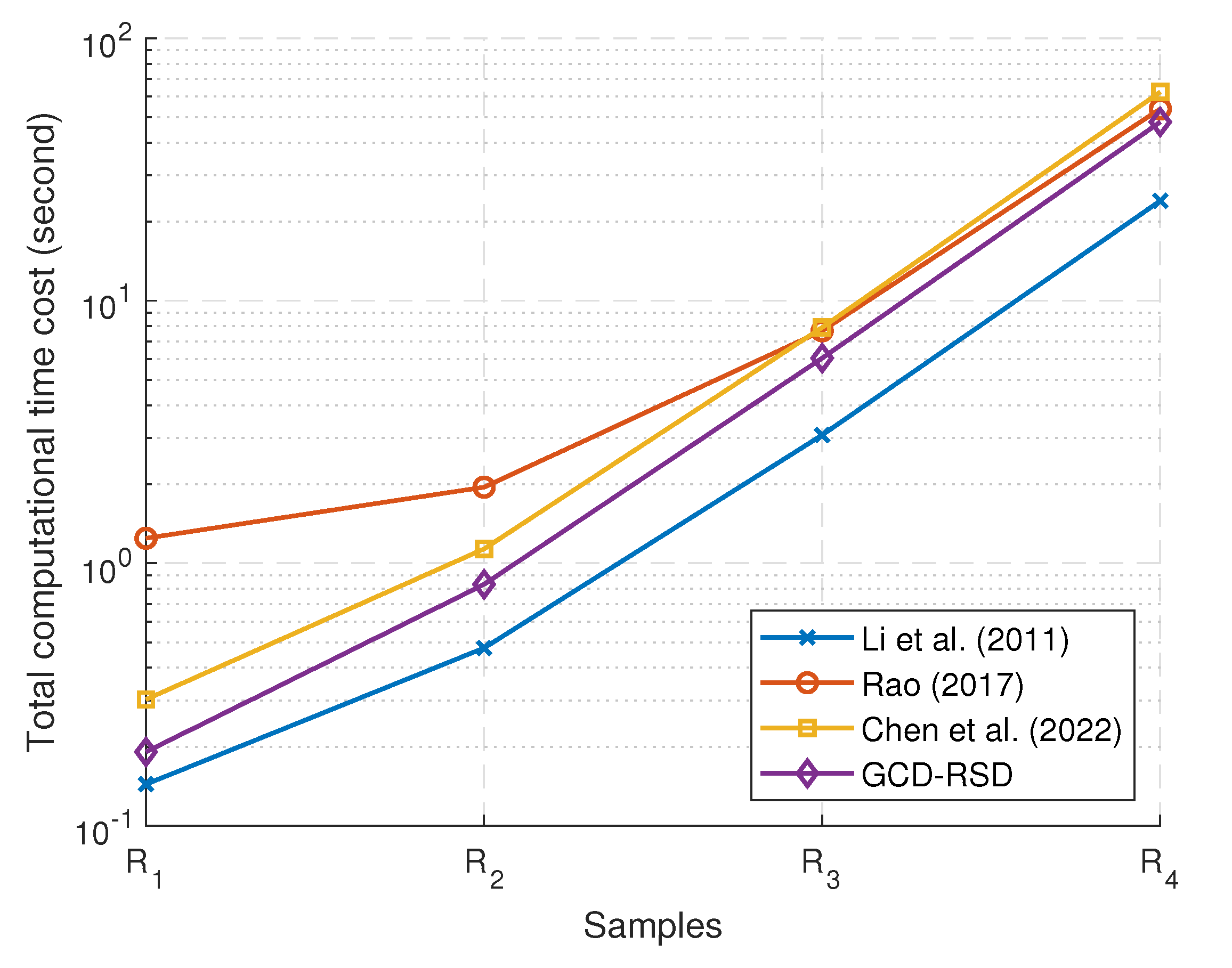
Figure 6.
The comparison of the total time cost for 4 schemes [17,19,28] and GCD-RSD to distribute , , , and , i.e., the total time consumption of Sign (or Signcrypt) and Verify (or Unsigncrypt).
In Figure 6, the total time consumption of signing and verifying to distribute the samples , , , and is reported. In this figure, four time-efficient schemes [17,19,28] and the GCD-RSD are compared because the schemes [15,16] are heavily time-consuming in the content distribution. The total computational time consumption grows with the size of the data for all four schemes. Apart from the scheme [17], which does not encrypt the distributed data to probably incur data leakage, our scheme GCD-RSD costs the least time in computation (27.6% faster than the scheme [28] and 43.6% faster than the scheme [19] on average) to complete the distributions of the four samples. Overall, our scheme GCD-RSD has the best computational time efficiency to achieve the content distribution while considering the confidentiality, integrity, and granularity control simultaneously in the comparison.
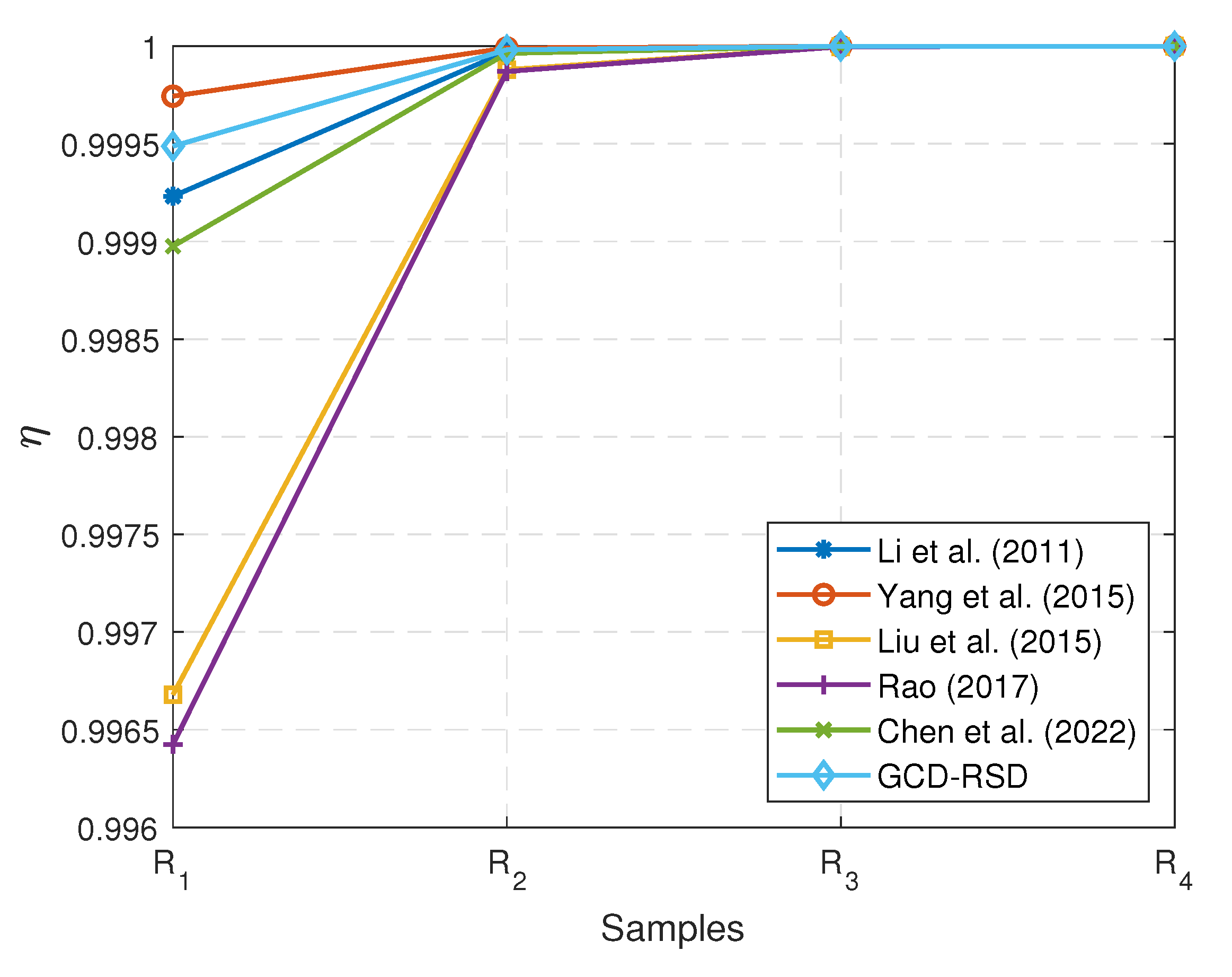
On the other hand, we measure the size of the ciphertext generated by the signing or signcryption algorithms for each scheme in our experiments and calculate the corresponding efficient data rate , where and denote the length of the distributed data and the length of the generated ciphertext. The reason for calculating is to evaluate the size of the extra data used in the different schemes. The extra data can be the keys for the decryption or some auxiliary parameters for verifying the signature. Fewer extra data mean a smaller and higher to reduce the time cost in the ciphertext transmission. Based upon the results presented in Figure 7, the GCD-RSD can achieve a higher when compared with the schemes [16,19,28], which indicates the GCD-RSD requires fewer extra data to realise the data integrity check and decryption for the ciphertext (encrypted data). When a data requester frequently requests small remote sensing data (e.g., IoT sensor data), our scheme has an obvious advantage of reducing the communication cost with a smaller transmitted data size. Because the extra data are quite tiny when compared with the samples, the of each scheme is over 99%, but the of the schemes [15,17] and GCD-RSD are observed to be higher than the of the schemes [16,19] which need about 7 times the data than the other three schemes on average. For example, the original data size of the sample (compressed) is 133.1 KB, and the schemes [16,19] add 0.406 KB and 0.438 KB extra data in the ciphertext, respectively. Meanwhile, our scheme GCD-RSD requires 0.063 KB extra data in the ciphertext and the schemes [15,17,28] add 0.031 KB, 0.094 KB, and 0.125 KB extra data, respectively. However, we emphasise again that the scheme [17] can expose the distributed data when eavesdropping occurs as the scheme [17] only signs the data without the necessary encryption. Meanwhile, the scheme [15] requires heavy computation to lead to the high time cost as shown in Figure 5. In addition, it may expose sensitive data to the data requester without the consideration of granularity control in the distribution of the remote sensing data. Furthermore, when the depth and width of the used attribute tree grow, the schemes [16,19] can generate more extra data in the ciphertext because the scale of the extra data in the ciphertext generated by the schemes [16,19] is related to the scale of the used attribute tree. Therefore, our scheme GCD-RSD can achieve not only a high-efficient data rate but also a low computational time cost for the granular content distribution when compared with the other related schemes [15,16,17,19,28] based on the conducted experiments.
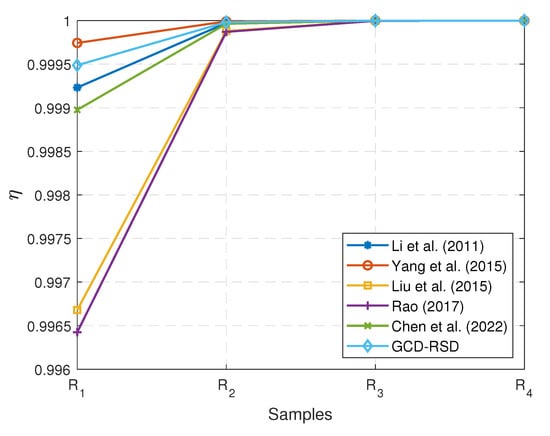
Figure 7.
The comparison of efficient data rate of the 6 schemes [15,16,17,19,28] and GCD-RSD in generating the ciphertext for the samples , , , and .
6. Conclusions
In this paper, we propose a granular content distribution scheme GCD-RSD for IoT remote sensing data distributions. The large data size feature brought by multimedia remote sensing data is considered in the GCD-RSD to avoid complicated public key operations in the data and hence to achieve high computational efficiency when compared with other content distribution methods in the experiments. Meanwhile, the GCD-RSD does not apply time-consuming public key operations, such as a bilinear pairing, to be lightweight for IoT devices as data requesters. Before the content distribution, the attribute tree is designed for granularity control to regulate different roles to access different parts of the data to safeguard the privacy of sensitive data. Furthermore, watermarks in remote sensing data are utilised to implement a dual data integrity check before and after decryption. It can help the data requester to perceive data tampering or forgery earlier. As a result, the data centre can employ our scheme GCD-RSD to provide a granular content distribution service more efficiently with privacy preservation.
Author Contributions
Conceptualization, X.Z., G.Z. and X.H.; methodology, X.Z.; software, G.Z. and X.H.; validation, X.Z. and G.Z.; formal analysis, X.Z.; data curation, G.Z. and X.H.; writing—original draft preparation, X.Z., G.Z. and X.H.; writing—review and editing, X.Z., S.P., G.Z. and X.H.; visualization, G.Z. and X.H.; supervision, X.Z. and S.P.; project administration, X.Z.; funding acquisition, X.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partly funded by the University of Glasgow and Queen Mary University of London.
Data Availability Statement
Data sharing not applicable.
Acknowledgments
This research was supported in part by a PhD scholarship funded jointly by the China Scholarship Council and Queen Mary University of London.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. IND-CCA Security (Confidentiality)
Appendix A.1. Security Model
Formally, the adversary defined to prove the theoretical security of our proposed scheme GCD-RSD is:
Type-IND adversary: The adversary cannot determine the message that the given challenge ciphertext is encrypted from with all the public keys and ciphertext in the remote sensing data distribution. This Type-IND adversary is used to prove our scheme is secure in the IND-CCA model, which is much stronger (more secure) than other models, such as IND-CPA and OW-CCA, in the confidentiality security [43].
The definition of the IND-CCA security model with the Type-IND adversary for our GCD-RSD scheme is as follows.
Game 1. is the given Type-IND adversary, and the index of the target data receiver is . The game between the challenger and is operated as follows:
Setup
first generates the public parameter via running the algorithm . Then, generates n public and private key pairs via running the algorithm KeyInitialise. Note that the data sender’s public and private key pair is defined as (). The generated and all are given to the adversary .
Queries
The following queries can be requested by for polynomial times:
1. Key retrieve query : responds with the private key ;
2. Decryption query : decrypts C with via running the algorithm , and responds with the output message.
Challenge
submits two equal-length messages and . picks , and then computes and returns the challenge ciphertext .
Constraints
(1) The target data receiver’s index t is not allowed to appear in the above Key retrieve query;
(2) The target data receiver’s index t and the challenge ciphertext is not allowed to appear in the above Decryption query.
Guess
can win the game if its output satisfies the condition .
Now, the advantage of could be defined as:
Definition A1
(IND-CCA Security). The GCD-RSD scheme is IND-CCA secure if the advantage of any probabilistic polynomial-time adversary is negligible.
Appendix A.2. Proof
Theorem A1.
According to the above Definition A1, the proposed scheme GCD-RSD is IND-CCA secure based on the ECCDH assumption against the Type-IND adversary in the random oracle model.
To be specific, let and be two random oracles and be a Type-IND adversary with the advantage against our proposed scheme. Hypothetically, requests a total of queries to the oracle , then there is an algorithm that can solve the ECCDH problem with the advantage at least .
Proof.
The elliptic curve group , and a secure hash function consist of an instance of the ECCDH problem, where G is the base point of . The target data receiver’s index is defined as t). aims to compute via executing . Next, and play the following game.
Setup
firstly generates the public parameter and then sends to . After that, operates the algorithm KeyInitialise to generate n public and private key pairs . In this process, the data sender’s public key and target data receiver’s public key are set as and , respectively. All are revealed to the adversary . Finally, initialises two empty lists and and updates them continuously in response to random oracle queries and . If the same input is asked multiple times, the same answer will be returned.
Queries
can respond to the queries requested by in the following ways:
1. : picks randomly and stores a new item into and returns as the answer;
2. : picks randomly and stores a new item into and returns as the answer;
3. : sends the private key to ;
4. : Note and there is a conditional branch caused by i to be discussed,
: For each item in the , performs the following operations:
(i) Recover by computing ;
(ii) If holds, returns to . If there is no item in the that satisfies the above condition, returns ⊥ to ,
: runs algorithm directly, then sends the output to as the answer.
Challenge
Firstly, submits two messages with the same length, then picks one random bit from the set and one random number . Finally, computes the ciphertext of via the following the operations defined in Signcrypt:
.
Note that the process of retrieving is by the definition of Unsigncrypt.
Finally, sends the ciphertext to the adversary .
Constraints
(1) The target data receiver’s index t is not allowed to appear in the ;
(2) The target data receiver’s index t and the challenge ciphertext are not allowed to appear in .
Guess
outputs one bit from the set , and at the same time, picks a random element from the as the answer to the above given instance of ECCDH problem.
Analysis
An event E is defined as that the adversary requests a query for retrieving during the described game above. Apparently, is at least in one item of at the end of this game if the event E happened.
However, if E does not happen, we can state that . On the other hand, based upon the definition of the Type-IND adversary (), holds. Then, we can present the following derivations.
Therefore, when the derivation (A1) is combined with the derivation (A2), the following derivation holds:
We can simplify this derivation to obtain that
In conclusion, at the end of the game between and , the probability of in the item(s) of is at least . Therefore, for , the probability of generating the correct answer is at least . □
Appendix B. EUF-CMA Security (Integrity)
Appendix B.1. Security Model
The security model we use to prove the integrity of our scheme GCD-RSD is existentially unforgeable under adaptively chosen-message attacks (EUF-CMA).
Definition A2
(EUF-CMA Security). The scheme to win the gameGCD-RSD is called EUF-CMA security, if for the adversary can access to a Signcrypt oracle , there is a negligible function such that:
where Q is the set of signatures that acquired from the Signcrypt oracle , is the public parameters, and l is the system security parameter. Note that is the data receiver’s public key whilst is the data sender’s private key.
To be specific, the adversary can play the following game with the challenger and win the game with the negligible probability .
Game 2. is a given adversary that can obtain valid signatures from queries. The game between the challenger and is operated as follows.
•Setup
firstly generates the public parameter via running the algorithm Setup and then utilises the algorithm KeyInitialise to set the public and private key pairs for all the data receivers in the scheme GCD-RSD. The data sender’s public and private key pair is defined as and the target date receiver’s key pair is .
•Queries
The following queries can be requested by for polynomial times.
1. responds with a random message .
2. responds with the receiver’s key pair .
3. executes the algorithm Signcrypt, then responds with the signature for the message M to the adversary . Note that the signature pair is appended to the list Q.
•Guess
The adversary first picks a random message via and a public key . Then, uses the algorithm Signcrypt to calculate the signature for with the public key . Finally, submits the signature to the challenger . can win the game if runs the algorithm and outputs true.
•Constrains
1. The picked message in Guess, i.e., cannot submit the message that has known its signature for .
2. cannot be obtained in .
The advantage of the adversary could be defined as:
We can state that GCD-RSD is EUF-CMA security if the probability is negligible with polynomial-time queries in the Queries phase and the mentioned constrains.
Appendix B.2. Proof
Theorem A2.
According to Definition A2, our GCD-RSD scheme is EUF-CMA secure based on ECCDH assumption against the adversary in the random oracle model.
To be specific, let be one random oracle; , , and be three real oracles; be the adversary with a non-negligible advantage against the scheme GCD-RSD. Hypothetically, requests a total of queries to the random oracle , then there is a challenger that can solve an instance of ECCDH problem with the advantage at least of .
Proof.
The elliptic curve group , and a secure hash function consist of an instance of the ECCDH problem, where G is the base point of . The target data receiver’s index is defined as t). aims to compute via executing . Next, and play the following game.
•Setup
firstly generates the public parameter and sets the public key pairs for all the data receivers in the scheme GCD-RSD. The data sender’s public and private key pair is defined as and the target receiver’s key pair is .
•Queries
The following queries can be requested by for polynomial times.
1. responds with a random message by querying , then appends to the list .
2. responds with the receiver’s key pair , then appends to the list .
3. executes the algorithm Signcrypt to obtain the signature . After that, responds with the signature for the message M to the adversary . Note that the signature pair is appended to the list .
•Guess
The adversary first picks a random message from . Then, uses the algorithm Signcrypt to calculate the signature for with the public key picked from randomly. Finally, submits the signature to the challenger to be verified by .
can win the game if the algorithm executed by the real oracle outputs true.
•Constrains
1. The picked message in Guess, i.e., cannot submit the message that has known its real signature for .
2. should not be queried in .
•Analysis We define the event E is that appears in . If E does not happen, . Based upon Definition. 2, the adversary has an advantage:
to win the game. It means has the advantage to find out from and hence to solve the ECCDH problem by calculating . Hence, the advantage of using as the subroutine to solve the ECCDH problem is at least
Therefore, we can state that the scheme GCD-RSD is EUF-CMA security, i.e., the probability is negligible if ECCDH assumption is intact. □
References
- Wikipedia. Internet of Things. Available online: https://en.wikipedia.org/wiki/Internet_of_things (accessed on 25 February 2022).
- Dang, L.M.; Piran, M.; Han, D.; Min, K.; Moon, H. A survey on internet of things and cloud computing for healthcare. Electronics 2019, 8, 768. [Google Scholar] [CrossRef]
- Facts & Factors. Global Internet of Things (IoT) Market Size To Hit USD 1842 Billion by 2028 at a 24.5% CAGR Growth (with COVID-19 Analysis): Facts & Factors. Available online: https://www.globenewswire.com/news-release/2022/01/13/2366783/0/en/Global-Internet-of-Things-IoT-Market-Size-To-Hit-USD-1-842-Billion-by-2028-at-a-24-5-CAGR-Growth-with-COVID-19-Analysis-Facts-Factors.html (accessed on 13 January 2022).
- Atzori, L.; Iera, A.; Morabito, G. The internet of things: A survey. Comput. Netw. 2010, 54, 2787–2805. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, C.; Poslad, S.; Chai, K.K. A provable semi-outsourcing privacy preserving scheme for data transmission from IoT devices. IEEE Access 2019, 7, 87169–87177. [Google Scholar] [CrossRef]
- Pallavi, S.; Mallapur, J.D.; Bendigeri, K.Y. Remote sensing and controlling of greenhouse agriculture parameters based on IoT. In Proceedings of the 2017 International Conference on Big Data, IoT and Data Science (BID), Pune, India, 20–22 December 2017; pp. 44–48. [Google Scholar]
- Mellit, A.; Kalogirou, S. Artificial intelligence and internet of things to improve efficacy of diagnosis and remote sensing of solar photovoltaic systems: Challenges, recommendations and future directions. Renew. Sustain. Energy Rev. 2021, 143, 110889. [Google Scholar] [CrossRef]
- Ullo, S.L.; Sinha, G. Advances in IoT and smart sensors for remote sensing and agriculture applications. Remote Sens. 2021, 13, 2585. [Google Scholar] [CrossRef]
- Li, W.; Awais, M.; Ru, W.; Shi, W.; Ajmal, M.; Uddin, S.; Liu, C. Review of sensor network-based irrigation systems using IoT and remote sensing. Adv. Meteorol. 2020, 2020. [Google Scholar] [CrossRef]
- Abraham, S.; Beard, J.; Manijacob, R. Remote environmental monitoring using Internet of Things (IoT). In Proceedings of the 2017 IEEE Global Humanitarian Technology Conference (GHTC), San Jose, CA, USA, 19–22 October 2017; pp. 1–6. [Google Scholar]
- Shafi, U.; Mumtaz, R.; Iqbal, N.; Zaidi, S.M.H.; Zaidi, S.A.R.; Hussain, I.; Mahmood, Z. A multi-modal approach for crop health mapping using low altitude remote sensing, internet of things (IoT) and machine learning. IEEE Access 2020, 8, 112708–112724. [Google Scholar] [CrossRef]
- Michler, J.D.; Josephson, A.; Kilic, T.; Murray, S. Privacy Protection, Measurement Error, and the Integration of Remote Sensing and Socioeconomic Survey Data. arXiv 2022, arXiv:2202.05220. [Google Scholar] [CrossRef]
- Zhang, Y.; Lu, Y.; Zhang, D.; Shang, L.; Wang, D. Risksens: A multi-view learning approach to identifying risky traffic locations in intelligent transportation systems using social and remote sensing. In Proceedings of the 2018 IEEE International Conference on Big Data (Big Data), Seattle, WA, USA, 10–13 December 2018; pp. 1544–1553. [Google Scholar]
- Voigt, P.; von dem Bussche, A. Organisational Requirements. In The EU General Data Protection Regulation (GDPR): A Practical Guide; Springer International Publishing: Cham, Switzerland, 2017; pp. 31–86. [Google Scholar] [CrossRef]
- Yang, J.J.; Li, J.Q.; Niu, Y. A hybrid solution for privacy preserving medical data sharing in the cloud environment. Future Gener. Comput. Syst. 2015, 43, 74–86. [Google Scholar] [CrossRef]
- Liu, J.; Huang, X.; Liu, J.K. Secure sharing of personal health records in cloud computing: Ciphertext-policy attribute-based signcryption. Future Gener. Comput. Syst. 2015, 52, 67–76. [Google Scholar] [CrossRef]
- Li, Z.R.; Chang, E.C.; Huang, K.H.; Lai, F. A secure electronic medical record sharing mechanism in the cloud computing platform. In Proceedings of the 2011 IEEE 15th International Symposium on Consumer Electronics (ISCE), Singapore, 14–17 June 2011; pp. 98–103. [Google Scholar]
- Li, M.; Yu, S.; Zheng, Y.; Ren, K.; Lou, W. Scalable and secure sharing of personal health records in cloud computing using attribute-based encryption. IEEE Trans. Parallel Distrib. Syst. 2012, 24, 131–143. [Google Scholar] [CrossRef]
- Rao, Y.S. A secure and efficient ciphertext-policy attribute-based signcryption for personal health records sharing in cloud computing. Future Gener. Comput. Syst. 2017, 67, 133–151. [Google Scholar] [CrossRef]
- Triantafyllou, A.; Sarigiannidis, P.; Bibi, S. Precision agriculture: A remote sensing monitoring system architecture. Information 2019, 10, 348. [Google Scholar] [CrossRef]
- Adi, W.; Mulhem, S.; Mars, A. Secured remote sensing by deploying clone-resistant Secret Unknown Ciphers. In Proceedings of the 2017 IEEE International Conference on Consumer Electronics-Taiwan (ICCE-TW), Taipei, Taiwan, 12–14 June 2017; pp. 133–134. [Google Scholar]
- Gao, P.; Zhang, H.; Yu, J.; Lin, J.; Wang, X.; Yang, M.; Kong, F. Secure cloud-aided object recognition on hyperspectral remote sensing images. IEEE Internet Things J. 2020, 8, 3287–3299. [Google Scholar] [CrossRef]
- Zheng, Y. Digital signcryption or how to achieve cost(signature & encryption) ≪ cost(signature) + cost(encryption). In Proceedings of the Advances in Cryptology—CRYPTO ’97, Santa Barbara, CA, USA, 17–21 August 1997; Kaliski, B.S., Ed.; Springer: Berlin/Heidelberg, Germany, 1997; pp. 165–179. [Google Scholar]
- Karati, A.; Islam, S.H.; Karuppiah, M. Provably secure and lightweight certificateless signature scheme for IIoT environments. IEEE Trans. Ind. Inform. 2018, 14, 3701–3711. [Google Scholar] [CrossRef]
- Truong, H.T.T.; Almeida, M.; Karame, G.; Soriente, C. Towards secure and decentralized sharing of IoT data. In Proceedings of the 2019 IEEE International Conference on Blockchain (Blockchain), Atlanta, GA, USA, 14–17 July 2019; pp. 176–183. [Google Scholar]
- Chen, Y.; Hu, B.; Yu, H.; Duan, Z.; Huang, J. A threshold proxy re-encryption scheme for secure IoT data sharing based on blockchain. Electronics 2021, 10, 2359. [Google Scholar] [CrossRef]
- Marr, B. Big Data in Practice: How 45 Successful Companies Used Big Data Analytics to Deliver Extraordinary Results; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Chen, J.; Wang, L.; Wen, M.; Zhang, K.; Chen, K. Efficient Certificateless Online/Offline Signcryption Scheme for Edge IoT Devices. IEEE Internet Things J. 2022, 9, 8967–8979. [Google Scholar] [CrossRef]
- Fadlullah, Z.M.; Kato, N. On Smart IoT Remote Sensing over Integrated Terrestrial-Aerial-Space Networks: An Asynchronous Federated Learning Approach. IEEE Netw. 2021, 35, 129–135. [Google Scholar] [CrossRef]
- Yuan, G.; Hao, Q. Digital watermarking secure scheme for remote sensing image protection. China Commun. 2020, 17, 88–98. [Google Scholar] [CrossRef]
- Stinson, D.R. Cryptography: Theory and Practice; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Barker, E.; Barker, W.; Burr, W.; Polk, W.; Smid, M. Recommendation for Key Management Part 1: General (Revision 5); Technical Report NIST.SP.800-57pt1r5; NIST: Gaithersburg, MD, USA, 2020; 57p. [Google Scholar]
- Szczechowiak, P.; Oliveira, L.B.; Scott, M.; Collier, M.; Dahab, R. NanoECC: Testing the limits of elliptic curve cryptography in sensor networks. In Proceedings of the European conference on Wireless Sensor Networks, Bologna, Italy, 30 January–1 February 2008; Springer: Berlin/Heidelberg, Germany, 2008; pp. 305–320. [Google Scholar]
- Lauter, K. The advantages of elliptic curve cryptography for wireless security. IEEE Wirel. Commun. 2004, 11, 62–67. [Google Scholar] [CrossRef]
- Potlapally, N.R.; Ravi, S.; Raghunathan, A.; Jha, N.K. A study of the energy consumption characteristics of cryptographic algorithms and security protocols. IEEE Trans. Mob. Comput. 2005, 5, 128–143. [Google Scholar] [CrossRef]
- Gupta, B.B.; Quamara, M. An overview of Internet of Things (IoT): Architectural aspects, challenges, and protocols. Concurr. Comput. Pract. Exp. 2020, 32, e4946. [Google Scholar] [CrossRef]
- Lowe, G. Casper: A compiler for the analysis of security protocols. In Proceedings of the 10th Computer Security Foundations Workshop, Rockport, MA, USA, 10–12 June 1997; pp. 18–30. [Google Scholar]
- Hoare, C.A.R. Communicating sequential processes. Commun. ACM 1978, 21, 666–677. [Google Scholar] [CrossRef]
- Gibson-Robinson, T.; Armstrong, P.; Boulgakov, A.; Roscoe, A.W. FDR3—A Modern Refinement Checker for CSP. In International Conference on Tools and Algorithms for the Construction and Analysis of Systems; Ábrahám, E., Havelund, K., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; Volume 8413, pp. 187–201. [Google Scholar]
- De Zan, F.; Guarnieri, A.M. TOPSAR: Terrain observation by progressive scans. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2352–2360. [Google Scholar] [CrossRef]
- Scott, M. MIRACL-Multiprecision Integer and Rational Arithmetic C/C++ Library. 2012. Available online: https://github.com/miracl/MIRACL (accessed on 21 August 2019).
- Viega, J.; Messier, M.; Chandra, P. Network Security with OpenSSL: Cryptography for Secure Communications; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2002. [Google Scholar]
- Paillier, P.; Villar, J.L. Trading One-Wayness Against Chosen-Ciphertext Security in Factoring-Based Encryption. In Proceedings of the Advances in Cryptology–ASIACRYPT 2006: 12th International Conference on the Theory and Application of Cryptology and Information Security, Shanghai, China, 3–7 December 2006; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006; Volume 4284, pp. 252–266. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).