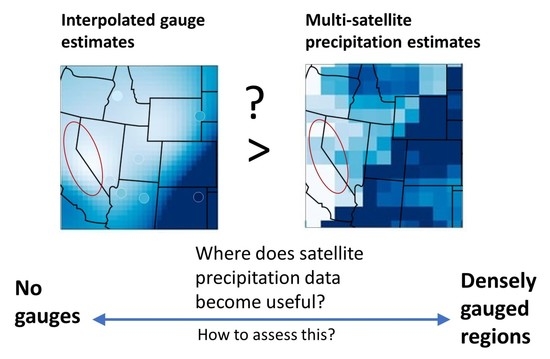
Where Can IMERG Provide a Better Precipitation Estimate than Interpolated Gauge Data?

Abstract

Although rain gauges provide valuable point-based precipitation observations, gauge data is globally sparse, necessitating interpolation between often-distant measurement locations. Interpolated gauge data is subject to uncertainty just as other precipitation data sources. Previous studies have focused either on the effect of decreasing gauge density on interpolated gauge estimate performance or on the ability of gauge data to accurately assess satellite multi-sensor precipitation data as a function of gauge density. No previous work has directly compared the performance of interpolated gauge estimates and satellite precipitation data as a function of gauge density to identify the gauge density at which satellite precipitation data and interpolated estimates have similar accuracy. This study seeks to provide insight into interpolated gauge product accuracy at low gage densities using a Monte Carlo interpolation scheme at locations across the continental U.S. and Brazil. We hypothesize that the error in interpolated precipitation estimates increases drastically at low rain gauge densities and at high distances to the nearest gauge. Results show that the multisatellite precipitation product, IMERG, has comparable performance in precipitation detection to interpolated gauge data at very low gauge densities (i.e., less than 2 gauges/10,000 km²) and that IMERG often outperforms interpolated data when the distance to the nearest gauge used during interpolation is greater than 80–100 km. However, there does not appear to be a consistent relationship between this performance ‘break point’ and the geographical variables of elevation, distance to coast, and annual precipitation.

1. Introduction

Many end users of rainfall data prefer to use gauge-based precipitation products based on the assumption that gauge products, even when interpolated over an area with sparse gauge data, are more accurate that remotely sensed satellite multi-sensor precipitation (SMP) products. SMP estimates are limited by sensor accuracy and sampling error, exhibiting errors at high elevations and in complex terrain and often performing poorly during orographic, extreme precipitation, and frozen or mixed phase precipitation events [1,2,3]. However, interpolated gauge precipitation products are also subject to limitations, including inconsistent quality control, higher-latency, short or intermittent records, and interpolation uncertainty due to sparse gauge locations or gauge network configuration [4,5,6,7,8,9]. Sparse gauge networks and SMP estimates both face considerable uncertainty in mountainous regions and during extreme precipitation events, making it interesting to understand whether one product has an advantage over the other in these challenging conditions. However, relatively little work has attempted to discern at what rain gauge density SMP data may become a useful supplement (or even replacement) to gauge-interpolated estimates. Intuitively, regions with high gauge density may not benefit greatly from supplemental SMP data, but in sparsely gauged or ungauged regions, SMP estimates may provide similarly accurate (or even more accurate) precipitation data compared to interpolated estimates. No work has, thus far, provided a practical assessment of where satellite precipitation products may outperform interpolated gauge data for end users with interests in maintaining accurate and near real-time records of precipitation, such as national agencies.

Despite the well-known decreasing performance of interpolated gauge estimates at low gauge densities and the impact of low gauge densities on, hydrologic models which ingest interpolated precipitation data, etc., no previous studies have compared the performance of interpolated gauge products to SMP products as a function of gauge density. The impact of low gauge density on interpolated estimates is important to understand; many regional gage networks are characterized by a few densely gauged regions (often near large cities) and large areas that are sparsely gaged and less populated [10,11]. Brazil’s national gage network exemplifies this pattern; in 2012, the coastal Atlantic region of Brazil had a gage density of approximately 1.0/1000 km² while the Amazon basin had an average gage density of 0.1/1000 km² [11].

Previous studies clearly document the decreased accuracy of interpolated gauge estimates at low gauge densities and the effect of varying gauge density and gauge network configuration on hydrologic model performance when using interpolated precipitation data to estimate streamflow [12,13,14,15]. Low gauge densities are associated with more variable performance of hydrologic models and generally lower accuracy of streamflow estimates. Low gauge density leads to underestimation and greater variance in estimates of debris flow triggering rainfall [16].

Nonetheless, SMP validation efforts continue to often use interpolated gauge data from sparse gauge networks to assess the performance of satellite precipitation products, assuming that interpolated gauge data is an accurate areal-average ground-reference [17,18]. Gadelha et al. [18] used inverse distance weighting to create a daily gauge-based precipitation product for Brazil and then evaluate NASA’s Integrated Multi-satellitE Retrievals for GPM (IMERG) product, further described in Section 2.3. This work found that IMERG-Final demonstrates particularly poor performance relative to the interpolated gauge product in areas with low gauge density (less than 5 gauges/10,000 km²) [18]. However, given the uncertainty surrounding interpolated precipitation estimates in regions with such low gauge density, it is unclear if the disagreement between IMERG-F and the interpolated product are a result of IMERG error, error in the interpolated product, or, most likely, a combination of both. The same relationship in which IMERG performance decreased with gauge density was found over a large study area in China [19]. Such results suggest that the suitability of interpolated gauge data to validate SMP estimates decreases with gauge density.

To address this issue, several studies assessed the gauge density required to produce accurate estimates of satellite precipitation product performance: In China, Tian et al. [19] found “a strong dependency of the evaluation metrics for the IMERG product on gauge density and rainfall intensity” and concluded that, “previous evaluations of the IMERG rainfall product based on a relatively low-density gauge network might have underestimated its performance”. In a study in southwestern England, Villarini et al. [9] found that “For evaluation of satellite products, to estimate areal rainfall (pixel of about 200 km²) within 20% of its true value, respectively over 25, around 25, 15, and 4 gauges are necessary at the 15-min, hourly, 3-hourly, and daily scale”. Similarly, Villarini [20] suggested that, at a minimum, five rain gauges should be used to interpolate and estimate ground reference areal-average precipitation at a 0.25° scale. One shortcoming of this study was the relatively short study period (4 months) and limited study area (two 0.25° TMPA pixels in Rome) [20]. Mandapaka and Lo [21] conducted a similar study based on eight IMERG pixels in Singapore, finding that at least 8–10 gauges per 0.1° pixel are required to limit the areal precipitation estimate error to 25% for daily precipitation estimates. However, the range of gauge densities analyzed in previous studies was much higher than what exists in most parts of the world; the lowest gauge densities evaluated were 1 gauge/0.1° pixel (equivalent to ~80 gages/10,000 km²), 1 gauge/0.25° pixel (equivalent to ~13 gages/10,000 km²), and 0.25 gauges/100 km² (equivalent to 25 gauges/10,000 km²) by Mandapaka and Lo [21], Villarini [20], and Tian et al. [19], respectively. Given that the Global Precipitation Climatology Center (GPCC) database contains approximately 75,000 stations [5], the average global gauge density over land is approximately 5 gauges/10,000 km² (assuming that all gauges in the GHCN database lie within the approximate 150 million km² of Earth’s land surface). Notably, the issue of uncertainty in interpolated gauge estimates is not limited to SMP validation, but also impacts gauge-correction of radar fields, with Peleg et al. [7] finding that “at least three rain stations are needed to adequately represent the rainfall on a typical radar pixel scale”.

Another challenge to understanding the relative performance of gauge interpolated estimates and SMPs across varying gauge densities is the lack of consistent units for gauge density across studies. While many studies quantify the density of a gauge network as a number of gauge stations per unit area, the unit area varies greatly, from stations per 100 km² or 10,000 km² [11,18,22] to stations per 0.25° pixel or 0.1° pixel [19,21,23]. Few studies utilize the distance to the nearest gauge used during interpolation to characterize gauge network density (i.e., Nikolopoulos et al. [16]), even though interpolated accuracy depends heavily on this metric and only 5.9% of the Earth’s land surface lies within 25 km of a rain gauge [5]. Nikolopoulos et al. [16] found that debris flow-triggering rainfall could be underestimated by up to 40% when the nearest available gauge data was 6–7 km away from a debris flow event.

Aforementioned studies also lack a robust scheme for evaluating low gauge density; at the lowest simulated gauge densities in Tian et al. [19], Mandapaka and Lo [21], and Villarini [20], the authors did not consider scenarios in which the nearest available gauge was not within a pixel or within 0.1° of a pixel; however, in data-limited regions across the world, the nearest gauge data is almost always located more than 0.1° away [5]. While these studies convincingly demonstrate that low gauge density impairs interpolated gauge estimates’ ability to evaluate SMP data, they do not directly compare the accuracy or utility of interpolated gauge data and SMP data as a function of gauge density.

This work extends past analyses of satellite precipitation products and interpolated gauge estimate performance over a longer study period and larger study area, a recommendation of previous studies [20]. We hypothesize that the variability in the performance of interpolated precipitation estimates increases at low rain gauge densities and at high distances to the nearest gauge used during interpolation. We hypothesize that SMP estimates have comparable performance to interpolated gauge data at low gauge densities. Unlike any previous studies, this work seeks to provide precipitation end-users with a quantitative estimate of the gauge density at which IMERG-Early and IMERG-Late performance can be reasonably expected to meet or exceed the performance of an interpolated gauge estimate at a daily, 0.1° resolution, both in terms of gauge density and distance to the nearest gauge. By studying the relative accuracy of daily IMERG and gauge-interpolated estimates across Brazil and the U.S. (study area in Figure 1) over 2015–2018, this study also assesses whether climatology and topography mediate IMERG’s performance relative to gauge interpolated estimates.

2. Data

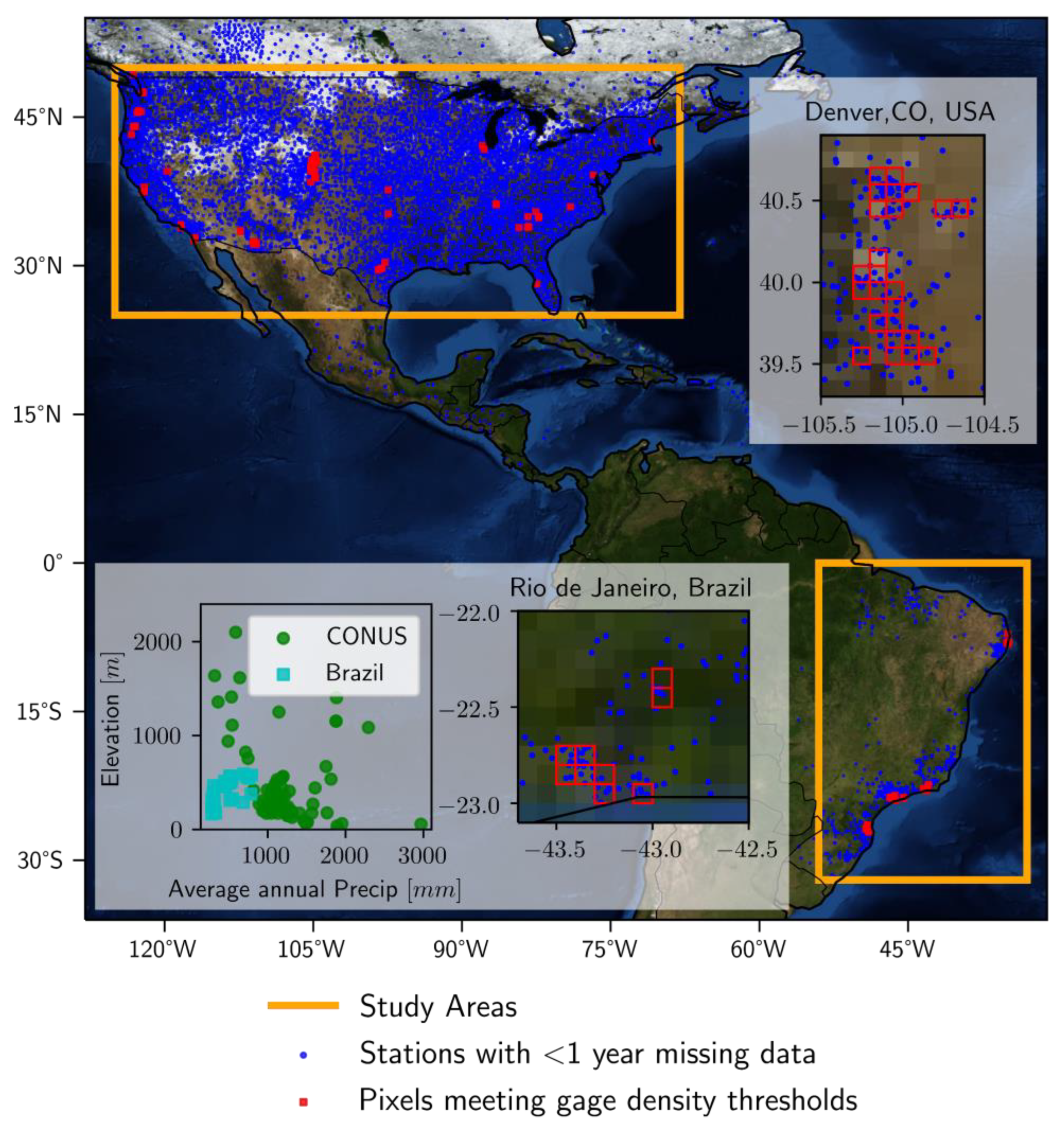
2.1. Study Area and Period

The study area covers the continental United States (CONUS) and eastern Brazil, roughly (125° W–68°W, 52° N–25°N) and (54° W–33°W, 0°–32°S), respectively (Figure 1). This study area covers a range of climates, elevations, and terrains, which will provide insight into how the relative performance of IMERG and gauge-interpolated products varies across these geographic features. The study period is 2015–2018, determined by the availability of CEMADEN gauge records (Section 2.2).

2.2. Gauge Data

Tipping bucket gage records for 2015–2018 from Brazil’s National Center for Natural Disaster Monitoring and Warning (CEMADEN) with a 10-min resolution during rainy periods and a 60-min resolution during non-rainy periods are used as the ground-reference in Brazil [24]. Tipping bucket timeseries were converted to daily resolution. Since no invalid data markers are present in the original gauge records, periods without observed precipitation in the tipping bucket record for greater than 30 days were assumed to be invalid data and were flagged with a missing precipitation marker in the dataset.

The station-based Serially Complete Dataset for North America (SCDNA) [25] is used as the ground-reference in CONUS. A precipitation flag is present in the SCDNA dataset to indicate where daily precipitation estimates are direct gauge observations and where they have been estimated based on other stations. Precipitation estimates that were not directly observed were flagged with a missing precipitation marker.

For both the CEMADEN and SCDNA gauge datasets, we excluded gauge records with missing or invalid precipitation data for greater than one year during the 2015-2018 study period. This resulted in relatively consistent spatial coverage of CONUS by the available SCDNA gauge records. Available gauge records from the CEMADEN dataset are heavily concentrated in the coastal east and southeast of Brazil, particularly near the cities of Rio de Janeiro and Sao Paolo (Figure 1).

2.3. Satellite Precipitation Data

Satellite-based precipitation estimates are extremely valuable due to their global coverage and near real-time, public availability. NASA’s multisatellite IMERG product combines remote sensing retrievals from a range of sensors, including passive microwave radiometers, active precipitation radar, and infrared sensors, to estimate precipitation at the earth’s surface [26,27]. IMERG is available globally from 2000 to present at a half-hourly, 0.1° resolution in three versions: IMERG-Early at a 4-h latency, available in near real-time but excluding remote sensing data following a satellite pass, IMERG-Late at a 12-h latency, which incorporates additional remote sensing retrievals, and IMERG-Final at an approximately 2.5 month latency, which assimilates gauge data to improve product accuracy [26,27]. In this work, IMERG-Early and -Late are used because of these products’ low latency and applicability to early warning systems and are aggregated to daily resolution. Since its release in 2014, the IMERG product has grown in popularity as an input to hydrologic modeling, landslide hazard assessment, and understanding extreme precipitation and trends in precipitation around the world, among other applications [28,29,30].

3. Methods

3.1. Pixel Selection

To be included in the analysis, 0.1° grid cells were required to meet two gauge density requirements: at least 6 gage stations must be located within 0.1° (~11 km) of the grid cell center, ensuring an accurate interpolated ground-reference of area-averaged precipitation for the grid cell, and at least 75 stations must be located within 1.0° (~110 km) of the center of the grid cell. The latter requirement ensures that the simulation of data-limited interpolation estimates described in the next subsection will be robust. This resulted in 38 pixels for analysis in Brazil using CEMADEN station data and 82 pixels for analysis in CONUS using SCDNA data (Figure 1).

3.2. Inverse Distance Weighting Interpolation Scheme

Inverse distance weighting (IDW) is used to interpolate SCDNA and CEMADEN gauge data, based on the findings of Xavier et al. [11] that IDW produced the most accurate gridded estimates of precipitation in Brazil. In IDW, the weight assigned to each station estimate is based on the distance of the station to the center of the grid cell for which an interpolated precipitation estimate is being calculated, with the nearest gauge stations being assigned the highest weights:

$$w_k=\frac{1}{d_k^p}$$

(1)

where w is the weight assigned to station k, d is the distance of station k from the center of the grid cell of interest, and p is the power parameter, which is equal to 2 in this study, following the methodology of similar studies [11,31]. In this implementation of IDW, a maximum of fifteen nearest stations are considered.

3.3. Monte Carlo “Data-Limited” Interpolation Scheme

Ground-truth precipitation is calculated using all gauge records available in proximity to a pixel (Figure 2a). The high gauge density thresholds required for all participating pixels (Section 3.1) ensures that this an accurate ground-truth record. To analyze the relationship between gauge density and the accuracy of gauge interpolated precipitation estimates, a Monte Carlo (MC) scheme is implemented at every pixel, described by the following steps:

(a)

n stations within 1.0° of a pixel are simulated as “available” and are used to generate a “data-limited” precipitation timeseries using IDW interpolation for that pixel (Figure 2a,b).

(b)

The resulting data-limited interpolated timeseries is compared against ground-truth precipitation. The following performance metrics are calculated for the data-limited timeseries: root mean square error (RMSE), probability of detection (POD), probability of false alarm (POFA), and Kling Gupta Efficiency (KGE). These performance metrics are further described in Section 3.4.

(c)

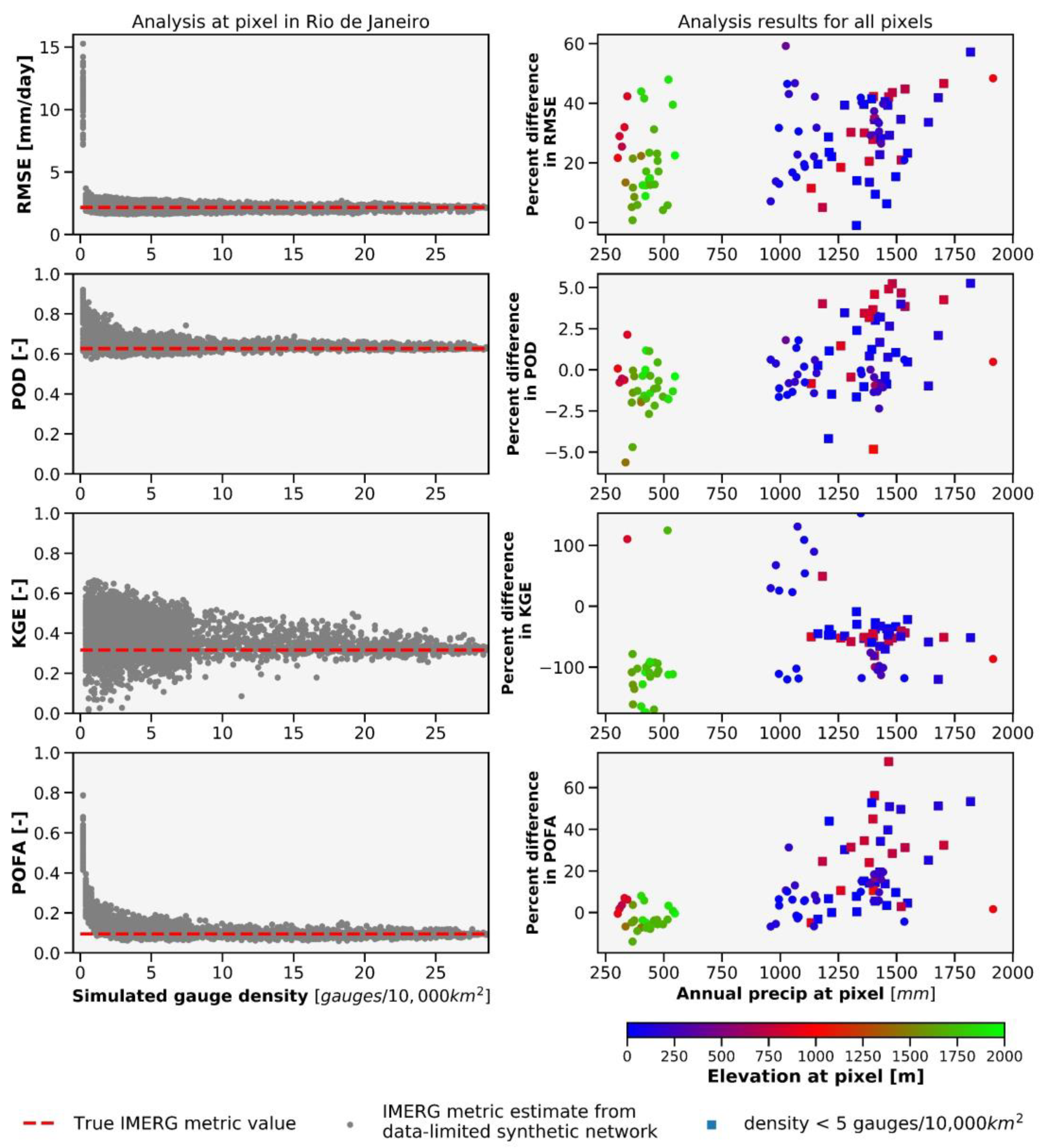
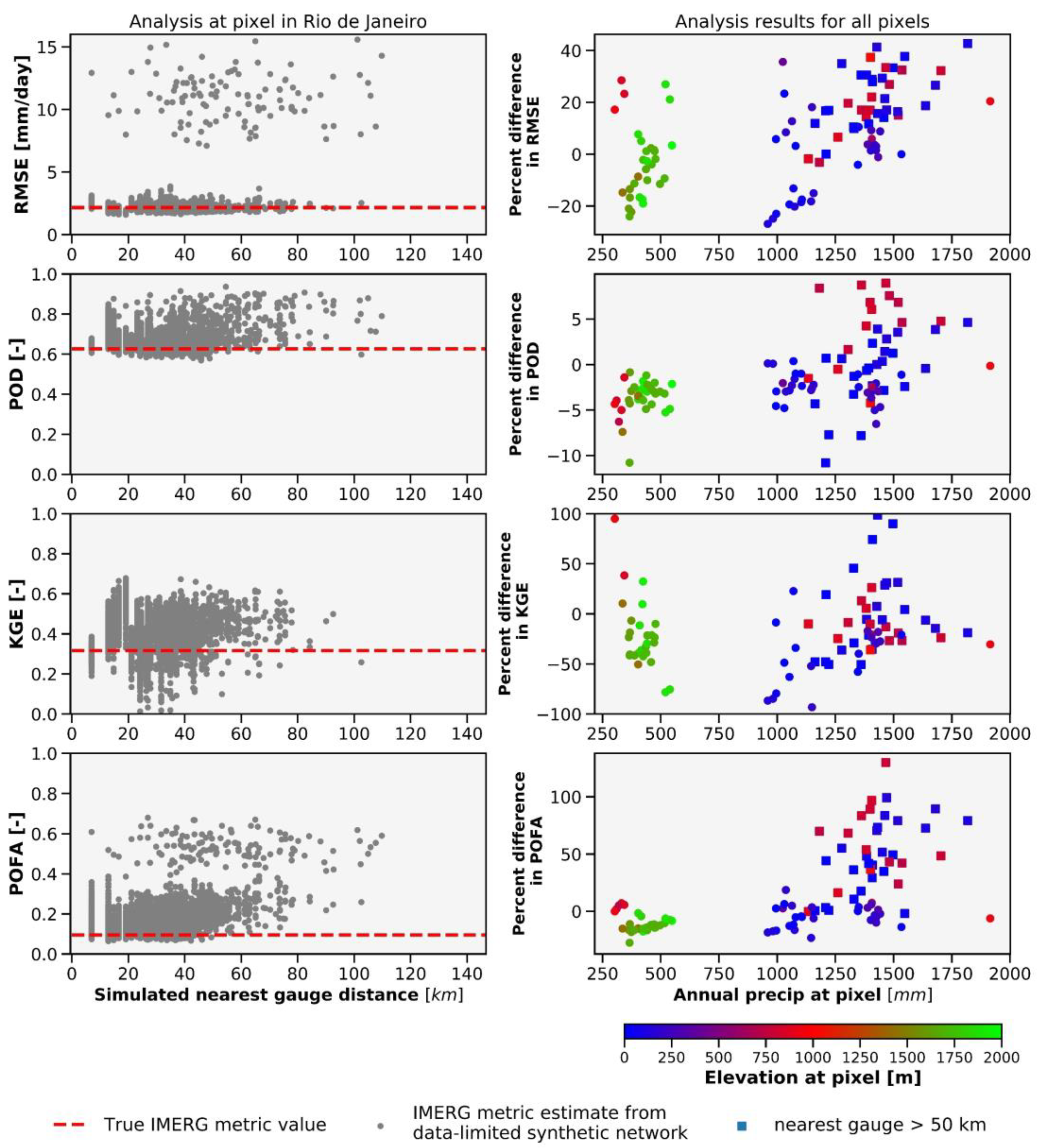
This scheme is repeated for a range of values of n, from n = 1 to n = nearly all available stations, resulting in a range of POD values and other performance metric values across the range of simulated gauge densities used during data-limited interpolation (Figure 2c). For each simulated value of n, n stations are randomly selected. At least 3000 iterations are performed at each pixel with a range of values for n to simulate a large variety of gauge densities and gauge network configurations.

Similar schemes have been implemented to study gauge network density in other studies [15,21]. The randomly sampled “data-limited” selection of gages shown in Figure 2a are referred to as the “synthetic network” in previous studies [21]. In addition to performing the above scheme to simulate a range of synthetic gauge densities, the distance from the center of the pixel to the nearest available gauge in each synthetic, data-limited gauge network is recorded. Thus, the performance of each synthetic gauge network is associated with a unique gauge density and nearest gauge distance.

3.4. Performance Metrics

The root mean square error (RMSE; ranges from 0 to infinity, and ideal score is 0), the Kling Gupta efficiency (KGE; ranges from −∞ to 0, and ideal score is 0), probability of detection (POD; ranges from 0 to 1, and ideal score is 1), and probability of false alarm (POFA; ranges from 0 to 1, and ideal score is 0) are used to evaluate the performance of precipitation data, consistent with previous precipitation studies [18,32,33]. KGE measures the correlation between estimated and ground truth precipitation as well as the ability of precipitation estimates to capture the mean and standard deviation of the ground truth.

$$RMSE=\sqrt{\frac{1}{n}{{\displaystyle \sum }}_{i=0}^n{\left(R_i-\widehat{R_i}\right)}^2}$$

(2)

where $R_i$ is the ground truth precipitation calculated using all available gauges and $\widehat{R_i}$ is the data-limited interpolated estimate at timestep, i.

$$KG=1-\sqrt{{\left(CC-1\right)}^2+{\left(\frac{{\mu }_{\widehat{R}}}{{\mu }_R}-1\right)}^2+{\left(\frac{{\sigma }_{\widehat{R}}}{{\sigma }_R}-1\right)}^2}$$

(3)

where CC is the Pearson correlation coefficient calculated between the data-limited and ground truth timeseries. ${\mu }_R$ (${\mu }_{\widehat{R}}$) and ${\sigma }_R$ (${\sigma }_{\widehat{R}}$) are the mean and standard deviation of the ground truth (data-limited) timeseries, respectively.

$$POD=\frac{H}{H+M}$$

(4)

$$POFA=\frac{F}{H+F}$$

(5)

H denotes instances when the data-limited estimate correctly detects precipitation; F represents instances when the data-limited estimate incorrectly detects precipitation; and M represents instances when the data-limited estimate fails to detect nonzero precipitation, as reported by the ground truth record.

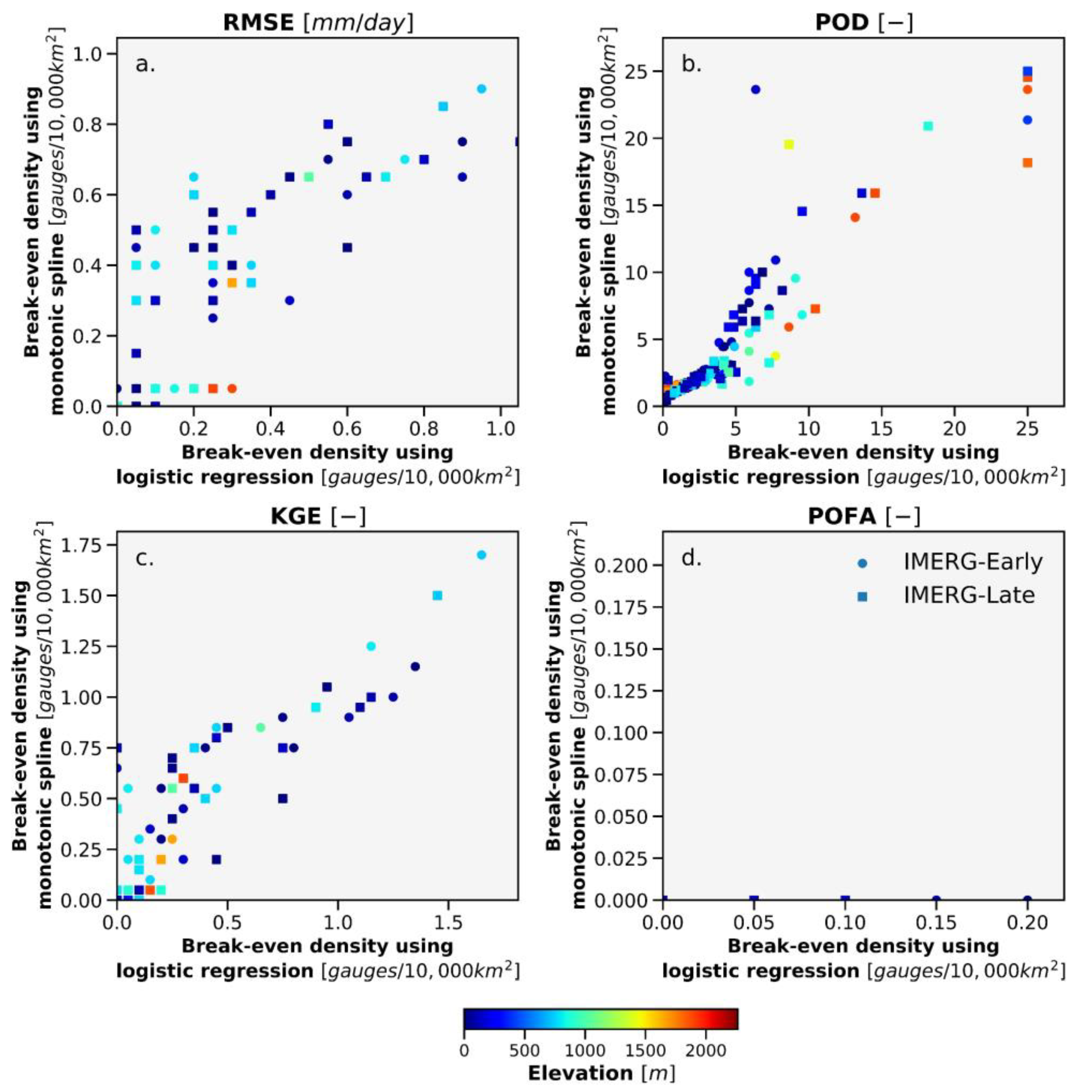
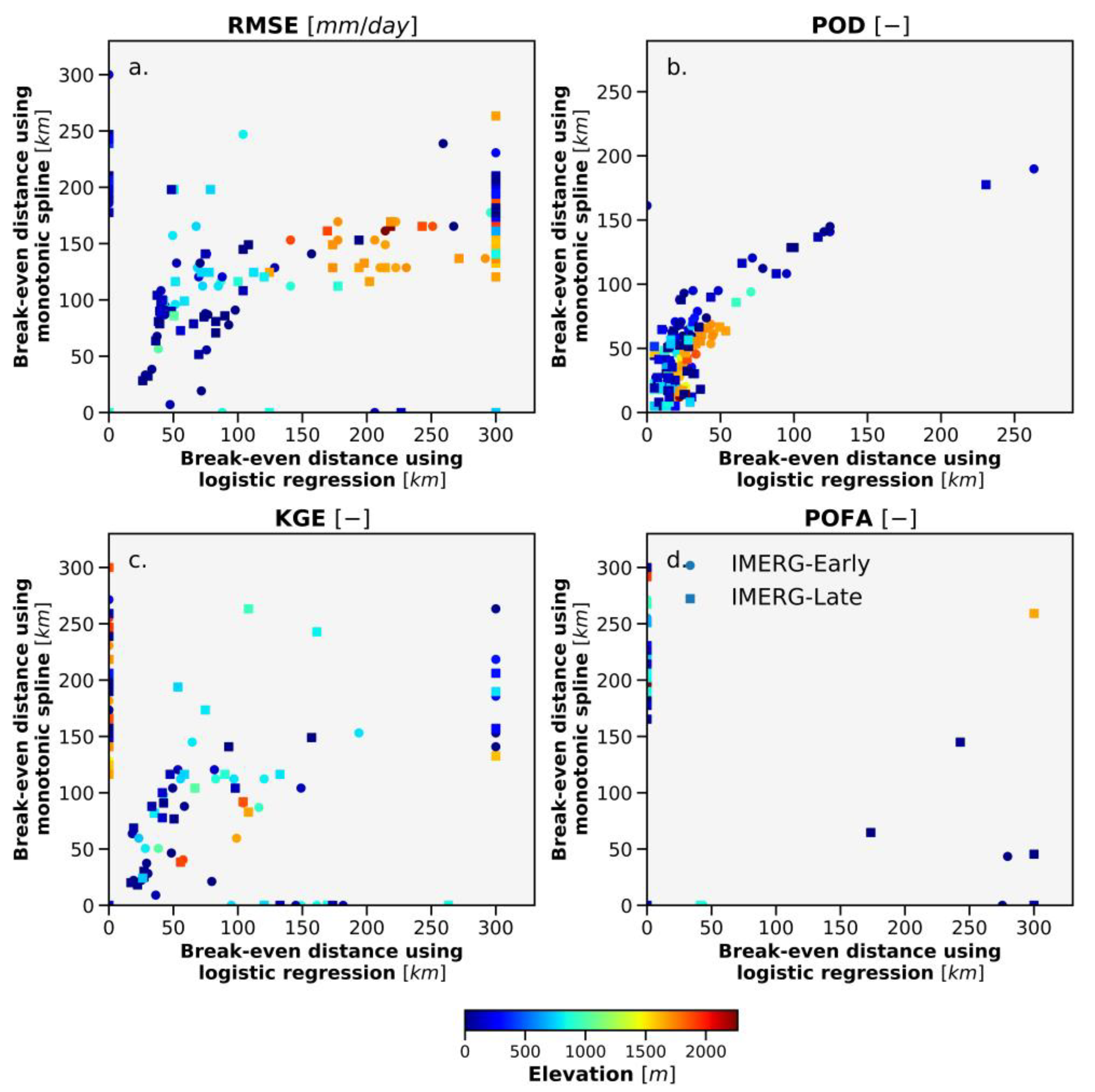
3.5. Regression Fitting

A logistic regression is fitted to the simulated error metric data obtained during the Monte Carlo data-limited interpolation scheme (Section 3.3) to capture the relationship between gauge density and each performance metric (see orange regression fitted to POD data in Figure 2c,d):

$$metric=\alpha ln\left(density\right)+\beta$$

(6)

Regression results with a r² value of less than 0.5 were not included in results due to lack of fit.

A monotonic cubic “smoothing” spline was also used to interpolate between data points and generate a “smoothed” monotonically increasing or decreasing line (depending on the performance metric) to describe the relationship between gauge density, nearest gauge distance, and performance metrics [34,35] (see smoothed olive line fitted to POD data in Figure 2c,d). The PCHIP 1-D monotonic cubic interpolation scheme from the SciPy interpolation package was used to implement this method [36]. The monotonic spline is useful because it can better reflect the relationship between gauge density and nearest gauge distance when it does not follow a logistic curve.

3.6. Comparison of Interpolated Gauge Performance to IMERG

The performance metrics RMSE, POD, KGE, and POFA of IMERG-Early and IMERG-Late are calculated for at every pixel using the ground-truth timeseries (Section 3.3). The logistic regression and monotonic splines fit to results of the data-limited MC scheme (Section 3.5) represent the expected change in performance of interpolated estimates as a function of gauge density and nearest gauge distance. The gauge density (or nearest gauge distance) at which the logistic regression intercepts the POD (or other performance metric) of IMERG is the “break-even” point of performance for that metric (Figure 2c,d). The break-even point is the gauge density (or nearest gauge distance) at which one can expect equal performance between IMERG and an interpolated gauge estimate. The break-even gauge density and break-even nearest gauge distance is calculated using both logistic regressions and monotonic splines fit to results of the data-limited MC scheme. The break-even points of all pixels are analyzed as a function of latitude, elevation, average annual precipitation, and distance from coast to understand if such physiographic features impact the relative performance of IMERG and interpolated gauge estimates.

3.7. Assessing the Ability of Interpolated Estimates to Evaluate IMERG

The performance metrics calculated for IMERG-Early and IMERG-Late at every pixel using the ground-truth timeseries (Section 3.3) are the “true” performance metrics of IMERG. These performance metrics are also calculated for IMERG-Early using the timeseries generated from synthetic “data-limited” networks during the MC interpolation scheme described in Section 3.3. The IMERG RMSE, POD, KGE, and POFA estimated by “data-limited” timeseries is compared to the true IMERG performance metrics and used to calculate the percent difference between these metrics. This analysis demonstrates how interpolated estimates’ ability to accurately evaluate IMERG changes depending on gauge density and nearest gauge distance during interpolation.

4. Results

Figure 3 shows the logistic regressions fitted following the MC interpolation scheme (Section 3.3) for all pixels in CONUS and Brazil for the four evaluation metrics identified in Section 3.2. Logistic regression fits with an r² lower than 0.5 are excluded. As could be expected, the performance of gauge interpolated estimates for all performance metrics is best at high gauge densities and decreases exponentially at low gauge densities, particularly below 10 gauges/10,000 km². The ‘break-even’ points for IMERG-Early and IMERG-Late show the gauge density at which IMERG performance metrics intersect with the predicted performance of interpolated estimates at each pixel. In 35% of CONUS pixels, IMERG-Early RMSE does not intersect with the logistic regression, indicating that generally the RMSE estimated by interpolated gauge data even at very low gauge densities outperforms that estimated by IMERG. For almost all pixels in CONUS and Brazil, IMERG POFA does not intersect with the predicted POFA of interpolated estimates, even at very low gauge densities and high distances to the nearest available gauge.

Figure 4 presents the monotonic smoothing regressions fit to data from the MC interpolation scheme. The flexibility of monotonic smoothing allows these regressions to better capture the relationship between gauge density and POFA. However, note that these functions will only monotonically increase (or decrease) if the training data is monotonically increasing (or decreasing); because the results of the Monte Carlo simulations sometimes generated performance metric data that was not monotonic, some of the monotonically smoothed regressions do not demonstrate monotonic behavior either (e.g., Figure 4a). The POFA breakpoint for IMERG-Early and IMERG-Late occurs at gauge densities of 0 and at high distances to nearest gauge, however, indicating that IMERG does not provide a more accurate assessment of POFA, event at low gauge density and high distance to nearest gauge. The breakpoints for RMSE and KGE, on the other hand, occur consistently between 0 and 2 gauges/10,000 km², and. POD breakpoints as a function of density demonstrate the greatest range, but generally occur at between 1 and 5 gauges/10,000 km². The decline in POD as a function of distance to nearest gauge is much more gradual when described using the monotonic smoothing spline (Figure 4d) than when fit to a logistic regression (Figure 3d).

Overall, the range of breakpoints as a function of distance to nearest gauge in Figure 4 is much wider than the breakpoint range as a function of gauge density in Figure 3. Some pixels appear to exhibit higher accuracy (in terms of RMSE, POD, and KGE) using IMERG data when the nearest available gauge is more than 10 km away, while in other pixels interpolated gauge estimates demonstrate better performance than IMERG until the nearest available gauge is farther than 100 km away. The several CONUS pixels that demonstrate sharp decreases in KGE with increasing distance to nearest gauge (Figure 4h) are located in the Pacific Northwest, where coastal and orographic dynamics play a role in creating highly heterogeneous precipitation fields; it makes sense that an interpolated precipitation timeseries would sharply decline in its ability to capture the mean and standard deviation of the true precipitation as the distance to the nearest available gauge increases in this region.

Figure 5 compares the break points for gauge density calculated using both logistic regression and monotonic splines fit to MC scheme data as shown in Figure 3 and Figure 4. POD and KGE break points show good agreement when calculated using both methods, and RMSE break points estimates by the logistic regression tend to be slightly higher than those estimated using monotonic spline fits. The results at each grid cell are colored according to grid cell elevation, and there does not appear to be a notable relationship between elevation and performance breakpoints.

Figure 6 compares break points for nearest gauge distance calculated using logistic regression and monotonic spline fits. Logistic regression fits show a tendency to sometimes estimate lower POD and KGE break points for nearest gauge distance than monotonic spline fits; however, both methods agree well on POD break points up to distances of 150 km. In both Figure 5 and Figure 6, the POFA break points are estimated to be at 0 gauges/10,000 km² and 0 km, indicating that IMERG does not meet or exceed interpolated estimate POFA performance even when barely any gauge data (i.e., one or two gauges) is available. Unlike in Figure 5, which analyzed MC scheme results as a function of simulated gauge density, there does appear to be a discernable relationship between elevation and the distance breakpoints for RMSE. At lower elevations, both logistic regression and monotonic spline fits agree on lower breakpoints, meaning that IMERG outperforms interpolated gauge estimates in terms of RMSE when the nearest gauge is closer at low elevations (~50–100 km) than at high elevations (nearest gauge must be >100 km away). RMSE appears to be exception however; there is no apparent relationship between elevation and distance breakpoints for POD, CC, and POFA.

Table 1. The average and ± standard deviation of break-even points in CONUS and Brazil study areas in terms of both gauge density and distance to nearest available gauge. IMERG-Early breakpoints are shown out of parentheses and IMERG-Late breakpoints are in parentheses.

	CONUS Average		Brazil Average
	Break-Even Density [Gauges/10,000 km2]	Break-Even Distance [km]	Break-Even Density [Gauges/10,000 km2]	Break-Even Distance [km]
RMSE [mm/day]	0.1 ± 0.1 (0.1 ± 0.1)	178 ± 38 (175 ± 35)	0.4 ± 0.3 (0.4 ± 0.2)	100 ± 45 (105 ± 40)
KGE [-]	0.3 ± 0.3 (0.2 ± 0.2)	172 ± 59 (179 ± 61)	0.6 ± 0.4 (0.5 ± 0.4)	94 ± 53 (113 ± 58)
POD [-]	4.7 ± 6.1 (5.9 ± 7.0)	42 ± 31 (38 ± 27)	2.4 ± 3.8 (1.6 ± 0.8)	47 ± 48 (46 ± 45)
POFA [-]	--	246 ± 42 (246 ± 41)	--	196 ± 58 (182 ± 65)

presents the CONUS- and Brazil-wide average break-even points and standard deviation of break-even points for all performance metrics. As demonstrated in Figure 3, Figure 4, Figure 5 and Figure 6, the break-even point for IMERG RMSE and KGE is relatively low in terms of density. The POD break-even point in CONUS shows that IMERG will generally have a higher POD than interpolated estimates when gauge density is less than roughly 5 gauges/10,000 km², which is comparable to the gauge density covering most parts of the world, or when the distance to the nearest gauge is greater than 40 km. No values are shown for the POFA break-even point as a function of density since IMERG-Early and Late POFA consistently failed to outperform interpolated estimates even when interpolated scheme results were extrapolated to extremely low densities using the monotonic smoothing spline and logistic regression (see Figure 3, Figure 4, Figure 5 and Figure 6). The average and standard deviation of IMERG Early and Late break points as a function of density and distance are generally similar in CONUS and Brazil, although the break-even distance for RMSE and KGE is substantially higher in CONUS than in Brazil.

Figure 7 presents IMERG-Early performance metrics calculated using interpolated data from the MC scheme. The left column shows results for a single pixel in Rio de Janeiro; estimated IMERG performance metrics vary most widely when calculated using interpolated data from low gauge density synthetic networks. IMERG RMSE, POFA, and POD all tend to be overestimated by interpolated gauge data at low densities, while estimated IMERG KGE varies widely depending on the synthetic network used during interpolation. Estimates of IMERG-Early POFA and POD converge to the true POFA and POD at this pixel when the simulated gauge density is 10 gauges/10,000 km² or higher. The right column of Figure 7 plots the average percent difference at every pixel between the true performance metrics of IMERG-Early and the metrics estimated using data-limited interpolations with a density less than 5 gauges/10,000 km² (low gauge density). Overestimation of POD by low density interpolations is generally higher in pixels with higher annual precipitation, reaching a 60% overestimation of the true POD in several pixels.

Similarly, Figure 8 shows how IMERG-Early performance metrics calculated using interpolated data differ from the the true IMERG-Early metric when the nearest gauge used during interpolation is 50 km or more away. Interpolated estimates show a high relative overestimation of RMSE and POFA (i.e., estimating a KGE that is double the true value). While the spread of error in estimates of KGE is wide, interpolated gauge estimates show an equal tendency to over- and under-estimate IMERG KGE when the nearest gauge is 50 km or farther away. As in Figure 7, there does not appear to be a discernabble relationship between the percent difference in metric estimation and the geographic variables of annual precipitation and elevation, except in the case of POFA.

5. Discussion

5.1. Accuracy of Interpolated Gauge Estimates as a Function of Gauge Density and Nearest Gauge Distance

The performance of low-density interpolated gauge estimates varies across error metrics; while interpolated estimates of precipitation achieve a relatively low POFA even at densities as low as 5 gauges/10,000 km² (Figure 3e and Figure 4e), the POD of interpolated estimates drops sharply at low gauge density. The performance variability for all error metrics increases at low gauge densities (Figure 3 and Figure 4).

Our finding that the RMSE at the daily scale is consistently low at densities greater than 20 gauges/10,000 km² (Figure 3a and Figure 4a) is consistent with findings by Tian et al. [19] that the MAE at the daily scale varied minimally as a function of gauge density, suggesting that low gauge density has less impact on the error of a gauge interpolated product at the daily scale than at the hourly scale. However, Tian et al.’s [19] finding that the MAE at the hourly scale was greater at low gauge densities suggests that the impacts of sampling error are greater at the hourly scale.

Our regression-fitting results demonstrate that logarithmic regressions are a suitable way to characterize the relationship between gauge density and interpolated gauge estimate accuracy in terms of RMSE and POD, but not POFA. The probability of false alarm (POFA) exhibits the least consistent relationship with gauge density; although the variability of data-limited interpolation POFA is high at low gauge densities, interpolated estimates are still able to obtain low POFA when available gauge data is located nearby (Figure 4). In terms of fit, POFA has the least direct relationship with distance to nearest gauge, as this metric is not easily fit to a linear or logistic regression within the framework of the MC scheme in Section 3.3 (Figure 3). Thus, POFA is poorly explained by gauge density alone and POFA results from the MC scheme are not easily fit to a logistic regression, resulting in relatively few POFA regression fits with R² greater than 0.5 (Figure 3). Estimating the breakpoint for POFA (i.e., the gauge density or nearest gauge distance at which IMERG and interpolated gauge estimates have similar POFA) is difficult because the monotonic cubic spline does not generate regressions that characterize POFA behavior at high distances (due to lack of ‘training data’), and, as previously mentioned, logistic regressions do not fit POFA data well.

The strong relationship exhibited between distance to nearest gauge and the RMSE, POD, and KGE of interpolated estimates (Figure 3 and Figure 4) demonstrates that incorporating this variable is beneficial to understanding the performance of interpolated gauge estimates at low densities.

5.2. Accuracy of Interpolated Gauge Estimates Relative to IMERG Early and Late

At gauge densities higher than 2 (10) gauges/10,000 km², interpolated gauge estimates consistently outperform IMERG-Early and IMERG-Late in terms of RMSE, KGE, and POFA (POFA; Figure 5, Table 1). IMERG appears to have the greatest relative advantage over low density interpolations when estimating probability of detection (POD), resulting in break points as high as 20–25 gauges/10,000 km² and as low as 5 km (Figure 3a, Figure 5b and Figure 6b). In several (but not most) pixels, results indicate that IMERG-Early and -Late can be expected to exhibit higher POD than interpolated gauge estimates where gauge densities are less than 20 gauges/10,000 km² or when the nearest available gauge is farther than 5 km away, i.e., nearly the entire world. However, this result may also reflect IMERG’s tendency to overestimate light precipitation occurrence [29,37]. The break-even densities for KGE and RMSE estimated using logistic regressions and the monotonic cubic spline agree quite well, although such relatively low break points indicate that interpolated estimates will generally outperform IMERG-Early and -Late (Figure 5a). The break-even distance for POD is lower when calculated using the logistic regression than the monotonic spline (Figure 6b), which may be due to the different ways that these methods extrapolate from the lowest simulated distance to nearest gauge.

The relative performance of interpolated estimates over IMERG is strongly mediated by the distance to the nearest gauge used during interpolation; the average break-even distance for IMERG-Early RMSE (KGE) in Brazil and CONUS is 100 (94) km and 178 (172) km (Table 1), respectively, indicating that IMERG-Early can be expected to have the same or better RMSE (KGE) than interpolated gauge estimates at a pixel when the nearest available gauge is farther away than these distances. The variability of the break-even distance within each country is highly variable, however (Table 1). It is also worth noting that there is not a large difference between the relative performance of IMERG-Early and IMERG-Late when compared to interpolated data (Figure 3, Figure 4, Figure 5 and Figure 6, Table 1).

5.3. Ability of Interpolated Estimates to Evaluate IMERG

Because different gauge network densities and configurations generate different interpolated estimates of precipitation, they also estimate different performance metrics when used to evaluate IMERG. IMERG-Early RMSE, POD, and POFA are generally overestimated by low density gauge-interpolations (Figure 7), suggesting that findings in Gadelha et al. [18], which demonstrate high IMERG RMSE in regions where the validation product has low gauge density, should be evaluated with caution. This aligns with findings from Tian et al. [19] that “…evaluations of the IMERG rainfall product based on a relatively low-density gauge network might have underestimated its performance”. The range of estimated IMERG-Early KGE is relatively high when calculated using low density interpolated data (Figure 7). Even though interpolated gauge estimates can exhibit lower RMSE than IMERG at very low gauge densities (Figure 3a and Figure 4a), and therefore may be considered more or comparably accurate to IMERG, this does not indicate that such interpolated estimates are suitable for evaluating IMERG. These findings support the results of Villarini [20] and Mandapaka and Lo [21] and highlight the difficulty of assessing IMERG performance when using low density interpolated gauge data as a ground-reference.

Adding to the understanding of interpolated gauge estimate performance, this analysis also shows that interpolated data based on gauge data 50 or more km away often overestimates IMERG error (Figure 8). The particularly high percent differences in metric values generated by interpolated estimates are mainly a result of the small values of IMERG RMSE, KGE, and POFA; for example, an estimate of 0.2 when the true POFA is 0.1 will result in a 100% difference between the true IMERG POFA and estimated POFA.

5.4. Interpolated Data Performance as a Function of Climate and Geographic Setting

A strong relationship does not appear to exist between the relative performance of IMERG and gauge-interpolated products as a function of geographical variables including elevation (Figure 5 and Figure 6), distance to coast, and annual precipitation (results not all shown), or at least not a relationship that can be captured using the Monte Carlo sampling and regression fitting schemes detailed in Section 3.3 and Section 3.5. On the other hand, the tendency of interpolated estimates based on low gauge densities to overestimate POFA does appear to increase with annual precipitation (Figure 7); otherwise, the ability of low density interpolated estimates to evaluate IMERG does not have a clear dependence on climate or geographic setting. One physiographic factor that was not explored in this work, but which may influence the accuracy of interpolated estimates, is seasonality. Especially in the CONUS study area, higher gauge density (or lower distance to nearest gauge) may be required to accurately estimate summer (i.e., highly convective) precipitation than winter precipitation fields.

6. Conclusions

Satellite multisensor precipitation products and rain gauge data interpolated to gridded datasets can both exhibit substantial errors when estimating precipitation; while satellite precipitation products experience uncertainty due to indirect measurement of precipitation and retrieval conditions, rain gauges only provide point measurements of precipitation, and any estimate of precipitation between gauges is subject to error and dependent on surrounding gauge density and topography. This work compares the daily performance of satellite precipitation products, IMERG-Early and IMERG-Late, with that of gauge-interpolated estimates as a function of the gauge density and distance to the nearest available gauge used during interpolation. A robust Monte Carlo sampling scheme is used to simulate interpolation under a range of gauge network densities and configurations in the continental US and Brazil. Unlike previous work, this analysis evaluates gauge-interpolated estimates as a function of gauge densities lower than 10 gauges/10,000 km² and as a function of distance to the nearest available gauge.

Results show that the performance of interpolated gauge data decreases with decreasing gauge density and increasing distance to nearest gauge. IMERG often demonstrates better performance in detecting precipitation when the gauge density used during interpolation is less than 5 gauges/10,000 km², which includes the gauge density values that are present in most parts of the world. The ability of interpolated gauge estimates to accurately characterize the probability of detection rapidly decreases at low gauge densities, making satellite products an attractive alternative source of precipitation data for applications which prioritize precipitation detection, such as landslide hazard monitoring systems. However, even at low gauge densities, interpolated gauge estimates provide a relatively robust estimate of IMERG RMSE.

The performance of interpolated gauge estimates is strongly mediated by the distance to the nearest gauge used during interpolation. IMERG Early and Late often demonstrate better probability of detection than gauge-interpolated estimates when the nearest gauge used during interpolation is more than 50 km away. These results affirm that distance to the nearest gauge used during interpolation is a useful predictor for the performance of interpolated gauge estimates that should be included in future studies on this topic in addition to the typical predictor, gauge density.

The ability of interpolated gauge estimates to accurately evaluate IMERG is also shown to decrease with decreasing gauge density, with interpolated estimates frequently overestimating IMERG error and probability of false alarm at low gauge densities (e.g., less than 5 gauges/10,000 km²). In line with previous, smaller-scale studies, this work demonstrates that it is critical that users of interpolated gauge data consider the gauge density, as well as distance to nearest gauge, used during interpolation before assuming that these estimates are more accurate than (or suitable for validating) satellite precipitation estimates.