Applying Deep Learning in the Prediction of Chlorophyll-a in the East China Sea
Abstract
1. Introduction
2. Materials and Methods
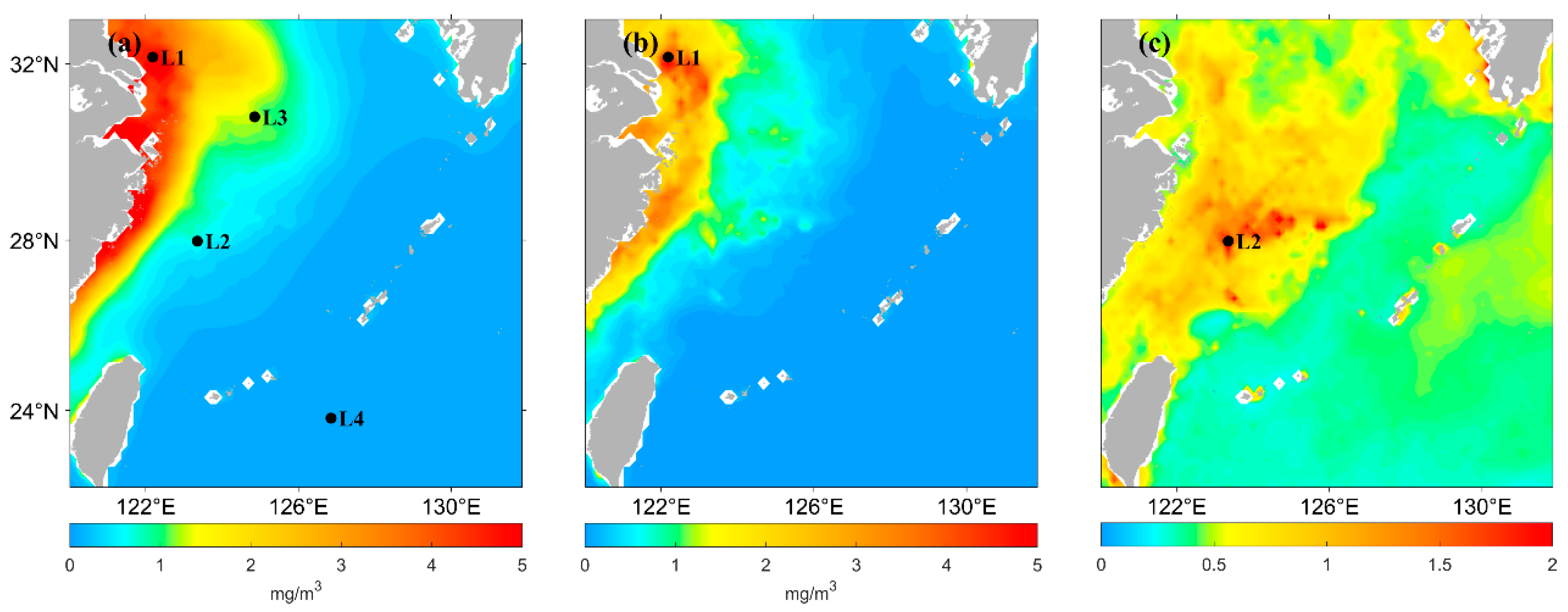
2.1. Materials
2.2. Methods
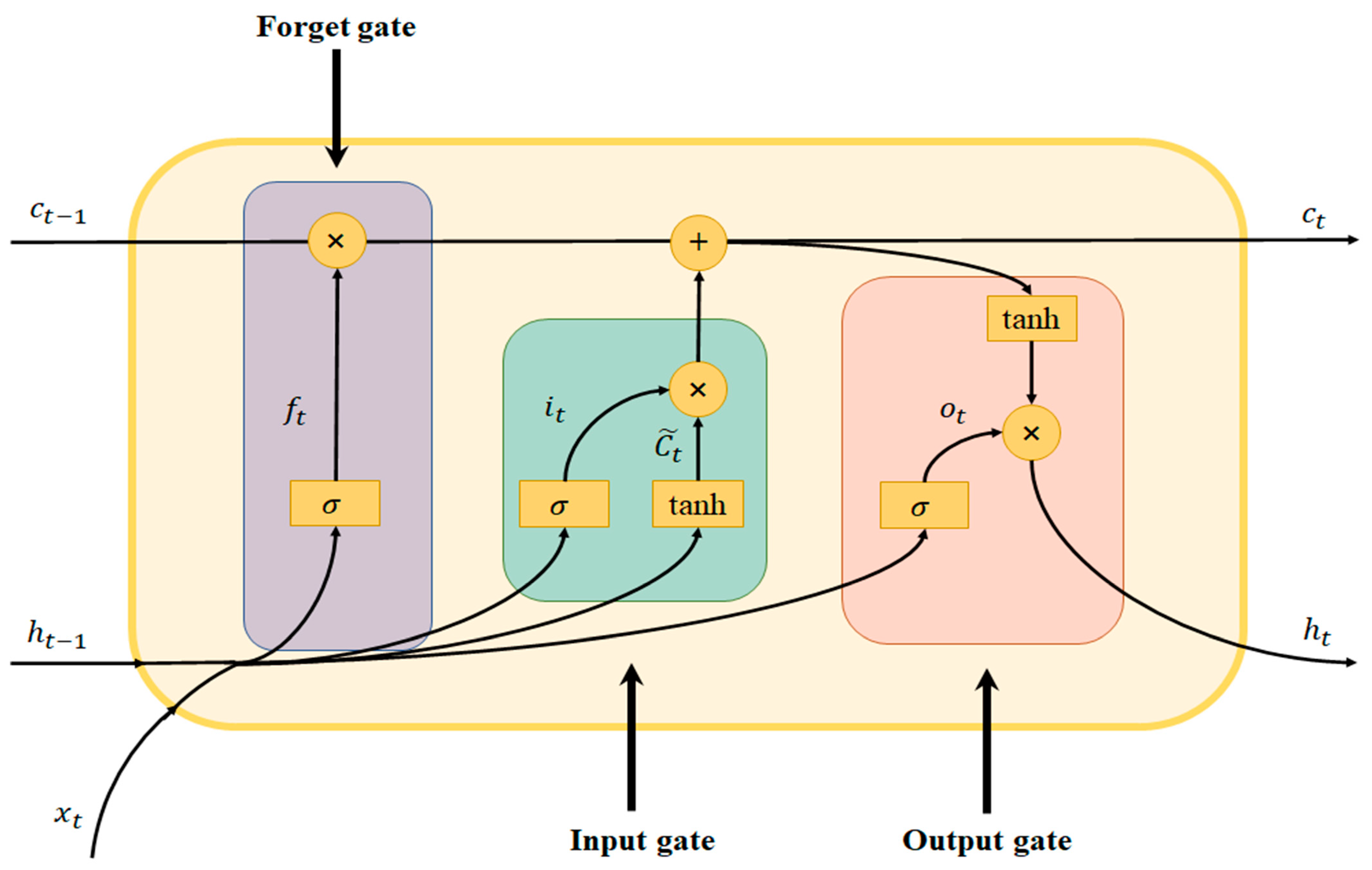
2.2.1. LSTM Neural Network
2.2.2. Architecture of the LSTM Model for Chl-a Forecasts
2.2.3. Data Pre-Processing
2.2.4. Evaluation Functions
3. Results
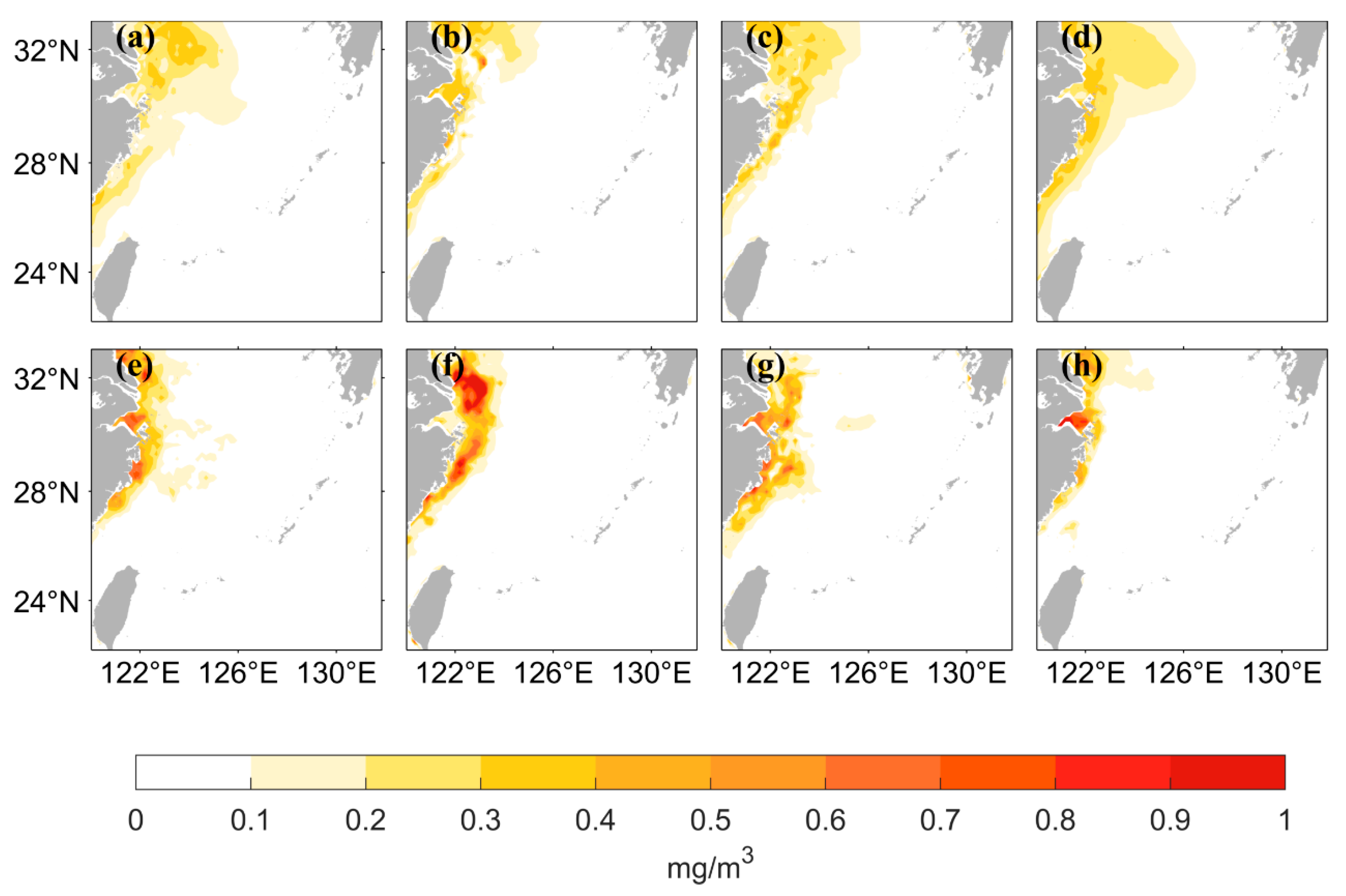
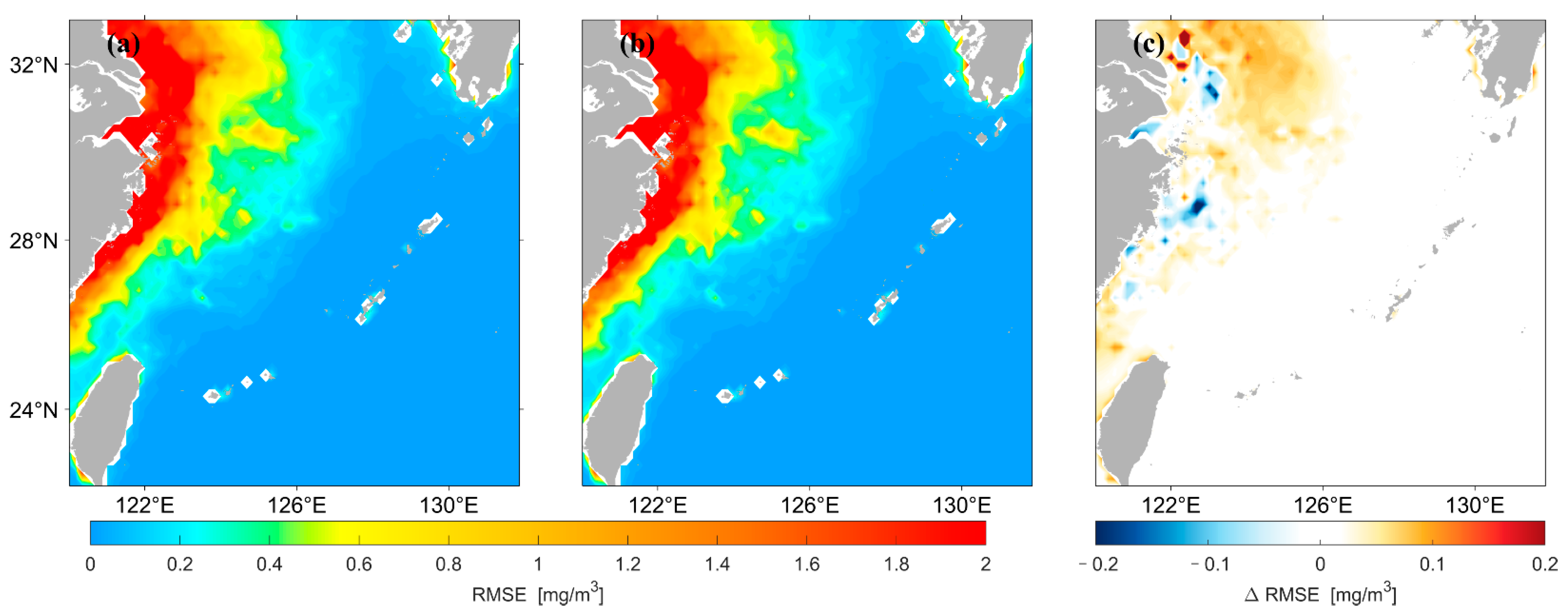
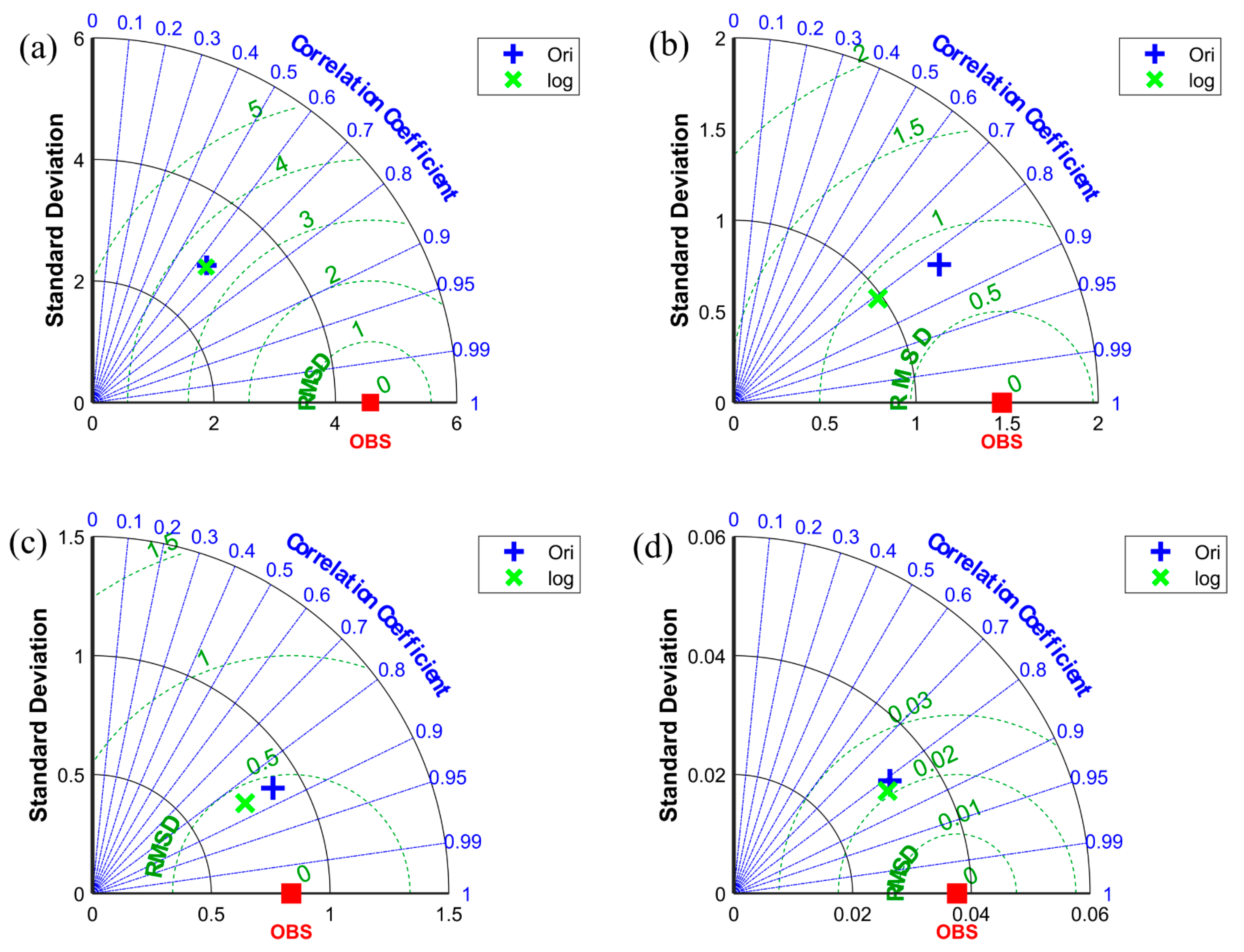
3.1. LSTM Prediction Results under Different Data Pre-Processing Methods
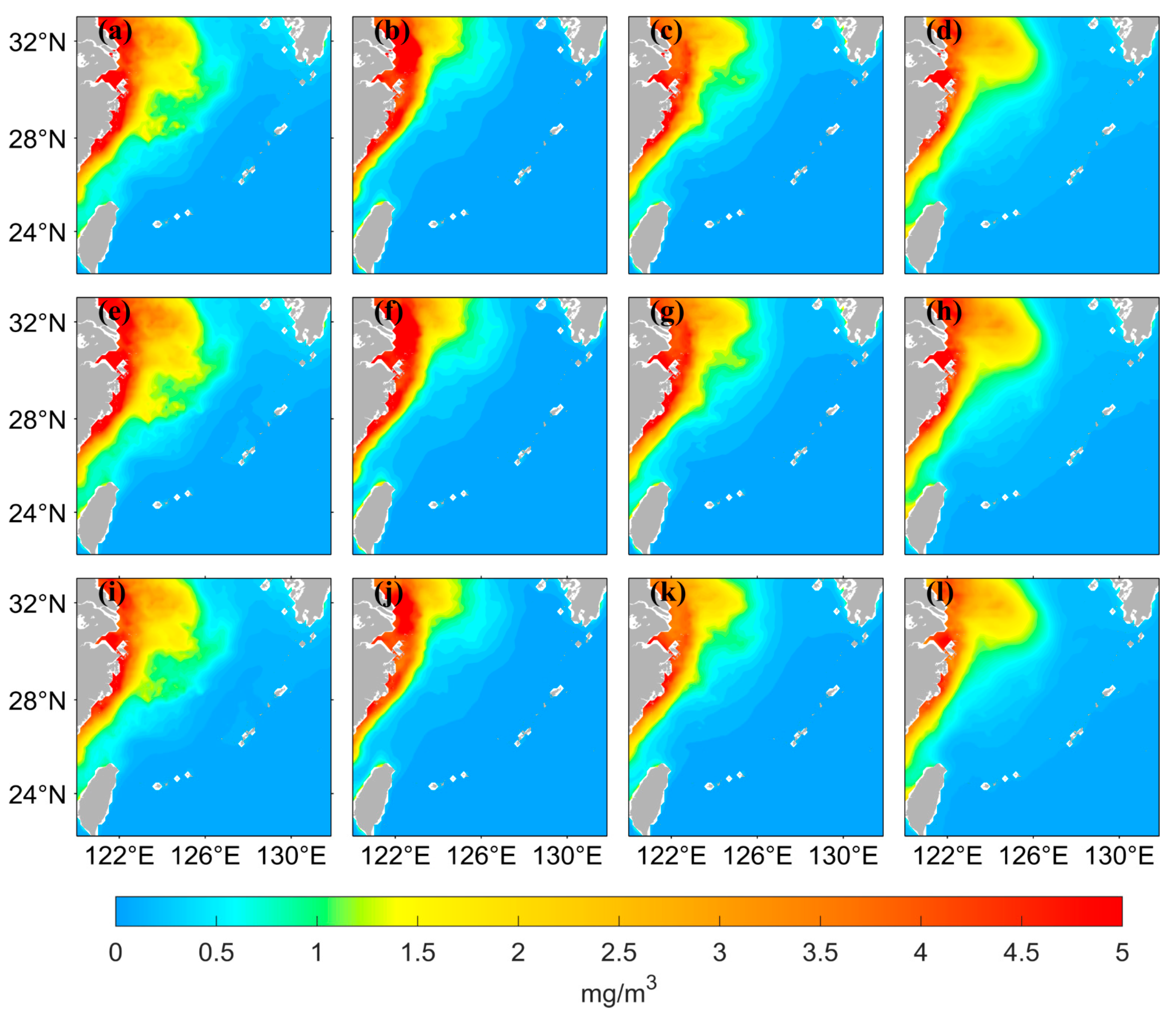
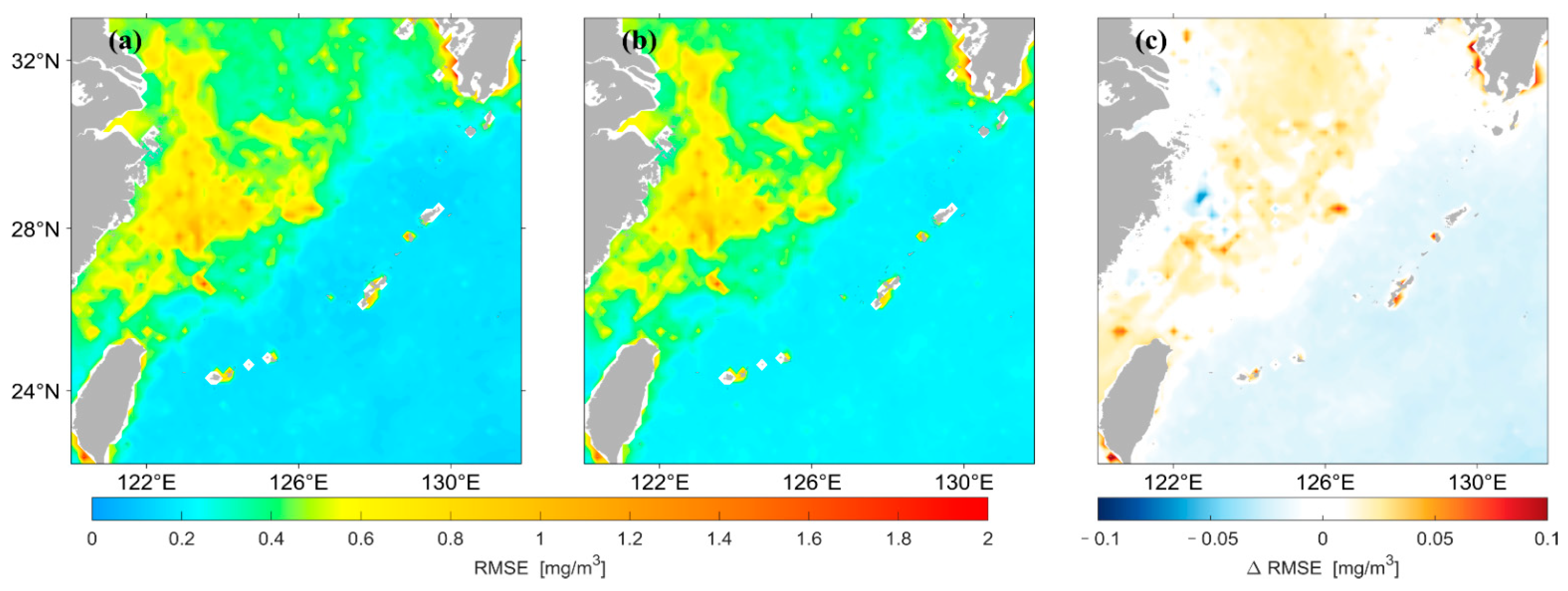
3.2. LSTM Prediction Results with Different Input and Output Lengths
4. Conclusions
5. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Iriarte, J.; González, H.; Liu, K.; Rivas, C.; Valenzuela, C. Spatial and Temporal Variability of Chlorophyll and Primary Productivity in Surface Waters of Southern Chile (41.5–43 S). Estuar. Coast. Shelf Sci. 2007, 74, 471–480. [Google Scholar] [CrossRef]
- Lee, Y.J.; Matrai, P.A.; Friedrichs, M.A.; Saba, V.S.; Antoine, D.; Ardyna, M.; Asanuma, I.; Babin, M.; Bélanger, S.; Benoît-Gagné, M.; et al. An Assessment of Phytoplankton Primary Productivity in the Arctic Ocean from Satellite Ocean Color/in Situ Chlorophyll-a Based Models. J. Geophys. Res. Ocean. 2015, 120, 6508–6541. [Google Scholar] [CrossRef] [PubMed]
- Arrigo, K.R.; Matrai, P.A.; Van Dijken, G.L. Primary Productivity in the Arctic Ocean: Impacts of Complex Optical Properties and Subsurface Chlorophyll Maxima on Large-Scale Estimates. J. Geophys. Res. Ocean. 2011, 116, C11022. [Google Scholar] [CrossRef]
- Ardyna, M.; Gosselin, M.; Michel, C.; Poulin, M.; Tremblay, J.-É. Environmental Forcing of Phytoplankton Community Structure and Function in the Canadian High Arctic: Contrasting Oligotrophic and Eutrophic Regions. Mar. Ecol. Prog. Ser. 2011, 442, 37–57. [Google Scholar] [CrossRef]
- Ardyna, M.; Babin, M.; Gosselin, M.; Devred, E.; Bélanger, S.; Matsuoka, A.; Tremblay, J.-É. Parameterization of Vertical Chlorophyll a in the Arctic Ocean: Impact of the Subsurface Chlorophyll Maximum on Regional, Seasonal, and Annual Primary Production Estimates. Biogeosciences 2013, 10, 4383–4404. [Google Scholar] [CrossRef]
- Sharada, M.; Yajnik, K. Seasonal Variation of Chlorophyll and Primary Productivity in Central Arabian Sea: A Macrocalibrated Upper Ocean Ecosystem Model. Proc. Indian Acad. Sci.-Earth Planet. Sci. 1997, 106, 33–42. [Google Scholar] [CrossRef]
- Thomalla, S.; Fauchereau, N.; Swart, S.; Monteiro, P. Regional Scale Characteristics of the Seasonal Cycle of Chlorophyll in the Southern Ocean. Biogeosciences 2011, 8, 2849–2866. [Google Scholar] [CrossRef]
- Hao, Y.; Tang, D.; Yu, L.; Xing, Q. Nutrient and Chlorophyll a Anomaly in Red-Tide Periods of 2003–2008 in Sishili Bay, China. Chin. J. Oceanol. Limnol. 2011, 29, 664–673. [Google Scholar] [CrossRef]
- Ishizaka, J.; Kitaura, Y.; Touke, Y.; Sasaki, H.; Tanaka, A.; Murakami, H.; Suzuki, T.; Matsuoka, K.; Nakata, H. Satellite Detection of Red Tide in Ariake Sound, 1998–2001. J. Oceanogr. 2006, 62, 37–45. [Google Scholar] [CrossRef]
- Zhang, C.; Zeng, Y.; Zhang, X.; Pan, W.; Lin, J. Ocean Chlorophyll a Derived from Satellite Data with Its Application to Red Tide Monitoring. J. Appl. Meteorol. Sci. 2007, 18, 821–831. [Google Scholar]
- Papenfus, M.; Schaeffer, B.; Pollard, A.I.; Loftin, K. Exploring the Potential Value of Satellite Remote Sensing to Monitor Chlorophyll-a for US Lakes and Reservoirs. Environ. Monit. Assess. 2020, 192, 1–22. [Google Scholar] [CrossRef] [PubMed]
- D’Croz, L.; O’Dea, A. Variability in Upwelling along the Pacific Shelf of Panama and Implications for the Distribution of Nutrients and Chlorophyll. Estuar. Coast. Shelf Sci. 2007, 73, 325–340. [Google Scholar] [CrossRef]
- Grodsky, S.A.; Carton, J.A.; McClain, C.R. Variability of Upwelling and Chlorophyll in the Equatorial Atlantic. Geophys. Res. Lett. 2008, 35, L03610. [Google Scholar] [CrossRef]
- Zhao, D.; Zhao, L.; Zhang, F.; Zhang, X. Temporal Occurrence and Spatial Distribution of Red Tide Events in China’s Coastal Waters. Hum. Ecol. Risk Assess. 2004, 10, 945–957. [Google Scholar] [CrossRef]
- Chen, M.; Li, J.; Dai, X.; Sun, Y.; Chen, F. Effect of Phosphorus and Temperature on Chlorophyll a Contents and Cell Sizes of Scenedesmus Obliquus and Microcystis Aeruginosa. Limnology 2011, 12, 187–192. [Google Scholar] [CrossRef]
- Wu, Q.; Xia, X.; Li, X.; Mou, X. Impacts of Meteorological Variations on Urban Lake Water Quality: A Sensitivity Analysis for 12 Urban Lakes with Different Trophic States. Aquat. Sci. 2014, 76, 339–351. [Google Scholar] [CrossRef]
- Carneiro, F.M.; Nabout, J.C.; Vieira, L.C.; Roland, F.; Bini, L.M. Determinants of Chlorophyll-a Concentration in Tropical Reservoirs. Hydrobiologia 2014, 740, 89–99. [Google Scholar] [CrossRef]
- de Oliveira Marcionilio, S.M.L.; Machado, K.B.; Carneiro, F.M.; Ferreira, M.E.; Carvalho, P.; Vieira, L.C.G.; de Moraes Huszar, V.L.; Nabout, J.C. Environmental Factors Affecting Chlorophyll-a Concentration in Tropical Floodplain Lakes, Central Brazil. Environ. Monit. Assess. 2016, 188, 1–9. [Google Scholar] [CrossRef]
- Vollenweider, R.A. Input-Output Models. Schweiz. Z. Hydrol. 1975, 37, 53–84. [Google Scholar] [CrossRef]
- Kiyofuji, H.; Hokimoto, T.; Saitoh, S.-I. Predicting the Spatiotemporal Chlorophyll-a Distribution in the Sea of Japan Based on SeaWiFS Ocean Color Satellite Data. IEEE Geosci. Remote Sens. Lett. 2006, 3, 212–216. [Google Scholar] [CrossRef]
- Jørgensen, S.E.; Mejer, H.; Friis, M. Examination of a Lake Model. Ecol. Model. 1978, 4, 253–278. [Google Scholar] [CrossRef]
- Wu, Z.; Wang, X.; Chen, Y.; Cai, Y.; Deng, J. Assessing River Water Quality Using Water Quality Index in Lake Taihu Basin, China. Sci. Total Environ. 2018, 612, 914–922. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Wu, Y.; Xu, J.; Zhang, H.; Wang, X.; Yu, J.; Sun, Q.; Zhao, Z. Nonlinear Dynamic Numerical Analysis and Prediction of Complex System Based on Bivariate Cycling Time Stochastic Differential Equation. Alex. Eng. J. 2020, 59, 2065–2082. [Google Scholar] [CrossRef]
- Liu, Y.; Guo, H.; Yang, P. Exploring the Influence of Lake Water Chemistry on Chlorophyll a: A Multivariate Statistical Model Analysis. Ecol. Model. 2010, 221, 681–688. [Google Scholar] [CrossRef]
- Kim, M.E.; Shon, T.S.; Shin, H.S. Forecasting Algal Bloom (Chl-a) on the Basis of Coupled Wavelet Transform and Artificial Neural Networks at a Large Lake. Desalination Water Treat. 2013, 51, 4118–4128. [Google Scholar] [CrossRef]
- Wang, H.; Yan, X.; Chen, H.; Chen, C.; Guo, M. Chlorophyll-a Predicting Model Based on Dynamic Neural Network. Appl. Artif. Intell. 2015, 29, 962–978. [Google Scholar] [CrossRef]
- Wei, B.; Sugiura, N.; Maekawa, T. Use of Artificial Neural Network in the Prediction of Algal Blooms. Water Res. 2001, 35, 2022–2028. [Google Scholar] [CrossRef]
- Lee, J.H.; Huang, Y.; Dickman, M.; Jayawardena, A.W. Neural Network Modelling of Coastal Algal Blooms. Ecol. Model. 2003, 159, 179–201. [Google Scholar] [CrossRef]
- Tian, W.; Liao, Z.; Zhang, J. An Optimization of Artificial Neural Network Model for Predicting Chlorophyll Dynamics. Ecol. Model. 2017, 364, 42–52. [Google Scholar] [CrossRef]
- Jimeno-Sáez, P.; Senent-Aparicio, J.; Cecilia, J.M.; Pérez-Sánchez, J. Using Machine-Learning Algorithms for Eutrophication Modeling: Case Study of Mar Menor Lagoon (Spain). Int. J. Environ. Res. Public Health 2020, 17, 1189. [Google Scholar] [CrossRef]
- Liao, Z.; Zang, N.; Wang, X.; Li, C.; Liu, Q. Machine Learning-Based Prediction of Chlorophyll-a Variations in Receiving Reservoir of World’s Largest Water Transfer Project—A Case Study in the Miyun Reservoir, North China. Water 2021, 13, 2406. [Google Scholar] [CrossRef]
- Li, X.; Sha, J.; Wang, Z.-L. Application of Feature Selection and Regression Models for Chlorophyll-a Prediction in a Shallow Lake. Environ. Sci. Pollut. Res. 2018, 25, 19488–19498. [Google Scholar] [CrossRef] [PubMed]
- Jia, W.; Cheng, J.; Hu, H. A Cluster-Stacking-Based Approach to Forecasting Seasonal Chlorophyll-a Concentration in Coastal Waters. IEEE Access 2020, 8, 99934–99947. [Google Scholar] [CrossRef]
- Kim, K.-M.; Ahn, J.-H. Machine Learning Predictions of Chlorophyll-a in the Han River Basin, Korea. J. Environ. Manag. 2022, 318, 115636. [Google Scholar] [CrossRef] [PubMed]
- Yajima, H.; Derot, J. Application of the Random Forest Model for Chlorophyll-a Forecasts in Fresh and Brackish Water Bodies in Japan, Using Multivariate Long-Term Databases. J. Hydroinformatics 2018, 20, 206–220. [Google Scholar] [CrossRef]
- Guo, Q.; Jin, S.; Li, M.; Yang, Q.; Xu, K.; Ju, Y.; Zhang, J.; Xuan, J.; Liu, J.; Su, Y.; et al. Application of Deep Learning in Ecological Resource Research: Theories, Methods, and Challenges. Sci. China Earth Sci. 2020, 63, 1457–1474. [Google Scholar] [CrossRef]
- Zhang, F.; Wang, Y.; Cao, M.; Sun, X.; Du, Z.; Liu, R.; Ye, X. Deep-Learning-Based Approach for Prediction of Algal Blooms. Sustainability 2016, 8, 1060. [Google Scholar] [CrossRef]
- Rostam, N.A.P.; Malim, N.H.A.H.; Abdullah, R.; Ahmad, A.L.; Ooi, B.S.; Chan, D.J.C. A Complete Proposed Framework for Coastal Water Quality Monitoring System With Algae Predictive Model. IEEE Access 2021, 9, 108249–108265. [Google Scholar] [CrossRef]
- Cho, H.; Park, H. Merged-LSTM and Multistep Prediction of Daily Chlorophyll-a Concentration for Algal Bloom Forecast. In Proceedings of the IOP Conference Series: Earth and Environmental Science, Kaohsiung, Taiwan, 1–4 July 2019; Volume 351, p. 012020. Available online: https://iopscience.iop.org/article/10.1088/1755-1315/351/1/012020/meta (accessed on 14 September 2022).
- Zheng, L.; Wang, H.; Liu, C.; Zhang, S.; Ding, A.; Xie, E.; Li, J.; Wang, S. Prediction of Harmful Algal Blooms in Large Water Bodies Using the Combined EFDC and LSTM Models. J. Environ. Manag. 2021, 295, 113060. [Google Scholar] [CrossRef]
- Yussof, F.N.; Maan, N.; Md Reba, M.N. LSTM Networks to Improve the Prediction of Harmful Algal Blooms in the West Coast of Sabah. Int. J. Environ. Res. Public Health 2021, 18, 7650. [Google Scholar] [CrossRef]
- Barzegar, R.; Aalami, M.T.; Adamowski, J. Short-Term Water Quality Variable Prediction Using a Hybrid CNN–LSTM Deep Learning Model. Stoch. Environ. Res. Risk Assess. 2020, 34, 415–433. [Google Scholar] [CrossRef]
- Gong, G.-C.; Wen, Y.-H.; Wang, B.-W.; Liu, G.-J. Seasonal Variation of Chlorophyll a Concentration, Primary Production and Environmental Conditions in the Subtropical East China Sea. Deep. Sea Res. Part II Top. Stud. Oceanogr. 2003, 50, 1219–1236. [Google Scholar] [CrossRef]
- Ji, C.; Zhang, Y.; Cheng, Q.; Tsou, J.; Jiang, T.; San Liang, X. Evaluating the Impact of Sea Surface Temperature (SST) on Spatial Distribution of Chlorophyll-a Concentration in the East China Sea. Int. J. Appl. Earth Obs. Geoinf. 2018, 68, 252–261. [Google Scholar] [CrossRef]
- Chen, C.-C.; Shiah, F.-K.; Chiang, K.-P.; Gong, G.-C.; Kemp, W.M. Effects of the Changjiang (Yangtze) River Discharge on Planktonic Community Respiration in the East China Sea. J. Geophys. Res. Ocean. 2009, 114, C03005. [Google Scholar] [CrossRef]
- Hsueh, Y. The Kuroshio in the East China Sea. J. Mar. Syst. 2000, 24, 131–139. [Google Scholar] [CrossRef]
- Guo, X.; Zhu, X.-H.; Wu, Q.-S.; Huang, D. The Kuroshio Nutrient Stream and Its Temporal Variation in the East China Sea. J. Geophys. Res. Ocean. 2012, 117, C01026. [Google Scholar] [CrossRef]
- Lou, X.; Shi, A.; Xiao, Q.; Zhang, H. Satellite Observation of the Zhejiang Coastal Upwelling in the East China Sea during 2007–2009. In Proceedings of the Remote Sensing of the Ocean, Sea Ice, Coastal Waters, and Large Water Regions 2011; Volume 8175, pp. 454–460. Available online: https://www.spiedigitallibrary.org/conference-proceedings-of-spie/8175/81751M/Satellite-observation-of-the-Zhejiang-Coastal-upwelling-in-the-East/10.1117/12.898140.short (accessed on 28 October 2022).
- Lou, X.; Hu, C. Diurnal Changes of a Harmful Algal Bloom in the East China Sea: Observations from GOCI. Remote Sens. Environ. 2014, 140, 562–572. [Google Scholar] [CrossRef]
- Peng, D.; Yang, Q.; Yang, H.-J.; Liu, H.; Zhu, Y.; Mu, Y. Analysis on the Relationship between Fisheries Economic Growth and Marine Environmental Pollution in China’s Coastal Regions. Sci. Total Environ. 2020, 713, 136641. [Google Scholar] [CrossRef]
- Chen, K.; Kuang, C.; Wang, L.; Chen, K.; Han, X.; Fan, J. Storm Surge Prediction Based on Long Short-Term Memory Neural Network in the East China Sea. Appl. Sci. 2021, 12, 181. [Google Scholar] [CrossRef]
- Xu, Y.; Cheng, C.; Zhang, Y.; Zhang, D. Identification of Algal Blooms Based on Support Vector Machine Classification in Haizhou Bay, East China Sea. Environ. Earth Sci. 2014, 71, 475–482. [Google Scholar] [CrossRef]
- Xiao, C.; Chen, N.; Hu, C.; Wang, K.; Xu, Z.; Cai, Y.; Xu, L.; Chen, Z.; Gong, J. A Spatiotemporal Deep Learning Model for Sea Surface Temperature Field Prediction Using Time-Series Satellite Data. Environ. Model. Softw. 2019, 120, 104502. [Google Scholar] [CrossRef]
- Xiao, C.; Chen, N.; Hu, C.; Wang, K.; Gong, J.; Chen, Z. Short and Mid-Term Sea Surface Temperature Prediction Using Time-Series Satellite Data and LSTM-AdaBoost Combination Approach. Remote Sens. Environ. 2019, 233, 111358. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep Learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]

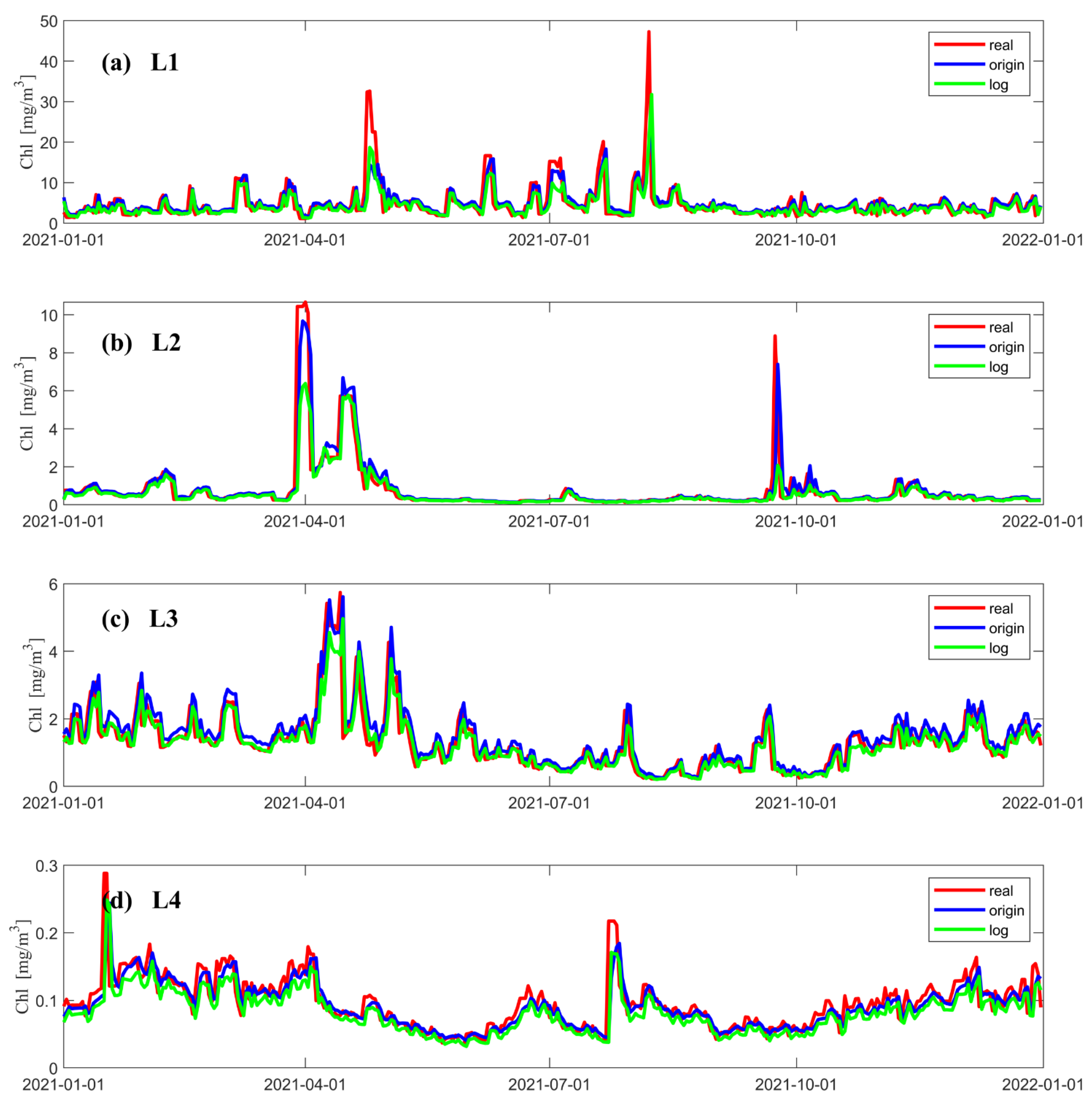

| L1 | L2 | L3 | L4 | |
|---|---|---|---|---|
| ori: 0.4133 | ori: 0.6806 | ori: 0.6732 | ori: 0.6482 | |
| log: 0.3936 | log: 0.66273 | log: 0.7337 | log: 0.5681 |
| L1 | L2 | L3 | L4 | |
|---|---|---|---|---|
| RMSE | 1d: 3.5012 | 1d: 0.8304 | 1d: 0.4779 | 1d: 0.0223 |
| 3d: 4.6445 | 3d: 1.2453 | 3d: 0.6867 | 3d: 0.0303 | |
| 5d: 4.6475 | 5d: 1.4237 | 5d: 0.7653 | 5d: 0.0320 | |
| STD | 1d: 2.9369 | 1d: 1.3581 | 1d: 0.8796 | 1d: 0.0324 |
| 3d: 1.6825 | 3d: 1.0272 | 3d: 0.7922 | 3d: 0.0312 | |
| 5d: 1.2218 | 5d: 0.8789 | 5d: 0.7349 | 5d: 0.0300 | |
| COR | 1d: 0.6431 | 1d: 0.8306 | 1d: 0.8368 | 1d: 0.8116 |
| 3d: 0.1495 | 3d: 0.5510 | 3d: 0.6755 | 3d: 0.6366 | |
| 5d: 0.1051 | 5d: 0.3504 | 5d: 0.5661 | 5d: 0.5841 | |
| 1d: 0.4133 | 1d: 0.6806 | 1d: 0.6732 | 1d: 0.6482 | |
| 3d: −0.0330 | 3d: 0.2820 | 3d: 0.3252 | 3d: 0.3553 | |
| 5d: −0.0356 | 5d: 0.0619 | 5d: 0.1599 | 5d: 0.2802 |
| L1 | L2 | L3 | L4 | |
|---|---|---|---|---|
| RMSE | 15d: 3.5012 | 15d: 0.8304 | 15d: 0.4799 | 15d: 0.0223 |
| 10d: 3.5972 | 10d: 0.8702 | 10d: 0.4845 | 10d: 0.0292 | |
| 7d: 3.5265 | 7d: 0.8530 | 7d: 0.4796 | 7d: 0.0217 | |
| STD | 15d: 2.9369 | 15d: 1.3581 | 15d: 0.8796 | 15d: 0.0324 |
| 10d: 3.2444 | 10d: 1.3997 | 10d: 0.9039 | 10d: 0.0263 | |
| 7d: 3.0379 | 7d: 1.3791 | 7d: 0.8783 | 7d: 0.0369 | |
| COR | 15d: 0.6431 | 15d: 0.8306 | 15d: 0.8368 | 15d: 0.8116 |
| 10d: 0.6235 | 10d: 0.8169 | 10d: 0.8591 | 10d: 0.8313 | |
| 7d: 0.6372 | 7d: 0.8228 | 7d: 0.8613 | 7d: 0.8316 | |
| 15d: 0.4133 | 15d: 0.6806 | 15d: 0.6732 | 15d: 0.6482 | |
| 10d: 0.3807 | 10d: 0.6492 | 10d: 0.6640 | 10d: 0.3955 | |
| 7d: 0.4048 | 7d: 0.6629 | 7d: 0.6708 | 7d: 0.6663 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cen, H.; Jiang, J.; Han, G.; Lin, X.; Liu, Y.; Jia, X.; Ji, Q.; Li, B. Applying Deep Learning in the Prediction of Chlorophyll-a in the East China Sea. Remote Sens. 2022, 14, 5461. https://doi.org/10.3390/rs14215461
Cen H, Jiang J, Han G, Lin X, Liu Y, Jia X, Ji Q, Li B. Applying Deep Learning in the Prediction of Chlorophyll-a in the East China Sea. Remote Sensing. 2022; 14(21):5461. https://doi.org/10.3390/rs14215461
Chicago/Turabian StyleCen, Haobin, Jiahan Jiang, Guoqing Han, Xiayan Lin, Yu Liu, Xiaoyan Jia, Qiyan Ji, and Bo Li. 2022. "Applying Deep Learning in the Prediction of Chlorophyll-a in the East China Sea" Remote Sensing 14, no. 21: 5461. https://doi.org/10.3390/rs14215461
APA StyleCen, H., Jiang, J., Han, G., Lin, X., Liu, Y., Jia, X., Ji, Q., & Li, B. (2022). Applying Deep Learning in the Prediction of Chlorophyll-a in the East China Sea. Remote Sensing, 14(21), 5461. https://doi.org/10.3390/rs14215461






