VirtuaLot—A Case Study on Combining UAS Imagery and Terrestrial Video with Photogrammetry and Deep Learning to Track Vehicle Movement in Parking Lots
Abstract
1. Introduction
- A computer vision pipeline which can detect and track vehicles that enter and exit a parking lot, using an available deep learning object detection network and traditional image processing techniques to improve the pipeline efficiency by reducing and constraining inputs and outputs to both deep learning object detection and more traditional tracking algorithms.
- Using monoplotting as a mechanism to automate the definition of tall, vertically occluding objects in a perspective camera image.
- An investigation into the effects of using a camera with unpredictably changing internal geometry as input for the monoplotting process, to evaluate its suitability as a mechanism for registering perspective video and uncrewed aircraft system (UAS) aerial imagery. Attention is also paid to challenges encountered while attempting to automate the monoplotting process using various keypoint descriptors.
2. Study Area and Datasets
3. Methods
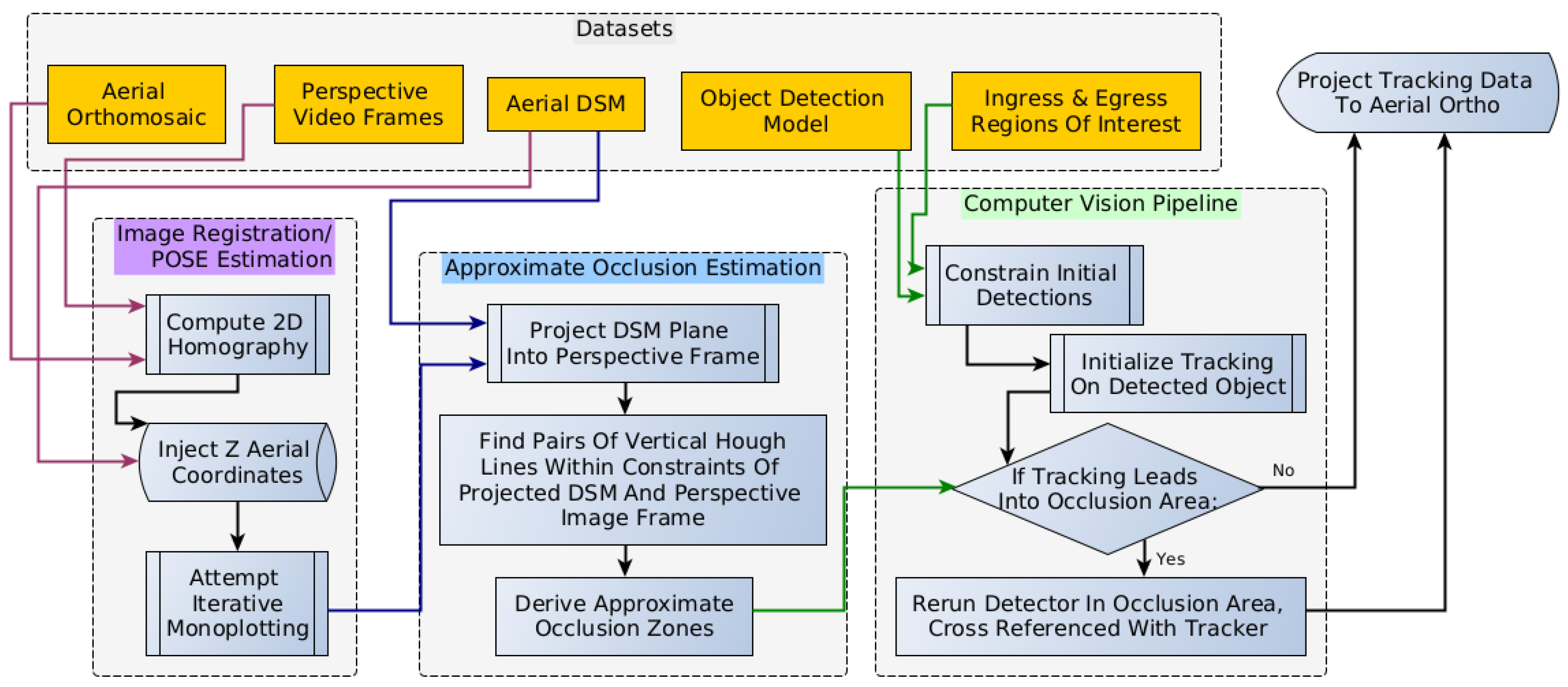
3.1. Computer Vision Pipeline
3.2. Single Frame Registration with Monoplotting
3.3. Automated Occlusion Detection

3.4. Automated Monoplotting
4. Results
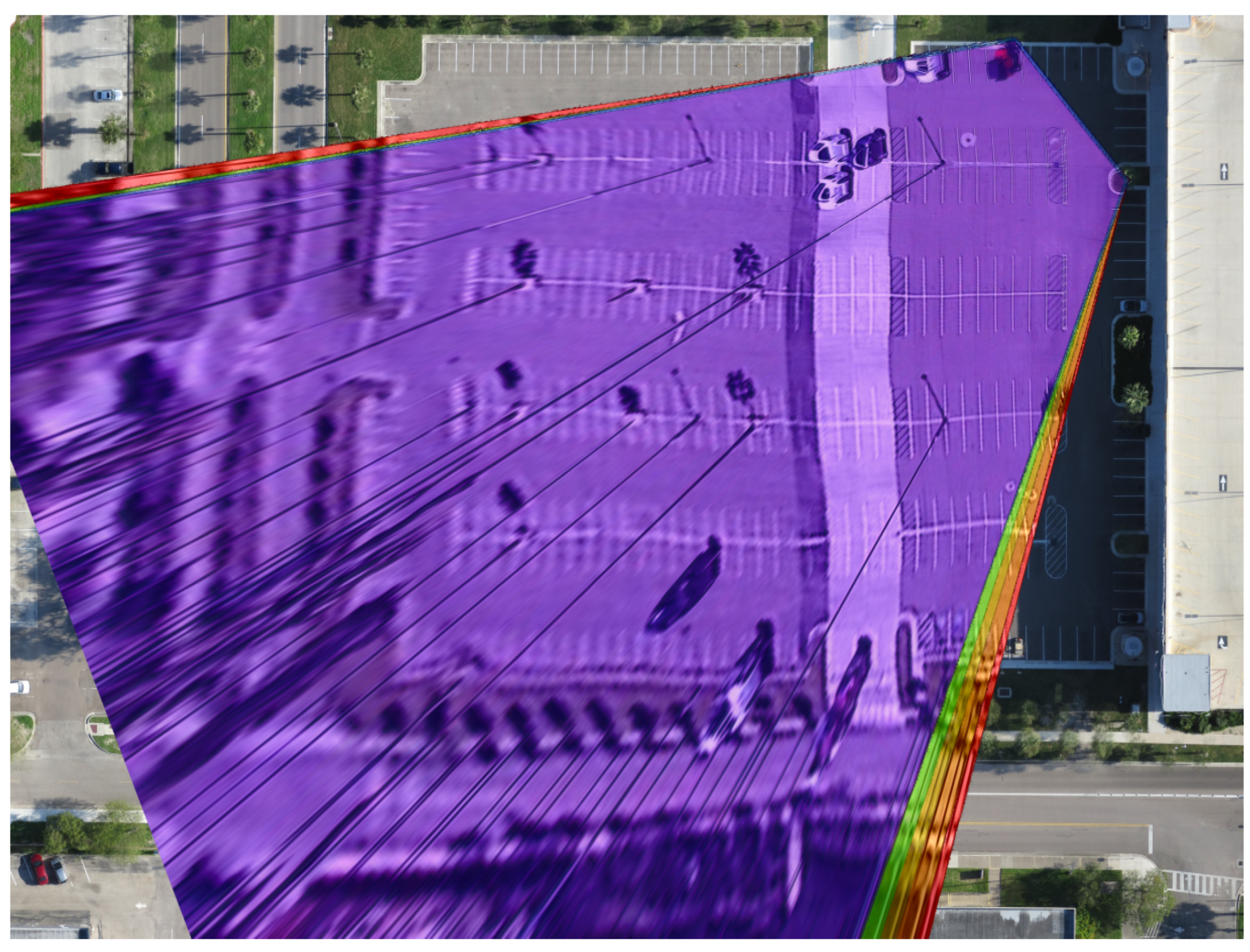
4.1. Single Frame Registration via Monoplotting Results
4.2. Object Detection and Tracking Results
4.3. Automated Occlusion Handling
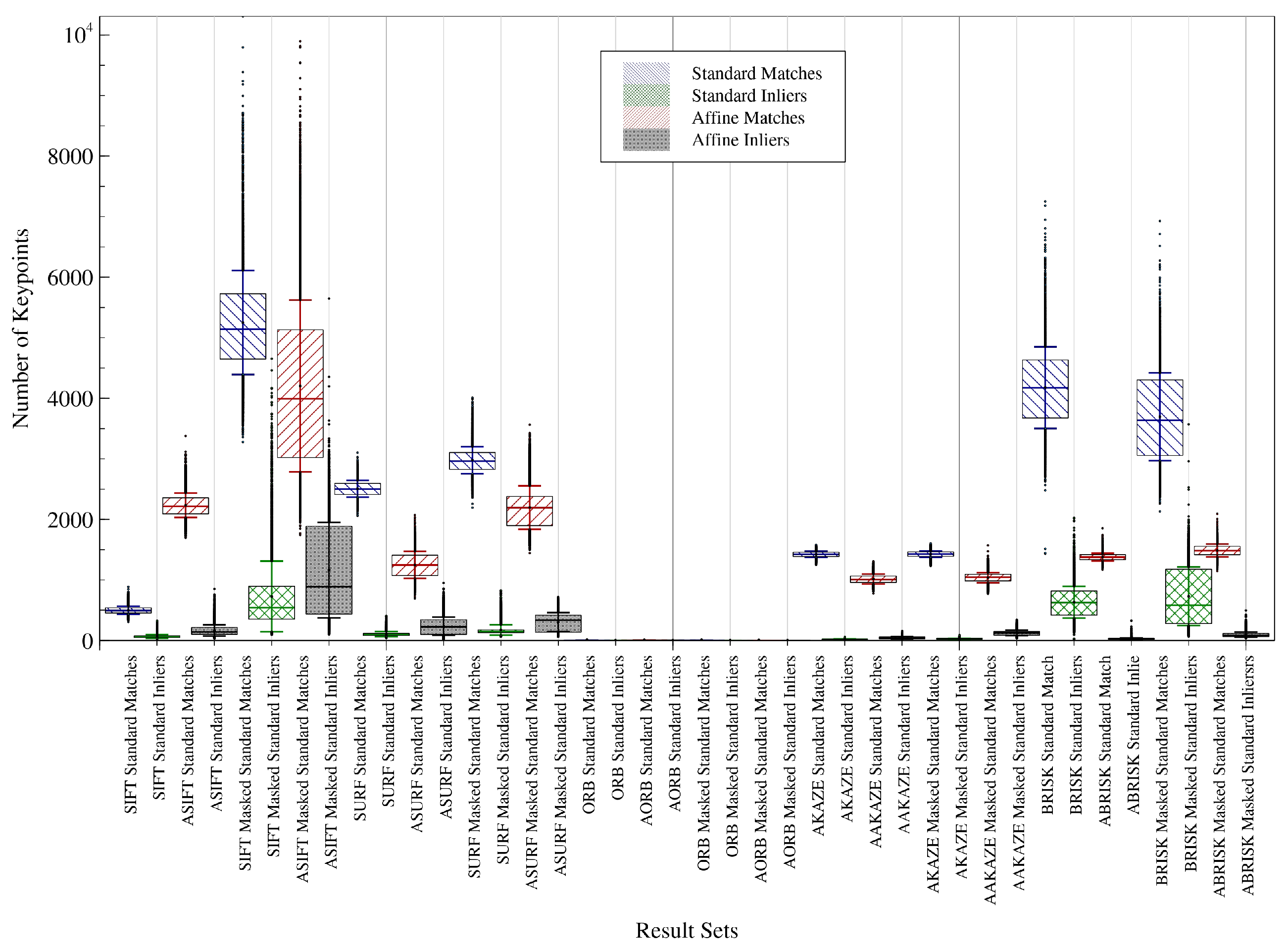
4.4. Automated Registration Results via Monoplotting
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chu, T.; Guo, N.; Backén, S.; Akos, D. Monocular Camera/IMU/GNSS Integration for Ground Vehicle Navigation in Challenging GNSS Environments. Sensors 2012, 12, 3162–3185. [Google Scholar] [CrossRef] [PubMed]
- Gupton, N. The Science of Self-Driving Cars; Technical Report; The Franklin Institute: Philadelphia, PA, USA, 2019. [Google Scholar]
- Behzadan, A.H.; Kamat, V.R. Georeferenced Registration of Construction Graphics in Mobile Outdoor Augmented Reality. J. Comput. Civ. Eng. 2007, 21, 247–258. [Google Scholar] [CrossRef]
- Boerner, R.; Kröhnert, M. Brute Force Matching Between Camera Shots and Synthetic Images From Point Clouds. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, XLI-B5, 771–777. [Google Scholar] [CrossRef]
- Oh, T.; Lee, D.; Kim, H.; Myung, H. Graph Structure-Based Simultaneous Localization and Mapping Using a Hybrid Method of 2D Laser Scan and Monocular Camera Image in Environments with Laser Scan Ambiguity. Sensors 2015, 15, 15830–15852. [Google Scholar] [CrossRef]
- Mair, E.; Strobl, K.H.; Suppa, M.; Burschka, D. Efficient camera-based pose estimation for real-time applications. In Proceedings of the 2009 IEEE/RSJ International Conference on Intelligent Robots and Systems, St. Louis, MO, USA, 10–15 October 2009. [Google Scholar] [CrossRef]
- Szelag, K.; Kurowski, P.; Bolewicki, P.; Sitnik, R. Real-time camera pose estimation based on volleyball court view. Opto-Electron. Rev. 2019, 27, 202–212. [Google Scholar] [CrossRef]
- Mur-Artal, R.; Montiel, J.M.M.; Tardos, J.D. ORB–SLAM: A Versatile and Accurate Monocular SLAM System. IEEE Trans. Robot. 2015, 31, 1147–1163. [Google Scholar] [CrossRef]
- Cavallari, T.; Golodetz, S.; Lord, N.; Valentin, J.; Prisacariu, V.; Stefano, L.D.; Torr, P.H. Real-Time RGB-D Camera Pose Estimation in Novel Scenes using a Relocalisation Cascade. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 42, 2465–2477. [Google Scholar] [CrossRef]
- Mishkin, D.; Matas, J.; Perdoch, M. MODS: Fast and Robust Method for Two-View Matching. Comput. Vis. Image Underst. 2016, 141, 81–93. [Google Scholar] [CrossRef]
- Bartol, K.; Bojanić, D.; Pribanić, T.; Petković, T.; Donoso, Y.D.; Mas, J.S. On the Comparison of Classic and Deep Keypoint Detector and Descriptor Methods. In Proceedings of the 2019 11th International Symposium on Image and Signal Processing and Analysis (ISPA), Dubrovnik, Croatia, 23–25 September 2020; pp. 64–69. [Google Scholar] [CrossRef]
- Wu, C. Towards Linear-Time Incremental Structure from Motion. In Proceedings of the 2013 International Conference on 3D Vision, Seattle, WA, USA, 29 June–1 July 2013. [Google Scholar] [CrossRef]
- Slocum, R.K.; Parrish, C.E. Simulated Imagery Rendering Workflow for UAS-Based Photogrammetric 3D Reconstruction Accuracy Assessments. Remote Sens. 2017, 9, 396. [Google Scholar] [CrossRef]
- Mouragnon, E.; Lhuillier, M.; Dhome, M.; Dekeyser, F.; Sayd, P. Generic and real-time structure from motion using local bundle adjustment. Image Vis. Comput. 2009, 27, 1178–1193. [Google Scholar] [CrossRef]
- Strasdat, H.; Montiel, J.M.M.; Davison, A.J. Real-time monocular SLAM: Why filter? In Proceedings of the 2010 IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–7 May 2010. [Google Scholar] [CrossRef]
- Lee, A.H.; Lee, S.H.; Lee, J.Y.; Choi, J.S. Real-time camera pose estimation based on planar object tracking for augmented reality environment. In Proceedings of the 2012 IEEE International Conference on Consumer Electronics (ICCE), Las Vegas, NV, USA, 13–16 January 2012. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, X.; Gu, T.; Zhang, Y.; Xing, G. Real-time camera pose estimation via line tracking. Vis. Comput. 2018, 34, 899–909. [Google Scholar] [CrossRef]
- Chakravarty, P.; Narayanan, P.; Roussel, T. GEN-SLAM: Generative Modeling for Monocular Simultaneous Localization and Mapping. arXiv 2019, arXiv:1902.02086v1. [Google Scholar]
- Schmuck, P.; Chli, M. CCM-SLAM: Robust and efficient centralized collaborative monocular simultaneous localization and mapping for robotic teams. J. Field Robot. 2018, 36, 763–781. [Google Scholar] [CrossRef]
- Wu, J.; Cui, Z.; Sheng, V.S.; Zhao, P.; Su, D.; Gong, S. A Comparative Study of SIFT and its Variants. Meas. Sci. Rev. 2013, 13, 122–131. [Google Scholar] [CrossRef]
- Rublee, E.; Rabaud, V.; Konolige, K.; Bradski, G. ORB: An efficient alternative to SIFT or SURF. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011. [Google Scholar] [CrossRef]
- Tola, E.; Lepetit, V.; Fua, P. DAISY: An Efficient Dense Descriptor Applied to Wide-Baseline Stereo. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 815–830. [Google Scholar] [CrossRef]
- Tola, E.; Lepetit, V.; Fua, P. A fast local descriptor for dense matching. In Proceedings of the 2008 IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, AK, USA, 23–28 June 2008. [Google Scholar] [CrossRef]
- Aanæs, H.; Dahl, A.L.; Pedersen, K.S. Interesting Interest Points. Int. J. Comput. Vis. 2011, 97, 18–35. [Google Scholar] [CrossRef]
- Bay, H.; Tuytelaars, T.; Van Gool, L. SURF: Speeded Up Robust Features. In Proceedings of the Computer Vision—ECCV 2006, Graz, Austria, 7–13 May 2006; Leonardis, A., Bischof, H., Pinz, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 404–417. [Google Scholar]
- Lowe, D.G. Distinctive Image Features from Scale-Invariant Keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Shi, J.; Tomasi, C. Good Features To Track. Comput. Vis. Pattern Recognit. 1994, 593–600. [Google Scholar] [CrossRef]
- Guo, Y.; Bennamoun, M.; Sohel, F.; Lu, M.; Wan, J.; Kwok, N.M. A Comprehensive Performance Evaluation of 3D Local Feature Descriptors. Int. J. Comput. Vis. 2015, 116, 66–89. [Google Scholar] [CrossRef]
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision, 2nd ed.; Cambridge University Press: Cambridge, MA, USA, 2003. [Google Scholar]
- Moulon, P.; Monasse, P.; Marlet, R. Adaptive Structure from Motion with a Contrario Model Estimation. In Proceedings of the Computer Vision—ACCV 2012, Daejeon, Korea, 5–9 November 2012; Lee, K.M., Matsushita, Y., Rehg, J.M., Hu, Z., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 257–270. [Google Scholar]
- Kendall, A.; Grimes, M.; Cipolla, R. PoseNet: A Convolutional Network for Real-Time 6-DOF Camera Relocalization. arXiv 2015, arXiv:1505.07427. [Google Scholar]
- Bae, H.; Golparvar-Fard, M.; White, J. High-precision vision-based mobile augmented reality system for context-aware architectural, engineering, construction and facility management (AEC/FM) applications. Vis. Eng. 2013, 1. [Google Scholar] [CrossRef]
- Cai, G.R.; Jodoin, P.M.; Li, S.Z.; Wu, Y.D.; Su, S.Z.; Huang, Z.K. Perspective-SIFT: An efficient tool for low-altitude remote sensing image registration. Signal Process. 2013, 93, 3088–3110. [Google Scholar] [CrossRef]
- Wilson, K.; Snavely, N. Robust Global Translations with 1DSfM. In Proceedings of the European Conference on Computer Vision (ECCV), Zurich, Switzerland, 6–12 September 2014. [Google Scholar]
- Morel, J.M.; Yu, G. ASIFT: A New Framework for Fully Affine Invariant Image Comparison. SIAM J. Imaging Sci. 2009, 2, 438–469. [Google Scholar] [CrossRef]
- Yu, G.; Morel, J.M. ASIFT: An Algorithm for Fully Affine Invariant Comparison. Image Process. Line 2011, 1, 11–38. [Google Scholar] [CrossRef]
- Maier, R.; Schaller, R.; Cremers, D. Efficient Online Surface Correction for Real-time Large-Scale 3D Reconstruction. arXiv 2017, arXiv:1709.03763v1. [Google Scholar]
- Yi, K.M.; Trulls, E.; Lepetit, V.; Fua, P. LIFT: Learned Invariant Feature Transform. In Proceedings of the European Conference On Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016. [Google Scholar]
- Strausz, D.A., Jr. An Application of Photogrammetric Techniques to the Measurement of Historic Photographs; Oregon State University: Corvallis, OR, USA, 2001. [Google Scholar]
- Bozzini, C.; Conedera, M.; Krebs, P. A New Monoplotting Tool to Extract Georeferenced Vector Data and Orthorectified Raster Data from Oblique Non-Metric Photographs by C. Bozzini, M. Conedera, P. Krebs. Int. J. Herit. Digit. Era 2012, 1, 499–518. [Google Scholar] [CrossRef]
- Produit, T.; Tuia, D. An open tool to register landscape oblique images and and generate their synthetic model. In Proceedings of the Open Source Geospatial Research and Education Symposium (OGRS), Yverdon les Bains, Switzerland, 24–26 October 2012; pp. 170–176. [Google Scholar]
- Petrasova, A.; Hipp, J.A.; Mitasova, H. Visualization of Pedestrian Density Dynamics Using Data Extracted from Public Webcams. ISPRS Int. J. Geo-Inf. 2019, 8, 559. [Google Scholar] [CrossRef]
- Chen, X.; Wang, Z.; Hua, Q.; Shang, W.L.; Luo, Q.; Yu, K. AI-Empowered Speed Extraction via Port-Like Videos for Vehicular Trajectory Analysis. IEEE Trans. Intell. Transp. Syst. 2022, 1–12. [Google Scholar] [CrossRef]
- Koskowich, B.J.; Rahnemoonfai, M.; Starek, M. Virtualot—A Framework Enabling Real-Time Coordinate Transformation & Occlusion Sensitive Tracking Using UAS Products, Deep Learning Object Detection & Traditional Object Tracking Techniques. In Proceedings of the IGARSS—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018. [Google Scholar] [CrossRef]
- Jiang, Q.; Liu, Y.; Yan, Y.; Xu, P.; Pei, L.; Jiang, X. Active Pose Relocalization for Intelligent Substation Inspection Robot. IEEE Trans. Ind. Electron. 2022, 99, 1–10. [Google Scholar] [CrossRef]
- Zhang, X.; Shi, X.; Luo, X.; Sun, Y.; Zhou, Y. Real-Time Web Map Construction Based on Multiple Cameras and GIS. ISPRS Int. J. Geo-Inf. 2021, 10, 803. [Google Scholar] [CrossRef]
- Han, S.; Dong, X.; Hao, X.; Miao, S. Extracting Objects’ Spatial–Temporal Information Based on Surveillance Videos and the Digital Surface Model. ISPRS Int. J. Geo-Inf. 2022, 11, 103. [Google Scholar] [CrossRef]
- Luo, X.; Wang, Y.; Cai, B.; Li, Z. Moving Object Detection in Traffic Surveillance Video: New MOD-AT Method Based on Adaptive Threshold. ISPRS Int. J. Geo-Inf. 2021, 10, 742. [Google Scholar] [CrossRef]
- Cao, X.; Wu, C.; Yan, P.; Li, X. Linear SVM classification using boosting HOG features for vehicle detection in low-altitude airborne videos. In Proceedings of the 2011 18th IEEE International Conference on Image Processing, Brussels, Belgium, 11–14 September 2011. [Google Scholar] [CrossRef]
- Choi, J.; Chang, H.J.; Yoo, Y.J.; Choi, J.Y. Robust moving object detection against fast illumination change. Comput. Vis. Image Underst. 2012, 116, 179–193. [Google Scholar] [CrossRef]
- Dollar, P.; Wojek, C.; Schiele, B.; Perona, P. Pedestrian Detection: An Evaluation of the State of the Art. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 743–761. [Google Scholar] [CrossRef]
- Redmon, J.; Farhadi, A. YOLOv3: An Incremental Improvement. arXiv 2018, arXiv:1804.02767v1. [Google Scholar]
- Simon, M.; Milz, S.; Amende, K.; Gross, H.M. Complex-YOLO: Real-time 3D Object Detection on Point Clouds. arXiv 2018, arXiv:1803.06199v2. [Google Scholar]
- Zhao, Z.Q.; Zheng, P.; Xu, S.T.; Wu, X. Object Detection with Deep Learning: A Review. arXiv 2018, arXiv:cs.CV/1807.05511. [Google Scholar] [CrossRef] [PubMed]
- Kalal, Z.; Mikolajczyk, K.; Matas, J. Tracking-Learning-Detection. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 34, 1409–1422. [Google Scholar] [CrossRef]
- Kalal, Z.; Mikolajczyk, K.; Matas, J. Forward-backward error: Automatic detection of tracking failures. In Proceedings of the 2010 20th International Conference on Pattern Recognition, Istanbul, Turkey, 23–26 August 2010; pp. 2756–2759. [Google Scholar]
- Babenko, B.; Yang, M.H.; Belongie, S. Visual Tracking with Online Multiple Instance Learning. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009. [Google Scholar] [CrossRef]
- Tao, M.; Bai, J.; Kohli, P.; Paris, S. SimpleFlow: A Non-iterative, Sublinear Optical Flow Algorithm. Comput. Graph. Forum 2012, 31, 345–353. [Google Scholar] [CrossRef]
- Henriques, J.F.; Caseiro, R.; Martins, P.; Batista, J. High-Speed Tracking with Kernelized Correlation Filters. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 583–596. [Google Scholar] [CrossRef] [PubMed]
- Xiang, Y.; Alahi, A.; Savarese, S. Learning to Track: Online Multi-object Tracking by Decision Making. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015. [Google Scholar] [CrossRef]
- Kristan, M.; Matas, J.; Leonardis, A.; Vojir, T.; Pflugfelder, R.; Fernandez, G.; Nebehay, G.; Porikli, F.; Čehovin, L. A Novel Performance Evaluation Methodology for Single-Target Trackers. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 2137–2155. [Google Scholar] [CrossRef] [PubMed]
- Bertinetto, L.; Valmadre, J.; Henriques, J.F.; Vedaldi, A.; Torr, P.H.S. Fully-Convolutional Siamese Networks for Object Tracking. In Computer Vision—ECCV 2016 Workshops. ECCV 2016; Hua, G., Jégou, H., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2016; Volume 9914, pp. 850–865. [Google Scholar] [CrossRef]
- Valmadre, J.; Bertinetto, L.; Henriques, J.; Vedaldi, A.; Torr, P.H.S. End-To-End Representation Learning for Correlation Filter Based Tracking. In Proceedings of the The IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Ondatec. Polycarbonate Systems. Available online: https://www.stabiliteuropa.com/sites/default/files/ondatec_english.pdf (accessed on 2 August 2022).
- Amerilux. Glossary. Available online: https://ameriluxinternational.com/wp-content/uploads/2021/pdf-downloads/general-resources/amerilux-glossary.pdf (accessed on 2 August 2022).
- Redmon, J.; Farhadi, A. YOLO9000: Better, Faster, Stronger. In Proceedings of the The IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; University of Washington, Allen Institute for AI: Washington, DC, USA, 2016. [Google Scholar]
- Grabner, H.; Grabner, M.; Bischof, H. Real-Time Tracking via On-line Boosting. In Proceedings of the British Machine Vision Conference 2006, Edinburgh, UK, 4–7 September 2006; 2006. [Google Scholar] [CrossRef]
- Everingham, M.; Van Gool, L.; Williams, C.K.I.; Winn, J.; Zisserman, A. The PASCAL Visual Object Classes Challenge 2012 (VOC2012) Results. 2012. Available online: http://www.pascal-network.org/challenges/VOC/voc2012/workshop/index.html (accessed on 2 August 2022).
- Duda, R.O.; Hart, P.E. Use of the Hough transformation to detect lines and curves in pictures. Commun. ACM 1972, 15, 11–15. [Google Scholar] [CrossRef]
- Alcantarilla, P.F.; Bartoli, A.; Davison, A.J. KAZE Features. In Proceedings of the Computer Vision—ECCV 2012, Florence, Italy, 7–13 October 2012; Springer: Berlin/Heidelberg, Germany, 2012; pp. 214–227. [Google Scholar] [CrossRef]
- Leutenegger, S.; Chli, M.; Siegwart, R.Y. BRISK: Binary Robust invariant scalable keypoints. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; Volume 22, pp. 2548–2555. [Google Scholar] [CrossRef]
- Texas Department of Licensing and Regulation. Texas Accessibility Standards, Chapter 5. In Texas Government Code Chapter 469; Texas Department of Licensing and Regulation: Austin, TX, USA, 2012; p. 110. [Google Scholar]
- Grand Prairie, Texas Planning Department. Appendix D: Parking Layout and Design standards. In Unified Development Code; Grand Prairie, Texas Planning Department: Grand Prairie, TX, USA, 2003; pp. 4–16. [Google Scholar]
- Zhao, X.; He, Z.; Zhang, S. Improved keypoint descriptors based on Delaunay triangulation for image matching. Opt. Int. J. Light Electron Opt. 2014, 125. [Google Scholar] [CrossRef]
- Liu, X.; Qu, X.; Ma, X. Improving flex-route transit services with modular autonomous vehicles. Transp. Res. Part Logist. Transp. Rev. 2021, 149, 102331. [Google Scholar] [CrossRef]





| Source | Data Set | Capture Metadata | Positioning Information | Recording Date |
|---|---|---|---|---|
| Perspective Footage: AXIS Q6044-E PTZ, Weatherproof housing; 1280 × 720 p @ 30 fps | Sample 1 Video: Low Traffic; (Reduced From 432 K Frames) | 6646 Frames ≈3 m 30 s ≈1 vehicle/5 s Sporadic | 15 m above ground plane, ≈20° below horizon observing south west | December 2016 |
| Sample 2 Video: High Traffic | 4616 Frames ≈2 m 30 s ≈1.5 vehicles/s Constant Motion | |||
| Aerial Imagery: SODA SenseFly Camera on eBee | UAS Flight | Sensor Resolution: 20 MP 1565 Images; Avg. GSD: 2.78 cm Image Resolution: 5472 × 3648 px; nadir observing; 80% sidelap/70% endlap | Flying a back and forth grid pattern ≈91 m altitude, covering 1.32 km2 | September 2017 |
| Digital Surface Model Derived from Aerial Imagery Point Cloud | Post Processed Data | Resolution: 12,042 × 8684 px @ 2.79 cm/px | 91.44 m altitude above ground, observing nadir, covering 0.029 km2 | |
| Georeferenced Orthomosaic: Region Of Interest |
| Sample 1 | Ground Truth | Object Tracking Methods | ||||
| Boosting | Centroid | KCF | MedianFlow | TLD | ||
| Detection Count | 46.1 +/− 12.94 | 38.45 +/− 8.57 | 49.67 +/− 8.64 | 46.74 +/− 12.1 | 51.5 +/− 7.39 | 38 +/− 7.07 |
| Tracking Stability | 0.86 +/− 2.13 | 0.16 +/− 0.37 | 3.21 +/− 7.97 | 0.22 +/− 0.66 | 0.18 +/− 0.4 | 0.1 +/− 0.23 |
| FPS | 18.63 +/− 9.50 | 15.53 +/− 10.43 | 29.06 +/− 16.07 | 31.06 +/− 16.7 | 17.97 +/− 14.58 | 25.28 +/− 15.79 |
| Sample 1 Min-Max | Ground Truth | Boosting | Centroid | KCF | MedianFlow | TLD |
| Detection Rate (%) | 21.74–100 | 26.09–54.35 | 45.65–100 | 21.74–67.39 | 39.13–67.39 | 23.91–50 |
| Tracking Stability | 0.05–3.46 | 0.03–0.34 | 0.86–3.46 | 0.09–0.69 | 0.1–0.31 | 0.05–0.17 |
| FPS | 3–44.5 | 5.8–48.4 | 16.7–123 | 4–63.5 | 3–61.9 | 4.1–63.3 |
| Sample 2 | Ground Truth | Boosting | Centroid | KCF | MedianFlow | TLD |
| Detection Count | 4.15 +/− 4.08 | 6.84 +/− 6.29 | 7.67 +/− 15.14 | 3.56 +/− 1.12 | 3.62 +/− 0.75 | 2.86 +/− 0.79 |
| Tracking Stability | 0.04 +/− 0.30 | 0.06 +/− 0.31 | 0.12 +/− 0.62 | 0.02 +/− 0.13 | 0.03 +/− 0.21 | 0.01 +/− 0.09 |
| FPS | 23.3 +/− 10.23 | 20.65 +/− 8.66 | 25.63 +/− 15.64 | 22.24 +/− 6.51 | 22.33 +/− 6.81 | 20.97 +/− 6.96 |
| Sample 2 Min-Max | Ground Truth | Boosting | Centroid | KCF | MedianFlow | TLD |
| Detection Rate (%) | 0–100 | 1.5–7 | 0–100 | 2–6 | 2–5 | 2–5 |
| Tracking Stability | 0–1 | 0.01–0.09 | 0–1 | 0–0.03 | 0.01–0.1 | 0–0.05 |
| FPS | 4–42.5 | 4–27.9 | 4.6–104.4 | 4–30.1 | 4.1–29.7 | 4–29.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koskowich, B.; Starek, M.; King, S.A. VirtuaLot—A Case Study on Combining UAS Imagery and Terrestrial Video with Photogrammetry and Deep Learning to Track Vehicle Movement in Parking Lots. Remote Sens. 2022, 14, 5451. https://doi.org/10.3390/rs14215451
Koskowich B, Starek M, King SA. VirtuaLot—A Case Study on Combining UAS Imagery and Terrestrial Video with Photogrammetry and Deep Learning to Track Vehicle Movement in Parking Lots. Remote Sensing. 2022; 14(21):5451. https://doi.org/10.3390/rs14215451
Chicago/Turabian StyleKoskowich, Bradley, Michael Starek, and Scott A. King. 2022. "VirtuaLot—A Case Study on Combining UAS Imagery and Terrestrial Video with Photogrammetry and Deep Learning to Track Vehicle Movement in Parking Lots" Remote Sensing 14, no. 21: 5451. https://doi.org/10.3390/rs14215451
APA StyleKoskowich, B., Starek, M., & King, S. A. (2022). VirtuaLot—A Case Study on Combining UAS Imagery and Terrestrial Video with Photogrammetry and Deep Learning to Track Vehicle Movement in Parking Lots. Remote Sensing, 14(21), 5451. https://doi.org/10.3390/rs14215451










