Abstract
On 22 July 2020, an Mw 6.3 earthquake occurred in Nima County, central Qinghai-Tibet Plateau, China. We used the synthetic aperture radar interferometry (InSAR) technique with Sentinel-1 images to retrieve the line of sight (LOS) coseismic deformation fields which indicate that the maximum surface displacement reached ~30 cm. We then processed a series of interferograms spanning one year after the Nima earthquake with the Small Baseline Subset Interferometric SAR (SBAS-InSAR) technique. The maximum cumulative postseismic LOS surface displacement reached ~8 cm and approximately followed a logarithmic function over time. The inversion of the fault geometry and co- and afterslip distribution shows that the epicenter location was (33.18°N, 86.88°E) at a depth of 7.4 km, and the causative fault had an N29.1°E strike and 50.2° dip. The most coseismic slip was concentrated at depths between 3 to 12 km with a peak value of 2.0 m at 7.4 km, whilst most afterslips were concentrated at depths between 0 to 12 km with a peak value of 0.2 m at 5 km. The postseismic moment energy was about 5.04 × 1017 N∙m 308 days after the event, which was approximately 13.8% of the coseismic moment energy. By analyzing the contribution of afterslip and poroelastic rebound to postseismic deformation, it was concluded that afterslip was the main early postseismic deformation mechanism. Future attention should be paid to the northern segment of the West Yibug Caka fault and East Yibug Caka fault.
1. Introduction
At 22:07 UTC on 22 July 2020, an Mw 6.3 earthquake occurred in Nima County, central Qinghai-Tibet Plateau. The epicenter was located at (33.14°N, 86.86°E), and the focal depth was 10 km (https://earthquake.usgs.gov/earthquakes, accessed on 1 March 2021). The focal mechanism solutions (Table 1) released by the China Earthquake Networks Center (CENC), United States Geological Survey (USGS) and Global Centroid Moment Tensor (GCMT) are all in agreement that this event was a normal fault earthquake, however, there are differences in their source parameters including the epicenter locations. Given the fact that normal faults play an important role in the east-west extension and north-south compression of the Qinghai-Tibet Plateau [], it is of great significance to investigate in detail the Nima earthquake, particularly its precise source parameters.

Table 1.
Fault plane parameters for the 2020 Mw 6.3 Nima earthquake.
The Qinghai-Tibet Plateau is the most intensely tectonically active region in China in modern times, with frequent earthquakes primarily due to the extrusion and collision of the Indian and Eurasian plates. The earthquake on 22 July 2020 occurred in the Qiangtang block, south of the Jinsha suture and north of the Bangong-Nujiang suture (Figure 1a). The eastern part of the block is primarily characterized by an E-SE trending motion, with deformation mainly distributed on both sides of the strike-slip boundaries; the central and western parts of the block are characterized by the diffuse deformation of a series of SN-trending normal faults and NE/NW-trending conjugate strike-slip faults []. Whilst in the western part, normal faults, and conjugate strike-slip faults play an important role in regulating SN-trending compression and EW-trending extension (Figure 1b) [,]. The NE-trending Riganpei Co–Yibug Caka–Jiangai Zangbo (RYJ) left-lateral strike-slip fault and the NW-trending right-slip Gyaring Co fault form a V-shaped conjugate strike-slip fault system with a deformation rate of 2 ± 0.6 mm/yr [,]. The total length of the RYJ fault zone is about 340 km, which is S-shaped on the map and is divided into three main segments, with the northern and southern segments dominated by left-lateral strike-slip faults striking ~N70°E and the central segment by normal faults striking N30°–40°E (Figure 1b,c) [,]. The central part is the most complex of the RYJ fault zone and is characterized by several fault-bounded titled blocks and interlaying NNE trending basins in between []. The epicenter was located near the West Yibug Caka fault (WYCF) and East Yibug Caka fault (EYCF) in the Yibug Caka Basin. The Yibug Caka Basin is a half-graben basin and is bounded by the West and East Yibug Caka faults. There has not been an Mw ≥ 6 earthquake in the Yibug Caka Basin since 1973 according to the USGS earthquake catalog (Figure 1c). Therefore, the study of the Nima earthquake is of great significance to the tectonic characteristics of the Yibug Caka Basin and the risk assessment of future earthquakes.
InSAR has been proven to be a powerful tool to monitor precise surface displacements with high spatial resolution and wide coverages, and it has been widely used to map coseismic and postseismic deformation [,,,,,,,,]. Several scholars have used InSAR to investigate the coseismic deformation of the 2020 Nima earthquake and then determine its source parameters, but obvious differences can be observed in the source parameters [,,,]. On the other hand, postseismic motion following large earthquakes represents the response of host rocks to the redistribution of coseismic stress changes, and its corresponding surface displacement time series is useful in identifying the potential physical mechanisms at depth, which might provide insight into future seismic hazards [,]. To our best knowledge, Yang et al. [] has been the only published work reporting the postseismic deformation following the Nima earthquake. Note that they acquired the postseismic deformation only for six months after the event using InSAR observations, but it is likely that the postseismic deformation would last for a longer period for earthquakes with similar magnitudes [,,]. The mechanisms of the postseismic deformation of the 2020 Nima earthquake remain unclear.
In this paper, we used InSAR to obtain the coseismic deformation, and SBAS-InSAR with the Generic Atmospheric Correction Online Service for InSAR (GACOS) correction to obtain the high-precision deformation time series one year after the Nima earthquake. The source parameters and slip distribution of this earthquake were inverted based on the Okada dislocation model in an elastic half-space. Then, the contributions of afterslip and poroelastic rebound to postseismic deformation were analyzed. Finally, the regional future seismic hazards were assessed based on Coulomb failure stress (CFS) changes.
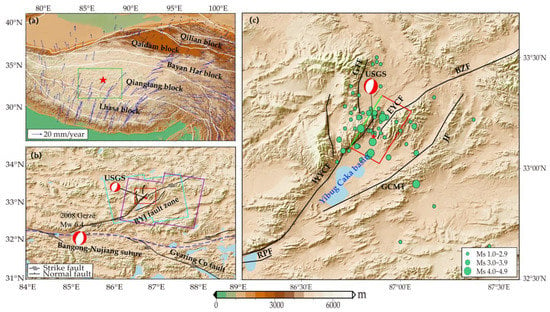
Figure 1.
Tectonic settings of the 2020 Mw 6.3 Nima earthquake. (a) Tectonic settings of the Qinghai-Tibet Plateau. The green rectangle represents the coverage of (b), and the red star indicates the epicenter of the 2020 Nima earthquake. (b) Tectonic settings of the Riganpei Co–Yibug Caka–Jiangai Zangbo (RYJ) fault zone. The red rectangle represents the coverage of (c) and the cyan and purple boxes indicate the coverage of Sentinel-1 images. (c) Regional tectonic settings of the 2020 Nima earthquake. The red box represents the surface projection of the distributed slip model determined in this study, and the solid green line is the intersection between the corresponding fault plane and the surface. Green dots show the aftershocks one year after the event from the China Earthquake Networks Center (CENC, https//news.seic.ac.cn, accessed on 1 March 2021). RPF, Riganpei Co fault; WYF, West Yibug Caka fault; EYC, East Yibug Caka fault; JF, Jiaomou fault; BZF, Bu Zang Ai fault; GTF, Gangtang fault. The GPS velocity field (blue arrows) is from Liang et al. [], and the block boundary data is from Deng et al. []. All faults shown are modified from Taylor and Yin [].
2. InSAR Observations
2.1. Coseismic Deformation
Sentinel-1A SAR images from both ascending and descending tracks were employed to investigate the 2020 Nima earthquake (Table 2), from which two interferograms were generated using the GAMMA software [] with the precise orbit product provided by the European Space Agency (ESA). The topographic phase contribution was removed using the Shuttle Radar Topography Mission (SRTM) 1-Arc-Second (~30 m) digital elevation model (DEM). The Goldstein filtering method was used to filter the wrapped interferograms [] and the minimum cost flow (MCF) method was used to unwrap the phase []. The atmospheric effect represents one of the main error sources of InSAR, especially the part due to tropospheric water vapor. In this study, tropospheric delays corresponding to the SAR acquisitions generated by GACOS [,,] were utilized to reduce atmospheric effects on InSAR observations. Two independent coseismic interferograms (Table A1 and Figure A1) were used to validate the coseismic deformation field. Detailed results can be found in Appendix A.

Table 2.
Coseismic interferograms for the 2020 Mw 6.3 Nima earthquake.
As shown in Figure 2, the descending interferogram shows an elliptical deforming area in the near field with a maximum LOS surface displacement of ~25 cm moving away from the satellite, whilst the ascending interferogram shows two elliptical deforming areas with a maximum surface displacement of ~30 cm moving away from the satellite as well as a maximum LOS surface displacement of ~10 cm moving toward the satellite. The coseismic deformation fields are continuous in both interferograms, indicating that the fault did not rupture to the surface (Figure 3a,b).
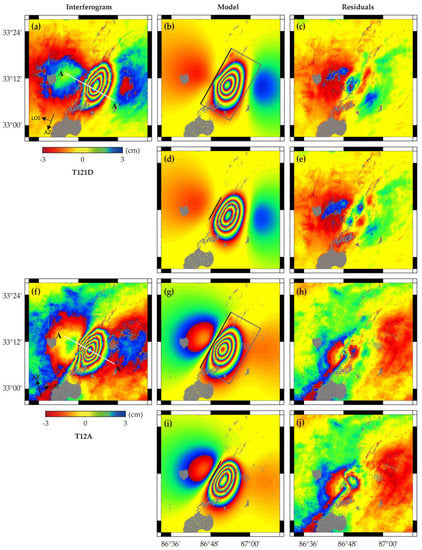
Figure 2.
(a,f) are interferograms for descending track 121 and ascending track 12, respectively. (b,g) are the modeled interferograms based on the distributed slip model determined in this study, and (c,h) are their corresponding residuals. (d,i) are the modeled interferograms based on the uniform slip model with fault parameters given in Table 1, and (e,j) are their corresponding residuals. Note that the gray box is the surface projection of the uniform model determined in this study, and the solid black line is the intersection between the corresponding fault plane and the surface. White lines A-A’ indicate profiles shown in Figure 3.
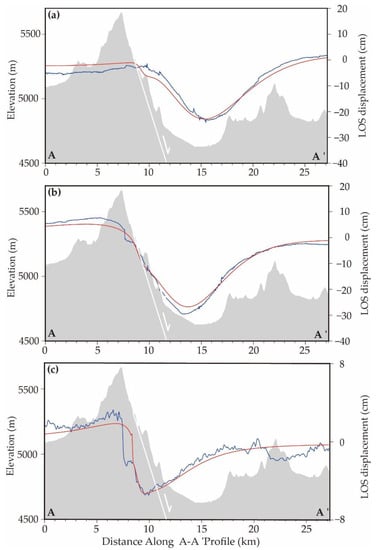
Figure 3.
(a,b) are profiles of coseismic LOS displacements and topography, and (c) are profiles of postseismic LOS displacements and topography. Note that (i) The lines of profiles (a,b) are shown in Figure 2a,f,c is the profile line of the LOS postseismic displacement 308 days after the event; and (ii) The observed LOS displacements along the profiles are shown in blue, the modeled LOS displacements in red, and the topography is shown as grayscale.
2.2. Postseismic Deformation
In this study, 24 Sentinel-1A ascending images acquired during the period from 30 July 2020 to 13 July 2021 were interferometrically processed to generate postseismic interferograms with small temporal baselines (<60 days) and small spatial baselines (<150 m) (Figure 4). Then the SBAS-InSAR technique was used to obtain the postseismic deformation time series (Figure 5). SBAS-InSAR is a commonly used InSAR time series approach to utilize multiple interferograms with short spatial and temporal baselines to minimize the effects of baseline decorrelation and inaccuracies in topographic data used []. To minimize atmospheric effects on InSAR observations, GACOS was incorporated into SBAS-InSAR with a spatial–temporal Atmospheric Phase Screen (APS) filter as demonstrated in []. We obtained 23 dates of accumulated LOS deformation and referenced it in time to the image acquired eight days after the event (30 July 2020). Based on the cumulative displacement maps, we inverted the afterslip at different time epochs.
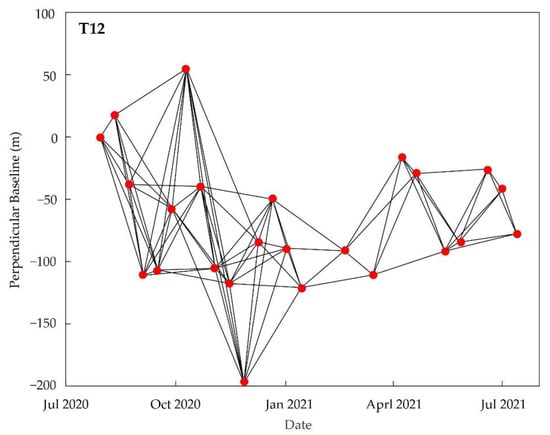
Figure 4.
Spatial–temporal baselines for Sentinel-1 interferograms from ascending track 12.
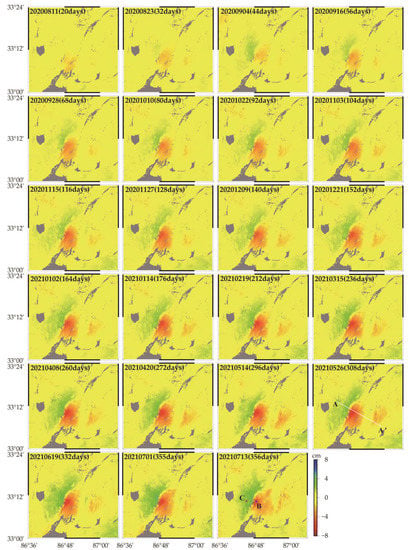
Figure 5.
Time series of the LOS surface displacements from ascending track 12 after the Mw 6.3 Nima earthquake. Days refer to those counted from 22 July 2020. Areas B and C were selected for further analysis.
It is clear in Figure 5 that obvious postseismic deformation can be observed, even only 20 days after the earthquake. In 356 days, the minimum surface displacement of −6.5 cm can be observed in the LOS direction (moving away from the satellite), while the maximum surface displacement of 2.5 cm can be observed in the LOS direction (moving toward the satellite). The postseismic deformation is mainly located on the eastern side of the fault and is dominated by subsidence. The western side of the fault is uplifting, but the displacements were relatively small. The coseismic and postseismic deformation maps of the A-A’ profile perpendicular to the surface trace of the fault have similar shapes (Figure 3b,c). The postseismic deformation on the profile is nearly an order of magnitude smaller than the coseismic deformation. In order to analyze the trend of postseismic deformation with time, the deformation of the two square areas was extracted from the postseismic deformation time series (Figure 5). The deformation time series of the extracted areas was fitted using the following logarithmic function [].
where y is the LOS deformation in cm, a, b and are constant coefficients, and is the number of postseismic days. It is clear in Figure 6 that the logarithmic function fits the postseismic deformation time series well, and the deformation evolution of the postseismic deformation follows the trend of the logarithmic decay. The postseismic deformation in area B started to stabilize 212 days after the event (Figure 6a), while the postseismic deformation in area C continued to increase even 356 days after the event (Figure 6b). It is also clear in Figure 6 that the observed LOS displacements agreed the best to the fitted lines 308 days than the following dates for both areas B and C, and hence the postseismic deformation 308 days after the event was selected for further analysis in this study.
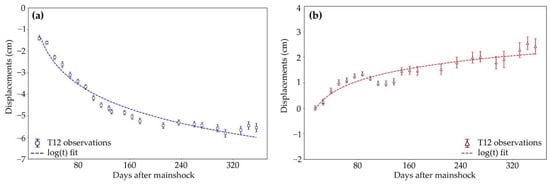
Figure 6.
The LOS postseismic displacement time series and logarithmic function fittings for areas B and C (indicated by squares in Figure 5). (a) The mean LOS surface displacement time series for area B (0.45 km × 0.45 km, blue square in Figure 5). (b) The mean LOS surface displacement time series for area C (0.45 km × 0.45 km, red square in Figure 5).
3. Coseismic Inversion
In order to reduce the number of data points in the inversion to expedite the modeling process, the quadtree downsampling method was used to downsample the interferograms [], and 1172 and 1671 data points were extracted from the descending and ascending interferograms, respectively. The ascending and descending datasets were set to equal weight.
A two-step inversion strategy was adopted to determine the fault parameters. In the first step, a nonlinear inversion was carried out to determine the fault geometry. In the second step, a linear inversion was performed to estimate the slip distribution on the ruptured fault plane. The interferometric phase was then modeled as that due to uniform slip on a rectangular fault using an elastic half-space dislocation model []. Given the fact that the earthquake ruptured on a blind fault (i.e., no rupture on the surface), we conducted a nonlinear global search to determine the fault parameters (i.e., the location, length, width, strike, dip, rake, depth and fault slip) with a commonly used geodetic inversion package, PSOKINV []. In the PSOKINV package, the multiple peak particle swarm optimization (MPSO) algorithm combining particle swarm optimization (PSO) [] and the downhill simplex algorithm (DSA) [] is employed to determine the optimal fault parameters by minimizing the squared misfits between the observed and the predicted surface displacements. MPSO takes advantage of the capability of PSO to perform a global search to find several local minima and the capability of DSA to accelerate the search process to ensure reliability and efficiency [].
The inversion results (Table 1) show that the causative fault was an SE-dipping normal fault with a small amount of left-lateral strike-slip component (the rake is about −74.7°), a length of about 11.4 km, and the top depth of the fault was 4.8 km.
To determine the parameter errors for the nonlinear MPSO inversion, a Monte Carlo simulation of correlated noise was utilized [,]. For each interferogram, a 1-D covariance function was estimated using the LOS range changes in the far field where there should be no deformation signal, and then 100 sets of correlated noise were simulated to create 100 perturbed datasets []. The MPSO inversion procedure was applied to each of these datasets and the distribution of best-fitting solutions provides information on the parameter errors and their trade-offs (Figure 7).
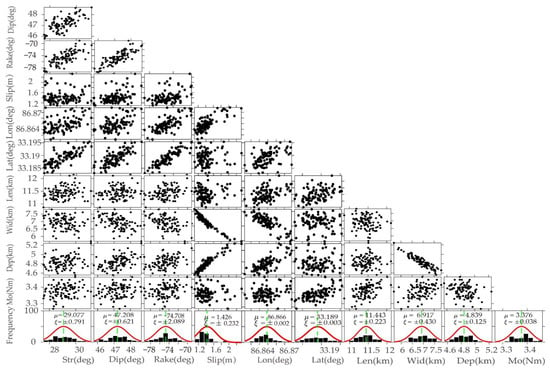
Figure 7.
Model parameter trade-offs (scatter plots) and standard deviations (black histograms) for the uniform-slip model. Each of the 100 dots is the best-fit solution for one data set to which Monte Carlo, correlated noise has been added (see text). Note the red waved lines represent probability distribution curves and the green dotted lines represent optimal model parameters solutions.
When the orientation of the fault plane was known, the slip distribution on the fault plane could be refined using a linear inversion. Based on the fault geometry from the uniform model, the fault length (along the strike) was extended to 30 km, the fault width (along the dip) was extended to 25 km, and the top depth was set to 0 km. The fault plane was divided into 750 small squared fault planes of 1 km × 1 km. The least square method was used to invert the slip of each small fault plane. Since the dip obtained by the previous inversion was not optimal for the inversion of fault-slip distribution, it was necessary to re-estimate the dip and determine the optimal dip []. In order to avoid the violent fluctuation of the slip on the fault plane, the optimal dip angle and smoothing factor of the fault were determined by comprehensively considering the model roughness and the model fitting residual []. The function was defined to estimate the optimal dip angle and smoothing factor []. Among them, is the dip angle, is the smoothing factor, is the fitting residual, and is the roughness of the slip distribution model. The optimal dip angle was determined as 50.2°, and the optimal smoothing factor was 6 (Figure 8a).
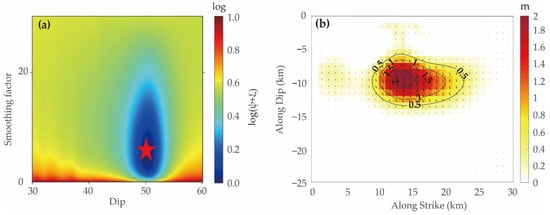
Figure 8.
(a) The map of log(ψ+ξ) with variations of dips and smoothing factors. The red star indicates the point of global minimum. (b) Slip distribution model of the 2020 Nima earthquake. Note the black lines indicate the coseismic slip contours and the black arrows within squares represent local coseismic slip directions.
Figure 8b shows that the slip was mainly concentrated in the depth range of 3–12 km, and the maximum slip amount was about 2 m at the depth of 7.4 km. A small amount of slip in the up-dip area of 0–3 km indicated that the slip did not rupture to the surface. The seismic moment released by the fault plane was 3.66 × 1018 N·m, which is equivalent to Mw 6.35. The correlation between the interferogram and the modeled interferogram reached 98%. The simulation results (Figure 2) show that the model predicted the coseismic deformation fields of ascending 12 and descending 121 well, with a small root mean square (RMS) misfits of 1.5 cm. There are obvious residuals close to the fault in Figure 2c,h, which are most likely due to the simplified fault plane model. Note that the aftershock and postseismic deformation could also account for part of the residuals since the coseismic interferograms spanned 4–6 days of the postseismic period.
4. Postseismic Deformation Mechanism
There are three mechanisms of postseismic deformation: afterslip [,], poroelastic rebound [,] and viscoelastic relaxation [,]. Afterslip occurs on unruptured fault patches near the surface or downdip of the coseismic rupture, where coseismic stress changes drive aseismic slip []. Poroelastic rebound is due to the flow of fluid driven by earthquake-induced pore pressure gradients with the upper crust []. Viscoelastic deformation of the lower crust and/or upper mantle, where coseismic stress changes imparted to the hot lower crust and upper mantle cannot be sustained and drive viscoelastic flow []. In the early postseismic period, viscoelastic relaxation generally does not play a dominant role in postseismic near-field deformation []. Therefore, afterslip and poroelastic rebound are considered in this paper.
4.1. Afterslip Inversion
Due to the small magnitude of deformation, the performance of the quadtree downsampling method is poor. Therefore, we instead used the downsampling method based on data resolution []. The same parameters were set for the downsampling of the selected six postseismic deformation maps. The fault geometry from coseismic inversion was used for afterslip inversion. The strike of the fault was 29.1°, and the dip angle was 50.2°. It can be seen in Figure 9 that the afterslip was mainly concentrated in the depth of 0–12 km, with a maximum slip of about 0.2 m at 5 km. The total seismic moment released by the afterslip was 5.04 × 1017 N·m in 308 days, which is about Mw 5.77, accounting for 13.8% of the energy released by the mainshock. The post- to coseismic moment ratio for strong (M > 6) earthquakes generally does not exceed ~0.3 [,]. The post- to coseismic moment release ratio was 13.8% in our study, which is consistent with previous studies. Figure 10 shows that the modeled interferograms have high similarity with the actual interferograms, and RMS misfits are less than 1 cm. Figure 11 reveals that the afterslip is mainly distributed in the up-dip direction of the coseismic slip (Figure 11a). The amount of afterslip is small and does not change the characteristics of the coseismic slip distribution (Figure 11b).
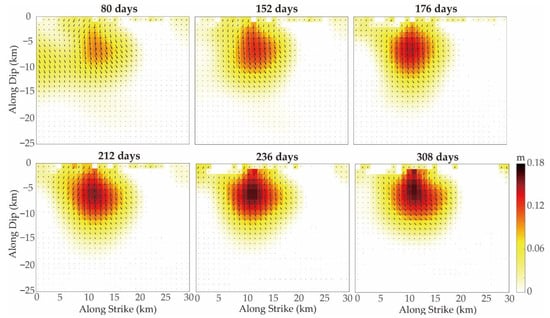
Figure 9.
The afterslip distribution of the Mw 6.3 Nima earthquake. Note the black arrows within squares represent local afterslip directions.
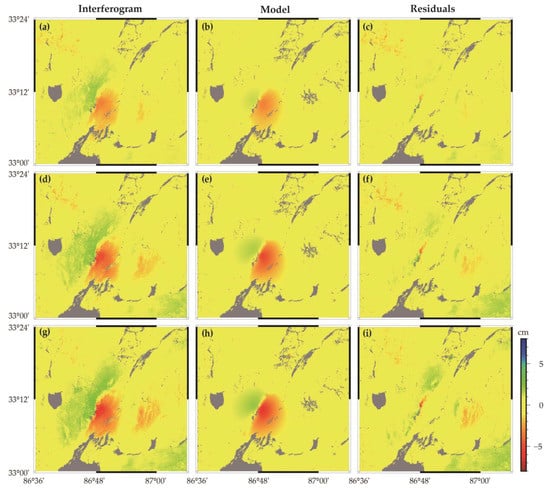
Figure 10.
(a,d,g) are interferograms of 80, 176, and 308 days, respectively. (b,e,h) are the modeled interferograms based on the afterslip models (Figure 9), and (c,f,i) are their corresponding residuals.
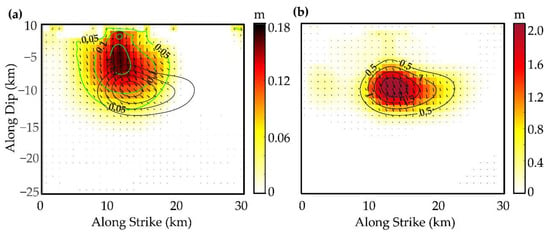
Figure 11.
(a) The afterslip distribution 308 days after the event. Note that the green lines represent the afterslip contours whilst the black lines indicate the coseismic slip contours; (b) The total slip distribution which is the sum of the postseismic slip after 308 days and the coseismic slip. Note the black lines represent the total slip contours.
4.2. Poroelastic Rebound
Both afterslip and poroelastic rebound could result in time-dependent postseismic deformation in the near field. Previous studies [] suggest that the poroelastic rebound mechanism could contribute to postseismic deformation in the region. Therefore, we conducted poroelastic rebound analyses [,] to examine the potential contributions of the poroelastic rebound to the postseismic deformation.
The deformation of poroelastic rebound is generally obtained by differencing the simulated coseismic displacements based on the Okada model in an elastic half-space with undrained and drained conditions (Figure 12a) [,]. The equation is shown below,
where is the surface deformation caused by poroelastic rebound at position , and and are the surface deformation at position in the drained and undrained conditions, respectively. The coseismic fault model was used to predict the surface deformation of undrained and drained conditions. The Poisson’s ratio of the drained model was fixed to 0.25, and the Poisson’s ratio of the undrained model was set to 0.27, 0.28, 0.29, and 0.3 to estimate the deformation of the poroelastic rebound [,]. It is clear in Figure 13b–e that the poroelastic rebound deformation bears no resemblance to the corresponding afterslip residuals in Figure 10. On the other hand, the poroelastic rebound deformation shows an elliptical pattern and is not similar to the deformation pattern in any postseismic interferogram (Figure 5). When the difference between the undrained Poisson’s ratio and the drained Poisson’s ratio increases, the surface deformation caused by the poroelastic rebound increases [,]. Even with a Poisson’s ratio of 0.3 in the undrained state, the maximum modeled poroelastic rebound deformation is 5 mm, which is much smaller than the observed 8 cm deformation. Therefore, the contributions of the poroelastic rebound should be marginal in this case and afterslip should be considered the primary mechanism of first-year postseismic deformation.
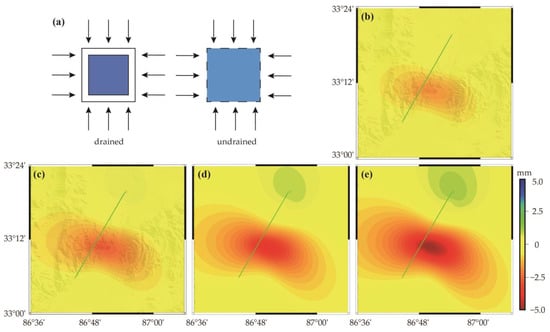
Figure 12.
(a) Poroelastic rebound principle. Note the arrows represent the stress direction. (b–e) are the results of poroelastic rebound modeling for ascending track 12. The drained Poisson’s ratio value was fixed at 0.25 while the undrained Poisson’s ratio values were set as 0.27, 0.28, 0.29, and 0.3. Note the solid green line is the intersection between the fault plane and the surface.
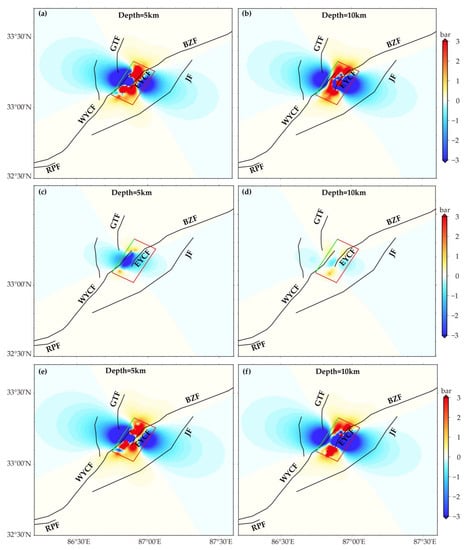
Figure 13.
(a,b) Static Coulomb failure stress (CFS) changes of the Mw 6.3 Nima earthquake calculated by the optimal coseismic slip distribution at depths of 5 km and 10 km. (c,d) CFS changes produced by the afterslip in 308 days. (e,f) CFS changes produced by the total slip distribution in 308 days. Note symbols as for Figure 1c.
5. Discussion
5.1. Comparisons of the Fault Geometry with Previous Studies
There have been several previous studies investigating the fault geometry of the 2020 Nima earthquake [,,,], showing that the fault plane with strikes ranging from 28° to 31.3° and dips ranging from 48.3° to 51.6°. For instance, Hu et al. [] used a modified resolution-based decomposition algorithm [] to downsample the interferograms and inverted the fault geometry using the Bayesian method []. In this study, we used the quadtree downsampling method to downsample the interferograms using the geodetic inversion package, PSOKINV, to determine the fault parameters. Our inversion results suggested that the causative fault occurred on an east-dipping normal fault with a strike of 29.1° and a dip of 50.2°. It is clear that our fault geometry was consistent with previous results, although different downsampling and inversion methods were employed in the geodetic inversion.
5.2. Static Coulomb Failure Stress Changes
Moderate and strong earthquakes can cause a readjustment of the surrounding crustal stress field, leading to the advance or delay of future seismic events [,]. The 2020 Nima earthquake, the largest earthquake in nearly 47 years in the Yibug Caka Basin, plays a significant role in evaluating the potential earthquake risk in the Nima area. Here we calculated the CFS changes using the Coulomb 3.3 software for 5 km and 10 km depths based on the coseismic slip distribution (Figure 13) [,,]. The friction coefficient was set as 0.4, and the receiver fault was a coseismic fault geometry (strike 29.1°, dip 50.2°, rake −72°). The Nima earthquake caused an increased CFS on the northern segment of the WYCF and GTF, EYCF, and the southern segment of the BZF (Figure 13a,b) []. We also calculated the CFS changes generated by afterslip in 308 days, a positive CFS on the northern part of the WYCF and EYCF (Figure 13c,d). Since the contribution in the early postseismic is relatively small, the coseismic CFS changes are basically the same as the sum of the coseismic and afterslip CFS changes in 308 days (Figure 13e,f). Considering the stress loading, the northern segment of the WYCF and EYCF may have a high rupture risk.
6. Conclusions
In this paper, Sentinel-1A satellite radar images were employed to acquire the coseismic and postseismic deformation fields of the 22 July 2020 Nima Mw 6.3 earthquake, and the Okada elastic dislocation model was used to invert its source parameters, slip distribution, and afterslip. The preferred slip distribution suggests: (1) this event occurred on an east-dipping normal fault with a strike of 29.1° and dip of 50.2°; (2) a maximum slip of 2.0 m at a depth of 7.4 km; (3) and the released moments were equivalent to a magnitude of Mw 6.35. The afterslip gives a maximum of 0.2 m at a depth of 5 km in 308 days. The contribution of poroelastic rebound to postseismic deformation was too small, suggesting that afterslip was the primary mechanism for early postseismic deformation. We also computed the static Coulomb stress changes caused by the Nima earthquake and afterslip in 308 days, indicating that the northern segment of WYCF and EYCF have a high rupture risk under positive stress loading.
Author Contributions
Conceptualization, Z.L. (Zhenhong Li); data curation, M.Z.; formal analysis, M.Z.; funding acquisition, Z.L. (Zhenhong Li); investigation, M.Z.; methodology, M.Z., Z.L. (Zhenhong Li), C.Y. and Z.L. (Zhenjiang Liu); project administration, Z.L. (Zhenhong Li); resources, Z.L. (Zhenhong Li); software, C.Y. and Z.L. (Zhenjiang Liu); supervision, Z.L. (Zhenhong Li), C.Y. and J.P. (Jianbing Peng); validation, M.Z., J.Y., X.Z. (Xuesong Zhang) and B.H.; visualization, J.W.; writing—original draft, M.Z.; writing—review and editing, Z.L. (Zhenhong Li) and C.Y. All authors have read and agreed to the published version of the manuscript.
Funding
The research was funded by the National Key Research and Development Program of China (2020YFC1512000), the National Natural Science Foundation of China (41941019), the Shaanxi Province Science and Technology Innovation Team (2021TD–51), the Shaanxi Province Geoscience Big Data and Geohazard Prevention Innovation Team (2022), and the Fundamental Research Funds for the Central Universities, CHD (Refs. 300102260301, 300102261108, and 300102262902).
Data Availability Statement
The Sentinel-1 images were freely downloaded from the Copernicus Open Access Hub, https://scihub.copernicus.eu/dhus/#/home (accessed on 1 March 2021). GACOS Atmospheric corrected data was downloaded from the Generic Atmospheric Correction Online Service for InSAR, http://www.gacos.net/ (accessed on 2 March 2021).
Acknowledgments
Part of this work was also supported by the Key Laboratory of Ecological Geology and Disaster Prevention, and the Key Laboratory of Mine Geological Hazards Mechanism and Control, Ministry of Natural Resources, China. The Sentinel-1 data were provided by the European Space Agency (ESA), and the SRTM DEM data were provided by the National Aeronautics and Space Administration (NASA).
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Validation of Coseismic Deformation Fields
Ground truth data (e.g., GNSS and leveling) is not available in the study area, but independent coseismic interferograms can be generated from Sentinel-1 images acquired from the same orbit. Therefore, two independent coseismic interferograms from ascending track 12 (Table A1 and Figure A1) were used to validate the coseismic deformation field.
Figure A1a,b show the two independent coseismic deformation fields in the radar LOS, and Figure A1c shows their differences which are generally close to zero with a mean of −0.3 cm. The R2 (correlation coefficient) between the two coseismic deformation fields is 0.97 (Figure A1d), indicating that the coseismic deformation fields are reliable.
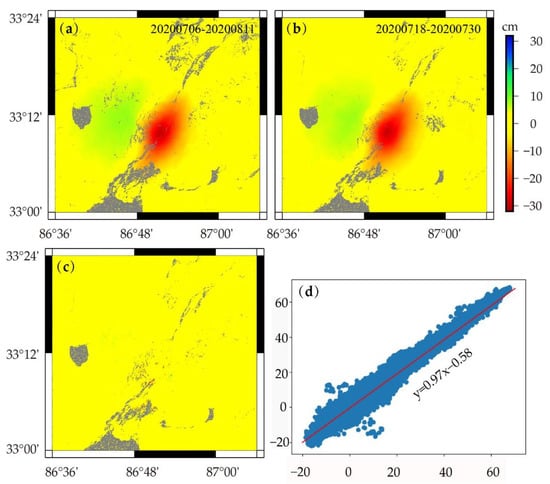
Figure A1.
(a,b) are two independent coseismic interferograms: 20200706–20200811 and 20200718–20200730; (c) is the difference map between (a,b); (d) is the correlation between (a,b).

Table A1.
Two independent coseismic interferograms for the 2020 Mw 6.3 Nima earthquake.
Table A1.
Two independent coseismic interferograms for the 2020 Mw 6.3 Nima earthquake.
| Tracks | Orbits | Master | Slave | ΔT (days) | B⊥ (m) | Inc (deg) |
|---|---|---|---|---|---|---|
| 12 | Ascending | 20200706 | 20200811 | 36 | −181 | 41.65 |
| 12 | Ascending | 20200718 | 20200730 | 12 | −84 | 41.65 |
References
- Elliott, J.R.; Walters, R.J.; England, P.C.; Jackson, J.A.; Li, Z.H.; Parsons, B. Extension on the Tibetan plateau: Recent normal faulting measured by InSAR and body wave seismology. Geophys. J. Int. 2010, 183, 503–535. [Google Scholar] [CrossRef]
- Yang, J.Y.; Xu, C.J.; Wen, Y.M.; Xu, G.Y. The July 2020 Mw 6.3 Nima Earthquake, Central Tibet: A Shallow Normal-Faulting Event Rupturing in a Stepover Zone. Seismol. Soc. Am. 2021, 93, 45–55. [Google Scholar] [CrossRef]
- Li, H.B.; Pan, J.A.; Sun, Z.M.; Si, J.L.; Pei, J.L.; Liu, D.L.; Chevalier, M.L.; Wang, H.; Lu, H.J.; Zheng, Y.; et al. Continental tectonic deformation and seismic activity: A case study from the Tibetan Plateau. Acta Geol. Sin. 2021, 95, 194–213. (In Chinese) [Google Scholar]
- Deng, Q.D.; Cheng, S.P.; Ma, J.; Du, P. Seismic Activities and Earthquake Potential in the Tibetan Plateau. Chin. J. Geophys. 2014, 57, 678–697. (In Chinese) [Google Scholar] [CrossRef]
- Wang, M.; Shen, Z.K. Present-Day Crustal Deformation of Continental China Derived from GPS and Its Tectonic Implications. J. Geophys. Res. Solid Earth 2020, 125, e2019JB018774. [Google Scholar] [CrossRef]
- Liu, F.C.; Pan, J.W.; Li, H.B.; Sun, Z.M.; Liu, D.L.; Lu, H.J.; Zheng, Y.; Wang, S.G.; Bai, M.K.; Chevalier, M.L.; et al. Characteristics of Quarternary activities along the Riganpei Co fault and seismogenic structure of the July 23, 2020 Mw6. 4 Nima earthquake, central Tibet. Acta Geosci. Sin. 2021, 43, 173–188. (In Chinese) [Google Scholar]
- Wang, H.; Wright, T.J.; Liu, Z.J.; Peng, L.C. Strain Rate Distribution in South-Central Tibet from Two Decades of InSAR and GPS. Geophys. Res. Lett. 2019, 46, 5170–5179. [Google Scholar] [CrossRef]
- Taylor, M.; Yin, A.; Ryerson, F.J.; Kapp, P.; Ding, L. Conjugate strike-slip faulting along the Bangong-Nujiang suture zone accommodates coeval east-west extension and north-south shortening in the interior of the Tibetan Plateau. Tectonics 2003, 22, 0278–7407. [Google Scholar] [CrossRef]
- Taylor, M.; Yin, A. Active structures of the Himalayan-Tibetan orogen and their relationships to earthquake distribution, contemporary strain field, and Cenozoic volcanism. Geosphere 2009, 5, 199–214. [Google Scholar] [CrossRef]
- Bürgmann, R.; Ayhan, M.E.; Fielding, E.J.; Wright, T.J.; McClusky, S.; Aktug, B.; Demir, C.; Lenk, O.; Türkezer, A. Deformation during the 12 November 1999 Düzce, Turkey, Earthquake, from GPS and InSAR Data. Bull. Seismol. Soc. Am. 2002, 92, 161–171. [Google Scholar] [CrossRef]
- Li, Z.H.; Elliott, J.R.; Feng, W.P.; Jackson, J.A.; Parsons, B.E.; Walters, R.J. The 2010 MW 6.8 Yushu (Qinghai, China) earthquake: Constraints provided by InSAR and body wave seismology. J. Geophys. Res. Solid Earth 2011, 116, B10302. [Google Scholar] [CrossRef]
- Massonnet, D.; Feigl, K.L. Radar interferometry and its application to changes in the Earth’s surface. Rev. Geophys. 1998, 36, 441–500. [Google Scholar] [CrossRef]
- Wen, Y.M.; Li, Z.H.; Xu, C.J.; Ryder, I.; Bürgmann, R. Postseismic motion after the 2001 MW 7.8 Kokoxili earthquake in Tibet observed by InSAR time series. J. Geophys. Res. Solid Earth 2012, 117, B08405. [Google Scholar] [CrossRef]
- Barnhart, W.D.; Brengman, C.M.; Li, S.Y.; Peterson, K.E. Ramp-flat basement structures of the Zagros Mountains inferred from co-seismic slip and afterslip of the 2017 Mw7. 3 Darbandikhan, Iran/Iraq earthquake. Earth Planet. Sci. Lett. 2018, 496, 96–107. [Google Scholar] [CrossRef]
- Melgar, D.; Ganas, A.; Taymaz, T.; Valkaniotis, S.; Crowell, B.W.; Kapetanidis, V.; Tsironi, V.; Yolsal-Çevikbilen, S.; Öcalan, T. Rupture kinematics of 2020 January 24 M w 6.7 Doğanyol-Sivrice, Turkey earthquake on the East Anatolian Fault Zone imaged by space geodesy. Geophys. J. Int. 2020, 223, 862–874. [Google Scholar] [CrossRef]
- Cheloni, D.; De Novellis, V.; Albano, M.; Antonioli, A.; Anzidei, M.; Atzori, S.; Avallone, A.; Bignami, C.; Bonano, M.; Calcaterra, S. Geodetic model of the 2016 Central Italy earthquake sequence inferred from InSAR and GPS data. Geophys. Res. Lett. 2017, 44, 6778–6787. [Google Scholar] [CrossRef]
- Pousse-Beltran, L.; Socquet, A.; Benedetti, L.; Doin, M.P.; Rizza, M.; d’Agostino, N. Localized afterslip at geometrical complexities revealed by InSAR after the 2016 Central Italy seismic sequence. J. Geophys. Res. Solid Earth 2020, 125, e2019JB019065. [Google Scholar] [CrossRef]
- Cheloni, D.; Giuliani, R.; D’Anastasio, E.; Atzori, S.; Walters, R.; Bonci, L.; D’Agostino, N.; Mattone, M.; Calcaterra, S.; Gambino, P. Coseismic and post-seismic slip of the 2009 L’Aquila (central Italy) MW 6.3 earthquake and implications for seismic potential along the Campotosto fault from joint inversion of high-precision levelling, InSAR and GPS data. Tectonophysics 2014, 622, 168–185. [Google Scholar] [CrossRef]
- Hu, X.P.; He, P.; Zhang, J. Source mechanism of the 2020 Mw 6.3 Nima earthquake derived from Bayesian inversions with InSAR observations: Insight into EW extensional activity in the central Tibet. Adv. Space Res. 2022, 70, 1721–1736. [Google Scholar] [CrossRef]
- JI, Z.T.; ZHANG, Y.Z.; WANG, S.J. Coseismic deformation field and fault slip distribution inversion of the Ms 6.6 Nima, Xizang earthquake by Sentinel-1A InSAR data. Prog. Geophys. 2021, 6, 2312–2319. (In Chinese) [Google Scholar]
- Li, C.T.; Li, Q.; Tan, K.; Lu, X.F. Coseismic deformation characteristics of the 2020 Nima, Xizang Mw6.3 earthquake from Sentinel-1A/B InSAR data and rupture slip distribution. Chin. J. Geophys. 2021, 64, 2297–2310. (In Chinese) [Google Scholar]
- Li, K.; Li, Y.S.; Tapponnier, P.; Xu, X.W.; Li, D.W.; He, Z.T. Joint InSAR and Field Constraints on Faulting During the Mw 6.4, July 23, 2020, Nima/Rongma Earthquake in Central Tibet. J. Geophys. Res. Solid Earth 2021, 126, e2021JB022212. [Google Scholar] [CrossRef]
- Bie, L.D.; Ryder, I.; Nippress, S.E.; Bürgmann, R. Coseismic and post-seismic activity associated with the 2008 M w 6.3 Damxung earthquake, Tibet, constrained by InSAR. Geophys. J. Int. 2014, 196, 788–803. [Google Scholar] [CrossRef]
- Liu, Y.; Xu, C.J.; Wen, Y.M.; Li, Z.C. Post-seismic deformation from the 2009 Mw 6.3 Dachaidan earthquake in the northern Qaidam Basin detected by small baseline subset InSAR technique. Sensors 2016, 16, 206. [Google Scholar] [CrossRef] [PubMed]
- Liang, S.M.; Gan, W.J.; Shen, C.Z.; Xiao, G.R.; Liu, J.; Chen, W.T.; Ding, X.Q.; Zhou, D.M. Three-dimensional velocity field of present-day crustal motion of the Tibetan Plateau derived from GPS measurements. J. Geophys. Res. Solid Earth 2013, 118, 5722–5732. [Google Scholar] [CrossRef]
- Werner, C.; Wegmüller, U.; Strozzi, T.; Wiesmann, A. Gamma SAR and interferometric processing software. In Proceedings of the Ers-Envisat Symposium, Gothenburg, Sweden, 16–20 October 2000. [Google Scholar]
- Goldstein, R.M.; Werner, C.L. Radar interferogram filtering for geophysical applications. Seismol. Res. Lett. 1998, 25, 4035–4038. [Google Scholar] [CrossRef]
- Flynn, T.J. Two-dimensional phase unwrapping with minimum weighted discontinuity. JOSA A 1997, 14, 2692–2701. [Google Scholar] [CrossRef]
- Yu, C.; Penna, N.T.; Li, Z.H. Generation of real-time mode high-resolution water vapor fields from GPS observations. J. Geophys. Res. Atmos. 2017, 122, 2008–2025. [Google Scholar] [CrossRef]
- Yu, C.; Li, Z.H.; Penna, N.T. Interferometric synthetic aperture radar atmospheric correction using a GPS-based iterative tropospheric decomposition model. Remote Sens. Environ. 2018, 204, 109–121. [Google Scholar] [CrossRef]
- Yu, C.; Li, Z.H.; Penna, N.T.; Crippa, P. Generic atmospheric correction model for interferometric synthetic aperture radar observations. J. Geophys. Res. Solid Earth 2018, 123, 9202–9222. [Google Scholar] [CrossRef]
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2375–2383. [Google Scholar] [CrossRef]
- Yu, C.; Li, Z.H.; Penna, N.T. Triggered afterslip on the southern Hikurangi subduction interface following the 2016 Kaikōura earthquake from InSAR time series with atmospheric corrections. Remote Sens. Environ. 2020, 251, 112097. [Google Scholar] [CrossRef]
- Wang, S.J.; Zhang, Y.Z.; Wang, Y.P.; Jiao, J.S.; Ji, Z.T.; Han, M. Post-seismic deformation mechanism of the July 2015 MW 6.5 Pishan earthquake revealed by Sentinel-1A InSAR observation. Sci. Rep. 2020, 10, 18536. [Google Scholar] [CrossRef] [PubMed]
- Jónsson, S.; Zebker, H.; Segall, P.; Amelung, F. Fault Slip Distribution of the 1999 Mw 7.1 Hector Mine, California, Earthquake, Estimated from Satellite Radar and GPS Measurements. Bull. Seismol. Soc. Am. 2002, 92, 1377–1389. [Google Scholar] [CrossRef]
- Okada, Y. Internal deformation due to shear and tensile faults in a half-space. Bull. Seismol. Soc. Am. 1992, 82, 1018–1040. [Google Scholar] [CrossRef]
- Feng, W.P.; Li, Z.H. A novel hybrid PSO/simplex algorithm for determining earthquake source parameters using InSAR data. Prog. Geophys. 2010, 25, 1189–1196. (In Chinese) [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Nelder, J.A.; Mead, R. A Simplex Method for Function Minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Funning, G.J. Source Parameters of Large Shallow Earthquakes in the Alpine-Himalayan Belt from InSAR and Waveform Modelling; University of Oxford: Oxford, UK, 2005. [Google Scholar]
- Li, Z.H.; Feng, W.P.; Xu, Z.H.; Cross, P.; Zhang, J.F. The 1998 Mw 5.7 Zhangbei-Shangyi (China) earthquake revisited: A buried thrust fault revealed with interferometric synthetic aperture radar. Geochem. Geophys. Geosyst. 2008, 9, Q04026. [Google Scholar] [CrossRef]
- Feng, W.P. Modelling Co-and Post-Seismic Displacements Revealed by InSAR, and Their Implications for Fault Behaviour; University of Glasgow: Glasgow, UK, 2015. [Google Scholar]
- Feng, W.P.; Li, Z.H.; Elliott, J.R.; Fukushima, Y.; Hoey, T.; Singleton, A.; Cook, R.; Xu, Z.H. The 2011 MW 6.8 Burma earthquake: Fault constraints provided by multiple SAR techniques. Geophys. J. Int. 2013, 195, 650–660. [Google Scholar] [CrossRef]
- Bürgmann, R.; Ergintav, S.; Segall, P.; Hearn, E.H.; McClusky, S.; Reilinger, R.E.; Woith, H.; Zschau, J. Time-dependent distributed afterslip on and deep below the Izmit earthquake rupture. Bull. Seismol. Soc. Am. 2002, 92, 126–137. [Google Scholar] [CrossRef]
- Marone, C.J.; Scholtz, C.H.; Bilham, R. On the mechanics of earthquake afterslip. J. Geophys. Res. Solid Earth 1991, 96, 8441–8452. [Google Scholar] [CrossRef]
- Jónsson, S.; Segall, P.; Pedersen, R.; Björnsson, G. Post-earthquake ground movements correlated to pore-pressure transients. Nature 2003, 424, 179–183. [Google Scholar] [CrossRef] [PubMed]
- Peltzer, G.; Rosen, P.; Rogez, F.; Hudnut, K. Poroelastic rebound along the Landers 1992 earthquake surface rupture. J. Geophys. Res. Solid Earth 1998, 103, 30131–30145. [Google Scholar] [CrossRef]
- Pollitz, F.F.; Peltzer, G.; Bürgmann, R. Mobility of continental mantle: Evidence from postseismic geodetic observations following the 1992 Landers earthquake. J. Geophys. Res. Solid Earth 2000, 105, 8035–8054. [Google Scholar] [CrossRef]
- Pollitz, F.F.; Wicks, C.; Thatcher, W. Mantle flow beneath a continental strike-slip fault: Postseismic deformation after the 1999 Hector Mine earthquake. Science 2001, 293, 1814–1818. [Google Scholar] [CrossRef] [PubMed]
- Freed, A.M. Afterslip (and only afterslip) following the 2004 Parkfield, California, earthquake. Geophys. Res. Lett. 2007, 34, L06312. [Google Scholar] [CrossRef]
- Lohman, R.B.; Simons, M. Some thoughts on the use of InSAR data to constrain models of surface deformation: Noise structure and data downsampling. Geochem. Geophys. Geosyst. 2005, 6, Q01007. [Google Scholar] [CrossRef]
- Wimpenny, S.; Copley, A.; Ingleby, T. Fault mechanics and post-seismic deformation at Bam, SE Iran. Geophys. J. Int. 2017, 209, 1018–1035. [Google Scholar] [CrossRef]
- Furuya, M.; Matsumoto, F. Post-Seismic to Co-Seismic Moment Ratios for the 2016 Moderate Earthquakes Along Chaman Fault. Geophys. Res. Lett. 2022, 49, e2021GL095236. [Google Scholar] [CrossRef]
- He, J.; Peltzer, G. Poroelastic triggering in the January 9-22, 2008 Nima-Gaize (Tibet) earthquake sequence. In AGU Fall Meeting Abstracts; American Geophysical Union: Washington, DC, USA, 2009; p. S51C-1434. [Google Scholar]
- Peltzer, G.; Rosen, P.; Rogez, F.; Hudnut, K. Postseismic rebound in fault step-overs caused by pore fluid flow. Science 1996, 273, 1202–1204. [Google Scholar] [CrossRef]
- Wang, S.; Xu, W.B.; Xu, C.J.; Yin, Z.; Bürgmann, R.; Liu, L.; Jiang, G.Y. Changes in groundwater level possibly encourage shallow earthquakes in central Australia: The 2016 Petermann Ranges earthquake. Geophys. Res. Lett. 2019, 46, 3189–3198. [Google Scholar] [CrossRef]
- Wang, K.; Fialko, Y. Space geodetic observations and models of postseismic deformation due to the 2005 M7. 6 Kashmir (Pakistan) earthquake. J. Geophys. Res. Solid Earth 2014, 119, 7306–7318. [Google Scholar] [CrossRef]
- Bagnardi, M.; Hooper, A. Inversion of surface deformation data for rapid estimates of source parameters and uncertainties: A Bayesian approach. Geochem. Geophys. Geosyst. 2018, 19, 2194–2211. [Google Scholar] [CrossRef]
- Stein, R.S. Earthquake Conversations. Sci. Am. 2003, 288, 72–79. [Google Scholar] [CrossRef] [PubMed]
- Lin, J.; Stein, R.S. Stress triggering in thrust and subduction earthquakes and stress interaction between the southern San Andreas and nearby thrust and strike-slip faults. J. Geophys. Res. Solid Earth 2004, 109, B02303. [Google Scholar] [CrossRef]
- King, G.C.; Stein, R.S.; Lin, J. Static stress changes and the triggering of earthquakes. Bull. Seismol. Soc. Am. 1994, 84, 935–953. [Google Scholar]
- Toda, S.; Stein, R.S.; Richards-Dinger, K.; Bozkurt, S.B. Forecasting the evolution of seismicity in southern California: Animations built on earthquake stress transfer. J. Geophys. Res. Solid Earth 2005, 110, B05S16. [Google Scholar] [CrossRef]
- Toda, S.; Stein, R.S.; Sevilgen, V.; Lin, J. Coulomb 3.3 Graphic-rich deformation and stress-change software for earthquake, tectonic, and volcano research and teaching—User guide. US Geol. Surv. Open-File Rep. 2011, 1060, 63. [Google Scholar]
- Ziv, A.; Rubin, A.M. Static stress transfer and earthquake triggering: No lower threshold in sight? J. Geophys. Res. Solid Earth 2000, 105, 13631–13642. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).