Distributed Scatterer Processing Based on Binary Partition Trees with Multi-Baseline PolInSAR Data
Abstract
1. Introduction
- (1)
- First, it is inappropriate to use the PolInSAR coherency matrix with a large data dimension, which seriously increases the burden of similarity measurement [24]. As mentioned in [25], the full-rank matrix for the similarity measurement should be filtered or regularized by at least 3N independent samples when the number of acquisitions is N. Thus, whether it is long time-series observation or point or line target monitoring; this method is not suitable due to the large computational burden.
- (2)
- Second, the similarity test indicator based on the PolInSAR coherency matrix is a trade-off between interferometry and polarimetry, of which the weight assignment is uncontrollable, and some undesirable pixels are selected [26].
- (3)
- Third, the observation geometries of multi-baseline PolInSAR data are different, leading to the uncertainty of the time-series similarity indicator [25]. In addition, the PIHP identification based on the hypothesis statistic test relies on the rationality of the statistical model [27]. An unreasonable statistical model will lead to incorrect PIHP extraction. Moreover, the similarity test between pixels is sensitive due to the inherent speckle noise in PolSAR images, of which the error can be amplified with the increase in the data amount.
- (1)
- First, the PolInSAR similarity measure for deformation monitoring is proposed, which combines polarimetric intensity, interferometric coherence, and phase. It considers static (polarimetric) and dynamic (interferometric) homogeneity and can easily control the weight of two kinds of homogeneity. By choosing proper weighting factors, the accurate deformation spatial distribution can be depicted.
- (2)
- Second, a novel object-oriented PIHP identification method based on BPT segmentation is proposed. Considering the advantage of hierarchical data representation, an image can be adaptively separated into multiple homogeneous regions with different sizes, which is beneficial for describing complex deformation scenes. Based on the BPT frame, a novel MT-InSAR processing strategy is proposed, which is not only useful for the reduction of the speckle noise effect but also useful for the reduction of interferometric phase noise.
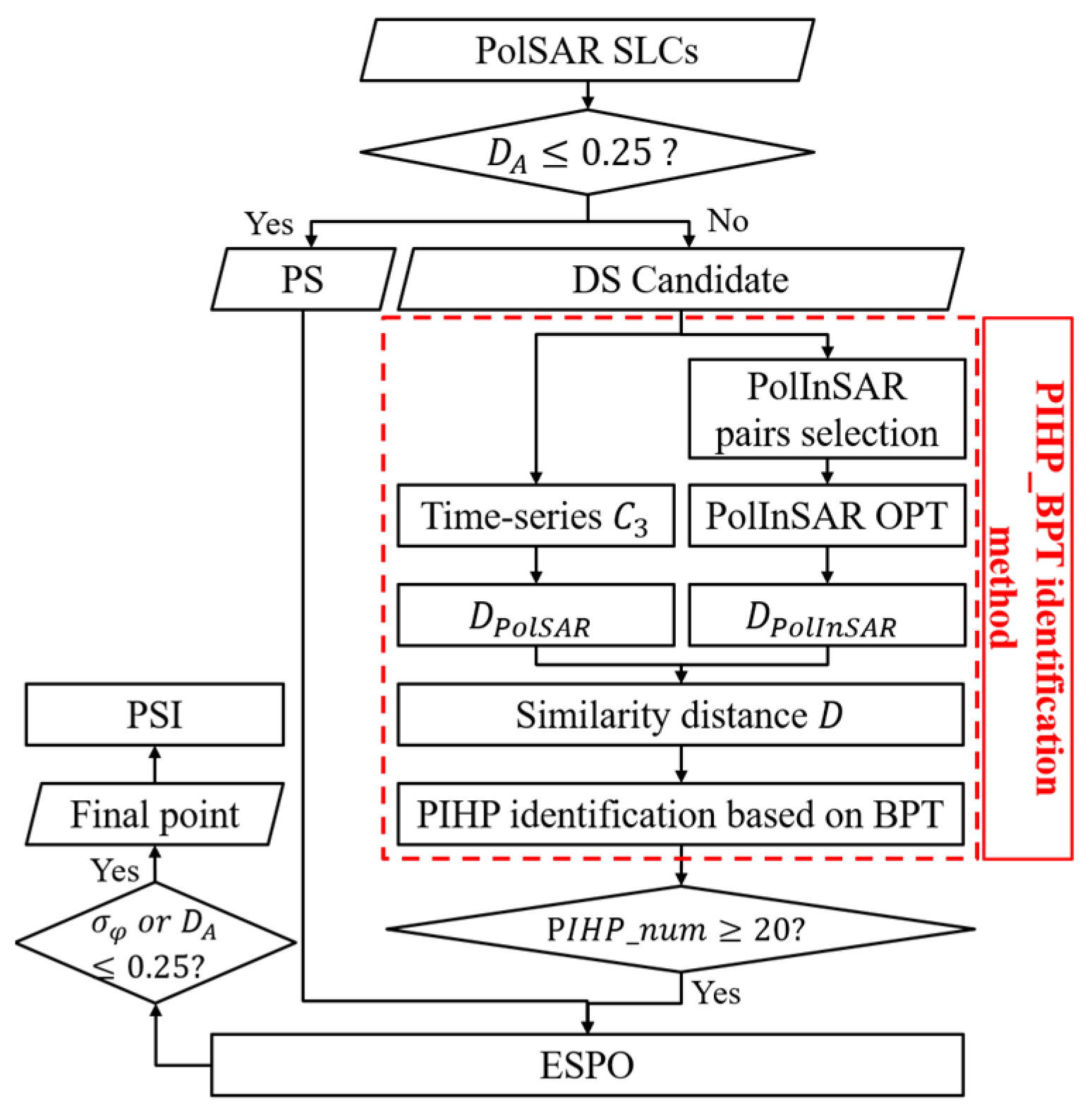
2. MT-InSAR with BPT-Based PIHP Identification
2.1. Similarity Measure
2.1.1. Polarimetric Similarity
2.1.2. Interferometric Similarity
2.1.3. The Weighted Co-Distance
2.2. PIHP Identification Based on BPT Framework
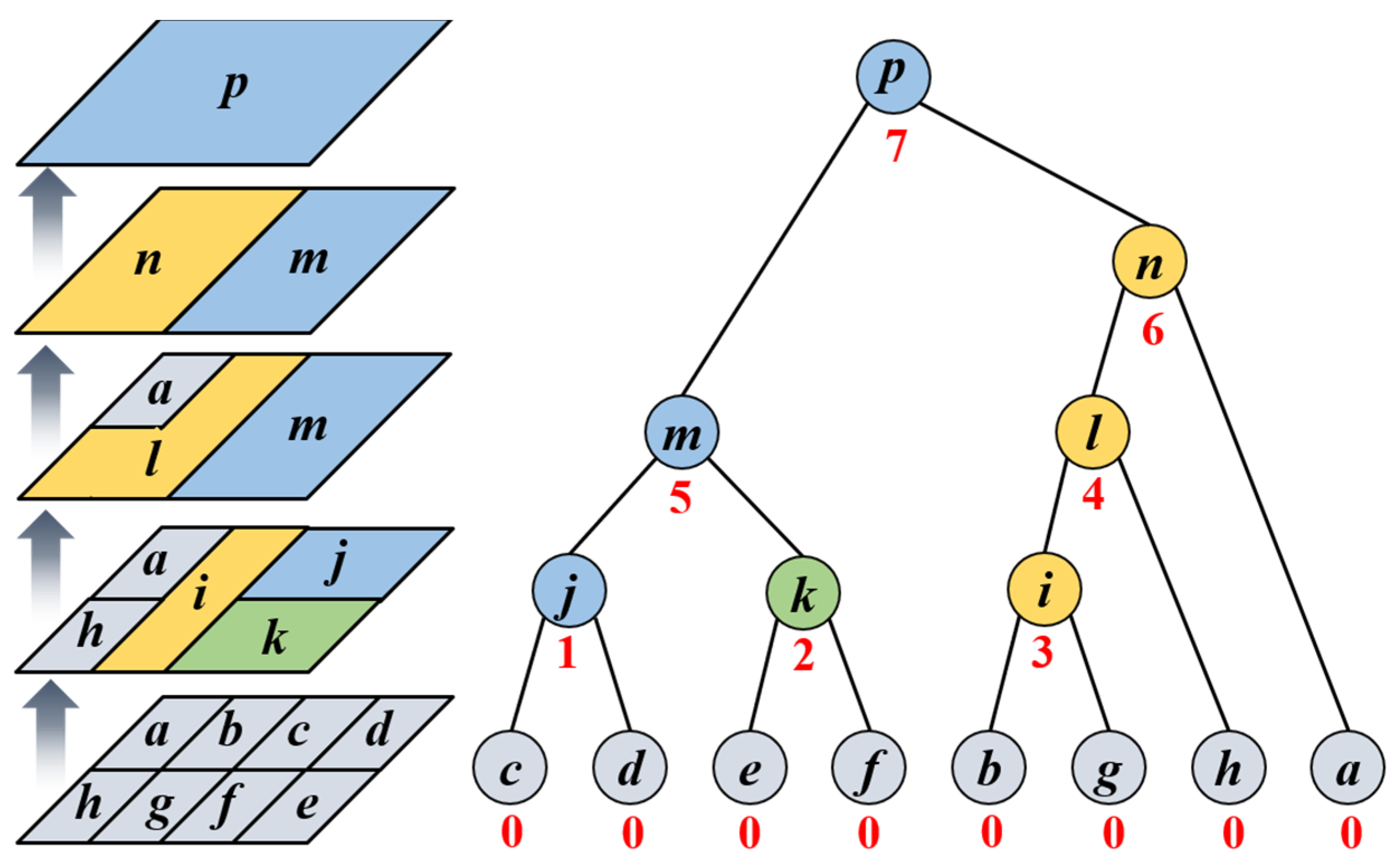
2.2.1. BPT Construction
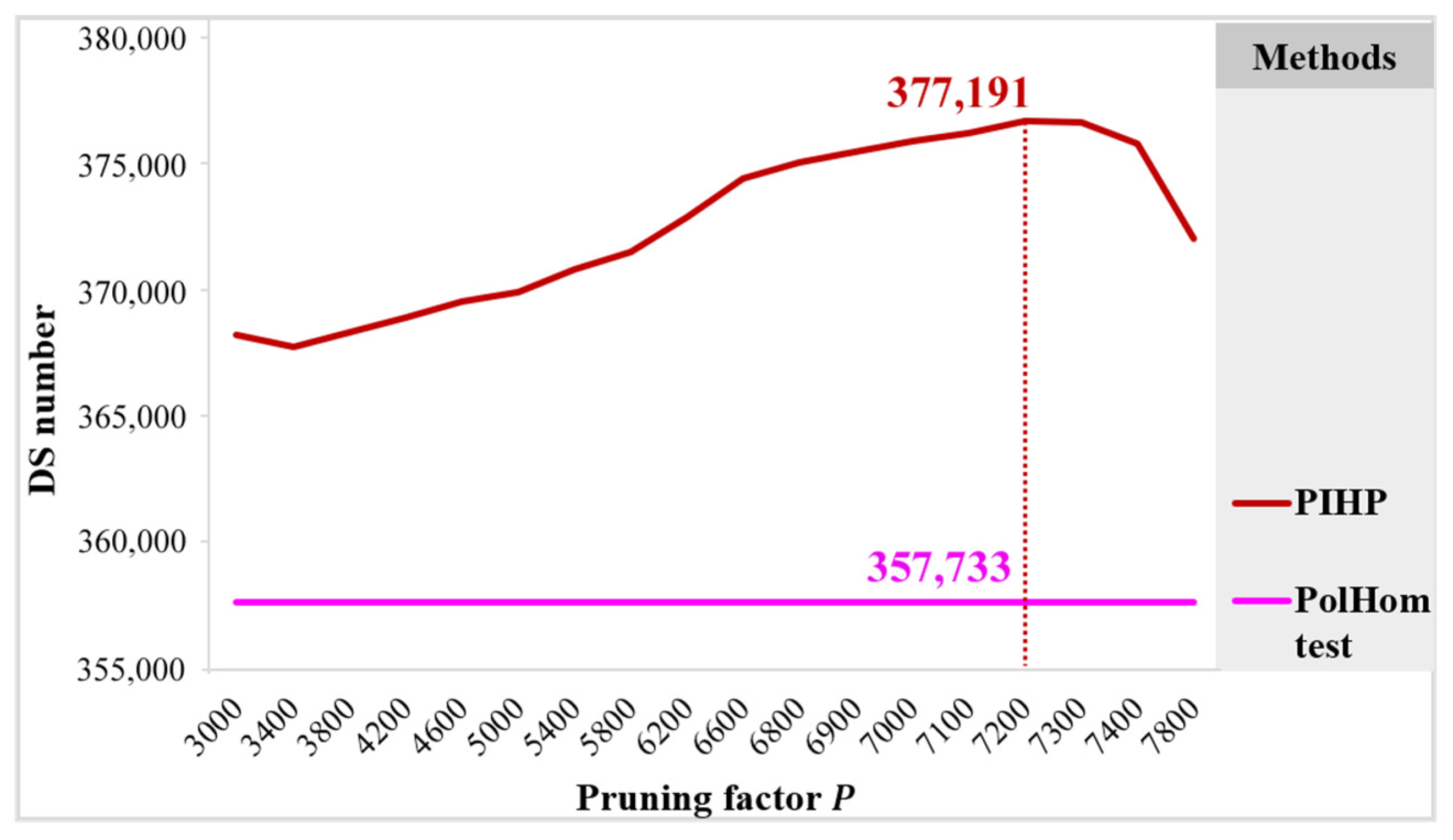
2.2.2. Branch Pruning
2.3. Improved MT-InSAR Processing Strategy
3. Experimental Datasets
3.1. Simulated Datasets Description and Parameter Settings
3.1.1. Time-Series PolSAR Data Generation
3.1.2. Multi-Temporal PolInSAR Data Generation
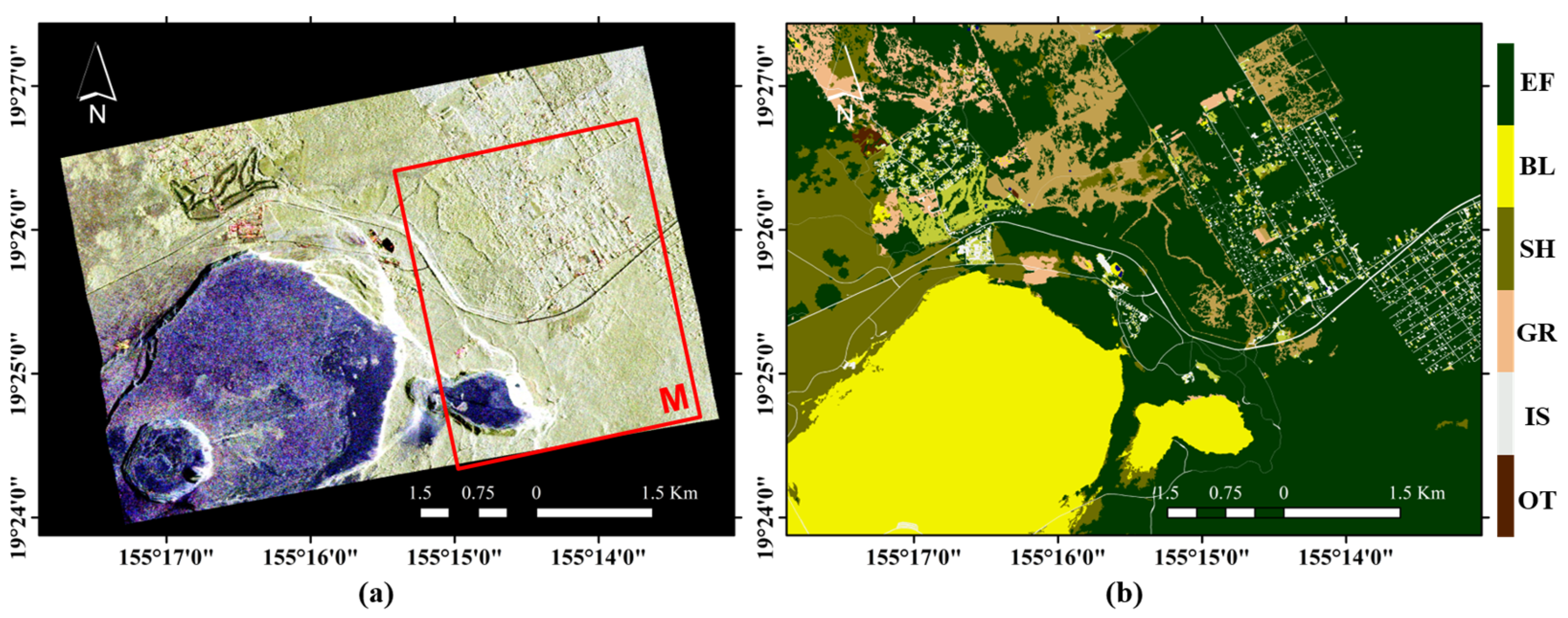
3.2. Real Datasets Description and Parameter Settings
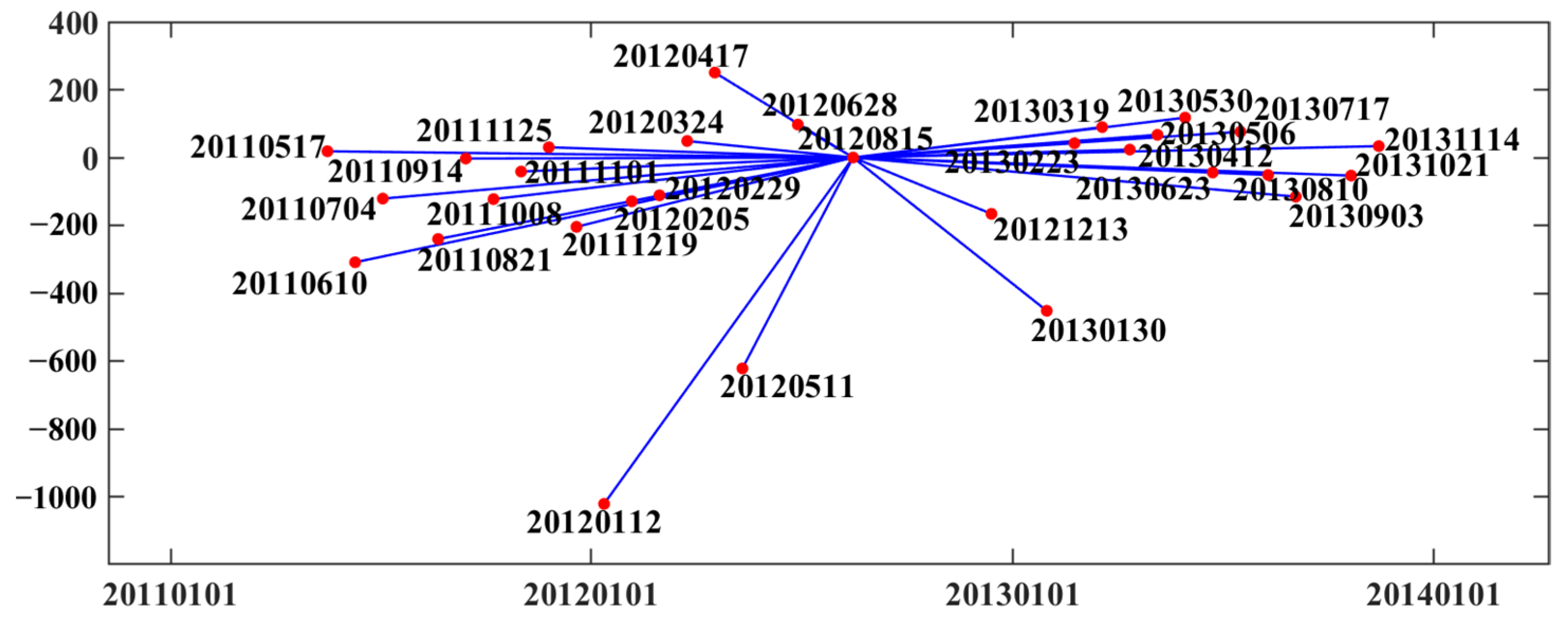
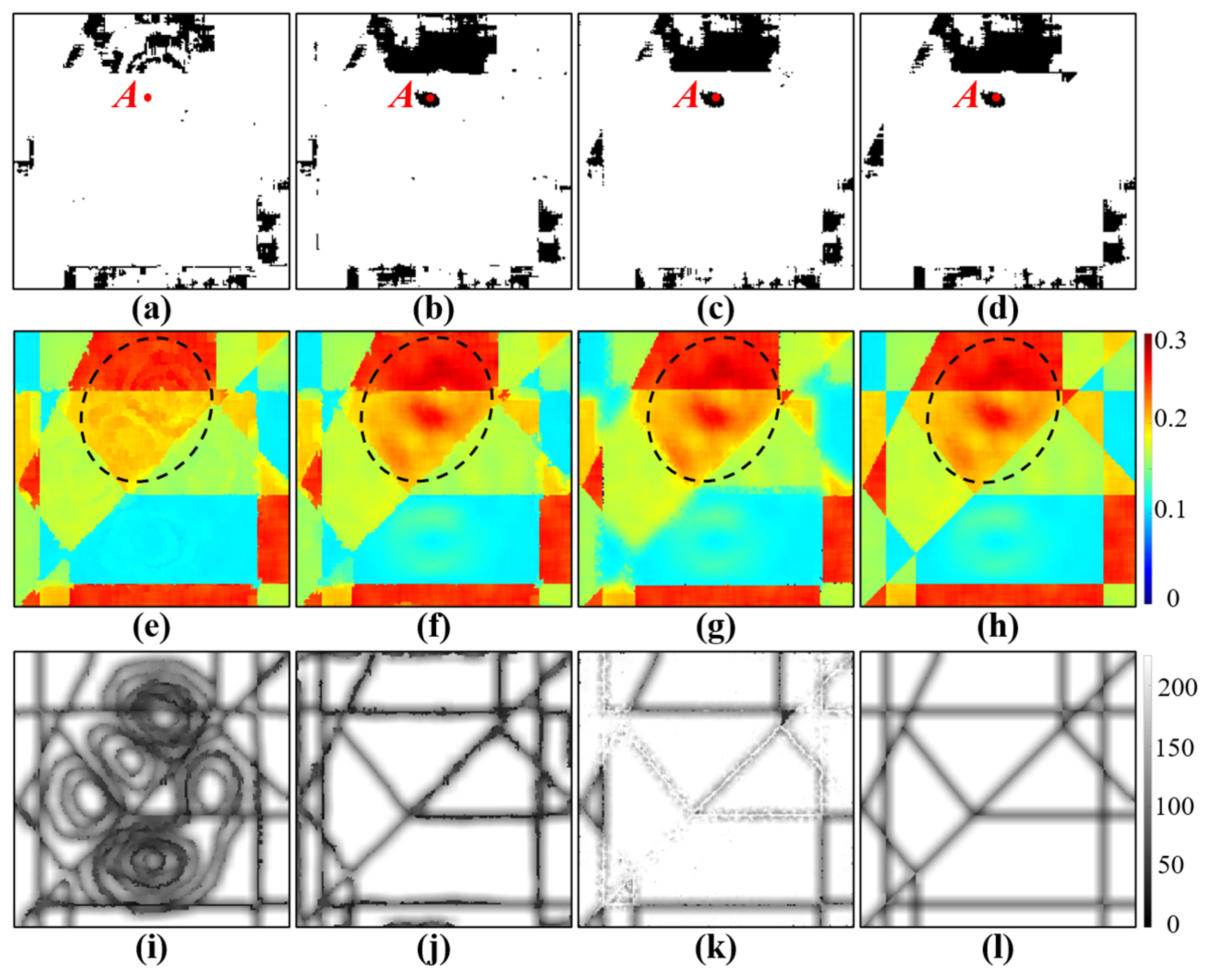
4. Result and Discussion
4.1. Comparison of Different Methods
4.1.1. Results of Simulated Datasets
4.1.2. Results of Real Datasets
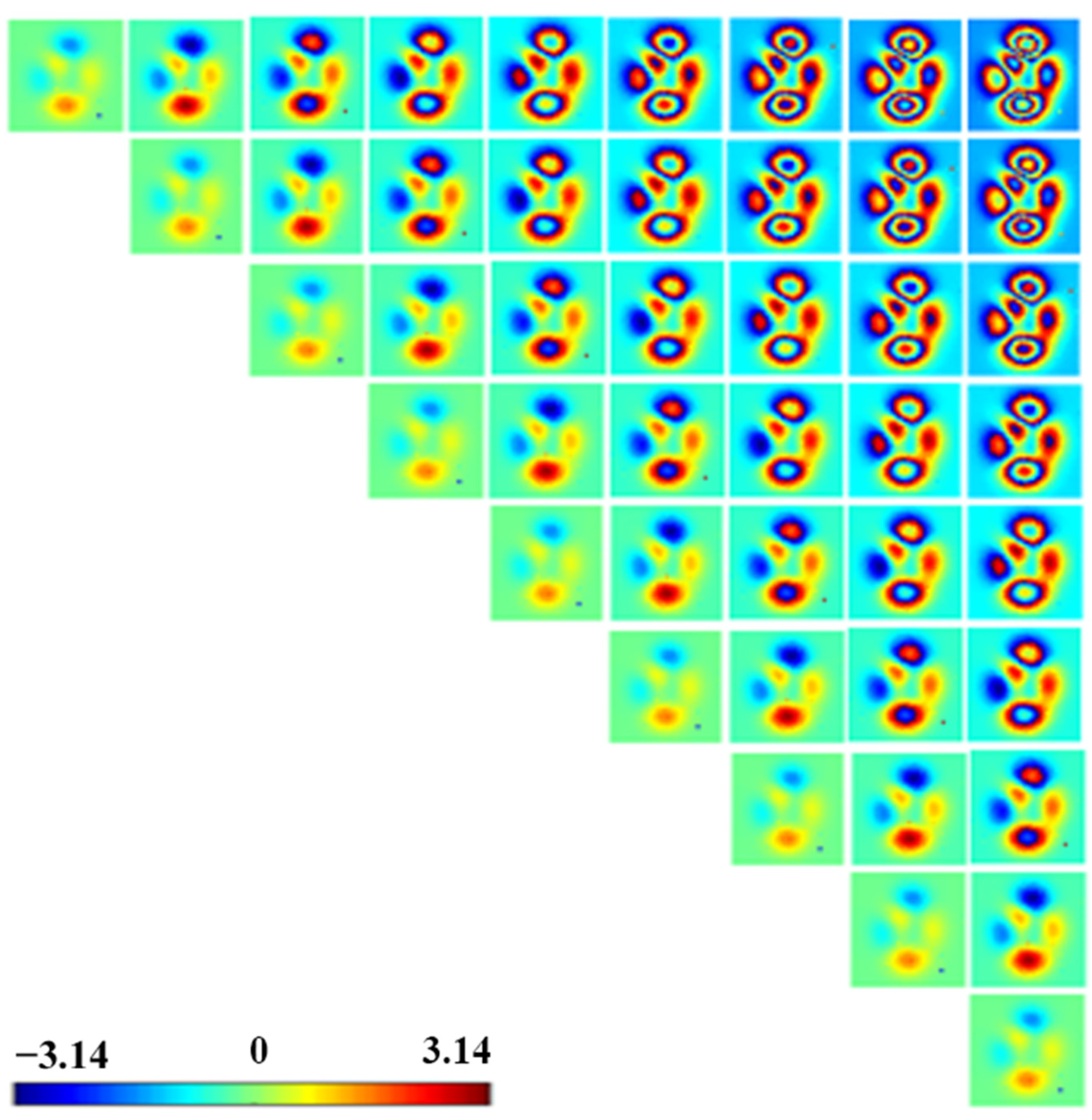
4.2. Comparison of Different Interferometric Similarities
4.3. Comparison of Different Polarimetric Similarities
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fatholahi, S.N.; He, H.; Wang, L.; Syed, A.; Li, J. Monitoring Surface Deformation Over Oilfield Using MT-Insar and Production Well Data. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 2298–2301. [Google Scholar]
- Luo, S.; Feng, G.; Xiong, Z.; Wang, H.; Zhao, Y.; Li, K.; Deng, K.; Wang, Y. An Improved Method for Automatic Identification and Assessment of Potential Geohazards Based on MT-InSAR Measurements. Remote Sens. 2021, 13, 3490. [Google Scholar] [CrossRef]
- Wu, S.; Zhang, B.; Liang, H.; Wang, C.; Ding, X.; Zhang, L. Detecting the Deformation Anomalies Induced by Underground Construction Using Multiplatform MT-InSAR: A Case Study in To Kwa Wan Station, Hong Kong. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 9803–9814. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, Z.; Zhang, H.; Zhang, B.; Tang, Y.; Wu, Q. Active Layer Thickness Retrieval of Qinghai–Tibet Permafrost Using the TerraSAR-X InSAR Technique. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 4403–4413. [Google Scholar] [CrossRef]
- Ruiz-Armenteros, A.M.; Lazecky, M.; Hlaváčová, I.; Bakoň, M.; Delgado, J.M.; Sousa, J.J.; Lamas-Fernández, F.; Marchamalo, M.; Caro-Cuenca, M.; Papco, J.; et al. Deformation Monitoring of Dam Infrastructures via Spaceborne MT-InSAR. The Case of La Viñuela (Málaga, Southern Spain). Procedia Comput. Sci. 2018, 138, 346–353. [Google Scholar] [CrossRef]
- Zhu, B.; Chu, Z.; Shen, F.; Tang, W.; Wang, B.; Wang, X. Land Subsidence (2004–2013) in Changzhou in Central Yangtze River Delta Revealed by MT-InSAR. Nat. Hazards 2019, 97, 379–394. [Google Scholar] [CrossRef]
- Mahmud, M.U.; Yakubu, T.A.; Adewuyi, T.O.; Sousa, J.J.; Ruiz Armenteros, A.M.; Bakon, M.; Lazecky, M.; Perissin, D. Subsidence Monitoring in the Coastal Region of Nigeria Using Multi Temporal Interferometric Synthetic Aperture Radar (MT-Insar). In Proceedings of the Living Planet Symposium, Prague, Czech Republic, 9–13 May 2016. [Google Scholar]
- Hooper, A. A Multi-Temporal InSAR Method Incorporating Both Persistent Scatterer and Small Baseline Approaches. Geophys. Res. Lett. 2008, 35, L16302. [Google Scholar] [CrossRef]
- Ferretti, A.; Fumagalli, A.; Novali, F.; Prati, C.; Rocca, F.; Rucci, A. A New Algorithm for Processing Interferometric Data-Stacks: SqueeSAR. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3460–3470. [Google Scholar] [CrossRef]
- Even, M.; Schulz, K. InSAR Deformation Analysis with Distributed Scatterers: A Review Complemented by New Advances. Remote Sens. 2018, 10, 744. [Google Scholar] [CrossRef]
- Sun, Q.; Jiang, L.; Jiang, M.; Lin, H.; Ma, P.; Wang, H. Monitoring Coastal Reclamation Subsidence in Hong Kong with Distributed Scatterer Interferometry. Remote Sens. 2018, 10, 1738. [Google Scholar] [CrossRef]
- Liu, Y.; Fan, H.; Wang, L.; Zhuang, H. Monitoring of Surface Deformation in a Low Coherence Area Using Distributed Scatterers InSAR: Case Study in the Xiaolangdi Basin of the Yellow River, China. Bull. Eng. Geol. Environ. 2021, 80, 25–39. [Google Scholar] [CrossRef]
- Du, Y.; Yan, S.; Yang, H.; Jiang, J.; Zhao, F. Investigation of Deformation Patterns by DS-InSAR in a Coal Resource-Exhausted Region with Spaceborne SAR Imagery. J. Asian Earth Sci. X 2021, 5, 100049. [Google Scholar] [CrossRef]
- Wang, G.; Xu, B.; Li, Z.; Fu, H.; Gao, H.; Wan, J.; Wang, C. A Phase Optimization Method for DS-InSAR Based on SKP Decomposition From Quad-Polarized Data. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Bao, J.; Luo, X.; Liu, G.; Chang, L.; Wang, X.; Shi, Y.; Wu, S. An Improved Distributed Scatterers Extraction Algorithm for Monitoring Tattered Ground Surface Subsidence with DSInSAR: A Case Study of Loess Landform in Tongren County. Int. J. Appl. Earth Obs. Geoinf. 2021, 99, 102322. [Google Scholar] [CrossRef]
- Narayan, A.B.; Tiwari, A.; Dwivedi, R.; Dikshit, O. A Novel Measure for Categorization and Optimal Phase History Retrieval of Distributed Scatterers for InSAR Applications. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5843–5849. [Google Scholar] [CrossRef]
- Jiang, M.; Ding, X.; Hanssen, R.F.; Malhotra, R.; Chang, L. Fast Statistically Homogeneous Pixel Selection for Covariance Matrix Estimation for Multitemporal InSAR. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1213–1224. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, X.X.; Bamler, R. Optimal Estimation of Distributed Scatterer Phase History Parameters from Meter-Resolution SAR Data. In Proceedings of the 2011 IEEE International Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 24–29 July 2011; pp. 3468–3471. [Google Scholar]
- Goel, K.; Adam, N. A Distributed Scatterer Interferometry Approach for Precision Monitoring of Known Surface Deformation Phenomena. IEEE Trans. Geosci. Remote Sens. 2014, 52, 5454–5468. [Google Scholar] [CrossRef]
- Parizzi, A.; Brcic, R. Adaptive InSAR Stack Multilooking Exploiting Amplitude Statistics: A Comparison Between Different Techniques and Practical Results. IEEE Geosci. Remote Sens. Lett. 2011, 8, 441–445. [Google Scholar] [CrossRef]
- Lee, J.; Pottier, E. Polarimetric Radar Imaging: From Basics to Applications; CRC Press: Boca Raton, FL, USA, 2017; ISBN 978-1-315-21933-2. [Google Scholar]
- Navarro-Sanchez, V.D.; Lopez-Sanchez, J.M. Spatial Adaptive Speckle Filtering Driven by Temporal Polarimetric Statistics and Its Application to PSI. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4548–4557. [Google Scholar] [CrossRef]
- Mullissa, A.G.; Perissin, D.; Tolpekin, V.A.; Stein, A. Polarimetry-Based Distributed Scatterer Processing Method for PSI Applications. IEEE Trans. Geosci. Remote Sens. 2018, 56, 3371–3382. [Google Scholar] [CrossRef]
- Dong, J.; Liao, M.; Zhang, L.; Gong, J. A Unified Approach of Multitemporal SAR Data Filtering Through Adaptive Estimation of Complex Covariance Matrix. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5320–5333. [Google Scholar] [CrossRef]
- Alonso-González, A.; López-Martínez, C.; Salembier, P. PolSAR Time Series Processing With Binary Partition Trees. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3553–3567. [Google Scholar] [CrossRef]
- Chen, S.-W.; Wang, X.-S.; Sato, M. PolInSAR Complex Coherence Estimation Based on Covariance Matrix Similarity Test. IEEE Trans. Geosci. Remote Sens. 2012, 50, 4699–4710. [Google Scholar] [CrossRef]
- Xiang, D.; Ban, Y.; Wang, W.; Su, Y. Adaptive Superpixel Generation for Polarimetric SAR Images With Local Iterative Clustering and SIRV Model. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3115–3131. [Google Scholar] [CrossRef]
- Salembier, P.; Garrido, L. Binary Partition Tree as an Efficient Representation for Image Processing, Segmentation, and Information Retrieval. IEEE Trans. Image Process. 2000, 9, 561–576. [Google Scholar] [CrossRef] [PubMed]
- Beaulieu, J.-M.; Touzi, R. Segmentation of Textured Polarimetric SAR Scenes by Likelihood Approximation. IEEE Trans. Geosci. Remote Sens. 2004, 42, 2063–2072. [Google Scholar] [CrossRef]
- Li, M.; Stein, A.; Bijker, W.; Zhan, Q. Region-Based Urban Road Extraction from VHR Satellite Images Using Binary Partition Tree. Int. J. Appl. Earth Obs. Geoinf. 2016, 44, 217–225. [Google Scholar] [CrossRef]
- Anfinsen, S.N.; Jenssen, R.; Eltoft, T. Spectral Clustering of Polarimetric SAR Data with the Wishart-Derived Distance Measures. In Proceedings of the 3rd International Workshop on Science and Applications of SAR Polarimetry and Polari-metric Interferometry, Frascati, Italy, 22–26 January 2007; Volume 644, p. 10. [Google Scholar]
- Gao, H.; Wang, C.; Xiang, D.; Ye, J.; Wang, G. TSPol-ASLIC: Adaptive Superpixel Generation With Local Iterative Clustering for Time-Series Quad- and Dual-Polarization SAR Data. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Cloude, S.R.; Papathanassiou, K.P. Polarimetric SAR Interferometry. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1551–1565. [Google Scholar] [CrossRef]
- Xing, C.; Zhang, T.; Wang, H.; Zeng, L.; Yin, J.; Yang, J. A Novel Four-Stage Method for Vegetation Height Estimation with Repeat-Pass PolInSAR Data via Temporal Decorrelation Adaptive Estimation and Distance Transformation. Remote Sens. 2021, 13, 213. [Google Scholar] [CrossRef]
- Neumann, M.; Ferro-Famil, L.; Reigber, A. Multibaseline Polarimetric SAR Interferometry Coherence Optimization. IEEE Geosci. Remote Sens. Lett. 2008, 5, 93–97. [Google Scholar] [CrossRef]
- Navarro-Sanchez, V.D.; Lopez-Sanchez, J.M.; Vicente-Guijalba, F. A Contribution of Polarimetry to Satellite Differential SAR Interferometry: Increasing the Number of Pixel Candidates. IEEE Geosci. Remote Sens. Lett. 2010, 7, 276–280. [Google Scholar] [CrossRef]
- Novak, L.M.; Burl, M.C. Optimal Speckle Reduction In Polarimetric Sar Imagery. In Proceedings of the Twenty-Second Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 31 October–2 November 1988; Volume 2, pp. 781–793. [Google Scholar]
- Shen, P.; Wang, C.; Hu, J.; Fu, H.; Zhu, J. Interferometric Phase Optimization Based on PolInSAR Total Power Coherency Matrix Construction and Joint Polarization-Space Nonlocal Estimation. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Shen, P.; Wang, C.; Fu, H.; Zhu, J.; Hu, J. Estimation of Equivalent Number of Looks in Time-Series Pol(In)SAR Data. Remote Sens. 2020, 12, 2715. [Google Scholar] [CrossRef]
- Sica, F.; Pulella, A.; Nannini, M.; Pinheiro, M.; Rizzoli, P. Repeat-Pass SAR Interferometry for Land Cover Classification: A Methodology Using Sentinel-1 Short-Time-Series. Remote Sens. Environ. 2019, 232, 111277. [Google Scholar] [CrossRef]
- Homer, C.; Dewitz, J.; Yang, L.; Jin, S.; Danielson, P.; Xian, G.; Coulston, J.; Herold, N.; Wickham, J.; Megown, K. Completion of the 2011 National Land Cover Database for the Conterminous United States—Representing a Decade of Land Cover Change Information. Photogramm. Eng. Remote Sens. 2015, 81, 346–354. [Google Scholar] [CrossRef]
- Mi, J.; Xiao-Li, D.; Xiu-Feng, H.E.; Zhi-Wei, L.I.; Guo-Qiang, S.H.I. FaSHPS-InSAR technique for distributed scatterers: A case study over the lost hills oil field, California. Chin. J. Geophys. 2016, 59, 3592–3603. [Google Scholar] [CrossRef]
- Ferretti, A.; Prati, C.; Rocca, F. Nonlinear Subsidence Rate Estimation Using Permanent Scatterers in Differential SAR Interferometry. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2202–2212. [Google Scholar] [CrossRef]
- Marino, A. Trace Coherence: A New Operator for Polarimetric and Interferometric SAR Images. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2326–2339. [Google Scholar] [CrossRef]




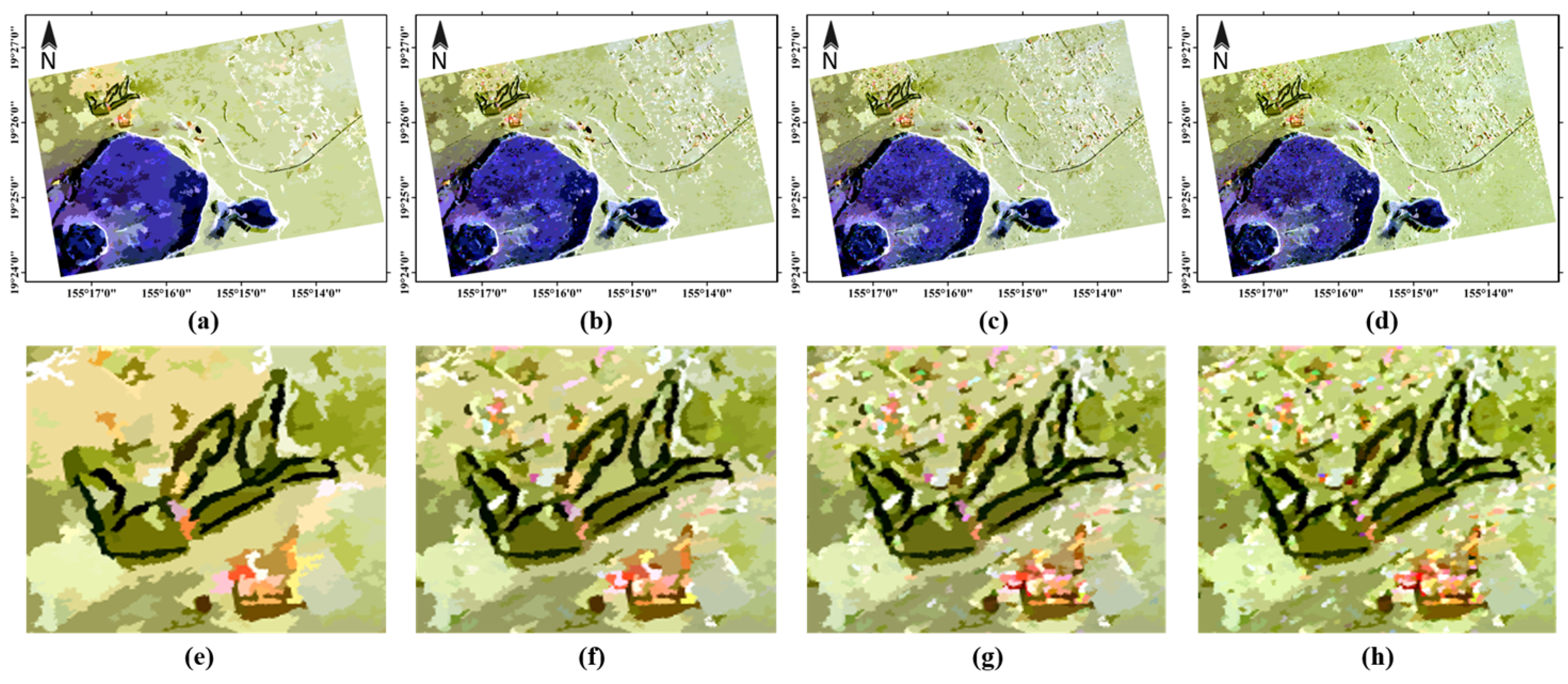
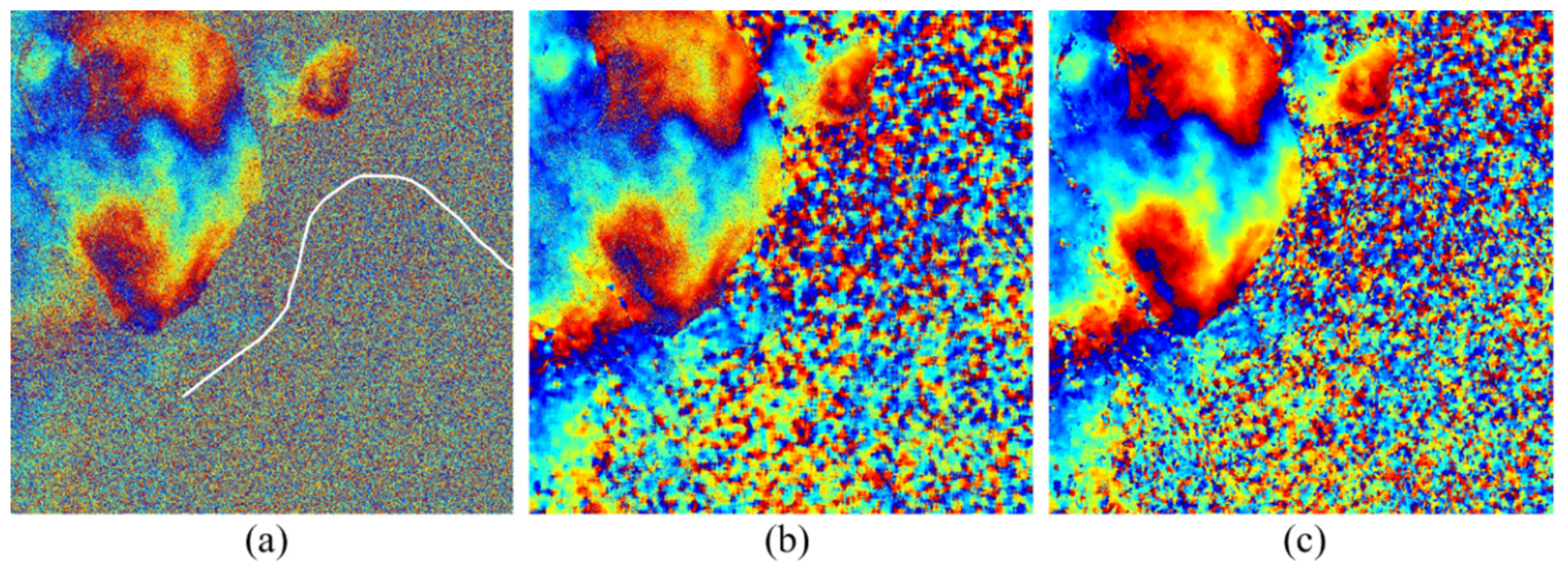

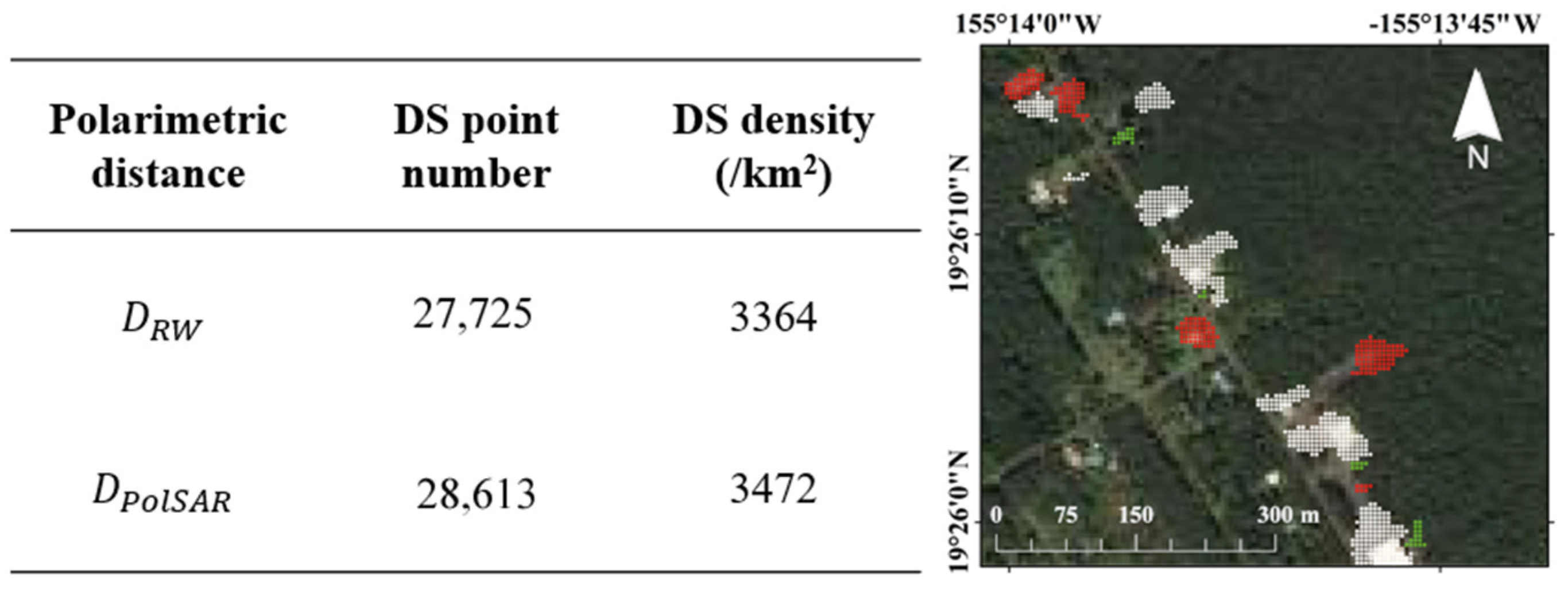
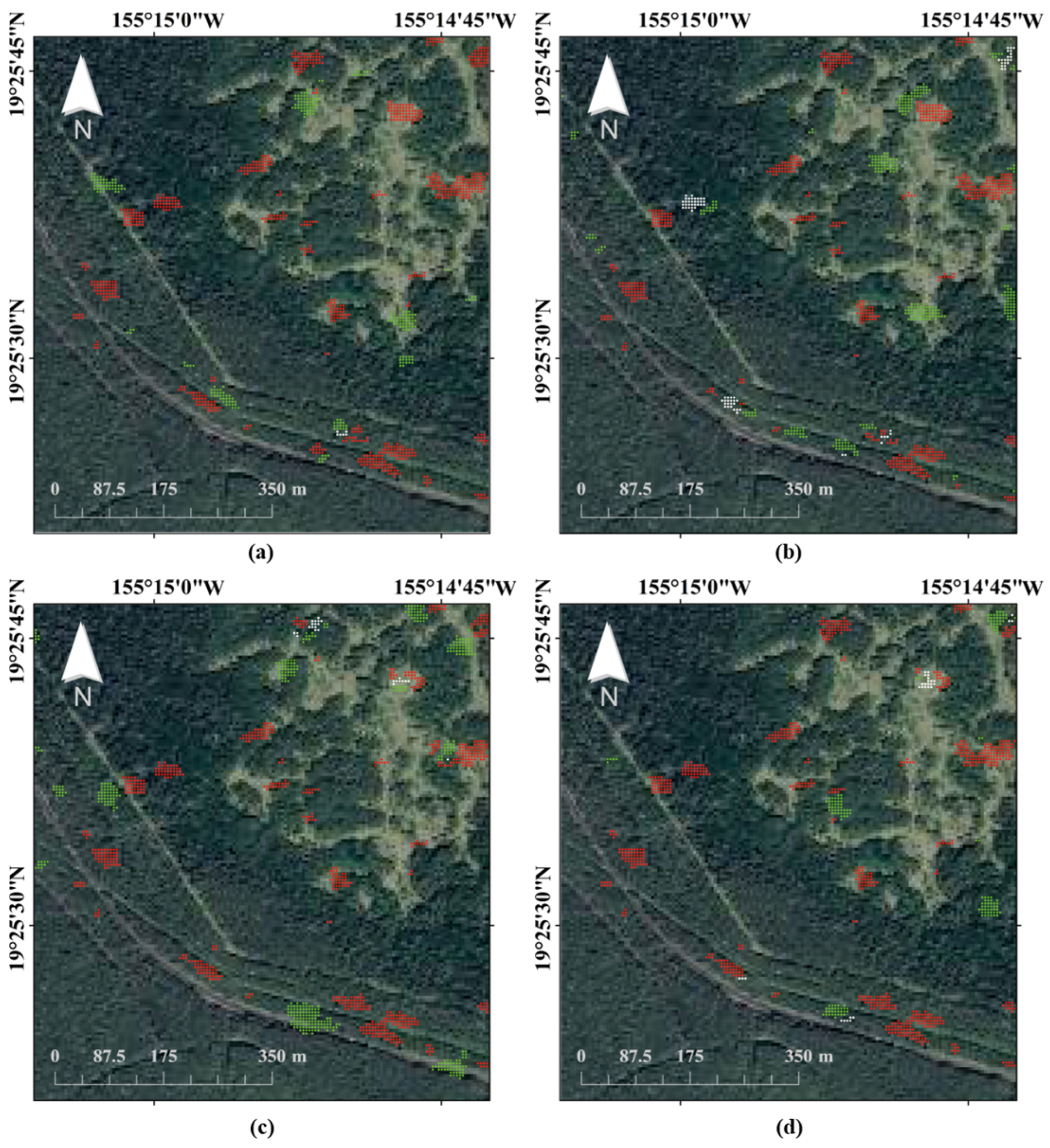
| Method | Mean | Standard Deviation | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Bare Land | Evergreen Forest | Grassland | Impervious Surface | Shrub | Bare Land | Evergreen Forest | Grassland | Impervious Surface | Shrub | |
| PolHom | 0.8228 | 0.1444 | 0.1312 | 0.1856 | 0.2519 | 0.0370 | 0.0152 | 0.0316 | 0.0205 | 0.0747 |
| PIHP | 0.8178 | 0.1900 | 0.1764 | 0.2417 | 0.2828 | 0.0352 | 0.0131 | 0.0278 | 0.0180 | 0.0711 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, G.; Deng, K.; Chen, Q.; Li, Z.; Gao, H.; Hu, J.; Xiang, D. Distributed Scatterer Processing Based on Binary Partition Trees with Multi-Baseline PolInSAR Data. Remote Sens. 2022, 14, 5367. https://doi.org/10.3390/rs14215367
Wang G, Deng K, Chen Q, Li Z, Gao H, Hu J, Xiang D. Distributed Scatterer Processing Based on Binary Partition Trees with Multi-Baseline PolInSAR Data. Remote Sensing. 2022; 14(21):5367. https://doi.org/10.3390/rs14215367
Chicago/Turabian StyleWang, Guanya, Kailiang Deng, Qi Chen, Zhiwei Li, Han Gao, Jun Hu, and Deliang Xiang. 2022. "Distributed Scatterer Processing Based on Binary Partition Trees with Multi-Baseline PolInSAR Data" Remote Sensing 14, no. 21: 5367. https://doi.org/10.3390/rs14215367
APA StyleWang, G., Deng, K., Chen, Q., Li, Z., Gao, H., Hu, J., & Xiang, D. (2022). Distributed Scatterer Processing Based on Binary Partition Trees with Multi-Baseline PolInSAR Data. Remote Sensing, 14(21), 5367. https://doi.org/10.3390/rs14215367






