Three-Dimensional Vulnerability Assessment of Peanut (Arachis hypogaea) Based on Comprehensive Drought Index and Vulnerability Surface: A Case Study of Shandong Province, China
Abstract
1. Introduction
2. Materials and Methods
Study Area and Data Sources
3. Methodology
3.1. Construction of Comprehensive Drought Index Based on the Atmosphere–Plant–Soil Continuum
3.1.1. Standardized Precipitation Evapotranspiration Index
3.1.2. Vegetation Condition Index
3.1.3. Soil Moisture Condition Index
3.2. CRITIC Weighting Method
3.3. Construction of Multi-Source Data Fusion Drought Index
3.4. Relative Meteorological Yield Reduction Rate
3.5. Mann–Kendall Trend Test
3.6. Run Theory
3.7. Vulnerability Surface Theory
4. Results and Discussion
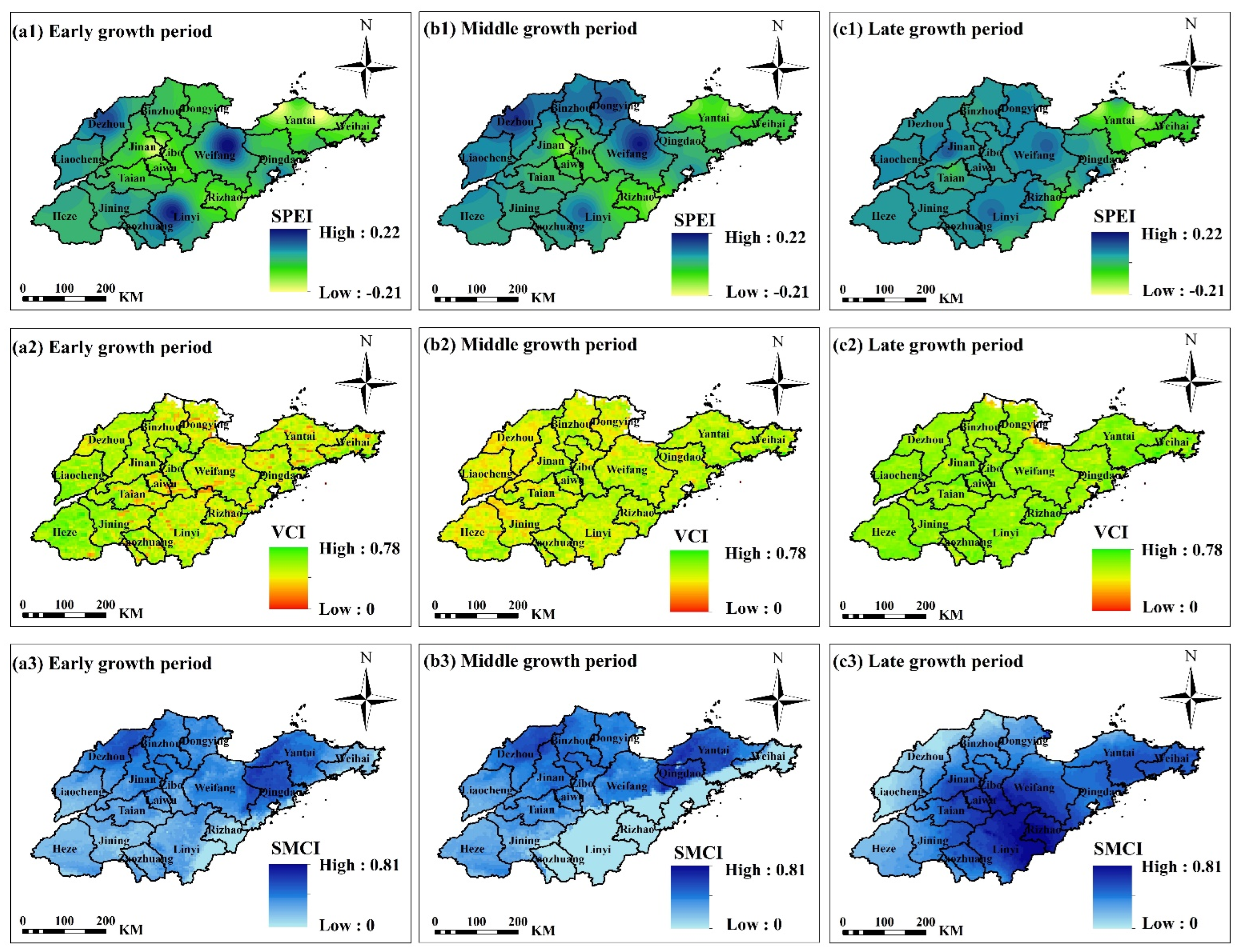
4.1. Single Drought Index Analysis
4.2. Establishment and Analysis of a Drought Index Based on Multi-Source Data Fusion
4.2.1. Drought Index Verification
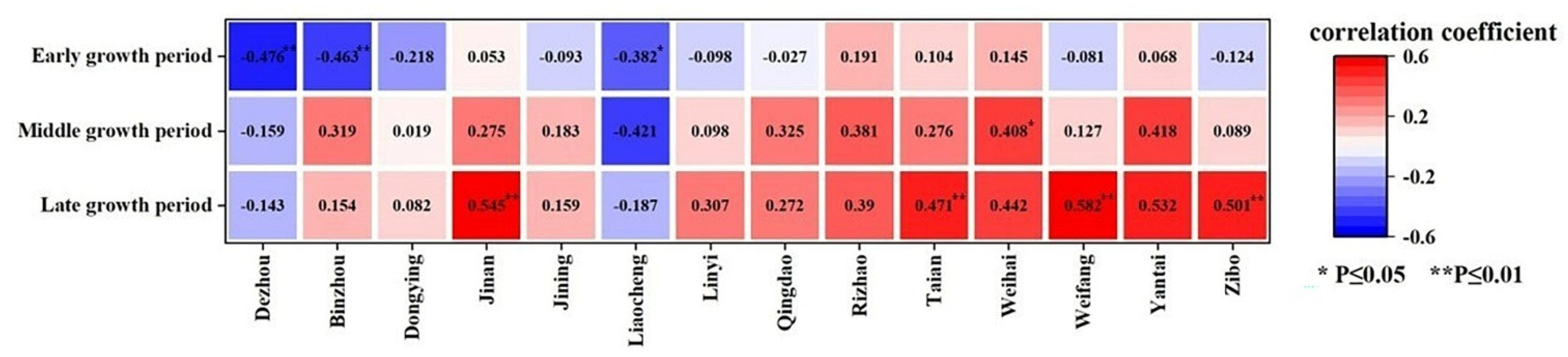
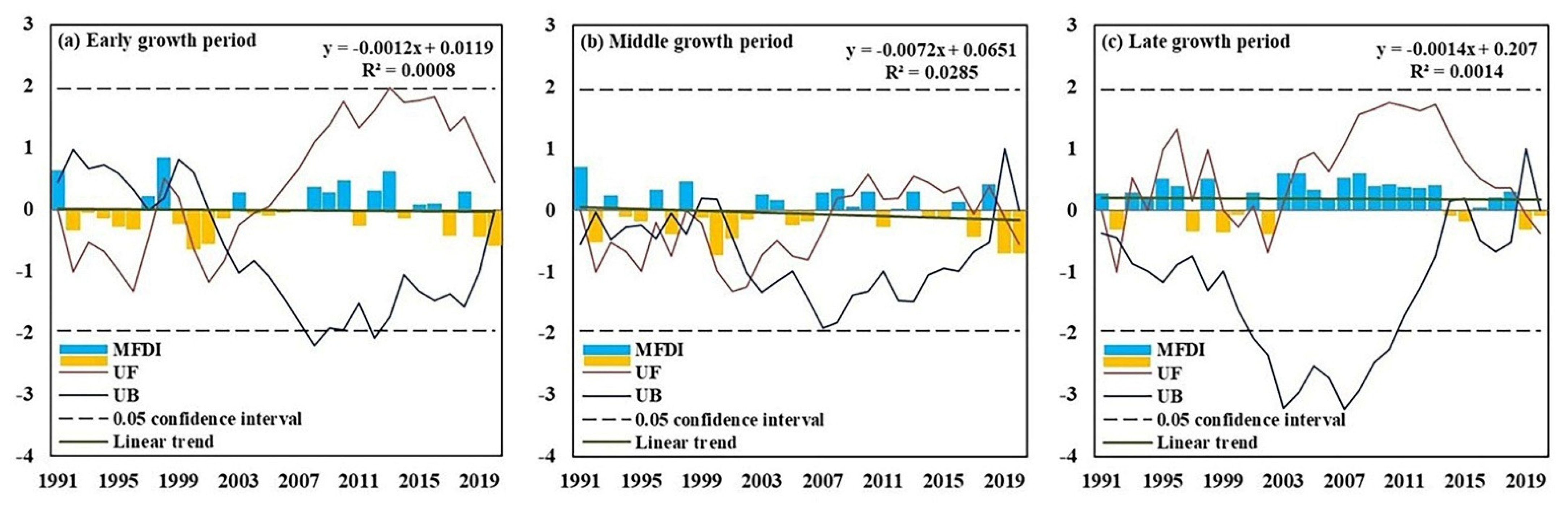
4.2.2. MFDI Time Series Analysis
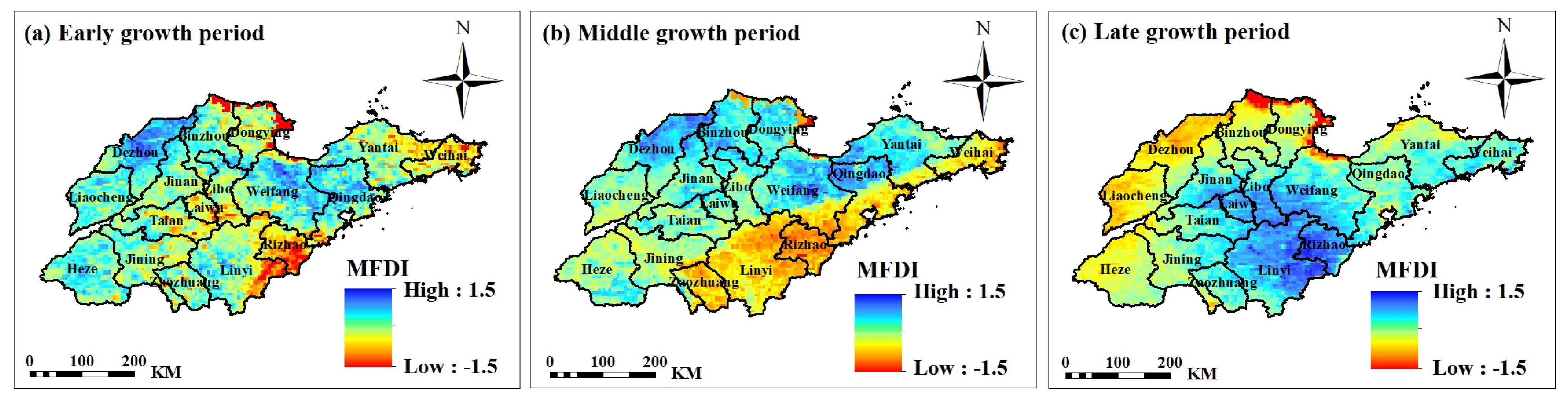
4.2.3. MFDI Spatial Distribution
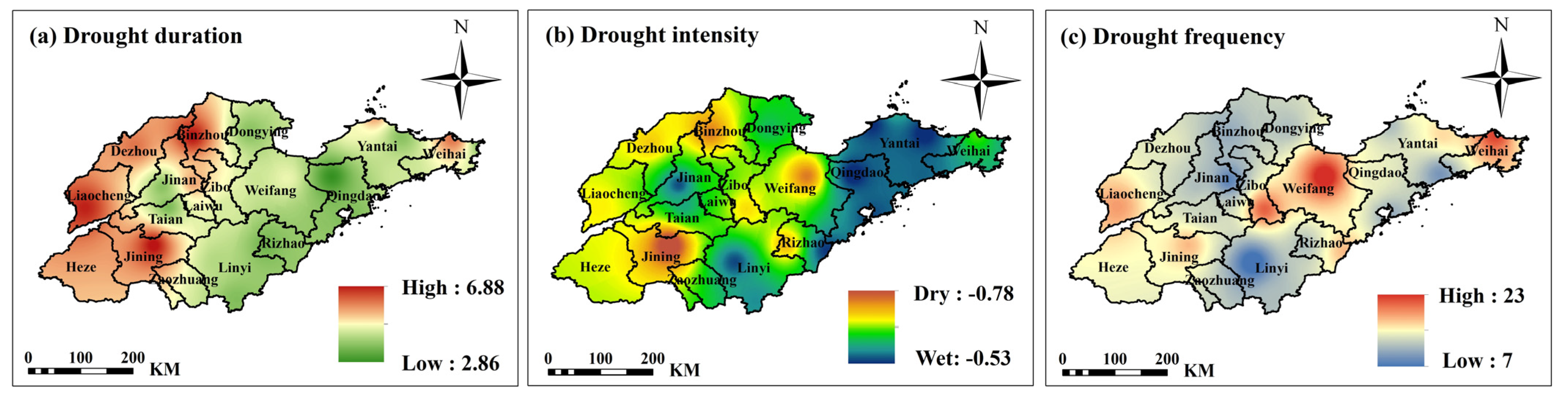
4.3. Analysis of Drought Characteristics Based on Run Theory
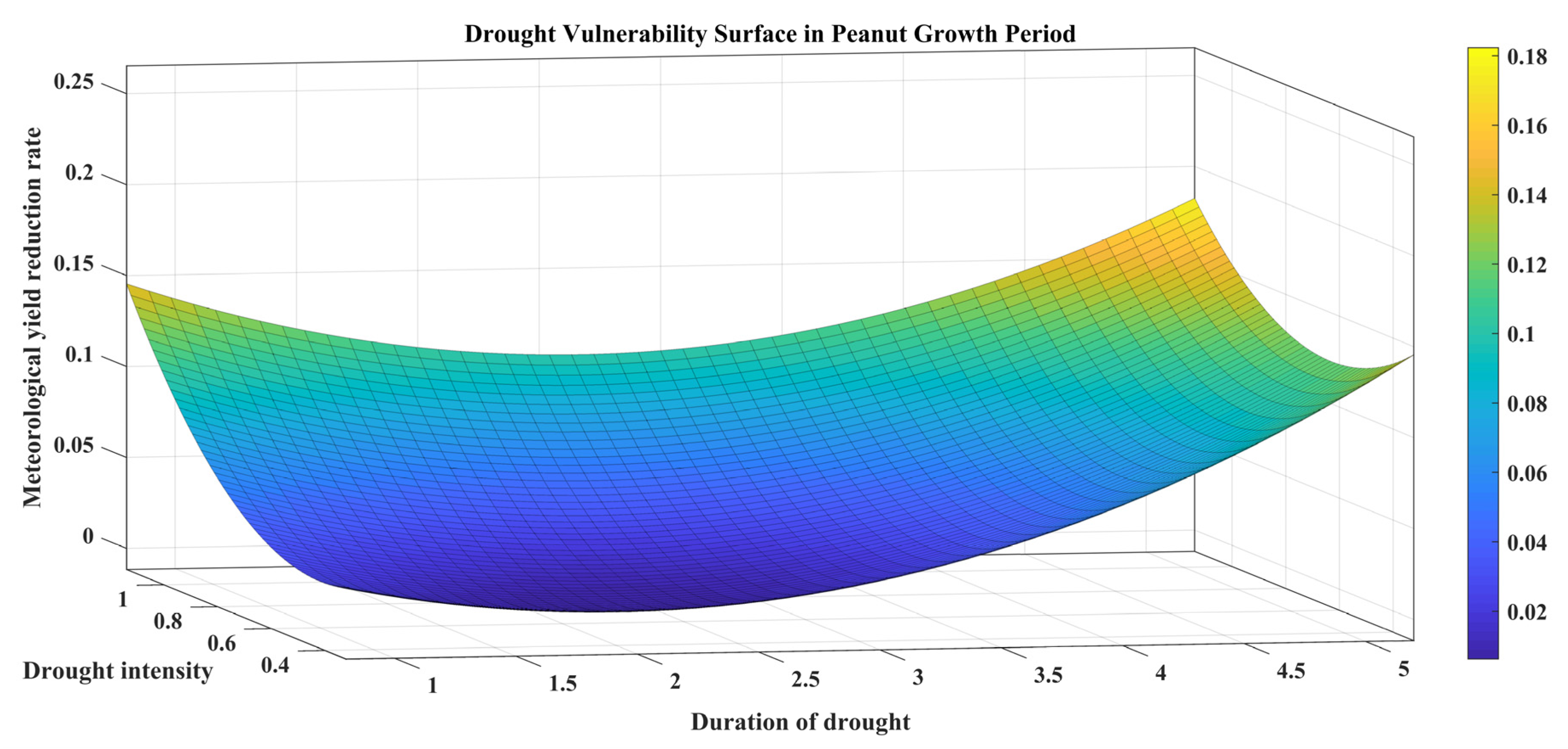
4.4. Vulnerability Surface Analysis
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Schmidhuber, J.; Tubiello, F.N. Global food security under climate change. Proc. Natl. Acad. Sci. USA 2007, 104, 19703–19708. [Google Scholar] [CrossRef] [PubMed]
- Raupach, M.R.; Marland, G.; Ciais, P.; Le Quéré, C.; Canadell, J.G.; Klepper, G.; Field, C.B. Global and regional drivers of accelerating CO2 emissions. Proc. Natl. Acad. Sci. USA 2007, 104, 10288–10293. [Google Scholar] [CrossRef] [PubMed]
- Ye, L.M.; Xiong, W.; Li, Z.G.; Yang, P.; Wu, W.B.; Yang, G.X.; Fu, Y.J.; Zou, J.Q.; Chen, Z.X.; Van Ranst, E.; et al. Climate change impact on China food security in 2050. Agron. Sustain. Dev. 2013, 33, 363–374. [Google Scholar] [CrossRef]
- Tollefson, J. IPCC climate report: Earth is warmer than it’s been in 125,000 years. Nature 2021, 596, 171–172. [Google Scholar] [CrossRef]
- Paparrizos, S.; Matzarakis, A. Assessment of future climate change impacts on the hydrological regime of selected Greek areas with different climate conditions. Hydrol. Res. 2017, 48, 1327–1342. [Google Scholar] [CrossRef]
- Wang, Y.J.; Zhou, B.T.; Qin, D.H.; Wu, J.; Gao, R.; Song, L.C. Changes in mean and extreme temperature and precipitation over the arid region of Northwestern China: Observation and projection. Adv. Atmos. Sci. 2017, 34, 289–305. [Google Scholar] [CrossRef]
- Tigkas, D.; Vangelis, H.; Tsakiris, G. Drought characterisation based on an agriculture-oriented standardised precipitation index. Theor. Appl. Climator. 2019, 135, 1435–1447. [Google Scholar] [CrossRef]
- Van Loon, A.F. Hydrological drought explained. Wires. Water 2015, 2, 359–392. [Google Scholar] [CrossRef]
- Wilhite, D.A.; Glantz, M.H. Understanding: The drought phenomenon: The role of definitions. Water Int. 2009, 10, 111–120. [Google Scholar] [CrossRef]
- Zhang, Y.F.; Qu, H.H.; Yang, X.G.; Wang, M.H.; Qin, N.S.; Zou, Y.J. Cropping system optimization for drought prevention and disaster reduction with a risk assessment model in Sichuan Province. Glob. Ecol. Conserv. 2020, 23, e01095. [Google Scholar] [CrossRef]
- Kolte, A.; Siggia, D.; Veer, N.B.; Daryani, A. Critical exploration of Indian economic reforms of 1991: A lesson for developing economies. Int. J. Eng. Adv. Technol. 2019, 8, 490–500. [Google Scholar] [CrossRef]
- Ma, Y.N.; Guga, S.; Xu, J.; Su, Y.L.; Liu, X.P.; Tong, Z.J.; Zhang, J.Q. Agricultural vulnerability assessment of high-temperature disaster in Shaanxi Province of China. Agriculture 2022, 12, 980. [Google Scholar] [CrossRef]
- Palmero, F.; Carcedo, A.J.P.; Haro, R.J.; Bigatton, E.D.; Salvagiotti, F.; Ciampitti, I.A. Modeling drought stress impacts under current and future climate for peanut in the semiarid pampas region of Argentina. Field Crop Res. 2022, 286, 108615. [Google Scholar] [CrossRef]
- Zhang, J.X.; Wang, Q.Q.; Xia, G.M.; Wu, Q.; Chi, D.C. Continuous regulated deficit irrigation enhances peanut water use efficiency and drought resistance. Agric. Water Manag. 2021, 255, 106997. [Google Scholar] [CrossRef]
- He, S.N.; Chen, Y.; Xiang, W.; Chen, X.Y.; Wang, X.L.; Chen, Y. Carbon and nitrogen footprints accounting of peanut and peanut oil production in China. J. Clean. Prod. 2021, 291, 125964. [Google Scholar] [CrossRef]
- Aninbon, C.; Jogloy, S.; Vorasoot, N.; Nuchadomrong, S.; Holbrook, C.C.; Kvien, C.; Patanothai, A. Effect of Terminal Drought on Arginine Content in Peanut Genotypes with Difference in Levels of Drought Resistance. Int. J. Plant Prod. 2019, 13, 155–162. [Google Scholar] [CrossRef]
- Zhen, X.X.; Zhang, Q.; Sanz-Saez, A.; Chen, C.Y.; Dang, P.M.; Batchelor, W.D. Simulating drought tolerance of peanut varieties by maintaining photosynthesis under water deficit. Field Crop Res. 2022, 287, 108650. [Google Scholar] [CrossRef]
- Zhang, M.; Wang, L.F.; Zhang, K.; Liu, F.Z.; Wan, Y.S. Drought-induced responses of organic osmolytes and proline metabolism during pre-flowering stage in leaves of peanut (Arachis hypogaea L.). J. Integr. Agr. 2017, 16, 2197–2205. [Google Scholar] [CrossRef]
- Jiang, M.Y.; Xue, X.P.; Zhang, L.J.; Chen, Y.Y.; Zhao, C.; Song, H.Y.; Wang, N. Peanut Drought Risk Zoning in Shandong Province, China. Sustainability 2022, 14, 3322. [Google Scholar] [CrossRef]
- Njouenwet, I.; Vondou, D.A.; Dassou, E.F.; Ayugi, B.O.; Nouayou, R. Assessment of agricultural drought during crop-growing season in the Sudano-Sahelian region of Cameroon. Nat. Hazards 2021, 106, 561–577. [Google Scholar] [CrossRef]
- Zhang, M.E.; Wang, C.Y.; Song, Y.L.; Sun, S.; Wu, D.R.; Liu, R.H. Risk assessment of summer peanut drought and waterlogging disaster during growth periods in Henan Province of China. Trans. Chin. Soc. Agric. Eng. 2022, 38, 158–168. [Google Scholar]
- Wang, R.; Zhang, J.Q.; Wang, C.Y.; Guo, E.L. Characteristic Analysis of Droughts and Waterlogging Events for Maize Based on a New Comprehensive Index through Coupling of Multisource Data in Midwestern Jilin Province, China. Remote Sens. 2020, 12, 60. [Google Scholar] [CrossRef]
- Challinor, A.J.; Koehler, A.K.; Ramirez-Villegas, J.; Whitfield, S.; Das, B. Current warming will reduce yields unless maize breeding and seed systems adapt immediately. Nat. Clim. Change 2016, 6, 954–958. [Google Scholar] [CrossRef]
- Guo, H.P.; Chen, J.; Pan, C.L. Assessment on agricultural drought vulnerability and spatial heterogeneity study in China. Int. J. Environ. Res. Public Health 2021, 18, 4449. [Google Scholar] [CrossRef] [PubMed]
- Wu, D.; Yan, D.H.; Yang, G.Y.; Wang, X.G.; Xiao, W.H.; Zhang, H.T. Assessment on agricultural drought vulnerability in the Yellow River basin based on a fuzzy clustering iterative model. Nat. Hazards 2013, 67, 919–936. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, Q.; Yao, Y.B. Drought vulnerability assessment for maize in the semiarid region of northwestern China. Theor. Appl. Climator. 2020, 140, 1207–1220. [Google Scholar] [CrossRef]
- Soufizadeh, S.; Munaro, E.; McLean, G.; Massignam, A.; van Oosterom, E.J.; Chapman, S.C.; Messina, C.; Cooper, M.; Hammer, G.L. Modelling the nitrogen dynamics of maize crops-Enhancing the APSIM maize model. Eur. J. Agron. 2018, 100, 118–131. [Google Scholar] [CrossRef]
- Shrivastava, S.; Kar, S.C.; Sharma, A.R. The DSSAT model simulations of soil moisture and evapotranspiration over central India and comparison with remotely-sensed data. Model. Earth Syst. Environ. 2018, 4, 27–37. [Google Scholar] [CrossRef]
- Yue, Y.J.; Wang, L.; Li, J.; Zhu, A.X. An EPIC model-based wheat drought risk assessment using new climate scenarios in China. Clim. Change 2018, 147, 539–553. [Google Scholar] [CrossRef]
- Dong, S.N.; Pang, Z.Y.; Zhang, J.Q.; Tong, Z.J.; Liu, X.P.; Sun, Z.Y. Research on Vulnerability Curve of Drought Disaster of Maize on CERES-Maize Model in Western Jilin Province. J. Catastrophol. 2014, 29, 115–119. [Google Scholar]
- Guo, H.; Wang, R.; Garfin, G.M.; Zhang, A.Y.; Lin, D.G.; Liang, Q.O.; Wang, J.A. Rice drought risk assessment under climate change: Based on physical vulnerability a quantitative assessment method. Sci. Total Environ. 2020, 751, 141481. [Google Scholar] [CrossRef] [PubMed]
- Ming, X.D.; Xu, W.; Li, Y.; Du, J.; Liu, B.Y.; Shi, P.J. Quantitative multi-hazard risk assessment with vulnerability surface and hazard joint return period. Stoch. Environ. Res. Risk A 2014, 29, 35–44. [Google Scholar] [CrossRef]
- Wang, Y.F.; Liu, G.X.; Guo, E.L.; Yun, X.J. Quantitative Agricultural Flood Risk Assessment Using Vulnerability Surface and Copula Functions. Water 2018, 10, 1229. [Google Scholar] [CrossRef]
- Yang, Y.T.; Wei, S.C.; Li, K.W.; Zhang, J.Q.; Wang, C.Y. Drought risk assessment of millet and its dynamic evolution characteristics: A case study of Liaoning Province, China. Ecol. Indic. 2022, 143, 109407. [Google Scholar] [CrossRef]
- Li, J.Y.; Wu, C.H.; Xia, C.A.; Yeh, P.J.F.; Chen, B.; Lv, W.H.; Hu, B.X. A voxel-based three-dimensional framework for flash drought identification in space and time. J. Hydrol. 2022, 608, 127568. [Google Scholar] [CrossRef]
- Zuo, D.P.; Cai, S.Y.; Xu, Z.X.; Li, F.L.; Sun, W.C.; Yang, X.J.; Kan, G.Y.; Liu, P. Spatiotemporal patterns of drought at various time scales in Shandong Province of Eastern China. Theor. Appl. Climator. 2018, 131, 271–284. [Google Scholar] [CrossRef]
- Wei, S.C.; Li, K.W.; Yang, Y.T.; Wang, C.Y.; Liu, C.; Zhang, J.Q. Comprehensive climatic suitability evaluation of peanut in Huang-Huai-Hai region under the background of climate change. Sci. Rep. 2022, 12, 11350. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Begueria, S.; Lopez-Moreno, J.I. A multiscalar drought index sensitive to global warming: The Standardized Precipitation Evapotranspiration Index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Zuo, D.P.; Cai, S.Y.; Xu, Z.X.; Peng, D.Z.; Kan, G.Y.; Sun, W.C.; Pang, B.; Yang, H. Assessment of meteorological and agricultural droughts using in-situ observations and remote sensing data. Agric. Water Manag. 2019, 222, 125–138. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements; FAO Irrigation and Drainage Paper 56; Food and Agriculture Organization of the United Nations (FAO): Rome, Italy, 1998; Volume 300, p. D05109. [Google Scholar]
- Durdu, O.F. Application of linear stochastic models for drought forecasting in the Büyük Menderes river basin, western Turkey. Stoch. Environ. Res. Risk A 2010, 24, 1145–1162. [Google Scholar] [CrossRef]
- Spennemann, P.C.; Rivera, J.A.; Saulo, A.C.; Penalba, O.C. A Comparison of GLDAS Soil Moisture Anomalies against Standardized Precipitation Index and Multisatellite Estimations over South America. J. Hydrometeorol. 2015, 16, 158–171. [Google Scholar] [CrossRef]
- Chang, Y.J.; Zhu, D.M. Urban water security of China’s municipalities: Comparison, features and challenges. J. Hydrol. 2020, 587, 125023. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R. A novel plithogenic TOPSIS- CRITIC model for sustainable supply chain risk management. J. Clean. Prod. 2020, 247, 119586. [Google Scholar] [CrossRef]
- Chen, S.; Yao, S.B. Evaluation and dynamic prediction of ecological security from the perspective of sustainable development: A case study of Shaanxi Province, China. Environ. Sci. Pollut. R. 2022, 29, 42331–42346. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.L.; Wu, W.B.; Yang, X.G.; Yang, P.; Sun, J. Exploring drought dynamics and its impacts on maize yield in the Huang-Huai-Hai farming region of China. Clim. Change 2020, 163, 415–430. [Google Scholar] [CrossRef]
- Zhou, W.; Guan, K.Y.; Peng, B.; Wang, Z.; Fu, R.; Li, B.; Ainsworth, E.A.; DeLucia, E.; Zhao, L.; Chen, Z.L. A generic risk assessment framework to evaluate historical and future climate-induced risk for rainfed corn and soybean yield in the U.S. Midwest. Weather Clim. Extrem. 2021, 33, 100369. [Google Scholar] [CrossRef]
- Chong, K.L.; Huang, Y.F.; Koo, C.H.; Ahmed, A.N.; El-Shafie, A. Spatiotemporal variability analysis of standardized precipitation indexed droughts using wavelet transform. J. Hydrol. 2022, 605, 127299. [Google Scholar] [CrossRef]
- Nury, A.H.; Hasan, K. Analysis of drought in northwestern Bangladesh using standardized precipitation index and its relation to Southern oscillation index. Environ. Eng. Res. 2016, 21, 58–68. [Google Scholar] [CrossRef]
- Guo, Y.; Lu, X.L.; Zhang, J.Q.; Li, K.W.; Wang, R.; Rong, G.Z.; Liu, X.P.; Tong, Z.J. Joint analysis of drought and heat events during maize (Zea mays L.) growth periods using copula and cloud models: A case study of Songliao Plain. Agric. Water Manag. 2021, 259, 107238. [Google Scholar] [CrossRef]
- Zhu, X.F.; Hou, C.Y.; Xu, K.; Liu, Y. Establishment of agricultural drought loss models: A comparison of statistical methods. Ecol. Indic. 2020, 112, 106084. [Google Scholar] [CrossRef]
- Zhao, Y.; Weng, Z.H.; Chen, H.; Yang, J.W. Analysis of the evolution of drought, flood, and drought-flood abrupt alternation events under climate change using the daily SWAP Index. Water 2020, 12, 1969. [Google Scholar] [CrossRef]
- Mokhtar, A.; He, H.M.; Alsafadi, K.; Mohammed, S.; Ayantobo, O.O.; Elbeltagi, A.; Abdelwahab, O.M.M.; Zhao, H.F.; Quan, Y.; Abdo, H.G.; et al. Assessment of the effects of spatiotemporal characteristics of drought on crop yields in southwest China. Int. J. Climator. 2022, 42, 3056–3075. [Google Scholar] [CrossRef]
- Mohammed, S.; Alsafadi, K.; Enaruvbe, G.O.; Bashir, B.; Elbeltagi, A.; Szeles, A.; Alsalman, A.; Harsanyi, E. Assessing the impacts of agricultural drought (SPI/SPEI) on maize and wheat yields across Hungary. Sci. Rep. 2022, 12, 8838. [Google Scholar] [CrossRef]
- Liu, L.Z.; Yang, X.; Zhou, H.K.; Liu, S.S.; Zhou, L.; Li, X.H.; Yang, J.H.; Han, X.Y.; Wu, J.J. Evaluating the utility of solar-induced chlorophyll fluorescence for drought monitoring by comparison with NDVI derived from wheat canopy. Sci. Total Environ. 2018, 625, 1208–1217. [Google Scholar] [CrossRef] [PubMed]
- Wan, W.; Liu, Z.; Li, J.H.; Xu, J.N.; Wu, H.Q.; Xu, Z.H. Spatiotemporal patterns of maize drought stress and their effects on biomass in the Northeast and North China Plain from 2000 to 2019. Agric. Forest Meteorol. 2022, 315, 108821. [Google Scholar] [CrossRef]
- Renwick, L.L.R.; Deen, W.; Silva, L.; Gilbert, M.E.; Maxwell, T.; Bowles, T.M.; Gaudin, A.C.M. Long-term crop rotation diversification enhances maize drought resistance through soil organic matter. Environ. Res. Lett. 2021, 16, 084067. [Google Scholar] [CrossRef]
- Ma, X.Y.; He, Q.J.; Zhou, G.S. Sequence of changes in maize responding to soil water deficit and related critical thresholds. Front. Plant Sci. 2018, 9, 511. [Google Scholar] [CrossRef]
- China Meteorological Administration (CMA). China Meteorological Disaster Yearbook (2006); Meteorological Press of China: Beijing, China, 2006.
- China Meteorological Administration (CMA). China Meteorological Disaster Yearbook (2009); Meteorological Press of China: Beijing, China, 2009.
- China Meteorological Administration (CMA). China Meteorological Disaster Yearbook (2017); Meteorological Press of China: Beijing, China, 2017.
- Tian, Q.; Lu, J.Z.; Chen, X.L. A novel comprehensive agricultural drought index reflecting time lag of soil moisture to meteorology: A case study in the Yangtze River basin, China. Catena 2021, 209, 105804. [Google Scholar] [CrossRef]
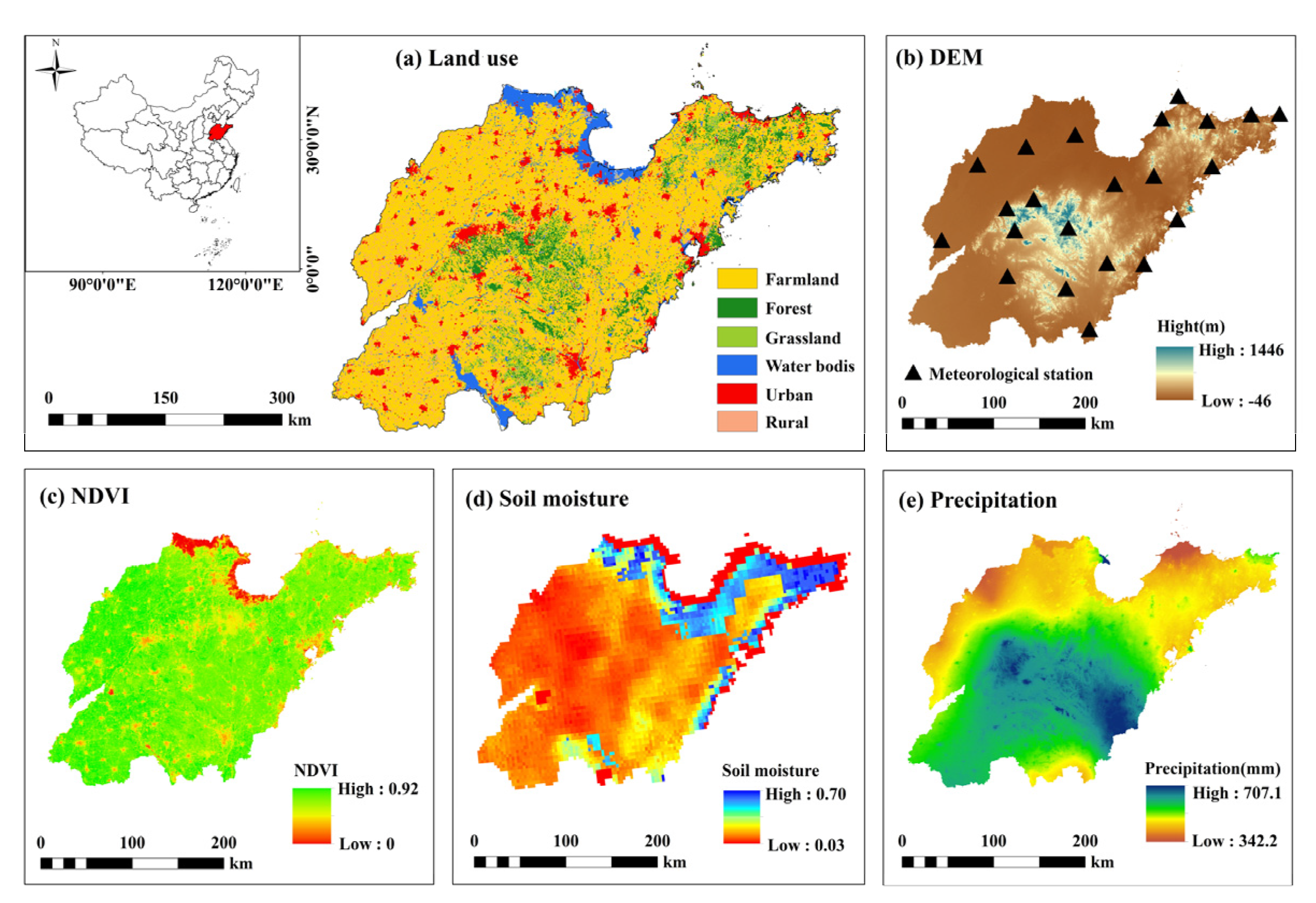

| Data Type | Data Contents | Resolution | Data Sources (1991–2020) |
|---|---|---|---|
| Daily meteorological data | Daily precipitation, Temperature, sunshine duration, wind speed and average relative humidity | 22 meteorological stations in Shandong Province | Meteorological Data Center of China Meteorological Administration (http://data.cma.cn/site/index.html, accessed on 10 May 2021) |
| Remote sensing data | Ten-day NDVI | 500 m | Computer Network Information Center International Scientific Data Mirror Website (http://www.gscloud.cn, accessed on 10 May 2021) |
| Soil data | Monthly soil moisture | 4 km × 4 km | Terra climate data sets (http://www.climatologylab.org, accessed on 10 May 2021) |
| Agricultural data | Peanut yield and sown area | Districts in Shandong Province | Institute of Meteorology, Department of Planting Management, Ministry of Agriculture, China (http://www.moa.gov.cn/, accessed on 10 May 2021) |
| Data of peanut development period | |||
| Other data | Historical disaster data | Districts in Shandong Province | Disaster Occurrence and China’s agricultural statistics |
| Basic data of research area | China Statistical Yearbook |
| Comprehensive Drought Index | Peanut Growth Period | ||
|---|---|---|---|
| Early Growth Period | Middle Growth Period | Late Growth Period | |
| Meteorological drought (SPEI) | 0.31 | 0.33 | 0.17 |
| Vegetation drought (VCI) | 0.34 | 0.32 | 0.37 |
| Soil drought (SMCI) | 0.35 | 0.35 | 0.46 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, S.; Yang, Y.; Li, K.; Guo, Y.; Zhang, J. Three-Dimensional Vulnerability Assessment of Peanut (Arachis hypogaea) Based on Comprehensive Drought Index and Vulnerability Surface: A Case Study of Shandong Province, China. Remote Sens. 2022, 14, 5359. https://doi.org/10.3390/rs14215359
Wei S, Yang Y, Li K, Guo Y, Zhang J. Three-Dimensional Vulnerability Assessment of Peanut (Arachis hypogaea) Based on Comprehensive Drought Index and Vulnerability Surface: A Case Study of Shandong Province, China. Remote Sensing. 2022; 14(21):5359. https://doi.org/10.3390/rs14215359
Chicago/Turabian StyleWei, Sicheng, Yueting Yang, Kaiwei Li, Ying Guo, and Jiquan Zhang. 2022. "Three-Dimensional Vulnerability Assessment of Peanut (Arachis hypogaea) Based on Comprehensive Drought Index and Vulnerability Surface: A Case Study of Shandong Province, China" Remote Sensing 14, no. 21: 5359. https://doi.org/10.3390/rs14215359
APA StyleWei, S., Yang, Y., Li, K., Guo, Y., & Zhang, J. (2022). Three-Dimensional Vulnerability Assessment of Peanut (Arachis hypogaea) Based on Comprehensive Drought Index and Vulnerability Surface: A Case Study of Shandong Province, China. Remote Sensing, 14(21), 5359. https://doi.org/10.3390/rs14215359






