Evaluation of Air-Cavities behind Concrete Tunnel Linings Using GPR Measurements
Abstract
1. Introduction
2. Experimental Program
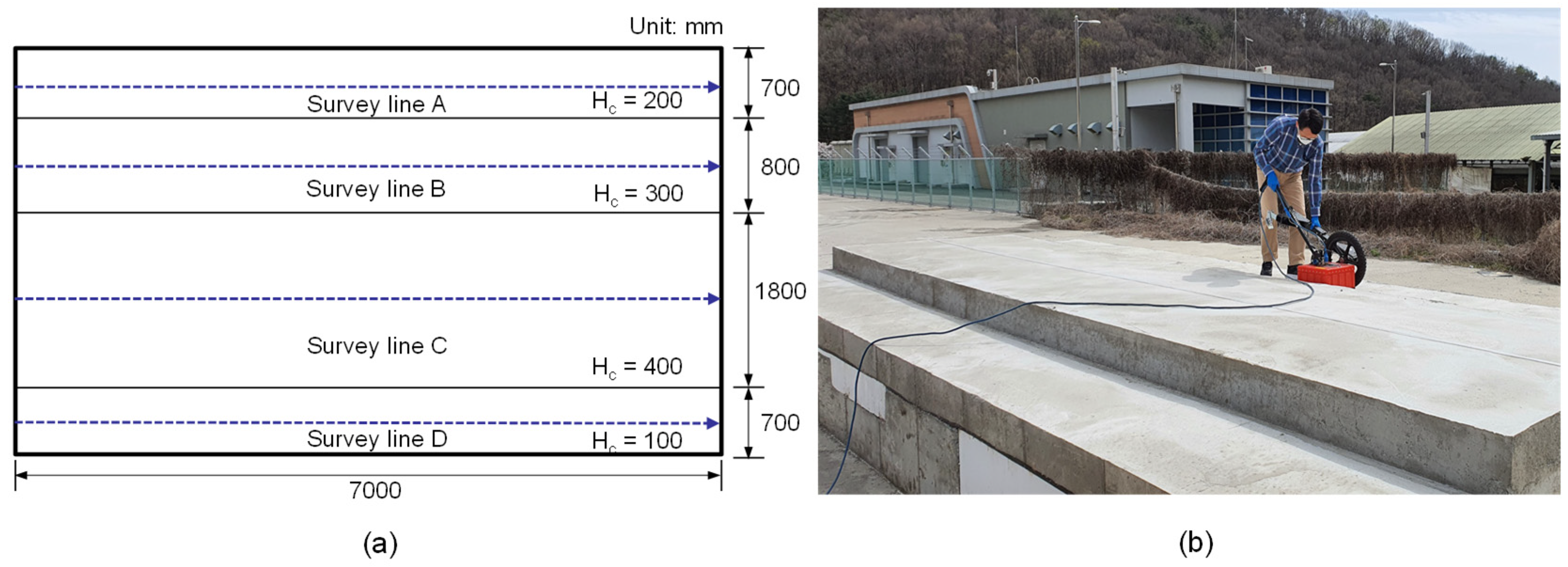
2.1. Concrete Tunnel Lining Model Spcimen
2.2. GPR Measurements
3. GPR Signal Analysis
3.1. Principle of GPR Survey for the Concrete Tunnel Lining Inspection
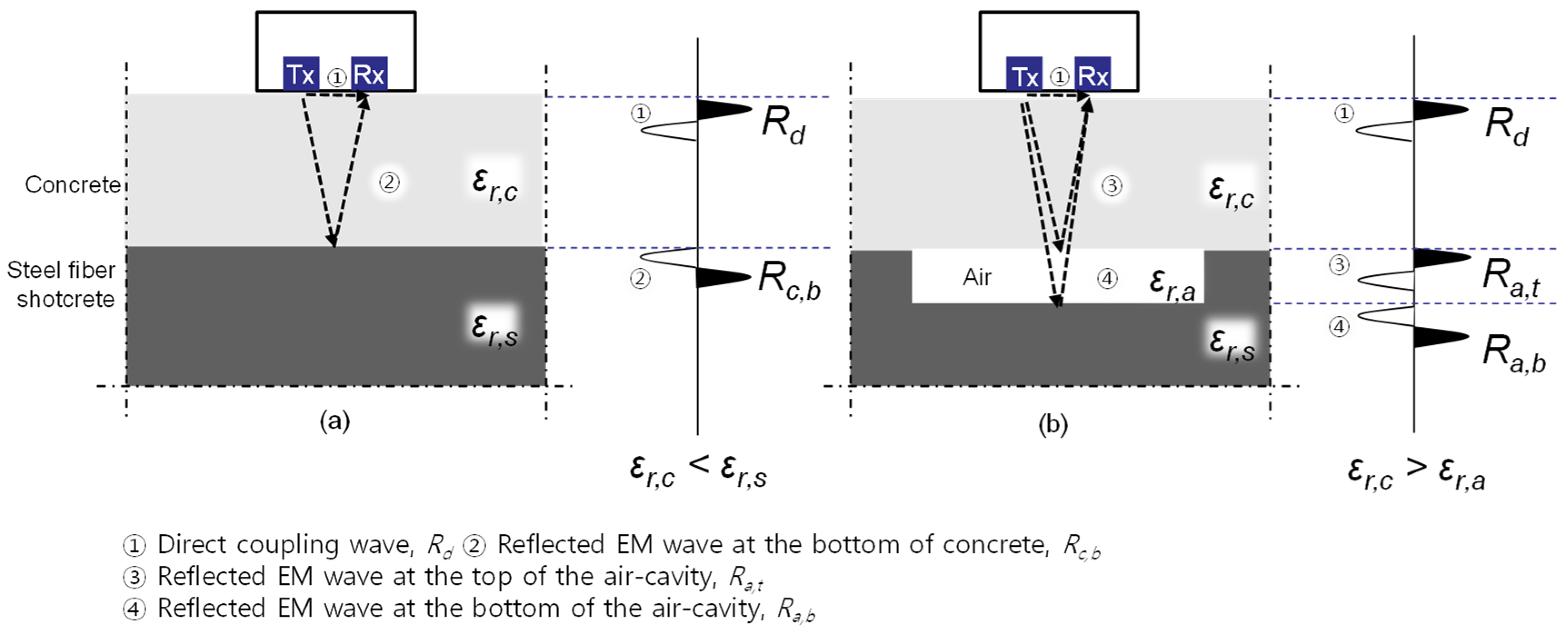
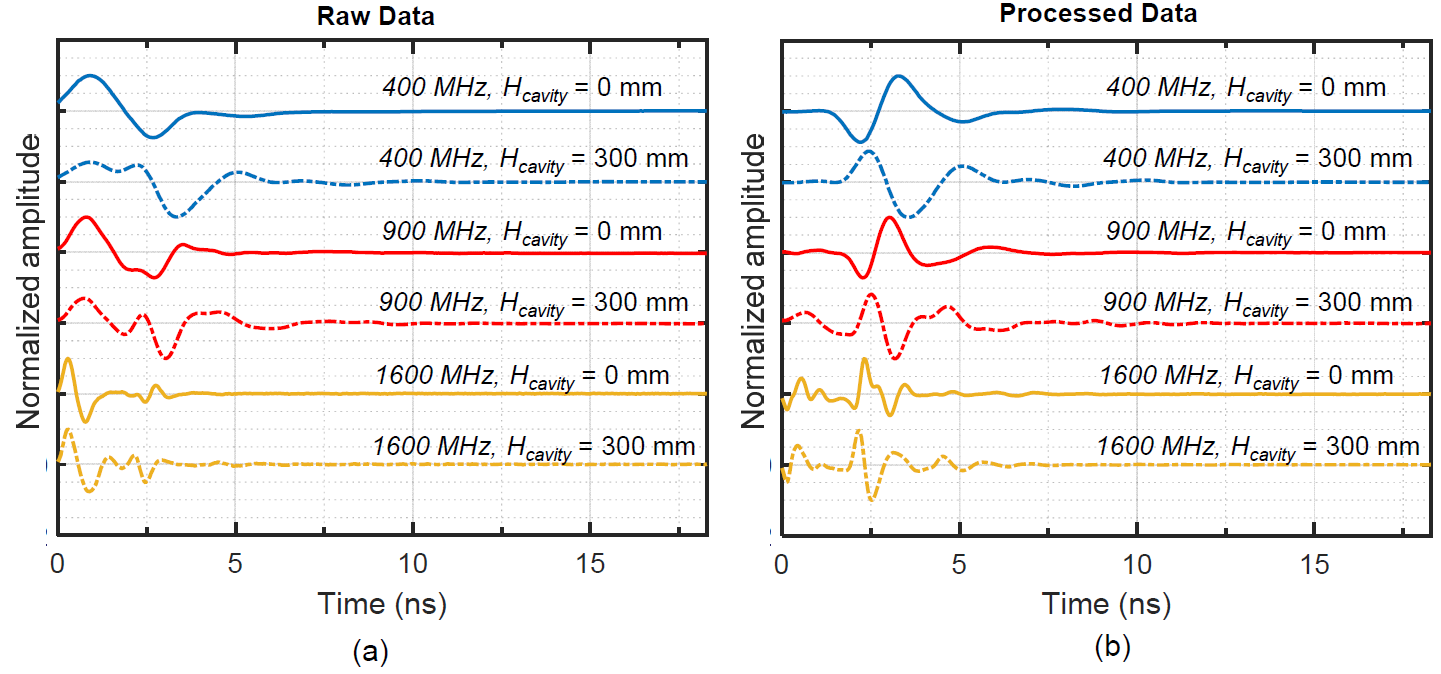
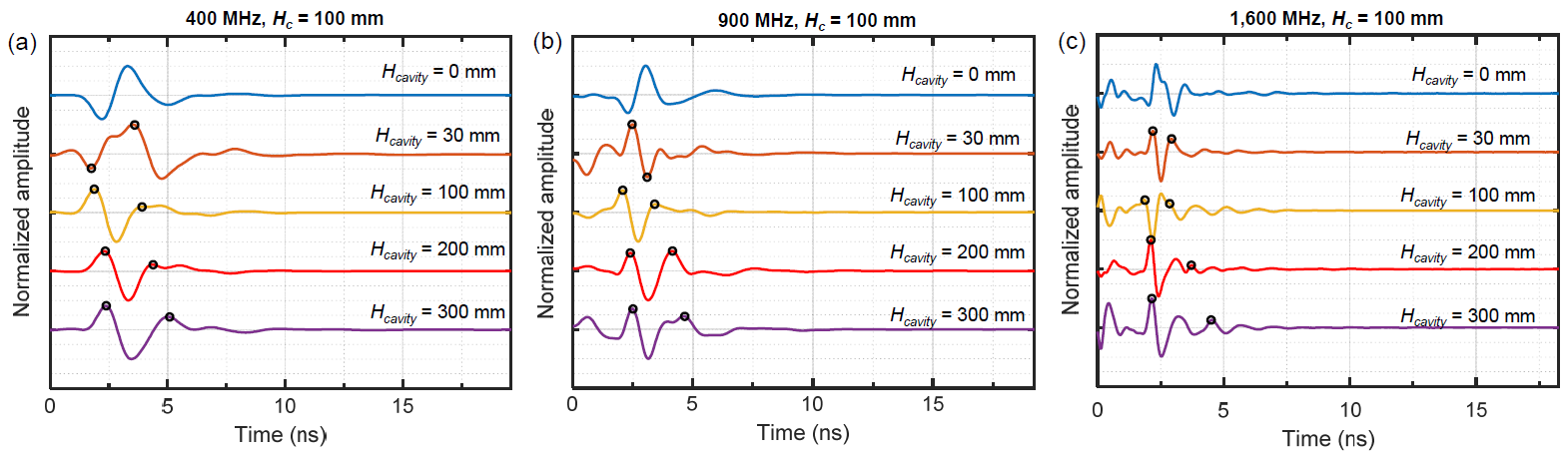
3.2. Typical GPR Signals
3.3. Detection of Air-Cavity Using Cross-Correlation Analysis
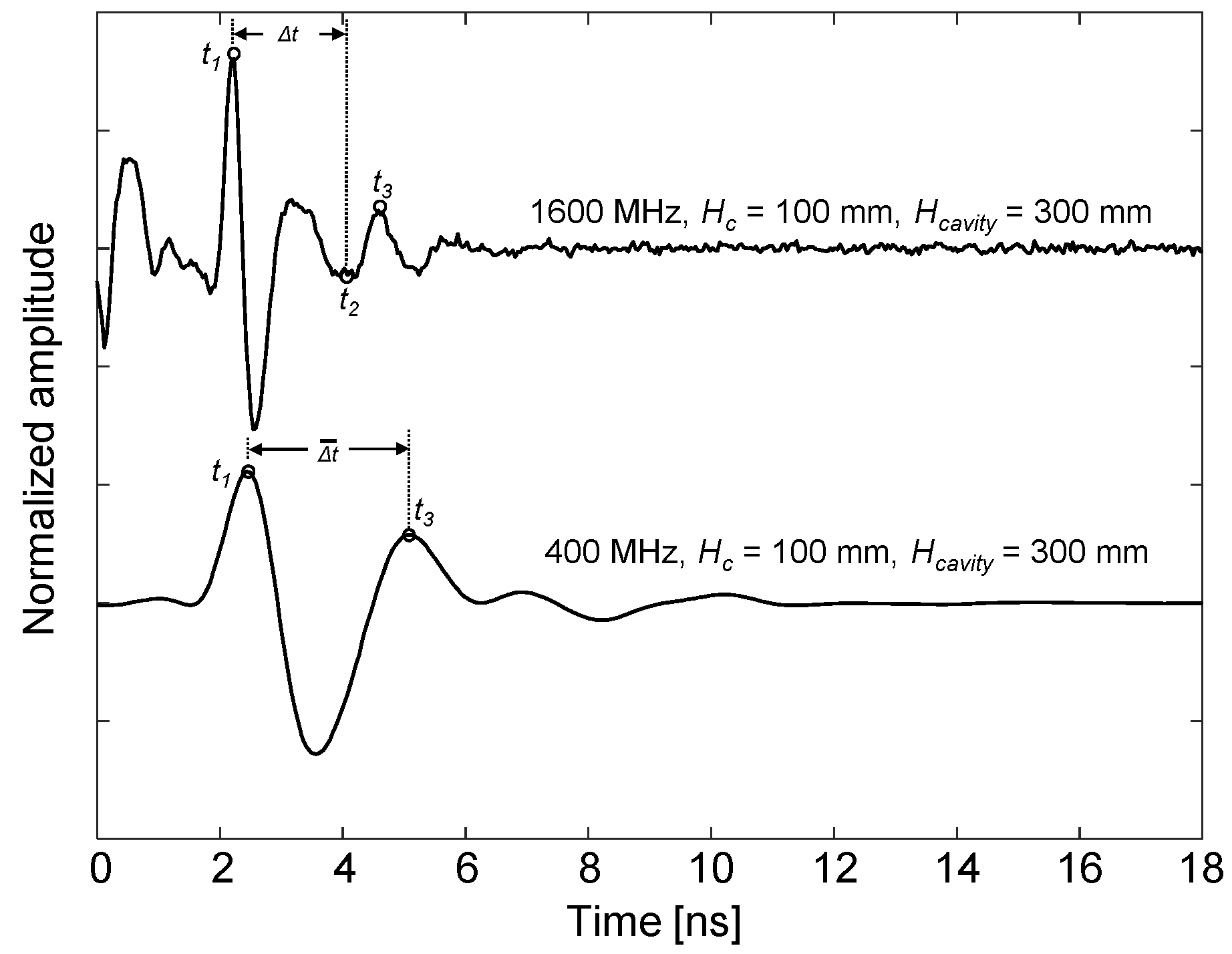
3.4. Two-Way Travel Time Method for the Thickness Evaluation of Air-Cavities
4. Results and Discussions
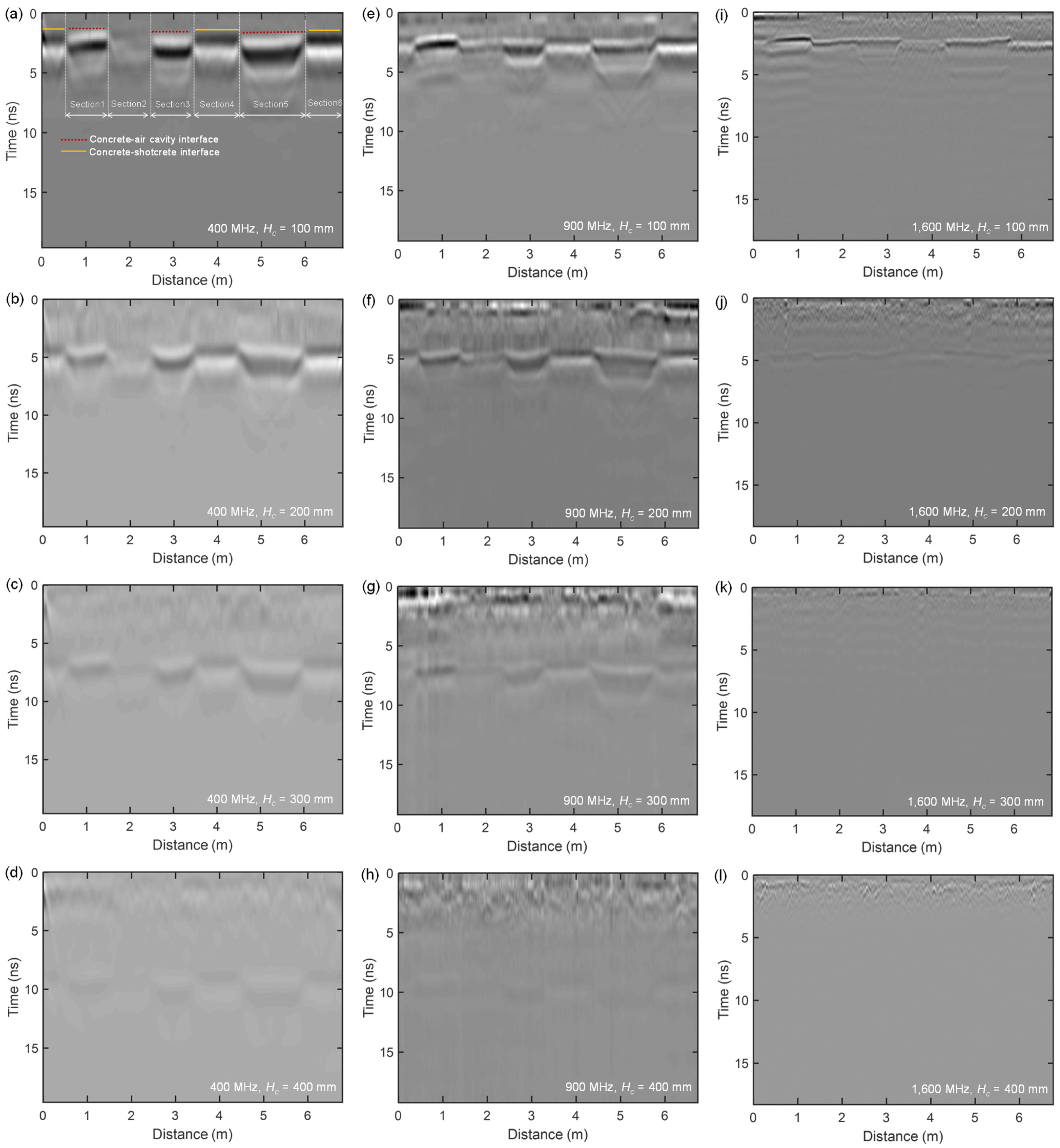
4.1. GPR Radargram
4.2. Relative Permittivity of Concrete
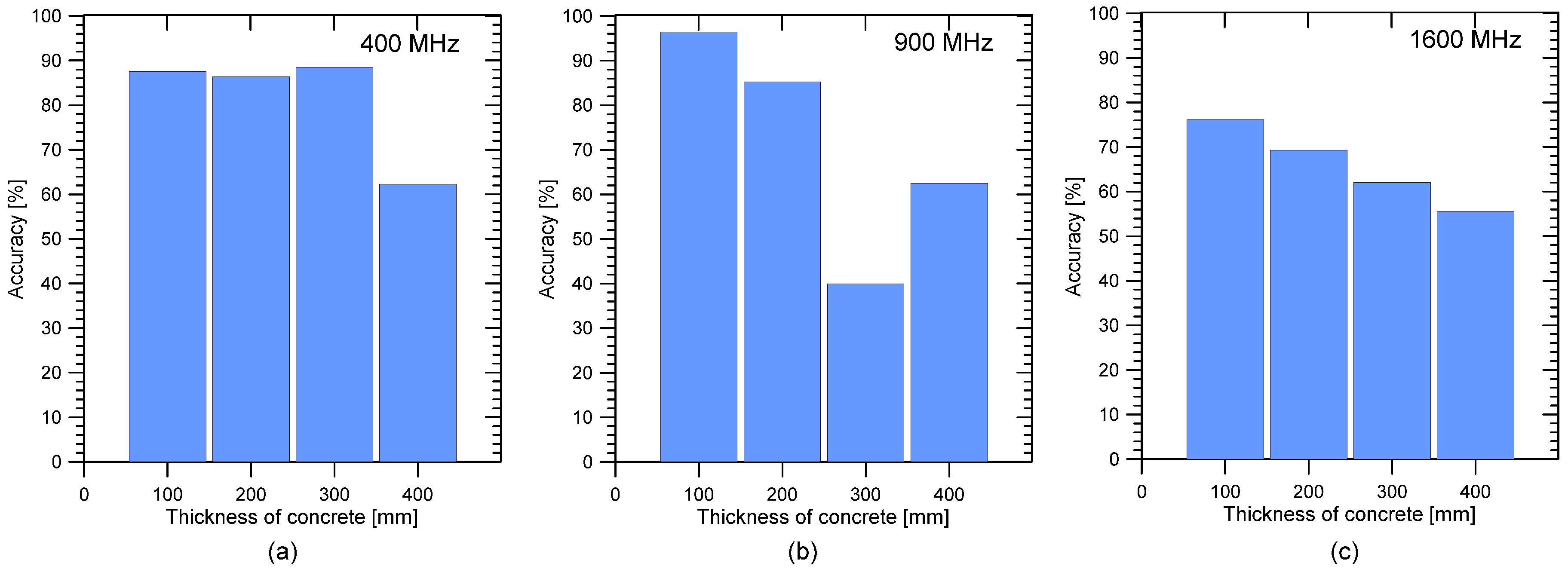
4.3. Detection of Air-Cavities behind Lining Concrete
4.4. Length of Air-Cavities behind Lining Concrete
4.5. Thickness of Air-Cavities behind Concrete
5. Conclusions
- (1)
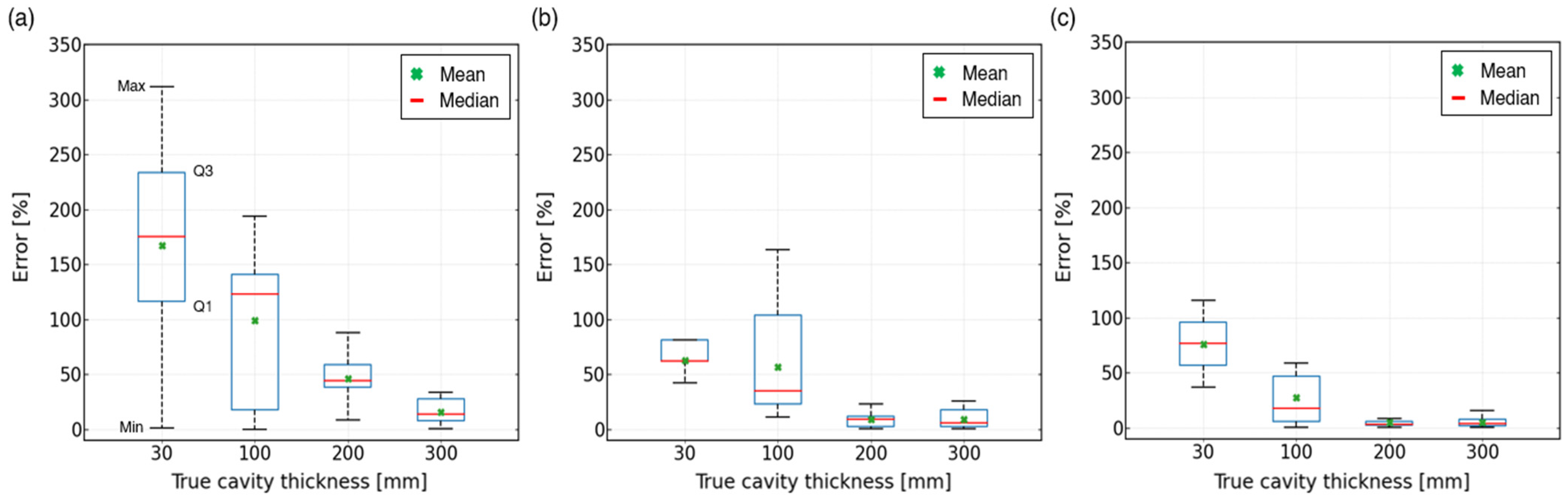
- The test regions over an air-cavity behind concrete were identified by the phase reversal of electromagnetic waves from the concrete–shotcrete (solid) and the concrete–air (defected) interfaces. In this study, a bilinear classification model based on the normalized cross-correlation coefficient of GPR signals was used to automatically identify the air-cavity regions from the solid ones (non-cavity regions), and characterize the length of the air-cavity regions. The accuracy of the classification model depends on the GPR frequency and concrete thickness.
- (2)
- The conventional two-way travel time method was effective for evaluating the thickness of concrete when the normalized thickness of air-cavities (the thickness of an air-cavity, Hcavitiy, normalized by the wavelength of primary GPR signals, λGPR) is greater than 0.5 (=Hcavitiy/λGPR ≥ 0.5). The thickness was estimated with an error within 5% for 1600 MHz data, and 10% for 900 MHz data.
- (3)
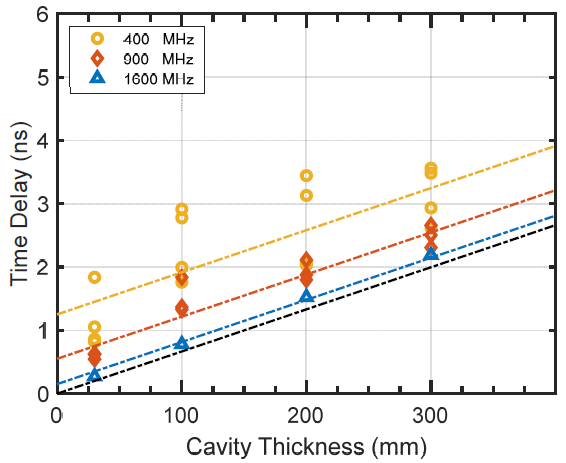
- The improved two-way travel time method, measuring the apparent time delay, , in the partially overlapped GPR waves, may not be effective as a deterministic tool for evaluating the thickness of air-cavities because of relatively great error levels, especially for relatively thin air-cavities. However, the statistical results in this study showed that the improved two-way travel time method could be effective for classifying the severity of an air-cavity according to its thickness. In this study, the use of a 900 MHz antenna led to the most promising results for the evaluation of the thickness of air-cavities after a compromise between the accuracy and penetration depth of the GPR signals.
- (4)
- The results of this study were obtained based on the GPR data on the concrete model specimen fabricated in the laboratory, with limited experimental variables (i.e., thickness of concrete, thickness of air-cavity, and GPR antenna frequency). The results in this study can provide a fundamental basis for better understanding the interference of a GPR signal with air-cavities behind concrete in tunnel structures. More studies are still needed to understand the effects of some important parameters (e.g., presence of reinforcing steel in concrete lining, types of materials filling cavities, water contents of concrete, and age of concrete) to obtain general conclusions on the use of GPR for concrete lining inspection in actual tunnel structures.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wimsatt, A.; White, J.; Leung, C.; Scullion, T.; Hurlebaus, S.; Zollinger, D.; Grasley, Z.; Nazarian, S.; Azari, H.; Yuan, D.; et al. Mapping Voids, Debonding, Delaminations, Moisture, and Other Defects Behind or Within Tunnel Linings. In SHRP 2 Report S2-R06G-RR-1; Transportation of Research Board of the National Academies: Washington, DC, USA, 2014. [Google Scholar]
- Meguid, M.A.; Dang, H.K. The effect of erosion voids on existing tunnel linings. Tunn. Undergr. Space Technol. 2009, 24, 278–286. [Google Scholar] [CrossRef]
- Lalagüe, A.; Lebens, M.A.; Hoff, I.; Grøv, E. Detection of Rockfall on a Tunnel Concrete Lining with Ground-Penetrating Radar (GPR). Rock Mech. Rock Eng. 2016, 49, 2811–2823. [Google Scholar] [CrossRef]
- Chiu, Y.-C.; Lee, C.-H.; Wang, T.-T. Lining crack evolution of an operational tunnel influenced by slope instability. Tunn. Undergr. Space Technol. 2017, 65, 167–178. [Google Scholar] [CrossRef]
- Li, C.; Li, M.-J.; Zhao, Y.-G.; Liu, H.; Wan, Z.; Xu, J.-C.; Xu, X.-P.; Chen, Y.; Wang, B. Layer recognition and thickness evaluation of tunnel lining based on ground penetrating radar measurements. J. Appl. Geophys. 2011, 73, 45–48. [Google Scholar] [CrossRef]
- Choo, J.H.; Yoo, C.K.; Oh, Y.C.; Lee, I.M. Assessment of NATM tunnel lining thickness and its behind state utilizing GPR survey. J. Korean Tunn. Undergr. Space Assoc. 2019, 21, 717–733. [Google Scholar]
- Zan, Y.; Li, Z.; Su, G.; Zhang, X. An innovative vehicle-mounted GPR technique for fast and efficient monitoring of tunnel lining structural conditions. Case Stud. Nondestruct. Test. Eval. 2016, 6, 63–69. [Google Scholar] [CrossRef]
- Parkinson, G.; Berger, K. Ground Penetrating Radar Evaluation of Concrete Tunnel Linings. In Proceedings of the 12th International Conference on Ground Penetrating Radar, Birmingham, UK, 16–19 June 2008. [Google Scholar]
- Kim, S.-I.; Chae, D.H.; Park, J.P.; Park, Y.J.; Song, C.H.; Kim, C.Y.; Lee, S.J. Applicability of ground penetrating radar antenna fre quency of tunnel lining structure. In Proceedings of the 2017 Spring Conference and Annual Meeting of the Korea Society for Railway, Daegu, Korea, 26–28 April 2017. [Google Scholar]
- Xiang, L.; Zhou, H.-L.; Shu, Z.; Tan, S.-H.; Liang, G.-Q.; Zhu, J. GPR evaluation of the Damaoshan highway tunnel: A case study. NDT E Int. 2013, 59, 68–76. [Google Scholar] [CrossRef]
- Cardarelli, E.; Marrone, C.; Orlando, L. Evaluation of tunnel stability using integrated geophysical methods. J. Appl. Geophys. 2003, 52, 93–102. [Google Scholar] [CrossRef]
- Zhang, F.; Xie, X.; Huang, H.-W. Application of ground penetrating radar in grouting evaluation for shield tunnel construction. Tunn. Undergr. Space Technol. 2010, 25, 99–107. [Google Scholar] [CrossRef]
- Davis, A.G.; Lim, M.K.; Petersen, C.G. Rapid and economical evaluation of concrete tunnel linings with impulse response and impulse radar non-destructive methods. NDT E Int. 2005, 38, 181–186. [Google Scholar] [CrossRef]
- Maekawa, S.; Fenner, T.J. Study of Cavity Depth Estimation behind Concrete Tunnel Lining Using GPR. In Proceedings of the Fifth International Conferention on Ground Penetrating, Kitchener, Canada, 12–16 June 1994; European Association of Geoscientists & Engineers: Kitchner, ON, USA, 1994. [Google Scholar]
- Rhim, H.C.; Lee, S.J.; Woo, S.K.; Song, Y.C. Detection of Delamination inside Concrete Using Ground Penetrating Radar. J. Korea Inst. Struct. Maint. Insp. 2003, 7, 177–184. [Google Scholar]
- Park, S.-K. An Experimental Study on Estimation of Size and Thickness of Cavitation(Void)s under Concrete Slabs and Tunnel Linings Using Law Frequency Type Radar (GPR). Korea Inst. Struct. Maint. Insp. 2006, 10, 95–104. [Google Scholar]
- Al-Qadi, I.L.; Lahouar, S. Measuring layer thicknesses with GPR—Theory to practice. Constr. Build. Mater. 2005, 19, 763–772. [Google Scholar] [CrossRef]
- Zhao, S.; Shangguan, P.; Al-Qadi, I.L. Application of regularized deconvolution technique for predicting pavement thin layer thicknesses from ground penetrating radar data. NDT E Int. 2015, 73, 1–7. [Google Scholar] [CrossRef]
- Liu, H.; Deng, Z.; Han, F.; Xia, Y.; Liu, Q.H.; Sato, M. Time-frequency analysis of air-coupled GPR data for identification of delamination between pavement layers. Constr. Build. Mater. 2017, 154, 1207–1215. [Google Scholar] [CrossRef]
- Dinh, K.; Gucunski, N. Factors affecting the detectability of concrete delamination in GPR images. Constr. Build. Mater. 2021, 274, 121837. [Google Scholar] [CrossRef]
- Takayama, J.-Y.; Ohara, Y.; Sun, W. Nondestructive evaluation of air voids in concrete structures using microwave radar technique. SCIE J. Control Meas. Syst. Integr. 2022, 15, 36–47. [Google Scholar] [CrossRef]
- Le Bastard, C.; Baltazart, V.; Dérobert, X.; Wang, Y. Support vector regression method applied to thin pavement thickness estimation by GPR. In Proceedings of the 14th International Conference on Ground Penetrating Radar (GPR 2012), Shanghai, China, 4–8 June 2012; IEEE: New York, NY, USA, 2012; pp. 349–353. [Google Scholar]
- Ministry of Land, Infrastructure, Transport and Tourism. Standard Specification of Tunnel; Ministry of Land, Infrastructure, Transport and Tourism: Sejong City, Korea, 2015.
- Rhim, H.C.; Buyukozturk, O. Electromagnetic Properties of Concrete at Microwave Frequency Range. ACI Mater. J. 1998, 95, 262–271. [Google Scholar]
- Rhee, J.Y.; Kee, S.-H.; Kim, H.-S.; Choi, J.-J. Seasonal Variation and Age-related Changes in the Relative Permittivity of Concrete Bridge Decks on Korea Expressways. Int. J. Concr. Struct. Mater. 2018, 12, 2. [Google Scholar] [CrossRef]
- Tzanis, A. MATGPR Release 2: A freeware MATLAB® package for the analysis & interpretation of common and single offset GPR data. FastTIMES 2010, 15, 17–43. [Google Scholar]
- Yelf, R. Where is true time zero? In Proceedings of the Tenth International Conference on Grounds Penetrating Radar 2004, GPR 2004, Delft, The Netherlands, 21–24 June 2004. [Google Scholar]
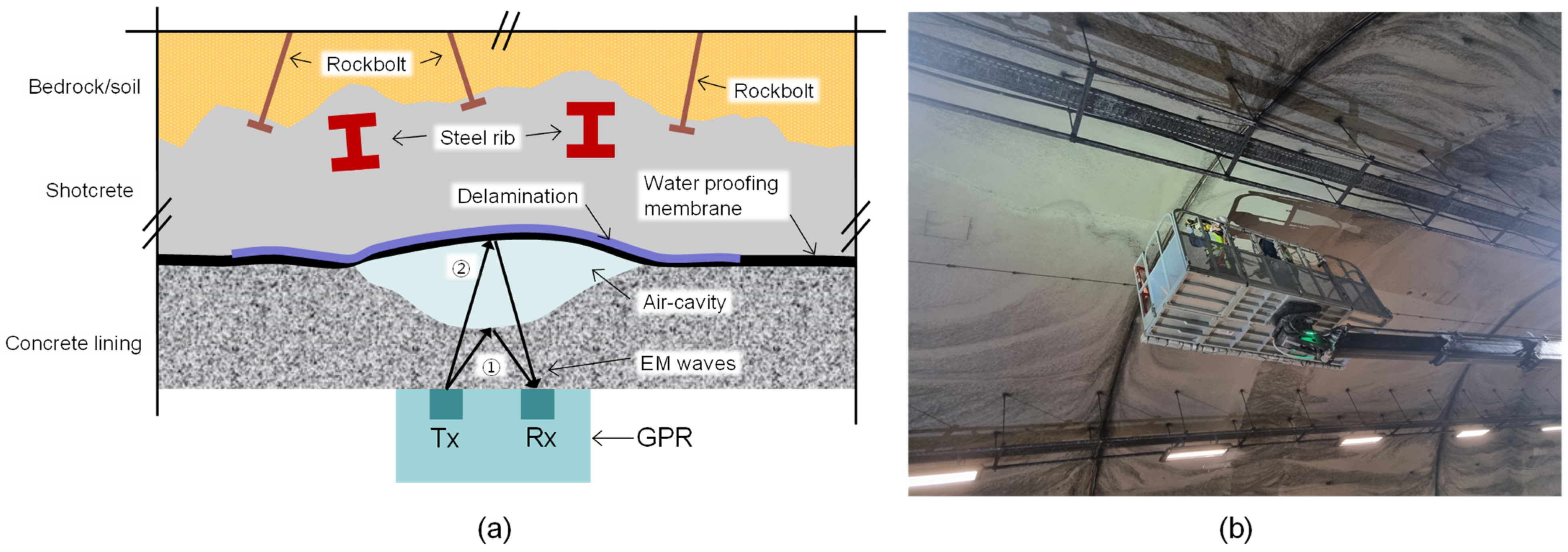




| Researchers | Target of GPR Survey | GPR Antenna | Tunnel | Remarks | ||
|---|---|---|---|---|---|---|
| Type | Frequency (MHz) | Type | Location | |||
| Li et al. [5] | Thickness of lining | Ground | 900 | Actual in-situ reinforced concrete tunnel | China (Long Hai Tunnel) | The automatic recognition method was used to evaluate the thickness of the second concrete lining in the tunnel based on the phase and amplitude features of reflected wave signals. |
| Choo et al. [6] | Thickness of lining, void state behind lining | Ground | NA | Metro lines and highway tunnels (unreinforced) | Korea | Lining thickness distribution and its behind state (particularly, its void state) were analyzed using the GPR survey data, performed on three currently operating NATM tunnels in South Korea. |
| Zan et al. [7] | Thickness of lining | Air-coupled | 300 | Metro lines | China | A vehicle-mounted GPR system was used to evaluate an entire railway line (integrity, deformation, conditions of the rock, steel arches inside the lining, and the surface conditions). |
| Parkingson and Ekes [8] | Condition of lining | Ground | 1000 | Water supply tunnel | Canada (Kapoor Water Supply Tunnel) | GPR was used to evaluate the condition of the tunnel concrete lining, specifically investigating water content, void spaces, embedded wood, faults, and metallic objects. |
| Kim et al. [9] | Condition of lining | Ground | 400, 900, 1600 | Metro lines | Korea | Three GPR antenna (400 MHz, 900 MHz, and 1600 MHz) were used to evaluate the condition of concrete lining in metro lines in Korea. |
| Xiang et al. [10] | Condition of lining | Ground | 500 | Highway tunnel | China (Damaoshan Tunnel) | GPR was used to evaluate the locations of reinforcing steel in lining, the thickness of the second lining, and the conditions of lining. The combined use of GPR and the finite difference time-domain method improved the accuracy of the GPR interpretation. |
| Cardarelli et al. [11] | Properties of rock, contact condition between lining and rock | Ground | 200, 225, 450 | Catchment tunnels of a potable water source | Italy | Three GPR antennas (200 MHz, 225 MHz, and 450 MHz) were used to evaluate the stability of tunnel structures with other geophysical methods (seismic refraction and seismic transmission method). |
| Zhang et al. [12] | Condition of the grout behind lining | Ground | 250, 500, 1000 | Metro | China | Three GPR antennas (250 MHz, 500 MHz, and 1000 MHz) were used to evaluate the overall condition of the ground behind the tunnel lining. 500 MHz antenna shows the most promising results. |
| David et al. [13] | Condition of the grout behind lining | NA | NA | Water supply tunnel | Argentina | Concrete tunnel lining was evaluated by using GPR and impulse response methods. |
| Lalagüe et al. [3] | Evaluating cavities behind linings, detecting rockfall from tunnel roof | Ground | 100 | Highway tunnel | Norway and United States | GPR was used to evaluate the air-cavities behind linings, and to detect rockfalls from the tunnel roof. |
| Maekaw and Fenner [14] | Thickness of lining and depth of air-cavity | Ground | 500, 900 | Model specimen and highway tunnel | Japan and United States | The depth of the air-cavity behind the tunnel lining was evaluated by the tunnel inspection vehicle, RAPIDAS, that is equipped with 500 MHz and 900 MHz GPR antennas. |
| Rhim et al. [15] | Detection of air-cavity behind concrete | Ground | 900, 1000, 1500 | Model specimen | Korea | Three GPR antennas (900 MHz, 1000 MHz, and 1500 MHz) were used to detect the air-cavity behind the concrete. |
| Park [16] | Thickness of air-cavity behind lining | Ground | 600 | Model specimen | Korea | The thickness of the air-cavity behind the concrete was evaluated by using the low-frequency GPR. |
| Antenna Frequency (MHz) | Concrete Thickness (mm) | Relative Permittivity of Concrete | |||||
|---|---|---|---|---|---|---|---|
| Section 1 | Section 2 | Section 3 | Section 4 | Section 5 | Section 6 | ||
| 400 | 100 | 8.75 | 8.70 | 8.50 | 8.63 | 7.28 | 8.28 |
| 200 | 8.10 | 8.45 | 9.30 | 8.46 | 9.30 | 9.30 | |
| 300 | 8.84 | 8.84 | 8.75 | 8.72 | 9.32 | 9.32 | |
| 400 | 9.30 | 9.40 | 9.47 | 8.94 | 9.49 | 8.79 | |
| 900 | 100 | 8.30 | 8.57 | 8.74 | 8.49 | 8.96 | 8.97 |
| 200 | 8.94 | 8.63 | 8.47 | 8.41 | 8.59 | 8.25 | |
| 300 | 9.08 | 8.47 | 9.66 | 8.72 | 8.12 | 8.84 | |
| 1600 | 100 | 7.94 | 8.48 | 8.71 | 8.75 | 8.10 | 9.26 |
| 200 | 8.94 | 9.35 | 8.12 | 9.35 | 9.12 | 8.94 | |
| Prediction | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Thickness of Concrete (mm) | |||||||||||
| 100 | 200 | 300 | 400 | ||||||||
| P | N | P | N | P | N | P | N | ||||
| Actual | Antenna frequency [MHz] | 400 | P | 773 (38.6%) | 0 (0.0%) | 756 (36.8%) | 17 (0.8%) | 746 (36.3%) | 27 (1.3%) | 526 (25.8%) | 227 (11.1%) |
| N | 260 (12.6%) | 1023 (49.8%) | 263 (12.8%) | 1020 (49.6%) | 209 (10.2%) | 1074 (52.2%) | 541 (26.6%) | 742 (36.4%) | |||
| Accuracy | 87.5% | 86.4% | 88.5% | 62.3% | |||||||
| 900 | P | 710 (34.7%) | 51 (2.5%) | 714 (35.2%) | 29 (1.4%) | 370 (18.1%) | 387 (19.0%) | 502 (24.8%) | 237 (11.7%) | ||
| N | 23 (1.1%) | 1260 (61.6%) | 271 (13.4%) | 1012 (50%) | 839 (41%) | 444 (21.8%) | 521 (25.8%) | 762 (37.7%) | |||
| Accuracy | 96.4% | 85.2% | 39.9% | 62.5% | |||||||
| 1600 | P | 535 (26.6%) | 194 (9.6%) | 558 (27.7%) | 171 (8.5%) | 542 (26.9%) | 187 (9.3%) | 436 (21.7%) | 293 (14.6%) | ||
| N | 286 (14.2%) | 997 (49.6%) | 446 (22.2%) | 837 (41.6%) | 575 (28.6%) | 708 (35.2%) | 603 (30.0%) | 680 (33.8%) | |||
| Accuracy | 76.1% | 69.3% | 62.1% | 55.5% | |||||||
| Antenna Frequency (MHz) | Concrete Thickness (mm) | Predicted length (mm) (error (%)) | |||||
|---|---|---|---|---|---|---|---|
| Section 1 (Cavity 1) | Section 2 (Cavity 2) | Section 3 (Cavity 3) | Section 4 (Solid 1) | Section 5 (Cavity 4) | Section 6 (Solid 2) | ||
| 400 | 100 | 1007 (1.0) | 947 (5.0) | 930 (7.0) | 1056 (5.6) | 1410 (6.0) | 914 (8.6) |
| 200 | 1036 (3.7) | 931 (8.7) | 1000 (0.0) | 1026 (2.7) | 1433 (4.4) | 920 (8.0) | |
| 300 | 1009 (1.0) | 973 (2.7) | 963 (3.7) | 1056 (5.7) | 1416 (5.6) | 916 (8.3) | |
| 400 | 1140 (14.0) | 963 (3.7) | 913 (8.7) | 1043 (4.3) | 1340 (10.7) | 876 (12.3) | |
| 900 | 100 | 1023 (2.0) | 1018 (1.9) | 924 (7.5) | 1070 (7.0) | 1433 (4.4) | 970 (3.0) |
| 200 | 1006 (0.7) | 976 (2.3) | 990 (1.0) | 980 (2.0) | 1546 (3.1) | 830 (17.0) | |
| 1600 | 100 | 1006 (0.7) | 931 (6.8) | 1104 (10.5) | 1023 (2.0) | 1419 (5.3) | 959 (4.0) |
| Statistic Parameter | Error (%) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 400 MHz | 900 MHz | 1600 MHz | ||||||||||
| 30 mm | 100 mm | 200 mm | 300 mm | 30 mm | 100 mm | 200 mm | 300 mm | 30 mm | 100 mm | 200 mm | 300 mm | |
| Maximum | 123.57 | 293.71 | 387.57 | 375.84 | 17.29 | 263.70 | 251.96 | 339.97 | 64.63 | 99.83 | 234.76 | 346.23 |
| Q3 | 100.10 | 240.90 | 317.17 | 287.84 | 11.43 | 203.56 | 210.90 | 310.63 | 58.76 | 93.96 | 211.30 | 322.76 |
| Median | 82.50 | 223.30 | 276.11 | 258.50 | 11.43 | 134.63 | 199.16 | 298.90 | 52.89 | 82.23 | 199.56 | 311.03 |
| Mean | 79.59 | 199.09 | 233.64 | 258.58 | 11.23 | 156.65 | 202.52 | 283.89 | 52.82 | 73.50 | 203.71 | 315.22 |
| Q1 | 64.90 | 117.70 | 123.57 | 217.44 | 5.56 | 122.89 | 181.56 | 246.10 | 47.03 | 52.89 | 193.70 | 305.16 |
| Minimum | 17.97 | 70.77 | 111.84 | 199.84 | 5.56 | 111.16 | 169.83 | 222.63 | 41.16 | 47.03 | 187.83 | 293.43 |
| Statistic Parameter | Error (%) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 400 MHz | 900 MHz | 1600 MHz | ||||||||||
| 30 mm | 100 mm | 200 mm | 300 mm | 30 mm | 100 mm | 200 mm | 300 mm | 30 mm | 100 mm | 200 mm | 300 mm | |
| Maximum | 311.90 | 193.71 | 87.92 | 33.39 | 81.47 | 163.70 | 23.05 | 25.79 | 115.42 | 58.49 | 8.58 | 15.41 |
| Q3 | 233.67 | 140.90 | 58.59 | 27.52 | 81.47 | 103.56 | 11.52 | 17.97 | 95.86 | 47.11 | 6.09 | 7.59 |
| Median | 175.01 | 123.30 | 43.92 | 13.83 | 61.91 | 34.63 | 9.22 | 5.50 | 76.31 | 17.77 | 3.15 | 3.68 |
| Mean | 167.07 | 99.20 | 45.90 | 15.93 | 62.73 | 56.65 | 8.84 | 8.94 | 76.07 | 27.47 | 5.20 | 5.23 |
| Q1 | 116.34 | 17.70 | 38.22 | 7.96 | 61.91 | 22.89 | 2.51 | 2.32 | 56.75 | 6.04 | 2.71 | 1.72 |
| Minimum | 1.00 | 0.10 | 8.72 | 0.14 | 42.36 | 11.16 | 0.42 | 0.37 | 37.20 | 0.17 | 0.22 | 0.23 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Harseno, R.W.; Lee, S.-J.; Kee, S.-H.; Kim, S. Evaluation of Air-Cavities behind Concrete Tunnel Linings Using GPR Measurements. Remote Sens. 2022, 14, 5348. https://doi.org/10.3390/rs14215348
Harseno RW, Lee S-J, Kee S-H, Kim S. Evaluation of Air-Cavities behind Concrete Tunnel Linings Using GPR Measurements. Remote Sensing. 2022; 14(21):5348. https://doi.org/10.3390/rs14215348
Chicago/Turabian StyleHarseno, Regidestyoko Wasistha, Sung-Jin Lee, Seong-Hoon Kee, and Sungmo Kim. 2022. "Evaluation of Air-Cavities behind Concrete Tunnel Linings Using GPR Measurements" Remote Sensing 14, no. 21: 5348. https://doi.org/10.3390/rs14215348
APA StyleHarseno, R. W., Lee, S.-J., Kee, S.-H., & Kim, S. (2022). Evaluation of Air-Cavities behind Concrete Tunnel Linings Using GPR Measurements. Remote Sensing, 14(21), 5348. https://doi.org/10.3390/rs14215348





