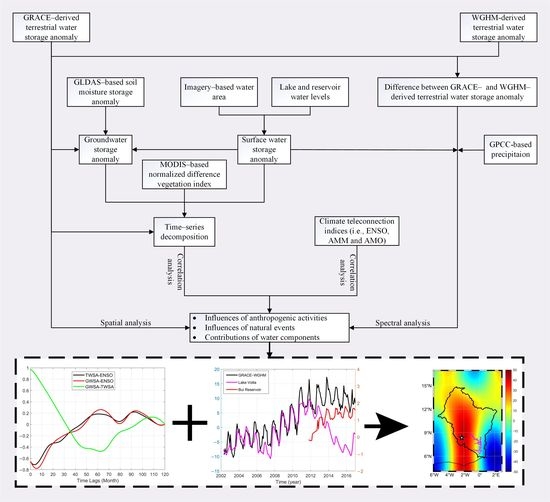
Water Storage Variation and Its Possible Causes Detected by GRACE in the Volta River Basin
Abstract
1. Introduction
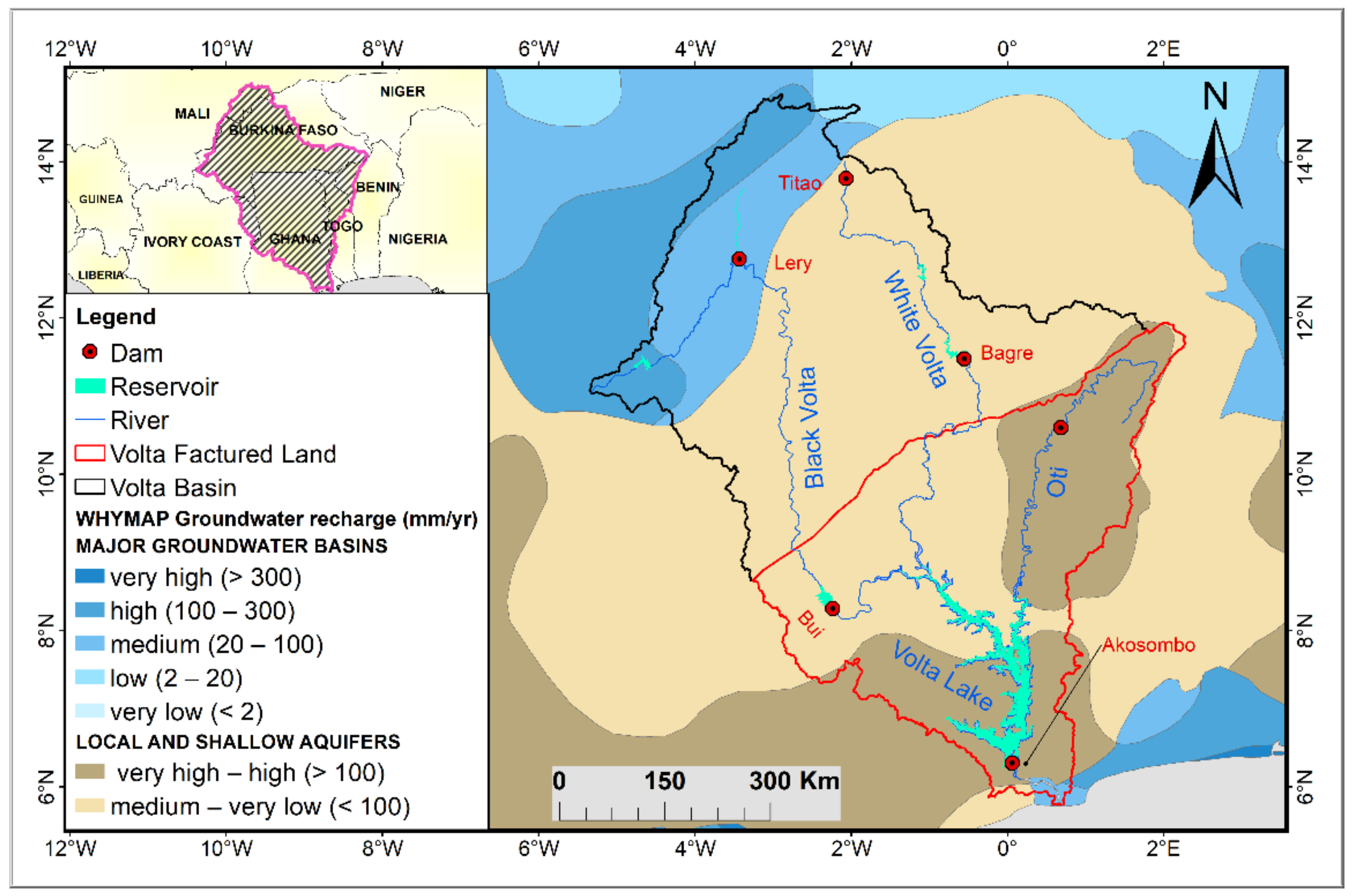
2. Study Area and Data Used Materials
2.1. The Volta River Basin
2.2. GRACE Data
2.3. TWSA from WGHM
2.4. SMSA from GLDAS
2.5. Precipitation Data, Climate Indices and Drought Index
2.6. Satellite Imagery and Altimetry
2.7. Normalized Difference Vegetation Index
3. Methods
3.1. Recovering of Lake Surface Water Storage Changes
3.2. Estimating GRACE-Derived TWSA and GWSA
3.3. The Cross Wavelet Transform Approach
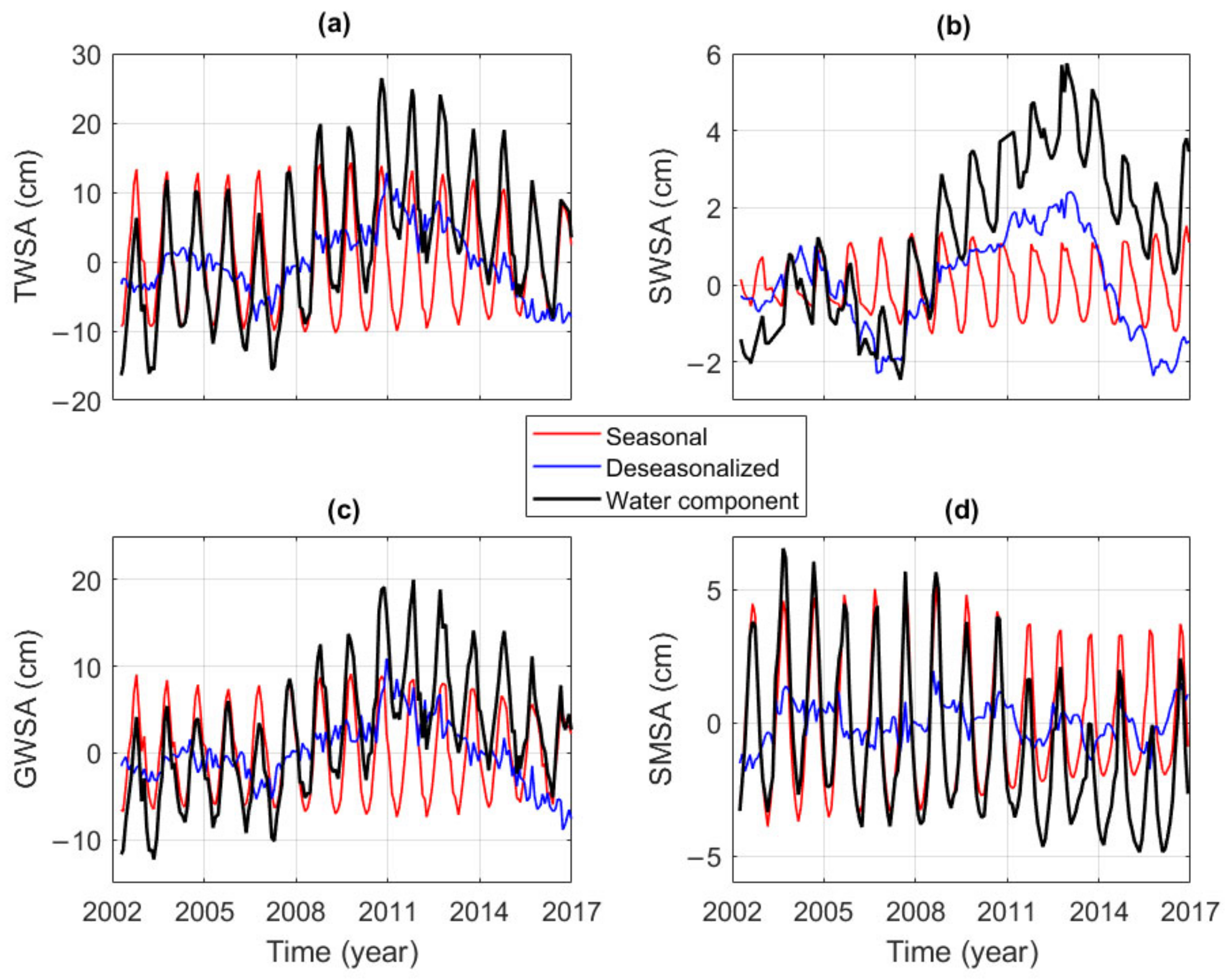
3.4. Decomposition of Time Series
4. Results
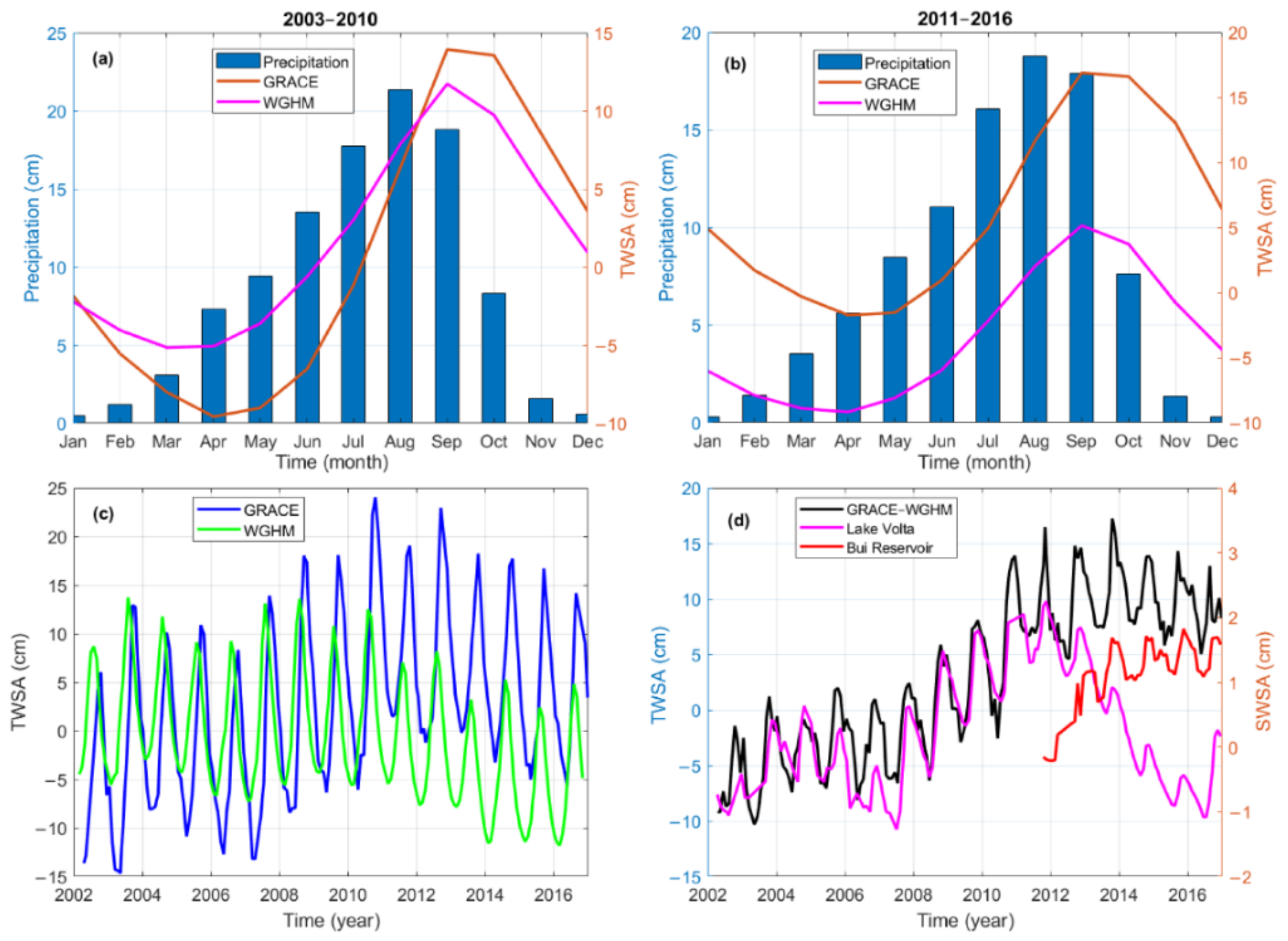
4.1. Terrestrial Water Storage Anomalies versus Changes in Precipitation
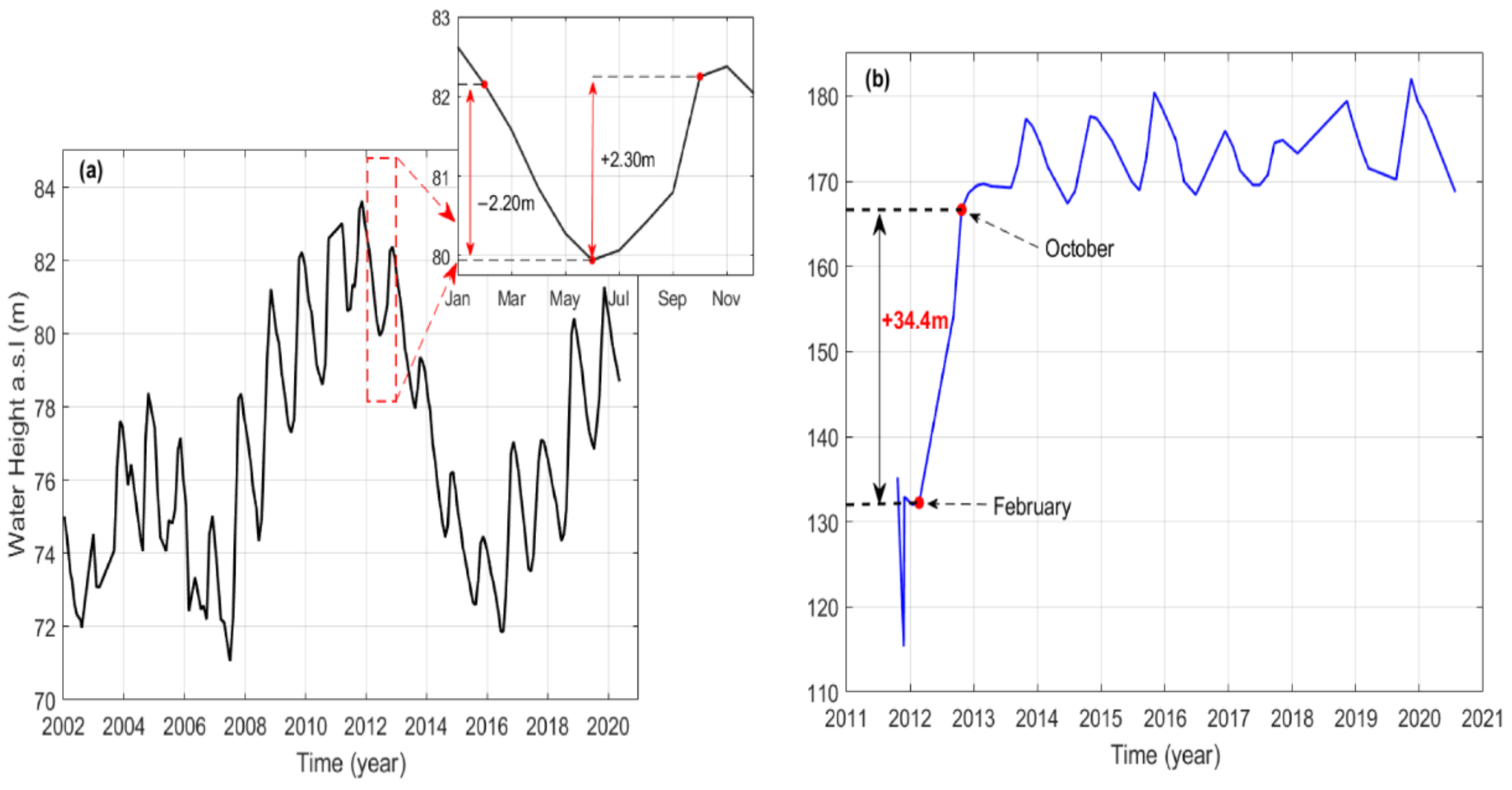
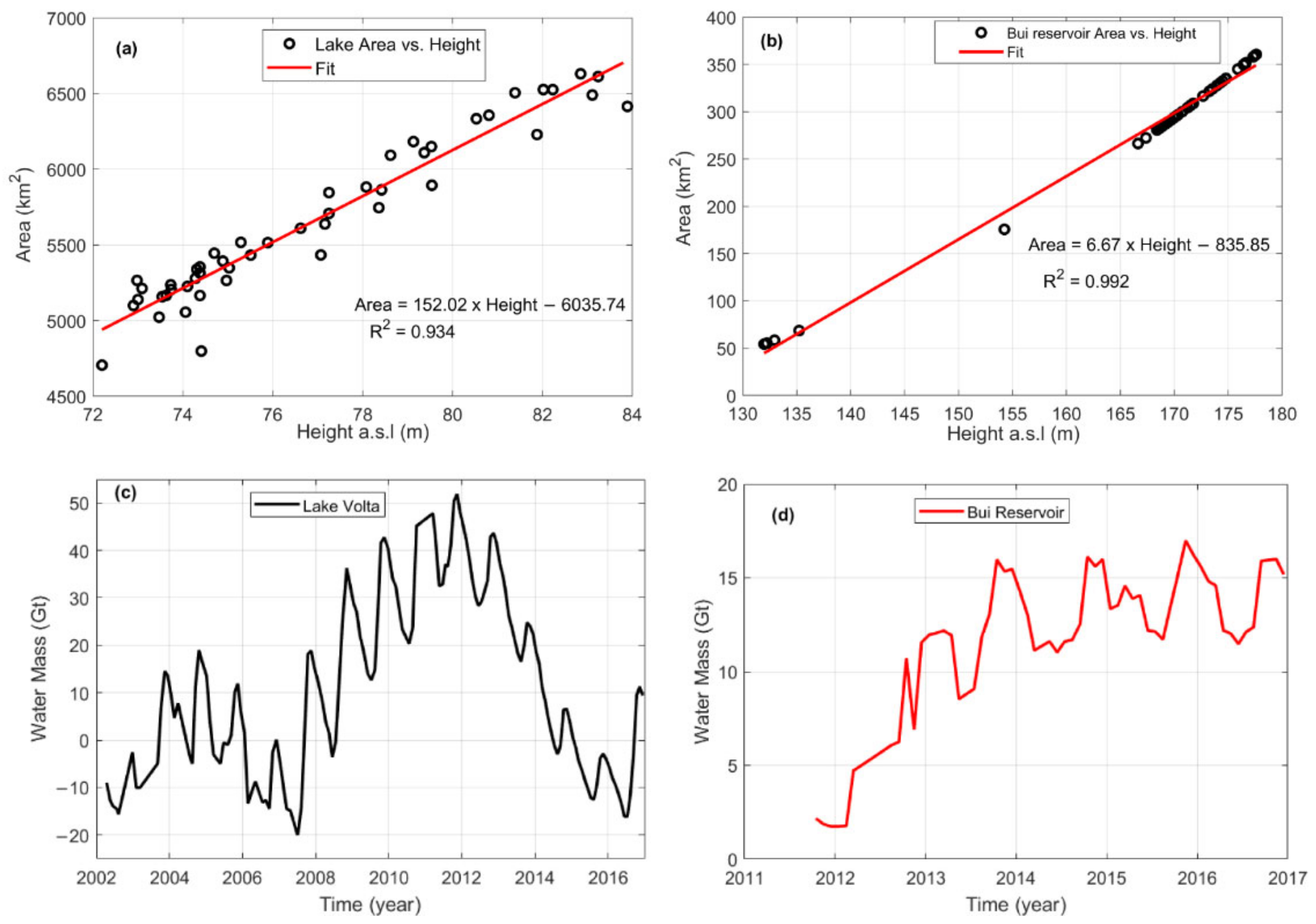
4.2. Water Mass and Level Changes in Both Lake Volta and Bui Reservoir
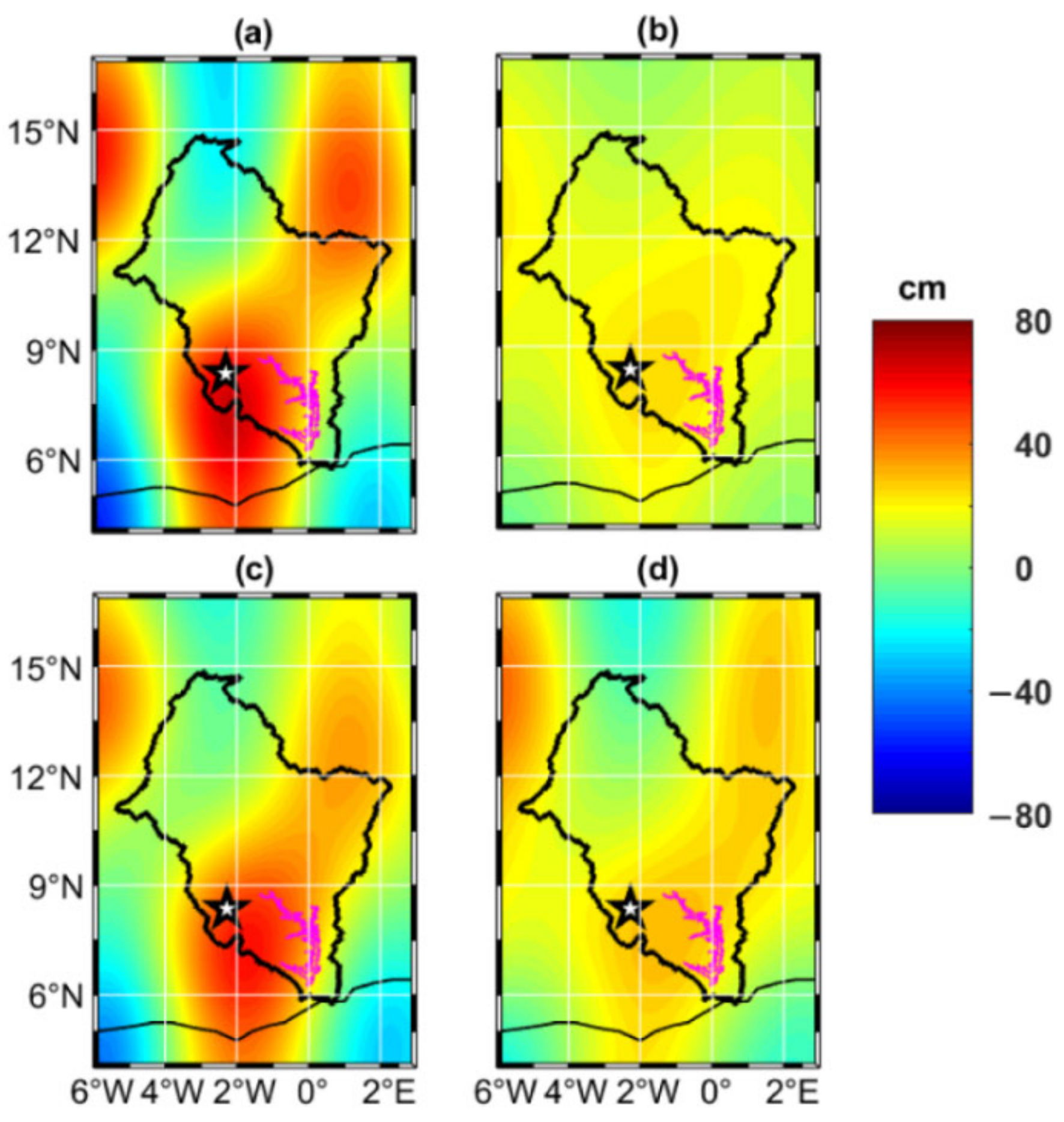
4.3. Influences of Bui Reservoir Operation on Changes in TWSAVRB in Spatial Domain
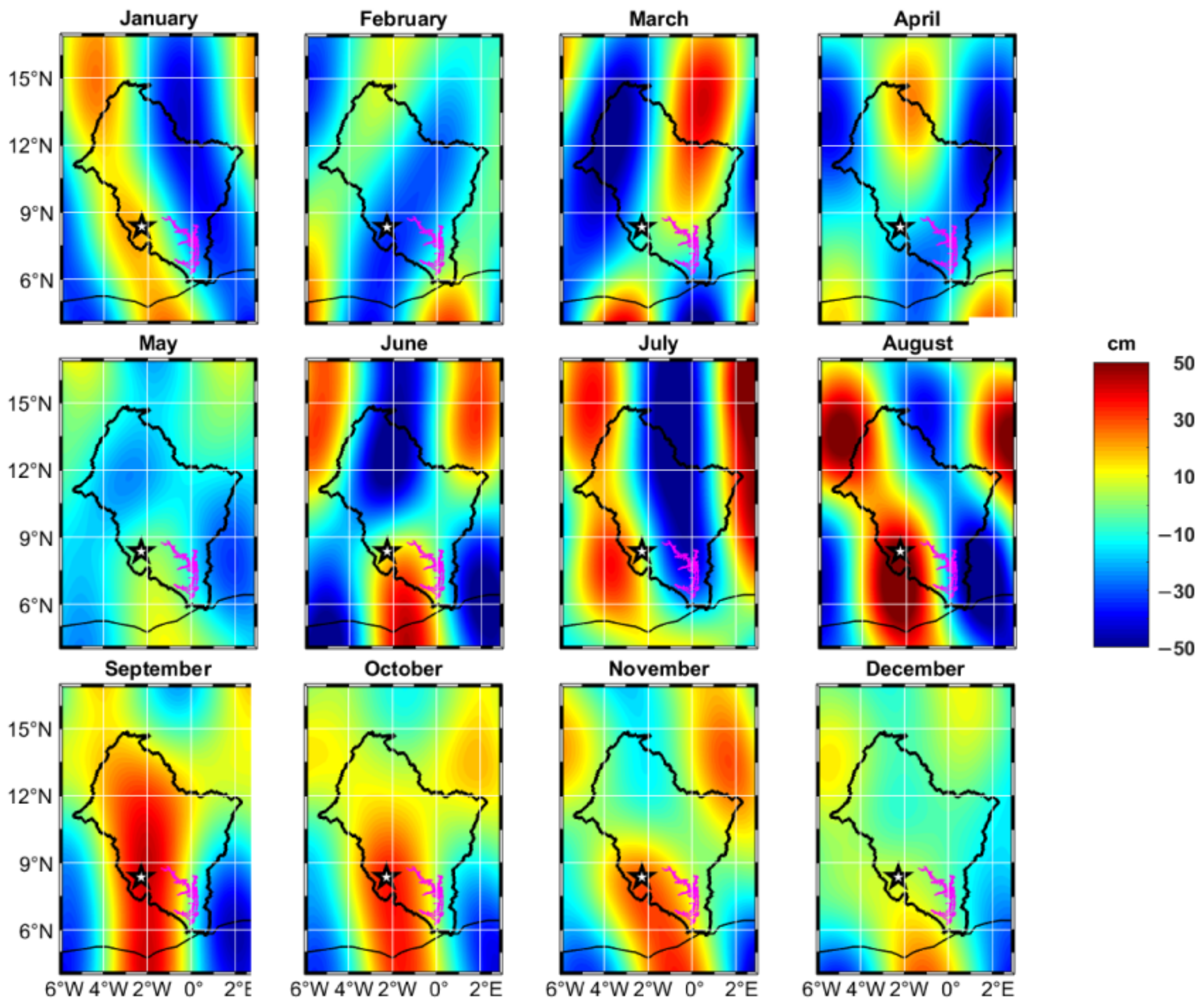
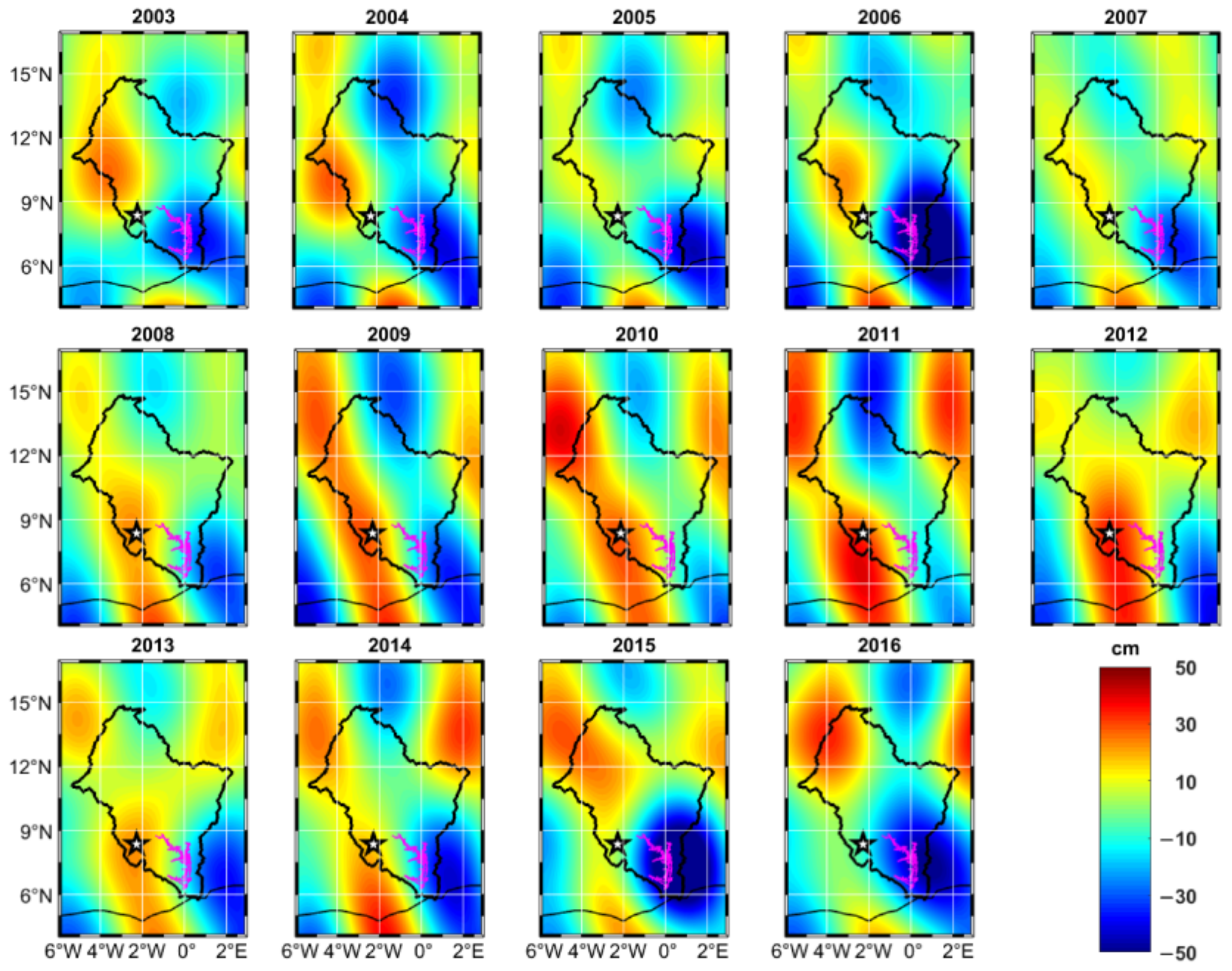
4.4. Influences of Bui Reservoir Operation on Changes in TWSAVRB Detected by GRACE in Spectral Domain
4.5. Temporal Variations of Water Storages within the Volta Fractured Land
5. Discussion
5.1. Water Storage Changes Influenced by Natural Causes
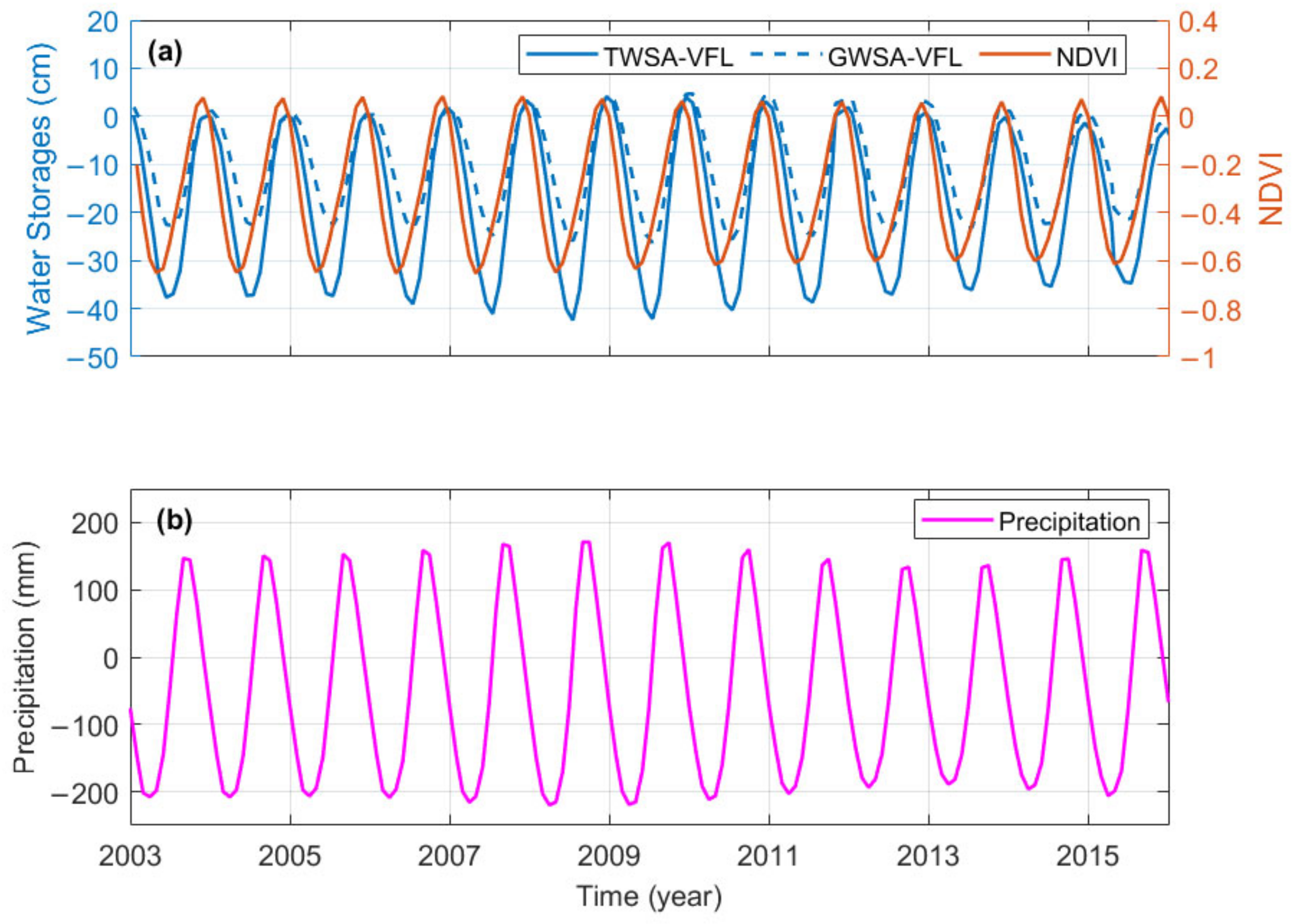
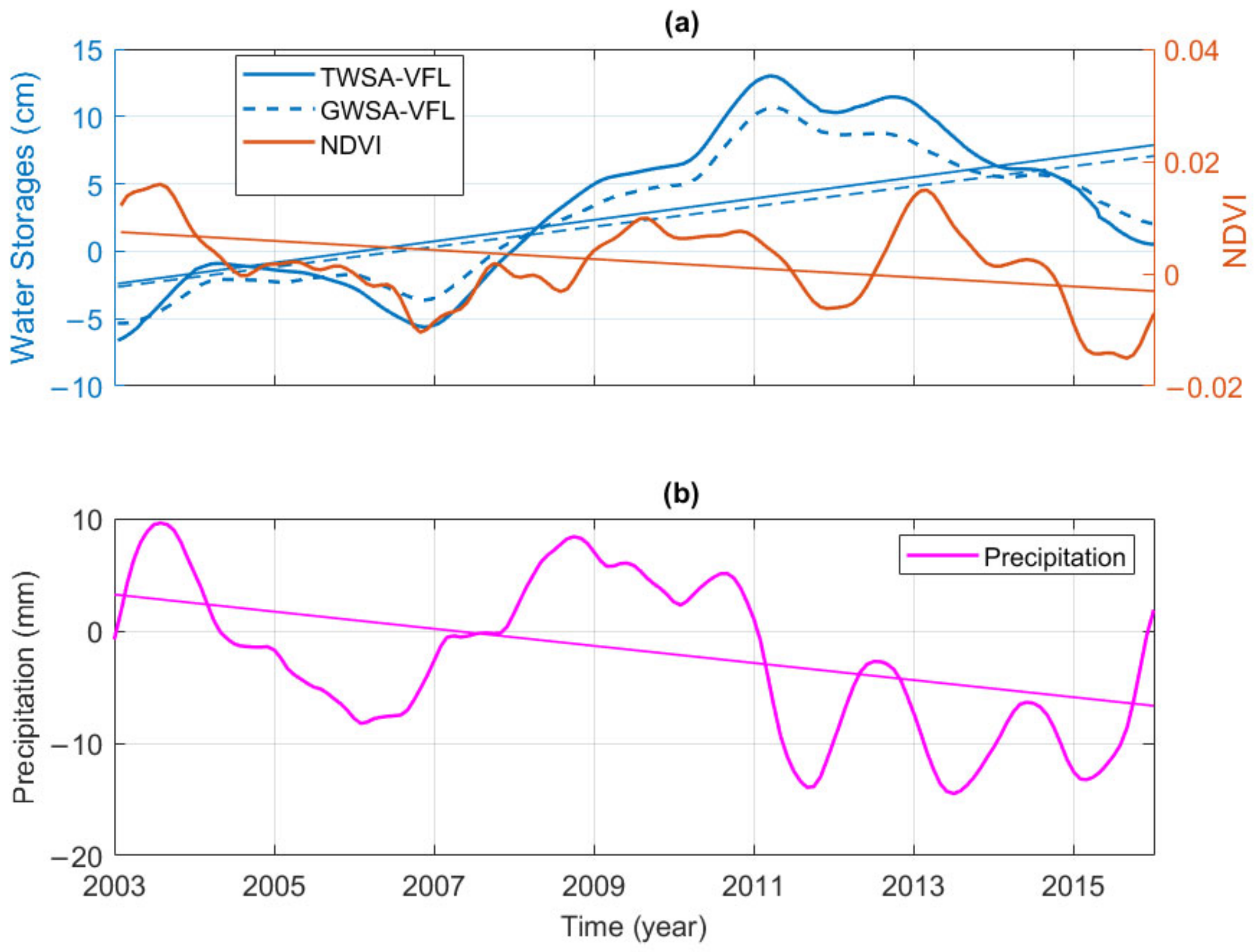
5.2. Surface Vegetation Dynamics from NDVI as Proxy for Infrastructure Influences on Water Storage Changes
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Roudier, P.; Ducharne, A.; Feyen, L. Climate Change Impacts on Runoff in West Africa: A Review. Hydrol. Earth Syst. Sci. 2014, 18, 2789–2801. [Google Scholar] [CrossRef]
- Roudier, P.; Sultan, B.; Quirion, P.; Berg, A. The Impact of Future Climate Change on West African Crop Yields: What Does the Recent Literature Say? Glob. Environ. Chang. 2011, 21, 1073–1083. [Google Scholar] [CrossRef]
- Ahmed, M.; Sultan, M.; Wahr, J.; Yan, E. The Use of GRACE Data to Monitor Natural and Anthropogenic Induced Variations in Water Availability across Africa. Earth-Sci. Rev. 2014, 136, 289–300. [Google Scholar] [CrossRef]
- Andam-Akorful, S.A.; Ferreira, V.G.; Ndehedehe, C.E.; Quaye-Ballard, J.A. An Investigation into the Freshwater Variability in West Africa during 1979–2010: Investigation of Freshwater Variability in West Africa. Int. J. Climatol. 2017, 37, 333–349. [Google Scholar] [CrossRef]
- Keenan, R.J.; Reams, G.A.; Achard, F.; de Freitas, J.V.; Grainger, A.; Lindquist, E. Dynamics of Global Forest Area: Results from the FAO Global Forest Resources Assessment 2015. For. Ecol. Manag. 2015, 352, 9–20. [Google Scholar] [CrossRef]
- Mul, M.; Obuobie, E.; Appoh, R.; Kankam-Yeboah, K.; Bekoe-Obeng, E.; Amisigo, B.; Logah, F.Y.; Ghansah, B.; McCartney, M. Water Resources Assessment of the Volta River Basin; International Water Management Institute (IWMI): Colombo, Sri Lanka, 2015. [Google Scholar]
- Yidana, S.M.; Vakpo, E.K.; Sakyi, P.A.; Chegbeleh, L.P.; Akabzaa, T.M. Groundwater–Lakewater Interactions: An Evaluation of the Impacts of Climate Change and Increased Abstractions on Groundwater Contribution to the Volta Lake, Ghana. Environ. Earth Sci. 2019, 78, 74. [Google Scholar] [CrossRef]
- Döll, P.; Hoffmann-Dobrev, H.; Portmann, F.T.; Siebert, S.; Eicker, A.; Rodell, M.; Strassberg, G.; Scanlon, B.R. Impact of Water Withdrawals from Groundwater and Surface Water on Continental Water Storage Variations. J. Geodyn. 2012, 59–60, 143–156. [Google Scholar] [CrossRef]
- Pfister, S.; Bayer, P.; Koehler, A.; Hellweg, S. Projected Water Consumption in Future Global Agriculture: Scenarios and Related Impacts. Sci. Total Environ. 2011, 409, 4206–4216. [Google Scholar] [CrossRef]
- Vörösmarty, C.J.; Douglas, E.M.; Green, P.A.; Revenga, C. Geospatial Indicators of Emerging Water Stress: An Application to Africa. Ambio 2005, 34, 230–236. [Google Scholar] [CrossRef]
- Ali, A.; Lebel, T. The Sahelian Standardized Rainfall Index Revisited. Int. J. Climatol. 2009, 29, 1705–1714. [Google Scholar] [CrossRef]
- Bader, J.; Latif, M. The 1983 Drought in the West Sahel: A Case Study. Clim. Dyn. 2011, 36, 463–472. [Google Scholar] [CrossRef]
- Diatta, S.; Fink, A.H. Statistical Relationship between Remote Climate Indices and West African Monsoon Variability. Int. J. Climatol. 2014, 34, 3348–3367. [Google Scholar] [CrossRef]
- Giannini, A.; Biasutti, M.; Held, I.M.; Sobel, A.H. A Global Perspective on African Climate. Clim. Chang. 2008, 90, 359–383. [Google Scholar] [CrossRef]
- Joly, M.; Voldoire, A. Role of the Gulf of Guinea in the Inter-Annual Variability of the West African Monsoon: What Do We Learn from CMIP3 Coupled Simulations? Int. J. Climatol. 2010, 30, 1843–1856. [Google Scholar] [CrossRef]
- Losada, T.; Rodríguez-Fonseca, B.; Janicot, S.; Gervois, S.; Chauvin, F.; Ruti, P. A Multi-Model Approach to the Atlantic Equatorial Mode: Impact on the West African Monsoon. Clim. Dyn. 2010, 35, 29–43. [Google Scholar] [CrossRef]
- Ndehedehe, C.E.; Awange, J.L.; Corner, R.J.; Kuhn, M.; Okwuashi, O. On the Potentials of Multiple Climate Variables in Assessing the Spatio-Temporal Characteristics of Hydrological Droughts over the Volta Basin. Sci. Total Environ. 2016, 557–558, 819–837. [Google Scholar] [CrossRef]
- Ndehedehe, C.E.; Awange, J.L.; Kuhn, M.; Agutu, N.O.; Fukuda, Y. Climate Teleconnections Influence on West Africa’s Terrestrial Water Storage: Climate Influence on West Africa’s Terrestrial Water Storage. Hydrol. Process. 2017, 31, 3206–3224. [Google Scholar] [CrossRef]
- Nicholson, S.E. The West African Sahel: A Review of Recent Studies on the Rainfall Regime and Its Interannual Variability. ISRN Meteorol. 2013, 2013, e453521. [Google Scholar] [CrossRef]
- Paeth, H.; Fink, A.H.; Pohle, S.; Keis, F.; Mächel, H.; Samimi, C. Meteorological Characteristics and Potential Causes of the 2007 Flood in Sub-Saharan Africa. Int. J. Climatol. 2011, 31, 1908–1926. [Google Scholar] [CrossRef]
- Ferreira, V.G.; Asiah, Z.; Xu, J.; Gong, Z.; Andam-Akorful, S.A. Land Water-Storage Variability over West Africa: Inferences from Space-Borne Sensors. Water 2018, 10, 380. [Google Scholar] [CrossRef]
- Ferreira, V.G.; Gong, Z.; Andam-Akorful, S.A. Monitoring Mass Changes in the Volta River Basin Using GRACE Satellite Gravity and TRMM Precipitation. Bol. Ciênc. Geod. 2012, 18, 549–563. [Google Scholar] [CrossRef]
- Grippa, M.; Kergoat, L.; Frappart, F.; Araud, Q.; Boone, A.; de Rosnay, P.; Lemoine, J.-M.; Gascoin, S.; Balsamo, G.; Ottlé, C.; et al. Land Water Storage Variability over West Africa Estimated by Gravity Recovery and Climate Experiment (GRACE) and Land Surface Models. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Ndehedehe, C.; Awange, J.; Agutu, N.; Kuhn, M.; Heck, B. Understanding Changes in Terrestrial Water Storage over West Africa between 2002 and 2014. Adv. Water Resour. 2016, 88, 211–230. [Google Scholar] [CrossRef]
- Ndehedehe, C.E.; Awange, J.L.; Kuhn, M.; Agutu, N.O.; Fukuda, Y. Analysis of Hydrological Variability over the Volta River Basin Using In-Situ Data and Satellite Observations. J. Hydrol. Reg. Stud. 2017, 12, 88–110. [Google Scholar] [CrossRef]
- Ni, S.; Chen, J.; Wilson, C.; Hu, X. Long-Term Water Storage Changes of Lake Volta from GRACE and Satellite Altimetry and Connections with Regional Climate. Remote Sens. 2017, 9, 842. [Google Scholar] [CrossRef]
- Kotchoni, D.O.V.; Vouillamoz, J.-M.; Lawson, F.M.A.; Adjomayi, P.; Boukari, M.; Taylor, R.G. Relationships between Rainfall and Groundwater Recharge in Seasonally Humid Benin: A Comparative Analysis of Long-Term Hydrographs in Sedimentary and Crystalline Aquifers. Hydrogeol. J. 2019, 27, 447–457. [Google Scholar] [CrossRef]
- Famiglietti, J.S.; Cazenave, A.; Eicker, A.; Reager, J.T.; Rodell, M.; Velicogna, I. Satellites Provide the Big Picture. Science 2015, 349, 684–685. [Google Scholar] [CrossRef]
- Bonsor, H.; Shamsudduha, M.; Marchant, B.; MacDonald, A.; Taylor, R. Seasonal and Decadal Groundwater Changes in African Sedimentary Aquifers Estimated Using GRACE Products and LSMs. Remote Sens. 2018, 10, 904. [Google Scholar] [CrossRef]
- Döll, P.; Douville, H.; Güntner, A.; Schmied, H.M.; Wada, Y. Modelling Freshwater Resources at the Global Scale: Challenges and Prospects. Surv. Geophys. 2016, 37, 195–221. [Google Scholar] [CrossRef]
- Rateb, A.; Scanlon, B.R.; Pool, D.R.; Sun, A.; Zhang, Z.; Chen, J.; Clark, B.; Faunt, C.C.; Haugh, C.J.; Hill, M.; et al. Comparison of Groundwater Storage Changes From GRACE Satellites With Monitoring and Modeling of Major U.S. Aquifers. Water Resour. Res. 2020, 56. [Google Scholar] [CrossRef]
- Wada, Y.; van Beek, L.P.H.; Kempen, C.M.; van Reckman, J.W.T.M.; Vasak, S.; Bierkens, M.F.P. Global Depletion of Groundwater Resources. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Wang, X.; de Linage, C.; Famiglietti, J.; Zender, C.S. Gravity Recovery and Climate Experiment (GRACE) Detection of Water Storage Changes in the Three Gorges Reservoir of China and Comparison with in Situ Measurements: GRACE DETECTION OF WATER STORAGE CHANGES IN TGR. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Rodgers, C.; van de Giesen, N.; Laube, W.; Vlek, P.L.G.; Youkhana, E. The GLOWA Volta Project: A Framework for Water Resources Decision-Making and Scientific Capacity Building in a Transnational West African Basin. Water Resour. Manag. 2007, 21, 295–313. [Google Scholar] [CrossRef]
- Resende, T.C.; Longuevergne, L.; Gurdak, J.J.; Leblanc, M.; Favreau, G.; Ansems, N.; der Gun, J.V.; Gaye, C.B.; Aureli, A. Assessment of the Impacts of Climate Variability on Total Water Storage across Africa: Implications for Groundwater Resources Management. Hydrogeol. J. 2019, 27, 493–512. [Google Scholar] [CrossRef]
- Sultan, B.; Baron, C.; Dingkuhn, M.; Sarr, B.; Janicot, S. Agricultural Impacts of Large-Scale Variability of the West African Monsoon. Agric. For. Meteorol. 2005, 128, 93–110. [Google Scholar] [CrossRef]
- Feng, W. GRAMAT: A Comprehensive Matlab Toolbox for Estimating Global Mass Variations from GRACE Satellite Data. Earth Sci. Inform. 2019, 12, 389–404. [Google Scholar] [CrossRef]
- Döll, P.; Trautmann, T.; Göllner, M.; Schmied, H.M. A Global-Scale Analysis of Water Storage Dynamics of Inland Wetlands: Quantifying the Impacts of Human Water Use and Man-Made Reservoirs as Well as the Unavoidable and Avoidable Impacts of Climate Change. Ecohydrology 2020, 13, e2175. [Google Scholar] [CrossRef]
- Müller Schmied, H.; Cáceres, D.; Eisner, S.; Flörke, M.; Herbert, C.; Niemann, C.; Peiris, T.A.; Popat, E.; Portmann, F.T.; Reinecke, R.; et al. The Global Water Resources and Use Model WaterGAP v2.2d: Model Description and Evaluation. Geosci. Model Dev. 2021, 14, 1037–1079. [Google Scholar] [CrossRef]
- Lehner, B.; Döll, P. Development and Validation of a Global Database of Lakes, Reservoirs and Wetlands. J. Hydrol. 2004, 296, 1–22. [Google Scholar] [CrossRef]
- Schneider, U.; Becker, A.; Finger, P.; Meyer-Christoffer, A.; Ziese, M.; Rudolf, B. GPCC’s New Land Surface Precipitation Climatology Based on Quality-Controlled in Situ Data and Its Role in Quantifying the Global Water Cycle. Theor. Appl. Climatol. 2014, 115, 15–40. [Google Scholar] [CrossRef]
- Awange, J.L.; Ferreira, V.G.; Forootan, E.; Khandu; Andam-Akorful, S.A.; Agutu, N.O.; He, X.F. Uncertainties in Remotely Sensed Precipitation Data over Africa. Int. J. Climatol. 2016, 36, 303–323. [Google Scholar] [CrossRef]
- Nicholson, S.E.; Some, B.; McCollum, J.; Nelkin, E.; Klotter, D.; Berte, Y.; Diallo, B.M.; Gaye, I.; Kpabeba, G.; Ndiaye, O.; et al. Validation of TRMM and Other Rainfall Estimates with a High-Density Gauge Dataset for West Africa. Part I: Validation of GPCC Rainfall Product and Pre-TRMM Satellite and Blended Products. J. Appl. Meteorol. Climatol. 2003, 42, 1337–1354. [Google Scholar] [CrossRef]
- Jones, S.; Fremier, A.; Declerck, F.; Smedley, D.; Ortega-Pieck, A.; Mulligan, M. Big Data and Multiple Methods for Mapping Small Reservoirs: Comparing Accuracies for Applications in Agricultural Landscapes. Remote Sens. 2017, 9, 1307. [Google Scholar] [CrossRef]
- Zhou, H.; Luo, Z.; Tangdamrongsub, N.; Zhou, Z.; He, L.; Xu, C.; Li, Q.; Wu, Y. Identifying Flood Events over the Poyang Lake Basin Using Multiple Satellite Remote Sensing Observations, Hydrological Models and In Situ Data. Remote Sens. 2018, 10, 713. [Google Scholar] [CrossRef]
- Crétaux, J.-F.; Jelinski, W.; Calmant, S.; Kouraev, A.; Vuglinski, V.; Bergé-Nguyen, M.; Gennero, M.-C.; Nino, F.; Rio, R.A.D.; Cazenave, A.; et al. SOLS: A Lake Database to Monitor in the Near Real Time Water Level and Storage Variations from Remote Sensing Data. Adv. Space Res. 2011, 47, 1497–1507. [Google Scholar] [CrossRef]
- Tapley, B.; Ries, J.; Bettadpur, S.; Chambers, D.; Cheng, M.; Condi, F.; Gunter, B.; Kang, Z.; Nagel, P.; Pastor, R.; et al. GGM02—An Improved Earth Gravity Field Model from GRACE. J. Geodesy. 2005, 79, 467–478. [Google Scholar] [CrossRef]
- Ji, L.; Zhang, L.; Wylie, B. Analysis of Dynamic Thresholds for the Normalized Difference Water Index. Photogramm. Eng. Remote Sens. 2009, 75, 1307–1317. [Google Scholar] [CrossRef]
- Zhang, J.; Hu, Q.; Li, Y.; Li, H.; Li, J. Area, Lake-Level and Volume Variations of Typical Lakes on the Tibetan Plateau and Their Response to Climate Change, 1972–2019. Geo-Spat. Inf. Sci. 2021, 24, 458–473. [Google Scholar] [CrossRef]
- Bhanja, S.N.; Malakar, P.; Mukherjee, A.; Rodell, M.; Mitra, P.; Sarkar, S. Using Satellite-Based Vegetation Cover as Indicator of Groundwater Storage in Natural Vegetation Areas. Geophys. Res. Lett. 2019, 46, 8082–8092. [Google Scholar] [CrossRef]
- Ndehedehe, C.E.; Ferreira, V.G.; Agutu, N.O. Hydrological Controls on Surface Vegetation Dynamics over West and Central Africa. Ecol. Indic. 2019, 103, 494–508. [Google Scholar] [CrossRef]
- Yi, S.; Song, C.; Wang, Q.; Wang, L.; Heki, K.; Sun, W. The Potential of GRACE Gravimetry to Detect the Heavy Rainfall-Induced Impoundment of a Small Reservoir in the Upper Yellow River. Water Resour. Res. 2017, 53, 6562–6578. [Google Scholar] [CrossRef]
- Wills, T.C.; Zorn, T.G.; Nuhfer, A.J. Manual of Fisheries Survey Methods II: With Periodic Updates; Fisheries Division, Michigan Department of Natural Resources: Lansing, MI, USA, 2006; p. 41. [Google Scholar]
- Han, D.; Wahr, J. The Viscoelastic Relaxation of a Realistically Stratified Earth, and a Further Analysis of Postglacial Rebound. Geophys. J. Int. 1995, 120, 287–311. [Google Scholar] [CrossRef]
- Cheng, M.; Ries, J.C.; Tapley, B.D. Variations of the Earth’s Figure Axis from Satellite Laser Ranging and GRACE. J. Geophys. Res. Solid Earth 2011, 116. [Google Scholar] [CrossRef]
- Swenson, S.; Chambers, D.; Wahr, J. Estimating Geocenter Variations from a Combination of GRACE and Ocean Model Output. J. Geophys. Res. Solid Earth 2008, 113. [Google Scholar] [CrossRef]
- Geruo, A.; Wahr, J.; Zhong, S. Computations of the Viscoelastic Response of a 3-D Compressible Earth to Surface Loading: An Application to Glacial Isostatic Adjustment in Antarctica and Canada. Geophys. J. Int. 2013, 192, 557–572. [Google Scholar] [CrossRef]
- Werth, S.; White, D.; Bliss, D.W. GRACE Detected Rise of Groundwater in the Sahelian Niger River Basin: Niger River Basin Water Storage Rise. J. Geophys. Res. Solid Earth 2017, 122, 10459–10477. [Google Scholar] [CrossRef]
- Grinsted, A.; Moore, J.C.; Jevrejeva, S. Application of the Cross Wavelet Transform and Wavelet Coherence to Geophysical Time Series. Nonlinear Process. Geophys. 2004, 11, 561–566. [Google Scholar] [CrossRef]
- Huang, S.; Huang, Q.; Chang, J.; Zhu, Y.; Leng, G.; Xing, L. Drought Structure Based on a Nonparametric Multivariate Standardized Drought Index across the Yellow River Basin, China. J. Hydrol. 2015, 530, 127–136. [Google Scholar] [CrossRef]
- Wang, F.; Wang, Z.; Yang, H.; Di, D.; Zhao, Y.; Liang, Q. Utilizing GRACE-Based Groundwater Drought Index for Drought Characterization and Teleconnection Factors Analysis in the North China Plain. J. Hydrol. 2020, 585, 124849. [Google Scholar] [CrossRef]
- Torrence, C.; Compo, G.P. A Practical Guide to Wavelet Analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Cleveland, R.B.; Cleveland, W.S.; McRae, J.E.; Terpenning, I. STL: A Seasonal-Trend Decomposition Procedure Based on Loess (with Discussion). J. Off. Stat. 1990, 6, 3–73. [Google Scholar]
- Abelen, S.; Seitz, F. Relating Satellite Gravimetry Data to Global Soil Moisture Products via Data Harmonization and Correlation Analysis. Remote Sens. Environ. 2013, 136, 89–98. [Google Scholar] [CrossRef]
- Ferreira, V.G.; Asiah, Z. An Investigation on the Closure of the Water Budget Methods Over Volta Basin Using Multi-Satellite Data. In IGFS 2014; Jin, S., Barzaghi, R., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 171–178. [Google Scholar]
- Li, B.; Rodell, M. Evaluation of a Model-Based Groundwater Drought Indicator in the Conterminous U.S. J. Hydrol. 2015, 526, 78–88. [Google Scholar] [CrossRef]
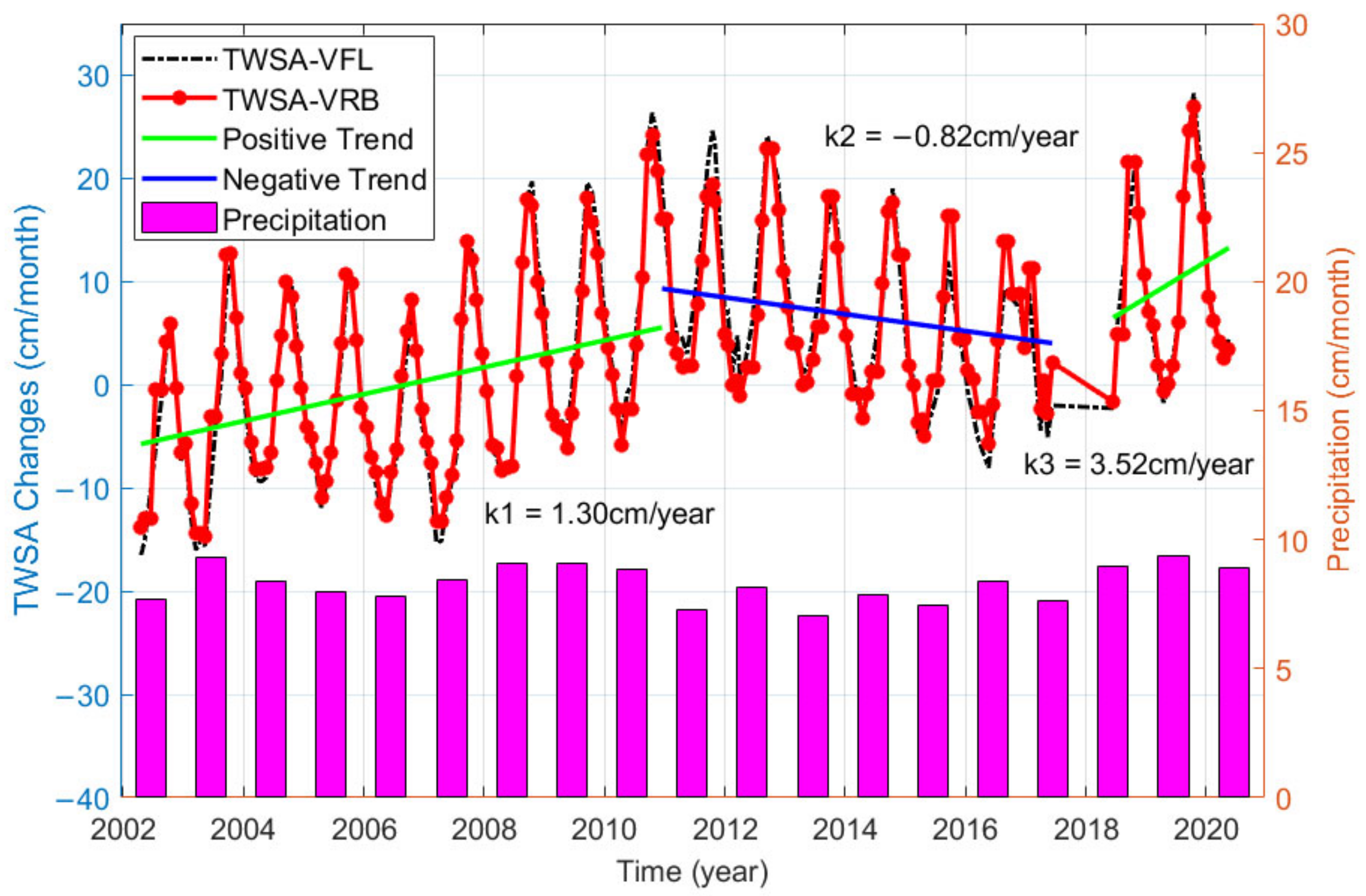



| Data Style | Annual Amplitude (cm) | RMSE (cm) | Annual Phase (month) | RMSE (cm) |
|---|---|---|---|---|
| TWSAVRB | 9.80 | 0.73 | 9.35 | 0.14 |
| Precipitation | 9.31 | 0.45 | 6.37 | 0.09 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Djessou, R.D.; Wan, X.; Yi, S.; Annan, R.F.; Su, X.; Wang, S. Water Storage Variation and Its Possible Causes Detected by GRACE in the Volta River Basin. Remote Sens. 2022, 14, 5319. https://doi.org/10.3390/rs14215319
Djessou RD, Wan X, Yi S, Annan RF, Su X, Wang S. Water Storage Variation and Its Possible Causes Detected by GRACE in the Volta River Basin. Remote Sensing. 2022; 14(21):5319. https://doi.org/10.3390/rs14215319
Chicago/Turabian StyleDjessou, Randal D., Xiaoyun Wan, Shuang Yi, Richard F. Annan, Xiaoli Su, and Sijia Wang. 2022. "Water Storage Variation and Its Possible Causes Detected by GRACE in the Volta River Basin" Remote Sensing 14, no. 21: 5319. https://doi.org/10.3390/rs14215319
APA StyleDjessou, R. D., Wan, X., Yi, S., Annan, R. F., Su, X., & Wang, S. (2022). Water Storage Variation and Its Possible Causes Detected by GRACE in the Volta River Basin. Remote Sensing, 14(21), 5319. https://doi.org/10.3390/rs14215319