Evaluating Optical Remote Sensing Methods for Estimating Leaf Area Index for Corn and Soybean
Abstract
1. Introduction
2. Data Used
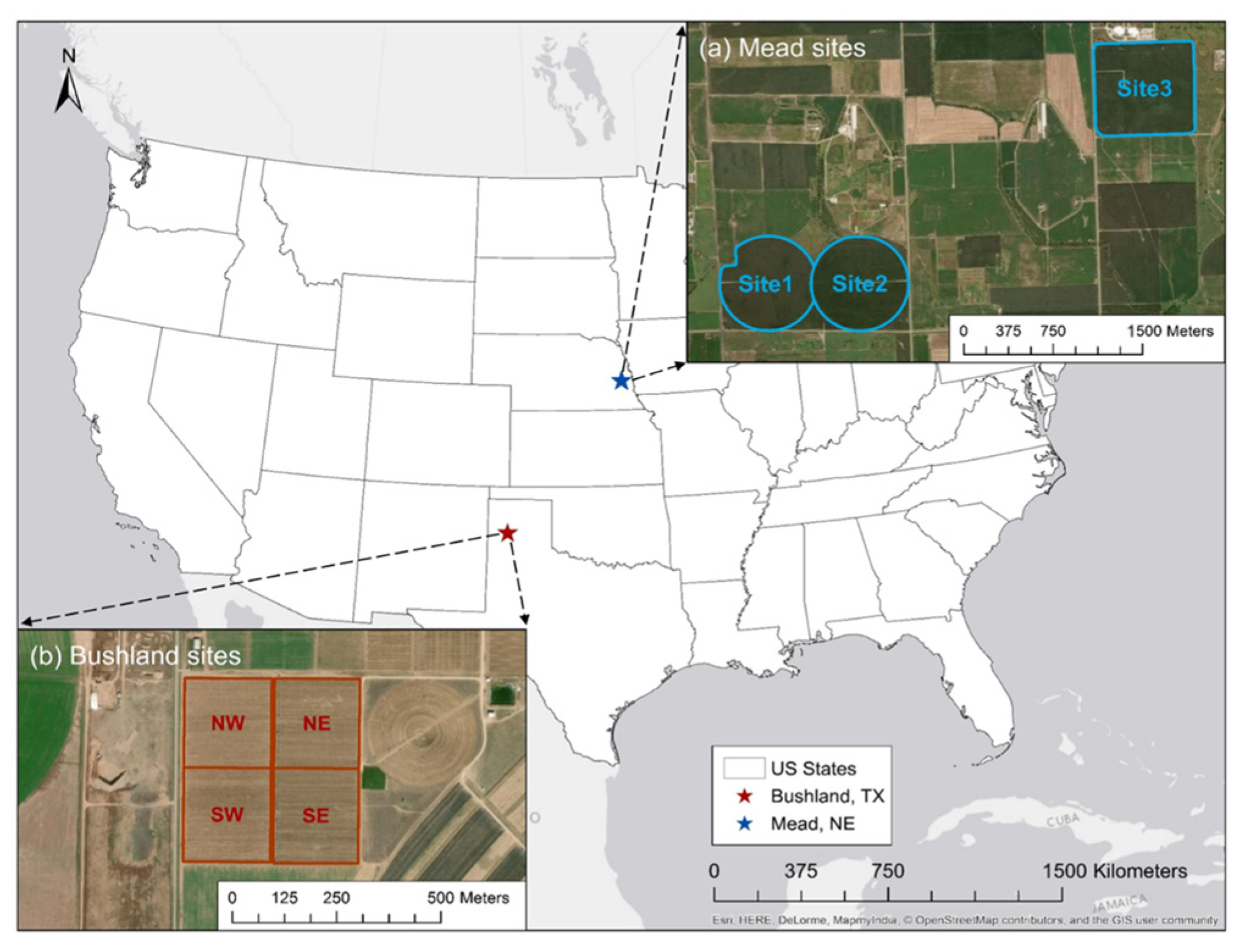
2.1. Study Sites and Field Observations
2.2. Remote Sensing Datasets
2.3. Landsat Data Preparation
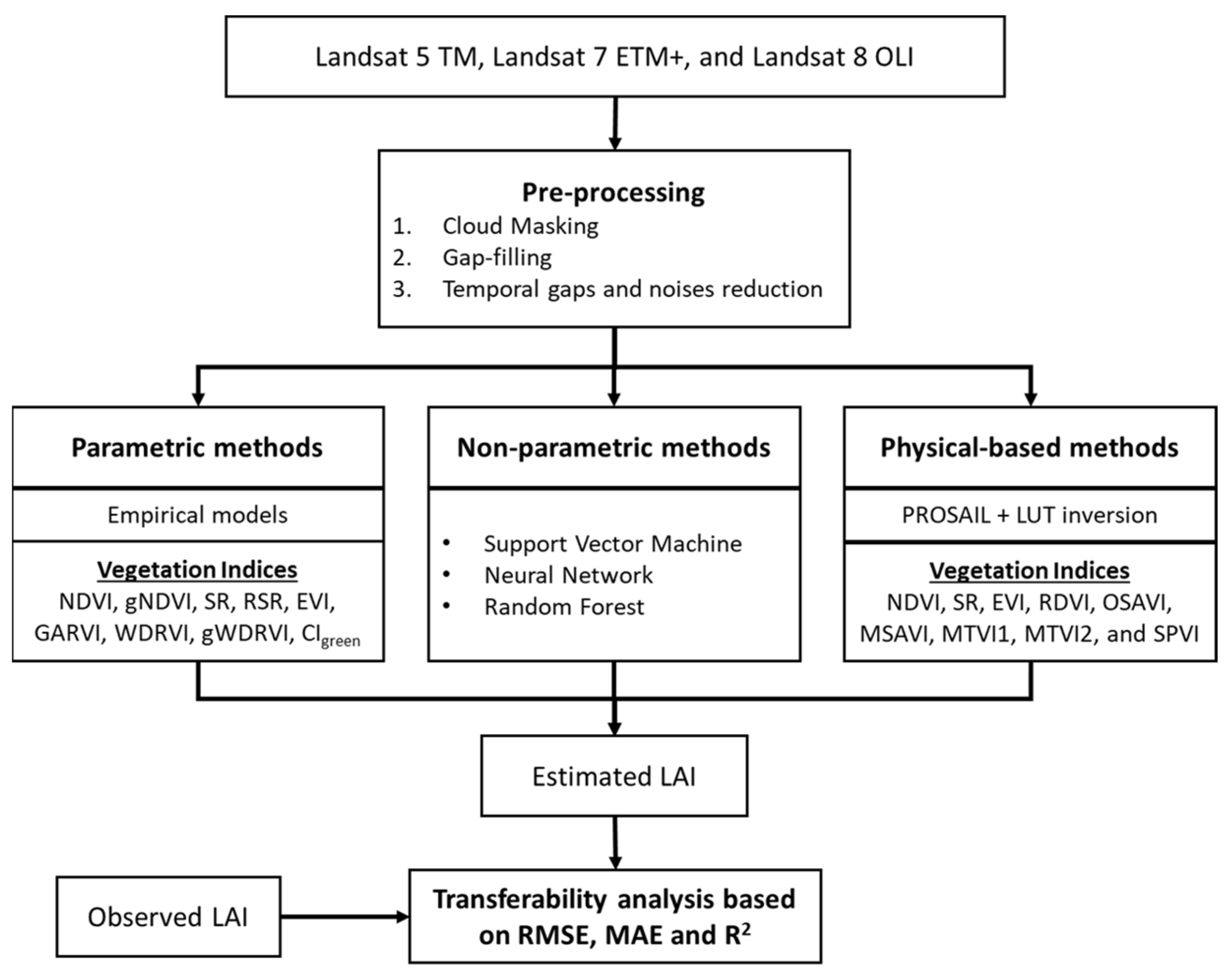
3. Crop LAI Estimation Methods
3.1. Empirical Modeling Methods
3.1.1. Parametric Equations
3.1.2. Non-Parametric Models
3.2. Physical-Based Methods
3.2.1. Physical-Based Parametric Equations
3.2.2. Physical-Based Non-Parametric Models
3.2.3. LUT-Based Inversion
3.3. Accuracy Assessment
4. Results
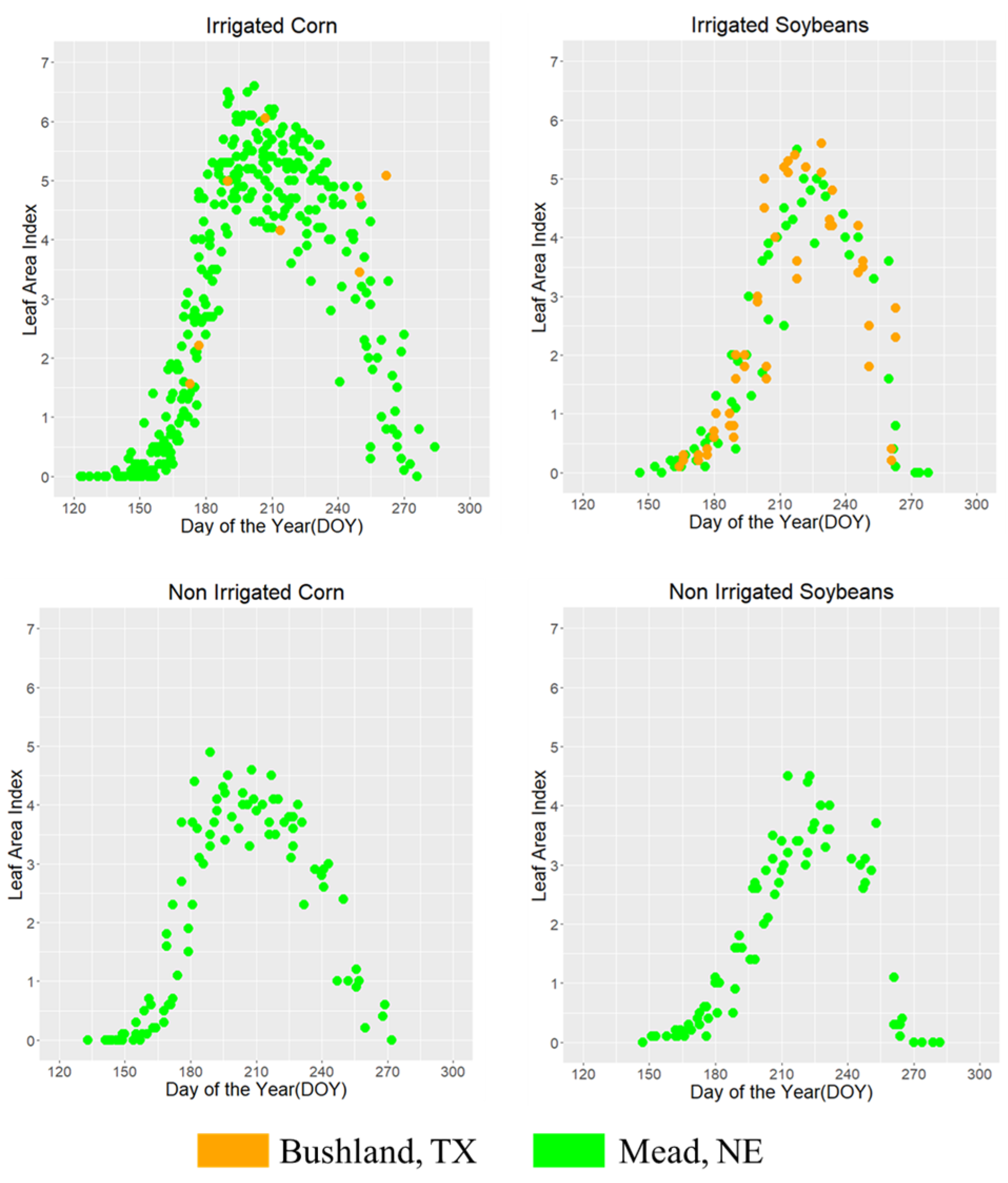
4.1. Variability in LAI Observations
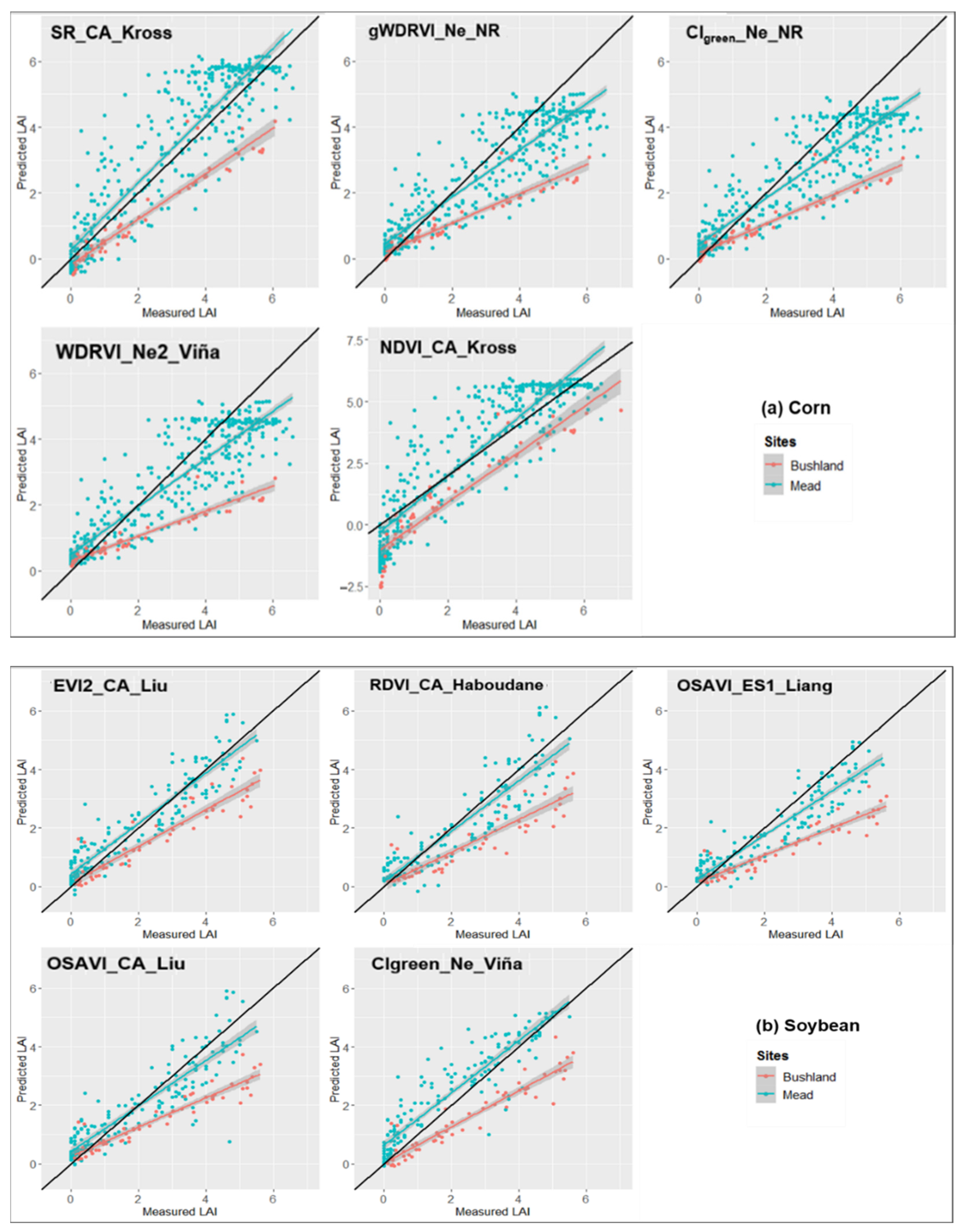
4.2. Empirical Approaches
4.3. Physical Approaches
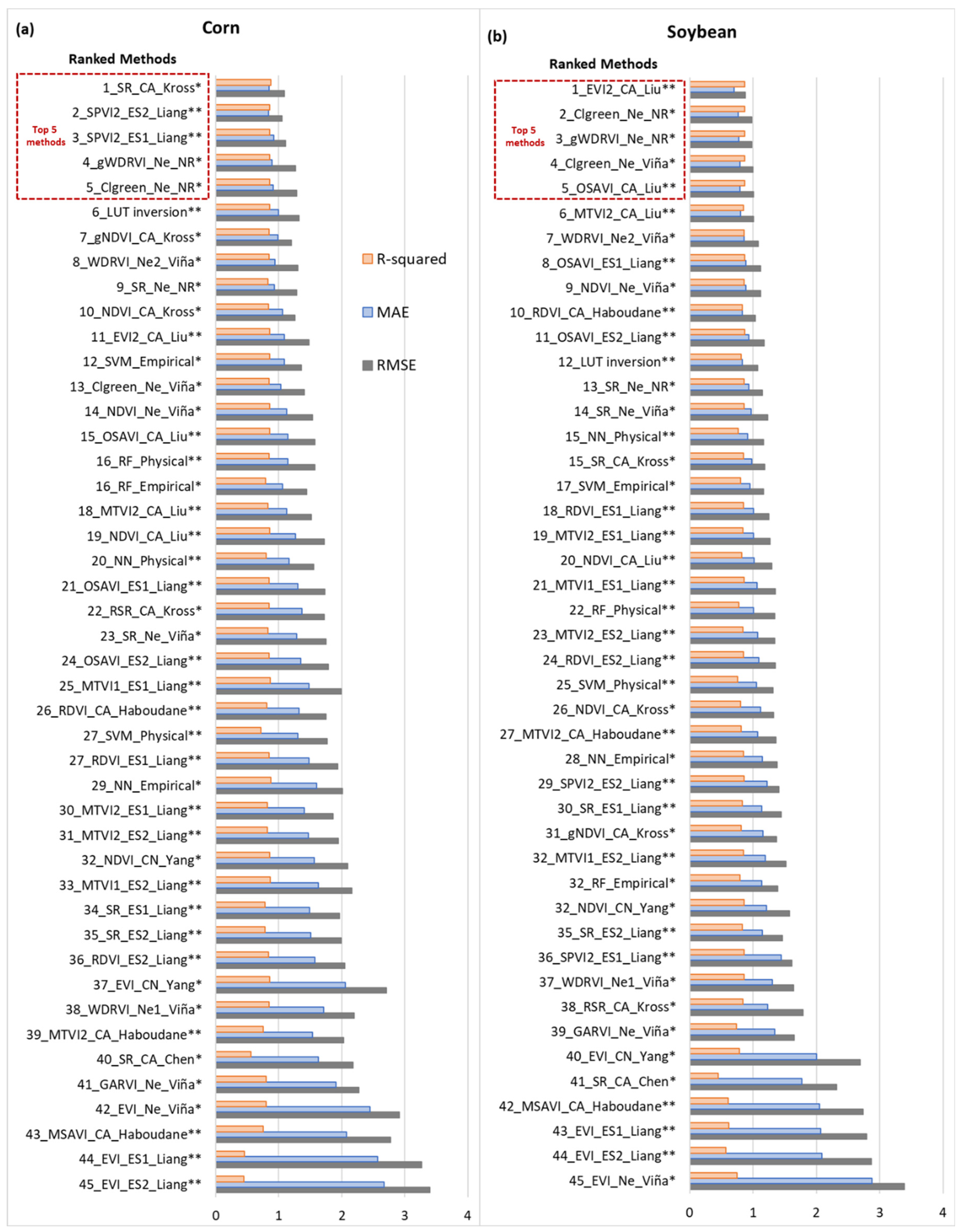
4.4. Overall Performance
5. Discussion
6. Conclusions
- The performance of LAI estimation methods varied based on the method used, vegetation indices, crop types and location, and the number of observations of LAI to evaluate or train the methods. Overall, parametric methods were found to be more effective to estimate LAI of the corn crop and at Mead site with less than 2.0 RMSE in most of the methods but showed greater variation in performance among the locations.
- After analyzing the RMSE, MAE, and R2 of different empirical and physical methods, it is found that the estimation accuracy of SR and EVI-based empirical and physical methods were higher than other methods considered in this study for corn and soybeans, respectively. These two were followed by vegetation indices such as OSAVI, MTVI2, gNDVI, and SPVI for corn and CIgreen, gWDRVI, and OSAVI for soybeans.
- The LUT-inversion physical approach performed reasonably well consistently irrespective of location and crop even though the performance was as good as some empirical methods. The consistency in its performance across locations for both crops is the advantage of the LUT-inversion approach over other methods and this approach is more suitable at regional scale LAI estimation.
- Since spectral data at red edge region and SAR microwave data are available, and they are found to be promising to estimate crop-specific LAI, future studies will focus on evaluating methods based on red edge spectral data and SAR.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Myneni, R.B. Estimation of Global Leaf Area Index and Absorbed Par Using Radiative Transfer Models. IEEE Trans. Geosci. Remote Sens. 1997, 35, 1380–1393. [Google Scholar] [CrossRef]
- Xiao, J.; Chevallier, F.; Gomez, C.; Guanter, L.; Hicke, J.A.; Huete, A.R.; Ichii, K.; Ni, W.; Pang, Y.; Rahman, A.F.; et al. Remote Sensing of the Terrestrial Carbon Cycle: A Review of Advances over 50 Years. Remote Sens. Environ. 2019, 233, 111383. [Google Scholar] [CrossRef]
- Xiao, Z.; Liang, S.; Sun, R.; Wang, J.; Jiang, B. Estimating the Fraction of Absorbed Photosynthetically Active Radiation from the MODIS Data Based GLASS Leaf Area Index Product. Remote Sens. Environ. 2015, 171, 105–117. [Google Scholar] [CrossRef]
- Chen, J.M.; Black, T.A. Defining Leaf Area Index for Non-flat Leaves. Plant Cell Environ. 1992, 15, 421–429. [Google Scholar] [CrossRef]
- Tian, L. Interdependent Dynamics of LAI-ET across Roofing Landscapes: The Mongolian and Tibetan Plateaus. J. Resour. Ecol. 2019, 10, 296–306. [Google Scholar] [CrossRef]
- Disney, M.; Muller, J.P.; Kharbouche, S.; Kaminski, T.; Voßbeck, M.; Lewis, P.; Pinty, B. A New Global FAPAR and LAI Dataset Derived from Optimal Albedo Estimates: Comparison with MODIS Products. Remote Sens. 2016, 8, 275. [Google Scholar] [CrossRef]
- Sánchez, J.M.; Kustas, W.P.; Caselles, V.; Anderson, M.C. Modelling Surface Energy Fluxes over Maize Using a Two-Source Patch Model and Radiometric Soil and Canopy Temperature Observations. Remote Sens. Environ. 2008, 112, 1130–1143. [Google Scholar] [CrossRef]
- He, B.; Li, X.; Quan, X.; Qiu, S. Estimating the Aboveground Dry Biomass of Grass by Assimilation of Retrieved LAI Into a Crop Growth Model. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 550–561. [Google Scholar] [CrossRef]
- Huang, J.; Gómez-Dans, J.L.; Huang, H.; Ma, H.; Wu, Q.; Lewis, P.E.; Liang, S.; Chen, Z.; Xue, J.-H.; Wu, Y.; et al. Assimilation of Remote Sensing into Crop Growth Models: Current Status and Perspectives. Agric. For. Meteorol. 2019, 276–277, 107609. [Google Scholar] [CrossRef]
- Chen, H.; Zhu, G.; Zhang, K.; Bi, J.; Jia, X.; Ding, B.; Zhang, Y.; Shang, S.; Zhao, N.; Qin, W. Evaluation of Evapotranspiration Models Using Different LAI and Meteorological Forcing Data from 1982 to 2017. Remote Sens. 2020, 12, 2473. [Google Scholar] [CrossRef]
- Strachan, I.B.; Stewart, D.W.; Pattey, E. Determination of Leaf Area Index in Agricultural Systems. Micrometeorol. Agric. Syst. 2015, 47, 179–198. [Google Scholar] [CrossRef]
- Kustas, W.P.; Anderson, M.C.; Semmens, K.A.; Alfieri, J.G.; Gao, F.; Hain, C.R.; Cammalleri, C. A Thermal-Based Remote Sensing Modelling System for Estimating Crop Water Use and Stress from Field to Regional Scales. In Proceedings of the Acta Horticulturae, Brisbane, Australia, 17–22 August 2014; Volume 1112, pp. 71–80. [Google Scholar]
- Anderson, M.C. Simple Method for Retrieving Leaf Area Index from Landsat Using MODIS Leaf Area Index Products as Reference. J. Appl. Remote Sens. 2012, 6, 063554. [Google Scholar] [CrossRef]
- Tang, H.; Brolly, M.; Zhao, F.; Strahler, A.H.; Schaaf, C.L.; Ganguly, S.; Zhang, G.; Dubayah, R. Deriving and Validating Leaf Area Index (LAI) at Multiple Spatial Scales through Lidar Remote Sensing: A Case Study in Sierra National Forest, CA. Remote Sens. Environ. 2014, 143, 131–141. [Google Scholar] [CrossRef]
- Kang, Y.; Özdoğan, M.; Zipper, S.C.; Román, M.O.; Walker, J.; Hong, S.Y.; Marshall, M.; Magliulo, V.; Moreno, J.; Alonso, L.; et al. How Universal Is the Relationship between Remotely Sensed Vegetation Indices and Crop Leaf Area Index? A Global Assessment. Remote Sens. 2016, 8, 597. [Google Scholar] [CrossRef]
- Delegido, J.; Verrelst, J.; Alonso, L.; Moreno, J. Evaluation of Sentinel-2 Red-Edge Bands for Empirical Estimation of Green LAI and Chlorophyll Content. Sensors 2011, 11, 7063–7081. [Google Scholar] [CrossRef] [PubMed]
- Delegido, J.; Verrelst, J.; Meza, C.M.; Rivera, J.P.; Alonso, L.; Moreno, J. A Red-Edge Spectral Index for Remote Sensing Estimation of Green LAI over Agroecosystems. Eur. J. Agron. 2013, 46, 42–52. [Google Scholar] [CrossRef]
- Nguy-Robertson, A.L.; Peng, Y.; Gitelson, A.A.; Arkebauer, T.J.; Pimstein, A.; Herrmann, I.; Karnieli, A.; Rundquist, D.C.; Bonfil, D.J. Estimating Green LAI in Four Crops: Potential of Determining Optimal Spectral Bands for a Universal Algorithm. Agric. For. Meteorol. 2014, 192–193, 140–148. [Google Scholar] [CrossRef]
- Kross, A.; McNairn, H.; Lapen, D.; Sunohara, M.; Champagne, C. Assessment of RapidEye Vegetation Indices for Estimation of Leaf Area Index and Biomass in Corn and Soybean Crops. Int. J. Appl. Earth Obs. Geoinf. 2015, 34, 235–248. [Google Scholar] [CrossRef]
- Dong, T.; Liu, J.; Shang, J.; Qian, B.; Ma, B.; Kovacs, J.M.; Walters, D.; Jiao, X.; Geng, X.; Shi, Y. Assessment of Red-Edge Vegetation Indices for Crop Leaf Area Index Estimation. Remote Sens. Environ. 2019, 222, 133–143. [Google Scholar] [CrossRef]
- Darvishzadeh, R.; Atzberger, C.; Skidmore, A.K.; Abkar, A.A. Leaf Area Index Derivation from Hyperspectral Vegetation Indicesand the Red Edge Position. Int. J. Remote Sens. 2009, 30, 6199–6218. [Google Scholar] [CrossRef]
- Deng, F.; Chen, J.M.; Plummer, S.; Chen, M.; Pisek, J. Algorithm for Global Leaf Area Index Retrieval Using Satellite Imagery. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2219–2229. [Google Scholar] [CrossRef]
- Kamal, M.; Phinn, S.; Johansen, K. Assessment of Multi-Resolution Image Data for Mangrove Leaf Area Index Mapping. Remote Sens. Environ. 2016, 176, 242–254. [Google Scholar] [CrossRef]
- Serbin, S.P.; Ahl, D.E.; Gower, S.T. Spatial and Temporal Validation of the MODIS LAI and FPAR Products across a Boreal Forest Wildfire Chronosequence. Remote Sens. Environ. 2013, 133, 71–84. [Google Scholar] [CrossRef]
- Tillack, A.; Clasen, A.; Kleinschmit, B.; Förster, M. Estimation of the Seasonal Leaf Area Index in an Alluvial Forest Using High-Resolution Satellite-Based Vegetation Indices. Remote Sens. Environ. 2014, 141, 52–63. [Google Scholar] [CrossRef]
- Biudes, M.S.; Machado, N.G.; Danelichen, V.H.d.M.; Souza, M.C.; Vourlitis, G.L.; Nogueira, J.d.S. Ground and Remote Sensing-Based Measurements of Leaf Area Index in a Transitional Forest and Seasonal Flooded Forest in Brazil. Int. J. Biometeorol. 2014, 58, 1181–1193. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Zhang, Y.; Bao, Y.; Luo, J.; Jin, X.; Xu, X.; Song, X.; Yang, G. Exploring the Best Hyperspectral Features for LAI Estimation Using Partial Least Squares Regression. Remote Sens. 2014, 6, 6221–6241. [Google Scholar] [CrossRef]
- Yuan, H.; Yang, G.; Li, C.; Wang, Y.; Liu, J.; Yu, H.; Feng, H.; Xu, B.; Zhao, X.; Yang, X. Retrieving Soybean Leaf Area Index from Unmanned Aerial Vehicle Hyperspectral Remote Sensing: Analysis of RF, ANN, and SVM Regression Models. Remote Sens. 2017, 9, 309. [Google Scholar] [CrossRef]
- Zemg, W.; Xu, C.; Gang, Z.; Wu, J.; Huamg, J. Estimation of Sunflower Seed Yield Using Partial Least Squares Regression and Artificial Neural Network Models. Pedosphere 2018, 28, 764–774. [Google Scholar] [CrossRef]
- De Peppo, M.; Taramelli, A.; Boschetti, M.; Mantino, A.; Volpi, I.; Filipponi, F.; Tornato, A.; Valentini, E.; Ragaglini, G. Non-Parametric Statistical Approaches for Leaf Area Index Estimation from Sentinel-2 Data: A Multi-Crop Assessment. Remote Sens. 2021, 13, 2841. [Google Scholar] [CrossRef]
- Féret, J.B.; Berger, K.; de Boissieu, F.; Malenovský, Z. PROSPECT-PRO for Estimating Content of Nitrogen-Containing Leaf Proteins and Other Carbon-Based Constituents. Remote Sens. Environ. 2021, 252, 112173. [Google Scholar] [CrossRef]
- Féret, J.B.; Gitelson, A.A.; Noble, S.D.; Jacquemoud, S. PROSPECT-D: Towards Modeling Leaf Optical Properties through a Complete Lifecycle. Remote Sens. Environ. 2017, 193, 204–215. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Baret, F. PROSPECT: A Model of Leaf Optical Properties Spectra. Remote Sens. Environ. 1990, 34, 75–91. [Google Scholar] [CrossRef]
- Verhoef, W. Light Scattering by Leaf Layers with Application to Canopy Reflectance Modeling: The SAIL Model. Remote Sens. Environ. 1984, 16, 125–141. [Google Scholar] [CrossRef]
- Verhoef, W.; Bach, H. Coupled Soil-Leaf-Canopy and Atmosphere Radiative Transfer Modeling to Simulate Hyperspectral Multi-Angular Surface Reflectance and TOA Radiance Data. Remote Sens. Environ. 2007, 109, 166–182. [Google Scholar] [CrossRef]
- Cheng, Q. Validation and Correction of MOD15-LAI Using In Situ Rice LAI in Southern China. Commun. Soil Sci. Plant Anal. 2008, 39, 1658–1669. [Google Scholar] [CrossRef]
- Claverie, M.; Vermote, E.F.; Weiss, M.; Baret, F.; Hagolle, O.; Demarez, V. Validation of Coarse Spatial Resolution LAI and FAPAR Time Series over Cropland in Southwest France. Remote Sens. Environ. 2013, 139, 216–230. [Google Scholar] [CrossRef]
- Kimes, D.S.; Knyazikhin, Y.; Privette, J.L.; Abuelgasim, A.A.; Gao, F. Inversion Methods for Physically-Based Models. Remote Sens. Rev. 2000, 18, 381–439. [Google Scholar] [CrossRef]
- Atzberger, C. Object-Based Retrieval of Biophysical Canopy Variables Using Artificial Neural Nets and Radiative Transfer Models. Remote Sens. Environ. 2004, 93, 53–67. [Google Scholar] [CrossRef]
- Durbha, S.S.; King, R.L.; Younan, N.H. Support Vector Machines Regression for Retrieval of Leaf Area Index from Multiangle Imaging Spectroradiometer. Remote Sens. Environ. 2007, 107, 348–361. [Google Scholar] [CrossRef]
- Mountrakis, G.; Im, J.; Ogole, C. Support Vector Machines in Remote Sensing: A Review. ISPRS J. Photogramm. Remote Sens. 2011, 66, 247–259. [Google Scholar] [CrossRef]
- Verger, A.; Baret, F.; Camacho, F. Optimal Modalities for Radiative Transfer-Neural Network Estimation of Canopy Biophysical Characteristics: Evaluation over an Agricultural Area with CHRIS/PROBA Observations. Remote Sens. Environ. 2011, 115, 415–426. [Google Scholar] [CrossRef]
- Liang, L.; Di, L.; Zhang, L.; Deng, M.; Qin, Z.; Zhao, S.; Lin, H. Estimation of Crop LAI Using Hyperspectral Vegetation Indices and a Hybrid Inversion Method. Remote Sens. Environ. 2015, 165, 123–134. [Google Scholar] [CrossRef]
- Jacquemoud, S. Inversion of the PROSPECT+ SAIL Canopy Reflectance Model from AVIRIS Equivalent Spectra: Theoretical Study. Remote Sens. Environ. 1993, 44, 281–292. [Google Scholar] [CrossRef]
- Fang, H.; Liang, S. A Hybrid Inversion Method for Mapping Leaf Area Index from MODIS Data: Experiments and Application to Broadleaf and Needleleaf Canopies. Remote Sens. Environ. 2005, 94, 405–424. [Google Scholar] [CrossRef]
- Fan, W.; Yan, B.; Xu, X. Crop Area and Leaf Area Index Simultaneous Retrieval Based on Spatial Scaling Transformation. Sci. China Earth Sci. 2010, 53, 1709–1716. [Google Scholar] [CrossRef]
- Xu, J.; Quackenbush, L.J.; Volk, T.A.; Im, J. Forest and Crop Leaf Area Index Estimation Using Remote Sensing: Research Trends and Future Directions. Remote Sens. 2020, 12, 2934. [Google Scholar] [CrossRef]
- Fang, H.; Baret, F.; Plummer, S.; Schaepman-Strub, G. An Overview of Global Leaf Area Index (LAI): Methods, Products, Validation, and Applications. Rev. Geophys. 2019, 57, 739–799. [Google Scholar] [CrossRef]
- Zheng, G.; Moskal, L.M. Retrieving Leaf Area Index (LAI) Using Remote Sensing: Theories, Methods and Sensors. Sensors 2009, 9, 2719–2745. [Google Scholar] [CrossRef]
- Tian, L.; Qu, Y.; Qi, J. Estimation of Forest LAI Using Discrete Airborne LiDAR: A Review. Remote Sens. 2021, 13, 2408. [Google Scholar] [CrossRef]
- Yan, G.; Hu, R.; Luo, J.; Weiss, M.; Jiang, H.; Mu, X.; Xie, D.; Zhang, W. Review of Indirect Optical Measurements of Leaf Area Index: Recent Advances, Challenges, and Perspectives. Agric. For. Meteorol. 2019, 265, 390–411. [Google Scholar] [CrossRef]
- Liu, K.; Zhou, Q.B.; Wu, W.B.; Xia, T.; Tang, H.J. Estimating the Crop Leaf Area Index Using Hyperspectral Remote Sensing. J. Integr. Agric. 2016, 15, 475–491. [Google Scholar] [CrossRef]
- Baret, F.; Buis, S. Estimating Canopy Characteristics from Remote Sensing Observations: Review of Methods and Associated Problems. Adv. Land Remote Sens. 2008, 173–201. [Google Scholar] [CrossRef]
- Song, C. Optical Remote Sensing of Forest Leaf Area Index and Biomass. Prog. Phys. Geogr. 2013, 37, 98–113. [Google Scholar] [CrossRef]
- Chen, J.M. Remote Sensing of Leaf Area Index of Vegetation Covers. In Remote Sensing of Natural Resources; CRC Press: Boca Raton, FL, USA, 2013; pp. 375–398. [Google Scholar]
- Marek, G.W.; Gowda, P.H.; Evett, S.R.; Baumhardt, R.L.; Brauer, D.K.; Howell, T.A.; Marek, T.H.; Srinivasan, R. Estimating Evapotranspiration for Dryland Cropping Systems in the Semiarid Texas High Plains Using SWAT. J. Am. Water Resour. Assoc. 2016, 52, 298–314. [Google Scholar] [CrossRef]
- Masek, J.G.; Vermote, E.F.; Saleous, N.E.; Wolfe, R.; Hall, F.G.; Huemmrich, K.F.; Gao, F.; Kutler, J.; Lim, T.K. A Landsat Surface Reflectance Dataset for North America, 1990–2000. IEEE Geosci. Remote Sens. Lett. 2006, 3, 68–72. [Google Scholar] [CrossRef]
- Vermote, E.; Justice, C.; Claverie, M.; Franch, B. Preliminary Analysis of the Performance of the Landsat 8/OLI Land Surface Reflectance Product. Remote Sens. Environ. 2016, 185, 46–56. [Google Scholar] [CrossRef] [PubMed]
- Yan, L.; Roy, D.P. Large-Area Gap Filling of Landsat Reflectance Time Series by Spectral-Angle-Mapper Based Spatio-Temporal Similarity (SAMSTS). Remote Sens. 2018, 10, 609. [Google Scholar] [CrossRef]
- Baret, F.; Jacquemoud, S.; Guyot, G.; Leprieur, C. Modeled Analysis of the Biophysical Nature of Spectral Shifts and Comparison with Information Content of Broad Bands. Remote Sens. Environ. 1992, 41, 133–142. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Verhoef, W.; Baret, F.; Bacour, C.; Zarco-Tejada, P.J.; Asner, G.P.; François, C.; Ustin, S.L. PROSPECT + SAIL Models: A Review of Use for Vegetation Characterization. Remote Sens. Environ. 2009, 113, S56–S66. [Google Scholar] [CrossRef]
- Viña, A.; Gitelson, A.A.; Nguy-Robertson, A.L.; Peng, Y. Comparison of Different Vegetation Indices for the Remote Assessment of Green Leaf Area Index of Crops. Remote Sens. Environ. 2011, 115, 3468–3478. [Google Scholar] [CrossRef]
- Gitelson, A.A. Wide Dynamic Range Vegetation Index for Remote Quantification of Biophysical Characteristics of Vegetation. J. Plant Physiol. 2004, 161, 165–173. [Google Scholar] [CrossRef]
- Tucker, C.J. Red and Photographic Infrared Linear Combinations for Monitoring Vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Kaufman, Y.J.; Merzlyak, M.N. Use of a Green Channel in Remote Sensing of Global Vegetation from EOS-MODIS. Remote Sens. Environ. 1996, 58, 289–298. [Google Scholar] [CrossRef]
- Jordan, C.F. Derivation of Leaf-Area Index from Quality of Light on the Forest Floor. Ecology 1969, 50, 663–666. [Google Scholar] [CrossRef]
- Brown, L.; Chen, J.M.; Leblanc, S.G.; Cihlar, J. A Shortwave Infrared Modification to the Simple Ratio for LAI Retrieval in Boreal Forests: An Image and Model Analysis. Remote Sens. Environ. 2000, 71, 16–25. [Google Scholar] [CrossRef]
- Huete, A.; Justice, C.; Liu, H. Development of Vegetation and Soil Indices for MODIS-EOS. Remote Sens. Environ. 1994, 49, 224–234. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Viña, A.; Arkebauer, T.J.; Rundquist, D.C.; Keydan, G.; Leavitt, B. Remote Estimation of Leaf Area Index and Green Leaf Biomass in Maize Canopies. Geophys. Res. Lett. 2003, 30, 1248. [Google Scholar] [CrossRef]
- Bacour, C.; Baret, F.; Béal, D.; Weiss, M.; Pavageau, K. Neural Network Estimation of LAI, FAPAR, FCover and LAI×Cab, from Top of Canopy MERIS Reflectance Data: Principles and Validation. Remote Sens. Environ. 2006, 105, 313–325. [Google Scholar] [CrossRef]
- Bsaibes, A.; Courault, D.; Baret, F.; Weiss, M.; Olioso, A.; Jacob, F.; Hagolle, O.; Marloie, O.; Bertrand, N.; Desfond, V.; et al. Albedo and LAI Estimates from FORMOSAT-2 Data for Crop Monitoring. Remote Sens. Environ. 2009, 113, 716–729. [Google Scholar] [CrossRef]
- Walthall, C.; Dulaney, W.; Anderson, M.; Norman, J.; Fang, H.; Liang, S. A Comparison of Empirical and Neural Network Approaches for Estimating Corn and Soybean Leaf Area Index from Landsat ETM+ Imagery. Remote Sens. Environ. 2004, 92, 465–474. [Google Scholar] [CrossRef]
- Verrelst, J.; Rivera, J.P.; Veroustraete, F.; Muñoz-Marí, J.; Clevers, J.G.P.W.; Camps-Valls, G.; Moreno, J. Experimental Sentinel-2 LAI Estimation Using Parametric, Non-Parametric and Physical Retrieval Methods—A Comparison. ISPRS J. Photogramm. Remote Sens. 2015, 108, 260–272. [Google Scholar] [CrossRef]
- Vuolo, F.; Neugebauer, N.; Bolognesi, S.F.; Atzberger, C.; D’Urso, G. Estimation of Leaf Area Index Using DEIMOS-1 Data: Application and Transferability of a Semi-Empirical Relationship between Two Agricultural Areas. Remote Sens. 2013, 5, 1274–1291. [Google Scholar] [CrossRef]
- Yang, F.; Sun, J.; Fang, H.; Yao, Z.; Zhang, J.; Zhu, Y.; Song, K.; Wang, Z.; Hu, M. Comparison of Different Methods for Corn LAI Estimation over Northeastern China. Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 462–471. [Google Scholar] [CrossRef]
- Atzberger, C.; Richter, K. Spatially Constrained Inversion of Radiative Transfer Models for Improved LAI Mapping from Future Sentinel-2 Imagery. Remote Sens. Environ. 2012, 120, 208–218. [Google Scholar] [CrossRef]
- Richter, K.; Atzberger, C.; Vuolo, F.; D’Urso, G. Evaluation of Sentinel-2 Spectral Sampling for Radiative Transfer Model Based LAI Estimation of Wheat, Sugar Beet, and Maize. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2011, 4, 458–464. [Google Scholar] [CrossRef]
- Thorp, K.R.; Wang, G.; West, A.L.; Moran, M.S.; Bronson, K.F.; White, J.W.; Mon, J. Estimating Crop Biophysical Properties from Remote Sensing Data by Inverting Linked Radiative Transfer and Ecophysiological Models. Remote Sens. Environ. 2012, 124, 224–233. [Google Scholar] [CrossRef]
- Haboudane, D.; Miller, J.R.; Pattey, E.; Zarco-Tejada, P.J.; Strachan, I.B. Hyperspectral Vegetation Indices and Novel Algorithms for Predicting Green LAI of Crop Canopies: Modeling and Validation in the Context of Precision Agriculture. Remote Sens. Environ. 2004, 90, 337–352. [Google Scholar] [CrossRef]
- Liu, J.; Pattey, E.; Jégo, G. Assessment of Vegetation Indices for Regional Crop Green LAI Estimation from Landsat Images over Multiple Growing Seasons. Remote Sens. Environ. 2012, 123, 347–358. [Google Scholar] [CrossRef]
- Roujean, J.-L.; Breon, F.-M. Estimating PAR Absorbed by Vegetation from Bidirectional Reflectance Measurements. Remote Sens. Environ. 1995, 51, 375–384. [Google Scholar] [CrossRef]
- Rondeaux, G.; Steven, M.; Baret, F. Optimization of Soil-Adjusted Vegetation Indices. Remote Sens. Environ. 1996, 55, 95–107. [Google Scholar] [CrossRef]
- Qi, J.; Chehbouni, A.; Huete, A.R.; Kerr, Y.H.; Sorooshian, S. A Modified Soil Adjusted Vegetation Index. Remote Sens. Environ. 1994, 48, 119–126. [Google Scholar] [CrossRef]
- Vincini, M.; Frazzi, E.; D’Alessio, P. Angular Dependence of Maize and Sugar Beet VIs from Directional CHRIS/Proba Data. In Proceedings of the 4th ESA CHRIS PROBA Workshop, Frascati, Italy, 19–21 September 2006; Volume 2006, pp. 19–21. [Google Scholar]
- Danson, F.M.; Rowland, C.S.; Baret, F. Training a Neural Network with a Canopy Reflectance Model to Estimate Crop Leaf Area Index. Int. J. Remote Sens. 2003, 24, 4891–4905. [Google Scholar] [CrossRef]
- Houborg, R.; McCabe, M.F. A Hybrid Training Approach for Leaf Area Index Estimation via Cubist and Random Forests Machine-Learning. ISPRS J. Photogramm. Remote Sens. 2018, 135, 173–188. [Google Scholar] [CrossRef]
- Pan, J.; Yang, H.; He, W.; Xu, P. Retrieve Leaf Area Index from HJ-CCD Image Based on Support Vector Regression and Physical Model. In Proceedings of the Remote Sensing for Agriculture, Ecosystems, and Hydrology XV, SPIE, Dresden, Germany, 24–26 September 2013; Volume 8887, p. 88871R. [Google Scholar]
- Duan, S.-B.; Li, Z.-L.; Wu, H.; Tang, B.-H.; Ma, L.; Zhao, E.; Li, C. Inversion of the PROSAIL Model to Estimate Leaf Area Index of Maize, Potato, and Sunflower Fields from Unmanned Aerial Vehicle Hyperspectral Data. Int. J. Appl. Earth Obs. Geoinf. 2014, 26, 12–20. [Google Scholar] [CrossRef]
- Rivera, J.P.; Verrelst, J.; Leonenko, G.; Moreno, J. Multiple Cost Functions and Regularization Options for Improved Retrieval of Leaf Chlorophyll Content and LAI through Inversion of the PROSAIL Model. Remote Sens. 2013, 5, 3280–3304. [Google Scholar] [CrossRef]
- Liu, C.; White, M.; Newell, G. Measuring and Comparing the Accuracy of Species Distribution Models with Presence-Absence Data. Ecography (Cop.) 2011, 34, 232–243. [Google Scholar] [CrossRef]
- Bennett, N.D.; Croke, B.F.W.; Guariso, G.; Guillaume, J.H.A.; Hamilton, S.H.; Jakeman, A.J.; Marsili-Libelli, S.; Newham, L.T.H.; Norton, J.P.; Perrin, C.; et al. Characterising Performance of Environmental Models. Environ. Model. Softw. 2013, 40, 1–20. [Google Scholar] [CrossRef]
- Li, J.; Heap, A.D. A Review of Spatial Interpolation Methods for Environmental Scientists. Aust. Geol. Surv. Organ. 2008, 68, 154. [Google Scholar]
- Li, J. Assessing the Accuracy of Predictive Models for Numerical Data: Not r nor R2, Why Not? Then What? PLoS ONE 2017, 12, e0183250. [Google Scholar] [CrossRef]
- Houborg, R.; Anderson, M.C. Utility of an Image-Based Canopy Reflectance Modeling Tool for Remote Estimation of LAI and Leaf Chlorophyll Content in Crop Systems. Int. Geosci. Remote Sens. Symp. 2008, 2, 141–144. [Google Scholar] [CrossRef][Green Version]
- Shibayama, M.; Sakamoto, T.; Takada, E.; Inoue, A.; Morita, K.; Yamaguchi, T.; Takahashi, W.; Kimura, A. Regression-Based Models to Predict Rice Leaf Area Index Using Biennial Fixed Point Continuous Observations of near Infrared Digital Images. Plant Prod. Sci. 2011, 14, 365–376. [Google Scholar] [CrossRef]
- Houborg, R.; Boegh, E. Mapping Leaf Chlorophyll and Leaf Area Index Using Inverse and Forward Canopy Reflectance Modeling and SPOT Reflectance Data. Remote Sens. Environ. 2008, 112, 186–202. [Google Scholar] [CrossRef]
- Aragão, L.E.O.C.; Shimabukuro, Y.E.; Espírito-Santo, F.D.B.; Williams, M. Spatial Validation of the Collection 4 MODIS LAI Product in Eastern Amazonia. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2526–2534. [Google Scholar] [CrossRef]
- Cohen, W.B.; Maiersperger, T.K.; Yang, Z.; Gower, S.T.; Turner, D.P.; Ritts, W.D.; Berterretche, M.; Running, S.W. Comparisons of Land Cover and LAI Estimates Derived from ETM+ and MODIS for Four Sites in North America: A Quality Assessment of 2000/2001 Provisional MODIS Products. Remote Sens. Environ. 2003, 88, 233–255. [Google Scholar] [CrossRef]
- Eklundh, L.; Harrie, L.; Kuusk, A. Investigating Relationships between Landsat ETM+ Sensor Data and Leaf Area Index in a Boreal Conifer Forest. Remote Sens. Environ. 2001, 78, 239–251. [Google Scholar] [CrossRef]
- Pu, R.; Yu, Q.; Gong, P.; Biging, G.S. EO-1 Hyperion, ALI and Landsat 7 ETM+ Data Comparison for Estimating Forest Crown Closure and Leaf Area Index. Int. J. Remote Sens. 2005, 26, 457–474. [Google Scholar] [CrossRef]
- He, L.; Ren, X.; Wang, Y.; Liu, B.; Zhang, H.; Liu, W.; Feng, W.; Guo, T. Comparing Methods for Estimating Leaf Area Index by Multi-Angular Remote Sensing in Winter Wheat. Sci. Rep. 2020, 10, 13943. [Google Scholar] [CrossRef]
- Hosseini, M.; McNairn, H.; Merzouki, A.; Pacheco, A. Estimation of Leaf Area Index (LAI) in Corn and Soybeans Using Multi-Polarization C- and L-Band Radar Data. Remote Sens. Environ. 2015, 170, 77–89. [Google Scholar] [CrossRef]
- Chen, J.M.; Pavlic, G.; Brown, L.; Cihlar, J.; Leblanc, S.G.; White, H.P.; Hall, R.J.; Peddle, D.R.; King, D.J.; Trofymow, J.A.; et al. Derivation and Validation of Canada-Wide Coarse-Resolution Leaf Area Index Maps Using High-Resolution Satellite Imagery and Ground Measurements. Remote Sens. Environ. 2002, 80, 165–184. [Google Scholar] [CrossRef]
| Year | Site 1 | Site 2 | Site 3 |
|---|---|---|---|
| 2001 | Corn | Corn | Corn |
| 2002 | Corn | Soybean | Soybean |
| 2003 | Corn | Corn | Corn |
| 2004 | Corn | Soybean | Soybean |
| 2005 | Corn | Corn | Corn |
| 2006 | Corn | Soybean | Soybean |
| 2007 | Corn | Corn | Corn |
| 2008 | Corn | Soybean | Soybean |
| 2009 | Corn | Corn | Corn |
| 2010 | Corn | Corn | Soybean |
| 2011 | Corn | Corn | Corn |
| 2012 | Corn | Corn | Soybean |
| 2013 | Corn | Corn | Corn |
| 2014 | Corn | Soybean | Soybean |
| 2015 | Corn | Corn | Corn |
| 2016 | Corn | Soybean | Soybean |
| Year | NE | SE | NW | SW |
|---|---|---|---|---|
| 1995 | - | - | Irrigated soybean | Irrigated soybean |
| 2003 | Irrigated soybean | Irrigated soybean | - | - |
| 2004 | Irrigated soybean | Irrigated soybean | - | - |
| 2006 | Irrigated corn | - | - | - |
| 2007 | - | Irrigated corn | - | - |
| 2010 | - | - | Dryland soybean | Dryland soybean |
| Sites | Spatial Resolution | Sensors | WRS2 Tiles |
|---|---|---|---|
| Mead, NE | 30 m | Landsat 5 TM, Landsat 7 ETM+, Landsat 8 OLI | Path 28 Row 31 |
| Bushland, TX | 30 m | Landsat 5 TM, Landsat 7 ETM+ | Path 30 Row 36, Path 31 Row 35, Path 31 Row 36 |
| Index | Formula | References |
|---|---|---|
| NDVI | [64] | |
| gNDVI | [65] | |
| SR | [66] | |
| RSR | [67] | |
| EVI | [68] | |
| GARVI | [65] | |
| WDRVI | [63] | |
| gWDRVI | [63] | |
| Clgreen | [69] |
| Models | Sites | Crop Types | Settings | References |
|---|---|---|---|---|
| SVM | Italy, Austria | Multiple types | Linear kernel function, least square | [74] |
| NN | Northeastern China | Corn | Back-propagation algorithm for minimizing misfit function | [75] |
| RF | Italy, Austria | Multiple types | Number of trees = 500 Number of input var at each split = 2 | [74] |
| Model | Parameters | Abbr. | Units | Ranges | Distribution |
|---|---|---|---|---|---|
| PROSPECT | Leaf structure index | N | Unitless | 1–2.5 | Uniform |
| Leaf chlorophyll content | Cab | μg/cm2 | 10–80 | Gaussian (μ:45, σ:20) | |
| Leaf dry matter content | Cm | g/cm2 | 0.001–0.03 | Uniform | |
| Leaf water content | Cw | cm | 0.002–0.05 | Uniform | |
| Brown pigments content | Cbp | Unitless | 0–2 | Uniform | |
| Leaf carotenoid content | Car | μg/cm2 | 0–16 | Uniform | |
| SAILH | Leaf area index | LAI | m2/m2 | 0.1–7 | Gaussian |
| Hot spot parameter | SL | Unitless | 0.05–1 | Uniform | |
| Soil reflectance factor | ρS | Unitless | 0–1 | Uniform | |
| Solar zenith angle | θS | Degree | Based on Landsat data acquisition conditions | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nandan, R.; Bandaru, V.; He, J.; Daughtry, C.; Gowda, P.; Suyker, A.E. Evaluating Optical Remote Sensing Methods for Estimating Leaf Area Index for Corn and Soybean. Remote Sens. 2022, 14, 5301. https://doi.org/10.3390/rs14215301
Nandan R, Bandaru V, He J, Daughtry C, Gowda P, Suyker AE. Evaluating Optical Remote Sensing Methods for Estimating Leaf Area Index for Corn and Soybean. Remote Sensing. 2022; 14(21):5301. https://doi.org/10.3390/rs14215301
Chicago/Turabian StyleNandan, Rohit, Varaprasad Bandaru, Jiaying He, Craig Daughtry, Prasanna Gowda, and Andrew E. Suyker. 2022. "Evaluating Optical Remote Sensing Methods for Estimating Leaf Area Index for Corn and Soybean" Remote Sensing 14, no. 21: 5301. https://doi.org/10.3390/rs14215301
APA StyleNandan, R., Bandaru, V., He, J., Daughtry, C., Gowda, P., & Suyker, A. E. (2022). Evaluating Optical Remote Sensing Methods for Estimating Leaf Area Index for Corn and Soybean. Remote Sensing, 14(21), 5301. https://doi.org/10.3390/rs14215301





