A Novel Waveform Decomposition and Spectral Extraction Method for 101-Channel Hyperspectral LiDAR
Abstract
1. Introduction
- To put forward a new decomposition method for HSL waveform data with 101 channels, including SCWD and MCMCD, which will help effectively extract target distance and intensity information in different channels of wavelengths;
- To restore and retrieve the feature spectrum of the target by selecting the wavelength based on the result of assessing HSL decomposition;
- To design an experiment to verify the correctness and effectiveness of this method and explore the spectral changes before and after the target is covered.
2. Materials and Methods
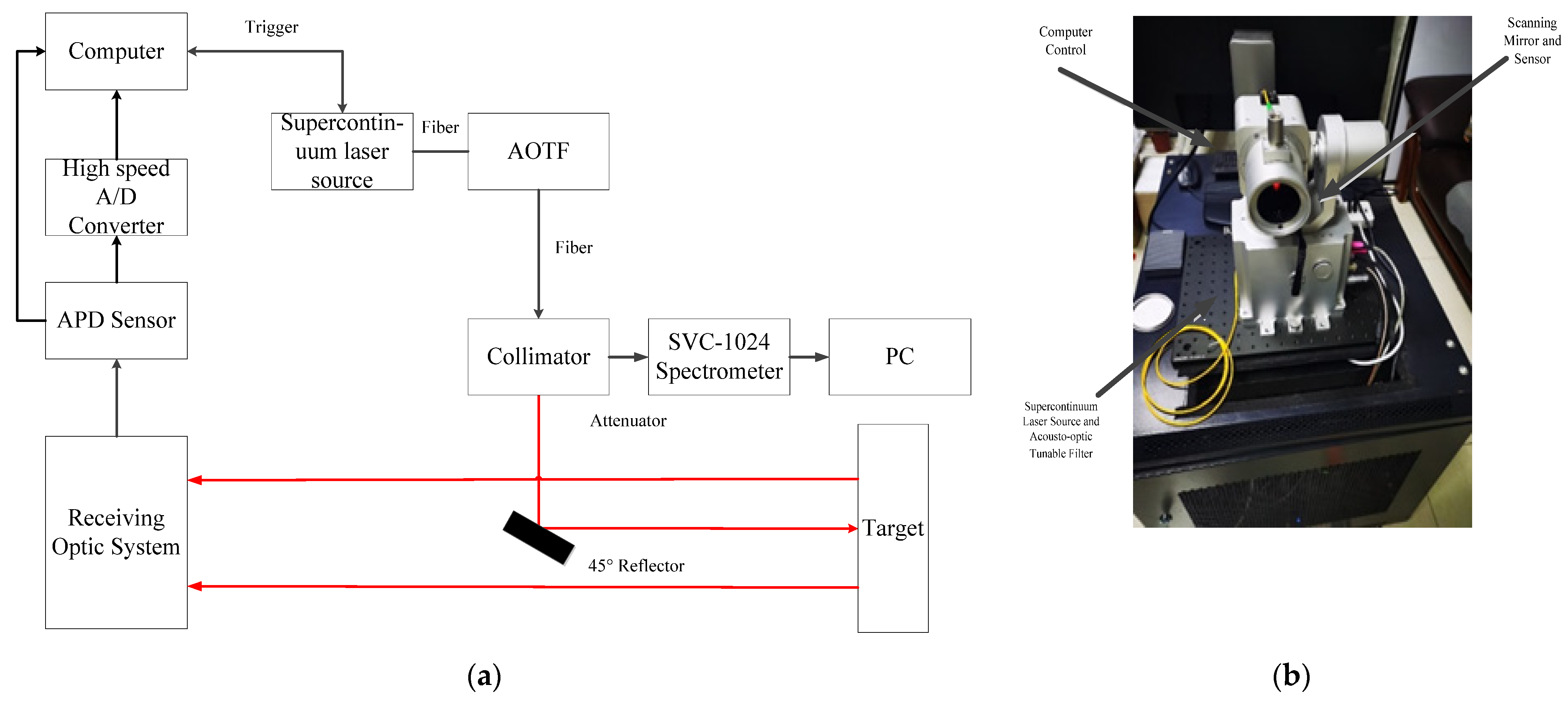
2.1. 101-Channel FWHSL System
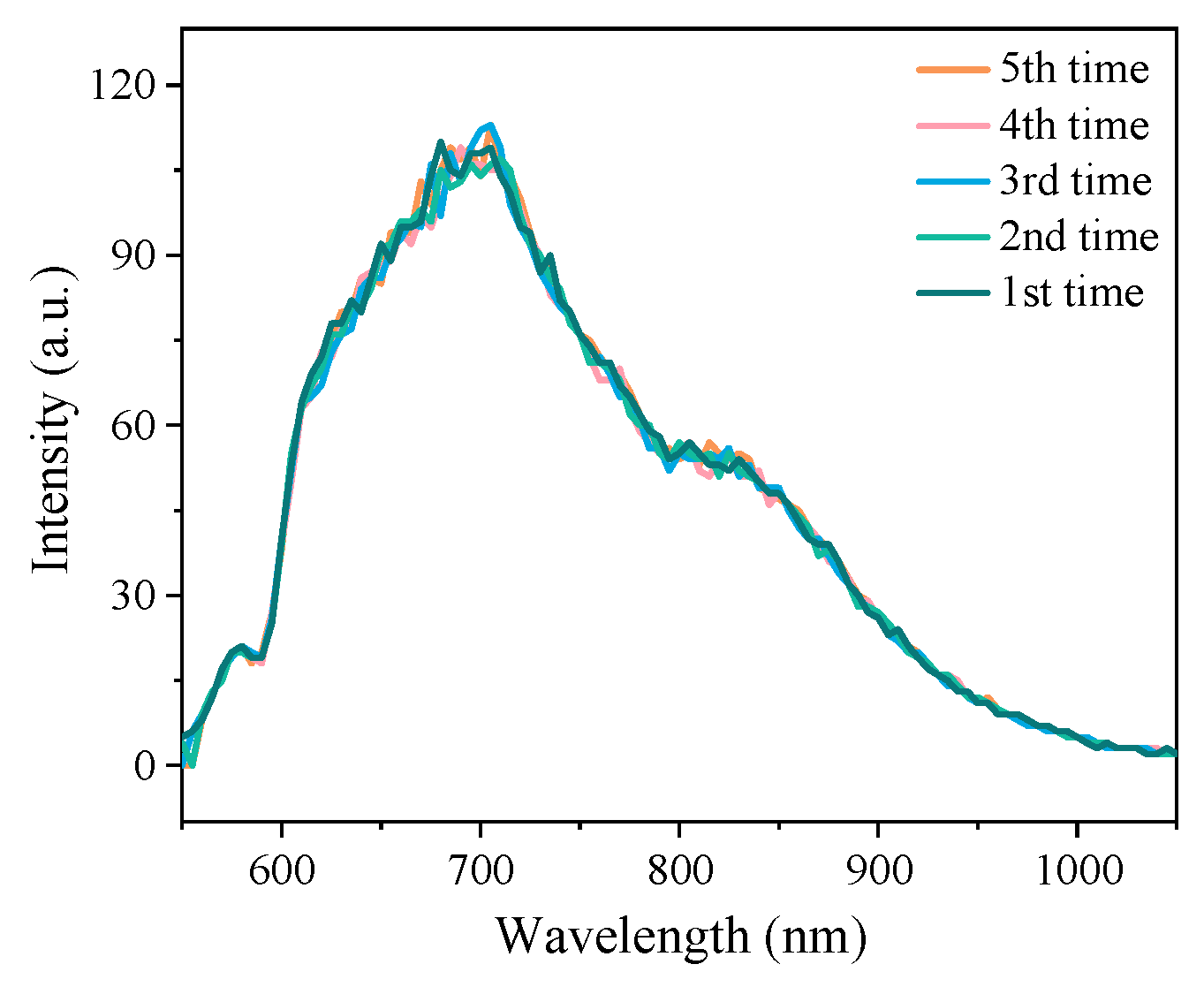
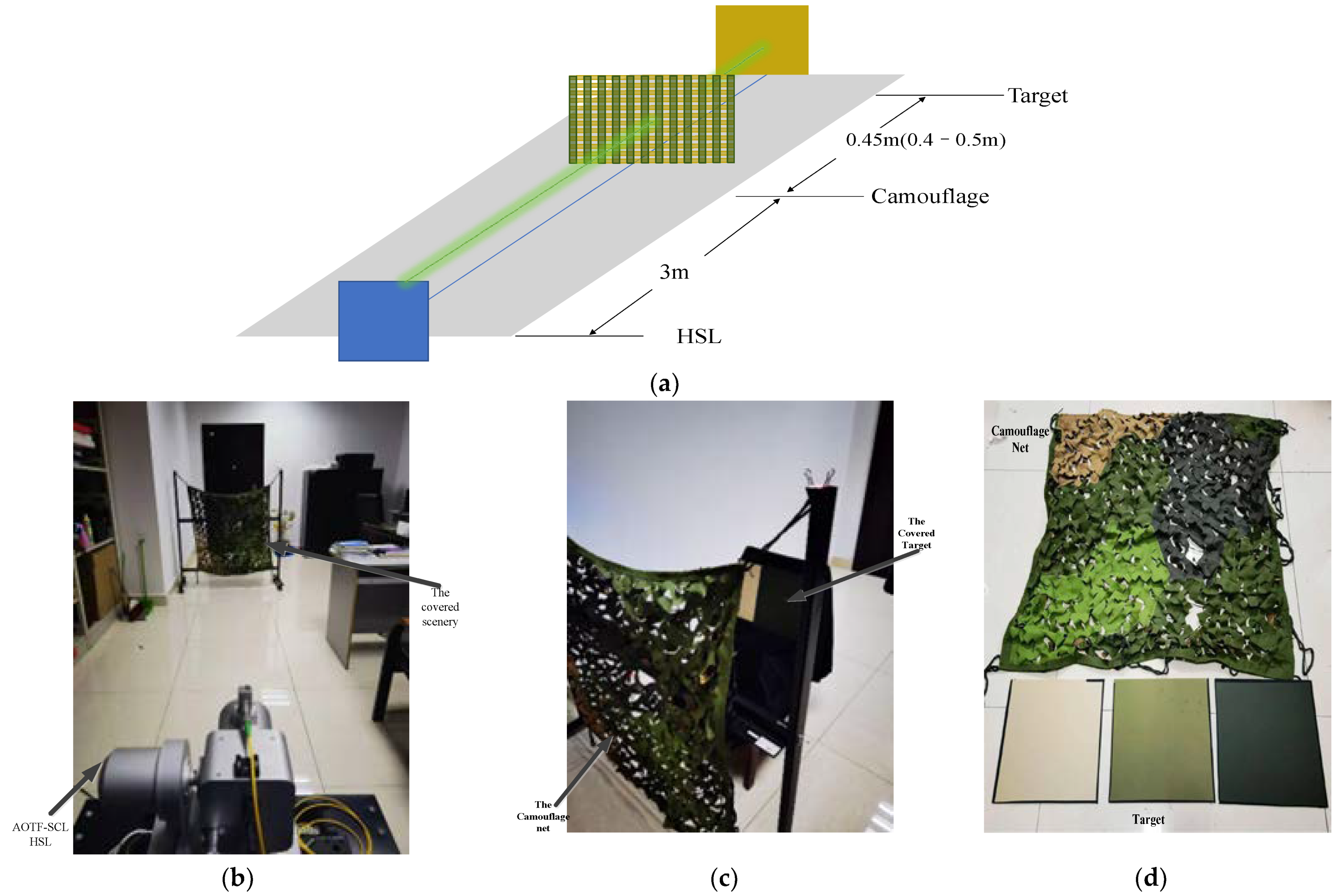
2.2. Experiment
2.3. Methods
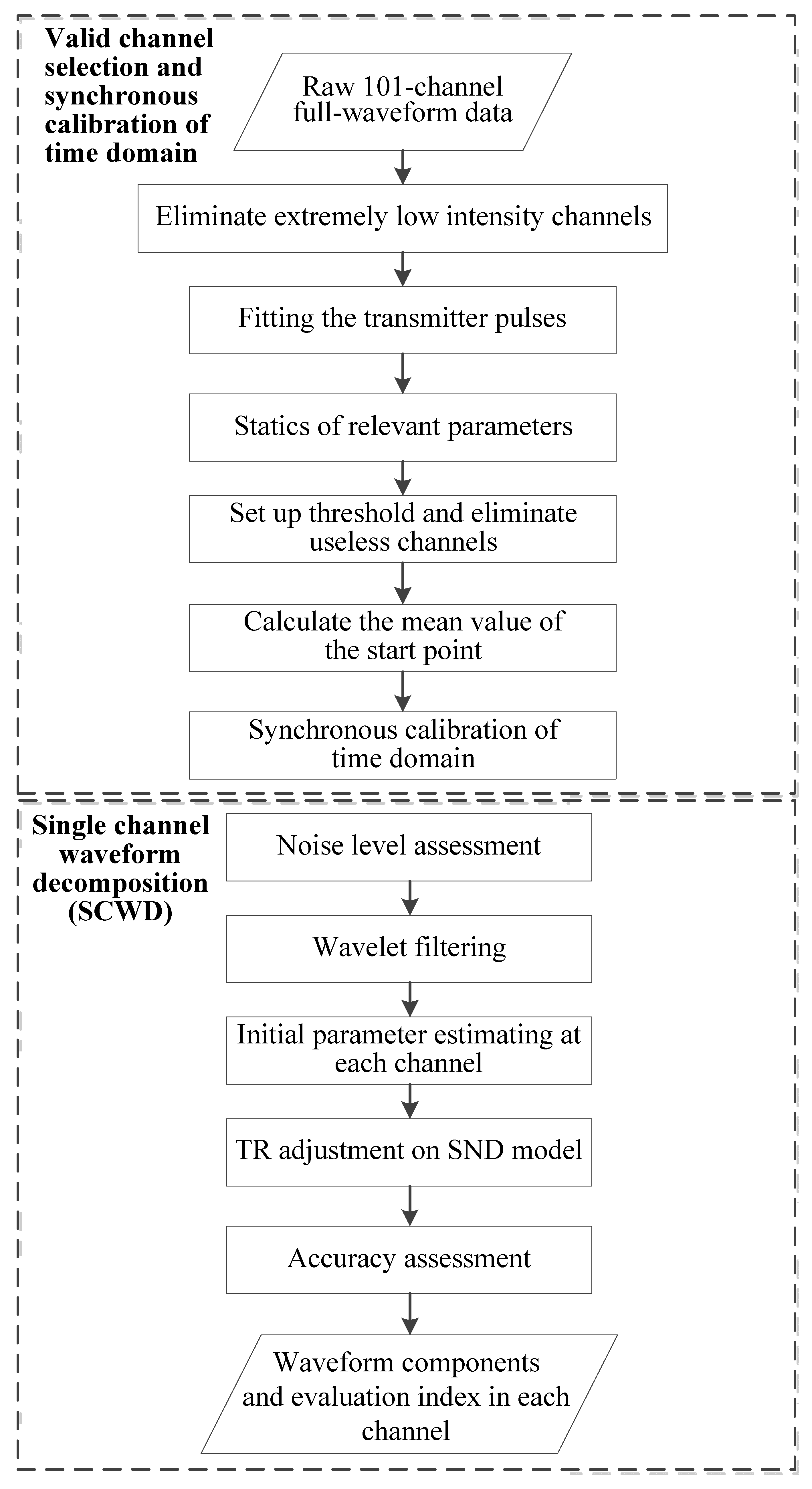
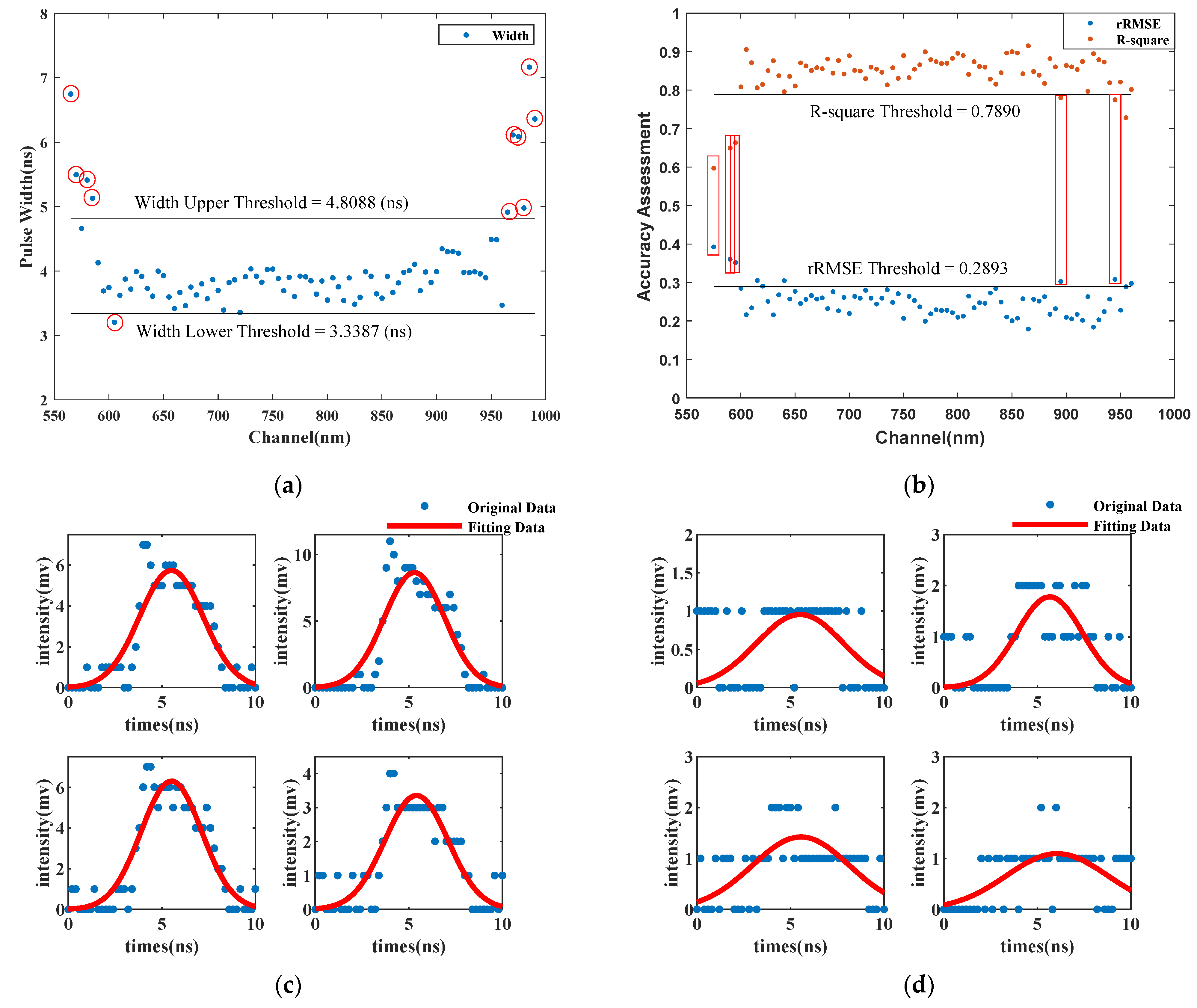
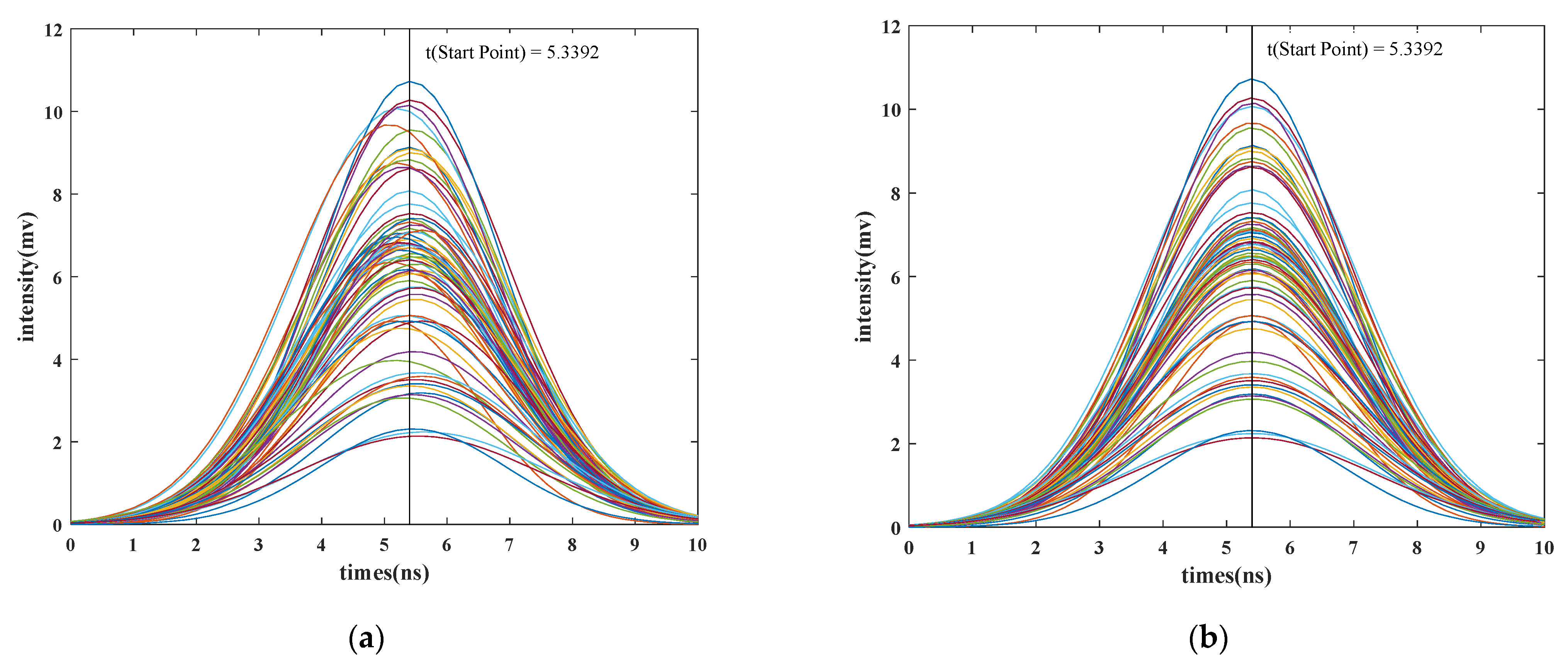
2.3.1. Valid Channel Selection and Synchronous Calibration of Time Domain
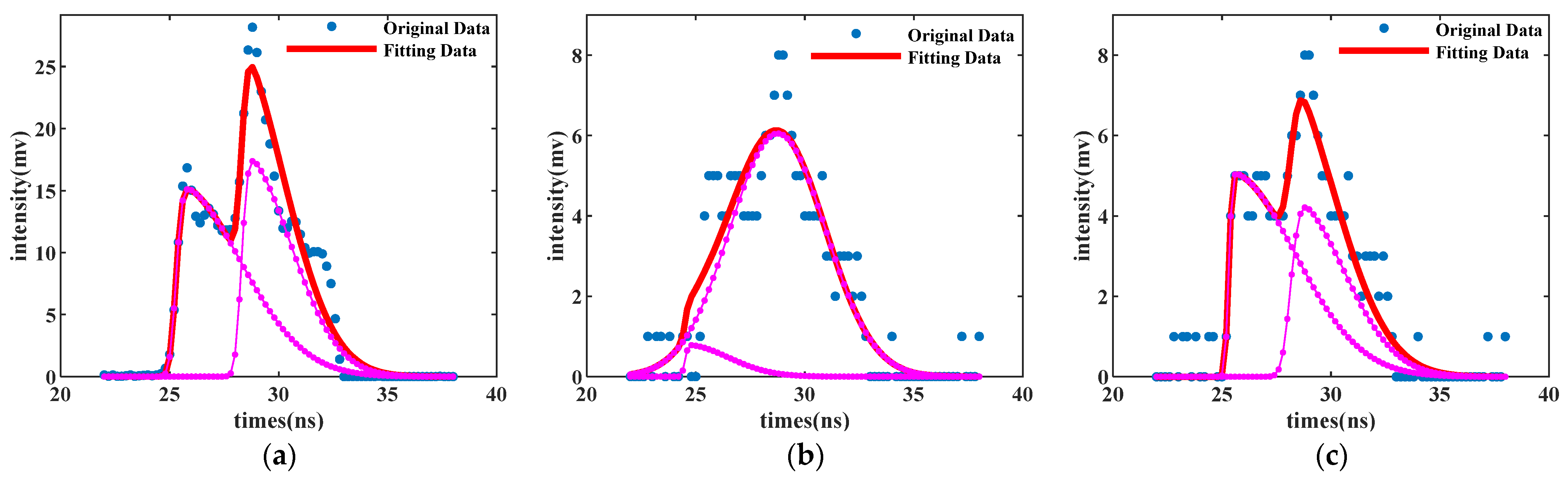
2.3.2. 101-Channel HSL Waveform Decomposition Method
- Denoising and Filtering
- Modeling
- Single-Channel Waveform Decomposition (SCWD) Step
- Multi-Channel Mutual Complementary Decomposition (MCMCD) Step
2.3.3. Channel Selection and Spectrum Restoration
- Standardize the initial indicators;
- Calculate the covariance matrix of the data and the eigenvalues and eigenvectors of the covariance matrix;
- Sort the eigenvalues from largest to smallest;
- Calculate the contribution rate and select the first several eigenvalues and corresponding eigenvectors whose contribution rate sum can summarize the most original data information;
- Transform the data into a new space constructed from the first several eigenvectors.
3. Results
3.1. Valid Channel Selection Results and Calibration of Data in Time Domain
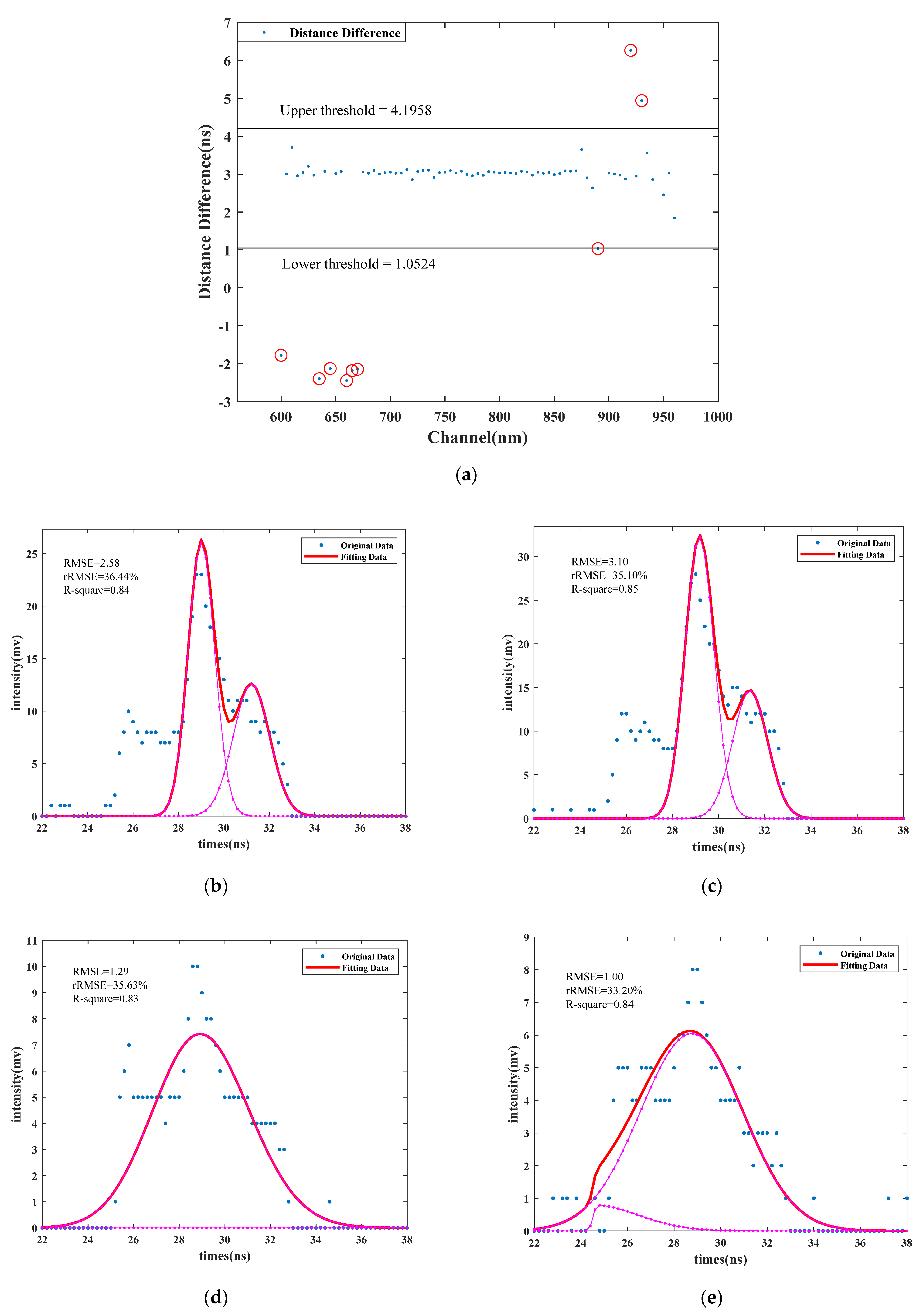
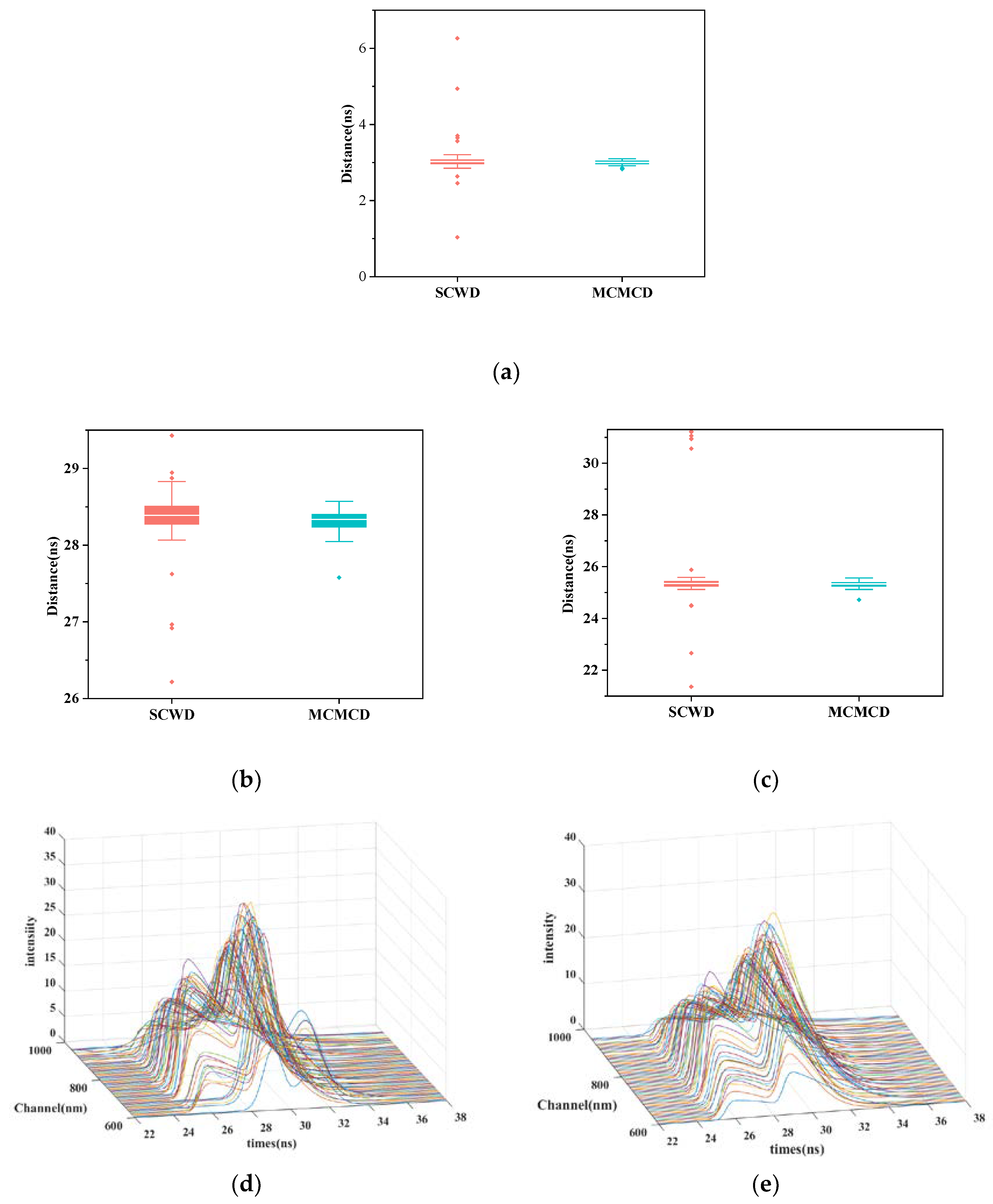
3.2. Distance Retrieval Results and Comparison between SCWD and MCMCD
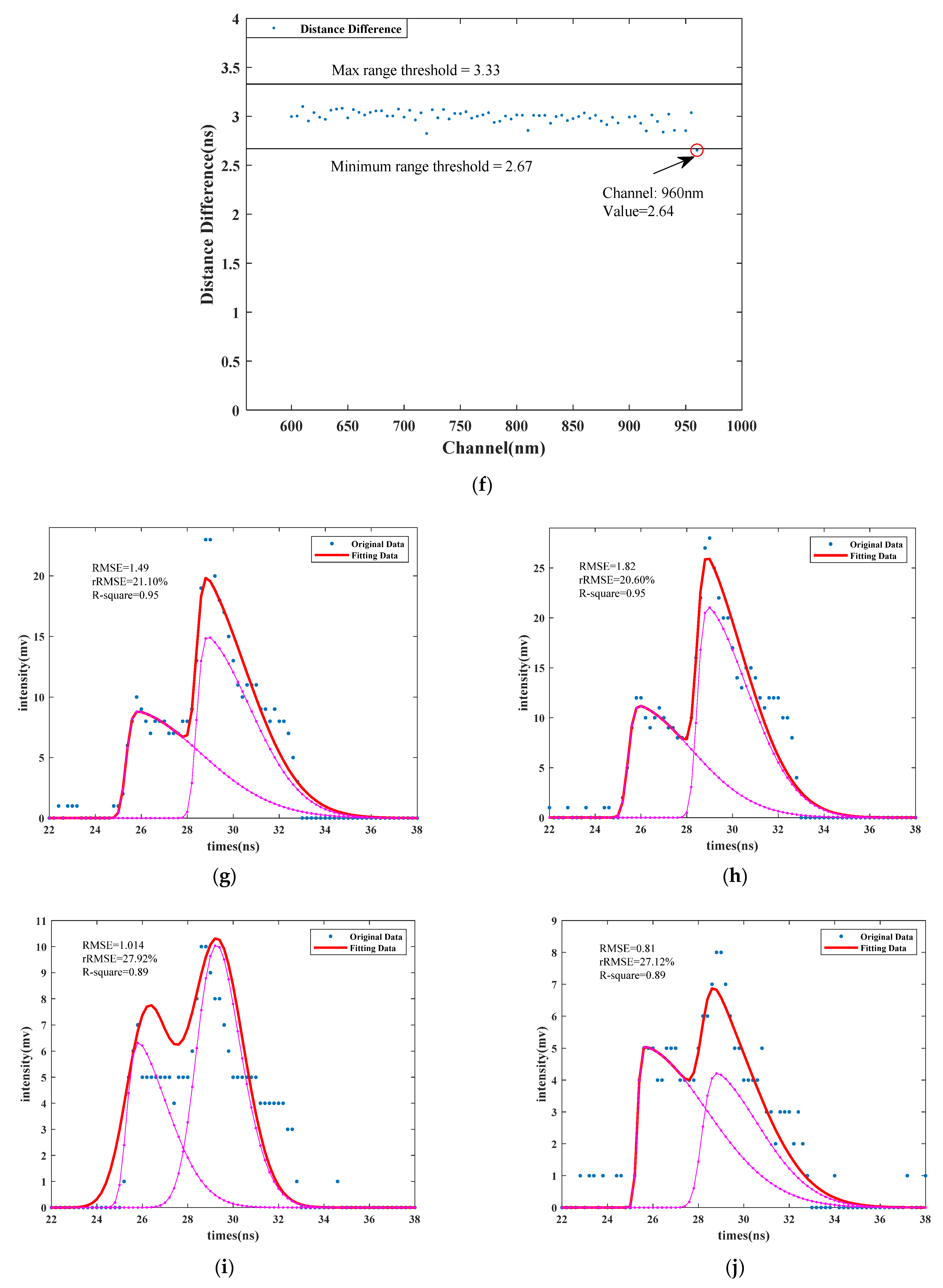
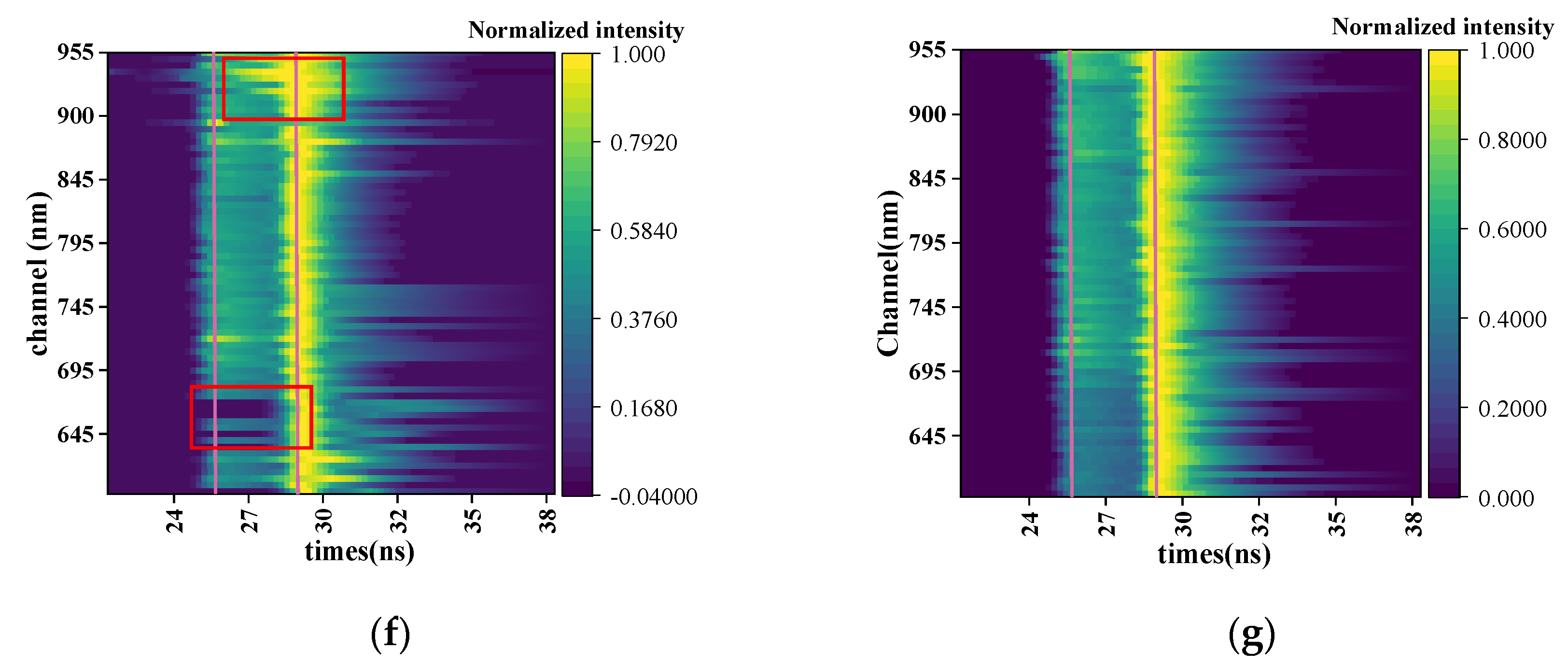
3.3. Comparison with Other Multi-Channel Decomposition Method
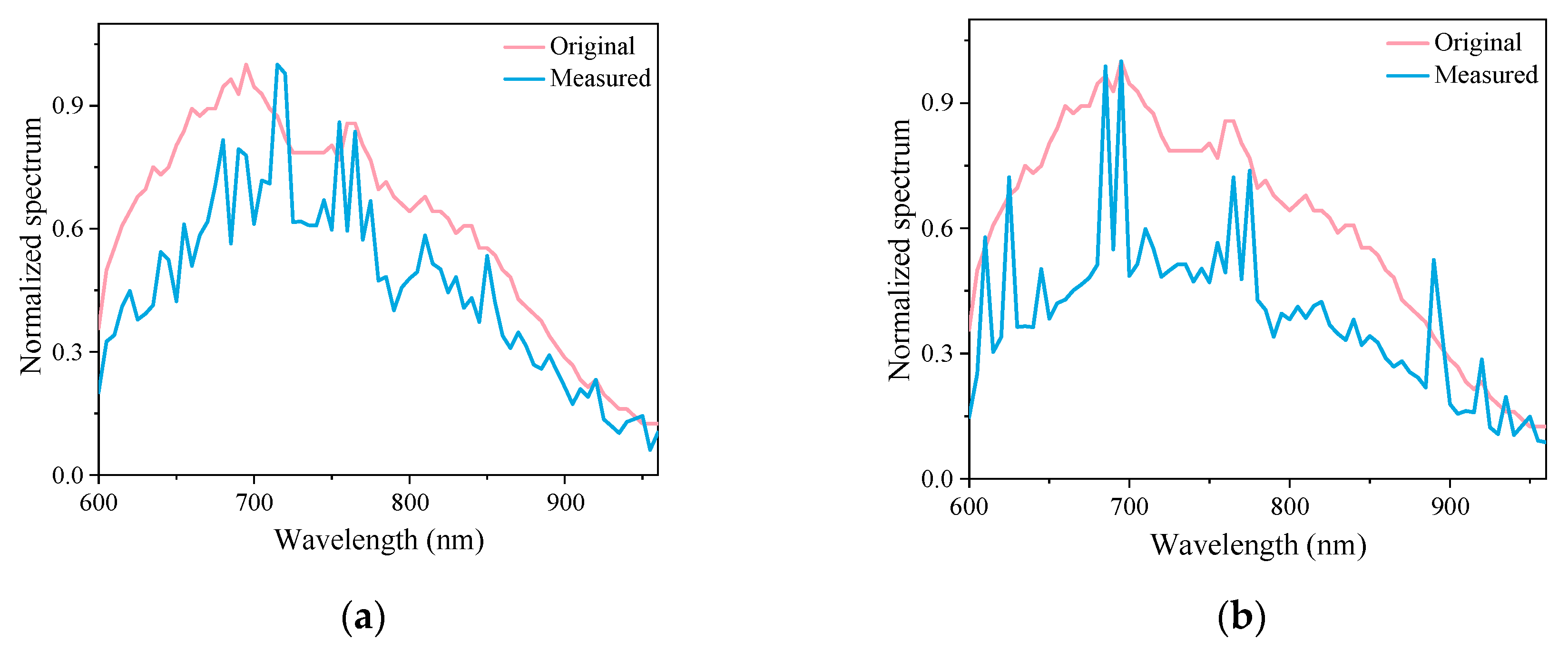
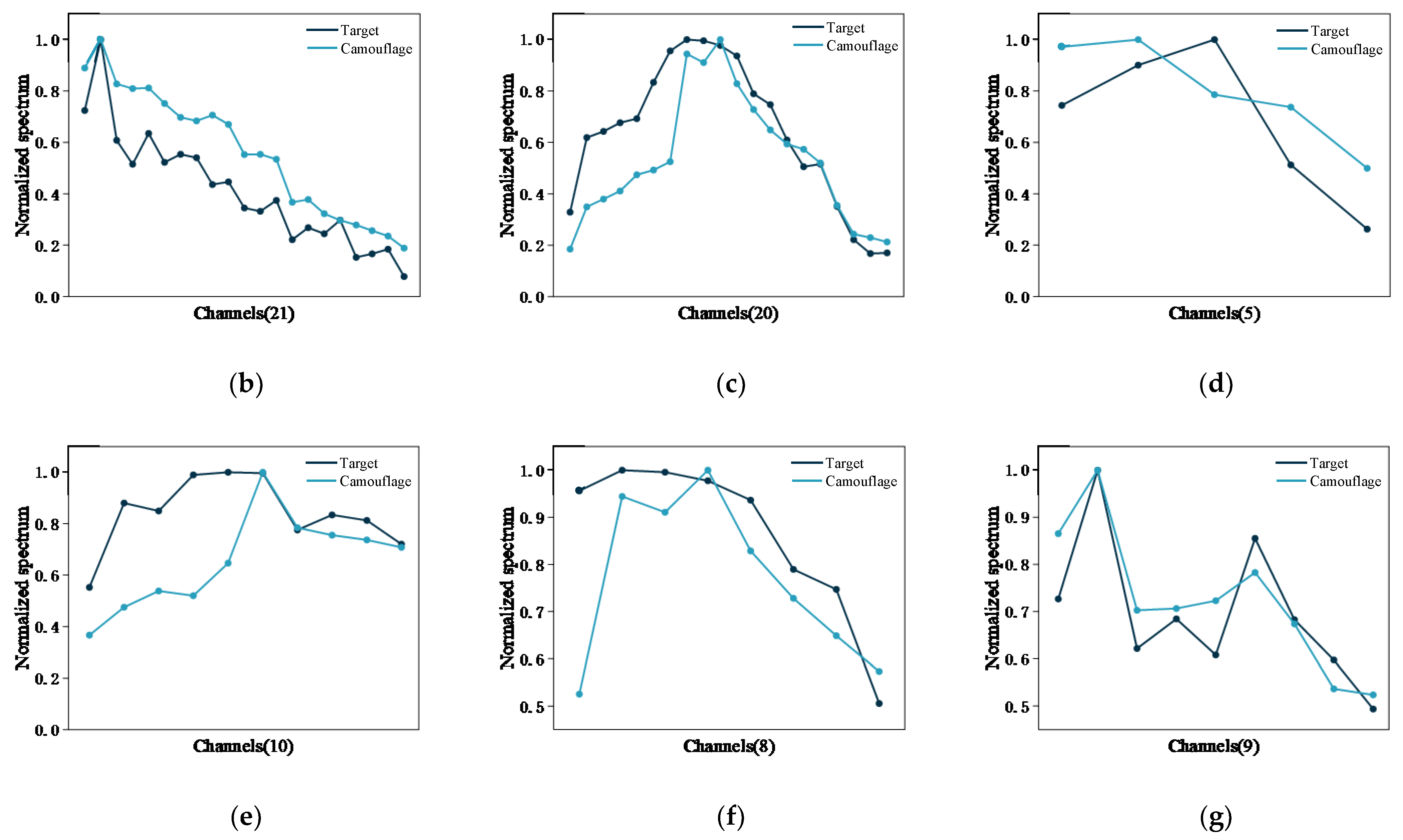
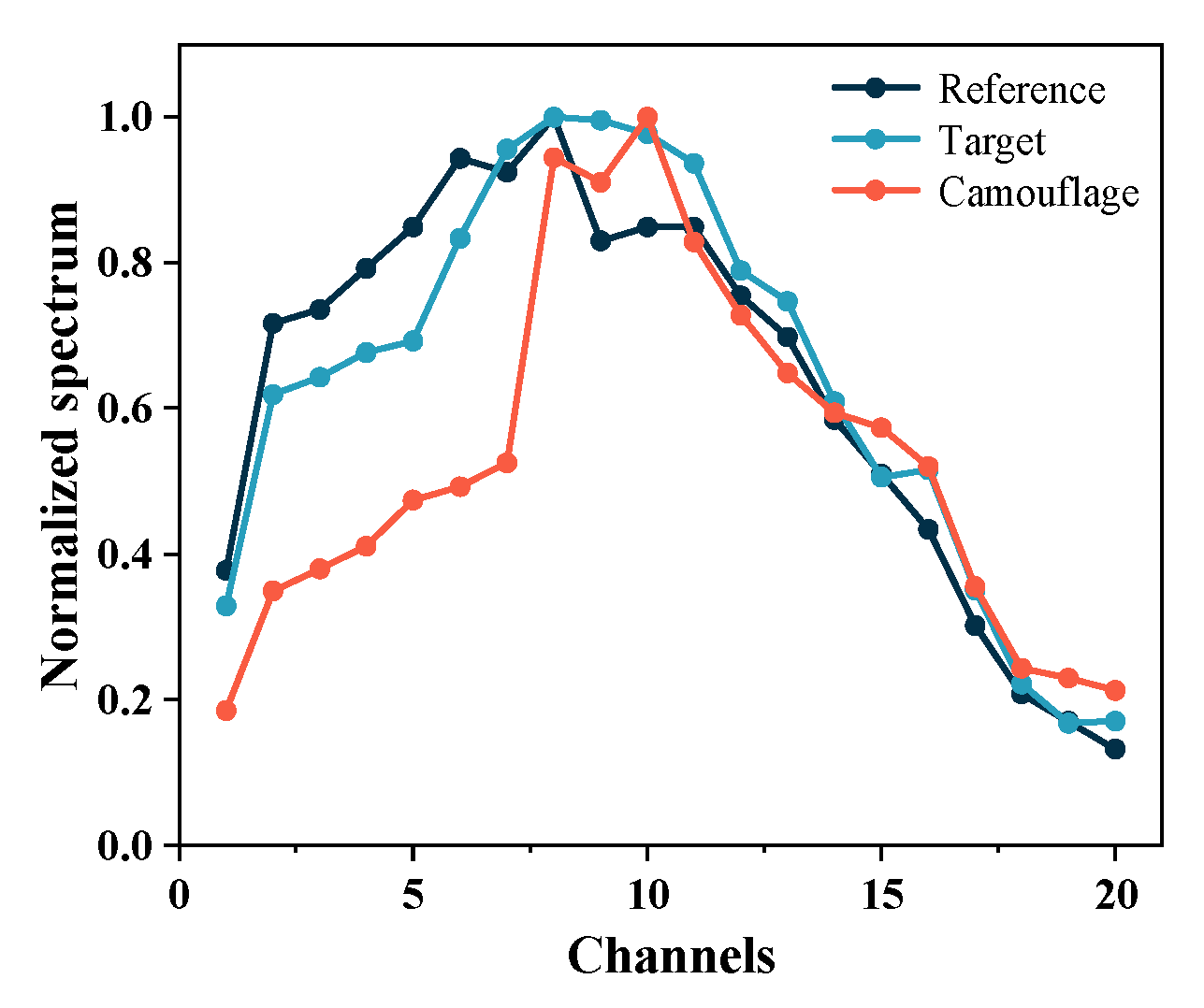
3.4. Characteristic Wavelength Selection and Spectral Restoration Result
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tan, K.; Cheng, X. Correction of Incidence Angle and Distance Effects on TLS Intensity Data Based on Reference Targets. Remote Sens. 2016, 8, 251. [Google Scholar] [CrossRef]
- Mallet, C.; Bretar, F. Full-Waveform Topographic Lidar: State-of-the-Art. ISPRS J. Photogramm. Remote Sens. 2009, 64, 1–16. [Google Scholar] [CrossRef]
- Wagner, W. Radiometric Calibration of Small-Footprint Full-Waveform Airborne Laser Scanner Measurements: Basic Physical Concepts. ISPRS J. Photogramm. Remote Sens. 2010, 65, 505–513. [Google Scholar] [CrossRef]
- Wang, C.-K.; Tseng, Y.-H.; Wang, C.-K. A Wavelet-Based Echo Detector for Waveform LiDAR Data. IEEE Trans. Geosci. Remote Sens. 2016, 54, 757–769. [Google Scholar] [CrossRef]
- Parrish, C.E.; Jeong, I.; Nowak, R.D.; Smith, R.B. Empirical Comparison of Full-Waveform Lidar Algorithms. Photogramm. Eng. Remote Sens. 2011, 77, 825–838. [Google Scholar] [CrossRef]
- Chen, B.; Shi, S.; Gong, W.; Zhang, Q.; Yang, J.; Du, L.; Sun, J.; Zhang, Z.; Song, S. Multispectral LiDAR Point Cloud Classification: A Two-Step Approach. Remote Sens. 2017, 9, 373. [Google Scholar] [CrossRef]
- Kukkonen, M.; Maltamo, M.; Korhonen, L.; Packalen, P. Comparison of Multispectral Airborne Laser Scanning and Stereo Matching of Aerial Images as a Single Sensor Solution to Forest Inventories by Tree Species. Remote Sens. Env. 2019, 231, 111208. [Google Scholar] [CrossRef]
- Sumnall, M.J.; Hill, R.A.; Hinsley, S.A. Comparison of Small-Footprint Discrete Return and Full Waveform Airborne Lidar Data for Estimating Multiple Forest Variables. Remote Sens. Env. 2016, 173, 214–223. [Google Scholar] [CrossRef]
- Lin, Y.; West, G. Retrieval of Effective Leaf Area Index (LAIe) and Leaf Area Density (LAD) Profile at Individual Tree Level Using High Density Multi-Return Airborne LiDAR. Int. J. Appl. Earth Obs. Geoinf. 2016, 50, 150–158. [Google Scholar] [CrossRef]
- Bi, K.; Xiao, S.; Gao, S.; Zhang, C.; Huang, N.; Niu, Z. Estimating Vertical Chlorophyll Concentrations in Maize in Different Health States Using Hyperspectral LiDAR. IEEE Trans. Geosci. Remote Sens. 2020, 58, 8125–8133. [Google Scholar] [CrossRef]
- Li, W.; Niu, Z.; Sun, G.; Gao, S.; Wu, M. Deriving Backscatter Reflective Factors from 32-Channel Full-Waveform LiDAR Data for the Estimation of Leaf Biochemical Contents. Opt. Express 2016, 24, 4771. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Gao, S.; Li, W.; Bi, K.; Huang, N.; Niu, Z.; Sun, G. Radiometric Calibration for Incidence Angle, Range and Sub-Footprint Effects on Hyperspectral LiDAR Backscatter Intensity. Remote Sens. 2020, 12, 1–18. [Google Scholar] [CrossRef]
- Chen, B.; Shi, S.; Sun, J.; Chen, B.; Guo, K.; Du, L.; Yang, J.; Xu, Q.; Song, S.; Gong, W. Using HSI Color Space to Improve the Multispectral Lidar Classification Error Caused by Measurement Geometry. IEEE Trans. Geosci. Remote Sens. 2021, 59, 3567–3579. [Google Scholar] [CrossRef]
- Wang, B.; Song, S.; Shi, S.; Chen, Z.; Li, F.; Wu, D.; Liu, D.; Gong, W. Multichannel Interconnection Decomposition for Hyperspectral LiDAR Waveforms Detected From Over 500 m. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Luo, B.; Yang, J.; Song, S.; Shi, S.; Gong, W.; Wang, A.; Du, L. Target Classification of Similar Spatial Characteristics in Complex Urban Areas by Using Multispectral LiDAR. Remote Sens. 2022, 14, 238. [Google Scholar] [CrossRef]
- Hakala, T.; Suomalainen, J.; Kaasalainen, S. Full waveform active hyperspectral LiDAR. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, XXXIX-B7, 459–462. [Google Scholar] [CrossRef]
- Suomalainen, J.; Hakala, T.; Kaartinen, H.; Räikkönen, E.; Kaasalainen, S. Demonstration of a Virtual Active Hyperspectral Lidar in Automated Point Cloud Classification. ISPRS J. Photogramm. Remote Sens. 2011, 66, 637–641. [Google Scholar] [CrossRef]
- Chen, Y.; Li, W.; Hyyppä, J.; Wang, N.; Jiang, C.; Meng, F.; Tang, L.; Puttonen, E.; Li, C. A 10-Nm Spectral Resolution Hyperspectral LiDAR System Based on an Acousto-Optic Tunable Filter. Sensors 2019, 19, 1620. [Google Scholar] [CrossRef]
- Hu, P.-L.; Chen, Y.-W.; Jiang, C.-H.; Lin, Q.-N.; Li, W.; Qi, J.-B.; Yu, L.-F.; Shao, H.; Huang, H.-G. Spectral Observation and Classification of Typical Tree Species Leaves Based on Indoor Hyperspectral Lidar. J. Infrared Millim. Waves 2020, 39, 372–380. [Google Scholar]
- Song, S.; Wang, B.; Gong, W.; Chen, Z.; Lin, X.; Sun, J.; Shi, S. A New Waveform Decomposition Method for Multispectral LiDAR. ISPRS J. Photogramm. Remote Sens. 2019, 149, 40–49. [Google Scholar] [CrossRef]
- Saini, T.S.; Baili, A.; Kumar, A.; Cherif, R.; Zghal, M.; Sinha, R.K. Design and Analysis of Equiangular Spiral Photonic Crystal Fiber for Mid-Infrared Supercontinuum Generation. J. Mod. Opt. 2015, 62, 1–7. [Google Scholar] [CrossRef]
- Yang, H.; Han, F.; Hu, H.; Wang, W.; Zeng, Q. Spectral-Temporal Analysis of Dispersive Wave Generation in Photonic Crystal Fibers of Different Dispersion Slope. J. Mod. Opt. 2014, 61, 409–414. [Google Scholar] [CrossRef]
- Eitel, J.U.H.; Magney, T.S.; Vierling, L.A.; Dittmar, G. Assessment of Crop Foliar Nitrogen Using a Novel Dual-Wavelength Laser System and Implications for Conducting Laser-Based Plant Physiology. ISPRS J. Photogramm. Remote Sens. 2014, 97, 229–240. [Google Scholar] [CrossRef]
- Qin, Y.; Yao, W.; Vu, T.T.; Li, S.; Niu, Z.; Ban, Y. Characterizing Radiometric Attributes of Point Cloud Using a Normalized Reflective Factor Derived from Small Footprint LiDAR Waveform. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 740–749. [Google Scholar] [CrossRef]
- Zhang, C. Key Techniques of Data Processing of Hyperspectral LiDAR for Earth Detection. Ph.D. Thesis, University of Chinese Academy of Sciences, Beijing, China, 2021. [Google Scholar]
- Yu, X.; Hyyppä, J.; Litkey, P.; Kaartinen, H.; Vastaranta, M.; Holopainen, M. Single-Sensor Solution to Tree Species Classification Using Multispectral Airborne Laser Scanning. Remote Sens. 2017, 9, 108. [Google Scholar] [CrossRef]
- Carrea, D.; Abellan, A.; Humair, F.; Matasci, B.; Derron, M.H.; Jaboyedoff, M. Correction of Terrestrial LiDAR Intensity Channel Using Oren-Nayar Reflectance Model: An Application to Lithological Differentiation. ISPRS J. Photogramm. Remote Sens. 2016, 113, 17–29. [Google Scholar] [CrossRef]
- Wagner, W.; Ullrich, A.; Ducic, V.; Melzer, T.; Studnicka, N. Gaussian Decomposition and Calibration of a Novel Small-Footprint Full-Waveform Digitising Airborne Laser Scanner. ISPRS J. Photogramm. Remote Sens. 2006, 60, 100–112. [Google Scholar] [CrossRef]
- Neuenschwander, A.L. Evaluation of Waveform Deconvolution and Decomposition Retrieval Algorithms for ICESat/GLAS Data. Canadian J. Remote Sens. 2008, 34, S240–S246. [Google Scholar] [CrossRef]
- Zhou, T.; Popescu, S.C.; Krause, K.; Sheridan, R.D.; Putman, E. Gold-A Novel Deconvolution Algorithm with Optimization for Waveform LiDAR Processing. ISPRS J. Photogramm. Remote Sens. 2017, 129, 131–150. [Google Scholar] [CrossRef]
- Zhang, Z.; Xie, H.; Tong, X.; Zhang, H.; Tang, H.; Li, B.; Wu, D.; Hao, X.; Liu, S.; Xu, X.; et al. A Combined Deconvolution and Gaussian Decomposition Approach for Overlapped Peak Position Extraction from Large-Footprint Satellite Laser Altimeter Waveforms. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 2286–2303. [Google Scholar] [CrossRef]
- Bruggisser, M.; Roncat, A.; Schaepman, M.E.; Morsdorf, F. Retrieval of Higher Order Statistical Moments from Full-Waveform LiDAR Data for Tree Species Classification. Remote Sens. Environ. 2017, 196, 28–41. [Google Scholar] [CrossRef]
- Shao, H.; Sa, B.; Li, W.; Chen, Y.; Liu, L.; Chen, J.; Sun, L.; Hu, Y. A Design and Implementation of Full-Waveform Hyperspectral LiDAR for Ancient Architecture Modelling. Infrared Laser Eng. 2022, 51, 20210786-1–20210786-10. [Google Scholar]
- Soudarissanane, S.; Lindenbergh, R.; Menenti, M.; Teunissen, P. Scanning Geometry: Influencing Factor on the Quality of Terrestrial Laser Scanning Points. ISPRS J. Photogramm. Remote Sens. 2011, 66, 389–399. [Google Scholar] [CrossRef]
- Hofton, M.A.; Minster, J.B.; Blair, J.B. Decomposition of Laser Altimeter Waveforms. IEEE Trans. Geosci. Remote Sens. 2000, 38, 1989–1996. [Google Scholar] [CrossRef]
- Dash, J.; Curran, P.J. The MERIS Terrestrial Chlorophyll Index. Int. J. Remote Sens. 2004, 25, 5403–5413. [Google Scholar] [CrossRef]
- Song, S.; Chen, Y.; Hu, H.; Hu, J.; Gong, Y.-M.; Shao, H. The Feasibility Study of Wavelength Selection of Multi-Spectral LIDAR for Autonomous Driving. J. Infrared Millim. Waves 2020, 39, 86–91. [Google Scholar] [CrossRef]
- Gitelson, A.; Merzlyak, M.N. Spectral Reflectance Changes Associated with Autumn Senescence of Aesculus Hippocastanum L. and Acer Platanoides L. Leaves. Spectral Features and Relation to Chlorophyll Estimation. J. Plant Physiol. 1994, 143, 286–292. [Google Scholar] [CrossRef]
- Barnes, E.M.; Clarke, T.R.; Richards, S.E.; Colaizzi, P.D.; Haberland, J.; Kostrzewski, M.; Waller, P.; Choi, C.R.E.; Thompson, T.; Lascano, R.J.; et al. Coincident Detection of Crop Water Stress, Nitrogen Status and Canopy Density Using Ground Based Multispectral Data. In Proceedings of the 5th International Conference Precis Agric, Bloomington, MN, USA, 16–19 July 2000. [Google Scholar]


| Parameter | Value |
|---|---|
| Spectral range | 550–1050 nm |
| Spectral resolution | 5 nm (101 channels) |
| Co-efficiency of AOTF crystal diffraction | >80% |
| Output efficiency | >40% |
| Polarization | Line polarization |
| Mono-pulse energy | >8 μJ |
| Divergence angle of light spot | ~0.35 mrad |
| Collimator focal length | 33 mm |
| Sampling rate | 5 GHz/s |
| FWHM | 2–4 ns |
| Channels | Range of (ns) | Range of rRMSE | Range of R2 | |||||
|---|---|---|---|---|---|---|---|---|
| Before | After | Before | After | Before | After | Before | After | |
| Laser footprint | 101 | 71 | 4.07 ± 0.74 | 3.83 ± 0.25 | 0.26 ± 0.06 | 0.24 ± 0.03 | 0.81 ± 0.12 | 0.85 ± 0.03 |
| Starting Position (ns) | Left Maximum Offset | Right Maximum Offset | |||
|---|---|---|---|---|---|
| Time (ns) | Distance (cm) | Time (ns) | Distance (cm) | ||
| Laser footprint | 5.3392 | 0.3134 | 4.7009 | 0.2383 | 3.5748 |
| Channel (nm) | RMSE | rRMSE | R-Square | ||||||
|---|---|---|---|---|---|---|---|---|---|
| S | MC | Inaccuracy | S | MC | Inaccuracy | S | MC | Promotion | |
| 600 | 1.59 | 1.26 | ↓ 20.74% | 48.96% | 38.72% | ↓ 20.92% | 0.7 | 0.81 | ↑ 15.71% |
| 610 | 1.59 | 1.15 | ↓ 27.67% | 29.77% | 21.59% | ↓ 27.48% | 0.89 | 0.94 | ↑ 5.62% |
| 635 | 2.58 | 1.49 | ↓ 42.25% | 36.45% | 21.10% | ↓ 42.11% | 0.84 | 0.95 | ↑ 13.10% |
| 670 | 3.27 | 1.8 | ↓ 44.95% | 35.16% | 19.27% | ↓ 45.19% | 0.85 | 0.95 | ↑ 11.77% |
| 875 | 1.08 | 1.35 | ↑ 25% | 16.42% | 20.32% | ↑ 23.75% | 0.96 | 0.95 | ↓ 1.04% |
| 890 | 1.88 | 1.26 | ↓ 32.98% | 35.06% | 23.42% | ↓ 33.20% | 0.83 | 0.87 | ↑ 4.82% |
| 920 | 1.29 | 0.96 | ↓ 25.58% | 35.63% | 26.37% | ↓ 25.99% | 0.83 | 0.91 | ↑ 9.64% |
| Overall average | 2.09 | 1.67 | ↓ 20.1% | 27.05% | 22.00% | ↓ 18.67% | 0.9 | 0.93 | ↑ 3.33% |
| Camouflage Position (cm) | Target Position (cm) | Distance Difference (cm) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| M | R | REOA | IOD | M | R | REOA | IOD | M | R | REOA | IOD | |
| SCWD (std) | 304.71 (25.64) | 300.00 | 0.1569 | 93.12% | 344.07 (6.52) | 345.00 | 0.0027 | 69.55% | 39.36 (23.41) | 45.00 | 0.1253 | 95.39% |
| MCMCD (std) | 298.76 (1.77) | 0.0041 | 343.59 (2.22) | 0.0041 | 44.83 (2.99) | 0.0037 | ||||||
| Method | Camouflage Net Position (cm) | Target Board Position (cm) | Distance Difference (cm) | RMSE | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| M | R | REOA | Std | M | R | REOA | Std | M | R | REOA | Std | ||
| Single accumulated waveform | 298.36 | 300 | 0.0055 | 343.07 | 345 | 0.0056 | 44.7 | 45 | 0.0067 | 1.853 | |||
| Overall average based on single accumulated waveform | 298.71 | 300 | 0.0043 | 0.34 | 342.84 | 345 | 0.0063 | 0.30 | 44.13 | 45 | 0.0193 | 0.50 | 2.15 |
| Proposed method | 298.76 | 300 | 0.0041 | 0.10 | 343.59 | 345 | 0.0047 | 0.13 | 44.83 | 45 | 0.0038 | 0.07 | 1.67 |
| Component | Initial Eigenvalue | Dimensionality Reduction Process | ||||
|---|---|---|---|---|---|---|
| Eigenvalue | Contribution | Total Contribution | Eigenvalue | Contribution | Total Contribution | |
| 1 | 4.81 | 43.70% | 43.70% | 4.81 | 43.70% | 43.70% |
| 2 | 2.09 | 19.04% | 62.74% | 2.09 | 19.04% | 62.74% |
| 3 | 1.39 | 12.65% | 75.38% | 1.39 | 12.65% | 75.38% |
| 4 | 1.08 | 9.84% | 85.22% | 1.08 | 9.84% | 85.22% |
| 5 | 0.92 | 8.33% | 93.55% | 0.92 | 8.33% | 93.55% |
| 6 | 0.30 | 2.77% | 96.32% | |||
| 7 | 0.19 | 1.70% | 98.01% | |||
| 8 | 0.11 | 0.98% | 99.00% | |||
| 9 | 0.06 | 0.59% | 99.58% | |||
| 10 | 0.04 | 0.36% | 99.94% | |||
| 11 | 0.007 | 0.006% | 100% | |||
| Spectrum | Target Uncovered vs. Target Covered | Target Uncovered vs. Camouflage Net | Target Covered vs. Camouflage Net |
|---|---|---|---|
| Before extraction | 0.8945 | 0.7635 | 0.8766 |
| After extraction | 0.9526 | 0.6984 | 0.8530 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, Y.; Xu, S.; Fang, J.; Hou, A.; Chen, Y.; Zhang, X.; Hu, Y. A Novel Waveform Decomposition and Spectral Extraction Method for 101-Channel Hyperspectral LiDAR. Remote Sens. 2022, 14, 5285. https://doi.org/10.3390/rs14215285
Xia Y, Xu S, Fang J, Hou A, Chen Y, Zhang X, Hu Y. A Novel Waveform Decomposition and Spectral Extraction Method for 101-Channel Hyperspectral LiDAR. Remote Sensing. 2022; 14(21):5285. https://doi.org/10.3390/rs14215285
Chicago/Turabian StyleXia, Yuhao, Shilong Xu, Jiajie Fang, Ahui Hou, Youlong Chen, Xinyuan Zhang, and Yihua Hu. 2022. "A Novel Waveform Decomposition and Spectral Extraction Method for 101-Channel Hyperspectral LiDAR" Remote Sensing 14, no. 21: 5285. https://doi.org/10.3390/rs14215285
APA StyleXia, Y., Xu, S., Fang, J., Hou, A., Chen, Y., Zhang, X., & Hu, Y. (2022). A Novel Waveform Decomposition and Spectral Extraction Method for 101-Channel Hyperspectral LiDAR. Remote Sensing, 14(21), 5285. https://doi.org/10.3390/rs14215285








