Analysis of Internal Angle Error of UAV LiDAR Based on Rotating Mirror Scanning
Abstract
1. Introduction
2. Materials and Methods
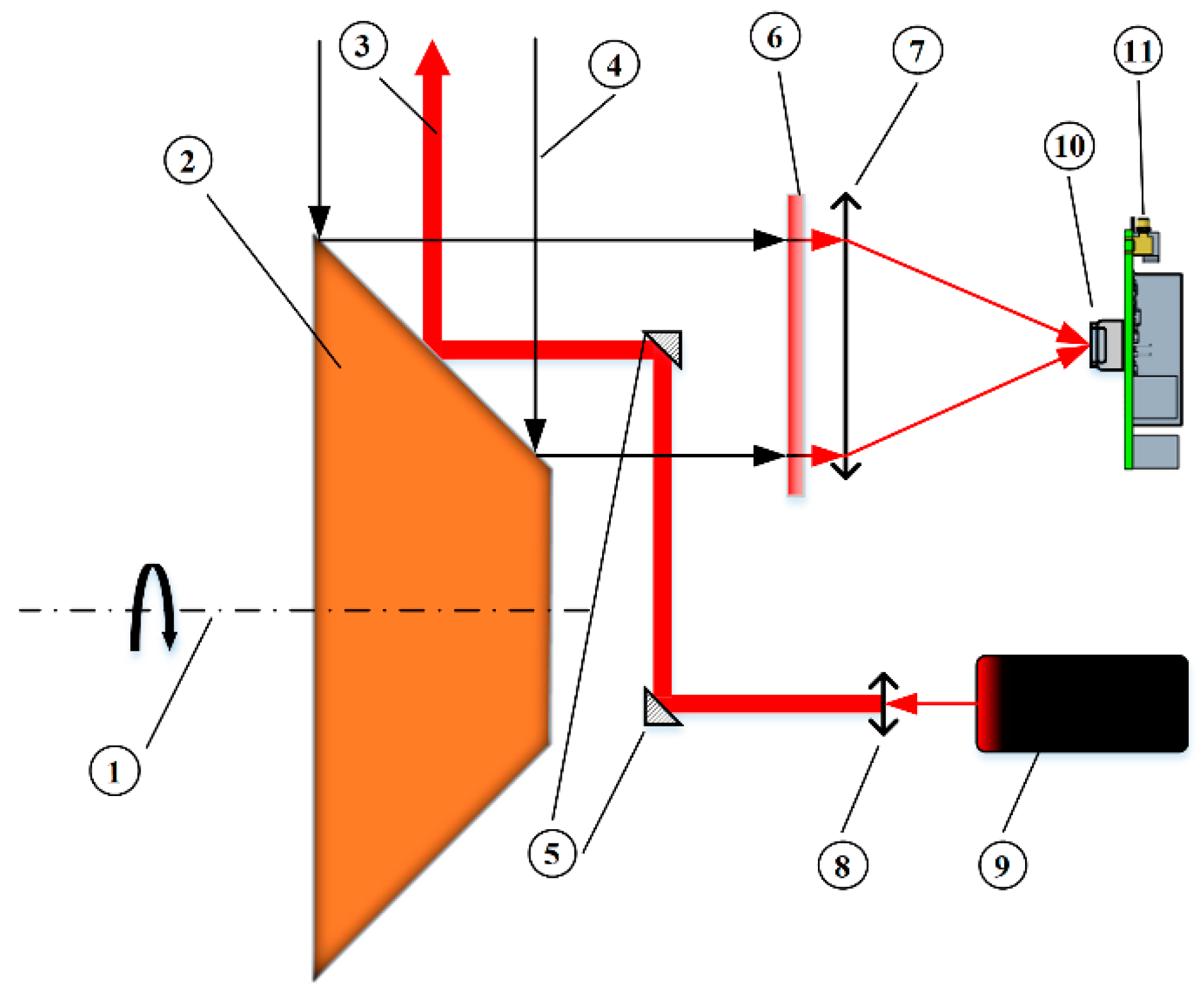
2.1. System Composition
2.1.1. Ranging Module
- 1
- Laser receiving subsystem
- 2
- Laser-receiving subsystem
- 3
- Online waveform processing
2.1.2. Scanning Module
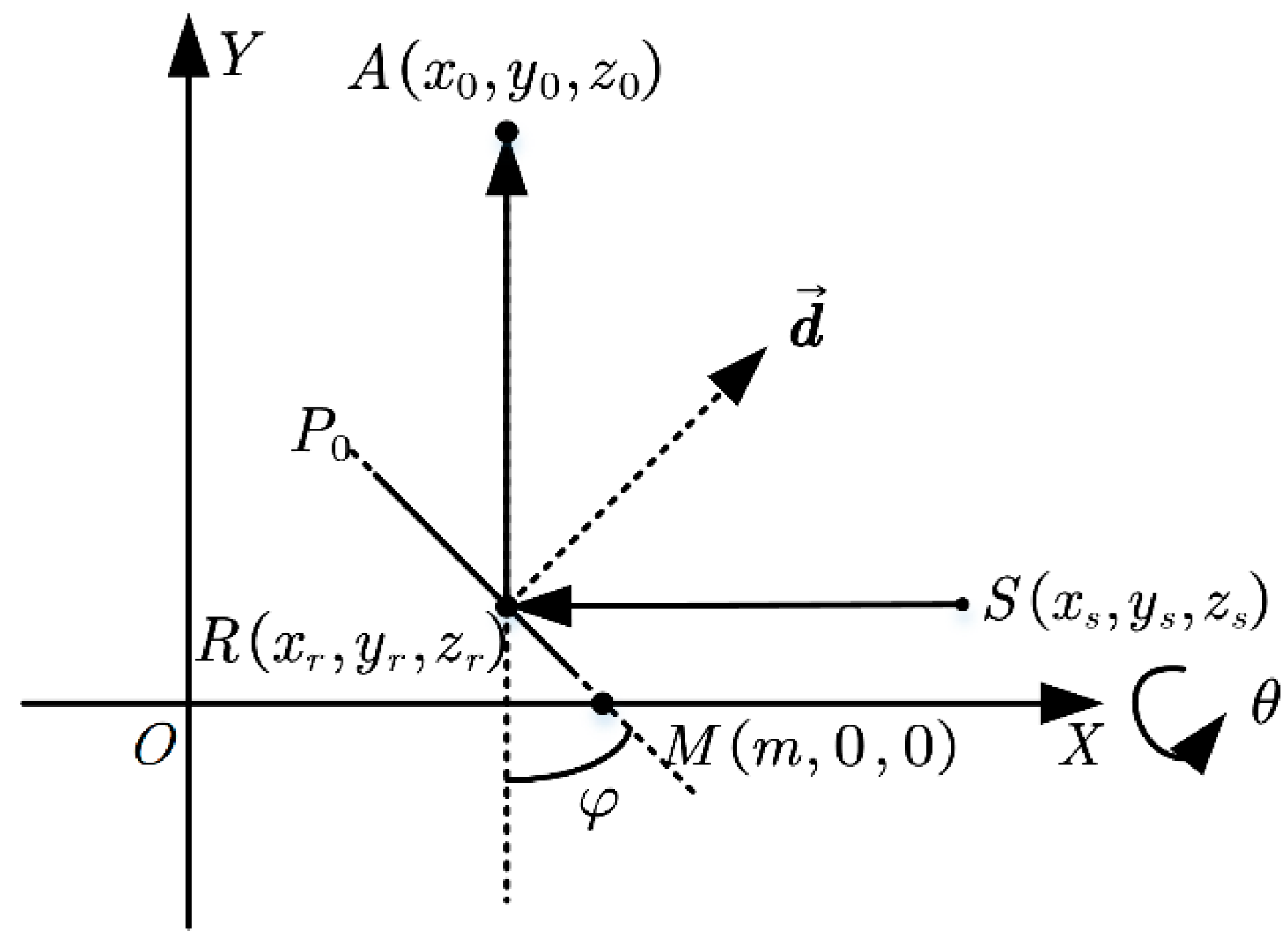
2.2. Mirror Scanning Model
2.2.1. Single-Sided Mirror Scanning Model
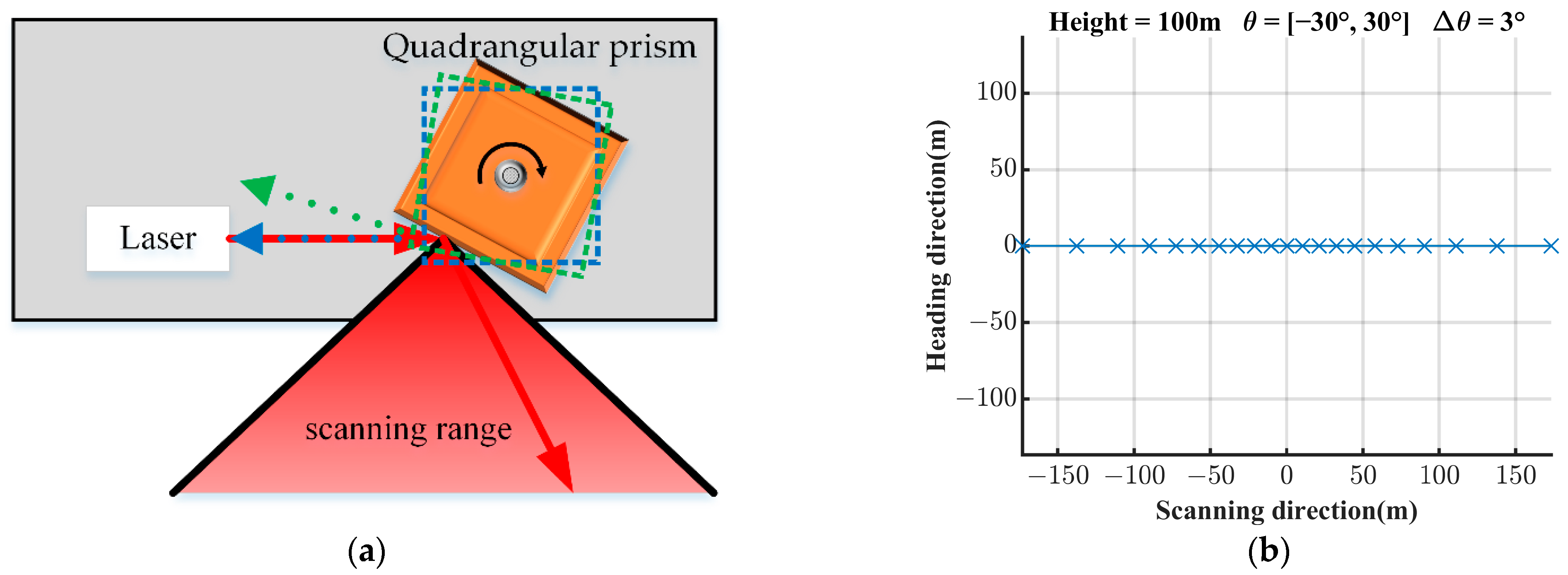
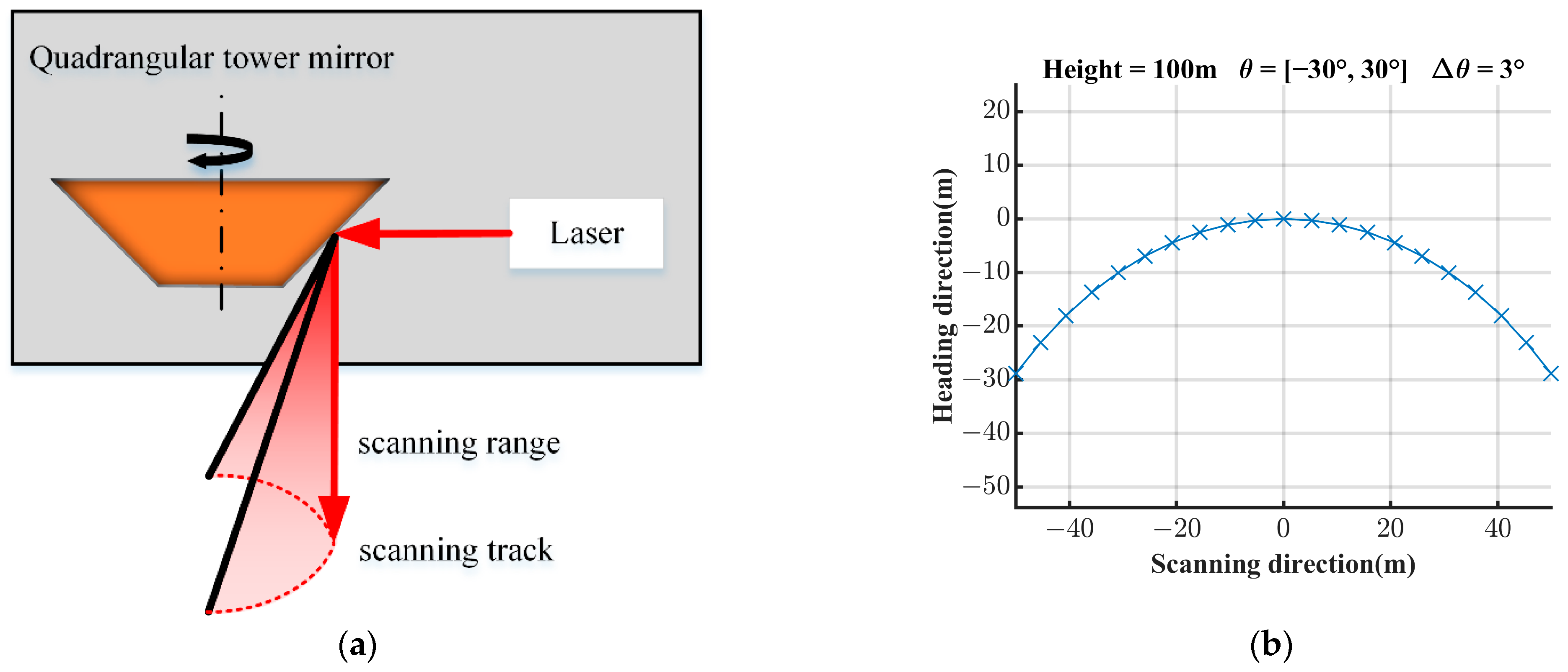
2.2.2. Polygon Prism and Polygon Tower Mirror Scanning Model
- 4
- Quadrangular prism scanning mode 1
- 5
- Quadrangular prism scanning mode 2
- 6
- Quadrangular tower mirror scanning mode 1
- 7
- Quadrangular tower mirror scanning mode 2
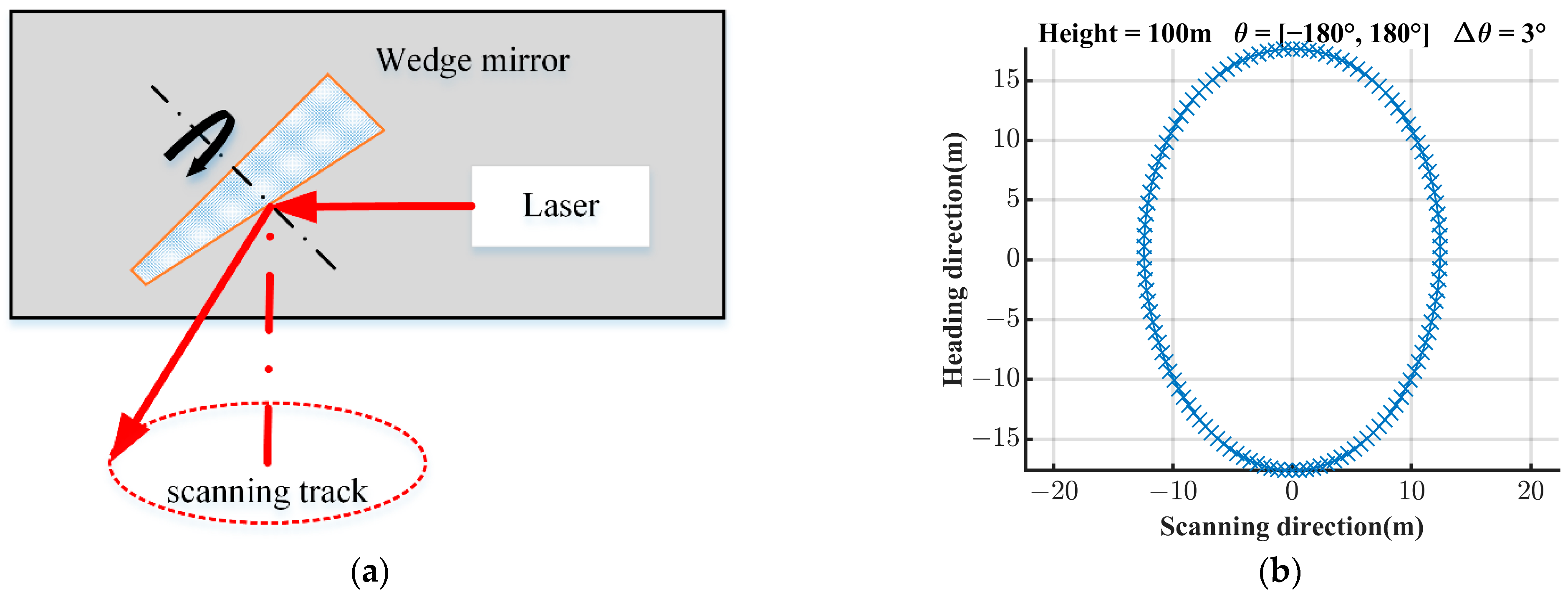
2.2.3. Wedge Mirror Scanning
2.3. Angle Errors of Mirror Scanning Model
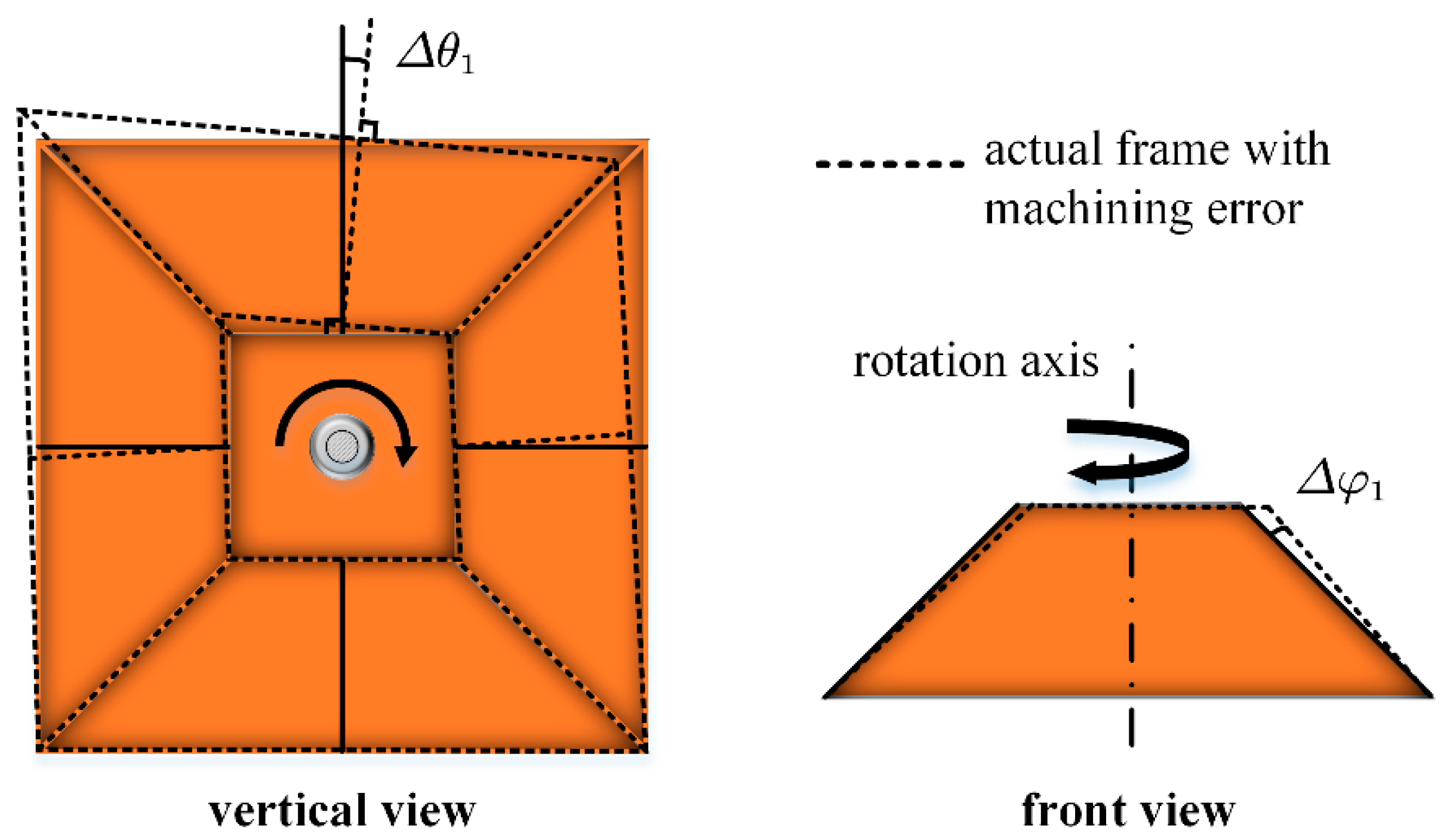
2.3.1. Laser and Rotation Axis Parallelism Deviation
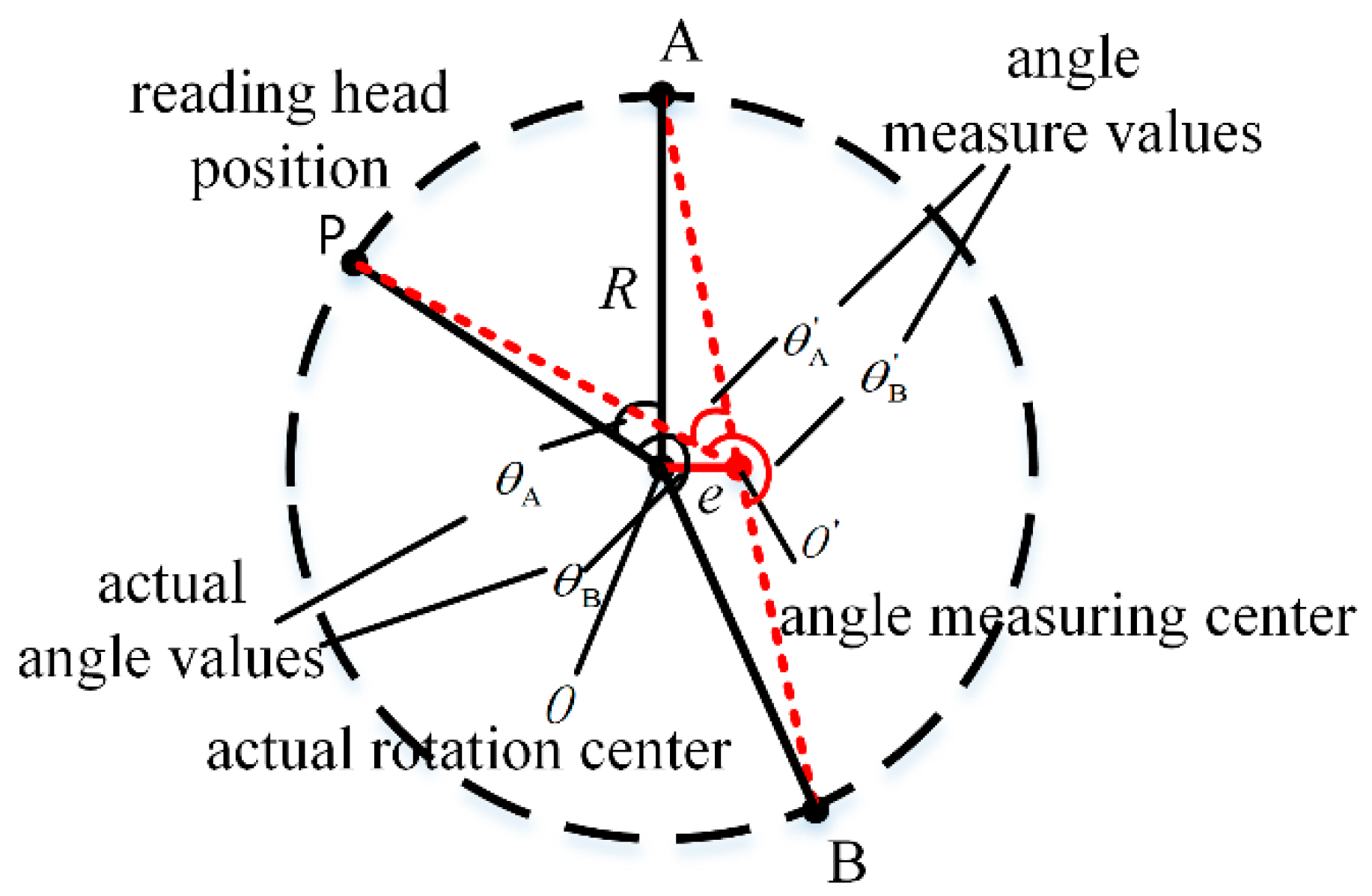
2.3.2. Eccentricity Error of Circular Grating Rotary Encoder
2.3.3. Surface Angle Deviation
3. Results
3.1. Simulation Experiments
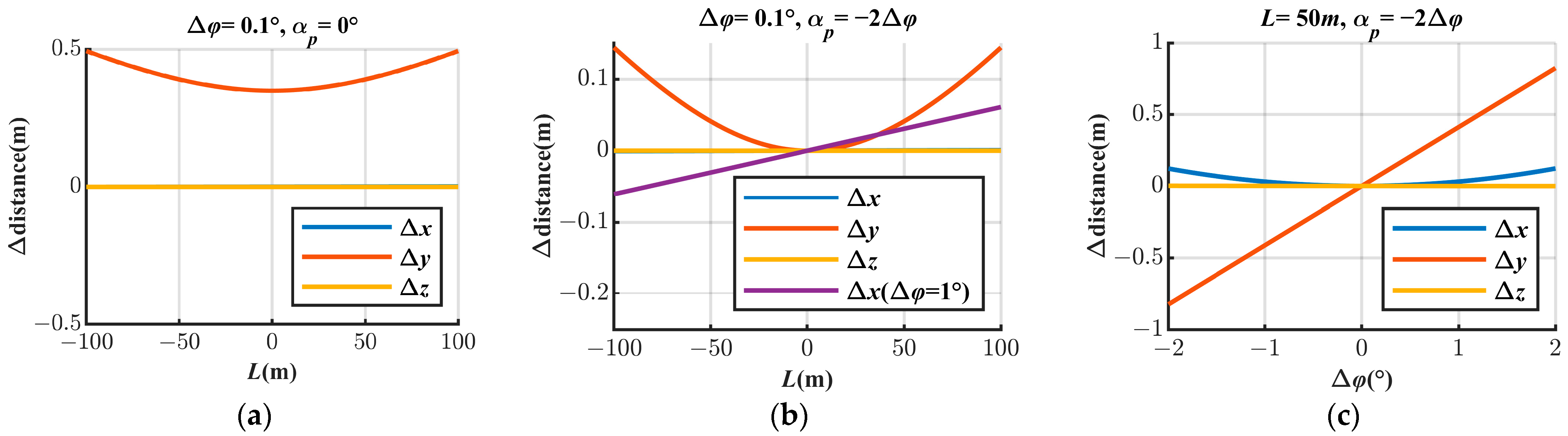
3.1.1. The Effect of on the Point Cloud
- 8
- Change or the distance from point to the yoz-plane;
- 9
- Use the Gauss–Newton method to solve the coordinate on the flight when the LiDAR scans to the point , as well as the ranging and the angle obtained by the LiDAR at this time;
- 10
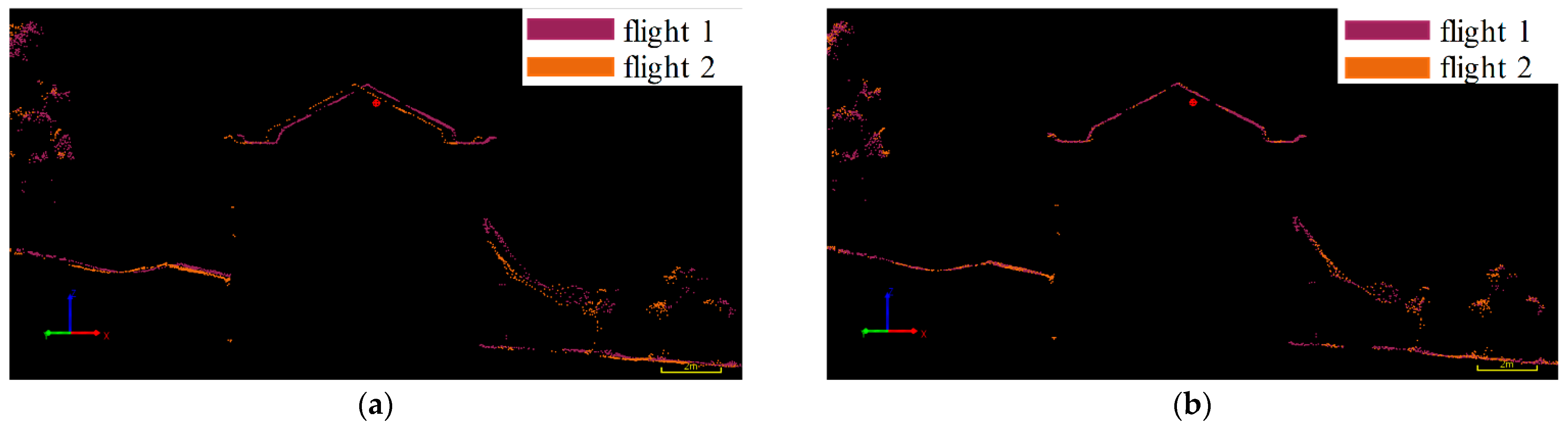
- According to the influence of on the point cloud, use to rotate the point cloud in the pitch direction, and then make , so as to ensure that the ground objects in flight 2 and flight 3 in Figure 11 coincide. Thus, the process of correcting the point cloud of multi-strip by using the installation angle when is ignored is simulated. Then, by , and , the coordinates of point in the point cloud are calculated as ;
- 11
- Finally, , , , etc., are calculated from the coordinates of and .
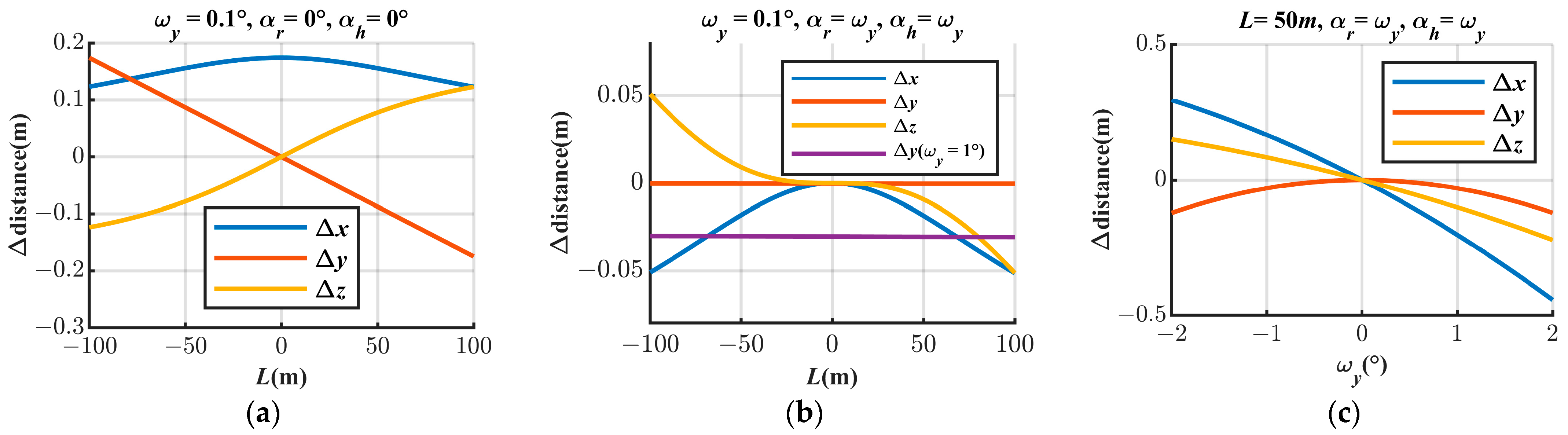
3.1.2. The Effect of on the Point Cloud
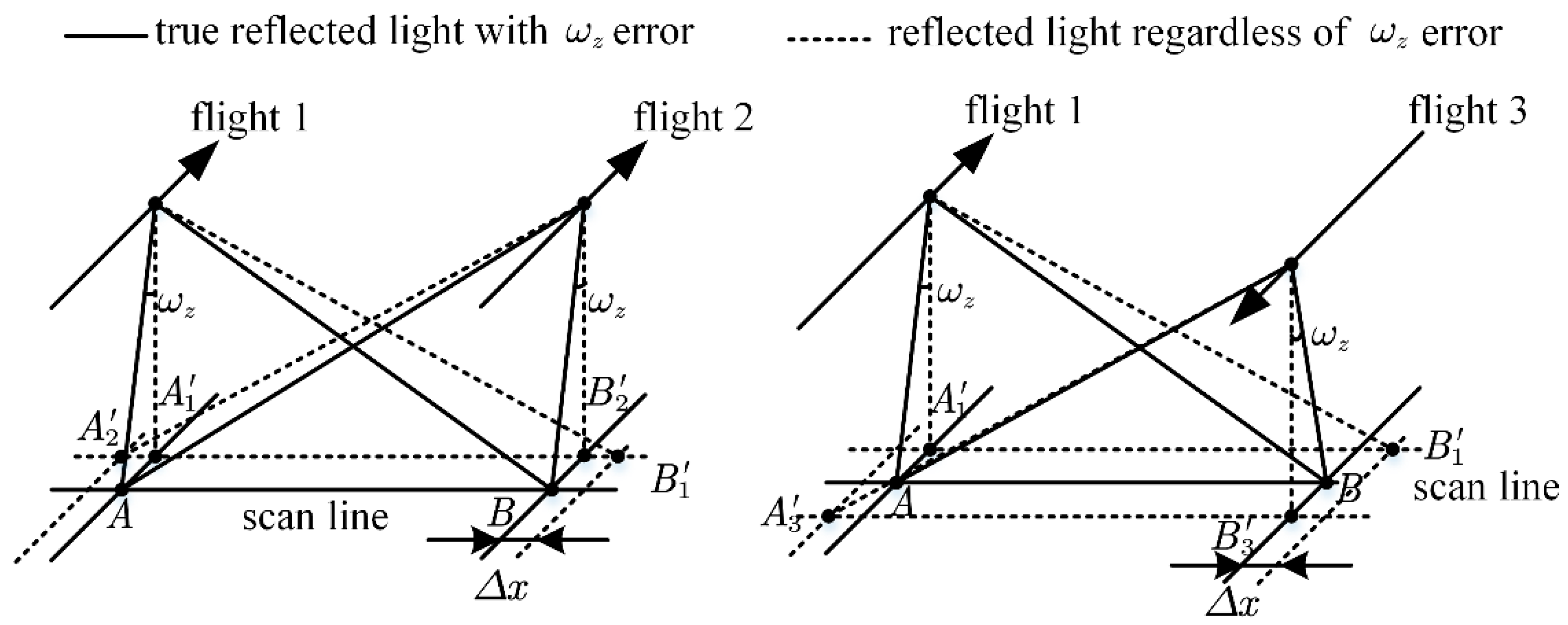
3.1.3. The Effect of on the Point Cloud
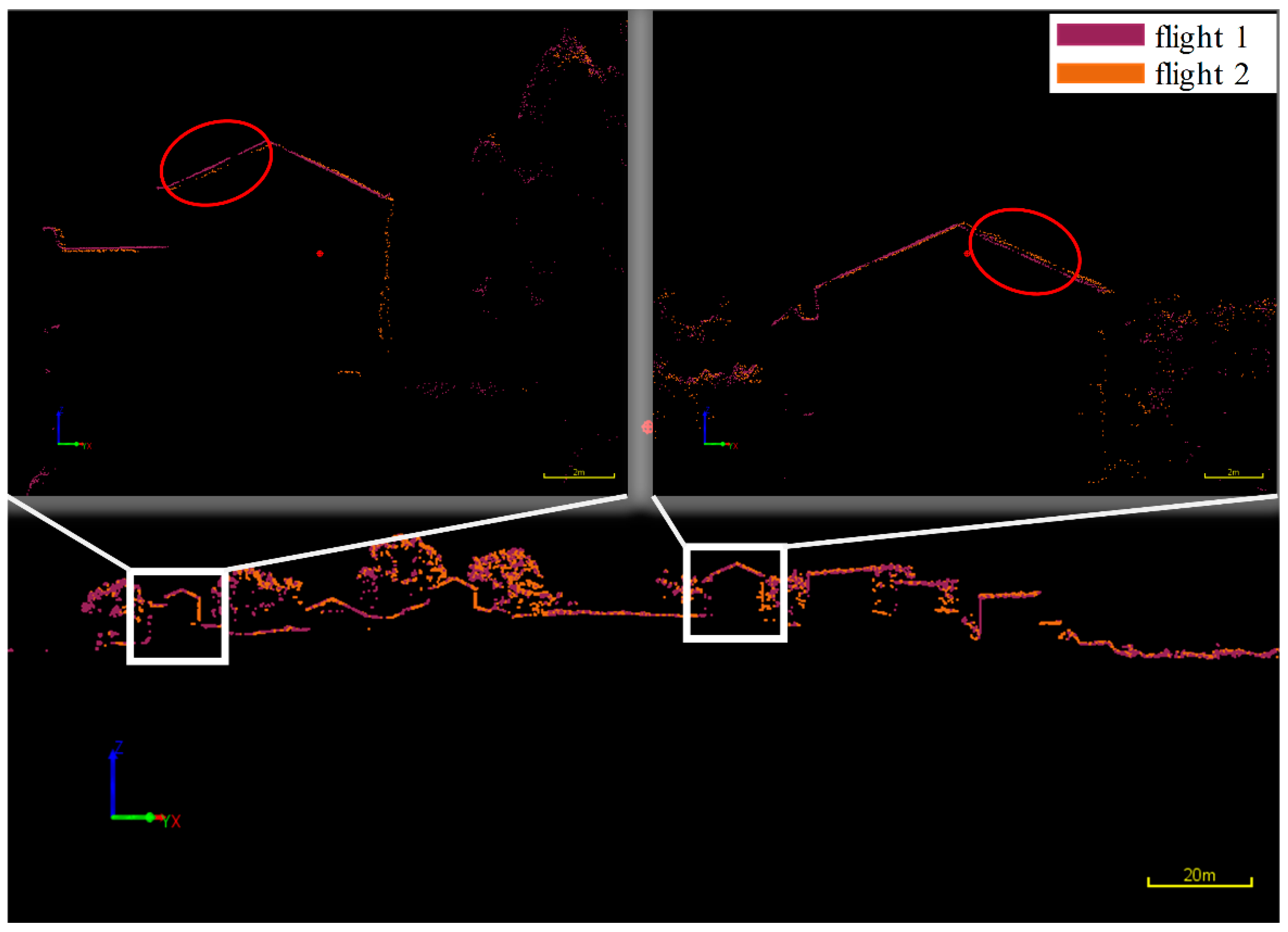
3.2. Flight Experiment
4. Discussion
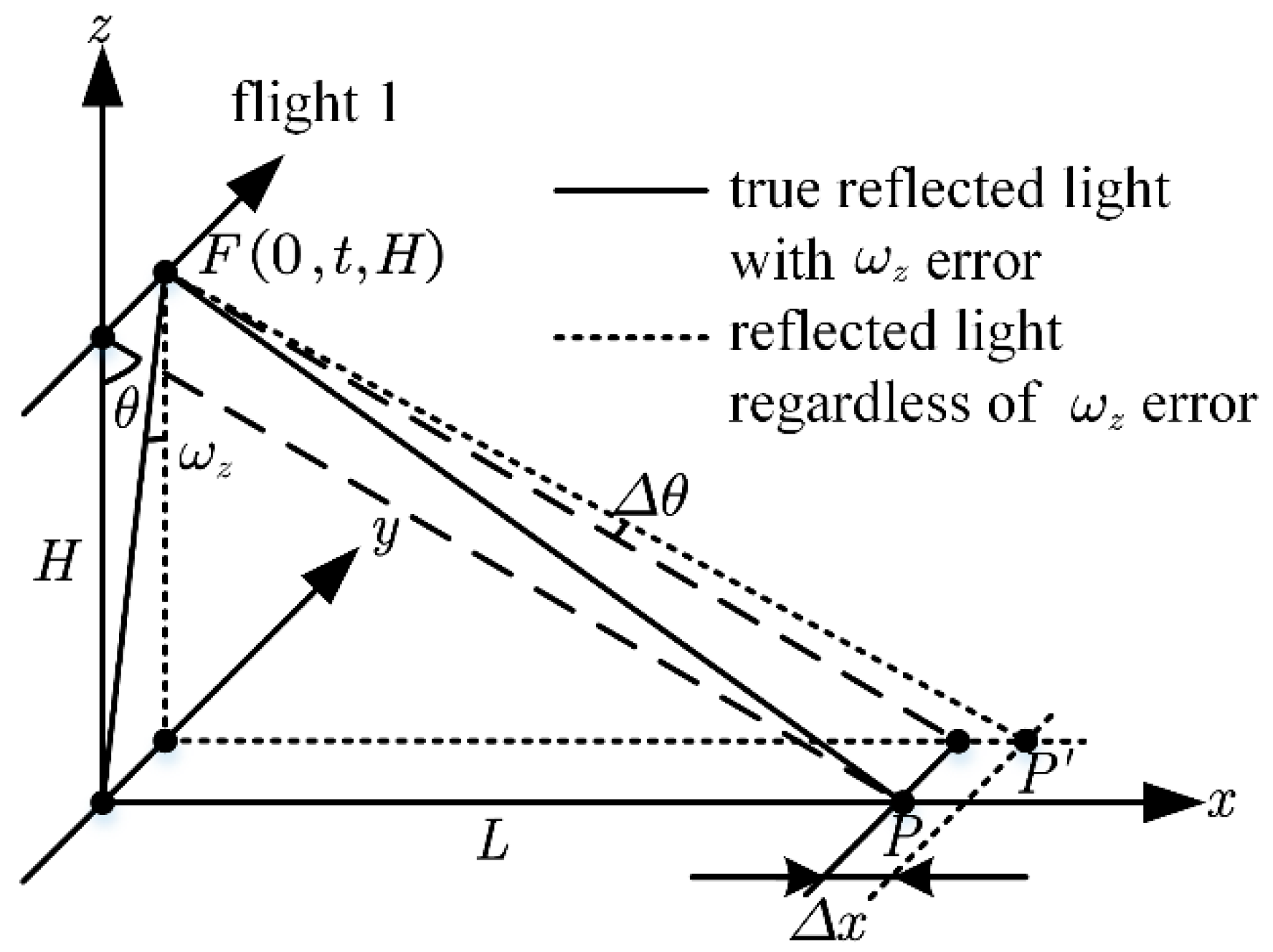
- The presence of will result in a perpendicular flight path, an offset, and an elevation offset. The offsets become larger as the scanning angle increases, and the trend is similar to outward or inward deformation of the point cloud, with respect to the real feature, centered on the flight path.
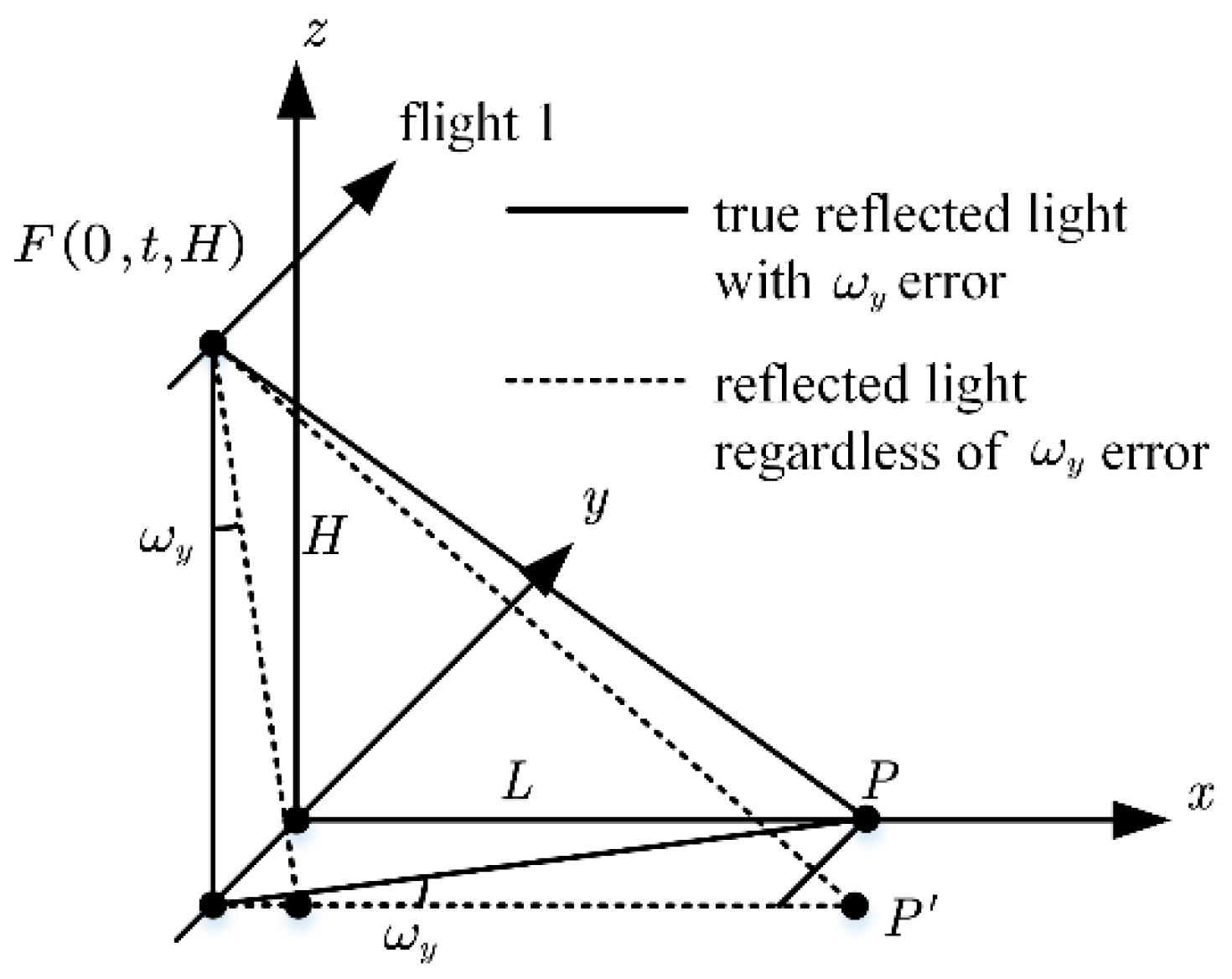
- The presence of will result in three directional offsets between the feature target in the point cloud and its true position. The offset perpendicular to the flight path and elevation and the offset in the elevation direction become larger as the scan angle becomes larger. The trend is similar to that of a point cloud with an overall left or right deformation relative to the real feature centered on the flight path. The offset of the parallel flight path is almost only related to the magnitude of but not to the scanning angle.
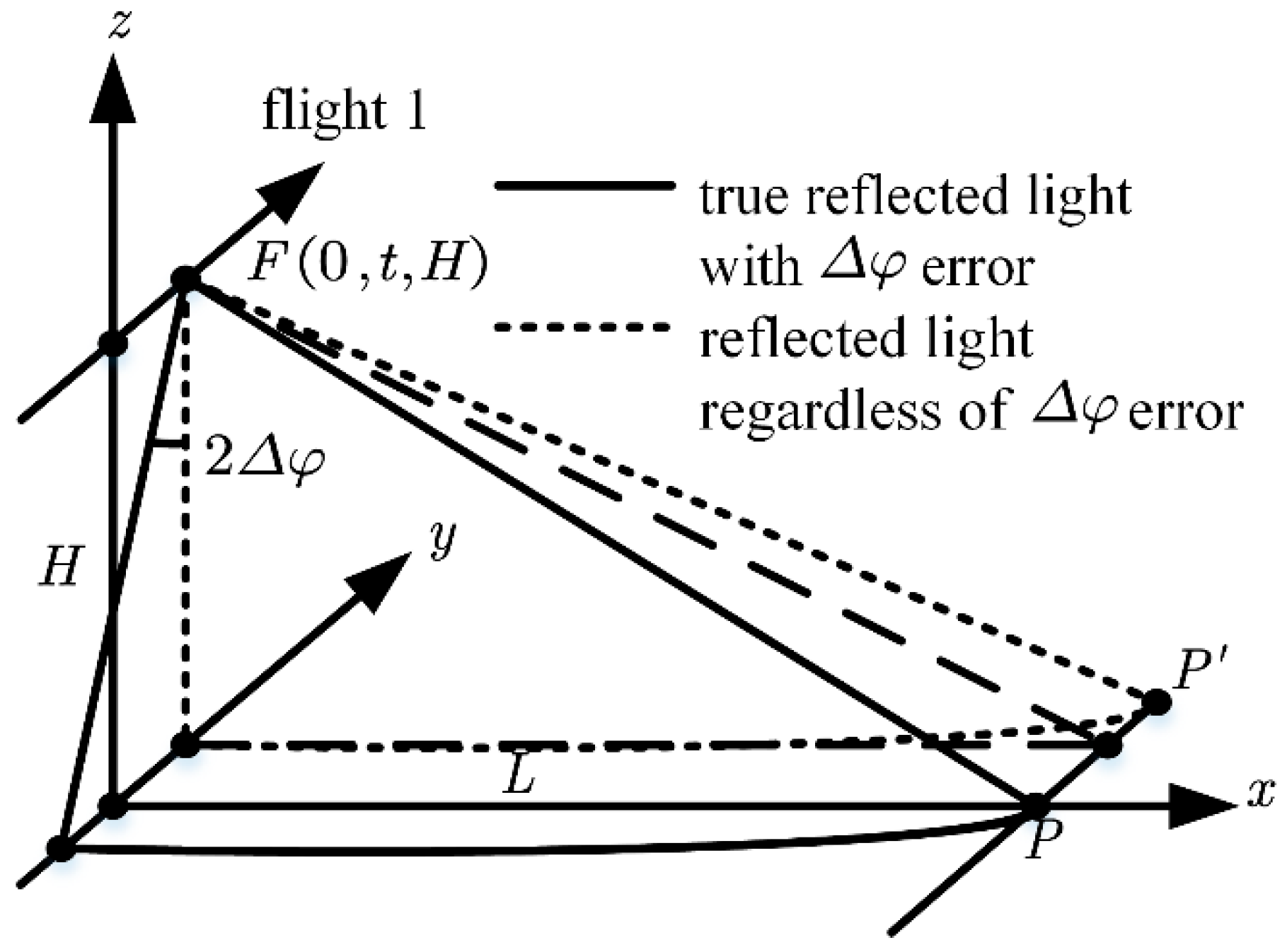
- The presence of will result in a parallel flight path offset between the feature target in the point cloud and its true position, which becomes larger as the scanning angle increases, and the scanning track changes from a straight line to a curve.
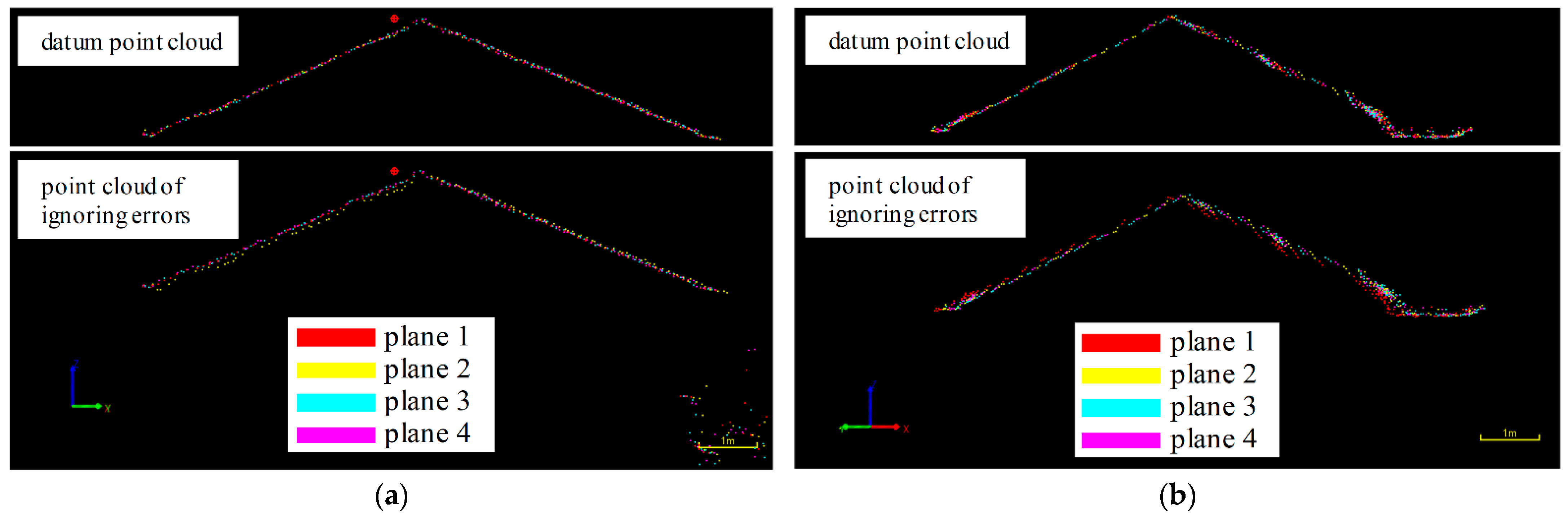
- In the presence of and , the point clouds of different reflecting surfaces in a single flight strip will be layered.
5. Conclusions
- 12
- Compact and efficient optomechanical structure
- 13
- Efficient and precise distance measurement
- 14
- Angle errors calibration and compensation
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ozcan, A.H.; Unsalan, C. LiDAR Data Filtering and DTM Generation Using Empirical Mode Decomposition. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 360–371. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, Q.; Liu, L.; Zheng, D.; Li, C.; Li, K. Supervised Classification of Power Lines from Airborne LiDAR Data in Urban Areas. Remote Sens. 2017, 9, 771. [Google Scholar] [CrossRef]
- Wallace, L.; Lucieer, A.; Watson, C.; Turner, D. Development of a UAV-LiDAR System with Application to Forest Inventory. Remote Sens. 2012, 4, 1519–1543. [Google Scholar] [CrossRef]
- Guo, K.; Li, Q.; Wang, C.; Mao, Q.; Liu, Y.; Zhu, J.; Wu, A. Development of a single-wavelength airborne bathymetric LiDAR: System design and data processing. ISPRS J. Photogramm. Remote Sens. 2022, 185, 62–84. [Google Scholar] [CrossRef]
- Hinterhofer, T.; Pfennigbauer, M.; Ullrich, A.; Rothbacher, D.; Schraml, S.; Hofstätter, M.; Guicheteau, J.A.; Fountain, A.W.; Howle, C.R. UAV-based LiDAR and gamma probe with real-time data processing and downlink for survey of nuclear disaster locations. In Proceedings of the Chemical, Biological, Radiological, Nuclear, and Explosives (CBRNE) Sensing, Orlando, FL, USA, 16 May 2018. [Google Scholar] [CrossRef]
- Rottensteiner, F.; Sohn, G.; Gerke, M.; Wegner, J.D.; Breitkopf, U.; Jung, J. Results of the ISPRS benchmark on urban object detection and 3D building reconstruction. ISPRS J. Photogramm. Remote Sens. 2014, 93, 256–271. [Google Scholar] [CrossRef]
- Lin, Y.; Hyyppa, J.; Rosnell, T.; Jaakkola, A.; Honkavaara, E. Development of a UAV-MMS-Collaborative Aerial-to-Ground Remote Sensing System–A Preparatory Field Validation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 1893–1898. [Google Scholar] [CrossRef]
- Crocker, R.I.; Maslanik, J.A.; Adler, J.J.; Palo, S.E.; Herzfeld, U.C.; Emery, W.J. A Sensor Package for Ice Surface Observations Using Small Unmanned Aircraft Systems. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1033–1047. [Google Scholar] [CrossRef]
- Wagner, W.; Ulrich, A.; Melzer, T. From single-pulse to full-waveform airborne laser scanners: Potential and practical challenges. In Proceedings of the International Society for Photogrammetry and Remote Sensing 20th Congress Commission 3, Istanbul, Turkey, 12–23 July 2004. [Google Scholar]
- She, J.; Mabi, A.; Liu, Z.; Sheng, M.; Dong, X.; Liu, F.; Wang, S. Analysis Using High-Precision Airborne LiDAR Data to Survey Potential Collapse Geological Hazards. Adv. Civ. Eng. 2021, 2021, 6475942. [Google Scholar] [CrossRef]
- LeWinter, A.L.; Pfennigbauer, M.; Gadomski, P.J.; Finnegan, D.C.; Schwarz, R.; Podoski, J.H.; Truong, M.; Singh, U.N.; Sugimoto, N. Unmanned aircraft system-based lidar survey of structures above and below the water surface: Hilo Deep Draft Harbor Breakwater, Hawaii. In Proceedings of the Lidar Remote Sensing for Environmental Monitoring, Honolulu, HI, USA, 24 October 2018. [Google Scholar] [CrossRef]
- Raj, T.; Hashim, F.H.; Huddin, A.B.; Ibrahim, M.F.; Hussain, A. A Survey on LiDAR Scanning Mechanisms. Electronics 2020, 9, 741. [Google Scholar] [CrossRef]
- Brazeal, R.G.; Wilkinson, B.E.; Hochmair, H.H. A Rigorous Observation Model for the Risley Prism-Based Livox Mid-40 Lidar Sensor. Sensors 2021, 21, 4722. [Google Scholar] [CrossRef]
- Wang, J.; Lindenbergh, R.; Shen, Y.; Menenti, M. Coarse point cloud registration by egi matching of voxel clusters. ISPRS Annals of Photogrammetry. Remote Sens. Spat. Inf. Sci. 2016, III-5, 97–103. [Google Scholar] [CrossRef]
- Aboujja, S.; Chu, D.; Bean, D.; Zediker, M.S.; Zucker, E.P. 1550nm triple junction laser diode for long range LiDAR. In Proceedings of the High-Power Diode Laser Technology, San Francisco, CA, USA, 4 March 2022. [Google Scholar] [CrossRef]
- Ullrich, A.; Reichert, R. Waveform digitizing laser scanners for surveying and surveillance applications. In Proceedings of the Electro-Optical Remote Sensing, Bruges, Belgium, 21 October 2005. [Google Scholar] [CrossRef]
- Wagner, W.; Ullrich, A.; Ducic, V.; Melzer, T.; Studnicka, N. Gaussian decomposition and calibration of a novel small-footprint full-waveform digitising airborne laser scanner. ISPRS J. Photogramm. Remote Sens. 2006, 60, 100–112. [Google Scholar] [CrossRef]
- Hao, Z.; Qingzhou, M.; Qingquan, L. Influence of sampling frequency and laser pulse width on ranging accuracy of full-waveform LiDAR. Infrared Laser Eng. 2022, 51, 20210363. (In Chinese) [Google Scholar]
- Mallet, C.; Bretar, F. Full-waveform topographic lidar: State-of-the-art. ISPRS J. Photogramm. Remote Sens. 2009, 64, 1–16. [Google Scholar] [CrossRef]
- Pfennigbauer, M.; Rieger, P.; Studnicka, N.; Ullrich, A. Detection of concealed objects with a mobile laser scanning system. In Proceedings of the Laser Radar Technology and Applications, Orlando, FL, USA, 2 May 2009. [Google Scholar] [CrossRef]
- Householder, A.S. The Theory of Matrices in Numerical Analysis; Blaisdell Pub. Co: New York, NY, USA, 1964. [Google Scholar] [CrossRef]








| Parameter | Luojia Yiyun FT1500 |
|---|---|
| Wavelength | 1550 nm |
| Measuring range | 1–1500 m @ ρ ≥ 80% |
| Accuracy/Precision | 10 mm/5 mm @ 100 m(1σ) |
| Pulse repetition rate | 100–2000 kHz |
| Maximum number of targets per pulse | up to 7 |
| Laser beam divergence | 0.5 mrad |
| Scanning mechanism | rotating polygon mirror |
| Field of view | 80° |
| Scan speed | up to 300 lines/second |
| Angle measurement resolution | 0.0006° |
| Weight | 2.7 kg |
| Parameter | Mean | The Equipment Used for Flight Experiment | |
|---|---|---|---|
| −0.13611° | 0.17958° | −0.04000° | |
| 0.84864° | 0.26278° | 1.01500° | |
| −0.00653° | 0.06561° | −0.02314° | |
| −0.00933° | 0.07006° | 0.00616° | |
| 0.00198° | 0.03897° | 0.00557° | |
| 0.00293° | 0.05526° | 0.01656° | |
| 0.02077° | 0.06028° | 0.01806° | |
| 0.00637° | 0.05194° | 0.01969° |
| Number | dz/m | Number | dz/m | Number | dz/m |
|---|---|---|---|---|---|
| pt25 | 0.009 | pt7 | −0.010 | pt10 | −0.027 |
| pt1 | 0.008 | pt15 | −0.012 | pt20 | −0.027 |
| pt3 | 0.008 | pt8 | −0.013 | pt24 | −0.034 |
| pt22 | 0.007 | pt27 | −0.014 | pt12 | −0.036 |
| pt4 | 0.003 | pt19 | −0.015 | pt16 | −0.037 |
| pt6 | 0.001 | pt9 | −0.015 | pt18 | −0.040 |
| pt21 | −0.002 | pt2 | −0.021 | pt11 | −0.065 |
| pt14 | −0.004 | pt26 | −0.025 | pt17 | −0.093 |
| pt23 | −0.006 | pt5 | −0.026 | pt13 | \ |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, H.; Mao, Q.; Song, Y.; Wu, A.; Hu, X. Analysis of Internal Angle Error of UAV LiDAR Based on Rotating Mirror Scanning. Remote Sens. 2022, 14, 5260. https://doi.org/10.3390/rs14205260
Zhou H, Mao Q, Song Y, Wu A, Hu X. Analysis of Internal Angle Error of UAV LiDAR Based on Rotating Mirror Scanning. Remote Sensing. 2022; 14(20):5260. https://doi.org/10.3390/rs14205260
Chicago/Turabian StyleZhou, Hao, Qingzhou Mao, Yufei Song, Anlei Wu, and Xueqing Hu. 2022. "Analysis of Internal Angle Error of UAV LiDAR Based on Rotating Mirror Scanning" Remote Sensing 14, no. 20: 5260. https://doi.org/10.3390/rs14205260
APA StyleZhou, H., Mao, Q., Song, Y., Wu, A., & Hu, X. (2022). Analysis of Internal Angle Error of UAV LiDAR Based on Rotating Mirror Scanning. Remote Sensing, 14(20), 5260. https://doi.org/10.3390/rs14205260






