Abstract
Multispectral satellite remote sensing imagery, together with appropriate modeling, have been proven to provide chlorophyll-a maps that are useful to evaluate the suitability of coastal areas for carrying out shellfish aquaculture. However, current approaches used for chlorophyll-a estimation in very shallow coastal areas often fail in their accuracy. To overcome this limitation, an algorithm that provides an accurate estimation of chlorophyll-a concentration in the coastal areas of the Ebro delta (North Western Mediterranean) using atmospherically corrected Sentinel 2 (S2) remote sensing reflectances (Rrs) has been calibrated and validated. The derived chlorophyll-a maps created have been used in a dynamic carrying capacity model that covers areas from very rich waters inside the embayment to the more oligotrophic waters in the open sea. The use of carrying capacity models is recommended to evaluate the potential of marine coastal areas for bivalve mollusk aquaculture. In this context, the depletion of chlorophyll-a is an indicator of negative environmental impact and thus a continuous monitoring of chlorophyll-a is key. The proposed methodology allows estimation of chlorophyll-a concentration from Sentinel-2 with an accuracy higher than 70% in most cases. The carrying capacity and the suitability of the external areas of the Ebro delta have been determined. The results show that these areas can hold a significant mussel production. The methodology presented in this study aims to provide a tool to the shellfish aquaculture industry.
Keywords:
sentinel-2; aquaculture; carrying capacity; chlorophyll-a; shellfish; bivalves; water quality 1. Introduction
Remote sensing enables the evaluation of the spatial and temporal variability of water quality worldwide, overcoming the lack of data from new, remote, or large marine areas. This has led to several applications of remote sensing in bivalve mollusk aquaculture, including spatial planning [1,2,3,4,5], early detection of harmful algal blooms [6,7,8,9,10,11], and detection of microbial contamination [12,13]. Among the different water quality parameters of interest that can be measured by sensors from satellites, chlorophyll-a concentration is commonly used in bivalve mollusk aquaculture because it is considered the best proxy of phytoplankton biomass [14], which is one of the ecosystem component Essential Ocean Variables (EOVs) [15,16]. The retrieval of water quality parameters (such as chlorophyll-a) using satellite remote sensing imagery and appropriate modelling is still challenging in coastal waters, especially in case-2 waters [17,18]. Although many approaches have been proposed, there is not yet any standardized approach. In case-2 waters, inorganic and/or organic sediments represent an important or dominant contribution to the optical properties [19], requiring high accuracy and precision in the atmospheric correction algorithms to successfully retrieve water constituents. Recently, several advances concerning enhanced modelling have been proposed to solve atmospheric correction [20], but their performances differ depending on the scenario (sun and observation geometry, atmospheric, optical) and site-specific conditions. The lack of a common approach and performance makes it necessary to continue validating different atmospheric correction approaches as well as water quality retrieval methods with in situ data accounting for a wide variety of water types and environmental conditions. Therefore, the estimation of chlorophyll-a concentration in coastal waters still has some difficulties in comparison to oceanic waters due to the more complex optical properties and to high spatial variability. Atmospheric correction and the correction of scale effects are necessary to accurately estimate chlorophyll-a concentration in coastal waters [21], where the retrieval of chlorophyll-a concentration through remote sensing has many applications, such as the evaluation of the environmental status of these water masses [17] or spatial planning for bivalve aquaculture [1].
Global aquaculture production in 2020 reached 17.7 million tons of mollusks, with bivalve aquaculture accounting for a high percentage of total aquaculture production in several countries such as New Zealand, France, Spain, republic of Korea, Italy, and Japan [22], with China being the main producer [23]. Bivalves do not require artificial feeds; they graze on phytoplankton communities present in marine waters [24]. Bivalve aquaculture, together with the cultivation of macroalgae and some herbivorous fish species, utilizes low trophic marine species that can provide alternatives for food production with lower environmental impacts [25]. Bivalve aquaculture is carried out in coastal waters, mainly in estuaries and embayments where phytoplankton biomass is higher than in offshore waters. The global production of bivalves is expected to continue growing [26]; however, seawater temperature in shallow coastal areas is currently reaching thresholds that are limiting the survival of some bivalve species.
Heat waves have been affecting, in recent years, shellfish species in different geographical areas such as the Pacific Northwest in 2021 [27,28], the eastern English channel in 2018 [29], and the coast of California in 2004 [30]. In the Mediterranean Sea, the warming trend in Sea Surface Temperature (SST) during the period 1992–2020 was 0.038 +/− 0.002 °C/year [31]. Marine heat wave (MHW) events in the Mediterranean Sea are increasing in intensity, duration, and frequency [32]. High seawater temperature in shallow coastal areas during MHW events produces high rates of mortality of Mytilus galloprovincialis [33], one of the main species in shellfish aquaculture in the Mediterranean Sea. These issues revealed the need for seeking new shellfish growing areas located in cooler waters, which requires the assessment of the production potential of new culture areas, with a sustainable approach. In this context, the coupling of remote sensing data and carrying capacity models has demonstrated a great potential for monitoring shellfish aquaculture and supporting management strategies [34,35].
Carrying capacity models are used to determine the total bivalve biomass supported by a given ecosystem as a function of the water residence time, primary production, and bivalve clearance rate [36,37]. Among them, the Dynamic Energy Budget (DEB) theory based on Kooijman [38] has been applied to model shellfish growth [39,40,41,42] in order to evaluate food limitation for different bivalve species such as Macoma balthica, Mya arenaria, Cerastoderma edule, Mytilus edulis, and Crassostrea gigas [43], and for Mytilus galloprovincialis [44], and to predict the impact of environmental changes on shellfish populations [45]. Used alone, or coupled with other biogeochemical [46], ecophysiological, and box models [47], DEB models have been proven to be a valid methodology to determine the quality of an area for shellfish aquaculture [34,35]. DEB models allow one to calculate the amount of energy used for shellfish growth and reproduction through the ingestion of the available food, thus they benefit from remote sensing estimates [48,49,50,51,52].
The Ebro delta, located in the western Mediterranean Sea, is a natural protected area where agriculture, fisheries, aquaculture, and tourism are the main economic activities. The aquaculture industry in the Ebro delta produces 3400 Tn of mussels and 300 Tn of oysters per year (average 2010–2021 [53]). Shellfish aquaculture is carried out in the two coastal embayments located in the northern (Fangar Bay) and the southern (Alfacs Bay) shores. The hydrodynamics in these embayments is highly sensitive to wind variability, which affects circulation patterns, water exchange times [54], and phytoplankton dynamics [55]. Drainage channels discharge freshwater from the rice fields into the embayments; the flow of freshwater is variable during the rice growing season from May to September, and it is almost negligible during the rest of the year. Shallowness and large water renewal times, coupled with the exacerbation of MHW events, is limiting the development of aquaculture in these embayments. Previous studies have focused on estimating chlorophyll-a concentration inside the embayments from remote sensing data (i.e., Sentinel-2 MultiSpectral imagery), either for monitoring phytoplankton biomass [56], or to evaluate the impact of coastal storms on water quality [57]. None of them have attempted to model the carrying capacity of the embayments or to evaluate the suitability of the nearby Mediterranean waters for shellfish aquaculture. These are crucial topics for the future of shellfish aquaculture in the region of the Ebro delta and other Mediterranean areas.
This study focuses on the development of a methodology to create, calibrate, and validate an algorithm that provides an accurate estimation of chlorophyll-a concentration in the coastal areas of the Ebro delta (NW Mediterranean) using atmospherically corrected Sentinel 2 (S2) remote sensing reflectances (Rrs) and a tool to calculate the carrying capacity of the potential new aquaculture areas and to evaluate its suitability. For this purpose, the DEB model has been implemented using two-year estimates of chlorophyll-a concentration derived from Sentinel-2 imagery and additional site-specific auxiliary data. The proposed approach is based on open-source data and open-source software tools. The use of remote sensing data will help the low trophic aquaculture industry to expand their activities to new suitable areas.
2. Materials and Methods
2.1. Study Area
The Ebro delta extends 25 km from the mainland and forms two embayments, Alfacs and Fangar (Figure 1). Fangar Bay, located in the north, has an extension of 12 km2 and a mean depth of 2 m, it contains 16 × 106 m3 of seawater, and the mouth of the Bay is 1 km wide. Alfacs Bay is in the south, its extension is 50 km2, the mean depth is 4 m, it contains 200 × 106 m3 of seawater, and its mouth is 3 km wide. Seawater temperature inside the embayments presents wide fluctuations in comparison to open waters. Both bays receive freshwater inputs from the agriculture drainage channels, favoring stratification during calm conditions [58]. The average salinity is similar in both bays: 34.6 in Fangar Bay and 34.8 in Alfacs. Freshwater inputs are 228 × 106 m3/year and 365 × 106 m3/year in Fangar and Alfacs, respectively. Water renewal time is approximately 1–2 days in Fangar and 10 days in Alfacs Bay [58]. Chlorophyll-a concentration increases during wind events due to horizontal mixing and bottom resuspension [55]. Both embayments currently hold mussel and oyster production; the location of mussels and oyster rafts is shown in Figure 2.
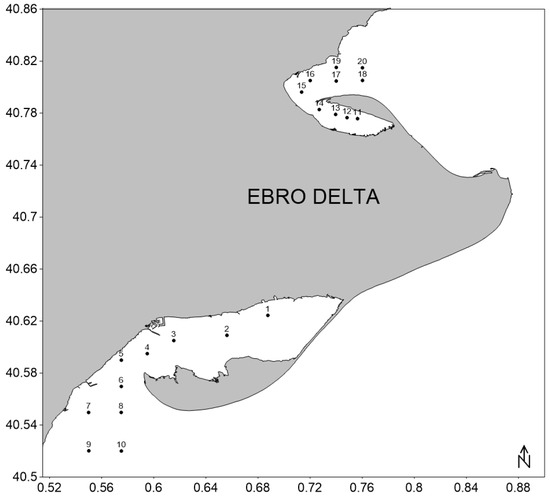
Figure 1.
Map showing the location of the sampling stations that were visited for in situ measurements and collection of water samples. Sampling stations in the southern area are numbered from 1 to 10, sampling stations in the northern area are numbered from 11 to 20.
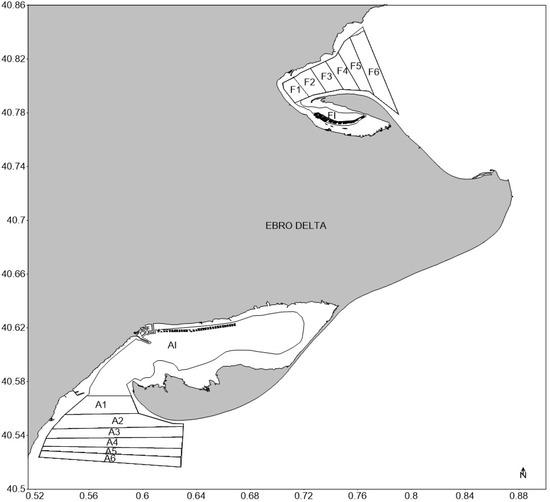
Figure 2.
Map showing the extent of the area of study divided in the area inside (AI, FI) and outside the coastal embayments. The external area is divided into different polygons (A1–A6, F1–F6).
2.2. In Situ Measurements
Sampling cruises were conducted, coinciding with a Sentinel-2 (S2) pass when the weather forecast was favorable. A total of 17 sampling cruises were carried out during the period 2 September 2020 to 27 October 2021, 9 of them covering the northern area and 8 for the southern area of the Ebro delta (western Mediterranean). Ten sampling stations were visited during each cruise, including waters inside and outside the bays. The location of the 20 sampling stations is shown in Figure 1. At each station, bottom depth, and the Secchi disk depth (ZSD) were measured; the profiles of temperature and salinity were obtained using a SeaBird19plus CTD and water samples were taken for chlorophyll-a analysis. Upon arrival at the laboratory, water samples were filtered through Whatman® glass microfiber filters, Grade GF/F (0.7 μm) 47 mm, using low vacuum. The filters were maintained at -80°C until analysis. Filter contents were extracted in acetone 90%, the absorbance of the extract was measured in a Shimadzu UV-1800 UV/Visible Scanning Spectrophotometer, and the chlorophyll-a concentration was calculated using the formula Chlorophyll-a = 11.85 E664 − 1.54 E647 − 0.08 E630 [59].
2.3. Maps of Chlorophyll-a from Sentinel-2
The Sentinel-2 (S2) constellation consists of two satellites (S2A and S2B) operated by The European Space Agency (ESA). Each satellite has on-board the MultiSpectral Instrument (S2-MSI). The S2-MSI Level-1 (L1C, Top of atmosphere) imagery includes 13 spectral bands centered at different wavelengths from 443 nm to 2200 nm with different spatial resolutions (10, 20, and 60 m). All available S2-L1C images between 1 October 2019 and 30 September 2021 were downloaded from the Copernicus Services Data Hub (https://cophub.copernicus.eu/dhus/#/home, accessed on 14 July 2022). The only orbit completely covering the study area was orbit #51. Every day the data from this orbit were available, the four tiles needed to cover the area were downloaded. This amounted to a total of 560 images (140 images per tile), covering a surface of 100 × 100 km2 for each tile.
Each image was visually checked for clouds and shadows over the region of study, leading to the rejection of 350 images (62.5%), implying the rejection of 46% of dates with chlorophyll-a in situ data. Due to project administrative deadlines, only images until September 2021 were used to accomplish the study.
The pre-processing of S2 imagery was performed through the Graphic Processing Tool (GTP) of SNAP v8.0 [60] and Rcore 3.6 [61]. For atmospheric correction of S2-MSI L1C imagery, the Case 2 Regional Coast Colour (C2RCC) and the C2X-COMPLEX (C2XC) processors (C2-Nets) [62] included in SNAP were applied on all valid S2 images. These processors are based on a multi-sensor per-pixel artificial neural network (NN) method, and differ in their training ranges of inherent optical properties [63]. The parametrization for the atmospheric correction of each image included: (a) pressure (hPa) from NCEP/DOE Reanalysis II data provided by the NOAA PSL, Boulder, Colorado, USA, from their website at https://psl.noaa.gov (accessed on 16 July 2022) [64]; (b) atmospheric ozone in Dobson units (DU) from the Aura OMI NASA dataset [65], downloaded for each location and date from https://oceancolor.gsfc.nasa.gov/ (accessed on 17 July 2022) [66]. Surface seawater temperature and salinity were obtained from the sampling cruises. For land/water segmentation, the valid pixel expression was set as a threshold on the short-wave infrared (SWIR) band of S2-MSI L1C images centered at 1600 nm (B11). The threshold was defined independently for each image with the triangle threshold method. From each C2-Net, remote sensing reflectance (Rrs) of visible and near infrared bands and the pigment absorption product (apig) were generated. C2-Nets flags, which include codes for quality control of pixels, were also exported. For C2RCC and C2XC, independently, images from the same date were merged when more than one tile were available.
A procedure to select match-ups between chlorophyll-a concentration measured from water samples and S2 Rrs was performed for the two C2-Nets. This procedure involves several steps. Firstly a 3 × 3 pixel window, centered at the coordinates of in situ measurements, was extracted for each date and sampling location, and C2-nets were quality-checked in all extracted pixels by applying the recommended flags [67]. Then, flagged pixels as well as pixels with negative Rrs at bands B1, B2, B3, and B4 were removed from the analysis, as recommended by Cui et al. [68]. The number of remaining pixels within each pixel window was checked; windows with less than 5 remaining pixels were removed from the analysis. Outliers were defined through Boxplot analysis applied to each available pixel window and spectral band (B1-B7 and B8A). Finally, the remaining pixel windows with less than 5 valid pixels were removed from the analysis.
A set of band combinations in the form of spectral indices were computed for all valid Rrs match-ups (Table 1). These spectral indices include visible and red edge S2 spectral bands (B1 to B6; ~443 nm to ~740 nm), exploiting specific chlorophyll-a absorption peaks in the blue and red spectral regions. The red edge bands are used for mitigating the effect of absorption by non-algal particles, yellow substances, and backscattering. For each C2-Net, chlorophyll-a was modelled with all the computed spectral indices and the apig band. Seventy percent of the data were used for model calibration (cal) and 30% for model validation (val). The cal/val datasets were generated randomly. Models were developed for raw and log-transformed Rrs/apig and chlorophyll-a data. Linear, linear piecewise (1 breakpoint), polynomial (2nd, 3rd, and 4th order), logarithmic, power, and exponential models were tested. The entire process was iterated 100 times with varying cal/val datasets. For each model (C2-Net × Band Combination × Type of fitting), performance was evaluated by means of the following statistics: mean average error (MAE), root mean squared error (RMSE), average percentage difference (APD), BIAS, and Pearson’s r.

Table 1.
Spectral bands and spectral combinations tested for chlorophyll-a estimation.
To generate the maps of chlorophyll-a, all flagged pixels (atmospheric correction flagging) were removed, as were pixels with negative Rrs in any of the spectral bands of each valid S2 image processed with the C2-Nets. The best performant model was selected according to lowest MAE, APD, RMSE, and BIAS, in this order, and it was applied to all valid images and pixels. Pixels with negative chlorophyll-a values were set to 0 mg/m3 and pixels with unreliably high chlorophyll-a concentration (>30 mg/m3) were removed. Pixels corresponding to the mussel farm structures or rafts were masked out using an available shapefile to mitigate/avoid pixel mixing problems.
2.4. Carrying Capacity Model
For the analysis and extraction of data from the generated images, QGIS 3.24 was used [74]. The area of interest corresponding to the masked images was divided into 2 different regions inside and outside the two coastal embayments (Figure 2). The studied area comprises 37.5 km2 inside and 37.8 km2 outside Alfacs Bay (southern area) and 2.7 km2 inside and 19.7 km2 outside Fangar Bay (northern area). The external area was divided into 12 polygons, 6 outside each embayment (Figure 2). The area inside each polygon was 5.5, 7.5, 7, 6.8, 4.8, 6.1 km2 for A1–A6 and 1.8, 2.5, 2.6, 2.9, 3.8, 6.1 km2 for F1–F6. Monthly chlorophyll-a concentration was averaged for each area of study, combining the available images for the period. The external areas were divided into different parts (polygons) to evaluate the gradient in chlorophyll-a concentration at different distances from the mouth of the bay. Each polygon was divided into three parts to evaluate the impact of the distance to the shore on the chlorophyll-a concentration.
The chlorophyll-a concentration, retrieved from the S2-L1C images treated with the algorithm calibrated and validated in this study, was used to determine the suitability of the different areas and their carrying capacity. To determine the suitability of each polygon for mussel aquaculture, the DEB model was applied. The model allows us to calculate the amount of energy used for growth and reproduction through the ingestion of the available food using the version from Rosland et al. [75] and the notation from Kooijman [76]. Mussel ingestion rate is proportional to the surface of the mussel, expressed as structural volume.
where is the ingestion rate; the values used for each parameter were obtained from van der Veer et al. [77] and are shown in Table 2. Clearance rates () were obtained from Galimany et al. [78]. The measured in situ seawater temperature (°C) at 1 m depth was converted to Kelvin degrees (K). In Equation (2), f is the Michaelis–Menten Equation to scale the ingestion rate to the food concentrations (X); this term scales the amount of food ingested as a function of the food (chlorophyll-a) available. In Equation (4), L is mussel length (cm), where δM is the dimensionless shape coefficient. Td in Equation (5) is the Arrhenius temperature function. The model (Equations (1)–(5)) was computed in Python.

Table 2.
Values used for the DEB model.
In a previous study [79], the DEB model was found to better reflect field observations of mussel ingestion in Alfacs Bay, in comparison with the Scope for Growth (SFG).
Carrying capacity was calculated by applying the recommendations of the Aquaculture Stewardship Council [80]. This standard provides indicators for a first approach to characterize the potential of an area. In the present study, the carrying capacity was defined as the number of rafts/ropes/mussels that can be grown in each area and was calculated as a function of the food availability measured through the chlorophyll-a concentration and the renewal time of the water masses. Chlorophyll-a concentration was obtained from the S2 images treated with the algorithm in this study, and the renewal time was calculated using the current speed at the different external areas.
In Formula (6), is the renewal time of the water in each area, is the total amount of chlorophyll-a in the whole volume of each area, and is the chlorophyll-a concentration of each area obtained from the Satellite images.
Different values of clearance rate, , were applied by selecting the corresponding values for each time of the year. The percentage of chlorophyll-a available for the cultivated mussels was assumed to be 0.75, and 0.25 was the remnant percentage. A standardized length of 3 m per rope that holds 1250 mussels was also used. These are the usual characteristics of the mussel ropes used in the Ebro delta. For the external areas, the average renewal times were calculated from the Copernicus Marine Service [81] using data from the years 2019 to 2021. For all areas, the volume was calculated for 3 m of depth as standard length of mussel ropes. The renewal times used for the areas inside the embayments were obtained from the bibliography [82]. We have not included primary production time because renewal times are short in the external areas.
The following diagram (Figure 3) shows the relation between in situ data, remote sensing data, and the different models used in this study.

Figure 3.
Diagram showing the relation between in situ data, remote sensing data, and the different models.
3. Results
3.1. In Situ Measurements
The results from the in situ measurements in October 2021 were not used for the calibration and validation of the satellite images but are included here to provide a wider view of the in situ environmental conditions of the area. The average depth of the 16 sampling stations was 7.7 ± 0.2 m (Mean ± Std. Error) and the range was 3.7–14.8 m. The average Secchi depth was 3.5 ± 0.2 m (Mean ± Std. Error) and the range was 1.3–10.4 m (Figure S1). The average chlorophyll-a concentration in the water samples was 2.4 ± 0.1 mg/m3 (Mean ± Std. Error) and the range was 0.1-8.9 mg/m3 (Figure 4). There was a statistically significant difference in chlorophyll-a concentration and Secchi disk depth (p ≤ 0.001) between the interior and the exterior sampling stations from the whole studied area (Kruskal–Wallis One Way Analysis of Variance on Ranks). In the southern area, there was no statistically significant difference in the mean values of chlorophyll-a concentration among the different sampling stations (p = 0.118) and dates (p = 0.251) (Two Way Analysis of Variance). In the northern area, there was a statistically significant difference (p ≤ 0.001) between sampling stations and dates.
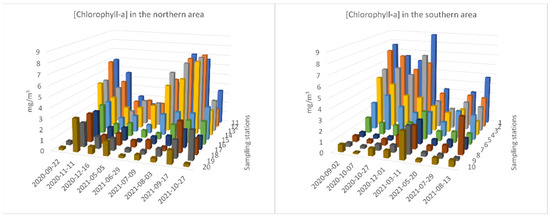
Figure 4.
Concentration of chlorophyll-a (mg/m3) at the different sampling stations.
The range in seawater temperature was 10.9–28.2 °C in the northern area outside Fangar Bay and 11.7–29.2 °C in the southern area outside Alfacs Bay. Minimum values were registered in January 2020 and maximum values in August 2020 (Figure 5). Higher temperature is measured in the southern area in comparison to the northern area.

Figure 5.
Seawater temperature (°C) in the external areas of the Ebro delta during the period of study.
3.2. Maps of Chlorophyll-a from Sentinel-2
Models performed better with C2XC than with C2RCC, particularly coupled with band combinations including spectral bands in the blue or green, and red or red edge regions. The best performance models for each C2-Net and band combinations are shown in Table 3. The best model for chlorophyll-a estimation was found with the C2XC processor, applying the REB1 band ratio (see Table 3) with a 2nd polynomial fitting ([chlorophyll-a] = −0.615 + 10.88 × REB1 + 8.704 × REB12).

Table 3.
Best performing models per C2-Net and spectral band combination.
The calibration and validation plots, as well as the fit between observed and estimated chlorophyll-a concentration values, are presented in Figure 6.
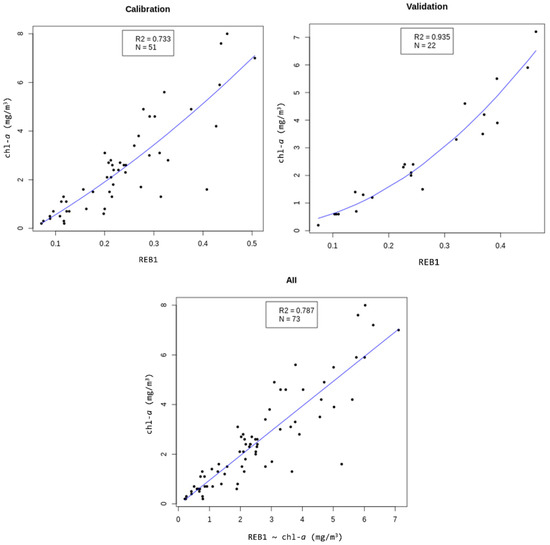
Figure 6.
Calibration, validation, and linear regression of the best model.
Maps of chlorophyll-a concentration from 56 different dates (Figure 7) along the period of study were generated using the methodology described in Section 2.3. A good agreement between estimated and observed chlorophyll-a concentration was observed within the sampling dates and the dynamic range of in situ data. However, unreliable high chlorophyll-a concentration was retrieved in some scenarios, such as the image of the 5 February 2020 (Figure 7), captured ~2 weeks after an extreme coastal storm. In those scenarios, dark brownish waters were visible in the RGB image composite, suggesting greater total suspended matter concentration and turbidity, leading to more optically complex waters.
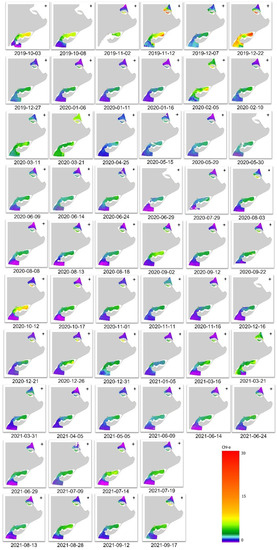
Figure 7.
Maps of chlorophyll-a concentration from the area of study (October 2019 to September 2021) derived from Sentinel-2.
3.3. Carrying Capacity Model
Monthly averages of chlorophyll-a concentration for the areas AI, A1–A6 together and FI, F1–F6 together are shown in Figure 8. Higher values of chlorophyll-a concentration were observed inside the two coastal embayments in comparison to the external area. The highest values occurred in Fangar Bay during autumn (13.6 mg/m3) and summer (8.5 mg/m3).
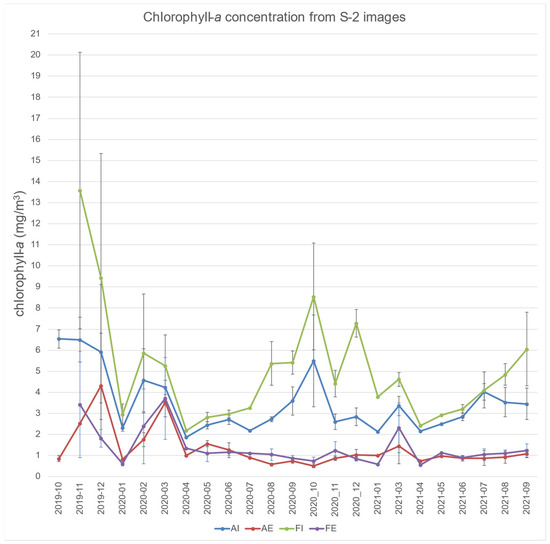
Figure 8.
Monthly chlorophyll-a concentration (Average ± Std. Error), from Sentinel-2 images, inside and outside the coastal embayments (AI: Alfacs interior, AE: Alfacs exterior, FI: Fangar Interior, FE: Fangar exterior).
In the north (F1–F6), the maximum averaged chlorophyll-a value per area and date (13.8 mg/m3) was detected in November 2019 in F1; in the south (A1–A6) it was detected in A2 in December 2019 (12.1 mg/m3). There are statistical differences between the different areas (Chi-square = 122, DF = 3, p < 0.001). The differences are between FI vs. AE, FI vs. FE, FI vs. AI, AI vs. AE, and AI vs. FE (Tukey test p < 0.05), but not between FE vs. AE (Tukey test p > 0.05). The averaged concentration of chlorophyll-a per date and polygon outside the embayments is shown in Figure S2. The minimum of the averaged values per image, external area, and date (0.12 mg/m3) was measured in July 2021 in A6 (southern area). In the same image, clouds where present in some of the areas, while in other areas of the same image the chlorophyll-a concentration could be measured. There are statistical differences between the different polygons (Tukey test p < 0.05); the results of the statistical analysis are shown in Figure S3. The gradient in chlorophyll-a concentration in the external areas at different distances from the bay’s mouth can be observed in Figure S4.
In the northern area outside Fangar Bay, apart from the gradient observed in chlorophyll-a at different distances from the mouth, a second gradient is observed inside each of the external areas at different distances from the shore, the closest areas to the shore being the richest in chlorophyll-a (Figure S3). A gradient is also observed in the southern areas, but in the opposite way. In polygons A1–A4, the areas closest to the shore contain less chlorophyll-a than those farther from the shore, except in polygons A5–A6, where the same pattern observed in the northern area occurs.
Ingestion rates () from October 2019 to September 2021 for the different polygons of the southern area and from November 2019 to September 2021 for the northern area are shown in Figure 9. In the external southern area, the mean value of was 8.7 ± 0.3 Jd−1 and the range was 1.6–14.2 Jd−1. The highest occurred from October 2019 to June 2020, when the range was 6.8–14.2 Jd−1; it decreased to values ≤ 8 Jd−1 from July to September 2020, increasing in October 2020 to values > 8 Jd−1 until May 2021, and decreasing again in June to September 2021 to values ≤ 8 Jd−1. In the external northern area, the mean value of was 7.7 ± 3.1 Jd−1 and the range was 1.7–12.5 Jd−1. In this area, the range was 6–12.5 Jd−1 from November 2019 to June 2020, decreasing to values < 6 Jd−1 from July to September 2020, increasing in October 2020 to values > 6 Jd−1 until May to June 2021, decreasing another time in July to September 2021. In both the northern and the southern area, there was a statistically significant difference (p ≤ 0.001; Two Way Analysis of Variance, General Linear Model) among the values for different dates and polygons.
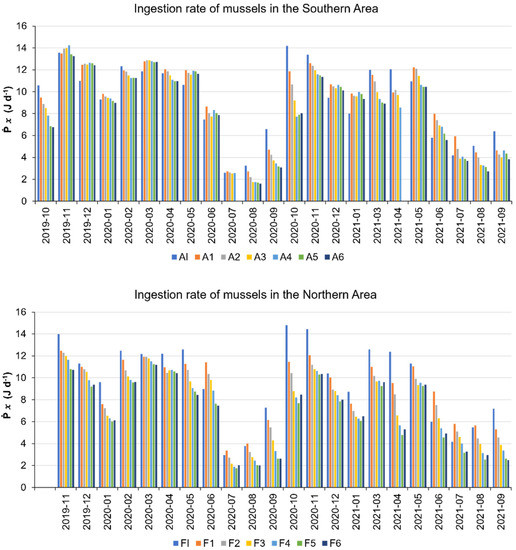
Figure 9.
Monthly average of the ingestion rates of mussels, (J d−1), inside the embayments and for the different polygons outside.
The carrying capacity (CC) calculated for each area is shown in Table 4 as the number of mussel rafts that can be held; a standardized raft in this study contains 1100 ropes of mussels that are 3 m in length. The renewal time for each area and the clearance rate time (h) calculated for the number of mussels and the chlorophyll-a stock of the area are also shown in Table 4. Renewal times are shorter than the clearance rate calculated because 0.75 of the chlorophyll-a stock was selected as available for CC. The renewal time used in Table 4 is the averaged renewal time for the year in each area. Because the renewal time is variable over the year, the CC was also modeled for different renewal times (Figure 10). We can observe that CC tends to stabilize at higher renewal times, depending on the internal areas below 50 rafts and the external areas below 200 rafts. The shaded red area in Figure 10 corresponds to the renewal time range described in previous studies and the red line is the CC calculated for this renewal time. In the external areas we observed the same exponential decreasing result.

Table 4.
Carrying capacity (CC) calculated for each area together with the corresponding surface and renewal times (Tr) and Clearance rate times. Note that the surface in AI and FI corresponds to the masked areas not to the whole surface of the embayments.
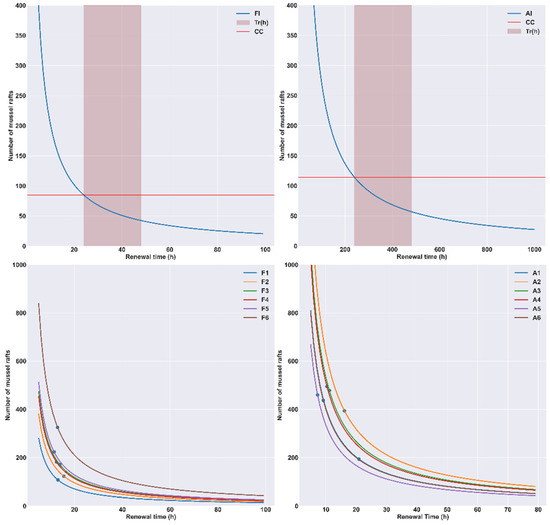
Figure 10.
Modeled number of rafts that each area can hold depending on the renewal time (h). The interior areas (FI, AI) are shown at the top of the image and the external areas (F1–F6, A1–A6) at the bottom. The horizontal red line represents the carrying capacity (CC) calculated for the average renewal time in hours (Tr) of the areas (FI, AI). The shaded area in FI, AI corresponds to the average renewal time of each embayment. The dots on the lines at the bottom of the figure correspond to the CC calculated for the average renewal time of each external area (F1–F6, A1–A6).
4. Discussion
The values of in situ Secchi disk depth and chlorophyll-a concentration measured in this study (2019–2021) differed slightly from those found in a previous study [82] conducted during the period 1982–1983. The Secchi disk depth (ZSD), at that time, was measured at some of the same sampling stations used for our study. The values obtained in [82] were 0.7–1.9 m deeper than our measurements when comparing the average values for each station. The same authors measured chlorophyll-a concentration and found yearly averages for the inner areas of 3.2 mg/m3 for AI and 3.44 mg/m3 for FI; these values are slightly lower than those found in our study: 5.2 mg/m3 for AI and 4 mg/m3 for FI. Therefore, the differences in Secchi disk depth can be partially explained by differences in chlorophyll-a concentration. Secchi disk depth (ZSD) is influenced by the phytoplankton biomass and other optical variables such as the colored dissolved organic matter (CDOM) and suspended particulate matter (SPM). Resuspension of sediments and the brownification of coastal waters influence ZSD, and therefore its relationship with chlorophyll-a concentration is not a straight inverse relation. The same authors detected maximum chlorophyll-a values in June–July (3.5–11 mg/m3) and September–October (25 mg/m3), and values in the range of 1–3.7 mg/m3 for the rest of the year. The maximum chlorophyll-a concentration in water samples measured in our study was 8.9 mg/m3 in December 2020 (AI). Higher values were observed from the satellite images. It is important to highlight that the values of chlorophyll-a retrieved from the Sentinel-2 images for the different polygons located at different distances from the mouth of the bays reflect the gradients observed in the in situ measurements of chlorophyll-a concentration.
Different methods exist for atmospheric correction in coastal waters, and some of them (C2-Nets, iCOR) are available in open-source tools such as SNAP. This feature opens the door to non-specialized users to generate atmospherically corrected S2 images by using this tool and following the proposed methodology. The model proposed here for mapping chlorophyll-a concentration, and the pixels quality control procedure, can also be implemented using the band-math’s functions provided by this tool.
The proposed methodology allows one to estimate chlorophyll-a concentration from Sentinel-2 with an accuracy higher than 70% in most cases (Table 3 and Figure 6). The best performant model was achieved with C2XC, which showed more consistent and accurate Rrs estimates than C2RCC in prior research [20]. However, empirical algorithms, such as the one used, can be expected to perform well only inside their range and for the area they were derived for. They are also limited in their ability to discriminate between non-unique signals from parameters that may be covariant, for example TSM and chlorophyll-a concentration [83]. The developed model is less reliable in conditions of high concentration of TSM and/or CDOM, which may occur after strong winds or storms (increased water turbulence, sediment resuspension, land runoff), as observed on 5 February 2020 (Figure 7). In these cases, the selected model tends to overestimate chlorophyll-a concentration because the red edge reflectance increases at high TSM values overlapping the absorption of chlorophyll-a in the blue region of the spectrum, which is also affected by greater CDOM concentration (CDOM strongly absorbs light up to 500 nm) [73,84]. In these cases, other empirical or semi-analytical algorithms may be more accurate. Further research should focus on the development of a multi-algorithm blending approach, which has proven to be more suitable across different types of water optical properties [85], albeit it will involve a more complex procedure. The development of an algorithm switching-based method requires the accurate definition of the optical water type pixel by pixel, accounting for the spectral shape, magnitude, and distinctive Rrs spectral features [86,87] and considering the uncertainty of the Rrs retrieval from C2-Nets across different optical water types [20]. In addition, in situ data covering all different scenarios are desirable, which may be difficult to reach due to complex logistics and meteorological limitations (i.e., cloud coverage), as occurred in our study.
The gradient observed in chlorophyll-a concentration from the inner areas towards the open sea is also observed in the values of ingestion rate (). The values of integrate the effect of chlorophyll-a concentration and seawater temperature on mussel physiology. Lower seawater temperature in summer in open waters in comparison to the inner areas could compensate the effect of having less phytoplankton available in these waters, obtaining similar or even better growth when high seawater temperature decreases mussel filtration rates. When we observe the mean values for the period of study in each area, in the north, we can see that the gradient decreases from 9.1 Jd−1 to 6.7 Jd−1 from area F1 to area F5, and it increases slightly to 6.9 Jd−1 in area F6. The gradient is less stepped in the southern area, from 9.3 Jd−1 in A1 to 8.3 Jd−1 in A6. We can employ the value of to rank the suitability of the different polygons for mussel aquaculture; the most suitable would be those with the highest , which are A1 and F1 followed by A2–5. The less suitable would be F3–6. We have based our model on the chlorophyll-a concentration measured in each area. The DEB model reflects well the decrease in food ingestion during summer months due to limiting seawater temperatures [88]. The use of chlorophyll-a as a proxy does not consider changes in food quality due, for example, to the presence of certain phytoplankton species with a different nutritional value. Some authors have detected gaps in DEB model parametrization and proposed to improve seston characterization [89,90], which should be tackled in further research.
A shellfish farm may exceed the ecological carrying capacity when the removal of phytoplankton biomass exceeds the renewal, resulting in a phytoplankton depleted water mass. In the proposed CC model, the renewal time of each area is shorter than the clearance rate time, thus complying with the ASC bivalve standard [80] that recommends comparing how long it takes to clear the body (CT) of water with the renewal time (RT), the ratio CT/RT should be >1. The same standard recommends that in locations where CT < RT, then the ratio CT/PPT should be >3. PPT is the number of days required for the replacement of phytoplankton biomass (PB) in the water body considering phytoplankton growth (PB/PPP; PPP = phytoplankton primary production). When the clearance rate is higher than the renewal rate plus the primary production, the body of water is depleted of phytoplankton and the bivalve stock will have less food available. Other authors suggest employing the regulation ratio defined as a fraction of the phytoplankton turnover rate RR = (1/CT)/(1/PT), where PT is the time it takes to renew the phytoplankton stock in an area [36,91]. We have applied the same formula for CC in the internal and external areas without considering primary production time. Renewal time in the internal areas is longer and it would be appropriate to include primary production time in the calculations. There are already mussel and oyster farms inside the embayments, therefore the chlorophyll-a concentration measured is affected already by the consumption of the bivalves from these farms. More complex models are needed to assess, with more detail, the carrying capacity inside the embayments. Renewal times are not uniform inside the embayments where hydrodynamic models are coupled with biological models such as the Regional Ocean Model System (ROMS) coupled to a biogeochemical nutrient-phytoplankton-zooplankton-detritus model (NPZD) such as in Dabrowski et al. [92]. Hydrodynamical modeling coupled to ecological modeling has been applied in other geographical areas to decide the most appropriate locations of the bivalve farms inside an embayment to avoid negative consequences for the ecosystem [93]. We have shown how small changes in renewal time affect the carrying capacity of the different water bodies in our study. The standard from the Aquaculture Stewardship Council [80] recommends to used retention time calculated as the number of days for tides to flush a volume of water equal to the volume of the area. In the Mediterranean Sea, tides have low amplitude, and so flushing time has to be calculated by other means.
The results on the modeled number of rafts in each area show that these external areas can hold a significant production of mussels in waters that are less impacted by warm events in summer. Mussel growth in these areas may be slower in comparison to the embayments due to lower chlorophyll-a concentration. The differences in seawater temperature measured during this study in summer were 1–2 °C for the same day and depth between internal and external areas; this small difference may be crucial to reduce mussel mortality in summer.
5. Conclusions
The proposed methodology can be reproduced using open-source tools such as SNAP software, enabling end-users to obtain their own maps of chlorophyll-a concentration from Sentinel-2 images. This methodology allows one to estimate chlorophyll-a concentration from Sentinel-2 with an accuracy higher than 70% in most cases. The best performant model was achieved with C2XC for atmospheric correction of S2-MSI L1C imagery. We have shown that the application of the DEB theory using multispectral remote sensing imagery allows one to rank the suitability of the different areas for shellfish aquaculture. It also allows one to determine the periods of the year with favorable and unfavorable conditions for shellfish growth. The results presented in this study show that the carrying capacity of the different areas is highly variable depending on the renewal times of the water, which at the same time are highly variable during the year. Nevertheless, the external areas located close to the Ebro delta embayments can hold a significant mussel production that would allow the reduction of mussel mortality during summer months due to the lower seawater temperature in these areas. This study shows the potential of the combined use of satellite remote sensing, in situ sampling, and carrying capacity models as a tool for helping the low trophic aquaculture industry to expand their activities to new suitable areas.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/rs14205235/s1, Figure S1. Secchi depth (m) at the different sampling stations. Note that the axis of sampling stations is reversed in the graphs showing chlorophyll-a concentration from Figure 3. Figure S2. Chlorophyll-a concentration, from Sentinel-2 images, averaged for each polygon and date outside the embayments. Figure S3. Matrix showing the results of the statistical analysis used to detect differences on the chlorophyll-a concentration, from Sentinel-2 images, averaged for each polygon and date outside the embayments. The squares colored in green correspond to polygons where statistical significant differences have been found, red color is for polygons where no differences have been detected, orange is for those polygons where no significant differences were found although they may exist. Figure S4. Chlorophyll-a concentration, from Sentinel-2 images, averaged for each of the 3 parts of each polygon outside the embayments, A-C are areas at different distances from the shore inside each polygon.
Author Contributions
Conceptualization, M.F.-T.; methodology, M.F.-T., J.E.V. and E.A.; software, J.E.V., E.A.; validation, M.F.-T., J.E.V. and E.A.; formal analysis, M.F.-T., J.E.V. and E.A.; investigation, M.F.-T., J.E.V. and E.A.; resources, M.F.-T.; data curation, J.E.V.; writing—original draft preparation, M.F.-T.; writing—review and editing, M.F.-T., J.E.V. and E.A.; visualization, M.F.-T., J.E.V. and E.A.; supervision, M.F.-T.; project administration, M.F.-T.; funding acquisition, M.F.-T. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the European Commission though the project New Technologies, Tools and Strategies for a Sustainable, Resilient and Innovative European Aquaculture (NewTechAqua), European Commission, Grant agreement ID: 862658 from Horizon 2020 Societal Challenges.
Data Availability Statement
Data supporting reported results can be found at the link https://github.com/E-Fis/Carrying-capacity-.
Acknowledgments
We acknowledge the support given by the technical staff of IRTA.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Brigolin, D.; Porporato, E.M.D.; Prioli, G.; Pastres, R. Making space for shellfish farming along the Adriatic coast. Ices J. Mar. Sci. 2017, 74, 1540–1551. [Google Scholar] [CrossRef]
- Giordano, L.; Portacci, G.; Caroppo, C. Multidisciplinary tools for sustainable management of an ecosystem service: The case study of mussel farming in the Mar Piccolo of Taranto (Mediterranean, Ionian Sea). Ocean Coast. Manag. 2019, 176, 11–23. [Google Scholar] [CrossRef]
- Habbane, M.; ElSabh, M.I.; Dubois, J.M. Determination of potential for aqua-culture activities via passive teledetection and a grid-based geographical information system—Application to coastal waters to the Baie-des-Chaleurs (Eastern Canada). Int. J. Remote Sens. 1997, 18, 3439–3457. [Google Scholar] [CrossRef]
- Hou, Y.; Zhao, G.; Chen, X.; Yu, X. Improving Satellite Retrieval of Coastal Aquaculture Pond by Adding Water Quality Parameters. Remote Sens. 2022, 14, 3306. [Google Scholar] [CrossRef]
- Radiarta, I.N.; Saitoh, S.-I. Biophysical models for Japanese scallop, Mizuhopecten yessoensis, aquaculture site selection in Funka Bay, Hokkaido, Japan, using remotely sensed data and geographic information system. Aquac. Int. 2009, 17, 403–419. [Google Scholar] [CrossRef]
- Babin, M.; Roesler, C.S.; Cullen, J.J. Real-Time Coastal Observing Systems for Marine Ecosystem Dynamics and Harmful Algal Blooms: Theory, Instrumentation and Modelling. In Monographs on Oceanographic Methodology; UNESCO: Paris, France, 2008. [Google Scholar]
- Silva, A.; Pinto, L.; Rodrigues, S.M.; de Pablo, H.; Santos, M.; Moita, T.; Mateus, M. A HAB warning system for shellfish harvesting in Portugal. Harmful Algae 2016, 53, 33–39. [Google Scholar] [CrossRef] [PubMed]
- Torres Palenzuela, J.M.; Gonzalez Vilas, L.; Bellas, F.M.; Garet, E.; Gonzalez-Fernandez, A.; Spyrakos, E. Pseudo-nitzschia Blooms in a Coastal Upwelling System: Remote Sensing Detection, Toxicity and Environmental Variables. Water 2019, 11, 1954. [Google Scholar] [CrossRef]
- Touza, I.S.; Rodriguez, J.E.A.; Pet, J.V.; Cumbreno, J.D.R. An Information System to Reduce the Effects of Red Tides in the Galician Rias. In Proceedings of the Systems of Optical Security 2003 Conference, Warsaw, Poland, 11–12 December 2003; pp. 33–37. [Google Scholar]
- Wakamatsu, L.; Britten, G.L.; Styles, E.J.; Fischer, A.M. Chlorophyll-a and Sea Surface Temperature Changes in Relation to Paralytic Shellfish Toxin Production off the East Coast of Tasmania, Australia. Remote Sens. 2022, 14, 665. [Google Scholar] [CrossRef]
- Wolny, J.L.; Tomlinson, M.C.; Uz, S.S.; Egerton, T.A.; McKay, J.R.; Meredith, A.; Reece, K.S.; Scott, G.P.; Stumpf, R.P. Current and Future Remote Sensing of Harmful Algal Blooms in the Chesapeake Bay to Support the Shellfish Industry. Front. Mar. Sci. 2020, 7, 337. [Google Scholar] [CrossRef]
- DeLuca, N.M.; Zaitchik, B.F.; Guikema, S.D.; Jacobs, J.M.; Davis, B.J.K.; Curriero, F.C. Evaluation of remotely sensed prediction and forecast models for Vibrio parahaemolyticus in the Chesapeake Bay. Remote Sens. Environ. 2020, 250, 112016. [Google Scholar] [CrossRef]
- Uz, S.S.; Ames, T.J.; Memarsadeghi, N.; McDonnell, S.M.; Blough, N.V.; Mehta, A.V.; McKay, J.R. Supporting Aquaculture in the Chesapeake Bay Using Artificial Intelligence to Detect Poor Water Quality with Remote Sensing. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Electr Network, Waikoloa, HI, USA, 26 September–2 October 2020; pp. 3629–3632. [Google Scholar]
- Huot, Y.; Babin, M.; Bruyant, F.; Grob, C.; Twardowski, M.S.; Claustre, H. Relationship between photosynthetic parameters and different proxies of phytoplankton biomass in the subtropical ocean. Biogeosciences 2007, 4, 853–868. [Google Scholar] [CrossRef]
- Muller-Karger, F.E.; Miloslavich, P.; Bax, N.J.; Simmons, S.; Costello, M.J.; Sousa Pinto, I.; Canonico, G.; Turner, W.; Gill, M.; Montes, E.; et al. Advancing Marine Biological Observations and Data Requirements of the Complementary Essential Ocean Variables (EOVs) and Essential Biodiversity Variables (EBVs) Frameworks. Front. Mar. Sci. 2018, 5, 211. [Google Scholar] [CrossRef]
- Miloslavich, P.; Bax, N.J.; Simmons, S.E.; Klein, E.; Appeltans, W.; Aburto-Oropeza, O.; Andersen Garcia, M.; Batten, S.D.; Benedetti-Cecchi, L.; Checkley Jr., D. M.; et al. Essential ocean variables for global sustained observations of biodiversity and ecosystem changes. Glob. Change Biol. 2018, 24, 2416–2433. [Google Scholar] [CrossRef] [PubMed]
- Staehr, S.U.; Van der Zande, D.; Staehr, P.A.U.; Markager, S. Suitability of multisensory satellites for long-term chlorophyll assessment in coastal waters: A case study in optically-complex waters of the temperate region. Ecol. Indic. 2022, 134, 108479. [Google Scholar] [CrossRef]
- Pahlevan, N.; Mangin, A.; Balasubramanian, S.V.; Smith, B.; Alikas, K.; Arai, K.; Barbosa, C.; Bélanger, S.; Binding, C.; Bresciani, M.; et al. ACIX-Aqua: A global assessment of atmospheric correction methods for Landsat-8 and Sentinel-2 over lakes, rivers, and coastal waters. Remote Sens. Environ. 2021, 258, 112366. [Google Scholar] [CrossRef]
- Gordon, H.R.; Morel, A.Y. Remote Assessment of Ocean Color for Interpretation of Satellite Visible Imagery. A Review; Springer: New York, NY, USA, 1983; p. 114. [Google Scholar]
- Soriano-González, J.; Urrego, E.P.; Sòria-Perpinyà, X.; Angelats, E.; Alcaraz, C.; Delegido, J.; Ruíz-Verdú, A.; Tenjo, C.; Vicente, E.; Moreno, J. Towards the Combination of C2RCC Processors for Improving Water Quality Retrieval in Inland and Coastal Areas. Remote Sens. 2022, 14, 1124. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, M.; Cui, T.; Wen, Z. A Review of Some Important Technical Problems in Respect of Satellite Remote Sensing of Chlorophyll-a Concentration in Coastal Waters. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 2275–2289. [Google Scholar] [CrossRef]
- FAO. The State of World Fisheries and Aquaculture 2022. Towards Blue Transformation; FAO: Rome, Italy, 2022. [Google Scholar]
- Naylor, R.L.; Hardy, R.W.; Buschmann, A.H.; Bush, S.R.; Cao, L.; Klinger, D.H.; Little, D.C.; Lubchenco, J.; Shumway, S.E.; Troell, M. A 20-year retrospective review of global aquaculture. Nature 2021, 591, 551–563. [Google Scholar] [CrossRef]
- Lucas, L.V.; Cloern, J.E.; Thompson, J.K.; Stacey, M.T.; Koseff, J.R. Bivalve Grazing Can Shape Phytoplankton Communities. Front. Mar. Sci. 2016, 3, 14. [Google Scholar] [CrossRef]
- Krause, G.; Le Vay, L.; Buck, B.; Costa-Pierce, B.; Dewhurst, T.; Heasman, K.; Nevejan, N.; Nielsen, P.; Nielsen, K.N.; Park, K.; et al. Prospects of Low Trophic Marine Aquaculture Contributing to Food Security in a Net Zero-Carbon World. Front. Sustain. Food Syst. 2022, 6, 875509. [Google Scholar] [CrossRef]
- Wijsman, J.W.M.; Troost, K.; Fang, J.; Roncarati, A. Global Production of Marine Bivalves. Trends and Challenges. In Goods and Services of Marine Bivalves; Smaal, A.C., Ferreira, J.G., Grant, J., Petersen, J.K., Strand, Ø., Eds.; Springer: Cham, Switzerland, 2019; pp. 7–26. [Google Scholar]
- Raymond, W.W.; Barber, J.S.; Dethier, M.N.; Hayford, H.A.; Harley, C.D.G.; King, T.L.; Paul, B.; Speck, C.A.; Tobin, E.D.; Raymond, A.E.T.; et al. Assessment of the impacts of an unprecedented heatwave on intertidal shellfish of the Salish Sea. Ecology 2022, 103, e3798. [Google Scholar] [CrossRef] [PubMed]
- White, R.; Anderson, S.; Booth, J.; Braich, G.; Draeger, C.; Fei, C.; Harley, C.; Henderson, S.; Jakob, M.; Lau, C.-A.; et al. The Unprecedented Pacific Northwest Heatwave of June 2021. Phys. Sci. 2022. [Google Scholar] [CrossRef]
- Seuront, L.; Nicastro, K.R.; Zardi, G.I.; Goberville, E. Decreased thermal tolerance under recurrent heat stress conditions explains summer mass mortality of the blue mussel Mytilus edulis. Sci. Rep. 2019, 9, 17498. [Google Scholar] [CrossRef] [PubMed]
- Harley, C.D.G. Tidal dynamics, topographic orientation, and temperature-mediated mass mortalities on rocky shores. Mar. Ecol. Prog. Ser. 2008, 371, 37–46. [Google Scholar] [CrossRef]
- Juza, M.; Tintoré, J. Multivariate Sub-Regional Ocean Indicators in the Mediterranean Sea: From Event Detection to Climate Change Estimations. Front. Mar. Sci. 2021, 8, 610589. [Google Scholar] [CrossRef]
- Juza, M.; Fernández-Mora, À.; Tintoré, J. Sub-Regional Marine Heat Waves in the Mediterranean Sea From Observations: Long-Term Surface Changes, Sub-Surface and Coastal Responses. Front. Mar. Sci. 2022, 9, 785771. [Google Scholar] [CrossRef]
- Ramon, M.; Fernandez, M.; Galimany, E. Development of mussel (Mytilus galloprovincialis) seed from two different origins in a semi-enclosed Mediterranean Bay (NE Spain). Aquaculture 2007, 264, 148–159. [Google Scholar] [CrossRef]
- Guyondet, T.; Roy, S.; Koutitonsky, V.G.; Grant, J.; Tita, G. Integrating multiple spatial scales in the carrying capacity assessment of a coastal ecosystem for bivalve aquaculture. J. Sea Res. 2010, 64, 341–359. [Google Scholar] [CrossRef]
- van der Veer, H.W.; Alunno-Bruscia, M. The DEBIB project: Dynamic Energy Budgets in Bivalves. J. Sea Res. 2006, 56, 81–84. [Google Scholar] [CrossRef]
- Smaal, A.C.; van Duren, L.A. Bivalve Aquaculture Carrying Capacity: Concepts and Assessment Tools. In Goods and Services of Marine Bivalves; Smaal, A.C., Ferreira, J.G., Grant, J., Petersen, J.K., Strand, Ø., Eds.; Springer: Cham, Switzerland, 2019; pp. 451–483. [Google Scholar]
- Dame, R.F.; Prins, T.C. Bivalve carrying capacity in coastal ecosystems. Aquat. Ecol. 1997, 31, 409–421. [Google Scholar] [CrossRef]
- Kooijman, S.A.L.M. Energy budgets can explain body size relations. J. Theor. Biol. 1986, 121, 269–282. [Google Scholar] [CrossRef]
- Cardoso, J.F.M.F.; van der Veer, H.W.; Kooijman, S.A.L.M. Body-size scaling relationships in bivalve species: A comparison of field data with predictions by the Dynamic Energy Budget (DEB) theory. J. Sea Res. 2006, 56, 125–139. [Google Scholar] [CrossRef]
- Dong, S.; Wang, F.; Zhang, D.; Yu, L.; Pu, W.; Shang, Y. Growth performance and ecological services evaluation of razor clams based on dynamic energy budget model. J. Environ. Manag. 2022, 306, 114329. [Google Scholar] [CrossRef] [PubMed]
- Fuentes-Santos, I.; Labarta, U.; Álvarez-Salgado, X.A. Modelling mussel shell and flesh growth using a dynamic net production approach. Aquaculture 2019, 506, 84–93. [Google Scholar] [CrossRef]
- Troost, T.A.; Wijsman, J.W.; Saraiva, S.; Freitas, V. Modelling shellfish growth with dynamic energy budget models: An application for cockles and mussels in the Oosterschelde (southwest Netherlands). Philos. Trans. R Soc. Lond. B Biol. Sci. 2010, 365, 3567–3577. [Google Scholar] [CrossRef]
- Cardoso, J.F.M.F.; Witte, J.I.J.; van der Veer, H.W. Intra- and interspecies comparison of energy flow in bivalve species in Dutch coastal waters by means of the Dynamic Energy Budget (DEB) theory. J. Sea Res. 2006, 56, 182–197. [Google Scholar] [CrossRef]
- Duarte, P.; Fernandez-Reiriz, M.J.; Labarta, U. Modelling mussel growth in ecosystems with low suspended matter loads using a Dynamic Energy Budget approach. J. Sea Res. 2012, 67, 44–57. [Google Scholar] [CrossRef]
- Stechele, B.; Maar, M.; Wijsman, J.; Van der Zande, D.; Degraer, S.; Bossier, P.; Nevejan, N. Comparing life history traits and tolerance to changing environments of two oyster species (Ostrea edulis and Crassostrea gigas) through Dynamic Energy Budget theory. Conserv. Physiol. 2022, 10, coac034. [Google Scholar] [CrossRef]
- Filgueira, R.; Guyondet, T.; Comeau, L.A.; Grant, J. A fully-spatial ecosystem-DEB model of oyster (Crassostrea virginica) carrying capacity in the Richibucto Estuary, Eastern Canada. J. Mar. Syst. 2014, 136, 42–54. [Google Scholar] [CrossRef]
- Pete, R.; Guyondet, T.; Bec, B.; Derolez, V.; Cesmat, L.; Lagarde, F.; Pouvreau, S.; Fiandrino, A.; Richard, M. A box-model of carrying capacity of the Thau lagoon in the context of ecological status regulations and sustainable shellfish cultures. Ecol. Model. 2020, 426, 109049. [Google Scholar] [CrossRef]
- Barille, L.; Le Bris, A.; Goulletquer, P.; Thomas, Y.; Glize, P.; Kane, F.; Falconer, L.; Guillotreau, P.; Trouillet, B.; Palmer, S.; et al. Biological, socio-economic, and administrative opportunities and challenges to moving aquaculture offshore for small French oyster-farming companies. Aquaculture 2020, 521, 735045. [Google Scholar] [CrossRef]
- Gernez, P.; Barille, L.; Lerouxel, A.; Mazeran, C.; Lucas, A.; Doxaran, D. Remote sensing of suspended particulate matter in turbid oyster-farming ecosystems. J. Geophys. Res. Ocean. 2014, 119, 7277–7294. [Google Scholar] [CrossRef]
- Graham, P.; Falconer, L.; Telfer, T.; Mossone, P.; Viale, I.; Carboni, S. A modelling approach to classify the suitability of shallow Mediterranean lagoons for pacific oyster, Crassostrea gigas (Thunberg, 1793) farming. Ocean Coast. Manag. 2020, 192, 105234. [Google Scholar] [CrossRef]
- Palmer, S.C.J.; Gornez, P.M.; Thomas, Y.; Simis, S.; Miller, P.I.; Glize, P.; Barille, L. Remote Sensing-Driven Pacific Oyster (Crassostrea gigas) Growth Modeling to Inform Offshore Aquaculture Site Selection. Front. Mar. Sci. 2020, 6, 802. [Google Scholar] [CrossRef]
- Stechele, B.; van der Zande, D.; Alvera-Azcárate, A.; Delbare, D.; Lacroix, G.; Nevejan, N. Biological site suitability for exposed self-regulating cultivation of blue mussel (Mytilus edulis): A Belgian case study. Aquac. Eng. 2022, 98, 102264. [Google Scholar] [CrossRef]
- Gencat. Evolució de la Producció Aqüícola Marina. Departament d’Acció Climàtica, Alimentació i Agenda Rural. Available online: http://agricultura.gencat.cat/ca/ambits/pesca/aquicultura/estadistica-aquicultura/evolucio-produccio-aquicola/ (accessed on 30 August 2022).
- Cerralbo, P.; Espino, M.; Grifoll, M. Modeling circulation patterns induced by spatial cross-shore wind variability in a small-size coastal embayment. Ocean Model. 2016, 104, 84–98. [Google Scholar] [CrossRef]
- F.-Pedrera Balsells, M.; Grifoll, M.; Fernández-Tejedor, M.; Espino, M. Short-Term Response of Chlorophyll a Concentration Due to Intense Wind and Freshwater Peak Episodes in Estuaries: The Case of Fangar Bay (Ebro Delta). Water 2021, 13, 701. [Google Scholar] [CrossRef]
- Soriano-González, J.; Angelats, E.; Fernández-Tejedor, M.; Diogene, J.; Alcaraz, C. First Results of Phytoplankton Spatial Dynamics in Two NW-Mediterranean Bays from Chlorophyll-a Estimates Using Sentinel 2: Potential Implications for Aquaculture. Remote Sens. 2019, 11, 1756. [Google Scholar]
- Angelats, E.; Soriano-González, J.; Fernández-Tejedor, M.; Alcaraz, C. Combined flooding and water quality monitoring during short extreme events using Sentinel-2: The caes study of Gloria storm in Ebro delta. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2022, V-3-2022, 361–368. [Google Scholar] [CrossRef]
- Camp, J.; Delgado, M. Hidrografía de las Bahías del Delta del Ebro. Investig. Pesq. 1987, 51, 351–369. [Google Scholar]
- Jeffrey, S.W.; Humphrey, G.F. New spectrophotometric equations for determining chlorophylls a, b, c1 and c2 in higher plants, algae and natural phytoplankton. Biochem. Und Physiol. Der Pflanz. 1975, 167, 191–194. [Google Scholar] [CrossRef]
- SNAP-ESA Sentinel Application Platform v 8.0. Available online: http://step.esa.int (accessed on 1 July 2022).
- RCoreTeam A Language and Environment for Statistical Computing, R Foundation for Statistical Computing: Vienna, Austria. Available online: https://www.R-project.org (accessed on 1 July 2022).
- Brockmann, C.; Doerffer, R.; Peters, M.; Kerstin, S.; Embacher, S.; Ruescas, A. Evolution of the C2RCC Neural Network for Sentinel 2 and 3 for the Retrieval of Ocean Colour Products in Normal and Extreme Optically Complex Waters. In Proceedings of the Living Planet Symposium, Prague, Czech Republic, 1 August 2016; p. 54. [Google Scholar]
- Warren, M.A.; Simis, S.G.H.; Martinez-Vicente, V.; Poser, K.; Bresciani, M.; Alikas, K.; Spyrakos, E.; Giardino, C.; Ansper, A. Assessment of atmospheric correction algorithms for the Sentinel-2A MultiSpectral Imager over coastal and inland waters. Remote Sens. Environ. 2019, 225, 267–289. [Google Scholar] [CrossRef]
- Kanamitsu, M.; Ebisuzaki, W.; Woollen, J.; Yang, S.-K.; Hnilo, J.J.; Fiorino, M.; Potter, G.L. NCEP–DOE AMIP-II Reanalysis (R-2). Bull. Am. Meteorol. Soc. 2002, 83, 1631–1644. [Google Scholar] [CrossRef]
- NASA Goddard Space Flight Center, O.E.L. Ocean Biology Processing Group. Ancillary Meteorological Ocean Color Data, NASA OB.DAAC. 2018. Available online: https://disc.gsfc.nasa.gov/datasets/OMTO3_003/summary (accessed on 17 July 2022).
- OceanColor Data. Available online: https://oceandata.sci.gsfc.nasa.gov (accessed on 27 September 2021).
- Pereira-Sandoval, M.; Ruescas, A.; Urrego, P.; Ruiz-Verdú, A.; Delegido, J.; Tenjo, C.; Soria-Perpinyà, X.; Vicente, E.; Soria, J.; Moreno, J. Evaluation of Atmospheric Correction Algorithms over Spanish Inland Waters for Sentinel-2 Multi Spectral Imagery Data. Remote Sens. 2019, 11, 1469. [Google Scholar] [CrossRef]
- Cui, T.; Zhang, J.; Groom, S.; Sun, L.; Smyth, T.; Sathyendranath, S. Validation of MERIS ocean-color products in the Bohai Sea: A case study for turbid coastal waters. Remote Sens. Environ. 2010, 114, 2326–2336. [Google Scholar] [CrossRef]
- Cairo, C.; Barbosa, C.; Lobo, F.; Novo, E.; Carlos, F.; Maciel, D.; Flores Júnior, R.; Silva, E.; Curtarelli, V. Hybrid Chlorophyll-a Algorithm for Assessing Trophic States of a Tropical Brazilian Reservoir Based on MSI/Sentinel-2 Data. Remote Sens. 2020, 12, 40. [Google Scholar] [CrossRef]
- O’Reilly, J.E.; Werdell, P.J. Chlorophyll algorithms for ocean color sensors—OC4, OC5 & OC6. Remote Sens. Environ. 2019, 229, 32–47. [Google Scholar] [CrossRef] [PubMed]
- Gitelson, A.A.; Gao, B.-C.; Li, R.-R.; Berdnikov, S.; Saprygin, V. Estimation of chlorophyll-a concentration in productive turbid waters using a Hyperspectral Imager for the Coastal Ocean—The Azov Sea case study. Environ. Res. Lett. 2011, 6, 024023. [Google Scholar] [CrossRef]
- Mishra, S.; Mishra, D.R. Normalized difference chlorophyll index: A novel model for remote estimation of chlorophyll-a concentration in turbid productive waters. Remote Sens. Environ. 2012, 117, 394–406. [Google Scholar] [CrossRef]
- Niroumand-Jadidi, M.; Bovolo, F.; Bruzzone, L.; Gege, P. Inter-Comparison of Methods for Chlorophyll-a Retrieval: Sentinel-2 Time-Series Analysis in Italian Lakes. Remote Sens. 2021, 13, 2381. [Google Scholar] [CrossRef]
- QGIS.org. QGIS Geographic Information System, QGIS Association. Available online: http://www.qgis.org (accessed on 21 April 2022).
- Rosland, R.; Strand, Ø.; Alunno-Bruscia, M.; Bacher, C.; Strohmeier, T. Applying Dynamic Energy Budget (DEB) theory to simulate growth and bio-energetics of blue mussels under low seston conditions. J. Sea Res. 2009, 62, 49–61. [Google Scholar] [CrossRef]
- Kooijman, S.A.L.M. Dynamic Energy and Mass Budgets in Biological Systems, 2nd ed.; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- van der Veer, H.W.; Cardoso, J.F.M.F.; van der Meer, J. The estimation of DEB parameters for various Northeast Atlantic bivalve species. J. Sea Res. 2006, 56, 107–124. [Google Scholar] [CrossRef]
- Galimany, E.; Ramón, M.; Ibarrola, I. Feeding behavior of the mussel Mytilus galloprovincialis (L.) in a Mediterranean estuary: A field study. Aquaculture 2011, 314, 236–243. [Google Scholar] [CrossRef]
- Ibáñez-Solé, J. Modelo Dinámico Para el Cálculo de la Capacidad de Carga de una Bahía Costera Para el Cultivo de Bivalvos; Universidad Nacional de Educación a Distancia (España); Facultad de Ciencias: Mexico City, Mexico, 2014. [Google Scholar]
- Aquaculture Stewardship Council. ASC Bivalve Standard, version 1.1; Aquaculture Stewardship Council: Utrecht, The Netherlands, 2019. [Google Scholar]
- Clementi, E.; Aydogdu, A.; Goglio, A.C.; Pistoia, J.; Escudier, R.; Drudi, M.; Grandi, A.; Mariani, A.; Lyubartsev, V.; Lecci, R.; et al. Mediterranean Sea Physical Analysis and Forecast (CMEMS MED-Currents, EAS6 system) (Version 1) set. Copernicus Monitoring Environment Marine Service (CMEMS). 2021. Available online: https://resources.marine.copernicus.eu/product-detail/MEDSEA_ANALYSISFORECAST_PHY_006_013/INFORMATION (accessed on 1 June 2022).
- Delgado, M. Fitoplancton de las Bahías del Delta del Ebro. Investig. Pesq. 1987, 51, 517–548. [Google Scholar]
- Matthews, M.W. A current review of empirical procedures of remote sensing in inland and near-coastal transitional waters. Int. J. Remote Sens. 2011, 32, 6855–6899. [Google Scholar] [CrossRef]
- Ligi, M.; Kutser, T.; Kallio, K.; Attila, J.; Koponen, S.; Paavel, B.; Soomets, T.; Reinart, A. Testing the performance of empirical remote sensing algorithms in the Baltic Sea waters with modelled and in situ reflectance data. Oceanologia 2017, 59, 57–68. [Google Scholar] [CrossRef]
- Moore, T.S.; Dowell, M.D.; Bradt, S.; Ruiz Verdu, A. An optical water type framework for selecting and blending retrievals from bio-optical algorithms in lakes and coastal waters. Remote Sens. Environ. 2014, 143, 97–111. [Google Scholar] [CrossRef]
- Spyrakos, E.; O’Donnell, R.; Hunter, P.D.; Miller, C.; Scott, M.; Simis, S.G.H.; Neil, C.; Barbosa, C.C.F.; Binding, C.E.; Bradt, S.; et al. Optical types of inland and coastal waters. Limnol. Oceanogr. 2018, 63, 846–870. [Google Scholar] [CrossRef]
- Uudeberg, K.; Ansko, I.; Põru, G.; Ansper, A.; Reinart, A. Using Optical Water Types to Monitor Changes in Optically Complex Inland and Coastal Waters. Remote Sens. 2019, 11, 2297. [Google Scholar] [CrossRef]
- Anestis, A.; Lazou, A.; Poertner, H.O.; Michaelidis, B. Behavioral, metabolic, and molecular stress responses of marine bivalve Mytilus galloprovincialis during long-term acclimation at increasing ambient temperature. Am. J. Physiol. Regul. Integr. Comp. Physiol. 2007, 293, R911–R921. [Google Scholar] [CrossRef] [PubMed]
- Filgueira, R.; Chica, M.; Palacios, J.J.; Strohmeier, T.; Lavaud, R.; Agüera, A.; Damas, S.; Strand, Ø. Embracing multimodal optimization to enhance Dynamic Energy Budget parameterization. Ecol. Model. 2020, 431, 109139. [Google Scholar] [CrossRef]
- Filgueira, R.; Strople, L.C.; Strohmeier, T.; Rastrick, S.; Strand, Ø. Mussels or tunicates: That is the question. Evaluating efficient and sustainable resource use by low-trophic species in aquaculture settings. J. Clean. Prod. 2019, 231, 132–143. [Google Scholar] [CrossRef]
- Gibbs, M.T. Sustainability performance indicators for suspended bivalve aquaculture activities. Ecol. Indic. 2007, 7, 94–107. [Google Scholar] [CrossRef]
- Dabrowski, T.; Lyons, K.; Curé, M.; Berry, A.; Nolan, G. Numerical modelling of spatio-temporal variability of growth of Mytilus edulis (L.) and influence of its cultivation on ecosystem functioning. J. Sea Res. 2013, 76, 5–21. [Google Scholar] [CrossRef]
- Filgueira, R.; Guyondet, T.; Thupaki, P.; Sakamaki, T.; Grant, J. The effect of embayment complexity on ecological carrying capacity estimations in bivalve aquaculture sites. J. Clean. Prod. 2021, 288, 125739. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).