Genetic Algorithm Captured the Informative Bands for Partial Least Squares Regression Better on Retrieving Leaf Nitrogen from Hyperspectral Reflectance
Abstract
1. Introduction
2. Materials and Methods
2.1. Datasets for LNC and Leaf Reflectance
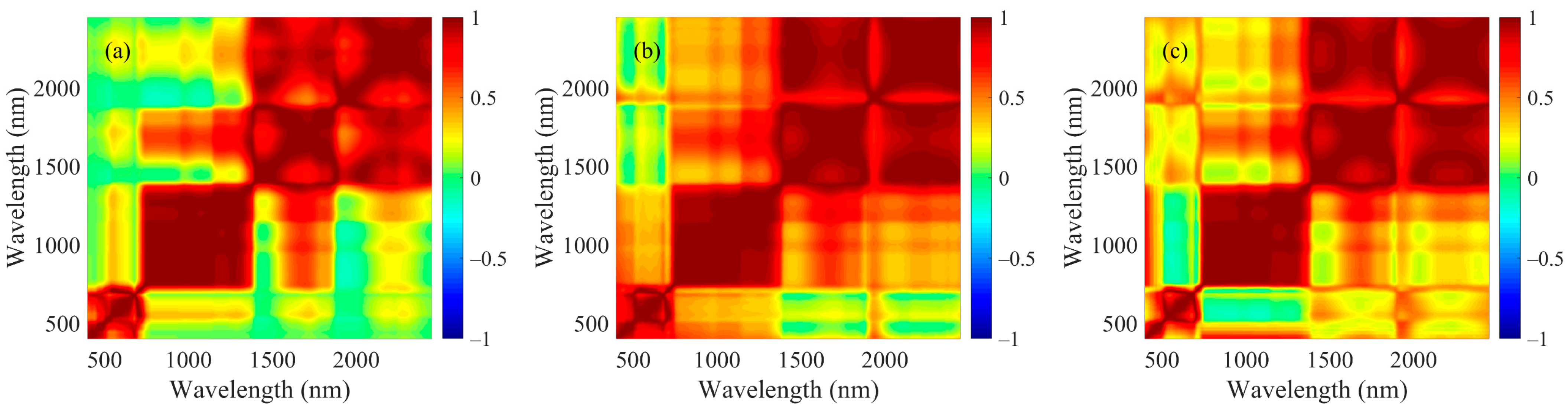
2.2. Spectral Data Processing
2.3. Informative Band Selections and Partial Least Squares Regression Analyses
2.4. Model Performance Evaluation
3. Results
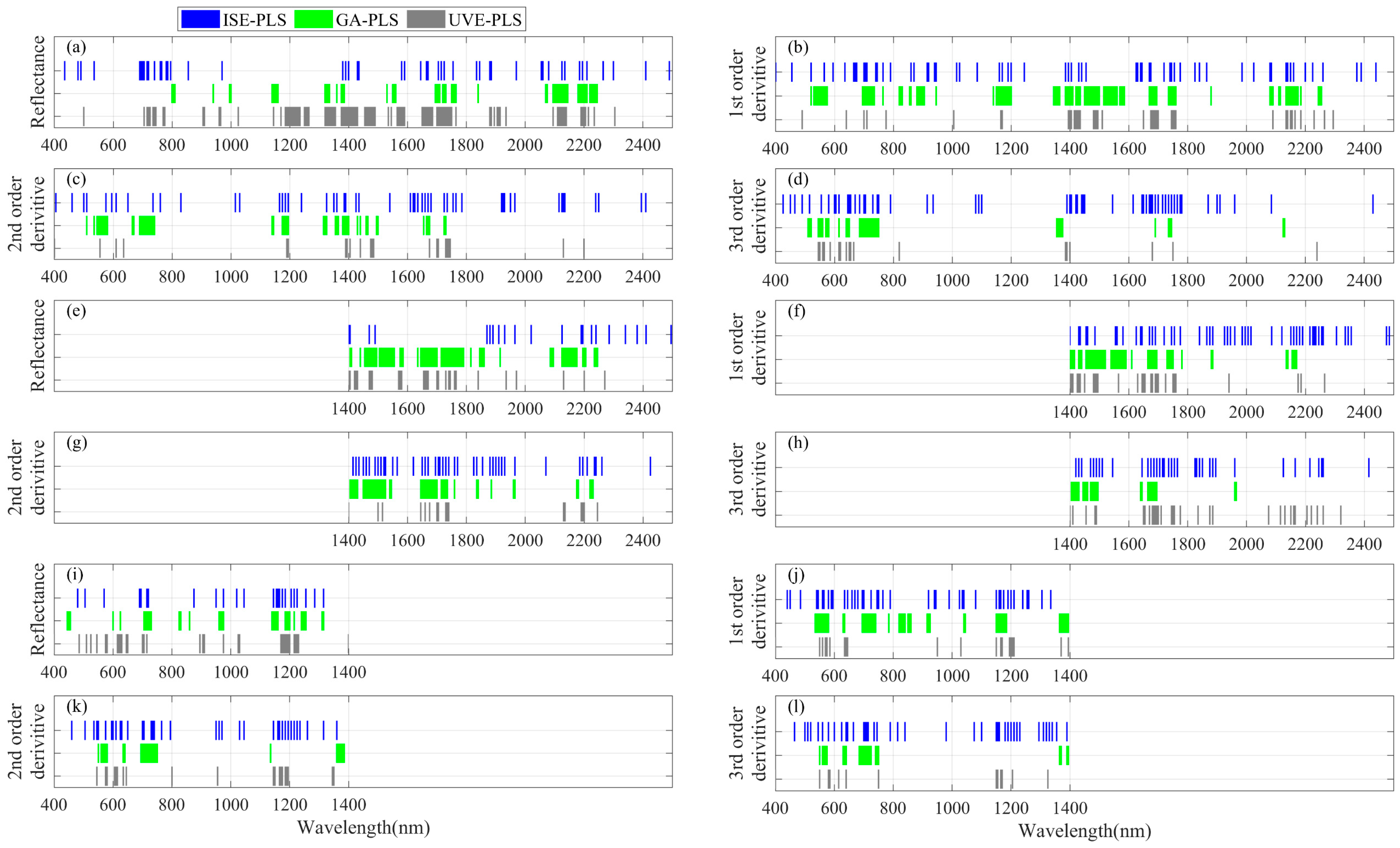
3.1. LNC Estimation from Spectra within 1400–2500 nm Using PLSR Models
3.2. LNC Estimation from Spectra within 400–2500 nm Using PLSR Models
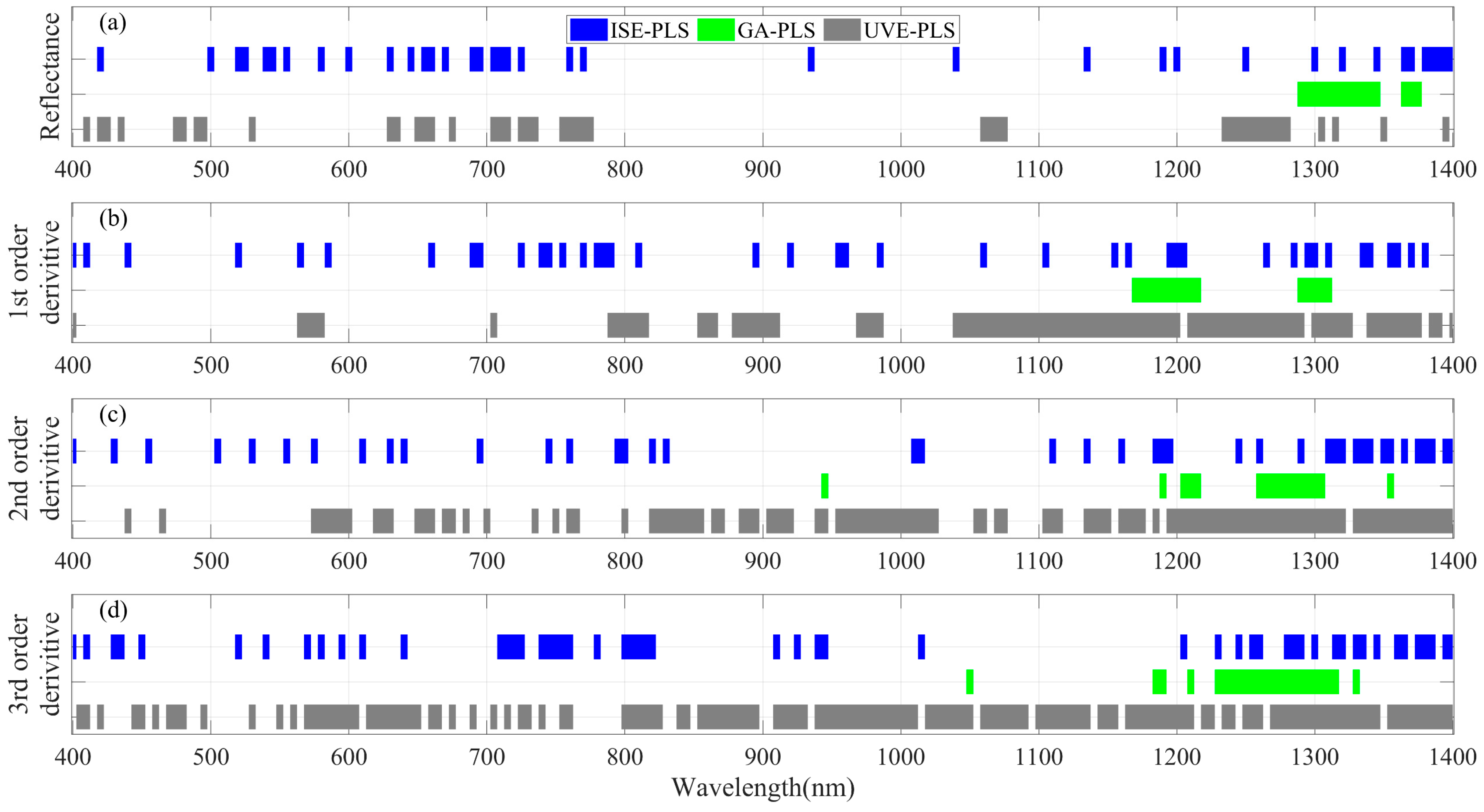
3.3. LNC Estimation from Spectra within 400–1400 nm Using PLSR Models
3.4. PLSR Models Developed from Field Datasets Directly
4. Discussion
4.1. Informative Band Selection—A Necessary Step for PLSR Models
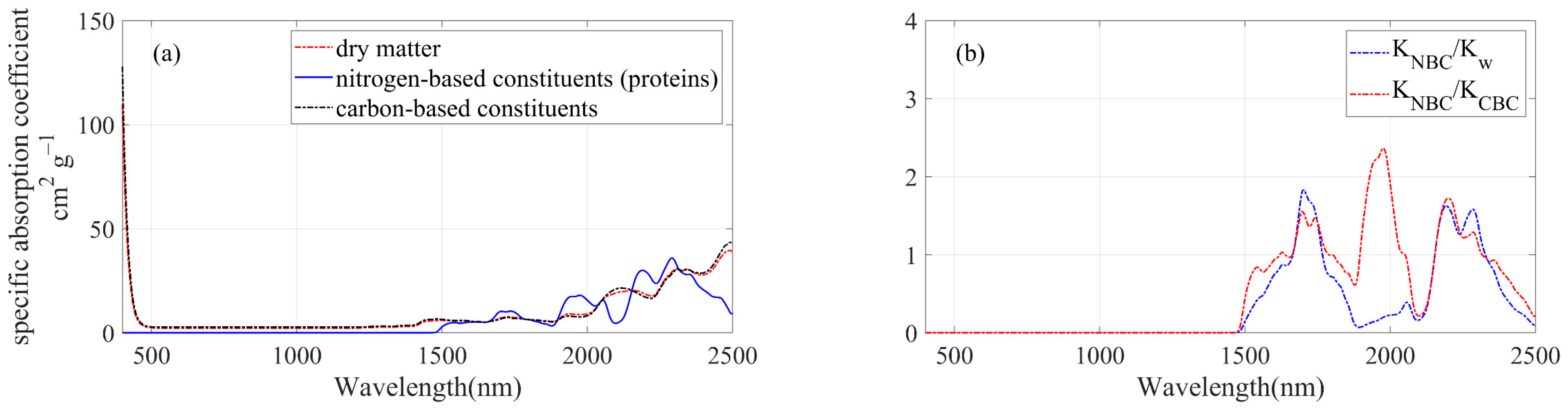
4.2. Informative Bands Selected for PLSR Models—Evidence from the PROSPECT-PRO Radiative Transfer Model
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wan, L.; Zhou, W.; He, Y.; Wanger, T.C.; Cen, H. Combining transfer learning and hyperspectral reflectance analysis to assess leaf nitrogen concentration across different plant species datasets. Remote Sens. Environ. 2022, 269, 112826. [Google Scholar] [CrossRef]
- Serbin, S.P.; Singh, A.; McNeil, B.E.; Kingdon, C.C.; Townsend, P.A. Spectroscopic determination of leaf morphological and biochemical traits for northern temperate and boreal tree species. Ecol. Appl. 2014, 24, 1651–1669. [Google Scholar] [CrossRef] [PubMed]
- Féret, J.-B.; Berger, K.; de Boissieu, F.; Malenovský, Z. PROSPECT-PRO for estimating content of nitrogen-containing leaf proteins and other carbon-based constituents. Remote Sens. Environ. 2021, 252, 112173. [Google Scholar] [CrossRef]
- Yang, X.; Tang, J.; Mustard, J.F.; Wu, J.; Zhao, K.; Serbin, S.; Lee, J.-E. Seasonal variability of multiple leaf traits captured by leaf spectroscopy at two temperate deciduous forests. Remote Sens. Environ. 2016, 179, 1–12. [Google Scholar] [CrossRef]
- Chavana-Bryant, C.; Malhi, Y.; Anastasiou, A.; Enquist, B.J.; Cosio, E.G.; Keenan, T.F.; Gerard, F.F. Leaf age effects on the spectral predictability of leaf traits in Amazonian canopy trees. Sci. Total Environ. 2019, 666, 1301–1315. [Google Scholar] [CrossRef]
- Zhang, Y.; Migliavacca, M.; Penuelas, J.; Ju, W. Advances in hyperspectral remote sensing of vegetation traits and functions. Remote Sens. Environ. 2021, 252, 112121. [Google Scholar] [CrossRef]
- Gamon, J.A.; Somers, B.; Malenovský, Z.; Middleton, E.M.; Rascher, U.; Schaepman, M.E. Assessing Vegetation Function with Imaging Spectroscopy. Surv. Geophys. 2019, 40, 489–513. [Google Scholar] [CrossRef]
- Jin, J.; Wang, Q. Hyperspectral indices developed from the low order fractional derivative spectra can capture leaf dry matter content across a variety of species better. Agric. For. Meteorol. 2022, 322, 109007. [Google Scholar] [CrossRef]
- Main, R.; Cho, M.A.; Mathieu, R.; O’Kennedy, M.M.; Ramoelo, A.; Koch, S. An investigation into robust spectral indices for leaf chlorophyll estimation. ISPRS-J. Photogramm. Remote Sens. 2011, 66, 751–761. [Google Scholar] [CrossRef]
- Féret, J.B.; Gitelson, A.A.; Noble, S.D.; Jacquemoud, S. PROSPECT-D: Towards modeling leaf optical properties through a complete lifecycle. Remote Sens. Environ. 2017, 193, 204–215. [Google Scholar] [CrossRef]
- Ali, A.M.; Darvishzadeh, R.; Skidmore, A.K.; Duren, I.v.; Heiden, U.; Heurich, M. Estimating leaf functional traits by inversion of PROSPECT: Assessing leaf dry matter content and specific leaf area in mixed mountainous forest. Int. J. Appl. Earth Obs. Geoinf. 2016, 45, 66–76. [Google Scholar] [CrossRef]
- Rubo, S.; Zinkernagel, J. Exploring hyperspectral reflectance indices for the estimation of water and nitrogen status of spinach. Biosys. Eng. 2022, 214, 58–71. [Google Scholar] [CrossRef]
- He, L.; Liu, M.-R.; Guo, Y.-L.; Wei, Y.-K.; Zhang, H.-Y.; Song, X.; Feng, W.; Guo, T.-C. Angular effect of algorithms for monitoring leaf nitrogen concentration of wheat using multi-angle remote sensing data. Comput. Electron. Agric. 2022, 195, 106815. [Google Scholar] [CrossRef]
- Burnett, A.C.; Serbin, S.P.; Davidson, K.J.; Ely, K.S.; Rogers, A. Detection of the metabolic response to drought stress using hyperspectral reflectance. J. Exp. Bot. 2021, 72, 6474–6489. [Google Scholar] [CrossRef] [PubMed]
- Berger, K.; Verrelst, J.; Féret, J.-B.; Wang, Z.; Wocher, M.; Strathmann, M.; Danner, M.; Mauser, W.; Hank, T. Crop nitrogen monitoring: Recent progress and principal developments in the context of imaging spectroscopy missions. Remote Sens. Environ. 2020, 242, 111758. [Google Scholar] [CrossRef] [PubMed]
- Ely, K.S.; Burnett, A.C.; Lieberman-Cribbin, W.; Serbin, S.P.; Rogers, A. Spectroscopy can predict key leaf traits associated with source-sink balance and carbon-nitrogen status. J. Exp. Bot. 2019, 70, 1789–1799. [Google Scholar] [CrossRef]
- Kawamura, K.; Watanabe, N.; Sakanoue, S.; Lee, H.J.; Inoue, Y.; Odagawa, S. Testing genetic algorithm as a tool to select relevant wavebands from field hyperspectral data for estimating pasture mass and quality in a mixed sown pasture using partial least squares regression. Grassl. Sci. 2010, 56, 205–216. [Google Scholar] [CrossRef]
- Huang, Z.; Turner, B.J.; Dury, S.J.; Wallis, I.R.; Foley, W.J. Estimating foliage nitrogen concentration from HYMAP data using continuum removal analysis. Remote Sens. Environ. 2004, 93, 18–29. [Google Scholar] [CrossRef]
- Thenkabail, P.S.; Lyon, J.G.; Huete, A. Hyperspectral Remote Sensing of Vegetation; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Hansen, P.M.; Schjoerring, J.K. Reflectance measurement of canopy biomass and nitrogen status in wheat crops using normalized difference vegetation indices and partial least squares regression. Remote Sens. Environ. 2003, 86, 542–553. [Google Scholar] [CrossRef]
- Yi, Q.; Jiapaer, G.; Chen, J.; Bao, A.; Wang, F. Different units of measurement of carotenoids estimation in cotton using hyperspectral indices and partial least square regression. ISPRS-J. Photogramm. Remote Sens. 2014, 91, 72–84. [Google Scholar] [CrossRef]
- Dorigo, W.A.; Zurita-Milla, R.; de Wit, A.J.W.; Brazile, J.; Singh, R.; Schaepman, M.E. A review on reflective remote sensing and data assimilation techniques for enhanced agroecosystem modeling. Int. J. Appl. Earth Obs. Geoinf. 2007, 9, 165–193. [Google Scholar] [CrossRef]
- Asner, G.P.; Martin, R.E. Spectral and chemical analysis of tropical forests: Scaling from leaf to canopy levels. Remote Sens. Environ. 2008, 112, 3958–3970. [Google Scholar] [CrossRef]
- le Maire, G.; François, C.; Soudani, K.; Berveiller, D.; Pontailler, J.-Y.; Bréda, N.; Genet, H.; Davi, H.; Dufrêne, E. Calibration and validation of hyperspectral indices for the estimation of broadleaved forest leaf chlorophyll content, leaf mass per area, leaf area index and leaf canopy biomass. Remote Sens. Environ. 2008, 112, 3846–3864. [Google Scholar] [CrossRef]
- Féret, J.-B.; François, C.; Gitelson, A.; Asner, G.P.; Barry, K.M.; Panigada, C.; Richardson, A.D.; Jacquemoud, S. Optimizing spectral indices and chemometric analysis of leaf chemical properties using radiative transfer modeling. Remote Sens. Environ. 2011, 115, 2742–2750. [Google Scholar] [CrossRef]
- Jin, J.; Wang, Q. Informative bands used by efficient hyperspectral indices to predict leaf biochemical contents are determined by their relative absorptions. Int. J. Appl. Earth Obs. Geoinf. 2018, 73, 616–626. [Google Scholar] [CrossRef]
- Wu, Q.; Wang, J.; Wang, C.; Xu, T. Study on the optimal algorithm prediction of corn leaf component information based on hyperspectral imaging. Infrared Phys. Technol. 2016, 78, 66–71. [Google Scholar] [CrossRef]
- Chen, H.; Chen, T.; Zhang, Z.; Liu, G. Variable Selection Using Adaptive Band Clustering and Physarum Network. Algorithms 2017, 10, 73. [Google Scholar] [CrossRef]
- Wang, Z.; Kawamura, K.; Sakuno, Y.; Fan, X.; Gong, Z.; Lim, J. Retrieval of Chlorophyll-a and Total Suspended Solids Using Iterative Stepwise Elimination Partial Least Squares (ISE-PLS) Regression Based on Field Hyperspectral Measurements in Irrigation Ponds in Higashihiroshima, Japan. Remote Sens. 2017, 9, 264. [Google Scholar] [CrossRef]
- Mehmood, T.; Liland, K.H.; Snipen, L.; Sæbø, S. A review of variable selection methods in Partial Least Squares Regression. Chemom. Intell. Lab. Syst. 2012, 118, 62–69. [Google Scholar] [CrossRef]
- Jin, J.; Wang, Q. Selection of informative spectral bands for PLS models to estimate foliar chlorophyll content using hyperspectral reflectance. IEEE Trans. Geosci. Remote Sens. 2019, 57, 3064–3072. [Google Scholar] [CrossRef]
- Centner, V.; Massart, D.-L.; de Noord, O.E.; de Jong, S.; Vandeginste, B.M.; Sterna, C. Elimination of Uninformative Variables for Multivariate Calibration. Anal. Chem. 1996, 68, 3851–3858. [Google Scholar] [CrossRef] [PubMed]
- Cai, W.; Li, Y.; Shao, X. A variable selection method based on uninformative variable elimination for multivariate calibration of near-infrared spectra. Chemom. Intell. Lab. Syst. 2008, 90, 188–194. [Google Scholar] [CrossRef]
- Leardi, R.; Boggia, R.; Terrile, M. Genetic algorithms as a strategy for feature selection. J. Chemom. 1992, 6, 267–281. [Google Scholar] [CrossRef]
- Burnett, A.C.; Serbin, S.P.; Rogers, A. Source:sink imbalance detected with leaf- and canopy-level spectroscopy in a field-grown crop. Plant Cell Environ. 2021, 44, 2466–2479. [Google Scholar] [CrossRef]
- Chavana-Bryant, C.; Malhi, Y.; Wu, J.; Asner, G.P.; Anastasiou, A.; Enquist, B.J.; Cosio Caravasi, E.G.; Doughty, C.E.; Saleska, S.R.; Martin, R.E.; et al. Leaf aging of Amazonian canopy trees as revealed by spectral and physiochemical measurements. New Phytol. 2017, 214, 1049–1063. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Nie, C.; Wei, C.; Xu, X.; Song, X.; Wang, J. Comparison of Four Chemometric Techniques for Estimating Leaf Nitrogen Concentrations in Winter Wheat (Triticum Aestivum) Based on Hyperspectral Features. J. Appl. Spectrosc. 2016, 83, 240–247. [Google Scholar] [CrossRef]
- Yao, X.; Huang, Y.; Shang, G.; Zhou, C.; Cheng, T.; Tian, Y.; Cao, W.; Zhu, Y. Evaluation of Six Algorithms to Monitor Wheat Leaf Nitrogen Concentration. Remote Sens. 2015, 7, 14939–14966. [Google Scholar] [CrossRef]
- Tahmasbian, I.; Xu, Z.; Abdullah, K.; Zhou, J.; Esmaeilani, R.; Nguyen, T.T.N.; Hosseini Bai, S. The potential of hyperspectral images and partial least square regression for predicting total carbon, total nitrogen and their isotope composition in forest litterfall samples. J. Soils Sed. 2017, 17, 2091–2103. [Google Scholar] [CrossRef]
- Wang, Q.; Jin, J.; Sonobe, R.; Chen, J.M. Derivative hyperspectral vegetation indices in characterizing forest biophysical and biochemical quantities. In Hyperspectral Indices and Image Classifications for Agriculture and Vegetation; Thenkabail, P.S., Lyon, J.G., Huete, A., Eds.; CRC Press: Boca Raton, FL, USA, 2018; pp. 27–63. [Google Scholar]
- Huguenin, R.L.; Jones, J.L. Intelligent information extraction from reflectance spectra: Absorption band positions. J. Geophys. Res. Solid Earth 1986, 91, 9585–9598. [Google Scholar] [CrossRef]
- Becker, B.L.; Lusch, D.P.; Qi, J. Identifying optimal spectral bands from in situ measurements of Great Lakes coastal wetlands using second-derivative analysis. Remote Sens. Environ. 2005, 97, 238–248. [Google Scholar] [CrossRef]
- Tsai, F.; Philpot, W. Derivative Analysis of Hyperspectral Data. Remote Sens. Environ. 1998, 66, 41–51. [Google Scholar] [CrossRef]
- Demetriades-Shah, T.H.; Steven, M.D.; Clark, J.A. High resolution derivative spectra in remote sensing. Remote Sens. Environ. 1990, 33, 55–64. [Google Scholar] [CrossRef]
- Abulaiti, Y.; Sawut, M.; Maimaitiaili, B.; Chunyue, M. A possible fractional order derivative and optimized spectral indices for assessing total nitrogen content in cotton. Comput. Electron. Agric. 2020, 171, 105275. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Baret, F. PROSPECT: A model of leaf optical properties spectra. Remote Sens. Environ. 1990, 34, 75–91. [Google Scholar] [CrossRef]
- Hosgood, B.; Jacquemoud, S.; Andreoli, G.; Verdebout, J.; Pedrini, G.; Schmuck, G. Leaf Optical Properties Experiment 93 (LOPEX93); European Commission—Joint Research Centre EUR 16095 EN: Ispra, Italy, 1994; p. 20. [Google Scholar]
- Stein, M. Large Sample Properties of Simulations Using Latin Hypercube Sampling. Technometrics 1987, 29, 143–151. [Google Scholar] [CrossRef]
- Ely, K.S.; Serbin, S.P.; Lieberman-Cribbin, W.; Rogers, A. Leaf Spectra, Structural and Biochemical Leaf Traits of Eight Crop Species. Ecological Spectral Information System (EcoSIS), 2018. Available online: http://ecosis.org (accessed on 2 September 2021). [CrossRef]
- Burnett, A.C.; Serbin, S.P.; Davidson, K.J.; Ely, K.S.; Rogers, A. Hyperspectral Leaf Reflectance, Biochemistry, and Physiology of Droughted and Watered Crops. Ecological Spectral Information System (EcoSIS), 2020. Available online: http://ecosis.org (accessed on 2 September 2021). [CrossRef]
- Vaiphasa, C. Consideration of smoothing techniques for hyperspectral remote sensing. ISPRS-J. Photogramm. Remote Sens. 2006, 60, 91–99. [Google Scholar] [CrossRef]
- Marang, I.J.; Filippi, P.; Weaver, T.B.; Evans, B.J.; Whelan, B.M.; Bishop, T.F.A.; Murad, M.O.F.; Al-Shammari, D.; Roth, G. Machine Learning Optimised Hyperspectral Remote Sensing Retrieves Cotton Nitrogen Status. Remote Sens. 2021, 13, 1428. [Google Scholar] [CrossRef]
- Boggia, R.; Forina, M.; Fossa, P.; Mosti, L. Chemometric Study and Validation Strategies in the Structure-Activity Relationships of New Cardiotonic Agents. Quant. Struct.-Act. Relat. 1997, 16, 201–213. [Google Scholar] [CrossRef]
- Leardi, R. Application of genetic algorithm–PLS for feature selection in spectral data sets. J. Chemom. 2000, 14, 643–655. [Google Scholar] [CrossRef]
- Leardi, R.; Lupiáñez González, A. Genetic algorithms applied to feature selection in PLS regression: How and when to use them. Chemom. Intell. Lab. Syst. 1998, 41, 195–207. [Google Scholar] [CrossRef]
- Burnett, A.C.; Anderson, J.; Davidson, K.J.; Ely, K.S.; Lamour, J.; Li, Q.; Morrison, B.D.; Yang, D.; Rogers, A.; Serbin, S.P. A best-practice guide to predicting plant traits from leaf-level hyperspectral data using partial least squares regression. J. Exp. Bot. 2021, 72, 6175–6189. [Google Scholar] [CrossRef] [PubMed]
- Fushiki, T. Estimation of prediction error by using K-fold cross-validation. Stat. Comput. 2011, 21, 137–146. [Google Scholar] [CrossRef]
- Deepak, M.; Keski-Saari, S.; Fauch, L.; Granlund, L.; Oksanen, E.; Keinänen, M. Leaf Canopy Layers Affect Spectral Reflectance in Silver Birch. Remote Sens. 2019, 11, 2884. [Google Scholar] [CrossRef]
- Mishra, P.; Asaari, M.S.M.; Herrero-Langreo, A.; Lohumi, S.; Diezma, B.; Scheunders, P. Close range hyperspectral imaging of plants: A review. Biosys. Eng. 2017, 164, 49–67. [Google Scholar] [CrossRef]
- McQuarrie, A.D.R.; Tsai, C.-L. Regression and Time Series Model Selection; World Scientific: Singapore, 1998. [Google Scholar]
- Hurvich, C.M.; Tsai, C.-L. Regression and Time Series Model Selection in Small Samples. Biometrika 1989, 76, 297–307. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Burnham, K.P.; Anderson, D.R. Multimodel Inference:Understanding AIC and BIC in Model Selection. Sociol. Methods Res. 2004, 33, 261–304. [Google Scholar] [CrossRef]
- Bozdogan, H. Model selection and Akaike’s Information Criterion (AIC): The general theory and its analytical extensions. Psychometrika 1987, 52, 345–370. [Google Scholar] [CrossRef]
- Verma, B.; Prasad, R.; Srivastava, P.K.; Yadav, S.A.; Singh, P.; Singh, R.K. Investigation of optimal vegetation indices for retrieval of leaf chlorophyll and leaf area index using enhanced learning algorithms. Comput. Electron. Agric. 2022, 192, 106581. [Google Scholar] [CrossRef]
- Jin, J.; Wang, Q. Evaluation of Informative Bands Used in Different PLS Regressions for Estimating Leaf Biochemical Contents from Hyperspectral Reflectance. Remote Sens. 2019, 11, 197. [Google Scholar] [CrossRef]
- Fan, L.; Zhao, J.; Xu, X.; Liang, D.; Yang, G.; Feng, H.; Yang, H.; Wang, Y.; Chen, G.; Wei, P. Hyperspectral-based Estimation of Leaf Nitrogen Content in Corn Using Optimal Selection of Multiple Spectral Variables. Sensors 2019, 19, 2898. [Google Scholar] [CrossRef] [PubMed]
- Thorp, K.R.; Wang, G.; Bronson, K.F.; Badaruddin, M.; Mon, J. Hyperspectral data mining to identify relevant canopy spectral features for estimating durum wheat growth, nitrogen status, and grain yield. Comput. Electron. Agric. 2017, 136, 1–12. [Google Scholar] [CrossRef]
- Yang, B.; He, Y.; Chen, W. A simple method for estimation of leaf dry matter content in fresh leaves using leaf scattering albedo. Glob. Ecol. Conserv. 2020, 23, e01201. [Google Scholar] [CrossRef]





| Spectral Form | Method | N_Bands | R2m | R2A | R2B | AICc |
|---|---|---|---|---|---|---|
| Original reflectance | FB-PLS | 221 | 1.00 | 0.00 | 0.02 | 2.60 |
| ISE-PLS | 58 | 1.00 | 0.05 | 0.20 | 2.90 | |
| GA-PLS | 41 | 0.98 | 0.64 | 0.63 | −2.44 | |
| UVE-PLS | 175 | 0.99 | 0.75 | 0.71 | −2.78 | |
| First-order derivative | FB-PLS | 221 | 1.00 | 0.06 | 0.00 | 3.02 |
| ISE-PLS | 92 | 1.00 | 0.04 | 0.01 | 3.07 | |
| GA-PLS | 19 | 0.97 | 0.39 | 0.40 | −1.90 | |
| UVE-PLS | 195 | 0.99 | 0.75 | 0.75 | −2.99 | |
| Second-order derivative | FB-PLS | 221 | 1.00 | 0.21 | 0.05 | 2.41 |
| ISE-PLS | 117 | 1.00 | 0.20 | 0.02 | 3.83 | |
| GA-PLS | 23 | 0.96 | 0.53 | 0.42 | −1.93 | |
| UVE-PLS | 201 | 0.99 | 0.68 | 0.72 | −2.82 | |
| Third-order derivative | FB-PLS | 221 | 1.00 | 0.15 | 0.02 | 4.47 |
| ISE-PLS | 126 | 1.00 | 0.06 | 0.02 | 4.43 | |
| GA-PLS | 62 | 0.98 | 0.51 | 0.51 | −2.10 | |
| UVE-PLS | 183 | 0.99 | 0.57 | 0.59 | −2.40 |
| Spectral Form | Method | N_Bands | R2m | R2A | R2B | AICc |
|---|---|---|---|---|---|---|
| Original reflectance | FB-PLS | 421 | 1.00 | 0.01 | 0.00 | 2.53 |
| ISE-PLS | 78 | 0.99 | 0.00 | 0.00 | 2.27 | |
| GA-PLS | 24 | 0.98 | 0.35 | 0.55 | −2.24 | |
| UVE-PLS | 301 | 0.98 | 0.34 | 0.64 | −2.30 | |
| First-order derivative | FB-PLS | 421 | 1.00 | 0.04 | 0.20 | −1.42 |
| ISE-PLS | 133 | 1.00 | 0.03 | 0.03 | −0.22 | |
| GA-PLS | 29 | 0.99 | 0.53 | 0.51 | −2.31 | |
| UVE-PLS | 300 | 0.99 | 0.69 | 0.78 | −3.05 | |
| Second-order derivative | FB-PLS | 421 | 0.99 | 0.01 | 0.16 | −0.24 |
| ISE-PLS | 135 | 1.00 | 0.17 | 0.02 | 1.14 | |
| GA-PLS | 51 | 0.99 | 0.59 | 0.55 | −2.43 | |
| UVE-PLS | 283 | 0.99 | 0.65 | 0.73 | −2.77 | |
| Third-order derivative | FB-PLS | 421 | 0.99 | 0.00 | 0.08 | 1.85 |
| ISE-PLS | 135 | 1.00 | 0.06 | 0.02 | 3.36 | |
| GA-PLS | 50 | 0.98 | 0.24 | 0.25 | −1.72 | |
| UVE-PLS | 259 | 0.99 | 0.49 | 0.63 | −2.43 |
| Spectral Form | Method | N_Bands | R2m | R2A | R2B | AICc |
|---|---|---|---|---|---|---|
| Original reflectance | FB-PLS | 201 | 0.43 | 0.04 | 0.21 | 3.81 |
| ISE-PLS | 38 | 0.94 | 0.00 | 0.01 | 6.12 | |
| GA-PLS | 15 | 0.40 | 0.15 | 0.31 | 0.11 | |
| UVE-PLS | 44 | 0.42 | 0.40 | 0.66 | 0.02 | |
| First-order derivative | FB-PLS | 201 | 0.51 | 0.06 | 0.05 | 5.68 |
| ISE-PLS | 41 | 0.96 | 0.04 | 0.03 | 8.21 | |
| GA-PLS | 15 | 0.30 | 0.11 | 0.24 | 0.25 | |
| UVE-PLS | 93 | 0.43 | 0.69 | 0.71 | 0.01 | |
| Second-order derivative | FB-PLS | 201 | 0.64 | 0.00 | 0.06 | 6.25 |
| ISE-PLS | 42 | 0.96 | 0.09 | 0.01 | 7.86 | |
| GA-PLS | 16 | 0.29 | 0.09 | 0.28 | 0.24 | |
| UVE-PLS | 114 | 0.42 | 0.52 | 0.73 | 0.02 | |
| Third-order derivative | FB-PLS | 201 | 0.63 | 0.00 | 0.00 | 7.65 |
| ISE-PLS | 53 | 0.92 | 0.01 | 0.02 | 6.04 | |
| GA-PLS | 23 | 0.30 | 0.01 | 0.16 | 0.25 | |
| UVE-PLS | 145 | 0.42 | 0.49 | 0.71 | 0.03 |
| Spectral Region | Spectral Form | Method | N_Bands | R2c | R2v | R2A | R2B | AICc |
|---|---|---|---|---|---|---|---|---|
| 400–2500 nm | Original reflectance | FB-PLS | 421 | 0.87 | 0.87 | 0.74 | 0.86 | 2.45 |
| ISE-PLS | 49 | 0.88 | 0.86 | 0.81 | 0.87 | −0.99 | ||
| GA-PLS | 61 | 0.80 | 0.81 | 0.75 | 0.79 | −0.47 | ||
| UVE-PLS | 110 | 0.87 | 0.89 | 0.75 | 0.88 | −0.75 | ||
| 1st order derivative | FB-PLS | 421 | 0.91 | 0.84 | 0.82 | 0.89 | 2.20 | |
| ISE-PLS | 64 | 0.91 | 0.84 | 0.81 | 0.89 | −1.08 | ||
| GA-PLS | 116 | 0.85 | 0.87 | 0.72 | 0.85 | −0.53 | ||
| UVE-PLS | 42 | 0.81 | 0.84 | 0.74 | 0.80 | −0.61 | ||
| 2nd order derivative | FB-PLS | 421 | 0.90 | 0.78 | 0.71 | 0.87 | 2.45 | |
| ISE-PLS | 52 | 0.89 | 0.80 | 0.79 | 0.86 | −0.93 | ||
| GA-PLS | 53 | 0.78 | 0.77 | 0.58 | 0.78 | −0.39 | ||
| UVE-PLS | 22 | 0.65 | 0.68 | 0.63 | 0.63 | −0.07 | ||
| 3rd order derivative | FB-PLS | 421 | 0.86 | 0.70 | 0.60 | 0.83 | 2.73 | |
| ISE-PLS | 58 | 0.82 | 0.73 | 0.58 | 0.80 | −0.46 | ||
| GA-PLS | 39 | 0.72 | 0.76 | 0.40 | 0.75 | −0.24 | ||
| UVE-PLS | 18 | 0.62 | 0.69 | 0.43 | 0.64 | −0.03 | ||
| 1400–2500 nm | Original reflectance | FB-PLS | 221 | 0.87 | 0.77 | 0.80 | 0.84 | 0.06 |
| ISE-PLS | 21 | 0.81 | 0.76 | 0.76 | 0.78 | −0.60 | ||
| GA-PLS | 81 | 0.81 | 0.82 | 0.81 | 0.81 | −0.46 | ||
| UVE-PLS | 28 | 0.80 | 0.82 | 0.78 | 0.79 | −0.61 | ||
| 1st order derivative | FB-PLS | 221 | 0.89 | 0.74 | 0.81 | 0.84 | 0.07 | |
| ISE-PLS | 51 | 0.87 | 0.74 | 0.80 | 0.83 | −0.74 | ||
| GA-PLS | 54 | 0.80 | 0.82 | 0.78 | 0.78 | −0.49 | ||
| UVE-PLS | 29 | 0.74 | 0.77 | 0.60 | 0.75 | −0.35 | ||
| 2nd order derivative | FB-PLS | 221 | 0.85 | 0.70 | 0.82 | 0.79 | 0.28 | |
| ISE-PLS | 43 | 0.85 | 0.68 | 0.83 | 0.78 | −0.53 | ||
| GA-PLS | 52 | 0.73 | 0.75 | 0.70 | 0.72 | −0.22 | ||
| UVE-PLS | 17 | 0.57 | 0.62 | 0.58 | 0.54 | 0.12 | ||
| 3rd order derivative | FB-PLS | 221 | 0.77 | 0.53 | 0.71 | 0.68 | 0.73 | |
| ISE-PLS | 36 | 0.81 | 0.68 | 0.77 | 0.76 | −0.46 | ||
| GA-PLS | 27 | 0.63 | 0.59 | 0.45 | 0.61 | 0.05 | ||
| UVE-PLS | 32 | 0.56 | 0.58 | 0.42 | 0.54 | 0.20 | ||
| 400–1400 nm | Original reflectance | FB-PLS | 201 | 0.81 | 0.81 | 0.58 | 0.82 | 0.13 |
| ISE-PLS | 24 | 0.81 | 0.78 | 0.58 | 0.81 | −0.62 | ||
| GA-PLS | 34 | 0.73 | 0.75 | 0.44 | 0.74 | −0.29 | ||
| UVE-PLS | 34 | 0.75 | 0.76 | 0.49 | 0.77 | −0.36 | ||
| 1st order derivative | FB-PLS | 201 | 0.85 | 0.79 | 0.65 | 0.83 | 0.02 | |
| ISE-PLS | 42 | 0.85 | 0.77 | 0.63 | 0.83 | −0.70 | ||
| GA-PLS | 51 | 0.72 | 0.75 | 0.49 | 0.73 | −0.19 | ||
| UVE-PLS | 20 | 0.68 | 0.72 | 0.63 | 0.68 | −0.18 | ||
| 2nd order derivative | FB-PLS | 201 | 0.83 | 0.73 | 0.52 | 0.82 | 0.16 | |
| ISE-PLS | 37 | 0.83 | 0.80 | 0.60 | 0.82 | −0.66 | ||
| GA-PLS | 27 | 0.69 | 0.71 | 0.37 | 0.73 | −0.16 | ||
| UVE-PLS | 20 | 0.74 | 0.77 | 0.57 | 0.75 | −0.37 | ||
| 3rd order derivative | FB-PLS | 201 | 0.81 | 0.73 | 0.44 | 0.80 | 0.26 | |
| ISE-PLS | 40 | 0.79 | 0.72 | 0.47 | 0.78 | −0.42 | ||
| GA-PLS | 24 | 0.66 | 0.72 | 0.44 | 0.69 | −0.10 | ||
| UVE-PLS | 13 | 0.54 | 0.60 | 0.42 | 0.53 | 0.17 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, J.; Wu, M.; Song, G.; Wang, Q. Genetic Algorithm Captured the Informative Bands for Partial Least Squares Regression Better on Retrieving Leaf Nitrogen from Hyperspectral Reflectance. Remote Sens. 2022, 14, 5204. https://doi.org/10.3390/rs14205204
Jin J, Wu M, Song G, Wang Q. Genetic Algorithm Captured the Informative Bands for Partial Least Squares Regression Better on Retrieving Leaf Nitrogen from Hyperspectral Reflectance. Remote Sensing. 2022; 14(20):5204. https://doi.org/10.3390/rs14205204
Chicago/Turabian StyleJin, Jia, Mengjuan Wu, Guangman Song, and Quan Wang. 2022. "Genetic Algorithm Captured the Informative Bands for Partial Least Squares Regression Better on Retrieving Leaf Nitrogen from Hyperspectral Reflectance" Remote Sensing 14, no. 20: 5204. https://doi.org/10.3390/rs14205204
APA StyleJin, J., Wu, M., Song, G., & Wang, Q. (2022). Genetic Algorithm Captured the Informative Bands for Partial Least Squares Regression Better on Retrieving Leaf Nitrogen from Hyperspectral Reflectance. Remote Sensing, 14(20), 5204. https://doi.org/10.3390/rs14205204