Optimization and Validation of Hyperspectral Estimation Capability of Cotton Leaf Nitrogen Based on SPA and RF
Abstract
1. Introduction
2. Materials and Methods
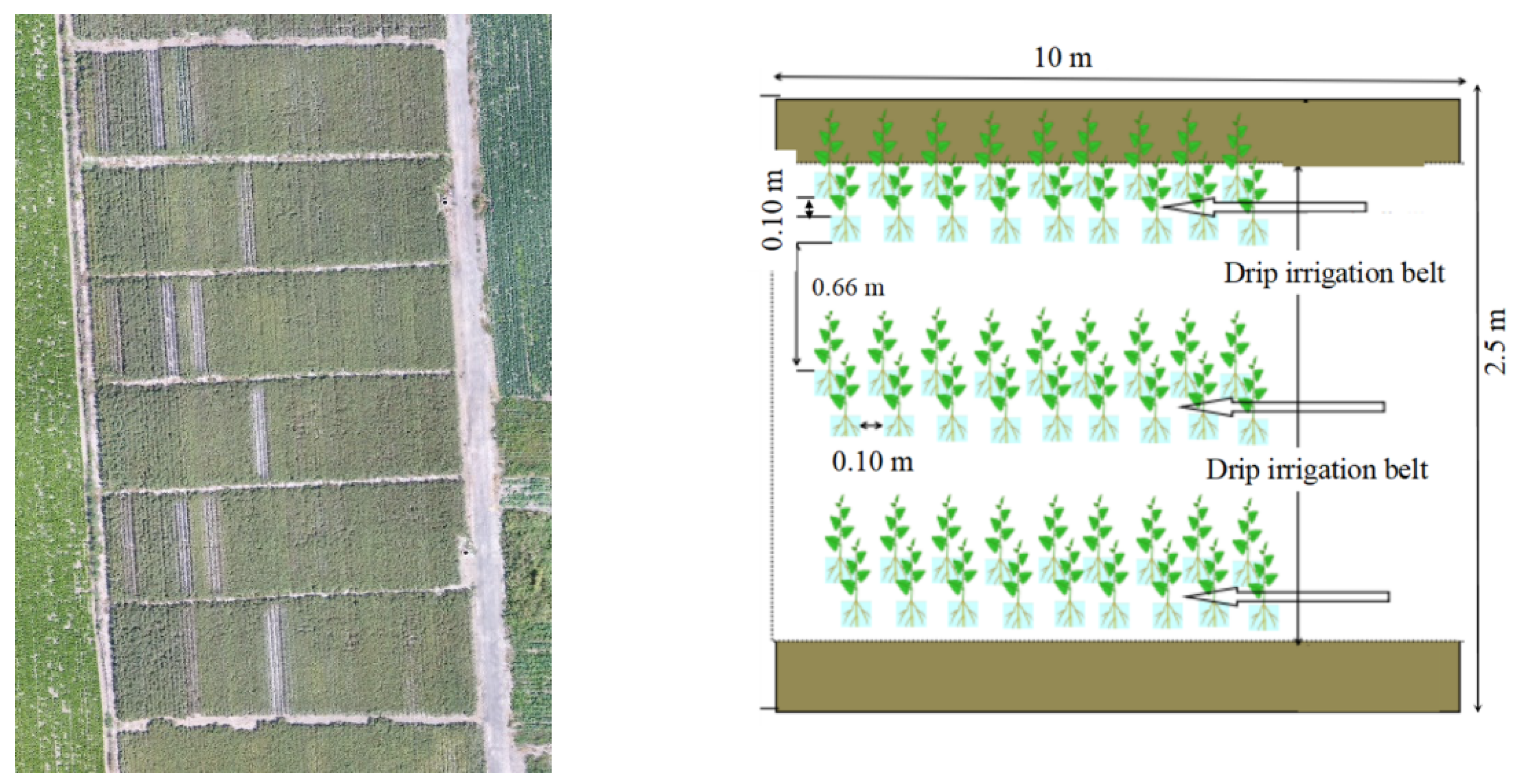
2.1. Study Area and Experimental Design
2.2. Hyperspectral Data Acquisition
2.3. Collection of Nitrogen Content in Cotton Canopy Leaves
2.4. Data Processing
3. Results
3.1. Variation in Canopy N Content
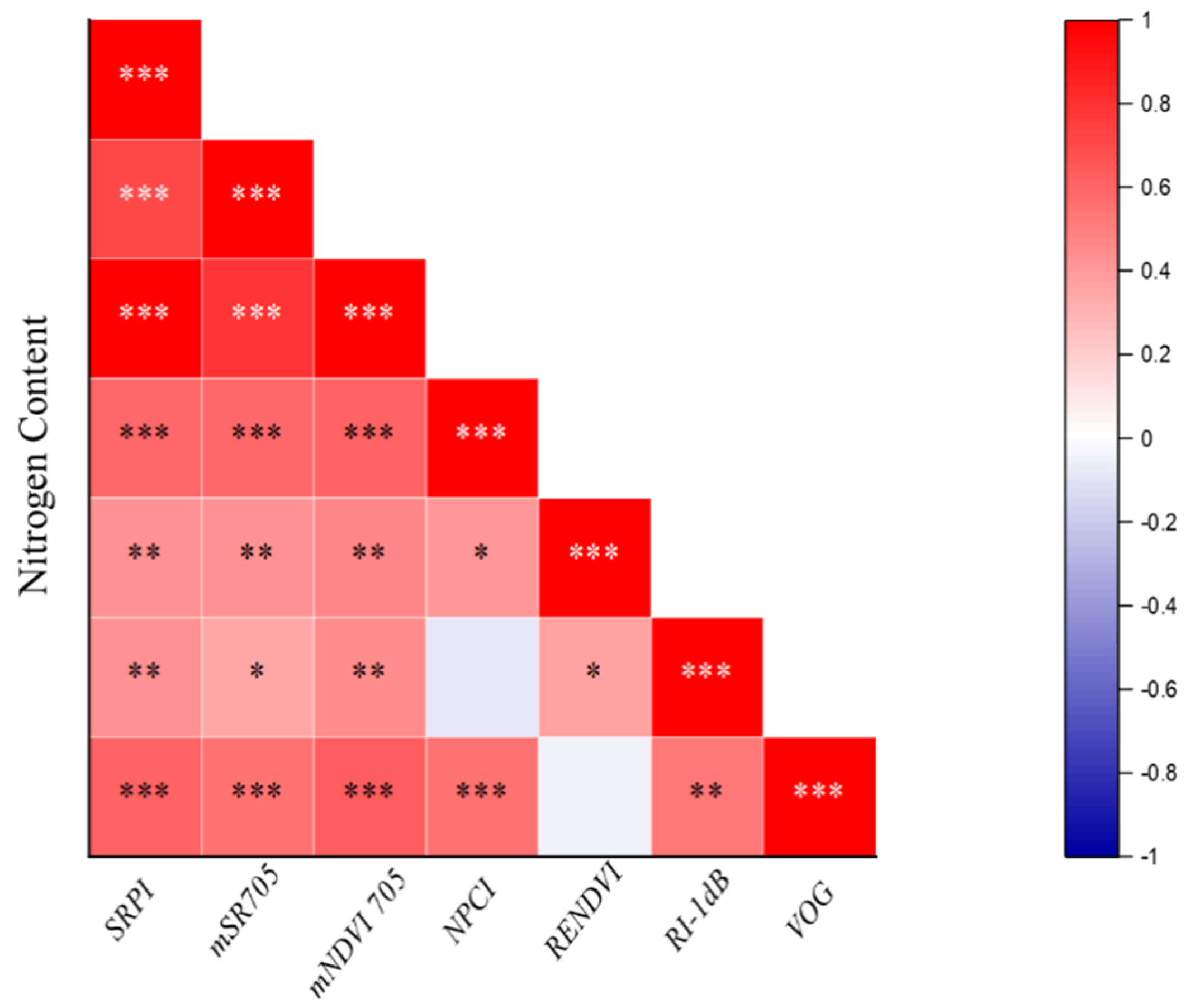
3.2. Relationship between Canopy N Content and Spectral Data
3.3. Screening Spectral Data
3.4. Evaluation of Optimised Spectral Indices
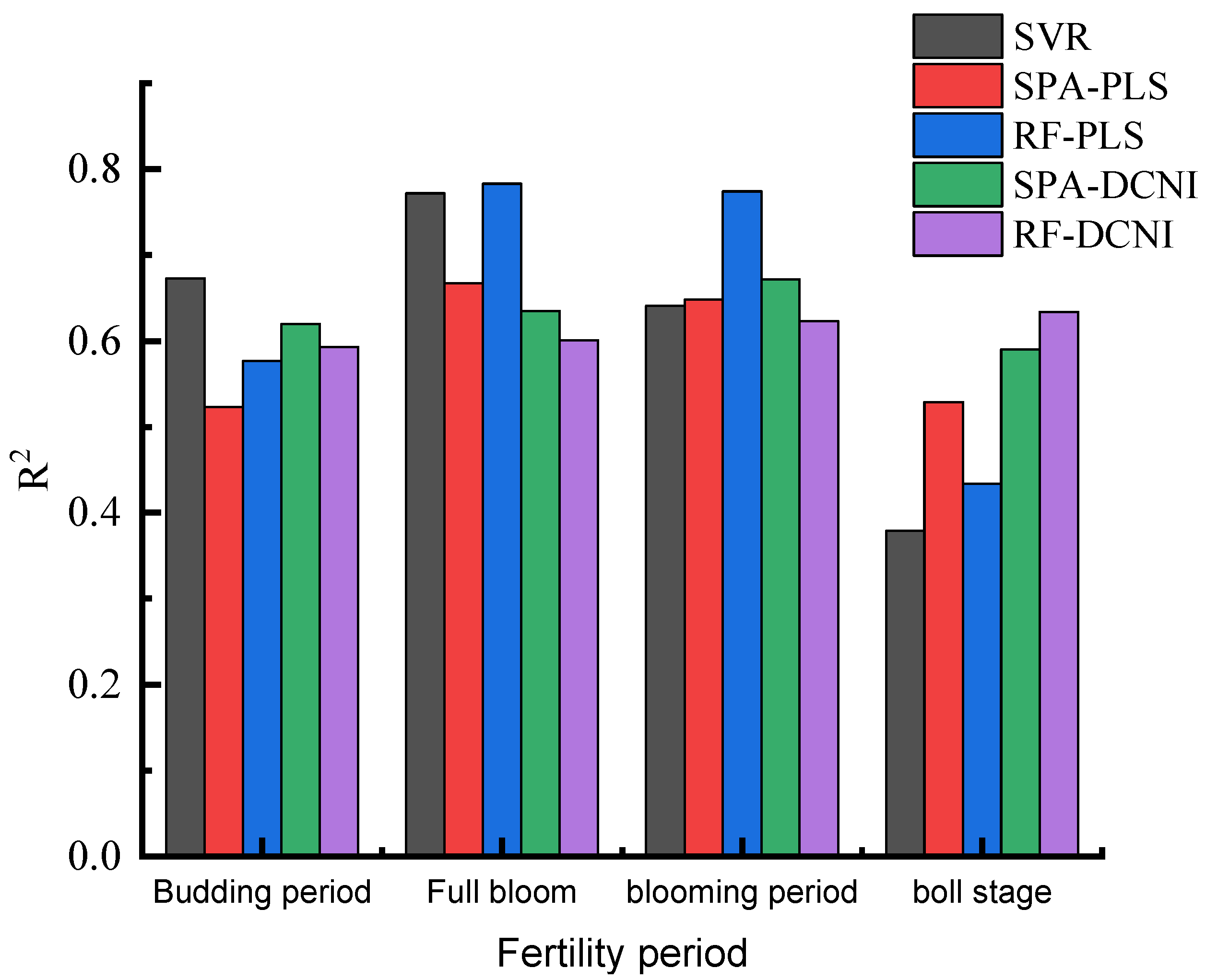
3.5. Testing of the Estimation Ability of the Model
4. Discussion
5. Conclusions
- (1)
- Among the three modeling methods, the inversion of the model constructed using eigenbands is the best at each fertility period. However, there is a problem of non-uniformity in the characteristic bands among the fertility periods. The accuracy of the model built using spectral indices decreased to some extent compared with the eigenbands, but the estimation was the most stable throughout the growth period, and it could effectively estimate the nitrogen content of cotton leaves.
- (2)
- In estimating the nitrogen content of leaves for a specific growth period, higher accuracy can be obtained with models built using characteristic spectral bands. However, with inversion of leaf nitrogen content at full growth period, the model built using spectral indices can invert cotton leaf nitrogen content better and more consistently. Combining the two, the optimized spectral index using the characteristic waveform has better correlation with the nitrogen content of cotton leaves, and the inversion effect is more stable, which is a good idea to optimize the accuracy of the model.
- (3)
- In the next step, we will continue to study the relationship between spectral incidence and nitrogen content of cotton leaves in depth, adopt more advanced algorithms, and consider the information differences brought by different cotton varieties and different growing regions on this basis, with a view to establishing a general model for cotton nitrogen nutrition estimation applicable to all cases.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Berger, K.; Verrelst, J.; Féret, J.B.; Wang, Z.; Wocher, M.; Strathmann, M.; Danner, M.; Mauser, W.; Hank, T. Crop nitrogen monitoring, Recent progress and principal developments in the context of imaging spectroscopy missions. Remote Sens. Environ. 2020, 242, 111758. [Google Scholar] [CrossRef]
- Zha, H.; Miao, Y.; Wang, T.; Li, Y.; Zhang, J.; Sun, W.; Feng, Z.; Kusnierek, K. Improving Unmanned Aerial Vehicle Remote Sensing-Based Rice Nitrogen Nutrition Index Prediction with Machine Learning. Remote Sens. 2020, 12, 215. [Google Scholar] [CrossRef]
- Mubarak, I.; Janat, M. Response of new cotton variety (Rassafa) to nitrogen fertilizer and partial rootzone drying drip irrigation. Open Agric. J. 2018, 12, 1–10. [Google Scholar] [CrossRef]
- Tuvdendorj, B.; Wu, B.; Zeng, H.; Batdelger, G.; Nanzad, L. Determination of appropriate remote sensing indices for spring wheat yield estimation in Mongolia. Remote Sens. 2019, 11, 2568. [Google Scholar] [CrossRef]
- Diao, C. Remote sensing phenological monitoring framework to characterize corn and soybean physiological growing stages. Remote Sens. Environ. 2020, 248, 111960. [Google Scholar] [CrossRef]
- Xu, W.; Chen, P.; Zhan, Y.; Chen, S.; Zhang, L.; Lan, Y. Cotton yield estimation model based on machine learning using time series UAV remote sensing data. Int. J. Appl. Earth Obs. Geoinf. 2021, 104, 102511. [Google Scholar] [CrossRef]
- Yadav, P.K.; Thomasson, J.A.; Hardin, R.; Searcy, S.W.; Braga-Neto, U.; Popescu, S.C.; Martin, D.E.; Rodriguez, R.; Meza, K.; Enciso, J.; et al. Detecting Volunteer Cotton Plants in a Corn Field with Deep Learning on UAV Remote-Sensing Imagery. arXiv 2022, arXiv:2207.06673. [Google Scholar]
- Ma, Y.; Zhang, Q.; Yi, X.; Ma, L.; Zhang, L.; Huang, C.; Zhang, Z.; Lv, X. Estimation of Cotton Leaf Area Index (LAI) Based on Spectral Transformation and Vegetation Index. Remote Sens. 2022, 14, 136. [Google Scholar] [CrossRef]
- Wright, D.L.; Rasmussen, V.P.; Ramsey, R.D.; Baker, D.J.; Ellsworth, J.W. Canopy reflectance estimation of wheat nitrogen content for grain protein management. GIScience Remote Sens. 2004, 41, 287–300. [Google Scholar] [CrossRef]
- Wei, F.; Yan, Z.; Yongchao, T.; Weixing, C.; Xia, Y.; Yingxue, L. Monitoring leaf nitrogen accumulation in wheat with hyper-spectral remote sensing. Acta Ecol. Sin. 2008, 28, 23–32. [Google Scholar] [CrossRef]
- Song, X.; Xu, D.; He, L.; Feng, W.; Wang, Y.; Wang, Z.; Coburn, C.A.; Guo, T. Using multi-angle hyperspectral data to monitor canopy leaf nitrogen content of wheat. Precis. Agric. 2016, 17, 721–736. [Google Scholar] [CrossRef]
- Huete, A.R.; Jackson, R.D.; Post, D.F. Spectral response of a plant canopy with different soil backgrounds. Remote Sens. Environ. 1985, 17, 37–53. [Google Scholar] [CrossRef]
- Yang, B.; Wang, M.; Sha, Z.; Wang, B.; Chen, J.; Yao, X.; Cheng, T.; Cao, W.; Zhu, Y. Evaluation of aboveground nitrogen content of winter wheat using digital imagery of unmanned aerial vehicles. Sensors 2019, 19, 4416. [Google Scholar] [CrossRef] [PubMed]
- Haijun, Q.; Xiu, J.; Liu, Z.; Maxime, D.I.; Shaowen, L. Predicting sandy soil moisture content with hyperspectral imaging. Int. J. Agric. Biol. Eng. 2017, 10, 175–183. [Google Scholar] [CrossRef]
- Tarpley, L.; Reddy, K.R.; Sassenrath-Cole, G.F. Reflectance indices with precision and accuracy in predicting cotton leaf nitrogen concentration. Crop Sci. 2000, 40, 1814–1819. [Google Scholar] [CrossRef]
- Yong YI, N.; Guanghui, W. Hyperspectral characteristic wavelength selection method for moldy maize based on continuous projection algorithm fusion information entropy. J. Nucl. Agric. Sci. 2020, 34, 356. [Google Scholar]
- Chan, J.C.W.; Paelinckx, D. Evaluation of Random Forest and Adaboost tree-based ensemble classification and spectral band selection for ecotope mapping using airborne hyperspectral imagery. Remote Sens. Environ. 2008, 112, 2999–3011. [Google Scholar] [CrossRef]
- Devos, O.; Ruckebusch, C.; Durand, A.; Duponchel, L.; Huvenne, J.P. Support vector machines (SVM) in near infrared (NIR) spectroscopy, Focus on parameters optimization and model interpretation. Chemom. Intell. Lab. Syst. 2009, 96, 27–33. [Google Scholar] [CrossRef]
- Daughtry, C.S.; Walthall, C.L.; Kim, M.S.; De Colstoun, E.B.; McMurtrey Iii, J.E. Estimating corn leaf chlorophyll concentration from leaf and canopy reflectance. Remote Sens. Environ. 2000, 74, 229–239. [Google Scholar] [CrossRef]
- Prado Osco, L.; Marques Ramos, A.P.; Roberto Pereira, D.; Akemi Saito Moriya, É.; Nobuhiro Imai, N.; Takashi Matsubara, E.; Estrabis, N.; de Souza, M.; Marcato Junior, J.; Gonçalves, W.N.; et al. Predicting canopy nitrogen content in citrus-trees using random forest algorithm associated to spectral vegetation indices from UAV-imagery. Remote Sens. 2019, 11, 2925. [Google Scholar] [CrossRef]
- Li, Z.; Jin, X.; Yang, G.; Drummond, J.; Yang, H.; Clark, B.; Li, Z.; Zhao, C. Remote Sensing of Leaf and Canopy Nitrogen Status in Winter Wheat (Triticum aestivum L.) Based on N-PROSAIL Model. Remote Sens. 2018, 10, 1463. [Google Scholar] [CrossRef]
- Chauhan, S.; Darvishzadeh, R.; Boschetti, M.; Nelson, A. Estimation of crop angle of inclinationfor lodged wheat using multi-sensor SAR data. Remote Sens. Environ. 2020, 236, 111488. [Google Scholar] [CrossRef]
- Fu, Y.; Yang, G.; Li, Z.; Li, H.; Li, Z.; Xu, X.; Song, X.; Zhang, Y.; Duan, D.; Zhao, C.; et al. Progress of hyperspectral data processing and modelling forcereal crop. Comput. Electron. Agric. 2020, 172, 105321. [Google Scholar] [CrossRef]
- Kobayashi, N.; Tani, H.; Wang, X.; Sonobe, R. Crop classification using spectral indices derived from Sentinel-2A imagery. J. Inf. Telecommun. 2020, 4, 67–90. [Google Scholar] [CrossRef]
- Deiss, L.; Margenot, A.J.; Culman, S.W.; Demyan, M.S. Tuning support vector machines regression models improves prediction accuracy of soil properties in MIR spectroscopy. Geoderma 2020, 365, 114227. [Google Scholar] [CrossRef]
- Golhani, K.; Balasundram, S.K.; Vadamalai, G.; Pradhan, B. A review of neural networks in plant disease detection using hyperspectral data. Inf. Processing Agric. 2018, 5, 354–371. [Google Scholar] [CrossRef]
- Wang, D.; Li, G.; Wu, S.; Lin, L. Apply a new characteristic wavelength screening method to improving the spectral quantitative analysis precision of multiple immune cell types. Infrared Phys. Technol. 2022, 123, 104140. [Google Scholar] [CrossRef]
- Li, Z.; Tang, X.; Shen, Z.; Yang, K.; Zhao, L.; Li, Y. Comprehensive comparison of multiple quantitative near-infrared spectroscopy models for Aspergillus flavus contamination detection in peanut. J. Sci. Food Agric. 2019, 99, 5671–5679. [Google Scholar] [CrossRef]
- Weih, M.; Hamnér, K.; Pourazari, F. Analyzing plant nutrient uptake and utilization efficiencies, comparison between crops and approaches. Plant Soil 2018, 430, 7–21. [Google Scholar] [CrossRef]
- Cummings, C.R. In-Season Corn Nitrogen Status Diagnosis and Precision Management with Proximal and Remote Sensing. Doctoral Dissertation, University of Minnesota, Minneapolis, MN, USA, 2020. [Google Scholar]
- Cai, Y.; Guan, K.; Nafziger, E.; Chowdhary, G.; Peng, B.; Jin, Z.; Wang, S.; Wang, S. Detecting in-season crop nitrogen stress of corn for field trials using UAV-and CubeSat-based multispectral sensing. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 5153–5166. [Google Scholar] [CrossRef]
- Bera, S.; Shrivastava, V.K. Analysis of various optimizers on deep convolutional neural network model in the application of hyperspectral remote sensing image classification. Int. J. Remote Sens. 2020, 41, 2664–2683. [Google Scholar] [CrossRef]
- Sims, D.A.; Gamon, J.A. Estimation of vegetation water content and photosynthetic tissue area from spectral reflectance, a comparison of indices based on liquid water and chlorophyll absorption features. Remote Sens. Environ. 2003, 84, 526–537. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, L.; Zhang, X.; Wang, S.; Tian, J.; Zhai, Y. Sensitivity of different spectral vegetation index for estimating winter wheat leaf nitrogen. Sci. Agric. Sin. 2017, 50, 474–485. [Google Scholar]
- Xue, J.; Su, B. Significant remote sensing vegetation indices, A review of developments and applications. J. Sens. 2017, 2017, 1353691. [Google Scholar] [CrossRef]
| Date | Fertilizer Application Ratio | ||
|---|---|---|---|
| N | P | K | |
| 7 June | 2.5 | 7.7 | 0 |
| 15 June | 7.5 | 11.7 | 6.7 |
| 24 June | 7.5 | 11.7 | 6.7 |
| 2 July | 12.5 | 19.2 | 20 |
| 18 July | 20 | 19.2 | 20 |
| 26 July | 25 | 15.4 | 13.3 |
| 5 August | 15 | 15.4 | 13.3 |
| 15 August | 10 | 0 | 13.3 |
| 25 August | 0 | 0 | 6.7 |
| Budding Period | Full Bloom | Blooming Period | Boll Stage | Spitting Period | |
|---|---|---|---|---|---|
| 41.9 ± 3.4 a | 36.0 ± 5.3 a | 33.9 ± 4.0 ab | 29.8 ± 4.3 b | 19.9 ± 3.5 c | |
| N0 | 41.2 ± 4.2 a | 36.6 ± 4.6 a | 34.9 ± 3.6 ab | 31.6 ± 3.5 b | 19.9 ± 5.5 c |
| 33.7 ± 4.8 a | 34.7 ± 3.6 a | 32.4 ± 3.2 ab | 31.4 ± 3.9 b | 21.5 ± 5.8 c | |
| 43.6 ± 5.0 a | 37.7 ± 4.5 a | 38.4 ± 4.2 a | 35.0 ± 4.2 ab | 23.3 ± 4.5 c | |
| N1 | 41.5 ± 5.2 a | 38.5 ± 3.2 a | 39.0 ± 4.8 a | 33.4 ± 4.7 b | 22.2 ± 3.9 c |
| 29.8 ± 4.1 a | 38.9 ± 3.9 a | 36.2 ± 4.8 ab | 29.7 ± 3.7 bc | 22.5 ± 2.3 c | |
| 41.1 ± 4.5 a | 41.1 ± 5.0 a | 39.0 ± 3.7 a | 30.0 ± 4.9 b | 17.8 ± 4.6 c | |
| N2 | 41.9 ± 3.9 a | 41.9 ± 5.4 a | 39.4 ± 4.4 a | 33.2 ± 3.6 b | 20.3 ± 3.4 c |
| 40.9 ± 4.4 a | 40.9 ± 5.6 a | 35.5 ± 4.3 ab | 30.3 ± 3.6 b | 20.9 ± 2.5 c | |
| 40.8 ± 3.6 a | 40.2 ± 3.8 a | 40.6 ± 3.1 a | 32.2 ± 4.7 b | 22.9 ± 2.3 c | |
| N3 | 42.6 ± 3.2 a | 41.3 ± 4.4 a | 39.9 ± 4.6 a | 32.6 ± 3.6 b | 22.7 ± 3.3 c |
| 35.6 ± 5.8 a | 38.3 ± 3.4 a | 37.6 ± 3.8 a | 30.6 ± 4.7 b | 22.9 ± 3.7 c | |
| 46.6 ± 4.6 a | 38.4 ± 5.7 a | 38.8 ± 3.2 a | 28.7 ± 4.7 b | 19.9 ± 5.3 c | |
| N4 | 43.8 ± 5.3 a | 39.0 ± 4.7 a | 40.0 ± 3.8 a | 35.7 ± 4.9 b | 20.4 ± 2.2 c |
| 39.5 ± 3.2 a | 37.4 ± 3.6 a | 38.4 ± 4.3 a | 32.1 ± 3.9 b | 22.2 ± 4.9 c | |
| 45.3 ± 5.1 a | 40.4 ± 4.0 a | 39.0 ± 5.1 a | 35.9 ± 4.7 b | 23.7 ± 4.8 c | |
| NC | 42.1 ± 4.8 a | 41.3 ± 4.2 a | 38.2 ± 3.1 a | 29.7 ± 4.1 b | 23.5 ± 3.9 c |
| 35.3 ± 5.3 a | 38.3 ± 3.2 a | 34.6 ± 3.3 ab | 30.7 ± 3.5 b | 23.5 ± 5.7 c |
| Serial Number | Abbreviation | Calculation Formula |
|---|---|---|
| 1 | SRPI | R430/R680 |
| 2 | mSR705 | (R750 − R445)/(R705 − R445) |
| 3 | mNDVI 705 | (R750 − R705)/(R750 + 2R445) |
| 4 | NPCI | (R680 − R430)/(R680 + R430) |
| 5 | RENDVI | (R750 − R705)/(R750 + R705) |
| 6 | RI-1dB | R735/R720 |
| 7 | VOG | R740/R720 |
| 8 | DCNI | (R720 − R700)/(R700 − R670) /(R720 − R670 + 0.03) |
| 9 | PRI | (R531 − R570/(R531 + R570) |
| 10 | RVI | R800/R670 |
| 11 | NDVI | (R800 − R670)/(R800 + R670) |
| 12 | VOG3 | (R734 − R747)/(R715 + R720) |
| 13 | ND705 | (R750 − R705)/(R750 + R705) |
| 14 | NRI | (R570 − R670)/(R570 + R670) |
| Math | Number | Result |
|---|---|---|
| SPA | 39 | 1987, 648, 2103, 700, 1706, 545, 694, 759, 561, 474, 740, 1806, 540, 1893, 783, 1058, 580, 628, 481, 602, 755, 1950, 677, 454, 1806, 671, 773, 424, 761, 393, 1991, 410, 714, 433, 351, 387, 438, 730, 687 |
| RF | 16 | 1847, 1851, 734, 1058, 1955, 687, 686, 1907, 783, 688, 1818, 541, 773, 1987, 513, 1901 |
| Abbreviation | Optimal Center Wavelength | R2 | RMSE | ||
|---|---|---|---|---|---|
| SPA-mSR705 | 755 | 445 | 708 | 0.764 | 3.97 |
| SPA-RI-1 dB | 738 | 719 | 0.702 | 4.69 | |
| SPA-DCNI | 725 | 706 | 677 | 0.832 | 4.01 |
| SPA-RVI | 789 | 677 | 0.710 | 4.56 | |
| SPA-ND705 | 755 | 708 | 0.709 | 4.09 | |
| RF-mSR705 | 750 | 448 | 707 | 0.780 | 4.48 |
| RF-RI-1 dB | 736 | 723 | 0.702 | 4.21 | |
| RF-DCNI | 723 | 705 | 673 | 0.791 | 3.74 |
| RF-RVI | 788 | 673 | 0.684 | 4.76 | |
| RF-ND705 | 750 | 707 | 0.694 | 3.92 | |
| Index | Equation | Before R2 | Before RMSE | After R2 | After RMSE |
|---|---|---|---|---|---|
| SPA-mSR705 | Y = 8.72X − 10.351 | 0.659 | 4.53 | 0.678 | 3.73 |
| SPA-RI-1 dB | Y = 32.016X − 13.283 | 0.601 | 4.87 | 0.613 | 4.57 |
| SPA-DCNI | Y = 1.868X + 18.515 | 0.673 | 4.46 | 0.762 | 3.06 |
| SPA-RVI | Y = 46.58X − 2.238 | 0.521 | 5.02 | 0.591 | 4.92 |
| SPA-ND705 | Y = 70.772X − 5.8457 | 0.616 | 4.55 | 0.638 | 4.45 |
| RF-mSR705 | Y = 7.631X − 9.176 | 0.402 | 4.59 | 0.659 | 4.89 |
| RF-RI-1 dB | Y = 34.13X − 14.752 | 0.542 | 4.57 | 0.642 | 4.77 |
| RF-DCNI | Y = 2.87X + 9.331 | 0.607 | 3.86 | 0.714 | 4.66 |
| RF-RVI | Y = 57.9X − 12.437 | 0.584 | 4.97 | 0.589 | 4.87 |
| RF-ND705 | Y = 76.532X − 7.788 | 0.538 | 4.51 | 0.597 | 4.11 |
| Model | Budding Period | Full Bloom | Blooming Period | Boll Stage | |
|---|---|---|---|---|---|
| SVR | R2 | 0.673 | 0.772 | 0.641 | 0.379 |
| RMSE | 4.62 | 3.37 | 4.88 | 6.21 | |
| SPA-PLS | R2 | 0.523 | 0.667 | 0.648 | 0.529 |
| RMSE | 5.33 | 4.61 | 4.79 | 5.15 | |
| RF-PLS | R2 | 0.577 | 0.783 | 0.774 | 0.434 |
| RMSE | 4.96 | 3.12 | 3.28 | 5.43 | |
| SPA-DCNI | R2 | 0.620 | 0.635 | 0.672 | 0.590 |
| RMSE | 3.76 | 3.82 | 3.76 | 4.68 | |
| RF-DCNI | R2 | 0.593 | 0.601 | 0.623 | 0.634 |
| RMSE | 4.72 | 4.11 | 3.97 | 3.52 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Lv, X.; Ma, L.; Chen, A.; Zhang, Q.; Zhang, Z. Optimization and Validation of Hyperspectral Estimation Capability of Cotton Leaf Nitrogen Based on SPA and RF. Remote Sens. 2022, 14, 5201. https://doi.org/10.3390/rs14205201
Chen X, Lv X, Ma L, Chen A, Zhang Q, Zhang Z. Optimization and Validation of Hyperspectral Estimation Capability of Cotton Leaf Nitrogen Based on SPA and RF. Remote Sensing. 2022; 14(20):5201. https://doi.org/10.3390/rs14205201
Chicago/Turabian StyleChen, Xiangyu, Xin Lv, Lulu Ma, Aiqun Chen, Qiang Zhang, and Ze Zhang. 2022. "Optimization and Validation of Hyperspectral Estimation Capability of Cotton Leaf Nitrogen Based on SPA and RF" Remote Sensing 14, no. 20: 5201. https://doi.org/10.3390/rs14205201
APA StyleChen, X., Lv, X., Ma, L., Chen, A., Zhang, Q., & Zhang, Z. (2022). Optimization and Validation of Hyperspectral Estimation Capability of Cotton Leaf Nitrogen Based on SPA and RF. Remote Sensing, 14(20), 5201. https://doi.org/10.3390/rs14205201






