Optimizing Radar-Based Rainfall Estimation Using Machine Learning Models
Abstract
1. Introduction
2. Radar Data and Ground Observations
2.1. Radar Data
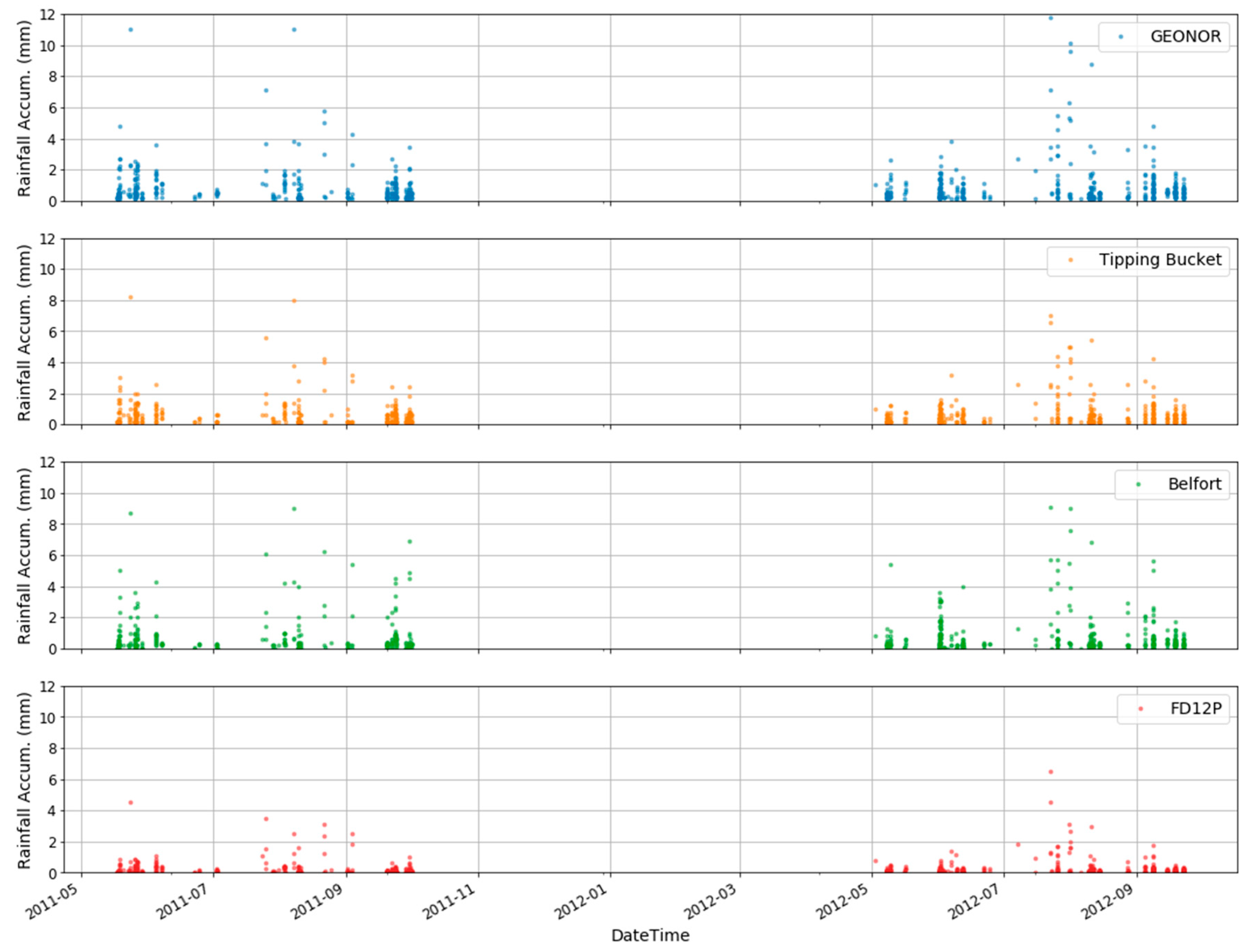
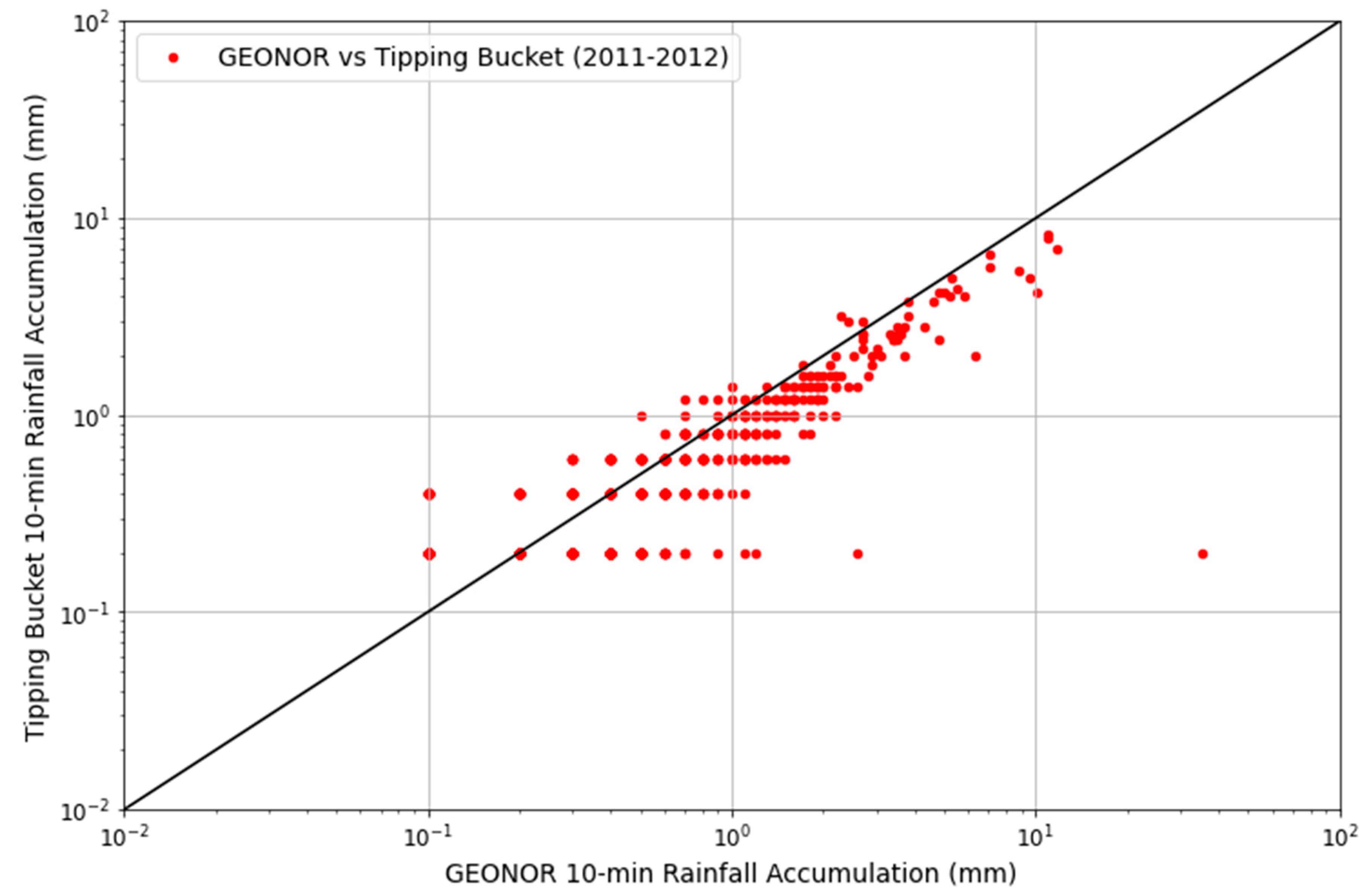
2.2. Rain Gauges
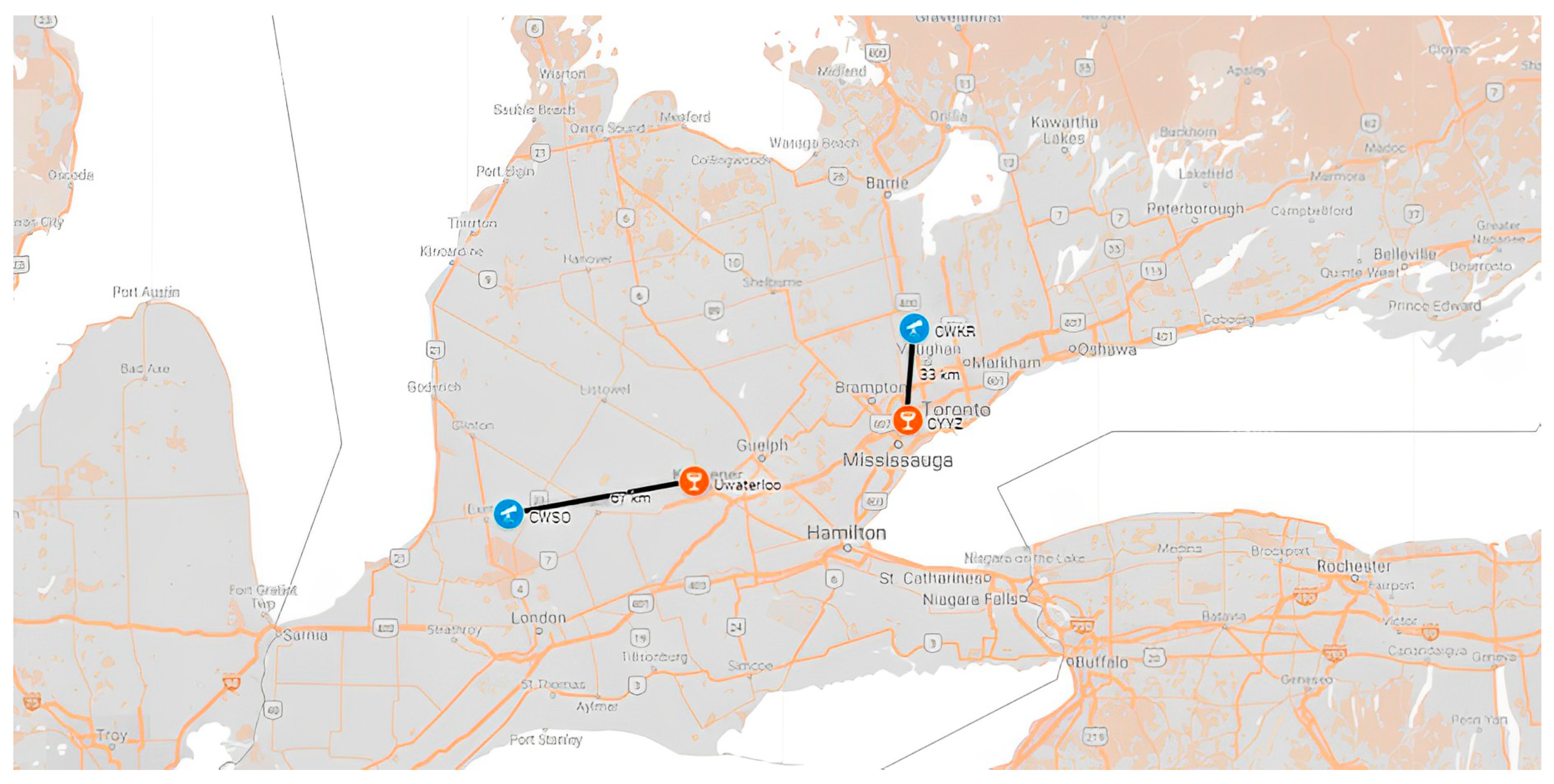
2.2.1. Pearson International Airport
2.2.2. Waterloo University Weather Station
3. Methodology: Rainfall Estimators and Decision Tree Models
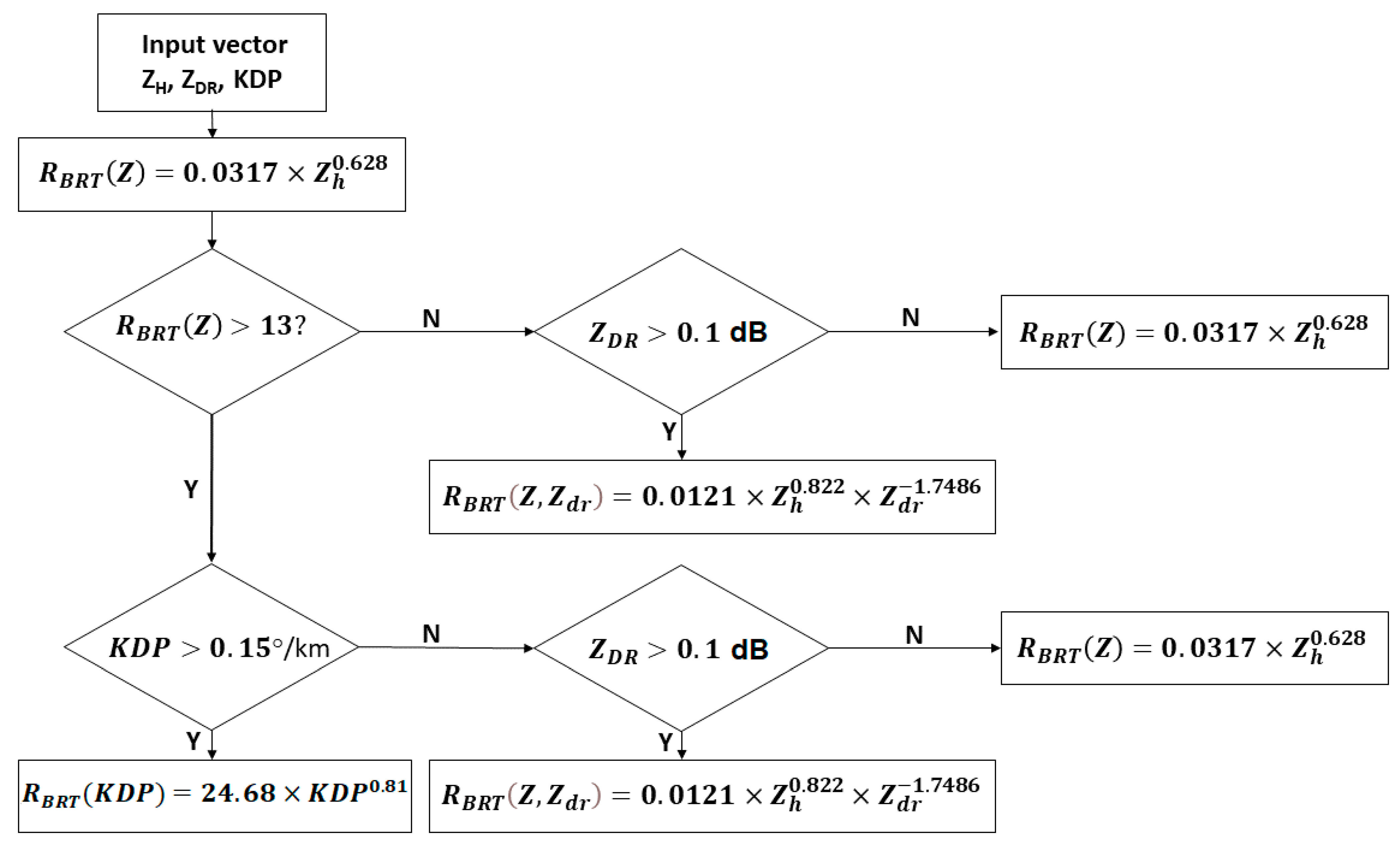
3.1. Rainfall Estimators
3.2. Supervised Decision Tree Machine Learning Method
3.3. Supervised Random Forest Machine Learning Method
3.4. Gradient Boosting, Ensemble Learning
3.5. Statistical Scores
3.6. Study Data and ML Models
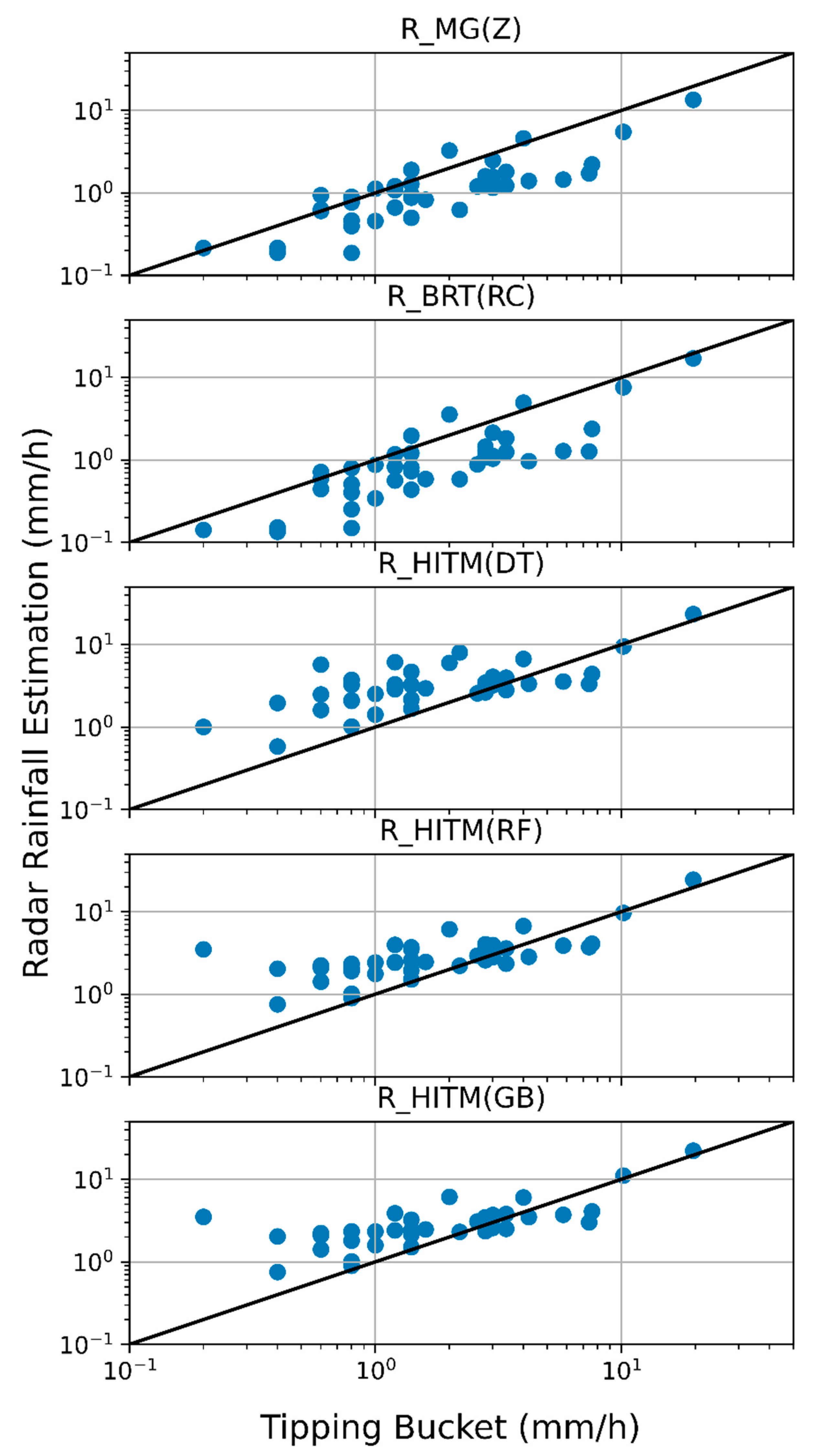
4. Evaluation Process
5. Case Study
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Boero, L.; Poffo, D.; Damino, V.; Villalba, S.; Barques, R.M.; Rodriguez, A.; Suarez, M.; Beccacece, H.M. Monitoring and characterizing temporal patterns of a large colony of Tadarida brasiliensis (Chiroptera: Molossidae) in Argentina using field observations and the weather radar RMA1. Remote Sens. 2020, 12, 210. [Google Scholar] [CrossRef]
- Ryzhkov, A.V.; Schuur, T.J.; Zrnic, D.S. Radar rainfall estimation using different polarimetric algorithms. In Proceedings of the 30th International Conference on Radar Meteorology, Munich, Germany, 19–24 July 2001; pp. 641–643. [Google Scholar]
- Baldini, L.; Gorgucci, E.; Romaniello, V. An integrated procedure for rainfall estimation using C-band dual-polarization weather radars. In Proceedings of the 2008 IEEE Radar Conference, Rome, Italy, 26–30 May 2008; pp. 1–4. [Google Scholar] [CrossRef]
- Vulpiani, G.; Giangrande, S.; Marzano, F.S. Rainfall estimation from Polarimetric S-Band Radar Measurements: Validation of a Neural Network Approach. J. Appl. Meteorol. Climatol. 2009, 48, 2022–2036. [Google Scholar] [CrossRef]
- Ryzhkov, A.V.; Giangrande, S.E.; Schuur, T.J. Rainfall estimation with a polarimetric prototype of WSR-88D. J. Appl. Meteorol. 2005, 44, 502–515. [Google Scholar] [CrossRef]
- Cremonini, R.; Bechini, R. Heavy rainfall monitoring by polarimetric C-band weather radars. Water 2010, 2, 838–848. [Google Scholar] [CrossRef]
- Crisologo, I.; Vulpiani, G.; Abon, C.C.; David, C.P.C.; Bronster, A.; Heistermann, M. Polarimetric rainfall retrieval from a C-band weather radar in a tropical environment (The Philippines). Asia Pac. J. Atmosp. Sci. 2014, 50, 595–607. [Google Scholar] [CrossRef]
- Thompson, E.J.; Rutledge, S.A.; Dolan, B.; Thurai, M.; Chandrasekar, V. Dual-polarization radar rainfall estimation over tropical oceans. J. Appl. Meteorol. Climatol. 2018, 57, 755–775. [Google Scholar] [CrossRef]
- Schleiss, M.; Olsson, J.; Berg, P.; Niemi, T.; Kokkonen, T.; Thorndahl, S.; Nielsen, R.; Nielsen, J.E.; Bozhinova, D.; Pulkkinen, S. The accuracy of weather radar in heavy rain: A comparative study for Denmark, the Netherlands, Finland and Sweden. Hydrol. Earth Syst. Sci. 2019, 427, 1–42. [Google Scholar] [CrossRef]
- Boodoo, S.; Hudak, D.; Ryzhkov, A.; Zhang, P.; Donaldson, N.; Sills, D.; Reid, J. Quantitative precipitation estimation from a C-band dual-polarized radar for the 8 July 2013 flood in Toronto, Canada. J. Hydrometeorol. 2015, 16, 2027–2044. [Google Scholar] [CrossRef]
- Boodoo, S.; Hudak, D.; Donaldson, N.; Reid, J.; Michelson, D.; Rodriguez, P.; Couture, M.; Stojanovic, V. The development of a Canadian operational dual-polarization rainfall estimation algorithm. In Proceedings of the 10th European Conference on Radar in Meteorology & Hydrology, Wageningen, The Netherlands, 1–6 July 2018. [Google Scholar]
- Wijayarathne, D.; Boodoo, S.; Coulibaly, P.; Sills, D. Evaluation of radar quantitative precipitation estimates (QPEs) as an input of hydrological models for hydrometeorological applications. J. Hydrometeorol. 2020, 21, 1847–1864. [Google Scholar] [CrossRef]
- Wijayarathne, D.; Coulibaly, P.; Boodoo, S.; Sills, D. Use of Radar Quantitative Precipitation Estimates (QPEs) for Improved Hydrological Model Calibration and Flood Forecasting. J. Hydrol. 2021, 22, 2033–2053. [Google Scholar] [CrossRef]
- Cuomo, J.; Chandrasekar, V. Use of deep learning for weather radar Nowcasting. J. Atmosp. Ocean. Technol. 2021, 38, 1641–1656. [Google Scholar] [CrossRef]
- Srinivas, T.A.S.; Somula, R.; Govinda, K.; Saxena, A.; Reddy, A.P. Estimating rainfall using machine learning strategies based on weather radar data. Int. J. Commun. Syst. 2019, 33, e3999. [Google Scholar] [CrossRef]
- Bonnet, S.M.; Evsukoff, A.; Rodriguez, C.A.M. Precipitation nowcasting with weather radar images and deep learning in Sao Paulo, Brasil. Atmosphere 2020, 11, 1157. [Google Scholar] [CrossRef]
- Marshall, J.S.; Gunn, K.L.S. Measurement of snow parameters by radar. J. Meteorol. 1952, 9, 322–327. [Google Scholar] [CrossRef]
- Bringi, V.N.; Rico-Ramirez, M.A.; Thurai, M. Rainfall estimation with an operational polarimetric C-band radar in the United Kingdom: Comparison with gauge network and error analysis. J. Hydrometeorol. 2011, 12, 935–954. [Google Scholar] [CrossRef]
- Hudak, D.; Rodriguez, P.; Lee, G.W.; Ryzhkov, A.V.; Fabry, F.; Donaldson, N. Winter precipitation studies with a dual-polarized C-band radar. In Proceedings of the ERAD 4th European Conference on Radar in Meteorology and Hydrology, Barcelona, Spain, 18–22 September 2006; pp. 9–12. [Google Scholar]
- Joe, P.; Lapczak, S. Evolution of the Canadian operational radar network. In Proceedings of the ERAD 2nd European Conference on Radar in Meteorology and Hydrology, Delft, The Netherlands, 18–22 November 2002; pp. 370–382. [Google Scholar]
- Taylor, B.M. Direct Comparisons of Polarimetric C-Band and S-Band Radar in Snow. Master’s Thesis, York University, Toronto, CA, USA, 2018. Available online: http://hdl.handle.net/10315/35034 (accessed on 1 June 2022).
- Isaac, G.A.; Bailey, M.; Boudala, F.; Cover, S.G.; Crawford, R.; Donaldson, N.; Gultepe, I.; Hansen, B.; Heckman, I.; Huang, L.; et al. The Canadian airport nowcasting systems (CAN-Now). Meteorol. Appl. 2014, 21, 30–40. [Google Scholar] [CrossRef]
- Milewska, E.J.; Vincent, L.A.; Hartwell, M.M.; Charlesworth, K.; Mekis, E. Adjusting precipitation amount from Geonor and Pluvio automated weighing gauges to preserve continuity of observations in Canada. Can. Water Resour. J. 2019, 44, 127–145. [Google Scholar] [CrossRef]
- Devine, K.A.; Mekis, É. Field accuracy of Canadian rain measurements. Atmosp. Ocean 2008, 46, 213–227. [Google Scholar] [CrossRef]
- Marshall, J.S.; Palmer, W.M.K. The distribution of raindrops with size. J. Meteorol. 1948, 5, 165–166. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, A.; Michel, V.; Thirion, B. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Raileanu, L.E.; Stoffel, K. Theoretical comparison between the Gini Index and Information Gain criteria. Ann. Math. Artif. Intell. 2004, 41, 77–93. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy boosting approximation: A gradient boosting machine. Ann. Stat. 2001, 20, 1189–1232. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models Part 1—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Irving, D. A Minimum Standard for Publishing Computational Results in the Weather and Climate Sciences. Bull. Am. Meteorol. Soc. 2016, 97, 1149–1158. [Google Scholar] [CrossRef]
- McCormick, G.C.; Hendry, A. Principles for the radar determination of the polarization properties of precipitation. Radio Sci. 1975, 10, 421–434. [Google Scholar] [CrossRef]
- McCormick, G.C.; Hendry, A. Techniques for the determination of the polarization properties of precipitation. Radio Sci. 1979, 14, 1027–1040. [Google Scholar] [CrossRef]
- McCormick, G.C. Polarization errors in a two-channel system. Radio Sci. 1981, 16, 67–75. [Google Scholar] [CrossRef]
- Fabry, F. Radar Meteorology, Principles and Practice, CUP; Cambridge University Press: Cambridge, UK, 2015; ISBN 9781108460392. [Google Scholar] [CrossRef]
- Bringi, V.; Zrnic, D. Polarization weather radar development from 1970–1995: Personal Reflections. Atmosphere 2019, 10, 714. [Google Scholar] [CrossRef]
- McKee, J.L. Evaluation of Gauge-Radar Merging Methods for Quantitative Precipitation Estimation in Hydrology: A Case Study in the Upper Thames River Basin. Master’s Thesis, University of Western Ontario, London, ON, Canada, 2015; p. 135. [Google Scholar]
- Adirosi, E.; Bladini, L.; Roberto, N.; Gatlin, P. Improvement of vertical profiles of raindrop size distribution from micro rain radar using 2D video disdrometer measurements. J. Atmosp. Res. 2018, 160, 404–415. [Google Scholar] [CrossRef]
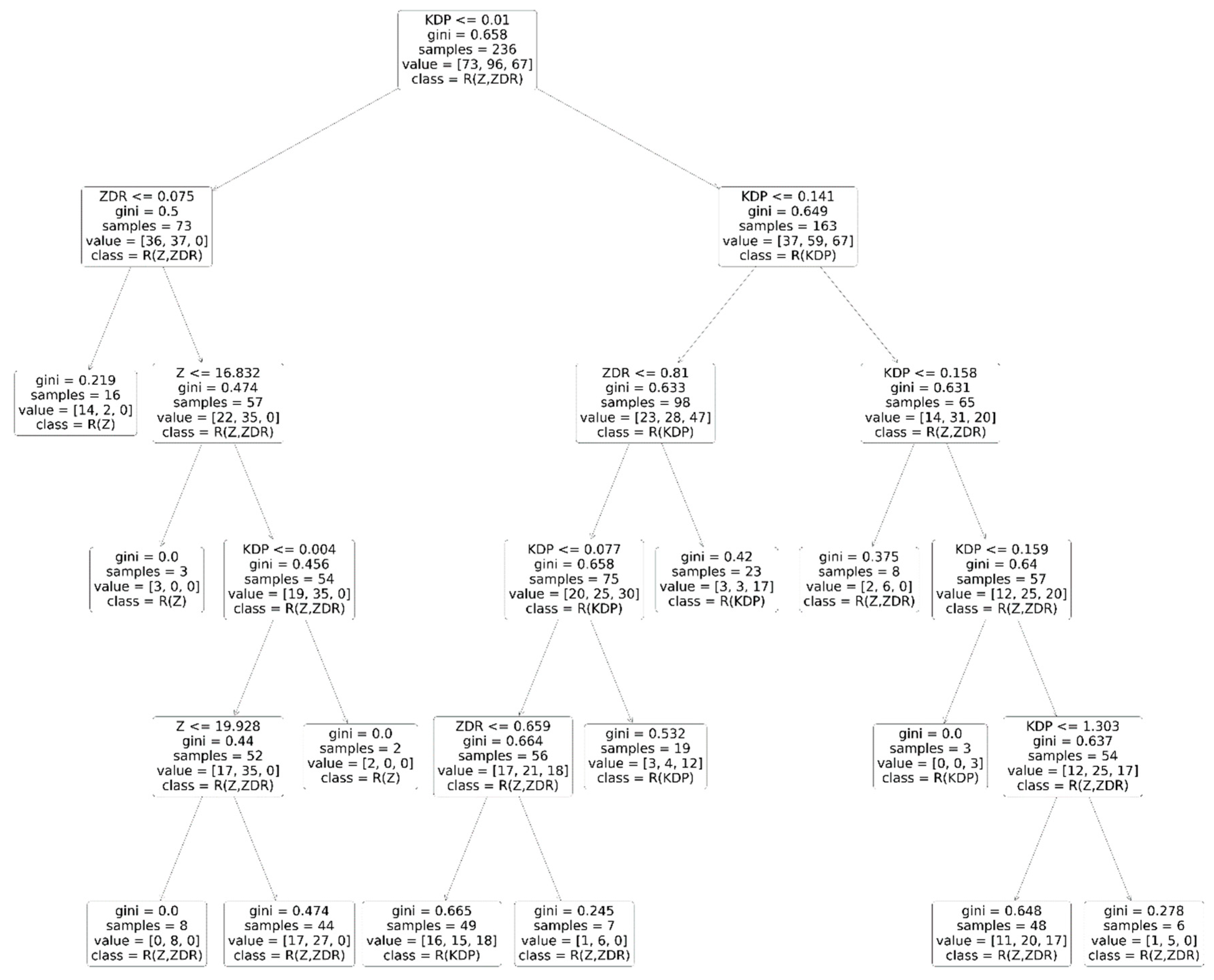
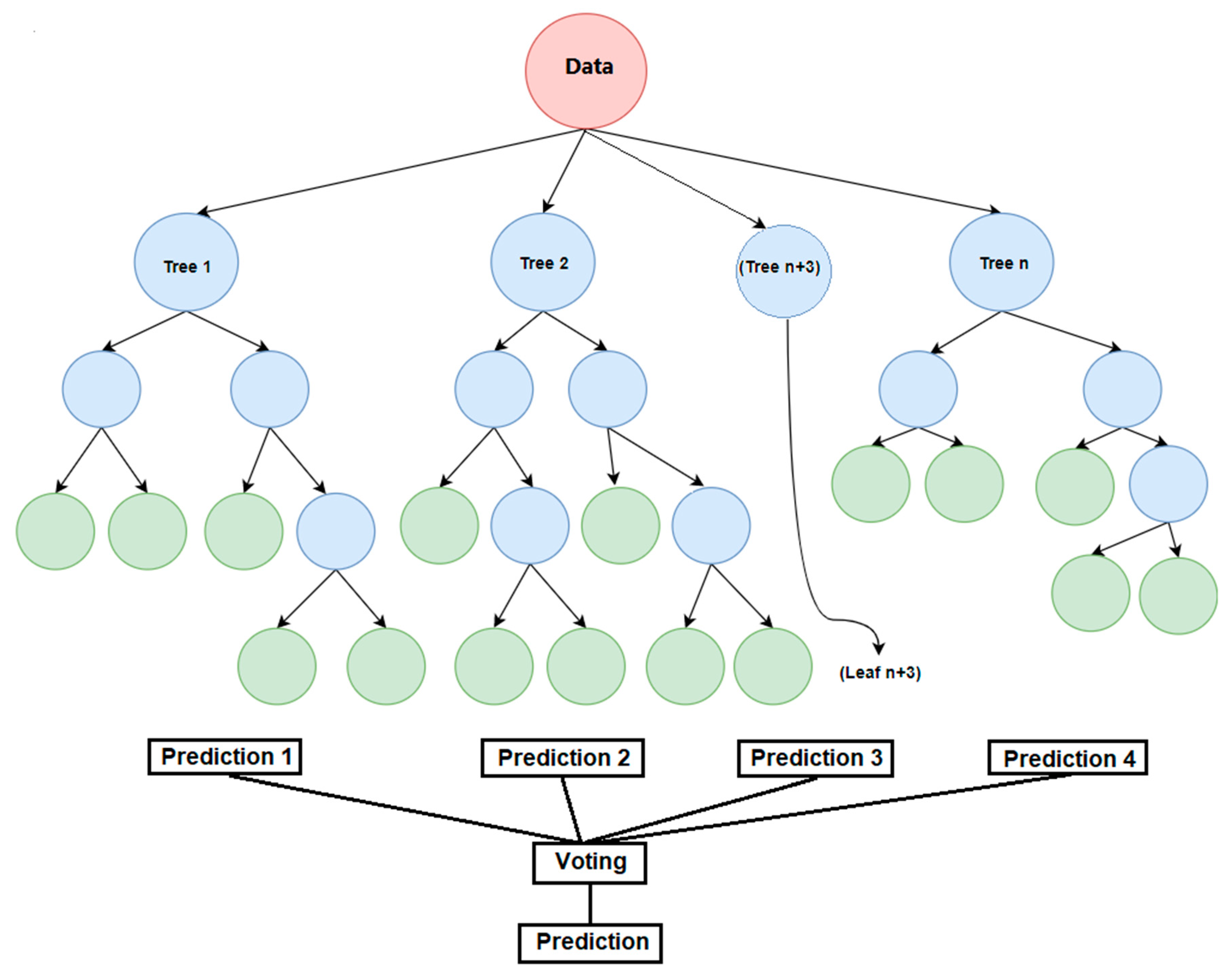
| Performance Evaluation | NSE |
|---|---|
| Very good | 0.75 < NSE ≤ 1.00 |
| Good | 0.65 < NSE ≤ 0.75 |
| Satisfactory | 0.5 < NSE ≤ 0.65 |
| Unsatisfactory | NSE ≤ 0.50 |
| RMG | RBRT(RC) | RHITM(DT) | RHITM(RF) | RHITM(GB) | |
|---|---|---|---|---|---|
| Corr | 0.901 | 0.898 | 0.842 | 0.895 | 0.901 |
| MAE | 1.32 | 1.30 | 1.71 | 1.37 | 1.27 |
| RMSE | 2.09 | 1.90 | 2.27 | 1.81 | 1.66 |
| NME | 0.650 | 0.642 | 0.846 | 0.677 | 0.626 |
| NSE | 0.623 | 0.688 | 0.553 | 0.716 | 0.763 |
| Est.% | 57.8 | 58.9 | 141 | 128 | 124 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hassan, D.; Isaac, G.A.; Taylor, P.A.; Michelson, D. Optimizing Radar-Based Rainfall Estimation Using Machine Learning Models. Remote Sens. 2022, 14, 5188. https://doi.org/10.3390/rs14205188
Hassan D, Isaac GA, Taylor PA, Michelson D. Optimizing Radar-Based Rainfall Estimation Using Machine Learning Models. Remote Sensing. 2022; 14(20):5188. https://doi.org/10.3390/rs14205188
Chicago/Turabian StyleHassan, Diar, George A. Isaac, Peter A. Taylor, and Daniel Michelson. 2022. "Optimizing Radar-Based Rainfall Estimation Using Machine Learning Models" Remote Sensing 14, no. 20: 5188. https://doi.org/10.3390/rs14205188
APA StyleHassan, D., Isaac, G. A., Taylor, P. A., & Michelson, D. (2022). Optimizing Radar-Based Rainfall Estimation Using Machine Learning Models. Remote Sensing, 14(20), 5188. https://doi.org/10.3390/rs14205188






