Abstract
In recent years, non-contact human–computer interactions have aroused much attention. In this paper, we mainly propose a dual view observation system based on the frontal and side millimeter-wave radars (MWR) to collect echo data of the Air writing digits “0~9”, simultaneously. Additionally, we also propose a novel distance approximation method to make the trajectory reconstruction more efficient. To exploit these characteristics of spatial-temporal adjacency in handwriting digits, we propose a novel clustering algorithm, named the constrained density-based spatial clustering of application with noise (CDBSCAN), to remove background noise or clutter. Moreover, we also design a robust gesture segmentation method by using twice-difference and high–low thresholds. In our trials and comparisons, based on the trajectories formulated by echo data series of time–distance and time–velocity of dual views, we present a lightweight-based convolution neural network (CNN) to realize these digits recognition. Experiment results show that our system has a relatively high recognition accuracy, which would provide a feasible application for future human–computer interaction scenarios.
1. Introduction
In recent years, millimeter wave radars (MWR)@77–79 GHz have been heavily focused on, especially in human activity monitoring areas. Typically, they are equipped with unique traits or advantages over cameras, lasers, and other sensors; are able capture subtle movements; and work well in dark environments, which protect users’ privacy. For these reasons, human posture recognition and gesture recognition based on MWR use in human–computer interactions, health care, intelligent control, and auxiliary information transmission have aroused researchers’ attention [1,2,3,4].
Authors in [5] consider the traffic gesture recognition problem and propose a point cloud-based graph neural network (GNN) network. Authors in [6] adopt a convolution neural network (CNN) and cyclic neural network to extract features from the point cloud data and track fingers’ movement online, so as to create cursor interaction between gestures and non-contact devices. Generally, the point cloud-based manner is to jointly calculate the distance and angle information of targets and further screen the spatial position of scattering points through constant false alarm rate detector (CFAR) mechanism, then extract features via manual or machine learning methods [7,8]. Despite the idea based on directly processing the echo point-cloud data, the characteristic spectrum idea has also been proposed to recognize gestures, which is aimed at exploiting the parameter estimations of range, Doppler, and angle information. Once various characteristics spectra are obtained, the classifier would be designed and attained. Authors in [9] combine the mix-up algorithm with an augmentation mechanism to expand gesture data and further propose a gesture recognition method based on a complementary multidimensional feature fusion network, which incorporates distance, speed, and angle information. The methods or algorithms above have provided valuable inspiration. Authors in [10] further propose a spiking neural network to improve hand gesture recognition, where a 2D fast Fourier transform (FFT) method is performed across fast-time and slow-time dimensions to generate a range of spectrograms, Doppler spectrograms, and angle spectrograms. Meanwhile, the meta-learning network has been proposed in order to learn a model and to adapt to unseen hand gesture tasks with few training observations [11]. However, most methods are focused on single radar view, which has some limitations to fully express the spatial linkage or correlation of gesture motions, even affecting gesture perception and recognition. Among gesture recognition, hand air writing recognition is more challenging. Traditional air writing observing mainly relies on cameras [12,13,14] or motion sensors [15]; however, the former cannot work in a dark environment and the latter requires the wearing of an auxiliary device. Obviously, MWR has some non-contact advantages and independence from illumination and further reconstructs the handwriting trajectory to form an intuitive interaction interface. In [16], authors use three radars to build a radar network, and refine range estimation with trilateration technology to detect and locate the hand marker. Authors in [17] propose a novel recognition scheme via two radars and formulate a one-dimensional time convolution network (TCN) to extract features from local target trajectories. Authors in [18] develop a novel air writing system using sparse radar network to reconstruct and classify the drawn characters. Moreover, authors in [19] utilize a single radar to locate hands with distance and angle estimation and then use the Hough transform to remove certain unnecessary trajectories. Moreover, a novel air writing framework based on a single ultra-wide-band radar has also been proposed but this idea cannot reconstruct the trajectory [20]. Authors in [21] propose a novel spatiotemporal path selection algorithm to separate the mixed gestures, and use a dual 3D CNN to extract feature and make recognition.
In this paper, we propose a novel MWR-based air writing trajectory reconstruction and recognition system by using two frequency modulated continuous wave (FMCW) radars. Via the theoretical derivation and experimental results, we find that the error between the approximated instantaneous radial distance and the longitudinal distance from hand to the radar plane is very small, so that we can adopt this simplification to tackle the hand location problem. Therein, a fast and robust gesture detection method based on a twice-time-difference and double-threshold is proposed, which has more reliable performance than the traditional single-threshold. Additionally, we presented a constrained density-based spatial clustering of applications with a noise (CDBSCAN) method to screen a hand motion trajectory, which borrows the sliding median filter to constrain the clustering effect and further remove outliers. Finally, compared with traditional trajectory reconstruction, we integrate the discriminative feature of velocity information into the trajectory to enrich the air writing digits information.
2. Raw Radar Data Preprocessing
Here, we use two MWRs of TI IWR 1443 board and DCA1000 board for data acquisition, simultaneously. The collection environment is a semi-open microwave darkroom as shown in Figure 1. Once obtain these echo data from two radars, an incoherent accumulation method is proposed to average 50 adjacent chirp data to obtain one stack-chirp, which can reduce random noise. Moreover, by conducting one-dimensional FFT on each chirp, the target distance information can be obtained. Meanwhile, by arranging these accumulated chirp-data along with time-units, we can obtain the time distance matrix (RTM). In this way, the frontal range time matrix (FRTM) and side range time matrix (SRTM) of these two views has been collected. Furthermore, the range-Doppler image can be obtained by performing 2D-FFT on each frame of the echo data with a Hamming window. In one frame of the range-Doppler image, the Doppler amplitude of gesture is obtained by searching the spectral peak-value, and the time velocity characteristic matrix (VTM) is obtained through a similar operation of frame accumulation. Finally, the frontal velocity time matrix (FVTM) and side velocity time matrix (SVTM) were able to be collected, respectively.
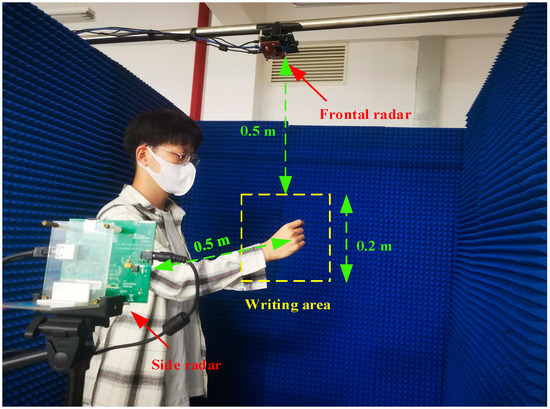
Figure 1.
The test scenarios based on frontal radar and side radar.
Note that when using the radars of the TI IWR 1443 board, due to the coupling effect of the transmitting antennas and receiving ones, a strong signal component always remains close to radar. Usually, supposing that this coupling effect may be seen as a low frequency signal but with large amplitude, we could use the high-pass filter to remove these low-frequency components. Typically, if the body, environmental parts and other targets also exist in echo data, the corresponding band-pass filter can be carried out where its boundary frequency is determined via the specific distance changing of a hand motion in FRTM and SRTM, respectively. Namely, the antenna coupling interference is equivalent to forming a false static target near radar, while the human body and test-environment can also be regarded as static targets. Therefore, the average elimination method can be used to remove the interference of static targets. This method first averages all received chirp data to obtain the referenced signal and then subtracts the referenced signal from each original chirp to obtain the echo signal of suspicious moving targets. Figure 2 shows the effect of clutter suppression through a high-pass filter, band-pass one and average elimination method. Considering that if the distance between the hand and radar changes little or remains unchanged for a period, the target signal may be greatly attenuated due to this average elimination method, so we mainly use the band-pass method to preliminarily remove the interference signal caused by the body and environmental clutter.
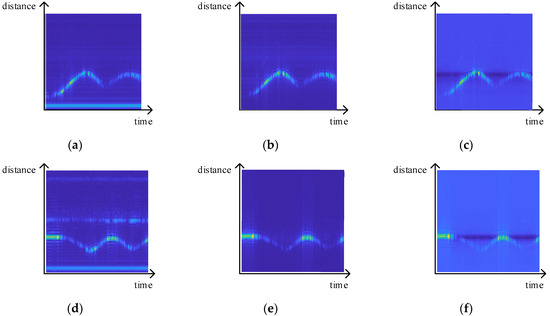
Figure 2.
Different methods of clutter suppression: (a) original RTM with antenna coupling interference only; (b) RTM after high-pass filter; (c) RTM after average elimination; (d) original RTM with antenna coupling interference and body interference; (e) RTM after band-pass filter; (f) RTM after average elimination.
3. Handwriting Trajectory Reconstruction
3.1. Distance Approximation Method
An experimental scenario is shown in Figure 1 of Section 2. When detecting the hand-writing digit “1”, we have found that its side trajectory is displayed as a horizontal straight line in SRTM. However, as the distance information reflects the radial distance from the target to radar, it should be a curve style from far to near and then from near to far; this result seems contradictory. Thus, the question is: how to define the spatial relative position of hand and radars?
Assuming the horizontal distance from target to radar is , the longitudinal distance is and the radial distance from the target to radar is . The absolute error (AE) of approximating the radial distance to the longitudinal distance is
where
can be represented as
The relative error (RE) is defined as
when the longitudinal distance is fixed, if the horizontal distance decreases, the angle between the target and radar also becomes smaller and the AE and RE would be smaller. Moreover, when the horizontal distance is fixed, the larger the longitudinal distance is, and the smaller the error will be. Figure 3 shows the AE and RE where the radial distance is replaced with the longitudinal distance when the horizontal distance varies from 0~15 cm and the longitudinal distance is 40 cm, 50 cm and 60 cm, respectively. Typically, the range of air writing in this experimental scenario is a square area with a side length of 20 cm and the square center is 50 cm away from the radar. Obviously, the maximum AE and RE appear simultaneously when the horizontal distance is 10 cm and the longitudinal distance is 40 cm. At this point, the maximum AE is 1.231 cm and the maximum RE is 3.077%. Particularly if the longitudinal distance is 60 cm, the maximum AE is only 0.828 cm and the RE is close to 1%. Consequently, we propose a distance approximation method which regards the radial distance measured by radar as the longitudinal distance. This distance approximation idea has little impact on the results of trajectory extraction and reconstruction. Furthermore, we conducted a simple experiment of moving the hand 20 cm along the horizontal direction and uniformly from left to right relative to radar over 2 s when the longitudinal distances are 40 cm and 80 cm, respectively, as shown in Figure 4. The trajectory is like a straight line both at 40 cm and 80 cm, which verifies the feasibility of the approximate distance method. Namely, by using this distance approximation method, the previous trilateration process can be directly omitted and the target angle does not need to be calculated, which greatly reduces the complexity of trajectory reconstruction.
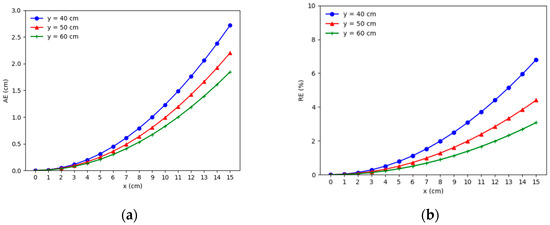
Figure 3.
Error of the distance approximation method: (a) Absolute error; (b) Relative error.

Figure 4.
Radial distance measured by radar with different longitudinal distances.
3.2. Trajectory Extraction Method Based on Peak-Value Search
As the FRTM and SRTM for one hand motion has some consistency, we further define FRTM and SRTM as where and denote the height and length of matrixes, respectively. Then, any element or at the distance unit and time unit could reflect the signal strength. The larger the value is, the more likely there is a target at this position. Via searching for the spectral peak-value, we were able to find the row index of the maximum signal intensity at each time unit, which represents the distance between the target and radar. Meanwhile, using the distance approximation method, this distance information can be regarded as the longitudinal distance between the hand and radar. In order to alleviate the impact of the noise part, we use the sliding average window to improve peak searching in each time unit, expressed as
where and denotes the length of sliding window. Note that the intensity of hand targets in RTM is very weak in some units. Moreover, the noise or clutter of the body and environment incurs some outliers in these time-distance series, which pollutes the trajectory reconstruction. In order to extract the accurate trajectory of the hand motion and suppress the clutter, we introduce a novel clustering algorithm with an adaptive neighborhood radius.
3.3. Trajectory Re-Extraction by CDBSCAN
Compared with k-means algorithm [22], DBSCAN does not need the number of clusters but needs two other parameters: one is the adjacent radius epsilon (denoted as EPS) and the other is the minimum number of points (denoted as Minpts) in the adjacent area [23]. DBSCAN is very sensitive to neighborhood radius where a slight change may lead to significant differences; therefore, the selection of the neighborhood radius is critical. In our echo data processing, we selected the appropriate neighborhood radius to achieve the ideal clustering effect for different trajectory cases. Through trials and comparison we found that the sliding median filter seems relatively stable and reliable in order to achieve trajectory smoothing, but it also has a poor effect on the continuous distribution of outliers. Thus, we tried to design a novel DBSCAN method that uses the adaptive determination mechanism of the neighborhood radius with the constraint of a sliding median filter (i.e., CDBSCAN), which could enhance the clustering task for different trajectories extraction. The detailed steps of this idea have been listed as follows. Firstly, we defined the sliding window length of this median filter, which was set as 1/10 of the data-sample length, then applied the sliding median filter to these samples. Subsequently, we also defined the state-flag on those outliers detected by the sliding median filter according to following principles:
where . Here, we set Minpts = 2, which means two points forming a cluster. Furthermore, we denoted the variation interval of the neighborhood radius as . As usual, if the number of noise points is less than that of hand trajectories, the cluster with the most points was seen as the hand trajectory. Naturally, all points of other clusters would form a novel set of outliers. Importantly, we selected each EPS parameter in to perform DBSCAN and set the state-flag by
Then we calculated the Hamming distance between two groups as follows:
Finally, the optimal neighborhood radius was selected through the EPS parameter to minimize the Hamming distance. Figure 5 shows the trajectory smoothing results using different methods. Note that the sliding mean filter can only remove the outliers with a sparse distribution. In contrast, the sliding median filter was able to remove most outliers but with a poor effect of suppressing outliers given the continuous distribution. As shown in (d), the minimum Hamming distance is fixed at 40 when EPS = 0.075. Namely, using appropriate EPS to perform CDBSCAN, we removed nearly all outliers and obtained excellent smoothing result.
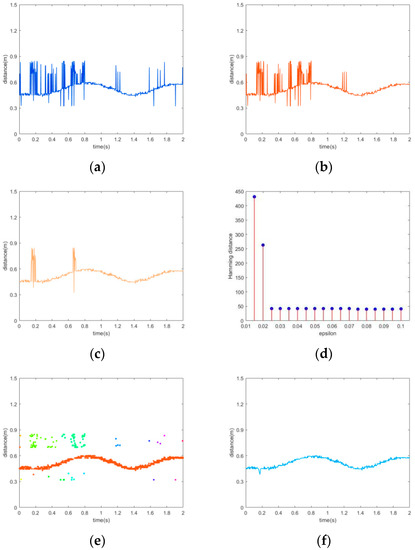
Figure 5.
Smoothing results using different methods: (a) original sample series; (b) sliding mean filter; (c) sliding median filter; (d) Hamming distance; (e) DBSCAN with given EPS; (f) our proposed CDBSCAN.
Additionally, if the number of points after CDBSCAN clustering is less than , to facilitate the trajectory reconstruction, we propose a novel interpolation idea. Suppose that the trajectory interval is , we should first carry out linear interpolation within this interval and then use following mechanism to obtain the final trajectory, i.e.,
The frontal- and side-trajectories of hand air writing digits “0~9” after CDBSCAN method have been shown in the Figure 6.
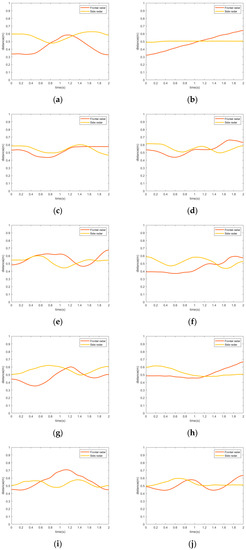
Figure 6.
The frontal- and side- trajectories of air writing digits: (a) 0; (b) 1; (c) 2; (d) 3; (e) 4; (f) 5; (g) 6; (h) 7; (i) 8; (j) 9.
3.4. Trajectory Reconstruction with Velocity Features
Similarly, we denote FVTM and SVTM as , respectively, and calculate the integrated velocity as follows:
where and denotes the height-size and length-size of matrixes. The integrated velocity curve of digits “0~9” is shown in Figure 7. We found that the velocity amplitude of these digits has some differences, but the statistical trend is consistent, which indicates that the velocity of air writing gesture has a good feature separability.
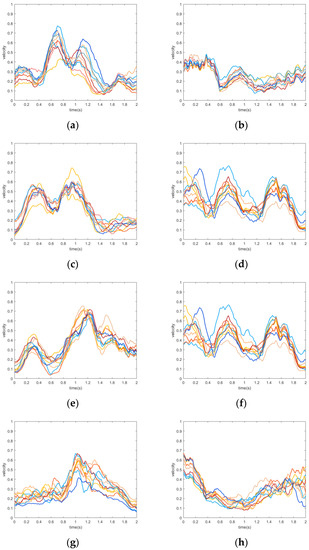
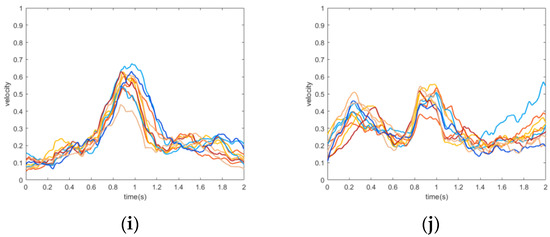
Figure 7.
The integrated velocity tendency of air writing digits where each color line denotes each sample: (a) 0; (b) 1; (c) 2; (d) 3; (e) 4; (f) 5; (g) 6; (h) 7; (i) 8; (j) 9.
Given the horizontal time-distance and time-velocity series and the vertical time-distance and time-velocity series, we constructed several graphs with different grid-size to demonstrate these handwriting trajectories. Figure 8 shows the typical trajectory of handwritten digit “3” when the grid length is chosen from 10 to 34 with an interval of 6 units. The color of the trajectory reflects the integrated velocity. The trajectories of digits “0~9” are shown in Figure 9. Generally, our proposed system supports any character input, but it is possibly not ideal for a character trajectory with more transitional strokes.
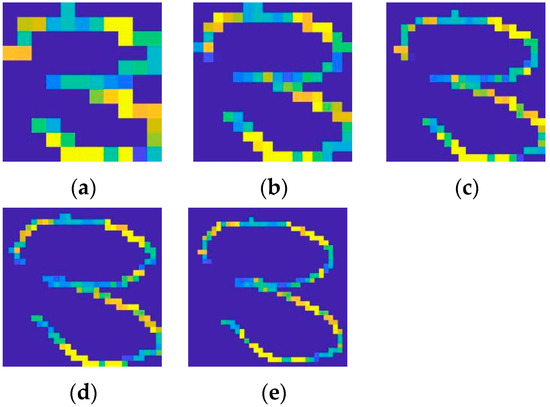
Figure 8.
Trajectories of different sizes of air writing digits “3”: (a) Size = 10; (b) Size = 16; (c) Size = 22; (d) Size = 28; (e) Size = 34.

Figure 9.
The trajectories of digits 0~9 with size of 28 × 28.
4. Gesture Segmentation Based on Twice-Difference and High–Low Thresholds
In this section, we propose a gesture segmentation idea with the twice-difference and high–low thresholds, which separate the trajectory regions from the static parts. Assume that after each hand motion, the hand remains stationary for a period before writing the next number. When the hand is stationary, the distance measured by the radar remains unchanged and the measured speed is nearly zero. Firstly, for the bidirectional time-distance series and after CDBSCAN, we calculated the first-order forward difference and the absolute value and :
Furthermore, we defined a novel threshold . If or is greater than this threshold, it will be judged as a suspicious point. Here, the first-order difference is calculated again corresponding to the suspicious point and the time interval is obtained. Normally, in the active area, these suspicious points should be continuously distributed, which means the interval at this moment should be 1. Consequently, we set the first suspicious point as the start point of the air writing digits and the last/end point as the suspicious point of the tail before the first interval. To judge the time interval in time series, namely, when the interval is less than threshold A (a high threshold), the action continues and the end point jumps to the suspicious point before the next interval. If the interval is greater than this threshold, it means the gesture has ended and then the duration is calculated. If the duration is greater than threshold B (a low threshold), it means that the duration is long enough to be recognized as a gesture (or part of one) and the first action detection ends. The last/end point is set as the suspicious tail point before the interval and the start and end point of the second gesture are reinitialized. If the point is less than threshold B, the gesture duration is too short to be admitted as a valid motion, so that we reinitialize the start and end point of first gesture in order and repeat the above operations. In particular, we set to 0.2, set the high threshold A = 2 s and low threshold to B = 0.4 s. Figure 10 shows the processing results of air writing “0” and “1” in order. Our proposed gesture segmentation method quickly achieved continuous gesture segmentation. For those transitional actions between gestures, e.g., the hand lifting action returning to the original position, a fixed sleep period can be set before the end of interval. Once the transitional gesture action has been completed, the gesture detection was started after this sleep period.
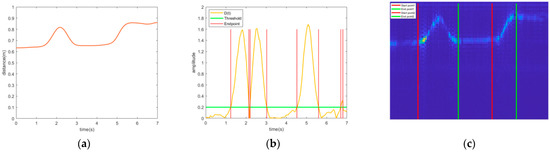
Figure 10.
Gesture Segmentation: (a) Sample to be segmented; (b) All detected endpoints; (c) Segmentation result.
In our scenarios, as the hand moves parallel to the radar, the radial distance changes little, which means the radial velocity calculated by the radar is almost zero. When there is only one view, the amplitude difference detection of RTM is misjudged and the result displays no hand movement. Fortunately, in the case of the dual view, as the gesture occurs, at least one of two radar systems (frontal or side) will detect the motion, and the final decision is obtained by the merged result of two radars:
where and denote the gesture motion detected by frontal and side radars, respectively.
5. Air Writing Trajectories Recognition
As discussed in Section 1, the collected echo data are transmitted to the PC terminal for further analysis and processing, where the PC system is Windows 10, Intel i7-8700 CPU. The deep learning framework is Tensorflow 2.4 and Keras. The parameter configuration of dual view radars is shown in Table 1.

Table 1.
Radar parameters configuration.
In this section, we build a lightweight-based CNN for trajectory classification and its structure is shown in Figure 11. This lightweight network mainly contains three Convolution layers with a size of 3 × 3 kernels, three Maxpooling layers with stride of 2, a Flatten layer, and a Fully connected output layer. Each Convolution layer applies the ReLU activation function, and Dropout operation is used in the Flatten layer. Finally, the Full Connected layer uses the Softmax activation function to output the probability of each digit.
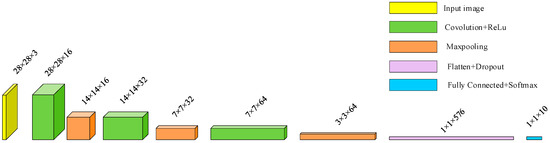
Figure 11.
The structure of lightweight convolutional neural network.
In order to build the whole dataset, we invited a total of 20 volunteers (aging from 19 to 23 years old) to complete the data collection in the semi-open microwave room, as shown in Figure 1, comprising 10 females and 10 males. When conducting the data collection, only one individual stood in the room and others remained outside the detection area of the radars. All participants wrote the same digits in order but there were some individual differences between the writing trajectories or speeds. A total dataset, including 12,000 FRTM and 12,000 SRTM and 12,000 FVTM and 12,000 SVTM was collected. After processing, we obtain 12,000 trajectories of 0~9 digits in total, where each of these categories had 1200 plane trajectories with velocity information. For each category, 1000 samples were randomly divided into training sets and 200 were divided into testing sets. The batch size of the network training is 32, the optimizer used the usual Adam one, the loss function is categorical cross-entropy, and the evaluation criterion is the accuracy metric. Table 2 has listed performance comparisons for trajectory recognition under different input sizes. Normally, the smaller of the input diagram size and fewer the network parameters are, then the faster the network training speed would be, but the recognition accuracy decreases. When the size is reduced to 10 × 10, the network recognition ability decreases rapidly but the average accuracy still reaches 93.62%. The accuracy changes for different sizes of the trajectory diagram with the training epoch increasing are shown in Figure 12. The input size with 28 × 28 and 34 × 34, in particular, almost achieved the best recognition performance. Thus, we recommend 28 × 28 as the final size of recognition, as the total amount of network training parameters is only 29,354 with average recognition rate 99.23%. Figure 13 shows the confusion matrix of the recognition results when the input trajectory is 28 × 28. Such a small input size can achieve excellent recognition accuracy due to fact that trajectory image has excellent spatial and velocity characteristics. These experiments have shown that this lightweight-based CNN may have the potential for various engineering applications.

Table 2.
Tests on the trajectory diagrams of different sizes.
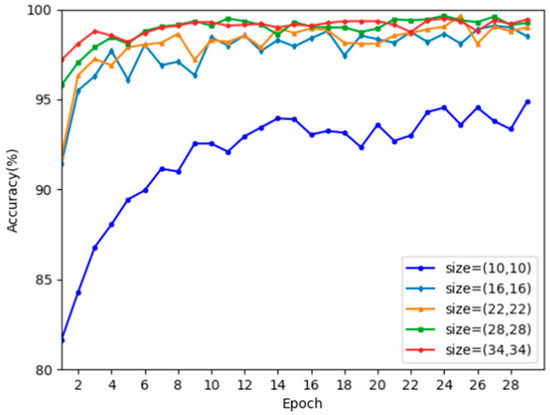
Figure 12.
Training accuracy curve of different input sizes.
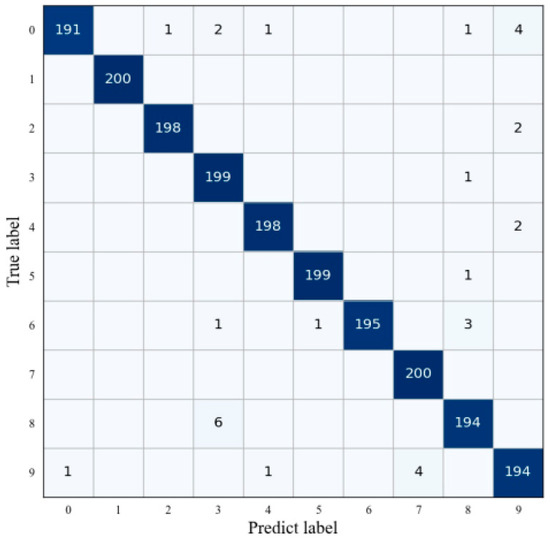
Figure 13.
Confusion matrix of the 28 × 28 size of the input trajectories.
To further evaluate the recognition performance for different feature-maps of air writing motions, we also present the ablation analysis. As shown in Table 3, the light-weighted network with single feature map, such as FRTM, SRTM, FVTM or SVTM, has not achieved the ideal result in comparison with the trajectories in Table 2, where only PVTM case obtained a high accuracy with 82.15%. Compared with the time-range feature of a single view, the time–velocity feature, i.e., FVTM and SVTM, outperformed FRTM and SRTM. Additionally, we introduce the two-stream CNN, which is formulated by two parallel light-weighted CNNs with similar parameters (seen in Figure 11) and attained the information fusion of a dual-view in the Flatten layer, as shown in Figure 14. In this case, two-stream CNNs using dual-view’s time–range or time–velocity feature map has achieved better results than the single case but also had a poorer performance compared with the results in Table 2.

Table 3.
Tests on different input feature maps.
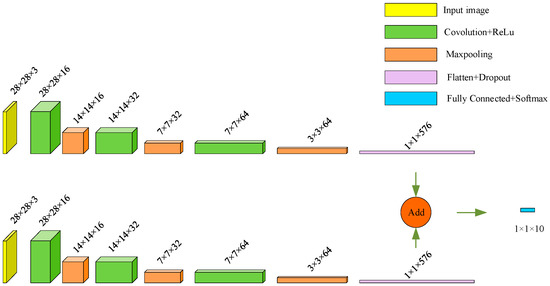
Figure 14.
The structure of two-stream CNN.
6. Conclusions
In this paper, we presented a novel dual-view MVR system to reconstruct and recognize air writing trajectories based on the sequential feature fusion idea. In addition, we provided corresponding novel denoising and gesture segmentation methods and established a dataset of air writing digits ”0~9”. Furthermore, by constructing a lightweight-based CNN model, we achieved relatively ideal classification results. In the future, we will focus on air writing recognition in more sophisticated scenarios and propose more robust methods to suppress noise and clutter. Moreover, typical multi-hand gesture recognition is also one of our research interests.
Author Contributions
Conceptualization, X.F. and T.L.; Data curation, X.F.; Formal analysis, T.L., Y.F., W.C. and Z.Z.; Funding acquisition, X.F.; Investigation, Y.Z.; Methodology, X.F., W.C., Z.Z. and Y.Z.; Project administration, X.F. and Y.Z.; Resources, Z.Z.; Supervision, Z.Z.; Validation, Y.F. and W.C.; Writing—original draft, T.L. and X.F.; Writing—review and editing, X.F. and Y.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant number 42127804.
Data Availability Statement
Not applicable.
Acknowledgments
This work was supported by the National Natural Science Foundation of China, grant number 42127804. We also appreciate the anonymous reviewers.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Li, X.; He, Y.; Fioranelli, F.; Jing, X. Semisupervised human activity recognition with radar micro-Doppler signatures. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5103112. [Google Scholar] [CrossRef]
- Erol, B.; Amin, M.G. Radar data cube processing for human activity recognition using multisubspace learning. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 3617–3628. [Google Scholar] [CrossRef]
- Skaria, S.; Al-Hourani, A.; Lech, M.; Evans, R.J. Hand-gesture recognition using two-antenna Doppler radar with deep convolutional neural networks. IEEE Sens. J. 2019, 19, 3041–3048. [Google Scholar] [CrossRef]
- Hazra, S.; Santra, A. Robust gesture recognition using millimetric-wave radar system. IEEE Sens. Lett. 2018, 2, 7001804. [Google Scholar] [CrossRef]
- Wu, J.; Zhu, Z.; Wang, H. Human Detection and Action Classification Based on Millimeter Wave Radar Point Cloud Imaging Technology. In Proceedings of the 2021 Signal Processing Symposium, Lodz, Poland, 20–23 September 2021; pp. 294–299. [Google Scholar]
- Li, Z.; Lei, Z.; Yan, A.; Solovey, E.; Pahlavan, K. ThuMouse: A Micro-gesture Cursor Input through mmWave Radar-based Interaction. In Proceedings of the 2020 IEEE International Conference on Consumer Electronics (ICCE), Las Vegas, NV, USA, 4–6 January 2020; pp. 1–9. [Google Scholar]
- Xia, Z.; Xu, F. Time-Space Dimension Reduction of Millimeter-Wave Radar Point-Clouds for Smart-Home Hand-Gesture Recognition. IEEE Sens. J. 2022, 22, 4425–4437. [Google Scholar] [CrossRef]
- Kim, Y.; Alnujaim, I.; Oh, D. Human activity classification based on point clouds measured by millimeter wave MIMO radar with deep recurrent neural networks. IEEE Sens. J. 2021, 21, 13522–13529. [Google Scholar] [CrossRef]
- Wang, Y.; Shu, Y.; Jia, X.; Zhou, M.; Xie, L.; Guo, L. Multifeature Fusion-Based Hand Gesture Sensing and Recognition System. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Arsalan, M.; Santra, A.; Issakov, V. RadarSNN: A Resource Efficient Gesture Sensing System Based on mm-Wave Radar. IEEE Trans. Microw. Theory Tech. 2022, 70, 2451–2461. [Google Scholar] [CrossRef]
- Shen, X.; Zheng, H.; Feng, X.; Hu, J. ML-HGR-Net: A Meta-Learning Network for FMCW Radar Based Hand Gesture Recognition. IEEE Sens. J. 2022, 22, 10808–10817. [Google Scholar] [CrossRef]
- Elshenaway, A.R.; Guirguis, S.K. On-Air Hand-Drawn Doodles for IoT Devices Authentication During COVID-19. IEEE Access 2021, 9, 161723–161744. [Google Scholar] [CrossRef]
- Kane, L.; Khanna, P. Vision-Based Mid-Air Unistroke Character Input Using Polar Signatures. IEEE Trans. Hum. Mach. Syst. 2017, 47, 1077–1088. [Google Scholar] [CrossRef]
- Hsieh, C.-H.; Lo, Y.-S.; Chen, J.-Y.; Tang, S.-K. Air-Writing Recognition Based on Deep Convolutional Neural Networks. IEEE Access 2021, 9, 142827–142836. [Google Scholar] [CrossRef]
- Pan, T.; Kuo, C.; Liu, H.; Hu, M. Handwriting Trajectory Reconstruction Using Low-Cost IMU. IEEE Trans. Emerg. Top. Comput. Intell. 2019, 3, 261–270. [Google Scholar] [CrossRef]
- Arsalan, M.; Santra, A. Character Recognition in Air-Writing Based on Network of Radars for Human-Machine Interface. IEEE Sens. J. 2019, 19, 8855–8864. [Google Scholar] [CrossRef]
- MArsalan; Santra, A.; Issakov, V. Radar Trajectory-based Air-Writing Recognition using Temporal Convolutional Network. In Proceedings of the 2020 19th IEEE International Conference on Machine Learning and Applications (ICMLA), Miami, FL, USA, 14–17 December 2020; pp. 1454–1459. [Google Scholar]
- Arsalan, M.; Santra, A.; Bierzynski, K.; Issakov, V. Air-Writing with Sparse Network of Radars using Spatio-Temporal Learning. In Proceedings of the 2020 25th International Conference on Pattern Recognition (ICPR), Milan, Italy, 10–15 January 2021; pp. 8877–8884. [Google Scholar]
- Lee, H.; Lee, Y.; Choi, H.; Lee, S. Digit Recognition in Air-Writing Using Single Millimeter-Wave Band Radar System. IEEE Sens. J. 2022, 22, 9387–9396. [Google Scholar] [CrossRef]
- Hendy, N.; Fayek, H.M.; Al-Hourani, A. Deep Learning Approaches for Air-Writing Using Single UWB Radar. IEEE Sens. J. 2022, 22, 11989–12001. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, D.; Fu, Y.; Yao, D.; Xie, L.; Zhou, M. Multi-Hand Gesture Recognition Using Automotive FMCW Radar Sensor. Remote Sens. 2022, 14, 2374. [Google Scholar] [CrossRef]
- Krishna, K.; Murty, M.N. Genetic K-means algorithm. IEEE Trans. Syst. Man Cybern. Part B Cybern. 1999, 29, 433–439. [Google Scholar] [CrossRef] [PubMed]
- Shen, J.; Hao, X.; Liang, Z.; Liu, Y.; Wang, W.; Shao, L. Real-time superpixel segmentation by DBSCAN clustering algorithm. IEEE Trans. Image Process. 2016, 25, 5933–5942. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).