L2AMF-Net: An L2-Normed Attention and Multi-Scale Fusion Network for Lunar Image Patch Matching
Abstract
1. Introduction
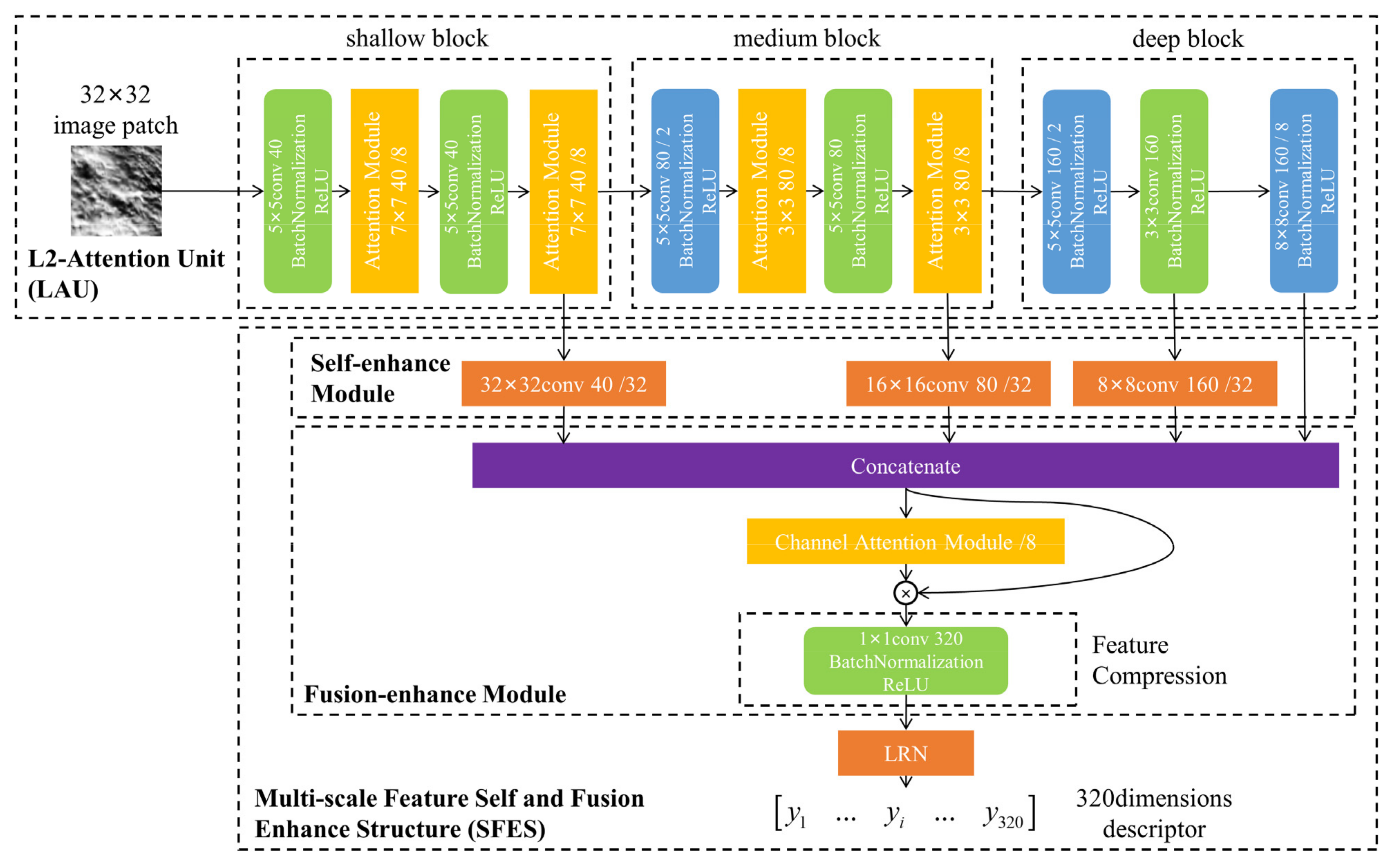
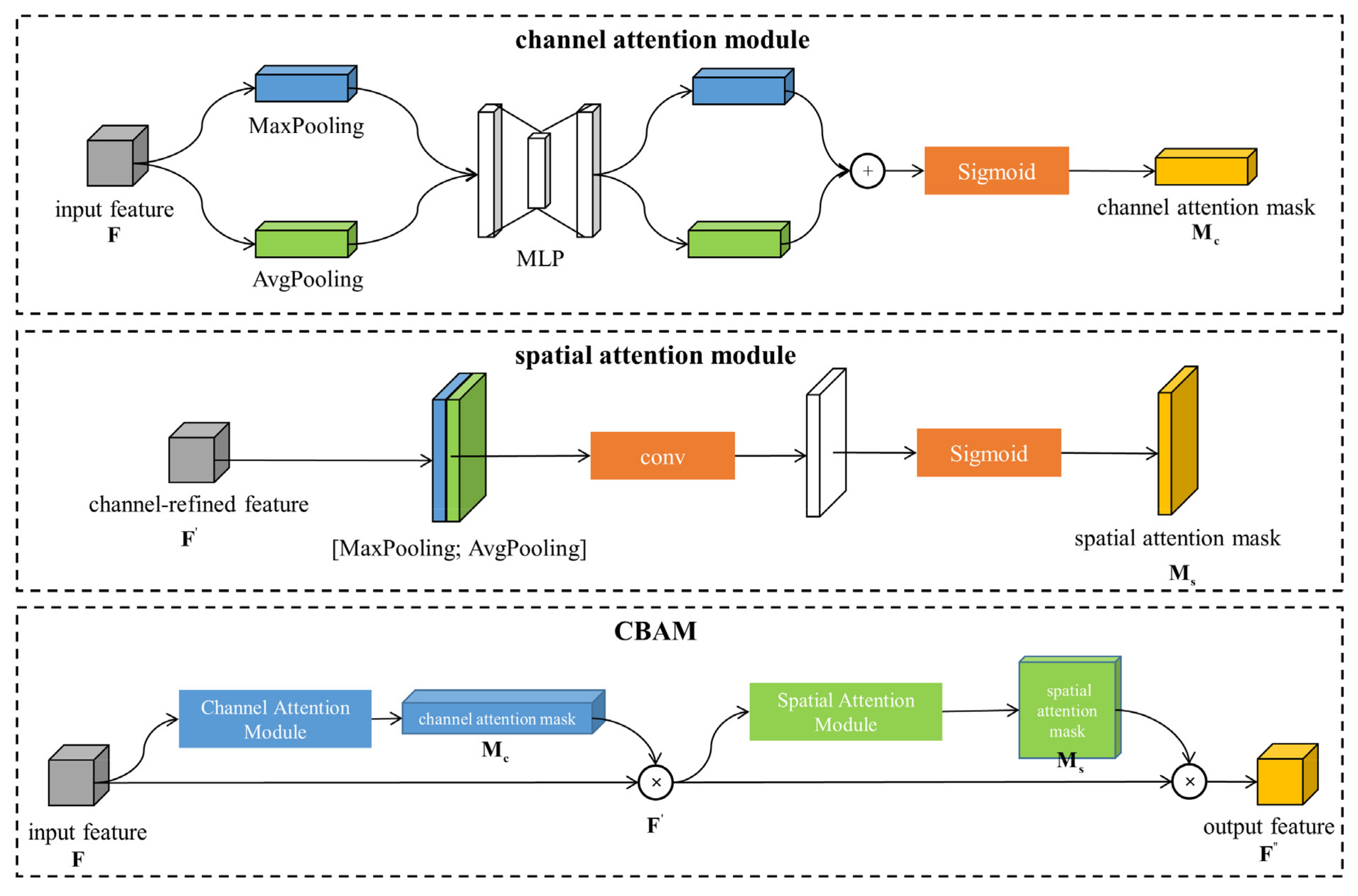
- An L2-Attention unit (LAU) was proposed to generate attention score maps in spatial and channel dimensions and enhance feature extraction. In the shallow and medium blocks, a spatial attention module filters pixel neighbourhoods to learn pixel interaction, and a channel attention module adopts a multi-layer perception (MLP) to explore the priority of features in different channels. An attention score map is generated and applied on a feature map to emphasize significant terrains or invariant features and weaken general features. In the deep block, a large-scale kernel convolution assigns weights to compact pixel features and accumulates them together as a more compact and abstract representation.
- A multi-scale feature self and fusion enhance structure (SFES) was proposed to fuse multi-scale features and enhance the feature representations. In the self-enhance module, a large-scale convolution assigns weights to shallow or deep features and refines a compact representation of a 1 × 1 map to achieve self enhancement, respectively. In the fusion-enhance module, a channel attention module identifies and assigns greater weights on invariant and significant features to enhance feature fusion, and a feature compression removes redundant features to increase the compactness of descriptors.
- The triplet loss and hard negative mining sampling strategy was introduced for network training in the TRN for EDL. The triplet loss maximizes the difference between matched descriptor pair distances and mismatched descriptor pair distances. This helps to simultaneously enhance the similarity of matched pairs and reduce the possibility of matching errors in the mini-batch.
2. Proposed Method
2.1. Backbone: L2-Net
2.2. L2-Attention Unit
2.3. Multi-Scale Feature Self and Fusion Enhance Structure
2.4. Loss Function and Sampling Strategy
- (1)
- The descriptor distance matrix is obtained according to Equation (2).
- (2)
- is set to 0 and the of is the index of the negative LCAM patch in the mini-batch. The is set to and is set to .
- (3)
- is set to . The second step is repeated until is equal to batch size .
- (4)
- The triplet loss is obtained through batch size tuples according to Equation (8).
3. Lunar Image Patch Datasets
3.1. Generation Procedure of Datasets
3.2. Datasets Overview
4. Experiment
4.1. Training and Testing Details
4.2. Comparison with Other Methods
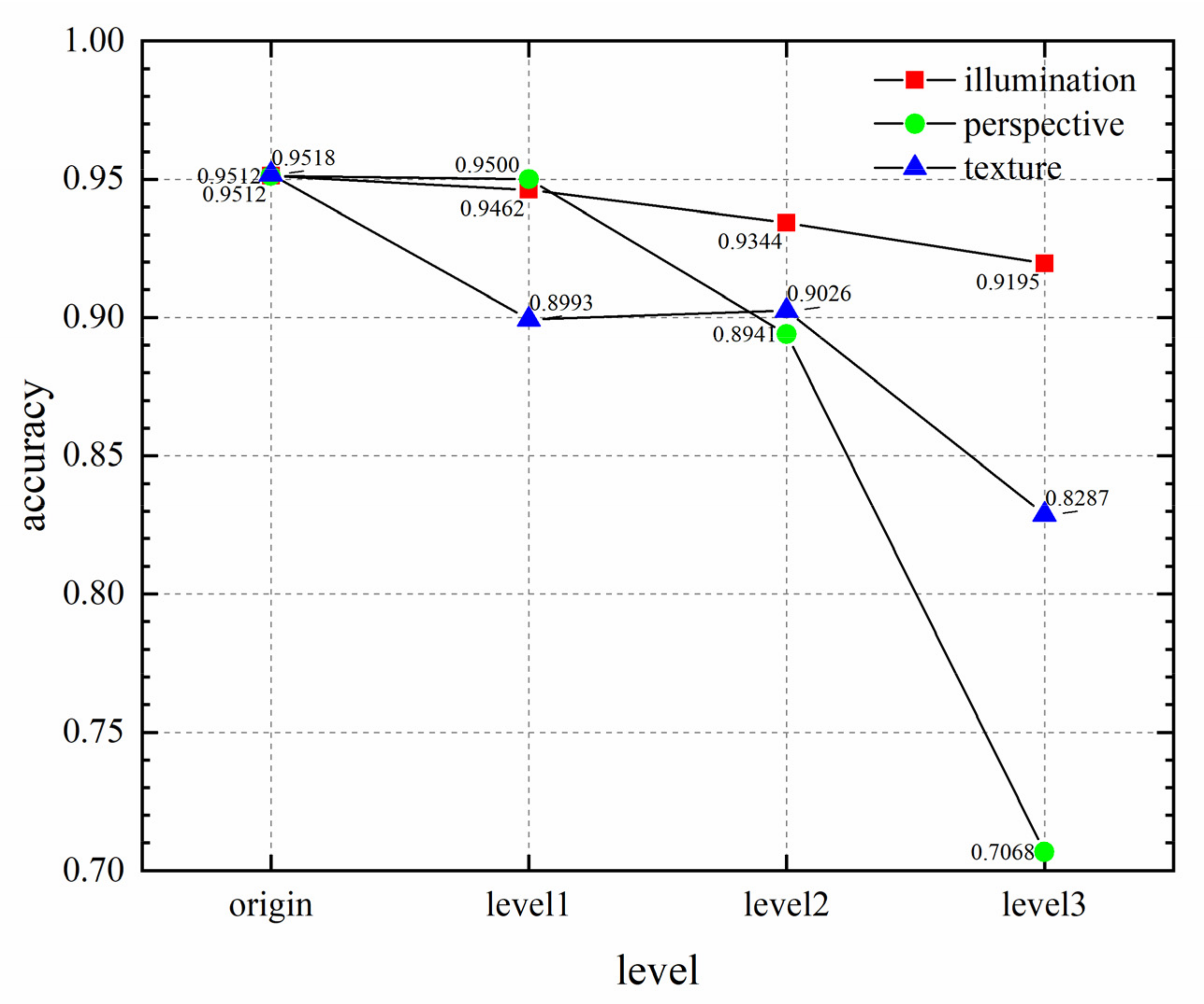
4.3. Robustness Testing
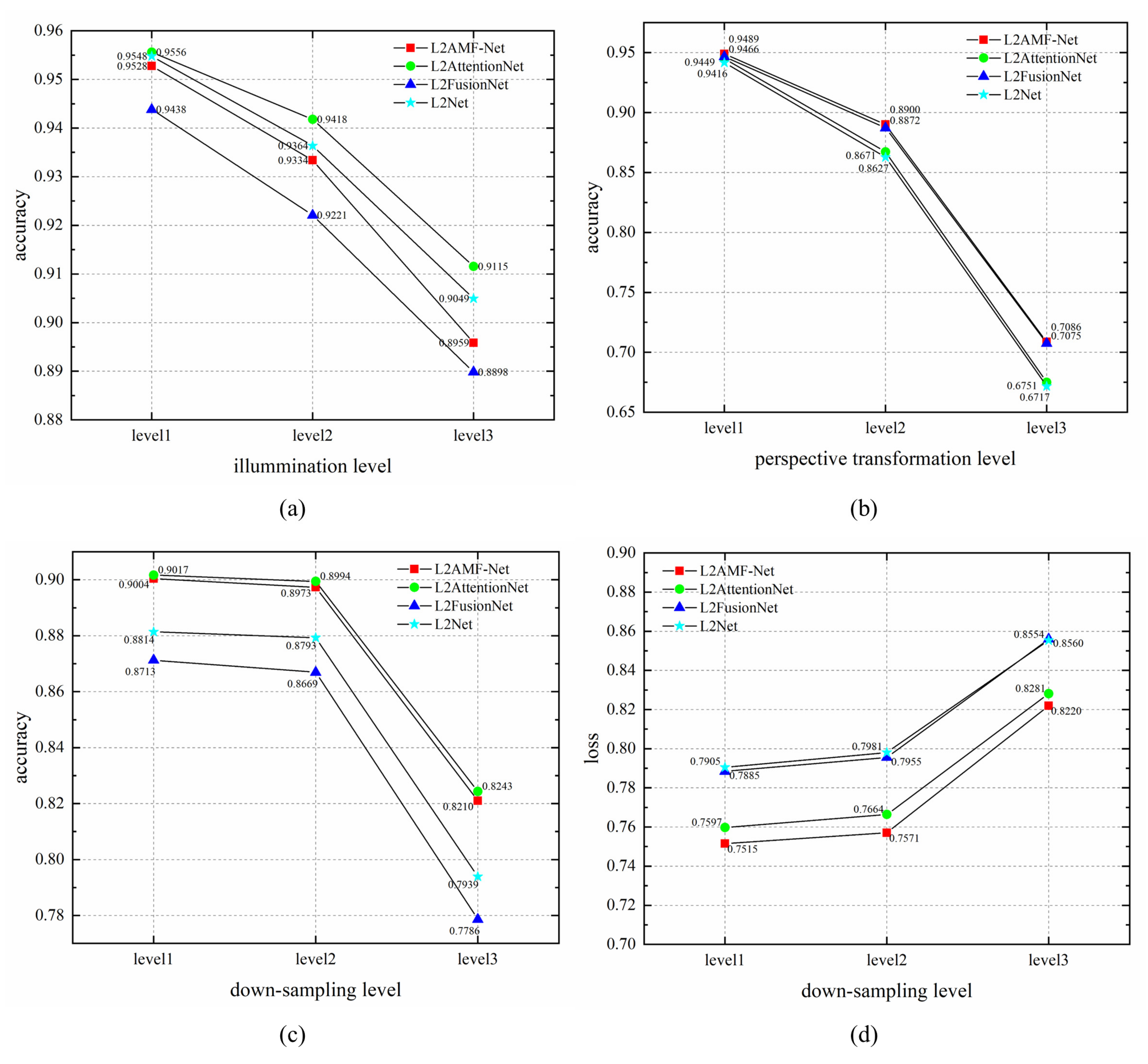
4.3.1. Illumination Robustness
4.3.2. Perspective Robustness
4.3.3. Texture Robustness
4.4. Ablation Study
4.4.1. L2-Attention Unit
4.4.2. Multi-Scale Feature Self and Fusion Enhance Structure
4.5. Further Discussion
4.5.1. Batch Size Characteristics
4.5.2. Patch Size Characteristics
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Johnson, A.; Aaron, S.; Chang, J.; Cheng, Y.; Montgomery, J.; Mohan, S.; Schroeder, S.; Tweddle, B.; Trawny, N.; Zheng, J. The lander vision system for mars 2020 entry descent and landing. In Proceedings of the AAS Guidance Navigation and Control Conference, Breckenridge, CO, USA, 2–8 February 2017. [Google Scholar]
- Johnson, A.E.; Montgomery, J.F. Overview of terrain relative navigation approaches for precise lunar landing. In Proceedings of the IEEE Aerospace Conference, Big Sky, MT, USA, 1–8 March 2008. [Google Scholar]
- Liu, J.; Ren, X.; Yan, W.; Li, C.; Zhang, H.; Jia, Y.; Zeng, X.; Chen, W.; Gao, X.; Liu, D.; et al. Descent trajectory reconstruction and landing site positioning of Chang’E-4 on the lunar farside. Nat. Commun. 2019, 10, 4229. [Google Scholar] [CrossRef]
- Wouter, D. Autonomous Lunar Orbit Navigation with Ellipse R-CNN. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 7 July 2021. [Google Scholar]
- Downes, L.; Steiner, T.J.; How, J.P. Deep learning crater detection for lunar terrain relative navigation. In Proceedings of the AIAA SciTech 2020 Forum, Orlando, FL, USA, 6 January 2020. [Google Scholar]
- Silburt, A.; Ali-Dib, M.; Zhu, C.; Jackson, A.; Valencia, D.; Kissin, Y.; Tamayo, D.; Menou, K. Lunar crater identification via deep learning. Icarus 2019, 317, 27–38. [Google Scholar] [CrossRef]
- Downes, L.M.; Steiner, T.J.; How, J.P. Lunar terrain relative navigation using a convolutional neural network for visual crater detection. In Proceedings of the American Control Conference, Denver, CO, USA, 1–3 July 2020. [Google Scholar]
- Lu, T.; Hu, W.; Liu, C.; Yang, D. Relative pose estimation of a lander using crater detection and matching. Opt. Eng. 2016, 55, 023102. [Google Scholar] [CrossRef]
- Johnson, A.; Villaume, N.; Umsted, C.; Kourchians, A.; Sterberg, D.; Trawny, N.; Cheng, Y.; Geipel, E.; Montgomery, J. The Mars 2020 lander vision system field test. In Proceedings of the AAS Guidance Navigation and Control Conference, Breckenridge, CO, USA, 30 January–5 February 2020. [Google Scholar]
- Matthies, L.; Daftry, S.; Rothrock, B.; Davis, A.; Hewitt, R.; Sklyanskiy, E.; Delaune, J.; Schutte, A.; Quadrelli, M.; Malaska, M.; et al. Terrain relative navigation for guided descent on titan. In Proceedings of the IEEE Aerospace Conference, Big Sky, MT, USA, 7–14 March 2020. [Google Scholar]
- Mulas, M.; Ciccarese, G.; Truffelli, G.; Corsini, A. Integration of digital image correlation of Sentinel-2 data and continuous GNSS for long-term slope movements monitoring in moderately rapid landslides. Remote Sens. 2020, 12, 2605. [Google Scholar] [CrossRef]
- Li, Z.; Mahapatra, D.; Tielbeek, J.A.; Stoker, J.; van Vliet, L.J.; Vos, F.M. Image registration based on autocorrelation of local structure. IEEE Trans. Image Processing 2015, 35, 63–75. [Google Scholar] [CrossRef]
- Ma, J.; Jiang, X.; Fan, A.; Jiang, J.; Yan, J. Image matching from handcrafted to deep features: A survey. Int. J. Comput. Vis. 2021, 129, 23–79. [Google Scholar] [CrossRef]
- Lowe, D.G. Object recognition from local scale-invariant features. In Proceedings of the Seventh IEEE International Conference on Computer Vision, Kerkyra, Greece, 20–25 September 1999. [Google Scholar]
- Bay, H.; Tuytelaars, T.; Gool, L.V. Surf: Speeded up robust features. In Proceedings of the European Conference on Computer Vision, Graz, Austria, 7–13 May 2006. [Google Scholar]
- Tola, E.; Lepetit, V.; Fua, P. Daisy: An Efficient Dense Descriptor Applied to Wide-baseline Stereo. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 32, 815–830. [Google Scholar] [CrossRef]
- Rublee, E.; Rabaud, V.; Konolige, K.; Bradski, G. ORB: An efficient alternative to SIFT or SURF. In Proceedings of the IEEE International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011. [Google Scholar]
- Leutenegger, S.; Chli, M.; Siegwart, R.Y. BRISK: Binary Robust Invariant Scalable Keypoints. In Proceedings of the IEEE International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011. [Google Scholar]
- Alahi, A.; Ortiz, R.; Vandergheynst, P. Freak: Fast Retina Keypoint. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 18–20 June 2012. [Google Scholar]
- Xi, J.; Ersoy, O.K.; Cong, M.; Zhao, C.; Qu, W.; Wu, T. Wide and Deep Fourier Neural Network for Hyperspectral Remote Sensing Image Classification. Remote Sens. 2022, 14, 2931. [Google Scholar] [CrossRef]
- Qing, Y.; Liu, W.; Feng, L.; Gao, W. Improved YOLO Network for Free-Angle Remote Sensing Target Detection. Remote Sens. 2021, 13, 2171. [Google Scholar] [CrossRef]
- Manos, E.; Witharana, C.; Udawalpola, M.R.; Hasan, A.; Liljedahl, A.K. Convolutional Neural Networks for Automated Built Infrastructure Detection in the Arctic Using Sub-Meter Spatial Resolution Satellite Imagery. Remote Sens. 2022, 14, 2719. [Google Scholar] [CrossRef]
- Chen, Y.; Jiang, J. A Two-Stage Deep Learning Registration Method for Remote Sensing Images Based on Sub-Image Matching. Remote Sens. 2021, 13, 3443. [Google Scholar] [CrossRef]
- Khorrami, B.; Valizadeh Kamran, K. A fuzzy multi-criteria decision-making approach for the assessment of forest health applying hyper spectral imageries: A case study from Ramsar forest, North of Iran. Int. J. Eng. Geosci. 2022, 7, 214–220. [Google Scholar] [CrossRef]
- Jiang, Z.; Zhang, J.; Ma, Y.; Mao, X. Hyperspectral Remote Sensing Detection of Marine Oil Spills Using an Adaptive Long-Term Moment Estimation Optimizer. Remote Sens. 2022, 14, 157. [Google Scholar] [CrossRef]
- Song, K.; Cui, F.; Jiang, J. An Efficient Lightweight Neural Network for Remote Sensing Image Change Detection. Remote Sens. 2021, 13, 5152. [Google Scholar] [CrossRef]
- Cui, F.; Jiang, J. Shuffle-CDNet: A Lightweight Network for Change Detection of Bitemporal Remote-Sensing Images. Remote Sens. 2022, 14, 3548. [Google Scholar] [CrossRef]
- Furano, G.; Meoni, G.; Dunne, A.; Moloney, D.; Ferlet-Cavrois, V.; Tavoularis, A.; Byrne, J.; Buckley, L.; Psarakis, M.; Voss, K.-O.; et al. Towards the use of artificial intelligence on the edge in space systems: Challenges and opportunities. IEEE Aerosp. Electron. Syst. Mag. 2020, 35, 44–56. [Google Scholar] [CrossRef]
- Keller, M.; Chen, Z.; Maffra, F.; Schmuck, P.; Chli, M. Learning deep descriptors with scale-aware triplet networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018. [Google Scholar]
- Simo-Serra, E.; Trulls, E.; Ferraz, L.; Kokkinos, I.; Fua, P.; Moreno-Noguer, F. Discriminative learning of deep convolutional feature point descriptors. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015. [Google Scholar]
- Wang, S.; Li, Y.; Liang, X.; Quan, D.; Yang, B.; Wei, S.; Jiao, L. Better and faster: Exponential loss for image patch matching. In Proceedings of the IEEE International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019. [Google Scholar]
- Barz, B.; Denzler, J. Deep learning on small dataset without pre-training using cosine loss. In Proceedings of the IEEE Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 2–5 March 2020. [Google Scholar]
- Regmi, K.; Shah, M. Bridging the domain gap for ground-to-aerial image matching. In Proceedings of the IEEE International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019. [Google Scholar]
- Wang, X.; Zhang, S.; Lei, Z.; Liu, S.; Guo, X.; Li, S.Z. Ensemble soft-margin softmax loss for image classification. arXiv 2018, arXiv:1805.03922. [Google Scholar]
- Kumar, B.G.V.; Carneiro, G.; Reid, I. Learning local image descriptors with deep siamese and triplet convolutional networks by minimising global loss functions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, CA, USA, 26 June–1 July 2016. [Google Scholar]
- Tian, Y.; Yu, X.; Fan, B.; Wu, F.; Heijnen, H.; Balntas, V. Sosnet: Second order similarity regularization for local descriptor learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019. [Google Scholar]
- Balntas, V.; Riba, E.; Ponsa, D.; Mikolajczyk, K. Learning local feature descriptors with triplets and shallow convolutional neural networks. In Proceedings of the British Machine Vision Conference, York, UK, 19–22 September 2016. [Google Scholar]
- Irshad, A.; Hafiz, R.; Ali, M.; Faisal, M.; Cho, Y.; Seo, J. Twin-net descriptor: Twin negative mining with quad loss for patch-based matching. IEEE Access 2019, 7, 136062–136072. [Google Scholar] [CrossRef]
- Han, X.; Leung, T.; Jia, Y.; Sukthankar, R.; Berg, A.C. Matchnet: Unifying feature and metric learning for patch-based matching. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016. [Google Scholar]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely connected convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Rocco, I.; Arandjelović, R.; Sivic, J. Convolutional Neural Network Architecture for Geometric Matching. IEEE Transactions on Pattern Analysis and Machine Intelligence 2019, 41, 2553–2567. [Google Scholar] [CrossRef]
- Quan, D.; Liang, X.; Wang, S.; Wei, S.; Li, Y.; Huyan, N.; Jiao, L. AFD-Net: Aggregated feature difference learning for cross-spectral image patch matching. In Proceedings of the IEEE International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019. [Google Scholar]
- Quan, D.; Wang, S.; Li, Y.; Yang, B.; Huyan, N.; Chanussot, J.; Hou, B.; Jiao, L. Multi-Relation Attention Network for Image Patch Matching. IEEE Trans. Image Processing 2021, 30, 7127–7142. [Google Scholar] [CrossRef]
- Zagoruyko, S.; Komodakis, N. Learning to compare image patches via convolutional neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015. [Google Scholar]
- Tian, Y.; Fan, B.; Wu, F. L2-Net: Deep learning of discriminative patch descriptor in euclidean space. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Noh, H.; Araujo, A.; Sim, J.; Weyand, T.; Han, B. Large-scale image retrieval with attentive deep local features. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017. [Google Scholar]
- Zhang, Z.; Lan, C.; Zeng, W.; Jin, X.; Chen, Z. Relation-aware global attention for person re-identification. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020. [Google Scholar]
- Lin, T.Y.; Dollár, P.; Girshick, R.; He, K.; Hariharan, B.; Belongie, S. Feature pyramid networks for object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Mishchuk, A.; Mishkin, D.; Radenovic, F.; Matas, J. Working hard to know your neighbor’s margins: Local descriptor learning loss. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–6 December 2012. [Google Scholar]
- Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.S. Cbam: Convolutional block attention module. In Proceedings of the European Conference on Computer Vision, Munich, Germany, 8–14 September 2018. [Google Scholar]
- Lunar and Deep Space Exploration Scientific Data and Sample Release System. Chang’E-2 CCD Stereoscopic Camera DOM-7m Dataset. Available online: http://moon.bao.ac.cn (accessed on 1 December 2021).
- Liu, J. Study on fast image template matching algorithm. Master’s Thesis, Central South University, Changsha, China, 1 March 2007. [Google Scholar]
- Zagoruyko, S.; Komodakis, N. Deep compare: A study on using convolutional neural networks to compare image patches. Comput. Vis. Image Underst. 2017, 164, 38–55. [Google Scholar] [CrossRef]





| Transformation Degree | ||||
|---|---|---|---|---|
| origin | 1 | 1 | 1 | 4–8 (random) |
| level1 | 0.7 | 1.4 | 0.6 | 9 |
| level2 | 0.55 | 1.9 | 0.5 | 10 |
| level3 | 0.4 | 2.4 | 0.4 | 11 |
| Methods | Test Accuracy |
|---|---|
| template matching (CCOEFF, 128) [1,54] | 0.5429 |
| template matching (CCORR, 128) [1,54] | 0.5408 |
| template matching (NORMED CCOEFF, 64) [1,54] | 0.7227 |
| template matching (NORMED CCORR, 64) [1,54] | 0.6852 |
| SIFT (32) [14] | 0.2088 |
| SURF (32) [15] | 0.2081 |
| ORB (64) [17] | 0.0728 |
| L2-Net (relative loss) [46] | 0.8896 |
| HardNet (triplet loss) [50] | 0.9370 |
| Siamese (hinge loss, base) [30] | 0.8694 |
| Siamese (soft-margin loss, base) [34] | 0.4663 |
| Siamese (cosine loss, base) [32] | 0.7262 |
| Siamese (hinge loss, 2ch2stream) [55] | 0.8422 |
| MatchNet (base) [39] | 0.9402 |
| MatchNet (2channel) [39,55] | 0.9576 |
| MatchNet (2ch2stream) [39,55] | 0.9398 |
| L2AMF-Net | 0.9557 |
| Network | LAU | SFES | Test Loss | Test Accuracy |
|---|---|---|---|---|
| L2AMF-Net | √ | √ | 0.6173 | 0.9499 |
| L2AttentionNet | √ | 0.6529 | 0.9468 | |
| L2FusionNet | √ | 0.6498 | 0.9457 | |
| L2-Net | 0.6808 | 0.9408 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhong, W.; Jiang, J.; Ma, Y. L2AMF-Net: An L2-Normed Attention and Multi-Scale Fusion Network for Lunar Image Patch Matching. Remote Sens. 2022, 14, 5156. https://doi.org/10.3390/rs14205156
Zhong W, Jiang J, Ma Y. L2AMF-Net: An L2-Normed Attention and Multi-Scale Fusion Network for Lunar Image Patch Matching. Remote Sensing. 2022; 14(20):5156. https://doi.org/10.3390/rs14205156
Chicago/Turabian StyleZhong, Wenhao, Jie Jiang, and Yan Ma. 2022. "L2AMF-Net: An L2-Normed Attention and Multi-Scale Fusion Network for Lunar Image Patch Matching" Remote Sensing 14, no. 20: 5156. https://doi.org/10.3390/rs14205156
APA StyleZhong, W., Jiang, J., & Ma, Y. (2022). L2AMF-Net: An L2-Normed Attention and Multi-Scale Fusion Network for Lunar Image Patch Matching. Remote Sensing, 14(20), 5156. https://doi.org/10.3390/rs14205156






