Time-Lagged Ensemble Quantitative Precipitation Forecasts for Three Landfalling Typhoons in the Philippines Using the CReSS Model, Part II: Verification Using Global Precipitation Measurement Retrievals
Abstract
1. Introduction
2. Data and Methodology
2.1. The CReSS Model and Hindcast Experiments
2.2. Observation Data for Model Verification
2.3. Verification of Model QPFs
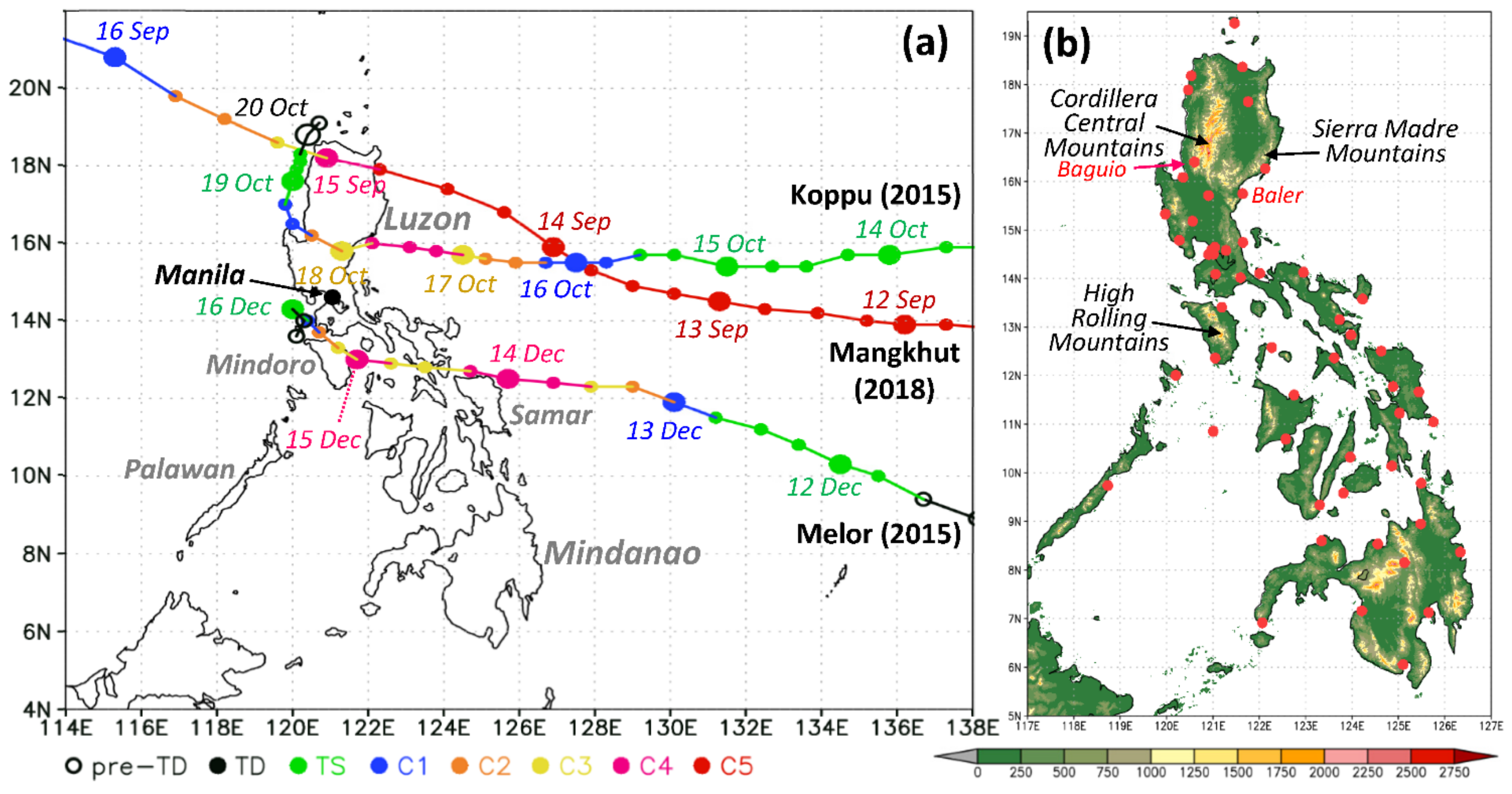
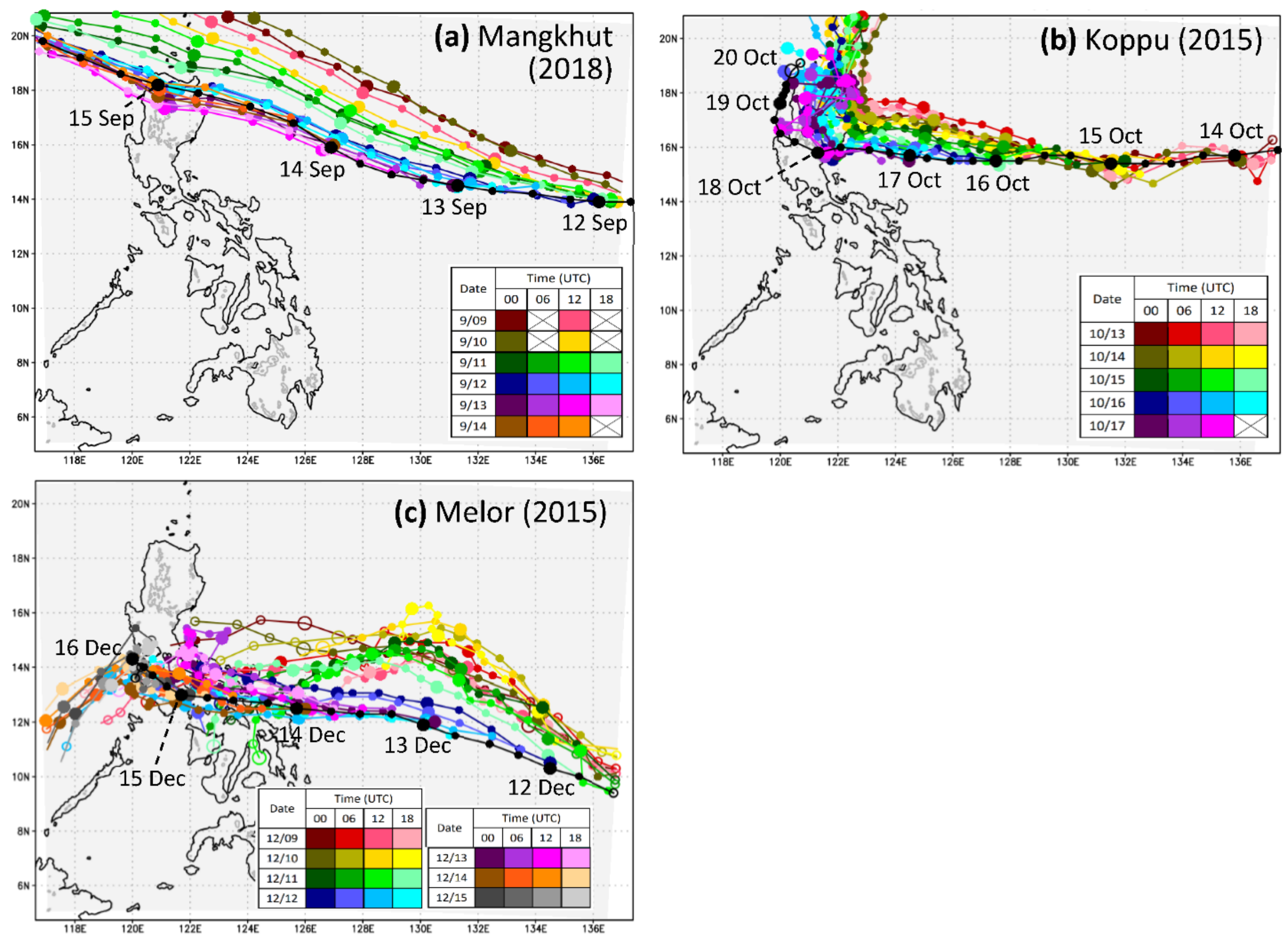
3. Time-Lagged Ensemble QPFs for TY Mangkhut (2018)
3.1. Track and Intensity of TY Mangkhut (2018)
3.2. Observed and Predicted Rainfall of TY Mangkhut (2018)
3.3. Heavy Rainfall Probabilities of TY Mangkhut (2018)
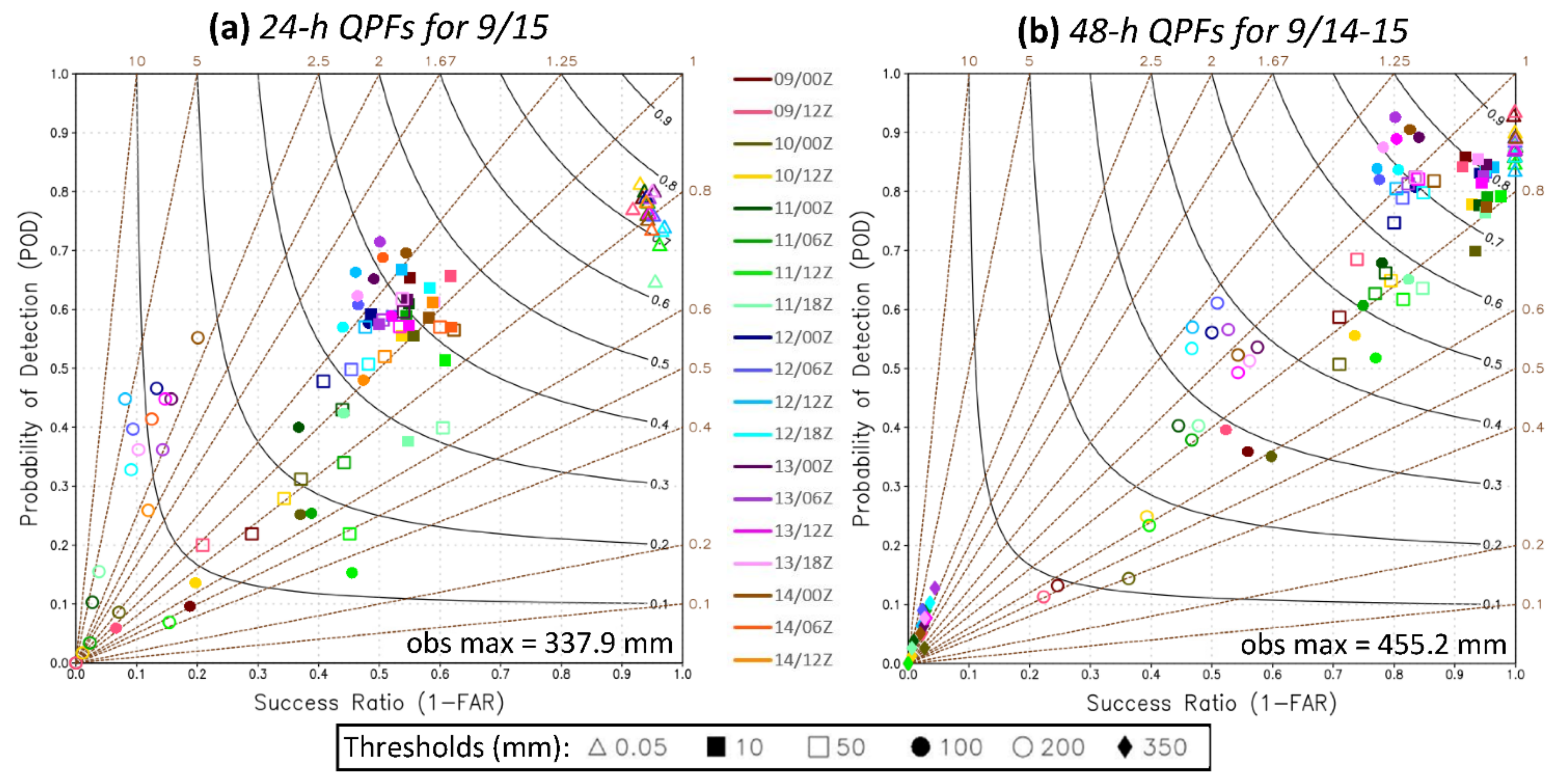
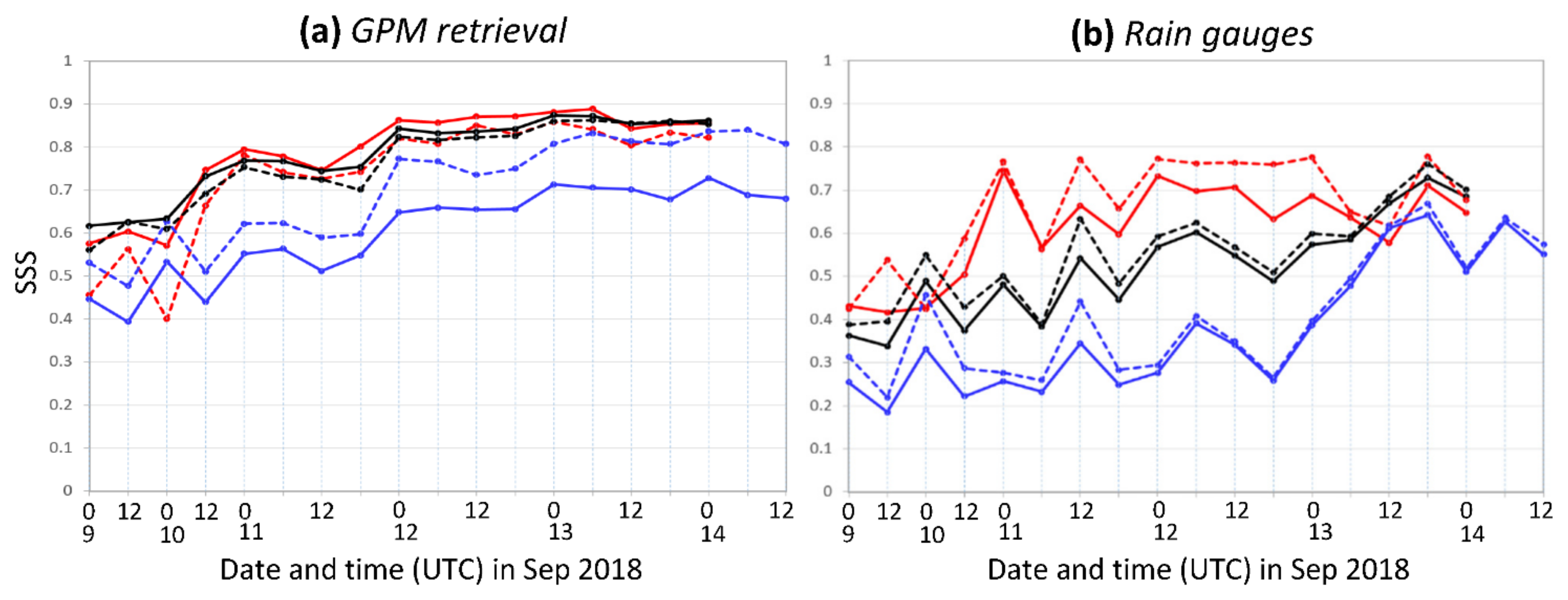
3.4. Objective Skill Scores of QPFs for TY Mangkhut (2018)
4. Time-Lagged Ensemble QPFs for TY Koppu (2015)
4.1. Track and Intensity of TY Koppu (2015)
4.2. Observed and Predicted Rainfall of TY Koppu (2015)
4.3. Heavy Rainfall Probabilities of TY Koppu (2015)
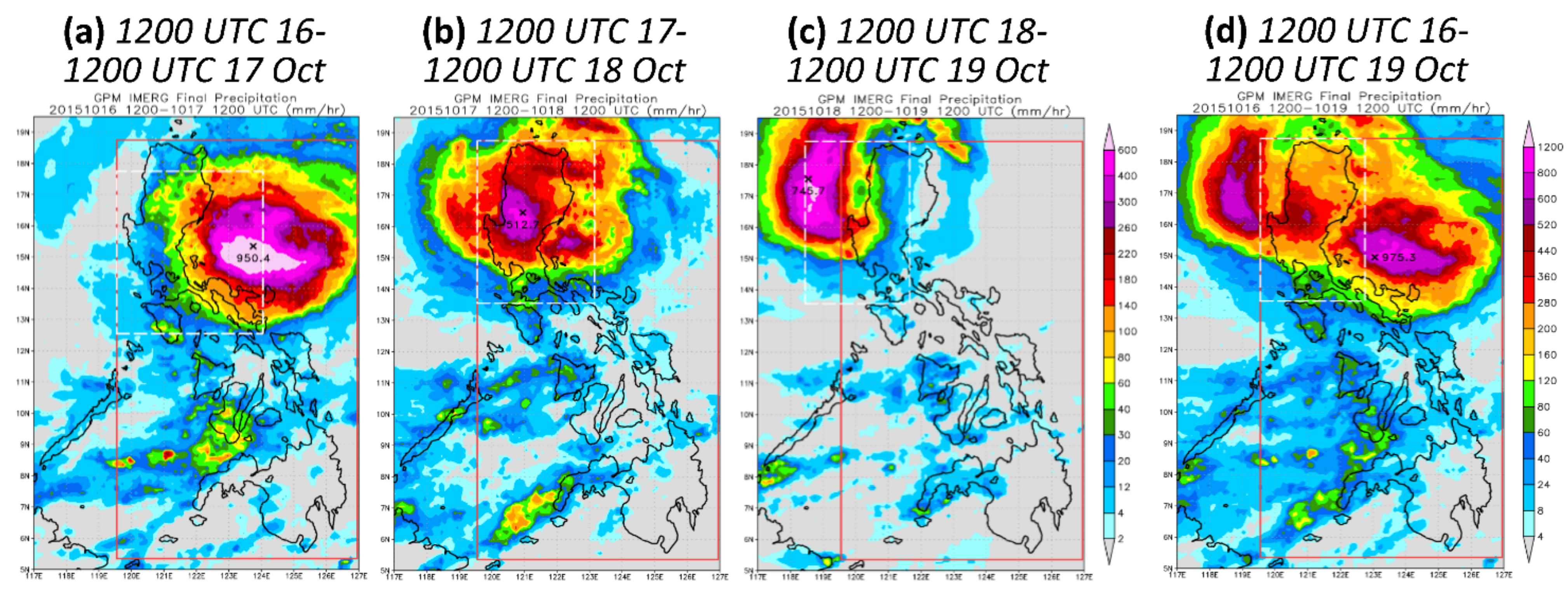
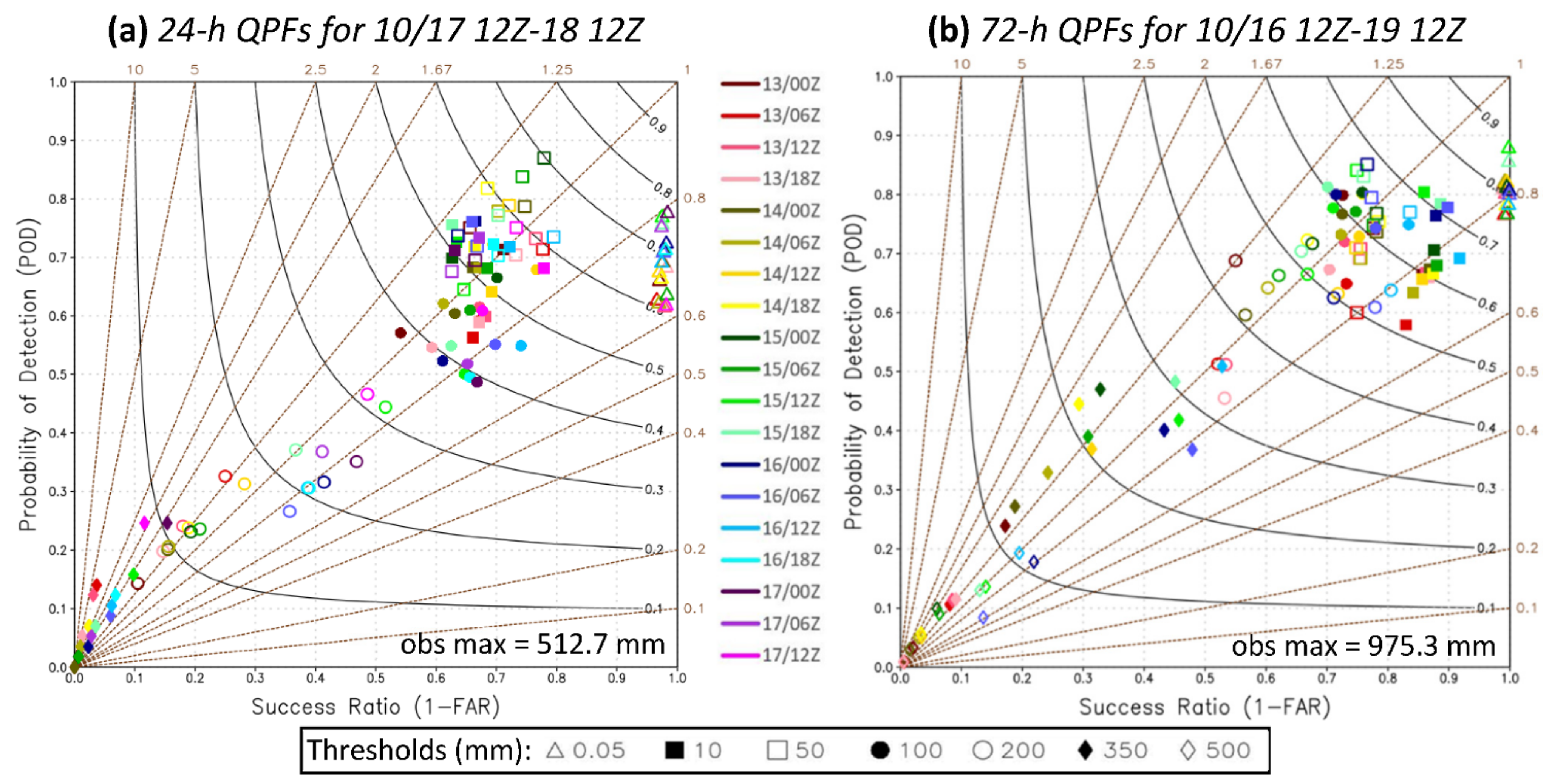
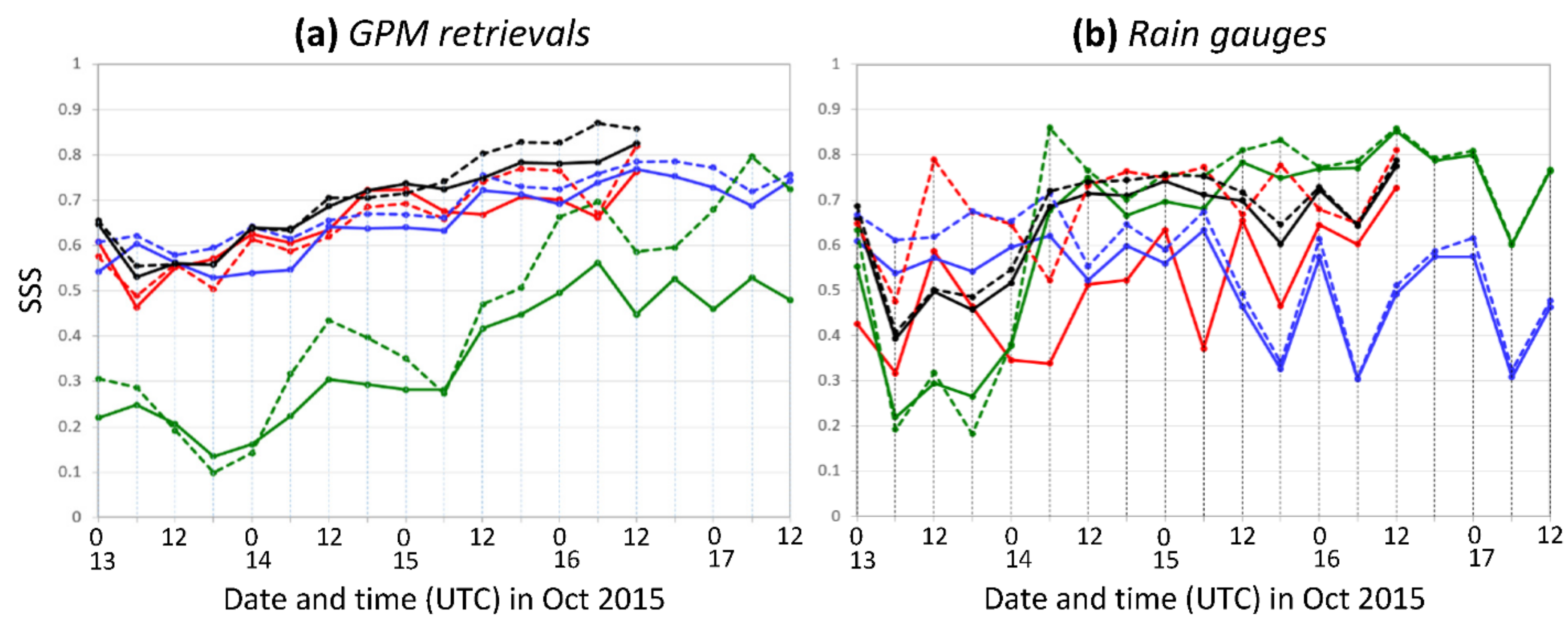
4.4. Objective Skill Scores of QPFs for TY Koppu (2015)
5. Time-Lagged Ensemble QPFs for TY Melor (2015)
5.1. Track and Intensity of TY Melor (2015)
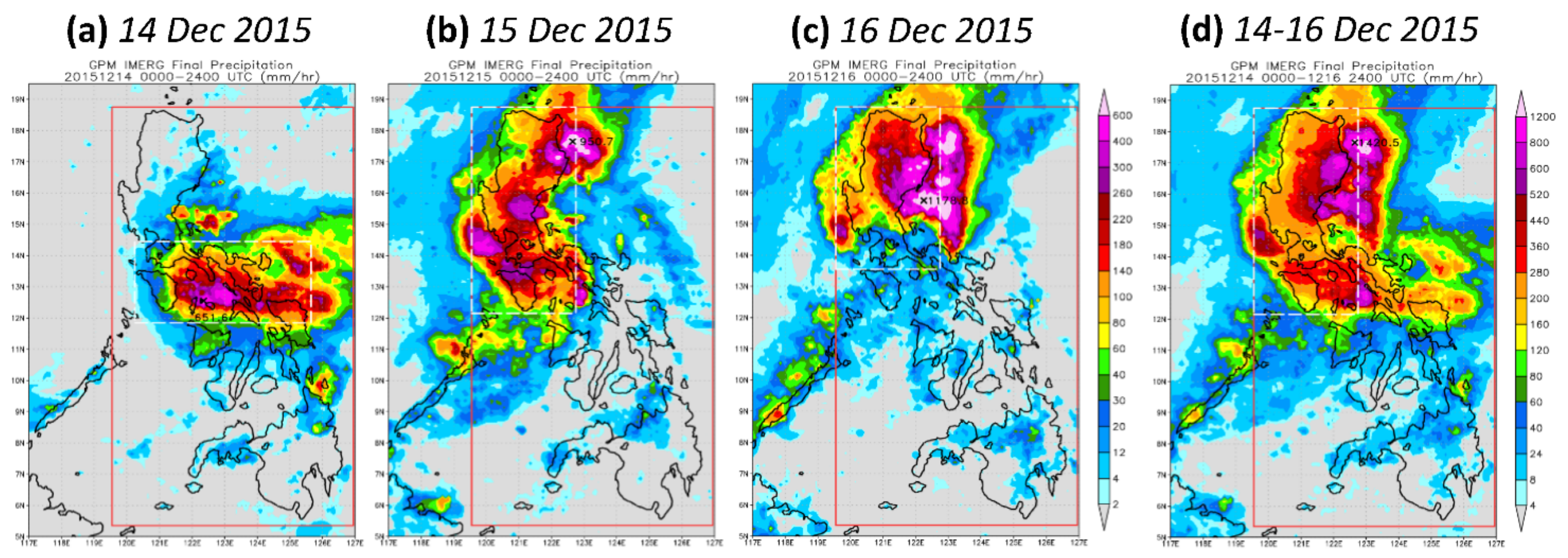
5.2. Observed and Predicted Rainfall of TY Melor (2015)
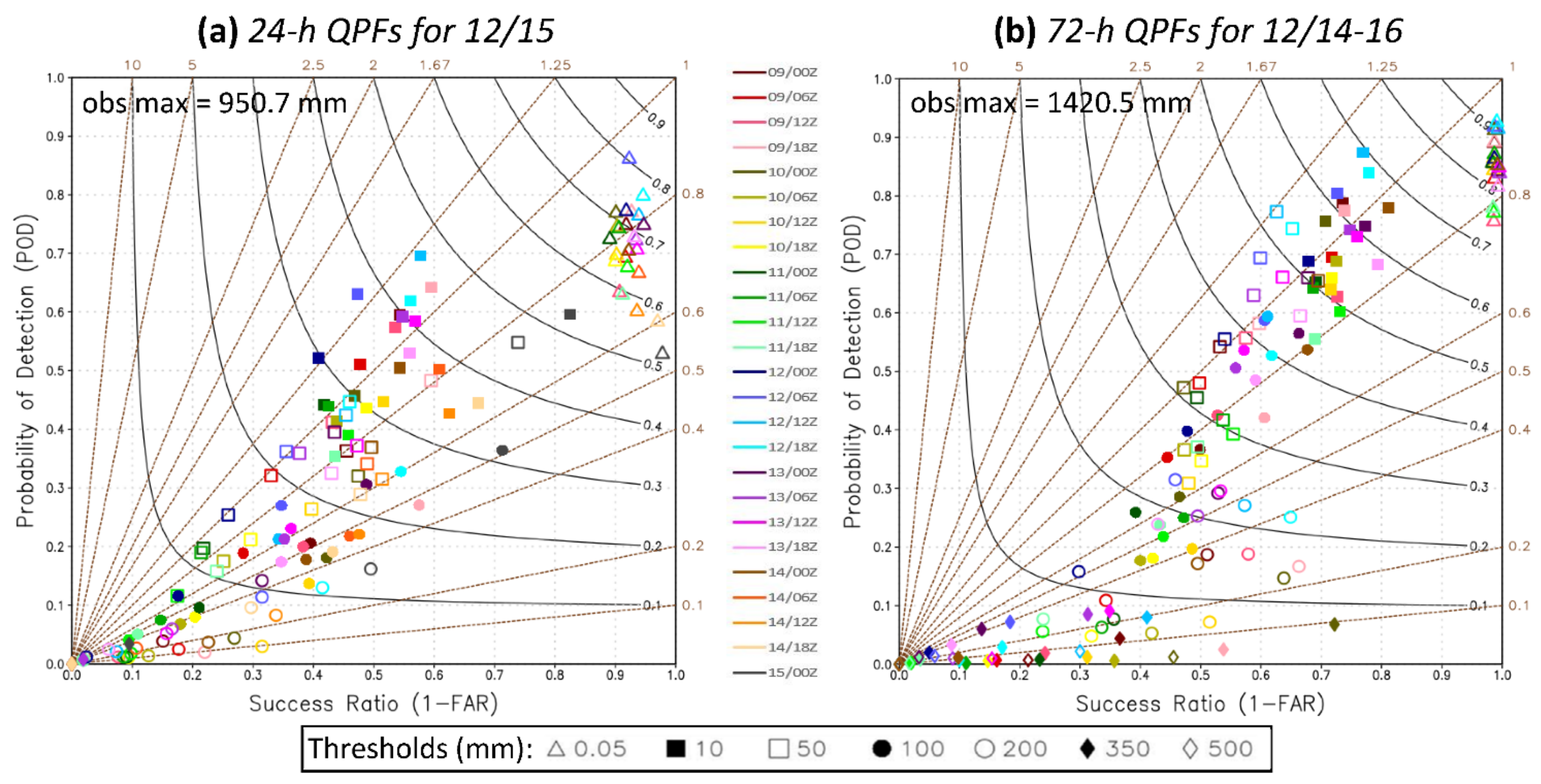
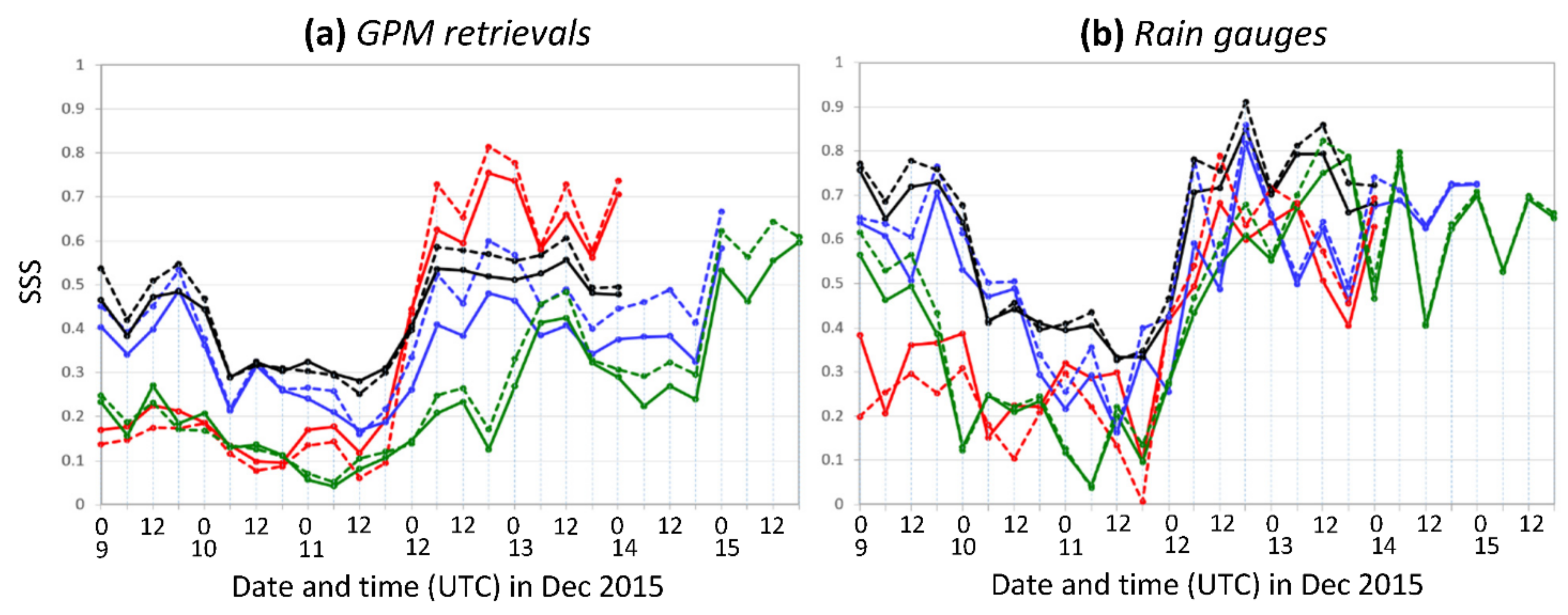
5.3. Heavy Rainfall Probabilities of TY Melor (2015)
5.4. Objective Skill Scores of QPFs for TY Melor (2015)
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Brown, S. The Philippines is the most storm-exposed country on Earth. Time, 11 November 2013. [Google Scholar]
- Wannewitz, S.; Hagenlocher, M.; Garschagen, M. Development and validation of a sub-national multi-hazard risk index for the Philippines. GI_Forum 2016, 1, 133–140. [Google Scholar] [CrossRef]
- Cinco, T.A.; de Guzman, R.G.; Ortiz, A.M.D.; Delfino, R.J.P.; Lasco, R.D.; Hilario, F.D.; Juanillo, E.L.; Barba, R.; Ares, E.D. Observed trends and impacts of tropical cyclones in the Philippines. Int. J. Climatol. 2016, 36, 4638–4650. [Google Scholar] [CrossRef]
- Guha-Sapir, D.; Hoyois, P.; Wallemacq, P.; Below, P. Annual Disaster Statistical Review 2016. The Numbers and Trends; Centre for Research on the Epidemiology of Disasters (CRED), Institute of Health and Society (IRSS), and Université Catholique de Louvain: Brussels, Belgium, 2017; 80p, Available online: https://www.emdat.be/sites/default/files/adsr_2016.pdf (accessed on 20 June 2022).
- NDRRMC (National Disaster Risk Reduction and Management Council). Effects of Typhoon “Yolanda” (Haiyan). SitRep. 108; NDRRMCL: Quezon City, Philippines, 2014; 67p. Available online: https://www.ndrrmc.gov.ph/attachments/article/1329/Effects_of_Typhoon_YOLANDA_(HAIYAN)_SitRep_No_108_03APR2014.pdf (accessed on 7 April 2020).
- Soria, J.L.A.; Switzer, A.D.; Villanoy, C.L.; Fritz, H.M.; Bilgera, P.H.T.; Cabrera, O.C.; Siringan, F.P.; Maria, Y.Y.S.; Ramos, R.D.; Fernandez, I.Q. Repeat storm surge disasters of Typhoon Haiyan and its 1897 predecessor in the Philippines. Bull. Am. Meteorol. Soc. 2016, 97, 31–48. [Google Scholar] [CrossRef]
- Wang, C.-C.; Lee, C.-Y.; Jou, B.J.-D.; Celebre, C.P.; David, S.; Tsuboki, K. High-resolution time-lagged ensemble prediction for landfall intensity of Super Typhoon Haiyan (2013) using a cloud-resolving model. Weather Clim. Extrem. 2022, 37, 100473. [Google Scholar] [CrossRef]
- Golding, B.W. Quantitative precipitation forecasting in the UK. J. Hydrol. 2000, 239, 286–305. [Google Scholar] [CrossRef]
- Fritsch, J.M.; Carbone, R.E. Improving quantitative precipitation forecasts in the warm season. A USWRP research and development strategy. Bull. Am. Meteorol. Soc. 2004, 85, 955–965. [Google Scholar] [CrossRef]
- Czajkowski, J.; Villarini, G.; Michel-Kerjan, E.; Smith, J.A. Determining tropical cyclone inland flooding loss on a large scale through a new flood peak ratio-based methodology. Environ. Res. Lett. 2013, 8, 044056. [Google Scholar] [CrossRef]
- Opiso, E.M.; Puno, G.R.; Alburo, J.L.P.; Detalla, A.L. Landslide susceptibility mapping using GIS and FR method along the Cagayan de Oro-Bukidnon-Davao City route corridor, Philippines. KSCE J. Civ. Eng. 2016, 20, 2506–2512. [Google Scholar] [CrossRef]
- Cabrera, J.S.; Lee, H.S. Flood risk assessment for Davao Oriental in the Philippines using geographic information system-based multi-criteria analysis and the maximum entropy model. J. Flood Risk Manag. 2020, 13, e12607. [Google Scholar] [CrossRef]
- Cuo, L.; Pagano, T.C.; Wang, Q.J. A review of quantitative precipitation forecasts and their use in short- to medium-range streamflow forecasting. J. Hydormeteorol. 2011, 12, 713–728. [Google Scholar] [CrossRef]
- Kneis, D.; Abona, C.; Bronsterta, A.; Heistermanna, M. Verification of short-term runoff forecasts for a small Philippine basin (Marikina). Hydrol. Sci. J. 2017, 62, 205–216. [Google Scholar] [CrossRef]
- MacLeod, D.; Easton-Calabria, E.; de Perez, E.C.; Jaime, C. Verification of forecasts for extreme rainfall, tropical cyclones, flood and storm surge over Myanmar and the Philippines. Weather Clim. Extrem. 2021, 33, 100325. [Google Scholar] [CrossRef]
- Yeh, T.-C.; Cayanan, E.O.; Hsiao, L.-F.; Chen, D.-S.; Tsai, Y.-T. A study of the rainfall and structural changes of Typhoon Koppu (2015) over northern Philippines. Terr. Atmos. Ocean. Sci. 2021, 32, 619–632. [Google Scholar] [CrossRef]
- Chang, C.-P.; Yeh, T.-C.; Chen, J.-M. Effects of terrain on the surface structure of typhoons over Taiwan. Mon. Weather Rev. 1993, 121, 734–752. [Google Scholar] [CrossRef]
- Cheung, K.K.W.; Huang, L.-R.; Lee, C.-S. Characteristics of rainfall during tropical cyclone periods in Taiwan. Nat. Hazards Earth Syst. Sci. 2008, 8, 1463–1474. [Google Scholar] [CrossRef]
- Su, S.-H.; Kuo, H.-C.; Hsu, L.-H.; Yang, Y.-T. Temporal and spatial characteristics of typhoon extreme rainfall in Taiwan. J. Meteorol. Soc. Jpn. 2012, 90, 721–736. [Google Scholar] [CrossRef]
- Lee, C.-S.; Huang, L.-R.; Shen, H.-S.; Wang, S.-T. A climatology model for forecasting typhoon rainfall in Taiwan. Nat. Hazards 2006, 37, 87–105. [Google Scholar] [CrossRef]
- Lee, C.-S.; Huang, L.-R.; Chen, D.Y.-C. The modification of the typhoon rainfall climatology model in Taiwan. Nat. Hazards Earth Syst. Sci. 2013, 13, 65–74. [Google Scholar] [CrossRef]
- Hong, J.-S.; Fong, C.-T.; Hsiao, L.-F.; Yu, Y.-C.; Tzeng, C.-Y. Ensemble typhoon quantitative precipitation forecasts model in Taiwan. Weather Forecast. 2015, 30, 217–237. [Google Scholar] [CrossRef]
- Wang, C.-C. The more rain, the better the model performs—The dependency of quantitative precipitation forecast skill on rainfall amount for typhoons in Taiwan. Mon. Weather Rev. 2015, 143, 1723–1748. [Google Scholar] [CrossRef]
- Wang, C.-C.; Chang, C.-S.; Wang, Y.-W.; Huang, C.-C.; Wang, S.-C.; Chen, Y.-S.; Tsuboki, K.; Huang, S.-Y.; Chen, S.-H.; Chuang, P.-Y.; et al. Evaluating quantitative precipitation forecasts using the 2.5 km CReSS model for typhoons in Taiwan: An update through the 2015 season. Atmosphere 2021, 12, 1501. [Google Scholar] [CrossRef]
- Wang, C.-C.; Paul, S.; Huang, S.-Y.; Wang, Y.-W.; Tsuboki, K.; Lee, D.-I.; Lee, J.-S. Typhoon quantitative precipitation forecasts by the 2.5 km CReSS model in Taiwan: Examples and role of topography. Atmosphere 2022, 13, 623. [Google Scholar] [CrossRef]
- Gentry, M.S.; Lackmann, G.M. Sensitivity of simulated tropical cyclone structure and intensity to horizontal resolution. Mon. Weather Rev. 2010, 138, 688–704. [Google Scholar] [CrossRef]
- Hoffman, R.N.; Kalnay, E. Lagged average forecasting, an alternative to Monte Carlo forecasting. Tellus A 1983, 35, 100–118. [Google Scholar] [CrossRef]
- Wang, C.-C.; Huang, S.-Y.; Chen, S.-H.; Chang, C.-S.; Tsuboki, K. Cloud-resolving typhoon rainfall ensemble forecasts for Taiwan with large domain and extended range through time-lagged approach. Weather Forecast. 2016, 31, 151–172. [Google Scholar] [CrossRef]
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Epstein, E.S. Stochastic dynamic prediction. Tellus 1969, 21, 739–759. [Google Scholar] [CrossRef]
- Toth, Z.; Kalnay, E. Ensemble forecasting at NMC: The generation of perturbations. Bull. Am. Meteorol. Soc. 1993, 74, 2317–2330. [Google Scholar] [CrossRef]
- Molteni, F.; Buizza, R.; Palmer, T.N.; Petroliagis, T. The ECMWF Ensemble Prediction System: Methodology and validation. Q. J. R. Meteorol. Soc. 1996, 122, 73–119. [Google Scholar] [CrossRef]
- Roebber, P.J.; Schultz, D.M.; Colle, B.A.; Stensrud, D.J. Toward improved prediction: High-resolution and ensemble modeling systems in operations. Weather Forecast. 2004, 19, 936–949. [Google Scholar] [CrossRef]
- Mittermaier, M.P. Improving short-range high-resolution model precipitation forecast skill using time-lagged ensembles. Q. J. R. Meteorol. Soc. 2007, 133, 1487–1500. [Google Scholar] [CrossRef]
- Lu, C.; Yuan, H.; Schwartz, B.E.; Benjamin, S.G. Short-range numerical weather prediction using time-lagged ensembles. Weather Forecast. 2007, 22, 580–595. [Google Scholar] [CrossRef]
- Yuan, H.; McGinley, J.A.; Schultz, P.J.; Anderson, C.J.; Lu, C. Short-range precipitation forecasts from time-lagged multimodel ensembles during the HMT-West-2006 campaign. J. Hydrometeorol. 2008, 9, 477–491. [Google Scholar] [CrossRef]
- Trilaksono, N.J.; Otsuka, S.; Yoden, S. A time-lagged ensemble simulation on the modulation of precipitation over West Java in January–February 2007. Mon. Weather Rev. 2012, 140, 601–616. [Google Scholar] [CrossRef]
- Wang, C.-C.; Chen, S.-H.; Tsuboki, K.; Huang, S.-Y.; Chang, C.-S. Application of time-lagged ensemble quantitative precipitation forecasts for Typhoon Morakot (2009) in Taiwan by a cloud-resolving model. Atmosphere 2022, 13, 585. [Google Scholar] [CrossRef]
- Chen, S.-H.; Wang, C.-C. Developing objective guidance for the quality of quantitative precipitation forecasts of westward-moving typhoons affecting Taiwan through machine learning. Atmos. Sci. 2022, 50, 78–124, (In Chinese with English Abstract). [Google Scholar]
- Wang, C.-C.; Tsai, C.-H.; Jou, B.J.-D.; David, S.J. Time-lagged ensemble quantitative precipitation forecasts for three landfalling Typhoons in the Philippines using the CReSS model, Part I: Description and verification against rain-gauge observations. Atmosphere 2022, 13, 1193. [Google Scholar] [CrossRef]
- Tsuboki, K.; Sakakibara, A. Large-scale parallel computing of cloud resolving storm simulator. In High Performance Computing; Zima, H.P., Jou, K., Sato, M., Seo, Y., Shimasaki, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2002; pp. 243–259. [Google Scholar]
- Tsuboki, K.; Sakakibara, A. Numerical Prediction of High-Impact Weather Systems. In The Textbook for the Seventeenth IHP Training Course in 2007; Hydrospheric Atmospheric Research Center, Nagoya University, and UNESCO: Nagoya, Japan, 2007; 273p. [Google Scholar]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, R.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM Multisatellite Precipitation Analysis: Quasi-global, multiyear, combined-sensor precipitation estimates at fine scale. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P. CMORPH: A method that produces global precipitation estimates from passive microwave and infrared data at high spatial and temporal resolution. J. Hydrometeorol. 2004, 5, 487–503. [Google Scholar] [CrossRef]
- Ashouri, H.; Hsu, K.; Sorooshian, S.; Braithwaite, D.K.; Knapp, K.R.; Cecil, L.D.; Nelson, B.R.; Prat, O.P. PERSIANN-CDR: Daily precipitation climate data record from multisatellite observations for hydrological and climate studies. Bull. Am. Meteorol. Soc. 2015, 96, 69–83. [Google Scholar] [CrossRef]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The climate hazards infrared precipitation with stations—A new environmental record for monitoring extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef] [PubMed]
- Hsu, J.; Huang, W.-R.; Liu, P.-Y. Performance assessment of GPM-based near-real-time satellite products in depicting diurnal precipitation variation over Taiwan. J. Hydrol. Reg. Stud. 2021, 38, 100957. [Google Scholar] [CrossRef]
- Hsu, J.; Huang, W.-R.; Liu, P.-Y.; Li, X. Validation of CHIRPS precipitation estimates over Taiwan at multiple timescales. Remote Sens. 2021, 13, 254. [Google Scholar] [CrossRef]
- Jamandre, C.A.; Narisma, G.T. Spatio-temporal validation of satellite-based rainfall estimates in the Philippines. Atmos. Res. 2013, 122, 599–608. [Google Scholar] [CrossRef]
- Peralta, J.C.A.C.; Narisma, G.T.T.; Cruz, F.A.T. Validation of high-resolution gridded rainfall datasets for climate applications in the Philippines. J. Hydrometeorol. 2020, 21, 1571–1587. [Google Scholar] [CrossRef]
- Huang, W.-R.; Hsu, J.; Liu, P.-Y.; Deng, L. Multiple satellite-observed long-term changes in the summer diurnal precipitation over Luzon and its adjacent seas during 2000–2019. Int. J. Appl. Earth Obs. Geoinf. 2022, 110, 102816. [Google Scholar] [CrossRef]
- Veloria, A.; Perez, G.J.; Tapang, G.; Comiso, J. Improved rainfall data in the Philippines through concurrent use of GPM IMERG and ground-based measurements. Remote Sens. 2021, 13, 2859. [Google Scholar] [CrossRef]
- Sunilkumar, K.; Yatagai, A.; Masuda, M. Preliminary evaluation of GPM-IMERG rainfall estimates over three distinct climate zones with APHRODITE. Earth Space Sci. 2019, 6, 1321–1335. [Google Scholar] [CrossRef]
- Liu, Z.; Ostrenga, D.; Teng, W.; Kempler, S. Tropical Rainfall Measuring Mission (TRMM) precipitation data and services for research and applications. Bull. Am. Meteorol. Soc. 2012, 93, 1317–1325. [Google Scholar] [CrossRef]
- Chen, S.; Hong, Y.; Cao, Q.; Kirstetter, P.-E.; Gourley, J.J.; Qi, Y.; Zhang, J.; Howard, K.; Hu, J.; Wang, J. Performance evaluation of radar and satellite rainfalls for Typhoon Morakot over Taiwan: Are remote-sensing products ready for gauge denial scenario of extreme events? J. Hydrol. 2013, 506, 4–13. [Google Scholar] [CrossRef]
- Zhou, Y.; Lau, W.K.-M.; Huffman, G.J. Mapping TRMM TMPA into average recurrence interval for monitoring extreme precipitation events. J. Appl. Meteorol. Climatol. 2015, 54, 979–995. [Google Scholar] [CrossRef]
- Hou, A.Y.; Kakar, R.K.; Neeck, S.; Azarbarzin, A.A.; Kummerow, C.D.; Kojima, M.; Oki, R.; Nakamura, K.; Iguchi, T. The Global Precipitation Measurement Mission. Bull. Am. Meteorol. Soc. 2014, 95, 701–722. [Google Scholar] [CrossRef]
- Kubota, T.; Aonashi, K.; Ushio, T.; Shige, S.; Takayabu, Y.N.; Kachi, M.; Arai, Y.; Tashima, T.; Masaki, T.; Kawamoto, N.; et al. Global Satellite Mapping of Precipitation (GSMaP) products in the GPM era. In Satellite Precipitation Measurement. Advances in Global Change Research; Levizzani, V., Kidd, C., Kirschbaum, D., Kummerow, C., Nakamura, K., Turk, F., Eds.; Springer: Cham, Switzerland, 2020; Volume 67, pp. 355–373. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.; Joyce, R.; Kidd, C.; Nelkin, E.J.; Sorooshian, S.; Tan, J.; Xie, P. Algorithm Theoretical Basis Document (ATBD) Version 06: NASA Global Precipitation Measurement (GPM) Integrated Multi-Satellite Retrievals for GPM (IMERG); NASA/GSFC: Greenbelt, MD, USA, 2020. Available online: https://gpm.nasa.gov/sites/default/files/2020–05/IMERG_ATBD_V06.3.pdf (accessed on 1 August 2019).
- Da Silva, N.A.; Webber, B.G.M.; Matthews, A.J.; Feist, M.M.; Stein, T.H.M.; Holloway, C.E.; Abdullah, M.F.A.B. Validation of GPM IMERG extreme precipitation in the Maritime Continent by station and radar data. Earth Space Sci. 2021, 8, e2021EA001738. [Google Scholar] [CrossRef]
- Lin, Y.-L.; Farley, R.D.; Orville, H.D. Bulk parameterization of the snow field in a cloud model. J. Clim. Appl. Meteorol. 1983, 22, 1065–1092. [Google Scholar] [CrossRef]
- Cotton, W.R.; Tripoli, G.J.; Rauber, R.M.; Mulvihill, E.A. Numerical simulation of the effects of varying ice crystal nucleation rates and aggregation processes on orographic snowfall. J. Clim. Appl. Meteorol. 1986, 25, 1658–1680. [Google Scholar] [CrossRef]
- Murakami, M. Numerical modeling of dynamical and microphysical evolution of an isolated convective cloud—The 19 July 1981 CCOPE cloud. J. Meteorol. Soc. Jpn. 1990, 68, 107–128. [Google Scholar] [CrossRef]
- Ikawa, M.; Saito, K. Description of a nonhydrostatic model developed at the Forecast Research Department of the MRI. MRI Tech. Rep. 1991, 28, 238. [Google Scholar]
- Murakami, M.; Clark, T.L.; Hall, W.D. Numerical simulations of convective snow clouds over the Sea of Japan: Two-dimensional simulation of mixed layer development and convective snow cloud formation. J. Meteorol. Soc. Jpn. 1994, 72, 43–62. [Google Scholar] [CrossRef]
- Deardorff, J.W. Stratocumulus-capped mixed layers derived from a three-dimensional model. Bound.-Layer Meteorol. 1980, 18, 495–527. [Google Scholar] [CrossRef]
- Louis, J.F.; Tiedtke, M.; Geleyn, J.F. A short history of the operational PBL parameterization at ECMWF. In Proceedings of the Workshop on Planetary Boundary Layer Parameterization, Reading, UK, 25–27 November 1981; ECMWF: Reading, UK, 1982; pp. 59–79. [Google Scholar]
- Kondo, J. Heat balance of the China Sea during the air mass transformation experiment. J. Meteorol. Soc. Jpn. 1976, 54, 382–398. [Google Scholar] [CrossRef]
- Segami, A.; Kurihara, K.; Nakamura, H.; Ueno, M.; Takano, I.; Tatsumi, Y. Operational mesoscale weather prediction with Japan Spectral Model. J. Meteorol. Soc. Jpn. 1989, 67, 907–924. [Google Scholar] [CrossRef]
- Kanamitsu, M. Description of the NMC global data assimilation and forecast system. Weather Forecast. 1989, 4, 335–342. [Google Scholar] [CrossRef]
- Kleist, D.T.; Parrish, D.F.; Derber, J.C.; Treadon, R.; Wu, W.S.; Lord, S. Introduction of the GSI into the NCEP global data assimilation system. Weather Forecast. 2009, 24, 1691–1705. [Google Scholar] [CrossRef]
- Schaefer, J.T. The critical success index as an indicator of warning skill. Weather Forecast. 1990, 5, 570–575. [Google Scholar] [CrossRef]
- Mason, I.B. Binary events. In Forecast Verification—A Practitioner’s Guide in Atmospheric Science; Jolliffe, I.T., Stephenson, D.B., Eds.; Wiley and Sons: West Sussex, UK, 2003; pp. 37–76. [Google Scholar]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences, 3rd ed.; Academic Press: Cambridge, MA, USA, 2011; 704p, ISBN 9780123850225. [Google Scholar]
- Roebber, P.J. Visualizing multiple measures of forecast quality. Weather Forecast. 2009, 24, 601–608. [Google Scholar] [CrossRef]
- Racoma, B.A.B.; David, C.P.C.; Crisologo, I.A.; Bagtasa, G. The change in rainfall from tropical cyclones due to orographic effect of the Sierra Madre Mountain Range in Luzon, Philippines. Philipp. J. Sci. 2016, 145, 313–326. [Google Scholar]
- Fang, X.; Kuo, Y.-H. Improving ensemble-based quantitative precipitation forecasts for topography-enhanced typhoon heavy rainfall over Taiwan with a modified probability-matching technique. Mon. Weather Rev. 2013, 141, 3908–3932. [Google Scholar] [CrossRef][Green Version]
- Ferrett, S.; Frame, T.H.A.; Methven, J.; Holloway, C.E.; Webster, S.; Stein, T.H.M.; Cafaro, C. Evaluating convection-permitting ensemble forecasts of precipitation over Southeast Asia. Weather Forecast. 2021, 36, 1199–1217. [Google Scholar] [CrossRef]




| Map projection | Lambert conformal (center at 123°E, secant at 5°N and 20°N) |
| Grid spacing (km) | 2.5 × 2.5 × 0.1–0.5695 (0.4) * |
| Grid dimension (x, y, z) | 864 × 696 × 50 |
| Domain size (km) | 2160 × 1740 × 20 |
| Forecast frequency | Every 6 h (at 0000, 0600, 1200, and 1800 UTC) |
| Forecast length | 8 days (192 h) |
| IC/BCs | NCEP GFS 0.5° × 0.5° analyses and forecasts (26 levels) |
| Cloud microphysics | Double-moment bulk cold-rain scheme |
| PBL parameterization | 1.5-order closure with turbulent kinetic energy prediction |
| Surface processes | Shortwave/longwave radiation and momentum/energy fluxes |
| Soil model | 43 levels, every 5 cm to 2.1 m in depth |
| Mangkhut | Against GPM | Against Rain Gauges | ||||||
|---|---|---|---|---|---|---|---|---|
| 24 h QPFs | Obs. Max | Threshold (mm) | Obs. Max | Threshold (mm) | ||||
| (mm) | 50 | 100 | 200 | (mm) | 50 | 100 | 200 | |
| t0 within 48 h (7) | ||||||||
| Mean TS | 337.9 | 0.39 | 0.39 | 0.12 | 535.6 | 0.30 | 0.42 | 0.21 |
| Range of TS | 0.08 | 0.13 | 0.09 | 0.13 | 0.46 | 1.00 | ||
| t0 beyond 48 h (12) | ||||||||
| Mean TS | 337.9 | 0.24 | 0.22 | 0.04 | 535.6 | 0.18 | 0.12 | 0.00 |
| Range of TS | 0.24 | 0.34 | 0.12 | 0.30 | 0.17 | 0.00 | ||
| 48 h QPFs | Obs. Max. | Threshold (mm) | Obs. Max. | Threshold (mm) | ||||
| (mm) | 100 | 200 | 350 | (mm) | 100 | 200 | 350 | |
| t0 within 48 h (9) | ||||||||
| Mean TS | 455.2 | 0.72 | 0.36 | 0.02 | 785.8 | 0.29 | 0.27 | 0.00 |
| Range of TS | 0.10 | 0.05 | 0.02 | 0.20 | 0.34 | 0.00 | ||
| t0 beyond 48 h (8) | ||||||||
| Mean TS | 455.2 | 0.43 | 0.18 | 0.01 | 785.8 | 0.15 | 0.12 | 0.00 |
| Range of TS | 0.29 | 0.20 | 0.02 | 0.21 | 0.29 | 0.00 | ||
| Koppu | Against GPM | Against Rain Gauges | ||||||
|---|---|---|---|---|---|---|---|---|
| 24 h QPFs | Obs. Max. | Threshold (mm) | Obs. Max. | Threshold (mm) | ||||
| Second period | (mm) | 10 | 50 | 100 | (mm) | 10 | 50 | 100 |
| t0 within 48 h (9) | ||||||||
| Mean TS | 512.7 | 0.54 | 0.54 | 0.42 | 188.8 | 0.53 | 0.24 | 0.11 |
| Range of TS | 0.07 | 0.14 | 0.08 | 0.20 | 0.12 | 0.18 | ||
| t0 beyond 48 h (10) | ||||||||
| Mean TS | 512.7 | 0.50 | 0.60 | 0.47 | 188.8 | 0.47 | 0.29 | 0.18 |
| Range of TS | 0.12 | 0.16 | 0.18 | 0.08 | 0.13 | 0.15 | ||
| 24 h QPFs | Obs. Max. | Threshold (mm) | Obs. Max. | Threshold (mm) | ||||
| Third period | (mm) | 100 | 200 | 350 | (mm) | 100 | 200 | 350 |
| t0 within 48 h (5) | ||||||||
| Mean TS | 400.0 # | 0.26 | 0.10 | 0.01 | 502.3 | 0.36 | 0.28 | 0.40 |
| Range of TS | 0.10 | 0.06 | 0.04 | 0.14 | 0.50 | 1.00 | ||
| t0 beyond 48 h (14) | ||||||||
| Mean TS | 400.0 # | 0.16 | 0.05 | 0.00 | 502.3 | 0.21 | 0.24 | 0.46 |
| Range of TS | 0.21 | 0.14 | 0.04 | 0.32 | 0.50 | 1.00 | ||
| 72 h QPFs | Obs. Max. | Threshold (mm) | Obs. Max. | Threshold (mm) | ||||
| (mm) | 200 | 350 | 500 | (mm) | 200 | 350 | 500 | |
| t0 within 48 h (9) | ||||||||
| Mean TS | 975.3 | 0.52 | 0.26 | 0.06 | 695.3 | 0.27 | 0.28 | 0.72 |
| Range of TS | 0.08 | 0.15 | 0.09 | 0.12 | 0.13 | 1.00 | ||
| t0 beyond 48 h (6) | ||||||||
| Mean TS | 975.3 | 0.39 | 0.09 | 0.01 | 695.3 | 0.21 | 0.13 | 0.06 |
| Range of TS | 0.13 | 0.11 | 0.02 | 0.13 | 0.33 | 0.33 | ||
| Melor | Against GPM | Against Rain Gauges | ||||||
|---|---|---|---|---|---|---|---|---|
| 24 h QPFs | Obs. Max. | Threshold (mm) | Obs. Max. | Threshold (mm) | ||||
| (mm) | 50 | 100 | 200 | (mm) | 50 | 100 | 200 | |
| t0 within 48 h (9) | ||||||||
| Mean TS | 950.7 | 0.18 | 0.06 | 0.00 | 209.2 | 0.46 | 0.3 | 0.12 |
| Range of TS | 0.19 | 0.12 | 0.03 | 0.29 | 0.39 | 1.00 | ||
| t0 beyond 48 h (16) | ||||||||
| Mean TS | 950.7 | 0.12 | 0.03 | 0.00 | 209.2 | 0.24 | 0.10 | 0.03 |
| Range of TS | 0.23 | 0.10 | 0.00 | 0.36 | 0.67 | 0.33 | ||
| 72 h QPFs | Obs. Max. | Threshold (mm) | Obs. Max. | Threshold (mm) | ||||
| (mm) | 100 | 200 | 350 | (mm) | 100 | 200 | 350 | |
| t0 within 48 h (9) | ||||||||
| Mean TS | 1420.5 | 0.39 | 0.20 | 0.04 | 407 | 0.48 | 0.32 | 0.08 |
| Range of TS | 0.16 | 0.12 | 0.07 | 0.35 | 0.58 | 0.33 | ||
| t0 beyond 48 h (12) | ||||||||
| Mean TS | 1420.5 | 0.21 | 0.09 | 0.02 | 407 | 0.22 | 0.11 | 0.00 |
| Range of TS | 0.19 | 0.12 | 0.06 | 0.32 | 0.31 | 0.00 | ||
| Forecast Range | Against GPM | Against Rain Gauges | ||||||
|---|---|---|---|---|---|---|---|---|
| 24 h QPFs | Obs. Max. | SSS values | Obs. Max. | SSS values | ||||
| Typhoon/period | (mm) | Mean | Median | Range | (mm) | Mean | Median | Range |
| t0 within 48 h | ||||||||
| Mangkhut, P1 (9) | 451.5 | 0.830 | 0.820 | 0.055 | 209.2 | 0.728 | 0.762 | 0.160 |
| Mangkhut, P2 (7) | 337.9 | 0.821 | 0.813 | 0.033 | 535.6 | 0.558 | 0.574 | 0.273 |
| Koppu, P1 (9) | 950.4 | 0.713 | 0.692 | 0.201 | 109.6 | 0.733 | 0.712 | 0.162 |
| Koppu, P2 (9) | 512.7 | 0.754 | 0.756 | 0.067 | 188.8 | 0.474 | 0.493 | 0.311 |
| Koppu, P3 (5) | 400.0 # | 0.676 | 0.679 | 0.209 | 502.3 | 0.767 | 0.792 | 0.254 |
| Melor, P1 (9) | 651.6 | 0.671 | 0.728 | 0.380 | 169.6 | 0.612 | 0.631 | 0.367 |
| Melor, P2 (9) | 950.7 | 0.488 | 0.461 | 0.265 | 209.2 | 0.649 | 0.657 | 0.248 |
| Melor, P3 (8) | 1178.8 | 0.457 | 0.444 | 0.352 | 273.8 | 0.618 | 0.647 | 0.388 |
| t0 beyond 48 h | ||||||||
| Mangkhut, P1 (8) | 451.5 | 0.634 | 0.695 | 0.382 | 209.2 | 0.591 | 0.575 | 0.346 |
| Mangkhut, P2 (12) | 337.9 | 0.634 | 0.622 | 0.296 | 535.6 | 0.321 | 0.291 | 0.237 |
| Koppu, P1 (6) | 950.4 | 0.555 | 0.567 | 0.124 | 109.6 | 0.626 | 0.647 | 0.313 |
| Koppu, P2 (10) | 512.7 | 0.631 | 0.631 | 0.091 | 188.8 | 0.641 | 0.649 | 0.162 |
| Koppu, P3 (14) | 400.0 # | 0.367 | 0.334 | 0.597 | 502.3 | 0.625 | 0.756 | 0.678 |
| Melor, P1 (12) | 651.6 | 0.128 | 0.136 | 0.125 | 169.6 | 0.208 | 0.215 | 0.303 |
| Melor, P2 (16) | 950.7 | 0.364 | 0.356 | 0.441 | 209.2 | 0.523 | 0.517 | 0.696 |
| Melor, P3 (20) | 1178.8 | 0.207 | 0.171 | 0.432 | 273.8 | 0.419 | 0.451 | 0.787 |
| 48/72 h QPFs | Obs. Max. | SSS values | Obs. Max. | SSS values | ||||
| Typhoon | (mm) | Mean | Median | Range | (mm) | Mean | Median | Range |
| t0 within 48 h | ||||||||
| Mangkhut (9) | 455.2 | 0.852 | 0.855 | 0.042 | 785.8 | 0.605 | 0.585 | 0.240 |
| Koppu (9) | 975.3 | 0.754 | 0.749 | 0.138 | 695.3 | 0.702 | 0.712 | 0.171 |
| Melor (9) | 1420.5 | 0.505 | 0.519 | 0.151 | 407.0 | 0.703 | 0.706 | 0.424 |
| t0 beyond 48 h | ||||||||
| Mangkhut (8) | 455.2 | 0.705 | 0.738 | 0.152 | 785.8 | 0.427 | 0.364 | 0.204 |
| Koppu (6) | 975.3 | 0.595 | 0.599 | 0.117 | 695.3 | 0.535 | 0.507 | 0.292 |
| Melor (12) | 1420.5 | 0.365 | 0.325 | 0.204 | 407.0 | 0.519 | 0.429 | 0.423 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.-C.; Tsai, C.-H.; Jou, B.J.-D.; David, S.J.; Pura, A.G.; Lee, D.-I.; Tsuboki, K.; Lee, J.-S. Time-Lagged Ensemble Quantitative Precipitation Forecasts for Three Landfalling Typhoons in the Philippines Using the CReSS Model, Part II: Verification Using Global Precipitation Measurement Retrievals. Remote Sens. 2022, 14, 5126. https://doi.org/10.3390/rs14205126
Wang C-C, Tsai C-H, Jou BJ-D, David SJ, Pura AG, Lee D-I, Tsuboki K, Lee J-S. Time-Lagged Ensemble Quantitative Precipitation Forecasts for Three Landfalling Typhoons in the Philippines Using the CReSS Model, Part II: Verification Using Global Precipitation Measurement Retrievals. Remote Sensing. 2022; 14(20):5126. https://doi.org/10.3390/rs14205126
Chicago/Turabian StyleWang, Chung-Chieh, Chien-Hung Tsai, Ben Jong-Dao Jou, Shirley J. David, Alvin G. Pura, Dong-In Lee, Kazuhisa Tsuboki, and Ji-Sun Lee. 2022. "Time-Lagged Ensemble Quantitative Precipitation Forecasts for Three Landfalling Typhoons in the Philippines Using the CReSS Model, Part II: Verification Using Global Precipitation Measurement Retrievals" Remote Sensing 14, no. 20: 5126. https://doi.org/10.3390/rs14205126
APA StyleWang, C.-C., Tsai, C.-H., Jou, B. J.-D., David, S. J., Pura, A. G., Lee, D.-I., Tsuboki, K., & Lee, J.-S. (2022). Time-Lagged Ensemble Quantitative Precipitation Forecasts for Three Landfalling Typhoons in the Philippines Using the CReSS Model, Part II: Verification Using Global Precipitation Measurement Retrievals. Remote Sensing, 14(20), 5126. https://doi.org/10.3390/rs14205126








