Rice Crop Height Inversion from TanDEM-X PolInSAR Data Using the RVoG Model Combined with the Logistic Growth Equation
Abstract
1. Introduction
2. Materials
2.1. Test Site and Ground-Truth Data
2.2. TanDEM-X Data and InSAR Processing
3. Methodology
3.1. RVoG Model Combined with the Logistic Growth Equation
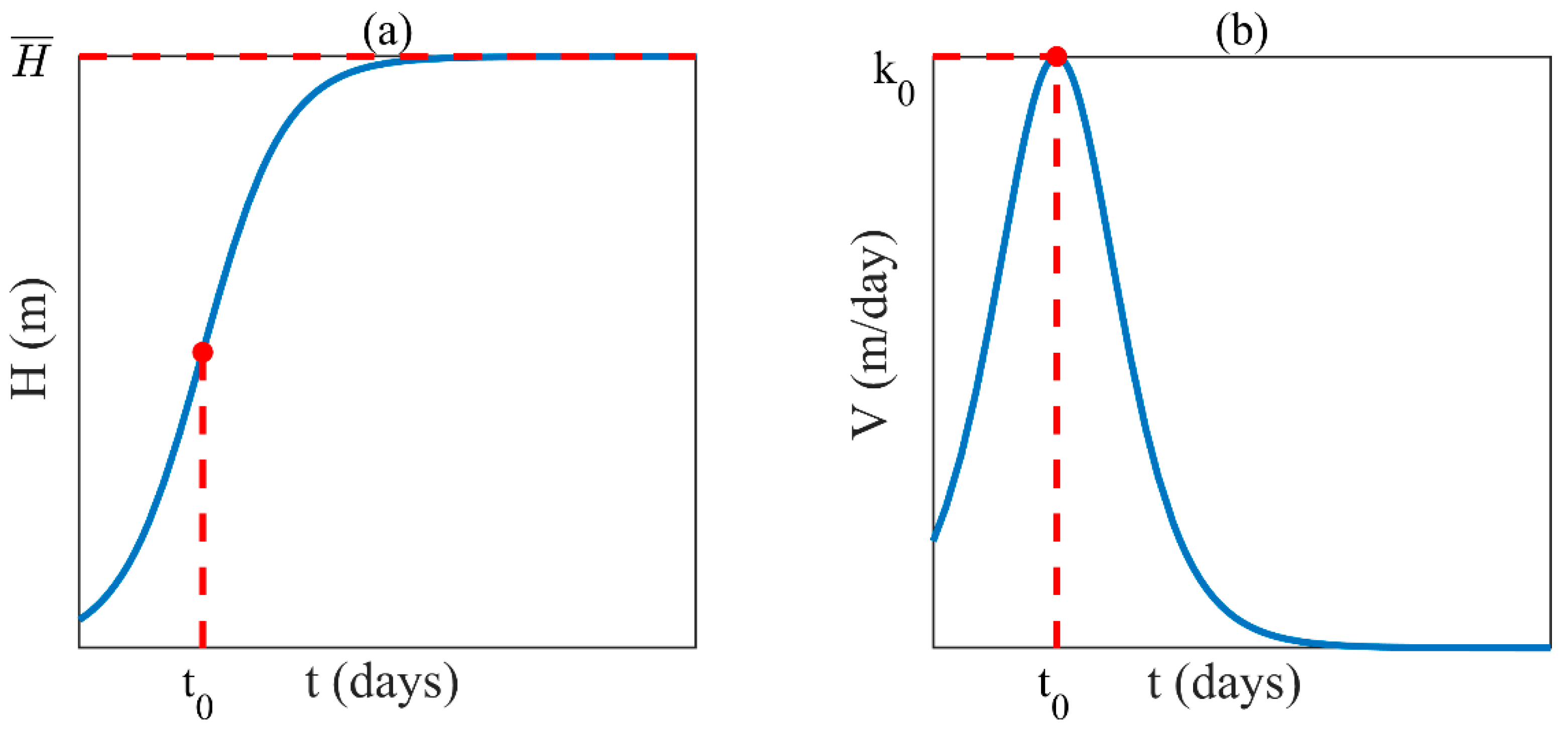
3.1.1. Logistic Growth Equation
3.1.2. The Modified RVoG Model
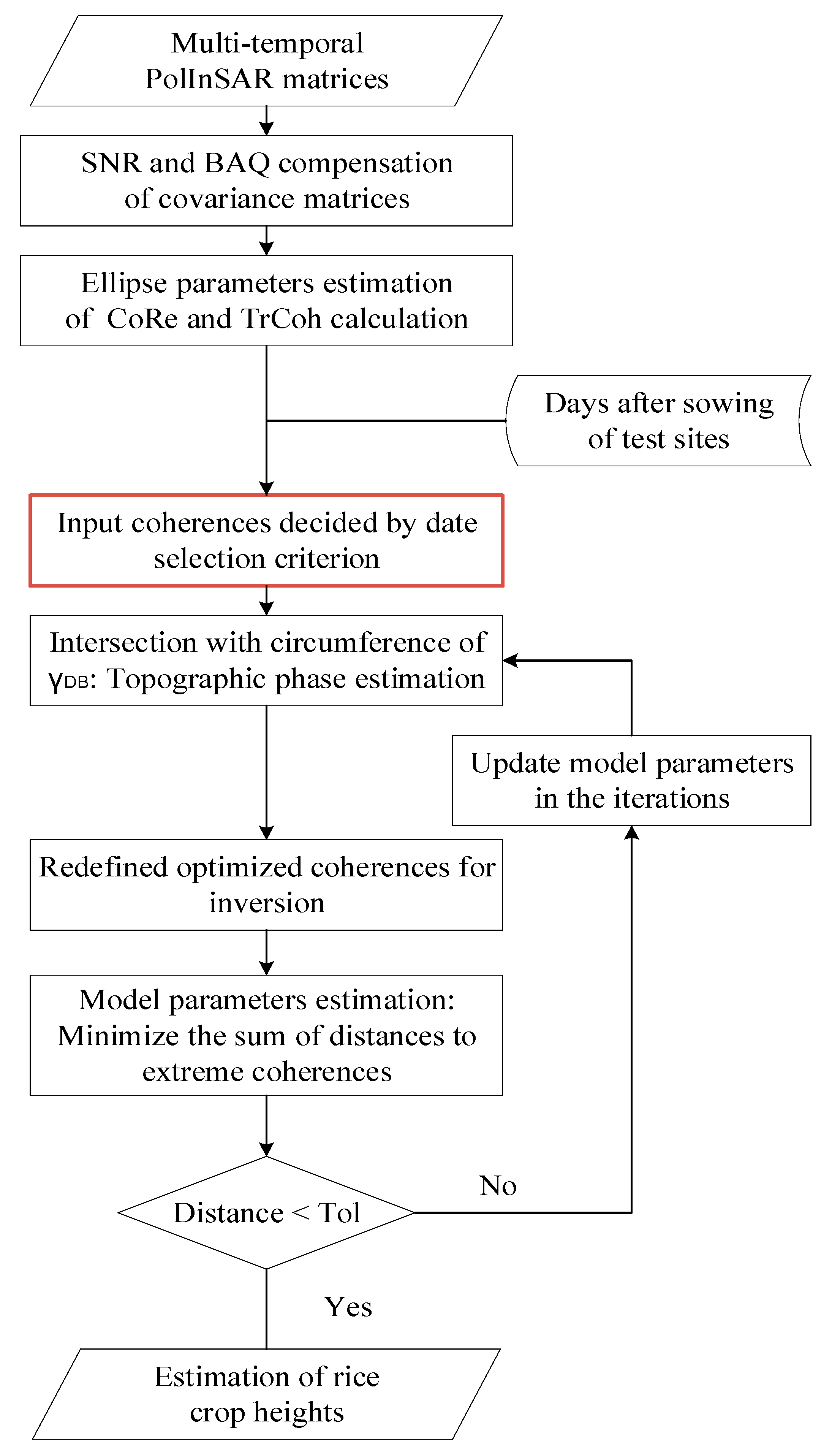
3.2. Inversion Scheme for Crop Height from TanDEM-X PolInSAR Data
3.2.1. Compensation of the SNR and BAQ Decorrelation of the Covariance Matrix
3.2.2. Calculation of the TrCoh and Estimation of the Two Coherences with Maximum Phase Separation
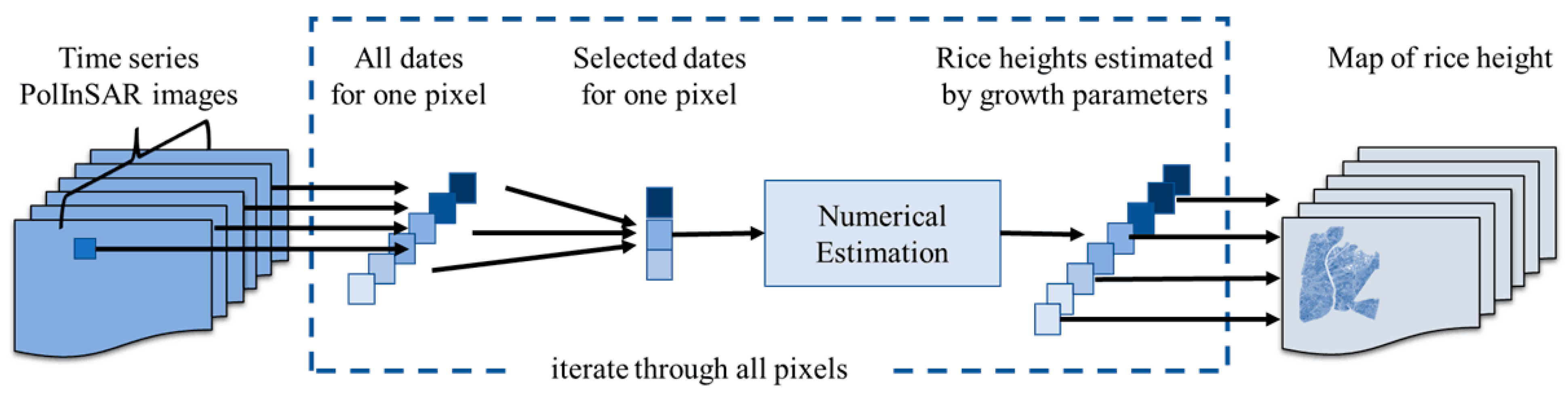
3.2.3. Determination of the Input Observations used for Inversion
3.2.4. Numerical Estimation of the Unknown Parameters
4. Results and Analysis
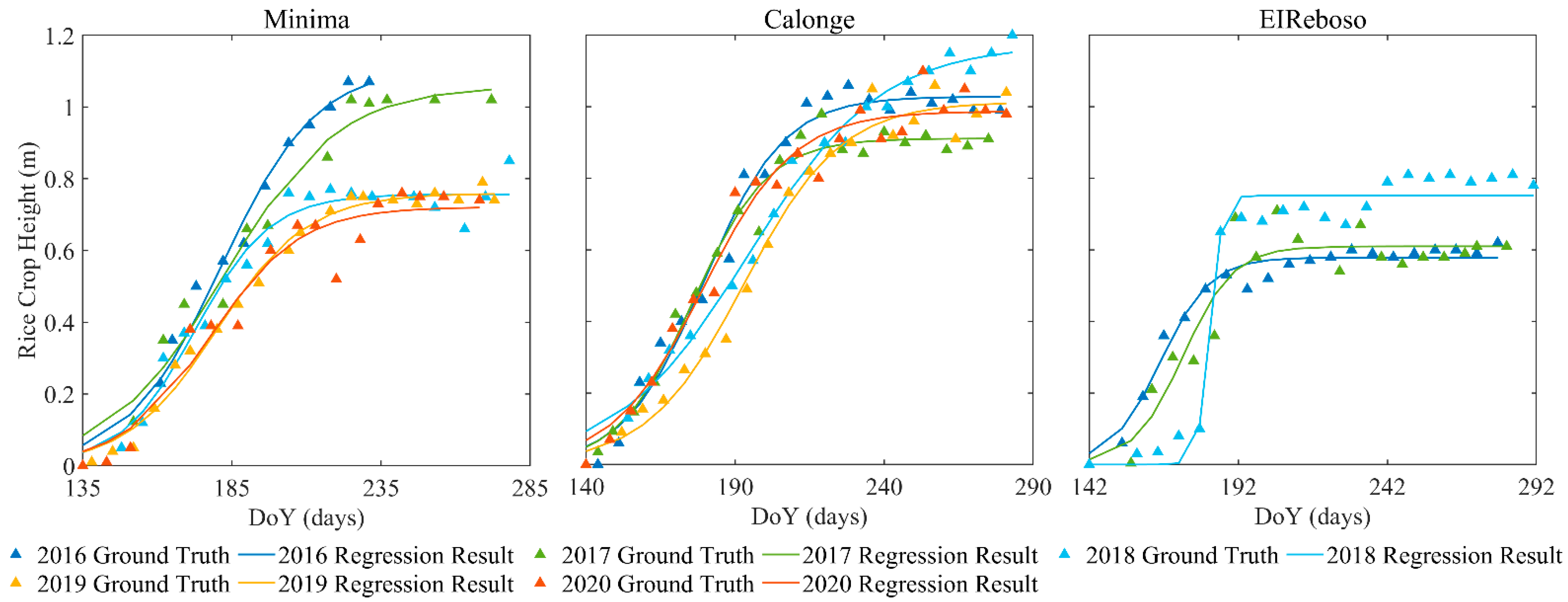
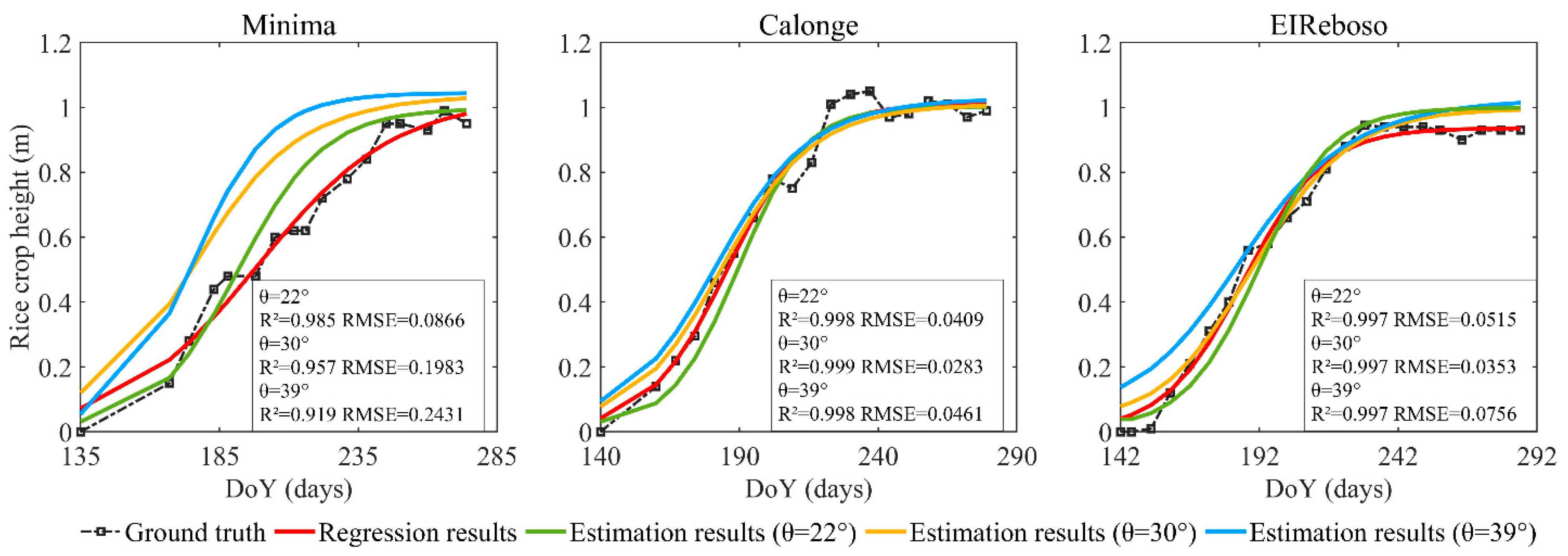
4.1. Feasibility Analysis of the Logistic Growth Equation
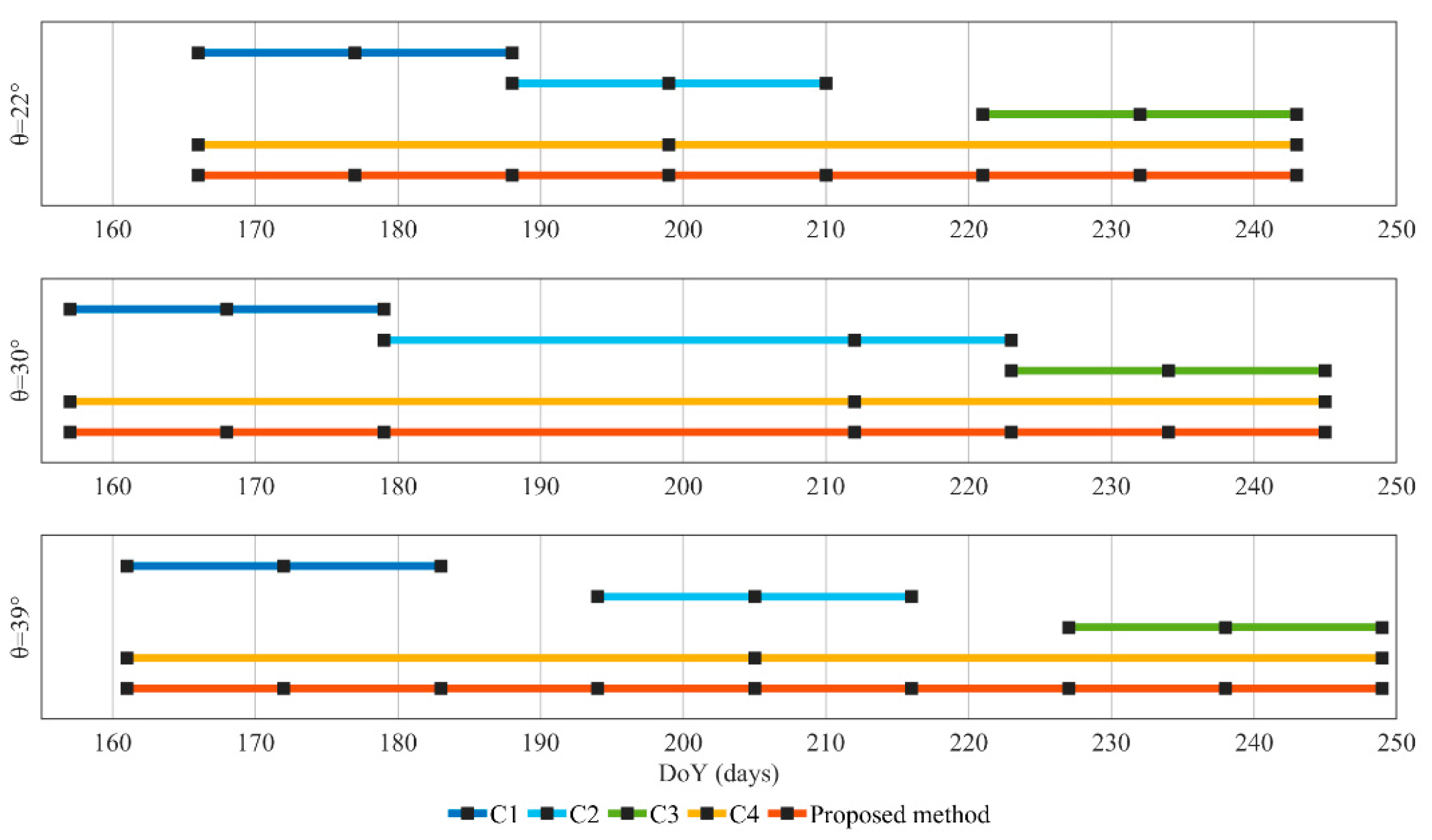
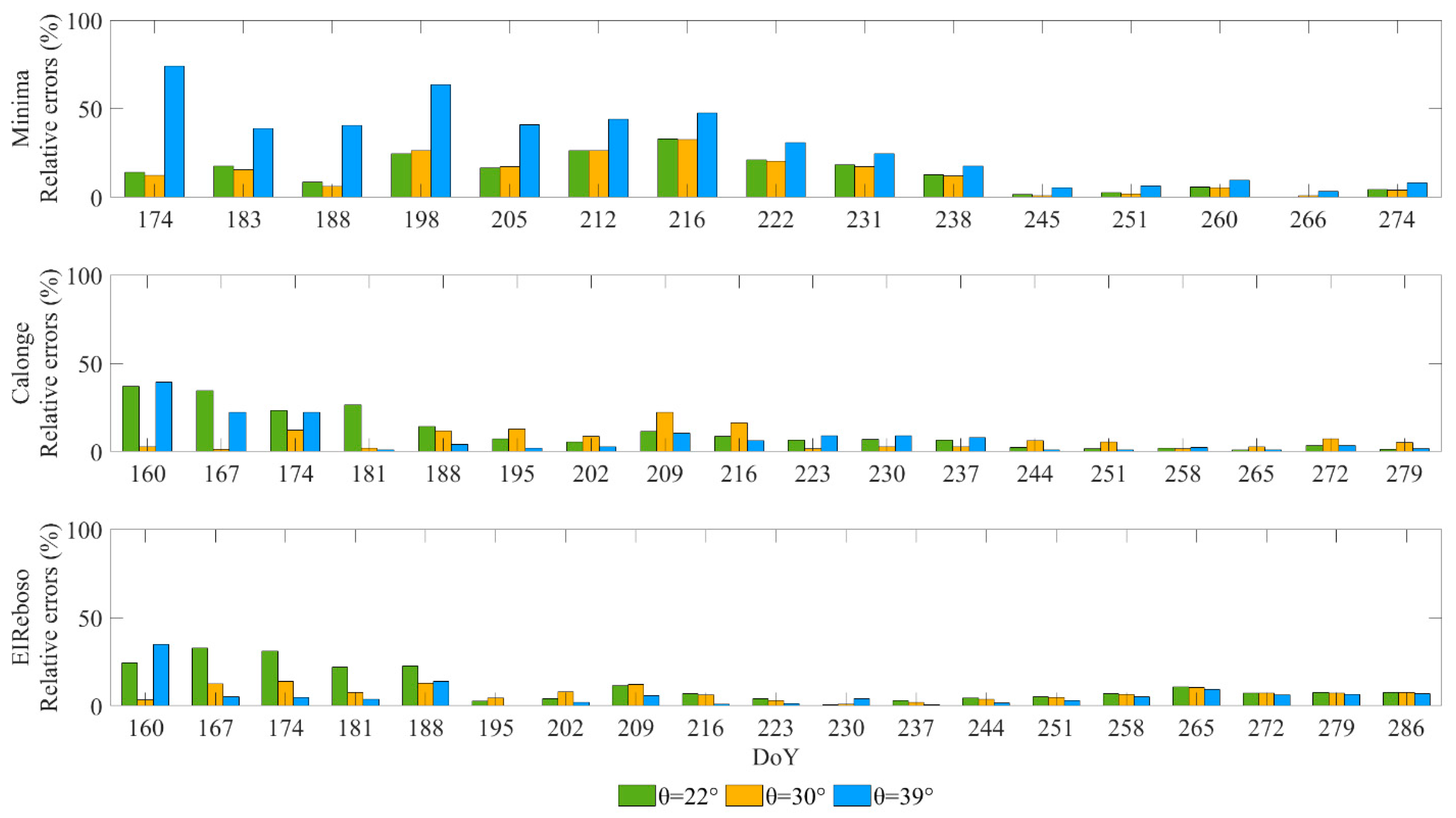
4.2. Effectiveness of the Date Selection Strategy
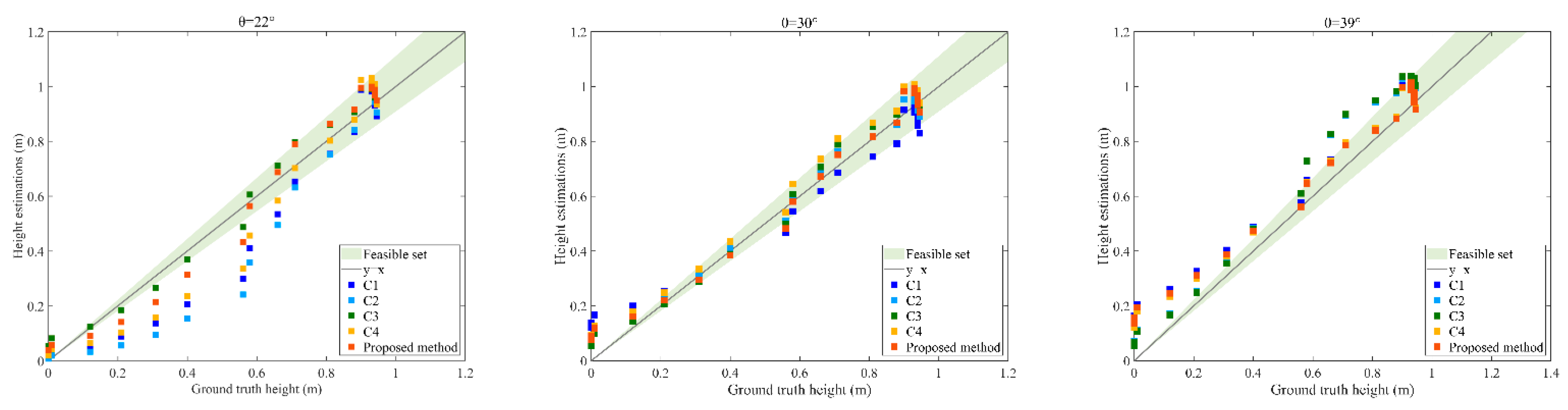
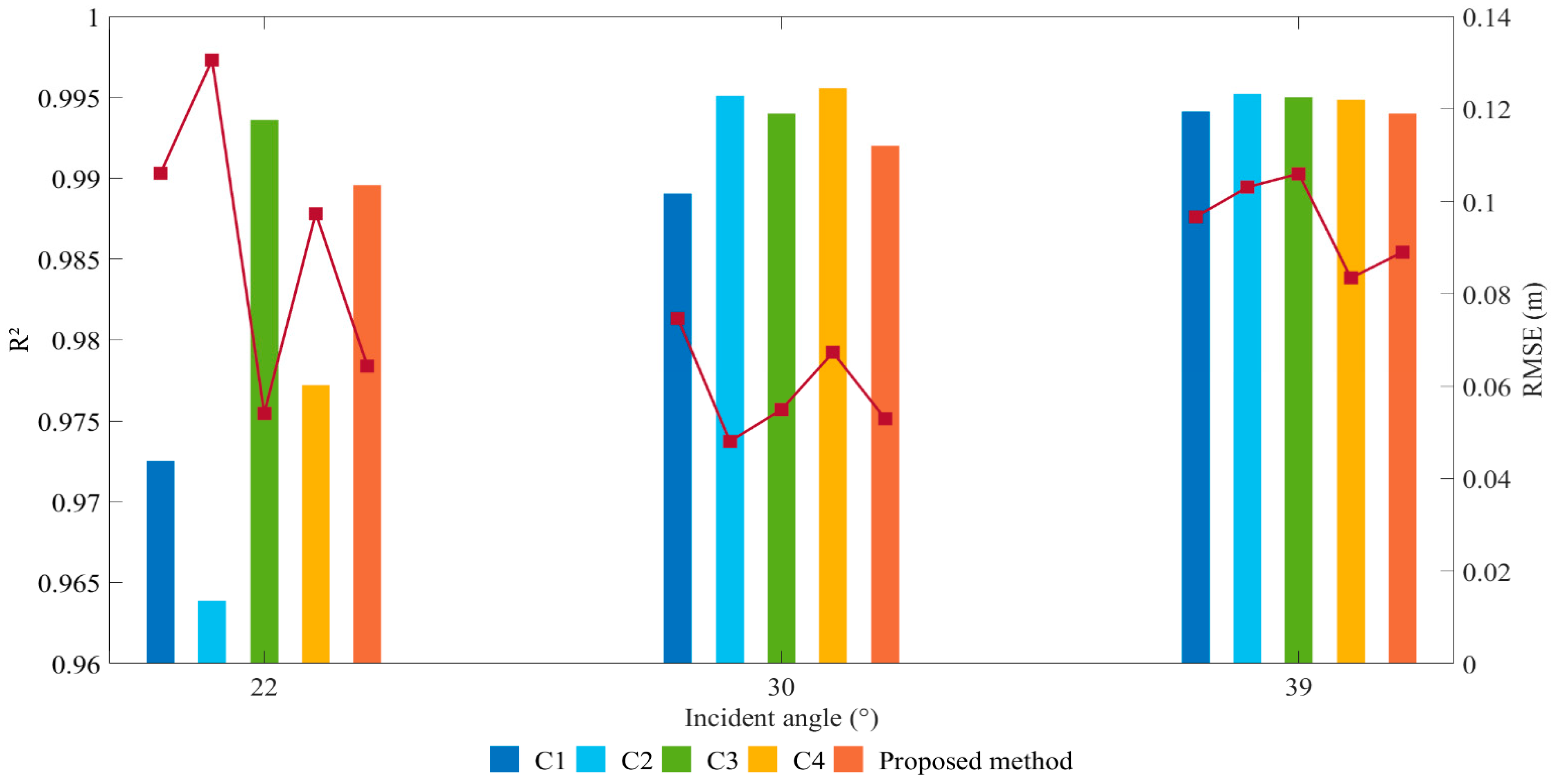
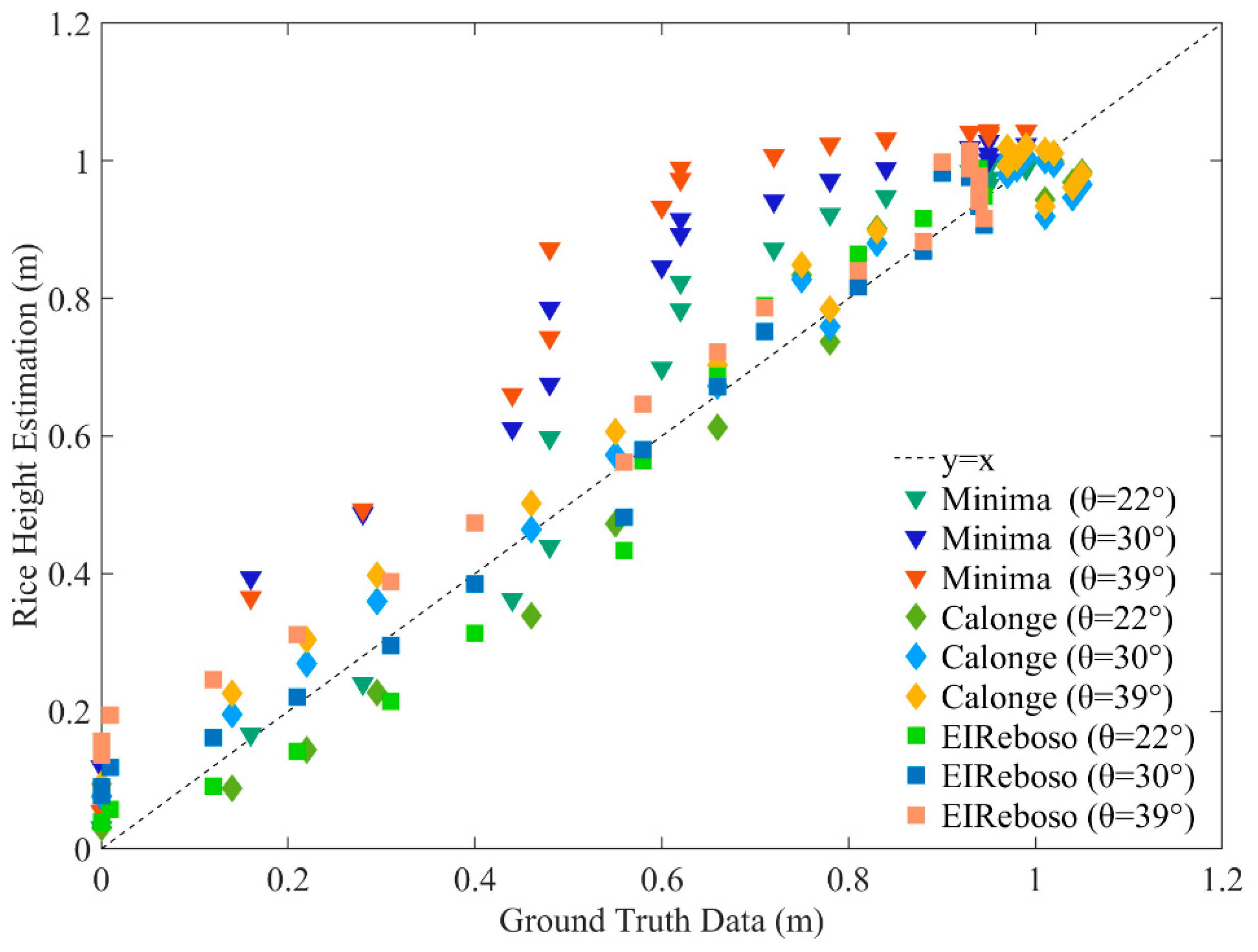
4.3. Inversion Results of Rice Crop Height
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mulla, D.J. Twenty Five Years of Remote Sensing in Precision Agriculture: Key Advances and Remaining Knowledge Gaps. Biosyst. Eng. 2013, 114, 358–371. [Google Scholar] [CrossRef]
- Allies, A.; Roumiguie, A.; Dejoux, J.-F.; Fieuzal, R.; Jacquin, A.; Veloso, A.; Champolivier, L.; Baup, F. Evaluation of Multiorbital SAR and Multisensor Optical Data for Empirical Estimation of Rapeseed Biophysical Parameters. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 7268–7283. [Google Scholar] [CrossRef]
- Garestier, F.; Dubois-Fernandez, P.; Dupuis, X.; Paillou, P.; Hajnsek, I. PolInSAR Analysis of X-Band Data over Vegetated and Urban Areas. IEEE Trans. Geosci. Remote Sens. 2006, 44, 356–364. [Google Scholar] [CrossRef]
- Ballester-Berman, J.D.; Lopez-Sanchez, J.M.; Fortuny-Guasch, J. Retrieval of Biophysical Parameters of Agricultural Crops Using Polarimetric SAR Interferometry. IEEE Trans. Geosci. Remote Sens. 2005, 43, 683–694. [Google Scholar] [CrossRef]
- Treuhaft, R.N.; Cloude, S.R. The Structure of Oriented Vegetation from Polarimetric Interferometry. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2620–2624. [Google Scholar] [CrossRef]
- Lopez-Sanchez, J.M.; Ballester-Berman, J.D.; Marquez-Moreno, Y. Model Limitations and Parameter-Estimation Methods for Agricultural Applications of Polarimetric SAR Interferometry. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3481–3493. [Google Scholar] [CrossRef]
- Ballester-Berman, J.D.; Lopez-Sanchez, J.-M.; Fortuny-Guasch, J. Retrieval of Height and Topography of Corn Fields by Polarimetric SAR Interferometry. In Proceedings of the IGARSS 2004. 2004 IEEE International Geoscience and Remote Sensing Symposium, Anchorage, AK, USA, 20–24 September 2004; IEEE: Piscataway NJ, USA, 2004; Volume 2, pp. 1228–1231. [Google Scholar]
- Hajnsek, I.; Cloude, S.R. Pol-InSAR for Agricultural Vegetation Parameter Estimation. In Proceedings of the IGARSS 2004. 2004 IEEE International Geoscience and Remote Sensing Symposium, Anchorage, AK, USA, 20–24 September 2004; IEEE: Piscataway NJ, USA, 2004; Volume 2, pp. 1224–1227. [Google Scholar]
- Pichierri, M.; Hajnsek, I. Comparing Performances of Crop Height Inversion Schemes From Multifrequency Pol-InSAR Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 1727–1741. [Google Scholar] [CrossRef]
- Lopez-Sanchez, J.M.; Hajnsek, I.; Ballester-Berman, J.D. First Demonstration of Agriculture Height Retrieval with PolInSAR Airborne Data. IEEE Geosci. Remote Sens. Lett. 2012, 9, 242–246. [Google Scholar] [CrossRef]
- Treuhaft, R.N. Vegetation Characteristics and Underlying Topography from Interferometric Radar. Radio Sci. 1996, 31, 1449–1485. [Google Scholar] [CrossRef]
- Maurer, E.; Kahle, R.; Mrowka, F.; Morfill, G.; Zimmermann, S. Operational Aspects of the TanDEM-X Science Phase. In Proceedings of the 14th International Conference on Space Operations, Daejeon, Korea, 16–20 May 2016. [Google Scholar]
- Erten, E.; Rossi, C.; Yuzugullu, O. Polarization Impact in TanDEM-X Data Over Vertical-Oriented Vegetation: The Paddy-Rice Case Study. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1501–1505. [Google Scholar] [CrossRef]
- Sun, Y.Y.; Lee, S.K.; Won, J.S. Rice Paddy Height Estimation from Single-Polarization TanDEM-X Science Phase Data. In Proceedings of the IGARSS 2017–2017 IEEE International Geoscience and Remote Sensing Symposium, Fort Worth, TX, USA, 23–28 July 2017; pp. 930–933. [Google Scholar]
- Lee, S.-K.; Yoon, S.Y.; Won, J.-S. Vegetation Height Estimate in Rice Fields Using Single Polarization TanDEM-X Science Phase Data. Remote Sens. Basel Switz. 2018, 10, 1702. [Google Scholar] [CrossRef]
- Ballester-Berman, J.D.; Lopez-Sanchez, J.M. Coherence Loci for a Homogeneous Volume Over a Double-Bounce Ground Return. IEEE Geosci. Remote Sens. Lett. 2007, 4, 317–321. [Google Scholar] [CrossRef]
- Ballester-Berman, J.D.; Lopez-Sanchez, J.M. Combination of Direct and Double-Bounce Ground Responses in the Homogeneous Oriented Volume Over Ground Model. IEEE Geosci. Remote Sens. Lett. 2011, 8, 54–58. [Google Scholar] [CrossRef]
- Erten, E.; Lopez-Sanchez, J.M.; Yuzugullu, O.; Hajnsek, I. Retrieval of Agricultural Crop Height from Space: A Comparison of SAR Techniques. Remote Sens. Environ. 2016, 187, 130–144. [Google Scholar] [CrossRef]
- Lopez-Sanchez, J.M.; Vicente-Guijalba, F.; Erten, E.; Campos-Taberner, M.; Garcia-Haro, F.J. Retrieval of Vegetation Height in Rice Fields Using Polarimetric SAR Interferometry with TanDEM-X Data. Remote Sens. Environ. 2017, 192, 30–44. [Google Scholar] [CrossRef]
- Romero-Puig, N.; Lopez-Sanchez, J.M.; Ballester-Berman, J.D. Estimation of RVoG Scene Parameters by Means of PolInSAR With TanDEM-X Data: Effect of the Double-Bounce Contribution. IEEE Trans. Geosci. Remote Sens. 2020, 58, 7283–7304. [Google Scholar] [CrossRef]
- Yuzugullu, O.; Erten, E.; Hajnsek, I. Assessment of Paddy Rice Height: Sequential Inversion of Coherent and Incoherent Models. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 3001–3013. [Google Scholar] [CrossRef]
- Romero-Puig, N.; Marino, A.; Lopez-Sanchez, J.M. Application of the Trace Coherence to HH-VV PolInSAR TanDEM-X Data for Vegetation Height Estimation. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–10. [Google Scholar] [CrossRef]
- Cloude, S. Polarisation: Applications in Remote Sensing, 1st ed.; Oxford University Press: New York, NY, USA; New York, NY, USA, 2010; ISBN 978-0-19-956973-1. [Google Scholar]
- Mascolo, L.; Martinez-Marin, T.; Lopez-Sanchez, J.M. Optimal Grid-Based Filtering for Crop Phenology Estimation with Sentinel-1 SAR Data. Remote Sens. Basel Switz. 2021, 13, 4332. [Google Scholar] [CrossRef]
- Xu, S.; Peng, G.; Deng, W.; Li, Z.; University, N.F. Optimal Fitting Study on Applying Genetic Algorithm to Five Theoretical Growth Equations. For. Eng. 2013, 29, 36–39+65. [Google Scholar]
- Rohner, B.; Waldner, P.; Lischke, H.; Ferretti, M.; Thürig, E. Predicting Individual-Tree Growth of Central European Tree Species as a Function of Site, Stand, Management, Nutrient, and Climate Effects. Eur. J. For. Res. 2017, 137, 29–44. [Google Scholar] [CrossRef]
- Tjørve, E.; Tjørve, K.M.C. A Unified Approach to the Richards-Model Family for Use in Growth Analyses: Why We Need Only Two Model Forms. J. Theor. Biol. 2010, 267, 417–425. [Google Scholar] [CrossRef]
- Rizzoli, P.; Dell’Amore, L.; Bueso-Bello, J.-L.; Gollin, N.; Carcereri, D.; Martone, M. On the Derivation of Volume Decorrelation From TanDEM-X Bistatic Coherence. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 3504–3518. [Google Scholar] [CrossRef]
- Marino, A. Trace Coherence: A New Operator for Polarimetric and Interferometric SAR Images. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2326–2339. [Google Scholar] [CrossRef]
- Fu, Y.; Min, H.; Wang, H.; Jiang, G. An Improved NSGA-II to Solve Multi-Objective Optimization Problem. In Proceedings of the 26th Chinese Control and Decision Conference (2014 CCDC), Changsha, China, 31 May–2 June 2014; pp. 1037–1040. [Google Scholar]
- Valcarce-Diñeiro, R.; Lopez-Sanchez, J.M.; Sánchez, N.; Arias-Pérez, B.; Martínez-Fernández, J. Influence of Incidence Angle in the Correlation of C-Band Polarimetric Parameters with Biophysical Variables of Rain-Fed Crops. Can. J. Remote Sens. 2018, 44, 643–659. [Google Scholar] [CrossRef]
- Papathanassiou, K.P.; Cloude, S.R.; Reiber, A.; Boerner, W.M. Multi-Baseline Polarimetric SAR Interferometry for Vegetation Parameters Estimation. In Proceedings of the IEEE International Geoscience & Remote Sensing Symposium, Honolulu, HI, USA, 24–28 July 2000; Volume 6, pp. 2762–2764. [Google Scholar]
- Kugler, F.; Lee, S.-K.; Papathanassiou, K.P. Estimation of Forest Vertical Sructure Parameter by Means of Multi-Baseline Pol-InSAR. In Proceedings of the 2009 IEEE International Geoscience and Remote Sensing Symposium, Cape Town, South Africa, 12–17 July 2009; IEEE: New York, NY, USA; Volume 4, p. IV–721. [Google Scholar]
- Kugler, F.; Lee, S.-K.; Hajnsek, I.; Papathanassiou, K.P. Forest Height Estimation by Means of Pol-InSAR Data Inversion: The Role of the Vertical Wavenumber. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5294–5311. [Google Scholar] [CrossRef]
- Romero-Puig, N. A Review of Crop Height Retrieval Using InSAR Strategies: Techniques and Challenges. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 20. [Google Scholar] [CrossRef]

| Parcel Name | Surface (ha) | Sowing Date | Harvest Date |
|---|---|---|---|
| Minima | 4.32 | 15 May 2015 | 6 October 2015 |
| Calonge | 12.93 | 20 May 2015 | 16 October 2015 |
| ElReboso | 17.25 | 22 May 2015 | 24 October 2015 |
| Incidence Angle | HoA (m) | Date Range | Number of Interferograms |
|---|---|---|---|
| 22° | 2.53 | 15 June 2015–31 August 2015 | 8 |
| 30° | 3.49 | 6 June 2015–2 September 2015 | 7 |
| 39° | 5.81 | 10 June 2015–6 September 2015 | 9 |
| TEST SITE | YEAR | R2 | RMSE (M) |
|---|---|---|---|
| MINIMA | 2016 | 0.984 | 5.52 × 10−3 |
| 2017 | 0.973 | 3.63 × 10−3 | |
| 2018 | 0.969 | 2.21 × 10−3 | |
| 2019 | 0.990 | 3.79 × 10−3 | |
| 2020 | 0.946 | 5.36 × 10−3 | |
| CALONGE | 2016 | 0.984 | 2.81 × 10−3 |
| 2017 | 0.983 | 2.75 × 10−3 | |
| 2018 | 0.989 | 2.89 × 10−3 | |
| 2019 | 0.984 | 1.16 × 10−3 | |
| 2020 | 0.973 | 3.70 × 10−3 | |
| EIREBOSO | 2016 | 0.975 | 2.23 × 10−3 |
| 2017 | 0.906 | 5.85 × 10−3 | |
| 2018 | 0.976 | 6.40 × 10−3 |
| Incidence Angle | Parameter | Test Plot | ||
| Minima | Calonge | EIReboso | ||
| θ = 22° | 0.903 | 0.938 | 0.915 | |
| 0.0617 | 0.0694 | 0.0699 | ||
| 59 | 57 | 61 | ||
| θ = 30° | 1.041 | 1.014 | 0.999 | |
| 0.0535 | 0.0638 | 0.0622 | ||
| 41 | 43 | 47 | ||
| θ = 39° | 1.045 | 1.029 | 1.027 | |
| 0.0726 | 0.0602 | 0.0500 | ||
| 40 | 41 | 42 | ||
| Incidence Angle θ | Precision Index | Test Plot | Total | ||
|---|---|---|---|---|---|
| Minima | Calonge | EIReboso | |||
| 22° | RMSE (m) | 0.101 | 0.061 | 0.064 | 0.075 |
| R2 | 0.970 | 0.989 | 0.990 | 0.980 | |
| 30° | RMSE (m) | 0.197 | 0.054 | 0.053 | 0.114 |
| R2 | 0.959 | 0.992 | 0.992 | 0.960 | |
| 39° | RMSE (m) | 0.244 | 0.065 | 0.089 | 0.145 |
| R2 | 0.926 | 0.992 | 0.994 | 0.949 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, N.; Lopez-Sanchez, J.M.; Fu, H.; Zhu, J.; Han, W.; Xie, Q.; Hu, J.; Xie, Y. Rice Crop Height Inversion from TanDEM-X PolInSAR Data Using the RVoG Model Combined with the Logistic Growth Equation. Remote Sens. 2022, 14, 5109. https://doi.org/10.3390/rs14205109
Li N, Lopez-Sanchez JM, Fu H, Zhu J, Han W, Xie Q, Hu J, Xie Y. Rice Crop Height Inversion from TanDEM-X PolInSAR Data Using the RVoG Model Combined with the Logistic Growth Equation. Remote Sensing. 2022; 14(20):5109. https://doi.org/10.3390/rs14205109
Chicago/Turabian StyleLi, Nan, Juan M. Lopez-Sanchez, Haiqiang Fu, Jianjun Zhu, Wentao Han, Qinghua Xie, Jun Hu, and Yanzhou Xie. 2022. "Rice Crop Height Inversion from TanDEM-X PolInSAR Data Using the RVoG Model Combined with the Logistic Growth Equation" Remote Sensing 14, no. 20: 5109. https://doi.org/10.3390/rs14205109
APA StyleLi, N., Lopez-Sanchez, J. M., Fu, H., Zhu, J., Han, W., Xie, Q., Hu, J., & Xie, Y. (2022). Rice Crop Height Inversion from TanDEM-X PolInSAR Data Using the RVoG Model Combined with the Logistic Growth Equation. Remote Sensing, 14(20), 5109. https://doi.org/10.3390/rs14205109










